Comparison among Voice Activity Detection Methods for Korean

Elderly Voice

JiYeoun Lee

Department of Biomedical Engineering, Jungwon University, Seoul, South Korea

Keywords: Elderly Voice, Auto-correlation Function, Average Magnitude Difference Function, Symmetric Higher

Order Differential Energy Operator, Voice Activity Detection.

Abstract: In the elderly voice, a large amount of noise is generated by physiological changes such as respiration,

vocalization, and resonance according to age. So it provides a cause for performance degradation when

operating a fusion healthcare device such as voice recognition, synthesis, and analysis software with elderly

voice. Therefore, it is necessary to analyze and research the voice of elderly people so that they can operate

various healthcare devices with their voices. This study investigated the voice activity detection algorithm

for the elderly voice using the existing symmetric higher order differential energy function. And it is

confirmed that it has better performance in detection of voice interval in the elderly voice compared with the

autocorrelation function and average magnitude difference function method. The voice activity detection

proposed in this paper can be applied to the voice interface for the elderly, thereby improving the

accessibility of the elderly to the smart device. Furthermore, it is expected that the performance

improvement and development of various fusion wearable devices for the elderly will be possible.

1 INTRODUCTION

It is estimated that the elderly population over 65

years old exceeded 7.2% in 2000 and entered an

aging society. The elderly population in 2018, which

exceeds 10% in 2010, is estimated at over 14%

(Song, 2012).

Despite the aging society, as shown in Table 1,

elderly people currently have poor utilization of

smart devices. So most Korean elderly people rarely

receive the benefits of smart devices including

wearable devices (Kim, 2016).

Table 1: Elderly using smart devices (%).

Age Utilization

Non-

utilization

Total

55- 64 3.9 96.1 100

Over 65

years old

0.7 99.3 100

One of the main reasons for the high entry

barriers to smart devices among the elderly is the

uncomfortable interface. That is, the voice interface

provided by the smart device was developed based

on the average voice of the young person and the

elderly person. Therefore the voice interface does

not work properly with the voice of the elderly (Kim,

2016).

In the old age, the speech speed is slowed down

and the number and length of the silence are

increased because of the vocal cords change due to

the reduced function of the vocal cords, thinning and

keratinized epithelial mucosa of the vocal cords, and

etc (Kim, 2016). Therefore, the elderly voice can be

regarded as one kind of impaired voice distinguished

from normal voice. These changes reduce the

performance of voice-interface-based convergence

devices by causing inaccuracies and noise in speech

(Kahane, 1981) and (Lee, 2011). It is necessary to

improve the algorithm through the construction of

the elderly voice database.

Pitch detection algorithm, which is one of the

methods for voice activity detection (VAD), can be

variously obtained in time domain, frequency

domain, and cepstrum domain (Hong, 2013).

Generally, auto-correlation function (ACF), average

magnitude difference function (AMDF) and zero

crossing rate (ZCR) are used (Iem, 2010). These

algorithms are based on the assumption that speech

is time-invariant. Among the algorithms that reflect

Lee J.

Comparison among Voice Activity Detection Methods for Korean Elderly Voice.

DOI: 10.5220/0006237502310235

In Proceedings of the 10th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2017), pages 231-235

ISBN: 978-989-758-212-7

231

the time-varying characteristics of speech developed

up to now, the symmetric higher order differential

energy function (SHODEO) with a symmetric

structure is known to show superior frequency

estimation performance compared to other methods

(Iem, 2010). It will be used as the basis for

developing fusion software and devices with elderly

voice (Seo, 2015).

2 VOICE ACTIVITY DETECTION

METHODS

2.1 Auto-Correlation Function (ACF)

ACF is an algorithm that extracts the pitch of a

speech signal through a correlation of a specific

signal at one time and at another time, and is defined

as Eq. (1) (Seo, 2015).

ACF





=

x





x(n+m)

N-1

n=0

 (1)

In the Eq. (1), N is a data length, x(n) is a data

value at a specific point n, and x(n + m) is a value

from n to m. For example, when the autocorrelation

function of the speech interval is analyzed for every

256 frames, a waveform with a maximum peak at

256 frames appears, and the point at which this peak

appears is determined as the pitch cycle (Lawfence,

1977).

2.2 Average Magnitude Difference

Function (AMDF)

AMDF is an algorithm that detects the pitch of a

speech signal in the time domain as in the

autocorrelation function, and is defined as follows

(Abdullah-Al-Mamun, 2019) and (Seo, 2006).

 D

AMDF





=

|x





-x(n+m)

N-1

n=0

|  (2)

In Eq. (2), the signal is used as the input signal

of the AMDF as a result of operation between the

original speech signal and a windowing function of

arbitrary length N (Seo, 2006). In case of AMDF,

for example, the minimum peak point of the

waveform within the 256 frame range of the speech

interval is determined as the pitch cycle (Abdullah-

Al-Mamun, 2019) and (Seo, 2006).

2.3 Symmetric Higher Order

Differential Energy Function

(SHODEO)

The instantaneous frequency is defined as the

derivative of the phase of the signal, which is a

function of time (Iem, 2010). In the Eq. (3), The k

differential energy function of the continuous signal

is expressed by the following equation (Iem, 2010).







=x







n+k-2



-x



n-1





n+k-1



(3)

k denotes an arbitrary order, n denotes a sampled

range of the signal, and x(n) denotes a data value

according to the discrete variable n. The higher-

order derivative energy function is expressed by two

mathematical expressions according to arbitrary

order k as follows (Iem, 2010).







= 







+Γ





n-k+2



 k=odd

x n-

+1 k=even

(4)

The instantaneous frequency is calculated by the

above Eq. (4) and (5) (Iem, 2010).

f





2π



k-1



cos

-1



2k-1







2·Ξ







   (5)

k is an arbitrary order, x (n) is a speech data

value at the current time n, 













/2∙















is defined as the ratio of the higher order

differential energy function to the degree k.

3 DATABASE

In this paper, author used the voices of ten men and

women in their seventies who were extracted from

the voice database of the elderly distributed by The

Speech Information Technology & Industry

Promotion Center (SiTEC). As shown in Table 2,

five words and two sentences were used as

experimental data. Five words and two sentences

were spoken once for each sex. That is, 20 sentences

and 20 words were used as experimental data. The

data was also sampled at 16 Hz.

BIOSIGNALS 2017 - 10th International Conference on Bio-inspired Systems and Signal Processing

232

Table 2: Database information.

Male Female

Word

Cheong-wadae

Ccleoango

udukeoni

Bogeolsungeo

Bohumryo

Sentence

Then somebody came forward the

her desk.

Then a stranger approached and

asked.

4 EXPERIMENTAL RESULTS

4.1 VAD Classification using Higher

Order Differential Energy

Figure 1(a) shows voice signal which passed 250Hz

low pass filter (LPF) and (b) shows the values using

SHODEO function. The differential energy function

is characterized by large amplitudes in the speech

region as shown Fig. 1(b). Therefore, the voice

interval is determined by designating an arbitrary

threshold value 800.

The low-pass filter is set to 250 Hz, the

instantaneous frequency to estimate the fundamental

frequency is set to k = 2, and the third-order energy

function obtained from order k = 2 is used as a

function for distinguishing between voiced and

unvoiced sounds. Finally, an instantaneous

frequency value is processed by a moving average

filter with a data length of 200 to calculate the

estimated value of the VAD (Iem, 2011).

Figure 1: (a) Waveform of voice signal (Male) (b)

Waveform of SHODEO function.

The fundamental frequency estimation using the

conventional symmetric differential energy function

uses only the instantaneous frequency determined as

the voiced sound as the input value of the filter.

However, in this paper, author calculates the

sections of VAD by processing all 0s except for the

voiced part to remove the noise section and

including the processed value of the moving average

filter range to 0.

4.2 Comparison among VAD Methods

VAD

Figure 2(a) shows the waveform of the phrase "then

someone came near her desk" when a 72-year-old

male spoke. Fig. 2(b), Fig. 2(c) and Fig. 2(d) show

the results of voice segment detection performance

comparison using the autocorrelation function, the

basic frequency estimation method using the AMDF

and the higher order differential energy function

(SHODEO), respectively. Compared with existing

methods, it can be seen that the voice interval

detection algorithm of Fig. 2(d) detects the voice

interval more accurately and shows excellent

performance in the noise section.

Figure 2: Comparison among VAD methods in sentence (a)

waveform of voice signal (b) ACF (c) AMDF (d)

SHODEO.

Figure 3, 4, 5 and 6 show the results of voice

segment detection in various database using

SHODEO function. Fig. 3(a) and Fig. 4(a) show the

Comparison among Voice Activity Detection Methods for Korean Elderly Voice

233

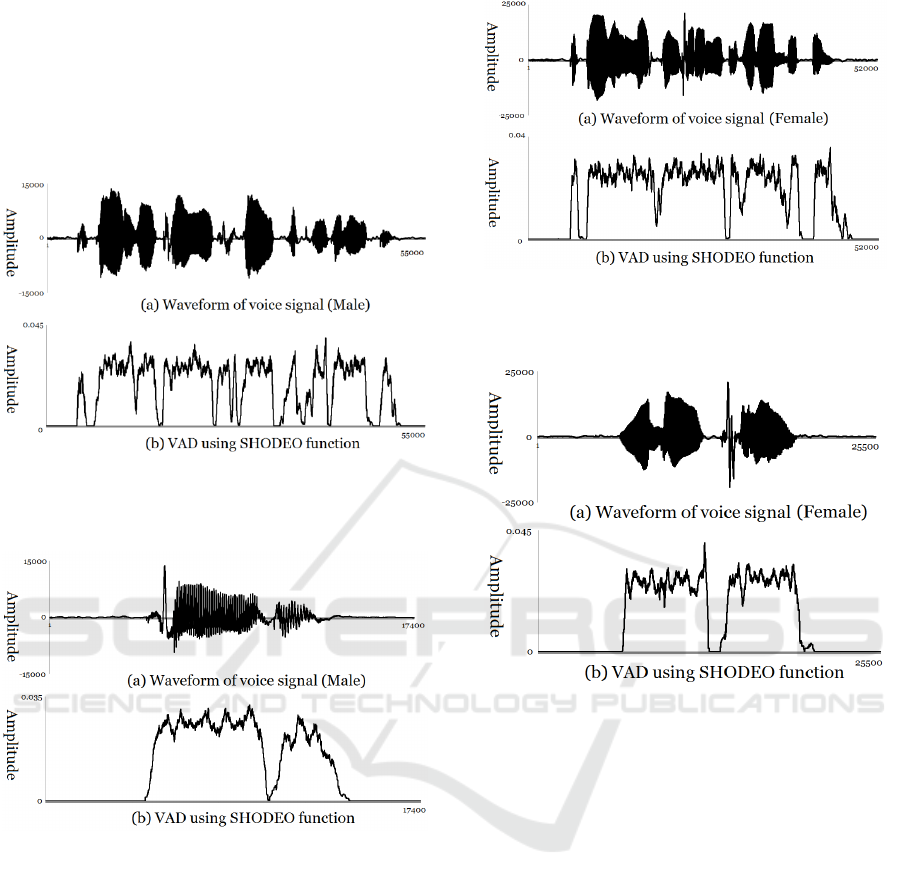
waveform of a sentence in which a 73-year-old male

pronounces "then someone came near her desk" and

“Cheongwadae”. When the speech segment is

detected using the proposed speech segment

detection algorithm, the noise segment is excluded

and only the speech segment is detected as shown in

fig. 3(b) and fig. 4(b).

Figure 3: Comparison among VAD methods in word

(male) (a) waveform of voice signal (b) VAD using

SHODEO function.

Figure 4: Comparison among VAD methods in sentence

(female) (a) voice signal (b) fundamental frequency (c)

VAD using SHODE function.

Fig. 5(a) and Fig. 6(a) show the waveform of a

sentence in which a 70-year-old female pronounces

"Then a stranger approached and asked." and

“Uducceni”. When the speech segment is detected

using the proposed speech segment detection

algorithm, the noise segment is excluded and only

the speech segment is detected as shown in fig. 5(b)

and fig. 6(b).

Figure 5: Comparison among VAD methods in sentence

(female) (a) voice signal (b) fundamental frequency (c)

VAD using SHODEO function.

Figure 6: Comparison among VAD methods in sentence

(female) (a) voice signal (b) fundamental frequency (c)

VAD using SHODEO function.

5 CONCLUSIONS

This study develops a speech segment detection

algorithm for the elderly voice using the existing

symmetric high order differential energy function

(SHODEO) in consideration of noise in the elderly

voice. In addition, it is confirmed that it has better

performance in the elderly voice detection than the

autocorrelation function and AMDF method.

The higher order differential energy function

enables more accurate VAD by eliminating noise

appearing in the elder voice based on the

characteristic that the amplitude difference is

prominent in the voiced and unvoiced interval and

the instantaneous frequency appears irregularly in

the unvoiced interval. It also has an advantage that it

can detect a voice interval by reflecting a time-

varying characteristic of a voice signal and requiring

a small calculation amount. Therefore, it is expected

BIOSIGNALS 2017 - 10th International Conference on Bio-inspired Systems and Signal Processing

234

that the voice segment detection algorithm proposed

in this paper can be applied to the voice interface for

the elderly to improve the accessibility of the elderly

to the smart devices and further develop various

wearable devices for the elderly.

ACKNOWLEDGEMENTS

This research was supported by the Basic Science

Research Program through the National Research

Foundation of Korea (NRF) funded by the Ministry

of Science, ICT & Future Planning (No. 2014-

00540001).

REFERENCES

Abdullah-Al-Mamun, K., 2009. A High Resolution Pitch

Detection Algorithm Based on AMDF and ACF. J. Sci. Res.

1, p. 508-515.

Hong, J., Park S., Jeong, S., Hahn, M., 2013. Robust Feature

Extraction for Voice Activity Detection in Nonstationary

Noisy Environments. Journal of the Korean society of

speech science, 6(1), p. 11-16.

Iem, B., 2010. An Instantaneous frequency estimators based on

the symmetric higher order differential energy operator.

IEICE Trans. Fundamentals, E93-A(1), p. 227-232.

Iem B., 2011. Estimation of Fundamental Frequency Using an

Instantaneous Frequency Based on the Symmetric Higher

Order Differential Energy Operator. The Korean Institute of

Electrical Engineers, 60(2), p. 2374-2379.

Kahane, J. C., 1981. Anatomic and physiologic changes in the

aging peripheral speech mechanism. In D. S. Beasley & G.

A. Davis (Eds.) Aging: Communication processes and

disorders New York: Grune & Stratton, p. 21-45.

Kim, S. and Hong, J., 2016. Application of Safety Analysis and

Management in Software Development Process. Journal of

Convergence Society for SMB, 6(1), p. 7-15.

Lee, S.Y., 2011. The overall speaking rate and articulation rate

of normal elderly people. Graduate program in speech and

language pathology, Master these, Yonsei University.

Lawfence, R. R., 1977. On the Use of Autocorrelation Analysis

for Pitch Detection. IEEE TRANSACTIONS ON

ACOUSTICS, SPEECH, AND SIGNAL PROCESSING,

ASSP-25(1).

Seo., H., 2006. Pitch Period Detection Algorithm Using

Modified AMDF. The Korea Institute of Information and

Communication Engineering, 10(1), p. 23-28.

Song, Y., 2012. Prevalence of Voice Disorders and

Characteristics of Korean Voice Handicap Index in the

Elderly. Journal of the Korean society of speech science,

4(3), p. 151-159.

Seo, I. and Lee, S., 2015. An Efficient Hospital Service Model of

Hierarchical Property information classified Bioinformatics

information of Patient. Journal of Convergence Society for

SMB, 5(4), p. 17-23.

Comparison among Voice Activity Detection Methods for Korean Elderly Voice

235