
A Case Base Approach to Cardiovascular Diseases using Chest X-ray
Image Analysis
Ricardo Faria
1
, Victor Alves
1
, Filipa Ferraz
1
, João Neves
2
, Henrique Vicente
1,3
and José Neves
1*
1
Centro Algoritmi, Universidade do Minho, Braga, Portugal
2
Mediclinic Arabian Ranches, PO Box 282602, Dubai, U.A.E.
3
Departamento de Química, Escola de Ciências e Tecnologia, Universidade de Évora, Évora, Portugal
Key
words: Chest X-ray Images, Knowledge Representation and Reasoning, Mathematical Logic and Logic
Programming, Case-based Reasoning, Similarity Analysis.
Abstract: Cardio Vascular Disease (CVD) also known as heart and circulatory disease comprises all the illnesses of
the heart and the circulatory system, namely coronary heart disease, angina, heart attack, congenital heart
disease or stroke. CVDs are, nowadays, one of the main causes of death. Indeed, this fact reveals the
centrality of prevention and how important is to be aware on these kind of situations. Thus, this work will
focus on the development of a decision support system to help to prevent these events from happening,
centred on a formal framework based on Mathematical Logic and Logic Programming for Knowledge
Representation and Reasoning, complemented with a Case Based Reasoning approach to computing that
caters to the handling of incomplete, unknown or even self-contradictory information or knowledge.
1 INTRODUCTION
Chest X-ray is a painless and non-invasive medical
procedure to get images of different structures inside
the thorax zone, turning easy the access to body
parts like heart, lungs or blood vessels. It stands for
a symptomatic approach to look at different kinds of
illnesses, namely pneumonia, heart failure, lung
cancer, lung tissue scarring or sarcoidosis. In this
study the X-ray images will be used to evaluate
cardiovascular problems, disease that cause 31.5 %
of the overall deaths in the world every year. Indeed,
this work is focused on the development of a hybrid
methodology for problem solving, aiming at the
elaboration of a decision support systems to detect
cardiovascular problems based on parameters
obtained from chest X-ray images, like the Cardiac
Width (Figure 1(a)), the Thoracic Width
(Figure 1(b)) and the Aortic Knuckle Perimeter
(AKP) (Figure 1(c)), according to a historical
dataset, under a Case Based Reasoning (CBR)
approach to problem solving (Aamodt and Plaza,
1994; Richter and Weber, 2013). Undeniably, CBR
provides the ability of solving new problems by
reusing knowledge acquired from past experiences
(Aamodt and Plaza, 1994), i.e., CBR is used
especially when similar cases have similar terms and
solutions, even when they have different
backgrounds (Richter and Weber, 2013). Its use may
be found in many different arenas, like in Online
Dispute Resolution (Carneiro et al. 2013) or
Medicine (Begum et al. 2011; Blanco et al. 2013),
just to name a few.
This article is subdivided into five sections. In
the former one a brief introduction to the problem is
made. Then a mathematical logic approach to
Knowledge Representation and Reasoning and a
CBR view to computing are introduced. In the third
and fourth sections a case study is set. Finally, in the
last section the most relevant attainments are
described and possible directions for future work are
outlined.
2 BACKGROUND
2.1 Knowledge Representation and
Reasoning
Many approaches to Knowledge Representation and
Reasoning have been proposed using the Logic
266
Faria R., Alves V., Ferraz F., Neves J., Vicente H. and Neves J.
A Case Base Approach to Cardiovascular Diseases using Chest X-ray Image Analysis.
DOI: 10.5220/0006237702660274
In Proceedings of the 9th International Conference on Agents and Artificial Intelligence (ICAART 2017), pages 266-274
ISBN: 978-989-758-220-2
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Programming (LP) epitome from Mathematical
Logic, namely in the area of Model Theory (Kakas.
et al. 1998; Pereira and Anh, 2009) and Proof
Theory (Neves, 1984; Neves et al. 2007). In the
present work the Proof Theoretical approach in
terms of an extension to the LP language is
followed. An Extended Logic Program, or Logic
Program, for short, is a finite set of clauses, given in
the form:
{
← ,
←
,⋯,
,
,⋯,
?
,⋯,
,
,⋯,
(
, 0
)
…
(
0
)
,
}
∷
where the first clause stand for predicate’s closure,
“,” denotes logical and, while “?” is a domain atom
denoting falsity. The “p
i
, q
j
, and p” are classical
ground literals, i.e., either positive atoms or atoms
preceded by the classical negation sign “
¬
” (Neves,
1984. Indeed, “
¬
” stands for a strong declaration
that speaks for itself, and not denotes negation-by-
failure, or in other words, a flop in proving a given
statement, once it was not declared explicitly. Every
program is also associated with a set of abducibles
(Kakas. et al. 1998; Pereira and Anh, 2009), given
here in the form of exceptions to the extensions of
the predicates that make the overall program, i.e.,
clauses of the form:
…
(
0
)
,
that stands for data, information or knowledge that
cannot be ruled out. On the other hand, clauses of
the type:
?
,⋯,
,
,⋯,
(
, 0
)
also named invariants or restrictions, allow one to
set the context under which the universe of discourse
has to be understood. The term scoring
value
stands for
the relative weight of the extension of a specific
predicate with respect to the extensions of the peers
ones that make the inclusive or global program.
Aiming to set one’s approach to Knowledge
Representation and Reasoning, two metrics were set,
namely the Quality-of-Information (QoI) and the
Degree-of-Confidence (DoC). The QoI of a logic
program should be understood as a mathematical
function that will return a truth-value ranging
between 0 and 1, once it is fed with the extension of
a given predicate, i.e., QoI
i
= 1 when the information
is known (positive) or false (negative) and QoI
i
= 0 if
the information is unknown. For situations where the
extensions of the predicates that make the program
also include abducible sets, its terms (or clauses)
present a QoI
i
ϵ ]0, 1[ (Fernandes et al. 2016).
Figure 1: The Chest X-ray`s parameters that were taken
into account in this study, i.e., Cardiac Width (a),
Thoracic Width (b), and Aortic Knuckle Perimeter (c).
A Case Base Approach to Cardiovascular Diseases using Chest X-ray Image Analysis
267

The DoCs, in turn, stand for one’s confidence
that the argument values or attributes of the terms
that make the extension of a given predicate, having
into consideration their domains, are in a given
interval (Neves et al. 2015). The DoC is figured out
using =
√
1−∆
, where ∆ stands for the
argument interval length, which was set to the
interval [0, 1], since the ranges of attributes values
for a given predicate and respective domains were
normalized, in terms of the expression ( −
)/(
−
), where the Y
s
stand for
themselves.
Thus, the universe of discourse is engendered
according to the information presented in the
extensions of such predicates, according to
productions of the type:
−
−
,
,
,⋯
⋯,
,
,
∷
∷
where
⋃
, m and l stand, respectively, for set union,
the cardinality of the extension of predicate
i
and the
number of attributes of each clause (Neves et al.
2015). On the other hand, either the subscripts of the
QoI
s
and the DoC
s
, or those of the pairs (A
s
, B
s
), i.e.,
x
1
, …, x
l
, stand for the attributes’ clauses values
ranges.
2.2 Case based Computing
The CBR approach to computing stands for an act of
finding and justifying a solution to a given problem
based on the consideration of the solutions of similar
past ones, either using old solutions, or by
reprocessing and generating new data or knowledge
from the old ones (Aamodt and Plaza, 1994; Richter
and Weber, 2013). In CBR the cases are stored in a
Cases repository, and those cases that are similar (or
close) to a new one are used in the problem solving
process.
The typical CBR cycle presents the mechanism
that should be followed to have a consistent model.
The first stage entails an initial description and a
reprocessing of the problem’s data or knowledge.
The new case is defined and it is used to retrieve one
or more cases from the repository, i.e., at this point
it is imperative to identify the characteristics of the
new case and retrieve cases with a higher degree of
similarity to it. Thereafter, a solution to the problem
emerges, on the Reuse phase, based on the blend of
the new case with the retrieved ones. The suggested
solution is reused (i.e., adapted to the new case), and
a solution is provided (Aamodt and Plaza, 1994;
Richter and Weber, 2013). However, when adapting
the solution it is crucial to have feedback from the
user, since automatic adaptation in existing systems
is almost impossible. This is the Revise stage, in
which the suggested solution is tested by the user,
allowing for its correction, adaptation and/or
modification, originating the test repaired case`s
phase that sets the solution to the new problem.
Thus, one is faced with an iterative process since the
solution must be tested and adapted, while the result
of considering that solution is inconclusive. During
the Retain (or Learning) stage the case is learned
and the repository is updated, by inserting the new
case (Aamodt and Plaza, 1994; Richter and Weber,
2013).
On the other hand, and despite promising results,
the current CBR systems are neither complete nor
adaptable for all domains. In some cases, the user
cannot choose the similarity(ies) method(s) used in
the retrieval phase and is required to follow the
system defined one(s), even if they do not meet their
needs. Moreover, in real problems, the access to all
necessary information is not always possible, since
existent CBR systems have limitations related to the
capability of dealing, explicitly, with unknown,
incomplete, and even self-contradictory information.
To make a change, a different CBR cycle was
induced (Figure 2). It takes into consideration the
case’s QoI and DoC metrics. It also contemplates a
cases optimization process present in the Case-base,
whenever they do not comply with the terms under
which a given problem as to be addressed (e.g., the
expected DoC on a prediction was not attained). In
this process may be used Artificial Neural Networks
(Haykin, 2009; Vicente et al. 2012), Particle Swarm
Optimization (Mendes et al. 2003) or Genetic
Algorithms
(Neves et al. 2007), just to name a few.
Indeed, the optimization process generates a set of
new cases which must be in conformity with the
invariant:
,
≠∅
(1)
that states that the intersection of the attribute’s
values ranges for the cases’ set that make the Case-
base or their optimized counterparts (B
i
) (being n its
cardinality), and the ones that were object of a
process of optimization (E
i
), cannot be empty.
ICAART 2017 - 9th International Conference on Agents and Artificial Intelligence
268
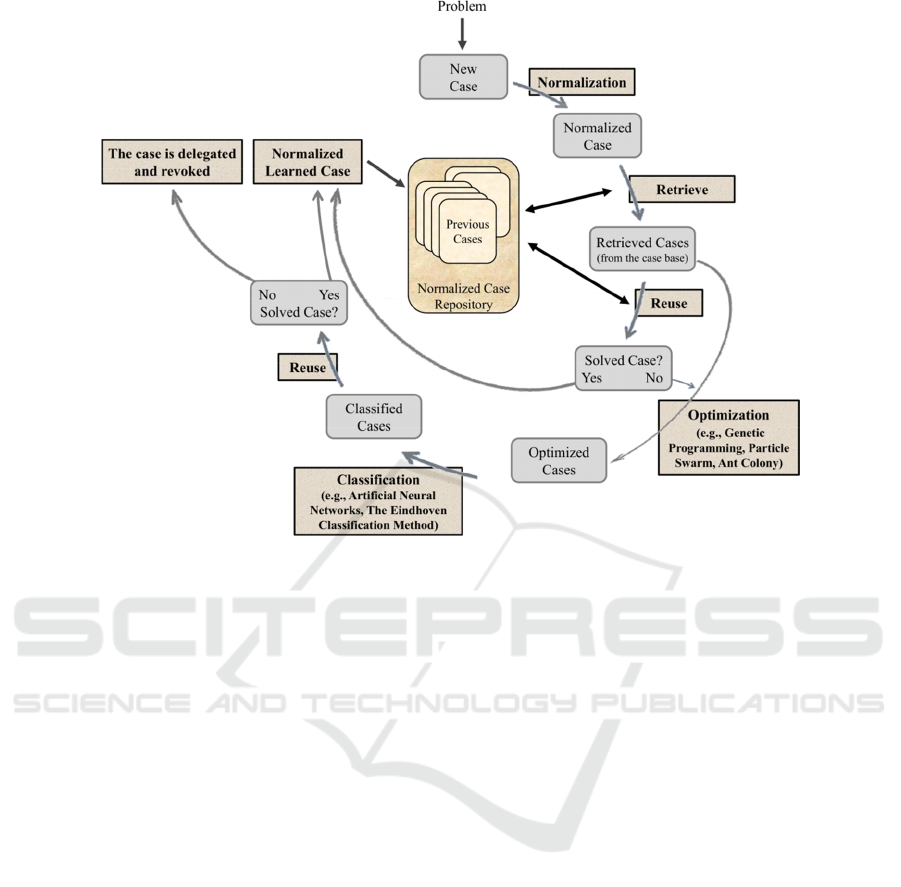
Figure 2: The extended view of the CBR cycle.
3 METHODS
Aiming to develop a predictive model to estimate
the risk of cardiovascular diseases, a database was
set, built on 388 health records of patients from a
major health care institution in the North of
Portugal.
The patients included in this study aged between
19 to 93 years old, with an average of 49±12 years
old. The gender distribution was 43.8% and 56.2%
for male and female, respectively.
After having collected the data it is possible to
build up a knowledge database given in terms of the
extensions of the relations or predicates depicted in
Figure 3, which stand for a situation where one has
to manage information aiming to access the
cardiovascular disease predisposing. The tables
include features obtained by both objective and
subjective methods. The physicians may populate
some issues and others may be perceived by
additional tests. The software imageJ (Rasband,
2016) was used to extract the necessary features
from X-ray images (Figure 1). Under this scenario
some incomplete and/or default data is also present.
For instance, the Triglycerides in case 2 are
unknown (depicted by the symbol
⊥
), while the Risk
Factors range in the interval [1, 2]. The values
presented in the Risk Factors column of
Cardiovascular Diseases Predisposing table is the
sum of the correspondent table values, ranging
between 0 and 4. The CTR column is the Cardiac
Thoracic Ratio computed using cardiac and thoracic
width. The Descriptions column stands for free text
fields that allow for the registration of relevant
patient features.
Applying the algorithm presented in Neves et al.
(2015) to the fields that make the knowledge base
for Cardiovascular Diseases Predisposing
(Figure 3), excluding at this stage of such a process
the Description one, and looking to the DoCs’
values, it is possible to set the arguments of the
predicate cardiovascular diseases predisposing
(cdp) referred to below, whose extension denote the
objective function with respect to the problem under
analyze:
:
,
,
,
,
,
,
,
→ 0, 1
where 0 (zero) and 1 (one) denote, respectively, the
truth values false and true.
A Case Base Approach to Cardiovascular Diseases using Chest X-ray Image Analysis
269

Figure 3: A fragment of the knowledge base for cardiovascular diseases predisposing assessment.
The application of the algorithm presented in
Neves et al. (2015) comprises several phases. In the
former one the clauses or terms that make extension
of the predicate under study are established. In the
next stage the boundaries of the attributes intervals
are set in the interval [0, 1] according to a
normalization process in terms of the expression
( −
)/(
−
), where the Y
s
stand for
themselves. Finally, the DoC is evaluated as
described in section 2.1. Exemplifying the
application of the algorithm referred to above, to a
term (patient) that presents the feature vector
Age = 64, SBP =
⊥
, Chol
LDL
= 128, Chol
HDL
= 47,
Trigly = 203, CTR = 0.45, AKP = 124, RF = [1, 2],
one may have:
%The predicate’s extension that sets the Univers
e
-
o
f
-
Discourse for the term under observation i
s
fixed
%
{
,
,
,
(
,
)(
,
)
, ⋯ ,
(
,
)(
,
)
←
,
,
,
(
,
)(
,
)
, ⋯ ,
(
,
)(
,
)
(
64,64
)
1
[, ]
,
[, ]
,70, 2001
[, ]
,
[, ]
, ⋯ ,
1, 21
[, ]
,
[, ]
∷1∷
[
19,93
]
[
70,200
]
⋯
[
0,4
]
`
}
∷1
ICAART 2017 - 9th International Conference on Agents and Artificial Intelligence
270

%The attribute’s boundaries are set to the interval [0, 1], according to a normalization process tha
t
uses the expression
( −
)/(
−
)
%
{
,
,
,
(
,
)(
,
)
, ⋯ ,
(
,
)(
,
)
←
,
,
,
(
,
)(
,
)
, ⋯ ,
(
,
)(
,
)
(
0.61,0.61
)
1
[., .]
,
[., .]
,0, 11
[, ]
,
[, ]
, ⋯ ,
0.25, 0.51
[., .]
,
[., .]
∷1∷
[
0,1
]
0, 1 ⋯ 0, 1
`
}
∷1
%The DoC’s values are evaluated
%
{
,
,
,
(
,
)(
,
)
, ⋯ ,
(
,
)(
,
)
←
,
,
,
(
,
)(
,
)
, ⋯ ,
(
,
)(
,
)
(
0.61,0.61
)
1, 1, 0, 11, 0, ⋯ ,0.25, 0.51, 0.97
`
∷1∷0.87
[
0,1
]
0, 1 ⋯ 0, 1
`
}
∷1
En
d
4 A CASE BASED REASONING
APPROACH TO COMPUTING
The framework presented previously shows how the
information comes together and how it is processed.
In this section, a soft computing approach was set to
model the universe of discourse, where the
computational part is based on a CBR approach to
computing. Contrasting with other problem solving
strategies (e.g., those that use Decision Trees or
Artificial Neural Networks), relatively little work is
done offline. Undeniably, in almost all the situations
the work is performed at query time. The main
difference between this approach and the typical
CBR one relies on the fact that not only all the cases
have their arguments set in the interval [0, 1], a
situation that is complemented with the prospect of
handling incomplete, unknown, or even self-
contradictory data, information or knowledge. Thus,
the classic CBR cycle was changed (Figure 2), being
the Case-base given in terms of the pattern:
=
,
,
(2)
A Case Base Approach to Cardiovascular Diseases using Chest X-ray Image Analysis
271

where the Description
data
field will not be object of
attention in this study.
Undeniably, when confronted with a new case,
the system is able to retrieve all cases that meet such
a case structure and optimize such a population,
having in consideration that the cases retrieved from
the Case-base must satisfy the invariant present in
equation (1), in order to ensure that the intersection
of the attributes range in the cases that make the
Case-base repository or their optimized
counterparts, and the equals in the new case cannot
be empty. Having this in mind, the algorithm given
in Neves et al. (2015) is applied to the new case that
presents the feature vector Age = 57, SBP = 118,
Chol
LDL
=
⊥
, Chol
HDL
=
⊥
, Trigly =
⊥
, CTR = 0.43,
AKP = 127, RF = [1, 3], with the outcome:
0.51, 0.511, 1,⋯,
0.25, 0.751, 0.87 ∷ 1 ∷ 0.61
Now, the new case may be portrayed on the
Cartesian plane in terms of its QoI and DoC, and by
using clustering methods (Neves et al. 2016) it is
feasible to identify the cluster(s) that intermingle
with the new one (epitomized as a square in
Figure 4). The new case is compared with every
retrieved case from the clusters using a similarity
function sim, given in terms of the average of the
modulus of the arithmetic difference between the
arguments of each case of the selected cluster and
those of the new case. Thus, one may have:
0.57, 0.571, 1,⋯,
0.5, 0.51, 1 ∷ 1 ∷ 0.73
0.49, 0.491, 1,⋯,
0.25, 0.51, 0.97 ∷ 1 ∷ 0.62
⋮
0.55, 0.551, 1,⋯,
0.75, 0.751, 1 ∷ 1 ∷ 0.88
Assuming that every attribute has equal weight,
for the sake of presentation, the di(similarity), in
terms of DoC, between
and the
, may be computed as follows:
→
=
‖
1−1
‖
⋯
‖
0.87 − 1
‖
8
= 0.16
(3)
Figure 4: A case’s set divided into clusters.
Therefore, the sim(ilarity), i.e.,
→
is
set as 1 – 0.16 = 0.84. Regarding QoI the procedure
is similar, returning
→
=1. Thus, one
may have:
→
,
= 1 0.84 = 0.84
(4)
These procedures should be applied to the
remaining cases of the retrieved clusters in order to
obtain the most similar ones, which may stand for
the possible solutions to the problem. This approach
allows users to define the most appropriate similarity
threshold to address the problem (i.e., it gives the
user the possibility to narrow the number of selected
cases with the increase of the similarity threshold).
The proposed model was tested on a real data set
with 388 examples. Thus, the dataset was divided in
exclusive subsets through a ten-folds cross
validation (Haykin, 2009). In the implementation of
the respective dividing procedures, ten executions
were performed for each one of them. Table 1
presents the coincidence matrix of the CBR model,
where the values presented denote the average of 25
(twenty five) experiments. A perusal to Table 1
shows that the model accuracy was 91.8% (i.e., 356
instances correctly classified in 388). Thus, the
predictions made by the CBR model are satisfactory,
attaining accuracies higher than 90%. The sensitivity
and specificity of the model were 92.8% and 90.5%,
while Positive and Negative Predictive Values were
91.9% and 91.5%, respectively. The ROC curve is
shown in Figure 5. The area under ROC curve (0.92)
denotes that the model exhibits a good performance
in the assessment of cardiovascular diseases
predisposing.
ICAART 2017 - 9th International Conference on Agents and Artificial Intelligence
272

Figure 5: The ROC curve regarding the proposed model.
Table 1: The coincidence matrix for the CBR model.
Target
Predictive
True (1) False (0)
True (1) 194 15
False (0) 17 162
5 CONCLUSIONS
This work presents a Logic Programming based
Decision Support System to estimate the
cardiovascular diseases predisposing, i.e., it is
centred on a formal framework based on LP for
Knowledge Representation and Reasoning,
complemented with a CBR approach to computing
that caters for the handling of incomplete, unknown,
or even self-contradictory information. The
proposed model is able to provide adequate
responses, once the overall accuracy is higher than
90%. The computational framework presented above
uses powerful knowledge representation and
reasoning methods to set the structure of the
information and the associate inference mechanisms.
Indeed, it has also the potential to be disseminated
across other prospective areas, therefore validating
an universal attitude. Additionally, it gives the user
the possibility to narrow the search space for similar
cases at runtime by choosing the most appropriate
strategy to address the problem.
ACKNOWLEDGEMENTS
This work has been supported by COMPETE: POCI-
01-0145-FEDER-007043 and FCT – Fundação para
a Ciência e Tecnologia within the Project Scope:
UID/CEC/00319/2013.
REFERENCES
Aamodt, A., Plaza, E., 1994. Case-Based Reasoning:
Foundational Issues, Methodological Variations, and
System Approaches. AI Communications, 7: 39-59.
Begum, S., Ahmed, M.U., Funk, P., Xiong, N., Folke, M.,
2011. Case-based reasoning systems in the health
sciences: a survey of recent trends and developments.
IEEE Transactions on Systems, Man, and Cybernetics,
Part C (Applications and Reviews), 41: 421-434.
Blanco, X., Rodríguez, S., Corchado, J.M., Zato, C., 2013.
Case-based reasoning applied to medical diagnosis and
treatment. In Distributed Computing and Artificial
Intelligence – Advances in Intelligent Systems and
Computing, Volume 217, 137-146.
Carneiro, D., Novais, P., Andrade, F., Zeleznikow, J.,
Neves, J., 2013. Using Case-Based Reasoning and
Principled Negotiation to provide decision support for
dispute resolution. Knowledge and Information
Systems, 36: 789-826.
Fernandes, A., Vicente, H., Figueiredo, M., Neves, M.,
Neves, J., 2016. An Adaptive and Evolutionary Model
to assess the Organizational Efficiency in Training
Corporations. In Future Data and Security
Engineering – Lecture Notes on Computer Science,
Volume 10018, 415–428.
Fernandes, F., Vicente, H., Abelha, A., Machado, J.,
Novais, P., Neves J., 2015. Artificial Neural Networks
in Diabetes Control. In Proceedings of the 2015
Science and Information Conference – SAI 2015, 362-
370.
Figueiredo, M., Esteves, L., Neves, J., Vicente, H., 2016.
A data mining approach to study the impact of the
methodology followed in chemistry lab classes on the
weight attributed by the students to the lab work on
learning and motivation. Chemistry Education
Research and Practice, 17: 156-171.
Haykin, S., 2009. Neural Networks and Learning Machines,
Pearson Education, New Jersey.
Kakas A., Kowalski R., Toni F., 1998. The role of
abduction in logic programming. In Handbook of
Logic in Artificial Intelligence and Logic
Programming, Volume 5, 235-324.
Mendes, R., Kennedy, J., Neves J., 2003. Watch thy
neighbor or how the swarm can learn from its
environment. In Proceedings of the 2003 IEEE Swarm
Intelligence Symposium – SIS’03, 88-94.
Neves J., 1984. A logic interpreter to handle time and
negation in logic data bases. In Proceedings of the
1984 annual conference of the ACM on the fifth
generation challenge, 50-54.
Neves J., Machado J., Analide C., Abelha A., Brito L.,
2007. The halt condition in genetic programming. In
Progress in Artificial Intelligence – Lecture Notes in
Computer Science, Volume 4874, 160-169.
A Case Base Approach to Cardiovascular Diseases using Chest X-ray Image Analysis
273

Pereira L., Anh H., 2009. Evolution prospection. In New
Advances in Intelligent Decision Technologies – Results
of the First KES International Symposium IDT, 51-64.
Rasband, W.S., 2016. ImageJ. U.S. National Institutes of
Health, Bethesda, Maryland, http://imagej.nih.gov/ij/.
Accessed 25 September 2016.
Richter, M., Weber, R., 2013. Case-Based Reasoning: A
Textbook, Springer, Berlin.
Vicente, H., Couto, C., Machado, J., Abelha, A., Neves, J.,
2012. Prediction of Water Quality Parameters in a
Reservoir using Artificial Neural Networks.
International Journal of Design & Nature and
Ecodynamics, 7: 310-319.
ICAART 2017 - 9th International Conference on Agents and Artificial Intelligence
274
