
Modulation of Impedance and Muscle Activation of the
Upper Limb Joints while Simultaneously Controlling
Manual-grasping and Walking
Joseph Mizrahi
1
, Navit Roth
1
and Rahamim Seliktar
2
1
Department of Biomedical Engineering, Technion, Israel Institute of Technology, Haifa, Israel
2
School of Biomedical Engineering, Science and Health Systems, Drexel University, Philadelphia, PA, U.S.A.
Keywords: Mechanical Impedance, Muscle Activation, Motor Control, Manual-grasping, Balanced Walking,
End-effector, Joint Constraints.
Abstract: The design of spring-based artificial and robotic arm joints presents a challenge in problems of transportation
of manually-held objects during walking. For maintaining stability of these objects, stiffness and damping of
the arm joints have to be adjusted by continuously tuning muscle activation. This necessitates knowledge
about the mechanisms by which stiffness and damping (mechanical impedance) are being modulated in
walking movement. The paradigm employed in this study consisted of modeling the impedance adjustments
from input data obtained in simultaneously controlled grasping and walking experiments. While walking on
a treadmill, tested subjects held a cup filled with liquid and were asked to aim at minimizing liquid spillage.
Monitoring liquid spillage served to quantify stability of the hand as the end-effector of the upper limb.
Kinematic data were obtained for the shoulder, elbow and wrist joints. Accelerometer data were obtained for
the wrist and for the knee. Electro-myography (EMG) data were collected for the wrist flexor and extensor
muscles. Based on the measured data, regressive functions were used to express stiffness and damping as a
function of angle and angular velocity. The joints of the upper limb were thereafter successively constrained
to study the effect of joint immobilization on joint impedance and muscle activation. The obtained results
indicate the nonlinearity of the joint impedances as required in tasks of manual grasping of objects during
locomotion, with and without joint constraints.
1 INTRODUCTION
Walking while grasping a cup filled with liquid (e.g.
tea, water) is a common daily activity necessitating
coordination of locomotion and prehension. Clearly,
the aim in this task is to navigate the moving hand in
space, so as to avoid or minimize spillage or dripping
of liquid from the cup. Following unintended
perturbations, it would also be desirable that the
grasping hand regains its stability through motion of
the joints of the upper limb. Thus, an interesting
question is how our body controls these joint
movements in order to perform the task in question.
Studying this question would provide an insight
into the mechanisms, by which the stiffness and
damping are adjusted to accommodate changes taking
place during manual transport of objects while
walking, if stability of the held object is to be
maintained.
Mechanically, the upper limb can be represented
by three major segments including the arm, forearm
and hand, connected through the shoulder, elbow and
wrist joints. Through the motion of its joints, the
upper limb provides the output to the terminal
segment or end-effector: the self-navigating free hand
grasping the cup of liquid being subjected to an
oscillatory-like motion.
The complex relationship between torque, angular
position and angular velocity, termed mechanical
impedance, defines the stiffness and damping
characteristics of the joint. Controlling the
mechanical impedance of the upper limb joints is an
important feature of the neuromuscular system
enabling to stabilize hand-held objects in space, or to
minimize the effect of externally applied forces
(Stroeve, 1999).
Past studies on the combined control of the
locomotor and prehensile systems have suggested
that locomotion and reaching are closely connected
motor activities (Georgopoulos and Grillner, 1989).
More recently, mechanical aspects of the interaction
between grasping and walking were reported (Roth et
194
Mizrahi J., Roth N. and Seliktar R.
Modulation of Impedance and Muscle Activation of the Upper Limb Joints while Simultaneously Controlling Manual-grasping and Walking.
DOI: 10.5220/0006239101940199
In Proceedings of the 10th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2017), pages 194-199
ISBN: 978-989-758-216-5
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

al, 2011). Muscle activity was not included in this
latter study.
The present study deals with the analysis of
motion of the hand grasping a cup filled with liquid
while walking. In order to explore the relative role of
each of the joint to the mechanical impedances,
different joint disabilities were simulated by the
successive immobilization of each of the shoulder,
elbow and wrist joints. Activation of the major
muscle groups of the elbow joint was also studied by
monitoring their EMG signals. Since impedance-
based control strategies require information on the
continuous nonlinear behavior of the joints, the
results of the present research should have
implications on the design of spring based artificial
and robotic arms.
2 METHODS
Subjects (n=4), aged 28-57 (average 35.5, SD 14.3)
provided informed consent to participate in the study
according to the University’s ethical committee’s
guidelines. The subjects walked on a treadmill
(Woodway PPS55-Med) at a constant speed of 1.25
m/s while holding in their right hand a cup filled with
liquid and fixing their look at a mark positioned in
front of them at eye level. While walking, the subjects
were instructed to maintain the liquid surface as level
as possible, to minimize "liquid spillage" from the
cup.
The walking tests, each of duration of 30 seconds,
were performed in the following testing conditions:
unrestricted joints of the upper limbs, followed by the
successive restriction of each of the right wrist, elbow
and shoulder joints. Joint restrictions were applied in
order to immobilize each joint (wrist 180 degrees,
elbow 90 degrees and shoulder 0 degrees). The
restrictions were accomplished by means of
constraining braces or straps. The tests were repeated
five times at each condition with a resting period of 2
min between the tests.
3 INSTRUMENTATION
3.1 Apparatus for Liquid Spillage
Quantitation
To observe the target of minimum liquid spillage, an
instrumented cup was designed to monitor liquid
level within the cup as follows, to simulate “liquid
spillage”. A plastic cup was wired at its inner surface
with circular conductive stripes, parallel to each other
and to the bottom of the cup, to indicate different
levels for the liquid. A signal was generated when the
liquid (salted water) level raised as a result of the
subject's motion and made contact with any of the
circular stripes to short a circuit.
3.2 Kinematics
Since the joint angles served as inputs for the model,
goniometers (Biometrics Ltd, Gwent, UK) were used
for two-dimensional measurements of elbow and
wrist angles. For kinematic measurements in the
sagittal plane video data were collected by two-
reflective markers located at the upper arm, near the
shoulder and elbow joints, as shown in Fig. 1.
Figure 1: Positioning of sensors (blue=positioning marker,
purple=goniometer, light green=EMG, yellow=accelero-
meter; the cup is shown in green color).
To monitor the foot-strike event, a light-weight
accelerometer (Kistler PiezoBeam, type 8634B50)
was attached onto the skin in closest position to the
bony prominence of the tibial tuberosity and was
aligned along the longitudinal axis of the tibia to
provide the axial component of the vertical impact
acceleration on the shank.
The signals from the accelerometer were fed to the
PC-based data acquisition system at a sampling rate
of 1000 Hz. A high sampling rate was required to
pick-up the timings of the spike acceleration resulting
from foot strike.
3.3 Electromyography (EMG)
Surface EMG signals from the right biceps and
triceps muscles were monitored to indicate the
activation of the major muscle groups of the elbow
joint. The signals were measured by means of two
pairs of bipolar Ag/AgCl disposable snap electrodes
(10mm diameter), amplified (Atlas Research Ltd.,
Hod-Hasharon, Israel) and sampled at 1000 samples/s
Modulation of Impedance and Muscle Activation of the Upper Limb Joints while Simultaneously Controlling Manual-grasping and Walking
195

(National Instrument AT-MIO-16E). The signals
were processed as follows: in the time domain, the
signals of each muscle were filtered (2-500 Hz),
normalized to their respective maximal voluntary
contraction (MVC) value, after which the root mean
squares (RMS) were calculated. The co-contraction
value of both muscles was calculated (Winter, 2009).
In the frequency domain, steadiness of the median
frequency was used to indicate the possible presence
of muscle fatigue.
4 BIOMECHANICAL MODEL
The input to the system in Figure 1 are the periodic
displacement signals due to the walking body-
movement, as transmitted to the upper limb through
the shoulder girdle, and the output of the system is the
self-navigated free hand holding the cup-of-liquid.
The model segments are assumed to be rigid bodies,
with known mass and inertia properties. The joint
angles are as defined in Fig. 2. The shoulder angle Øs
is defined between the upper arm and the vertical.
Angles Øe and Øw represent the elbow and wrist joint
angles, respectively, and their corresponding θ’ are
the external angles of these joints. Angles θ (no
prime) are between segments and the horizontal. The
model segments are connected together by the joints
via lumped impedances representing damped springs.
The damped spring coefficients are expressible in
terms of joint angles and angular velocities (Mizrahi,
2015).
Thus,
()
()
()
jjjjjjjj
kkkk
02010
φφφφφ
−+−+=
(1)
()
jjoint of stiffness−
φ
j
k
() ( )
jjjjj
bbb
010
φφφ
−+=
(2)
()
jjoint of damping−
φ
j
b
The reference angle
0 j
φ
was taken in the neutral
position of each joint.
These coefficients are related to joint torques M
j
as follows:
j
j
j
M
k
φ
∂
∂
=
(3)
j
j
j
M
b
φ
∂
∂
=
(4)
Figure 2: Sagittal view of segments and joints of the upper
limb: A=upper arm, in relation of vertical axis of the body
representing the walking body; B=forearm; C=hand.
The joint torque is M
j
obtainable by integration
and by summing up the elastic and damping torques.
=+=
btjstjtj
MMM
()()
+−+−
2
0
1
00
2
jtj
j
jtjj
k
k
φφφφ
()
()
[]
+−−
jtjjtjj
k
002
φφφφ
()()
2
0
1
00
2
jtj
j
jtjj
b
b
φφφφ
−+−
(5)
The torques of the wrist, elbow and shoulder
joints were obtained by solving the inverse dynamics
for the upper limb using Kane’s method (Kane and
Levinson, 1985). These torques were thereafter used
for the calculation of the stiffness and damping
coefficients at each joint.
4.1 Parameter Estimation and
Reduction of the Model
The stiffness and damping coefficients in Eqs. (5)
were resolved from the calculated torques in the
dynamic model by parameter estimation using
optimization procedures. Parameter estimation was
performed by using quadratic programming-
LSQLIN. Comparison between the various testing
conditions was carried out by using T-test for
repeated measures and statistical significance was
established at p-value p<0.05. Parameter identificati-
on was made to reveal the joint impedance model
which best fits all the tests made with and without
joint restrictions, and to indicate whether the general
impedance expressions could be reduced to a simpler
form. To ensure correct parameter estimation, all
predictor variables in the multiple linear regression
analysis must be uncorrelated and the model
BIODEVICES 2017 - 10th International Conference on Biomedical Electronics and Devices
196

parameters should be independent of each other.
Multiple collinearity diagnostic criteria combined
with F-test (Rapoport et al 2003) were used to reveal
dependencies and eliminate redundancies in the
numerical solution of the stiffness and damping
coefficients and reduce the variables in the stiffness
and damping functions. The reduction procedure of
the basic model was made separately for each joint.
5 RESULTS
In all four subjects, the liquid level did not reach the
highest conductive stripe during steady-state motion.
This indicated that the subjects succeeded in
stabilizing their end-effector, irrespective of whether
or not restrictions were introduced to the joints.
5.1 Joints Angles
Fig. 3 shows typical traces of the upper limb joint
angles while walking and holding the cup-of-liquid.
The traces shown are for the shoulder, elbow and
wrist angles. The dark dots designate heel-strike
events of the right foot.
5.2 Model Reduction
By applying the multiple collinearity diagnostic
criteria, the most significant stiffness coefficients
(with p-value p<0.05) were k
0
and k
2
, for the elbow
and shoulder joints and k
0
for the wrist joint (Eq 1).
The damping coefficient b
0
(Eq 2) was significant
only in the wrist joint. Thus, it was concluded that
reducing the optimal model to a 3-parameter model,
with nonlinearly variable stiffness and constant
damping would be sufficient, as follows:
For the wrist joint:
()
jj
kk
0
=
φ
(6)
(
)
jj
bb
0
=
φ
(7)
For the elbow and shoulder joints:
()
(
)
jjjjj
kkk
020
φφφ
−+=
(8)
Table 1 presents values of the overall stiffness
(Eqs. 6,8), in N*m/rad, with and without joint
restriction. The values designate averages of 5 tests,
each over the period of 30 s. The 'no restriction' case
served as a reference for comparisons (t-test), with
significance p level of p<0.05.
During the tests with no restriction, the overall
stiffness values were higher in the shoulder joint than
Figure 3: Typical traces of shoulder, elbow and wrist angles
during test. The dark dots designate heel-strike events of the
right foot.
Table 1: Overall stiffness (for the wrist, elbow and
shoulder, expressed in N*m/rad) with and without joint
restrictions. The values presented are averages of 5 tests,
each over the period of 30 s (SD).
Wrist Elbow Shoulder
SubjectRestriction
3.53 (0.01) 3.02 (0.05) 46.63 (12.83)
1
No
1.74 (0.01) 1.66 (0.36) 18.33 (0.45)
2
2.141(0.03)2.05 (0.24) 42.02 (8.39)
3
8.97 (0.00) 2.10 (0.14) 21.02 (1.16)
4
22.26 (0.06)2.90 (0.49) 57.36 (8.42)
1
Wrist
1.42 (0.02) 1.73 (0.14) 36.28 (3.99)
2
16.86 (0.27)1.99 (0.08) 54.74 (6.56)
3
126.65 (0.35)1.99 (0.16) 19.58 (1.57)
4
2.50 (0.01) 4.28 (0.43) 39.39 (4.14)
1
Elbow
1.90 (0.04) 3.39 (0.26) 47.61 (2.44)
2
1.42 (0.00) 2.51 (0.24) 53.84 (5.73)
3
4.14 (0.01) 3.03 (0.06) 19.70 (1.39)
4
2.67 (0.00) 3.60 (0.11) 64.91 (1.07)
1
Shoulder
5.82 (0.19) 1.95 (0.49) 26.52 (1.89) 2
2.18 (0.04) 1.72 (0.28) 52.77 (3.42) 3
6.58 (0.02) 2.67 (0.08) 59.92 (8.74) 4
in the elbow and wrist joints. Wrist restriction
resulted in an increase in stiffness (and damping) in
that joint in 3 out of the 4 subjects. The effect on the
elbow stiffness was a decrease in 3 out of 4 subjects.
The effect on the shoulder stiffness was an increase
in 3 out of 4 subjects. Elbow restriction demonstrated
a stiffness increase in that joint. The effect on the
wrist was a decrease in stiffness in 3 out of the 4
subjects (the effect on damping was not uniform).
Elbow restriction did not cause any uniform effect on
Modulation of Impedance and Muscle Activation of the Upper Limb Joints while Simultaneously Controlling Manual-grasping and Walking
197
the stiffness of the shoulder. Shoulder restriction
resulted in an increase in stiffness on that joint. In 2
subjects this restriction resulted in a decrease in
stiffness in the wrist and in 3 subjects an increase in
stiffness in the elbow.
5.3 EMG Results
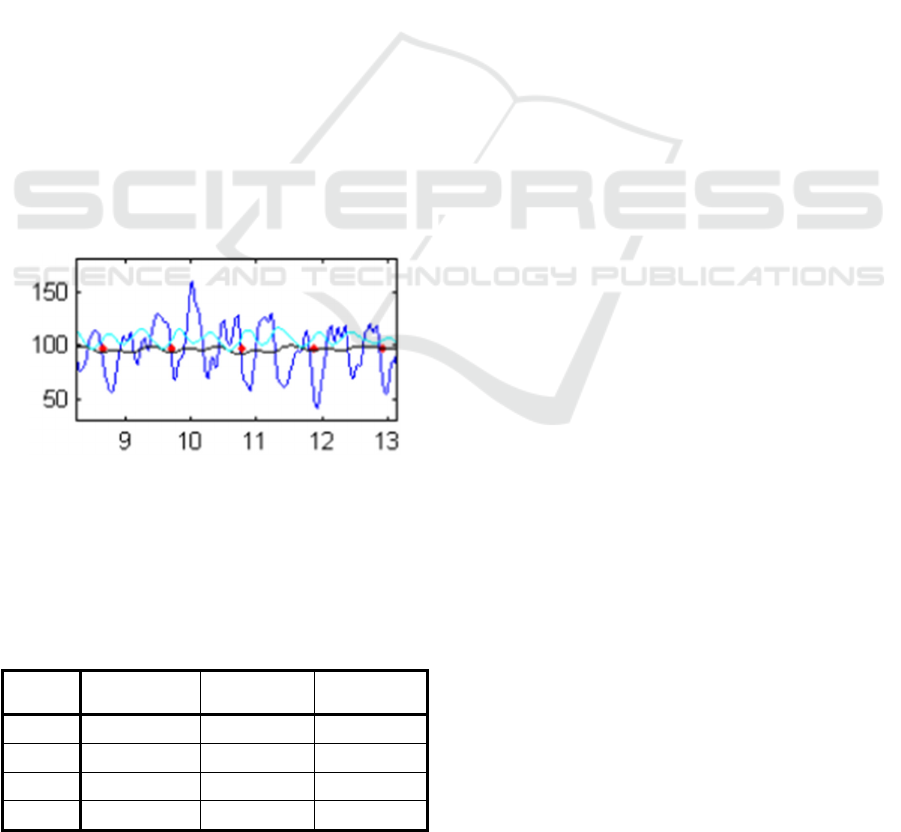
EMG traces (linear envelope of filtered data) of the
biceps muscle alongside the elbow joint angle
variation and elbow stiffness during a typical test
without joint constraint are demonstrated in Fig. 4.
The heel-strike signals are also shown by the red dots.
It is seen that biceps EMG and elbow overall stiffness
are opposite in phase. No correlation, however, was
observed between EMG and joint angle. It should be
remembered that stiffness is estimated from the
model and is not directly expressed by the angle.
Summary of time-domain processing of the root
mean square (RMS) values of the EMG signals is
presented in Table 2 for one of the tested subjects. It
is noted that activation intensity of the triceps is
nearly 50% of that of the biceps. The results indicate
that activation of both the biceps and the triceps were
not significantly affected by constraining any of the
wrist, elbow or shoulder joints. Likewise was the case
for co-contraction of these two muscles. Median
frequency results did not indicate development of
fatiguing during the course of the tests.
Figure 4: Filtered EMG signal of biceps (linear envelope)
with no joint restriction (Blue line = EMG, light blue =
elbow joint stiffness, black line = elbow joint angle, red dots
= heel-strike events of right foot).
Table 2: Representative RMS values of the EMG results
(normalized to MVC) of Biceps and Triceps muscles and of
co-contraction. Both unconstrained and joint-constrained
cases are reported.
Joint
constraint
Biceps RMS Triceps RMS Co-contraction
No 3.284 (0.0130) 1.659 (0.0090) 68.20 (0.080)
Wrist 3.284 (0.0086) 1.664 (0.0037) 68.25 (0.080)
Elbow 3.274 (0.0082) 1.655 (0.0041) 68.15 (0.045)
Shoulder 3.266 (0.0078) 1.653 (0.0057) 68.21 (0.093)
6 DISCUSSION
Although coordination between locomotion and
control has been studied in the past (Georgopoulos
and Grillner, 1989; van der Wel and Rosenbaum
2007, Roth et al 2011), no works were found dealing
with adjustment of the mechanical impedance by
continuously tuning muscle activation during
simultaneous control of grasping and walking.
The basic muscle-tendon model used was made to
include elastic and damping elements. The elastic
element depended on angular displacement and
angular velocity (Woo and Young, 1991) and the
damping element depended on angular velocity
(Milner and Cloutier, 1998). By checking for multi
co-linearity, this model was separately reduced and
adapted to each of the joints, in accordance with the
goodness of fit of parameter estimation.
The wrist joint was found to have constant
stiffness and damping (Eqs 6,7), and no regulation of
these coefficients was necessary during the gait cycle.
It should be reminded, however, that the finger joints
were not represented in the end-effector and this
segment was considered a rigid body attached to the
wrist joint. This representation was consistent with
the two-dimensional assumption of the model. The
other two joints had non-linear stiffness representa-
tions (Eq 7). Non-linear models are widespread in the
description of human joints (Rakheja et al 1993;
Karniel and Inbar, 1999; Konczack et al, 1999;
Rapoport et al 2003). Both in the elbow and shoulder
joints, stiffness included a constant coefficient as well
as an angular velocity-dependent coefficient.
The EMG results did not confirm a definite
relation between any of the elbow stiffness or elbow
joint angle and the activation of the flexor and
extensor muscles studied. It should be mentioned that
intensity of these muscles relative to their respective
MVC was only around 5% for the triceps and 10% for
the biceps muscles. This low activation suggests that,
most probably, other muscles (not monitored in this
study) also take part in controlling the elbow joint,
hindering the correlation sought. From the data of
stride timing versus biceps EMG it can be noted that
activation of this muscle decreases upon heel-strike
and increases again towards the next strike. In view
of the obvious presence of additional muscles in the
process of elbow control, this particular behavior of
the biceps should not be considered representative of
the other muscles. Siegler et al (1985) also reported
that joint torque and muscle activation are not
uniquely correlated.
We did not find in this study a pre-activation of
the muscles studied, prior to the impact loading
BIODEVICES 2017 - 10th International Conference on Biomedical Electronics and Devices
198

introduced by heel strike. Previous studies have
indicated the presence of pre-activation in non-
repetitive activities such as ball-catching (Lacqaniti et
al, 1993). In the present study, loading was rather
repetitive, due to the cyclic nature of steady walking.
7 CONCLUSIONS
We investigated how the stiffness and damping of the
upper limb joints are being modulated in combined
activity of hand grasping and locomotion. Kinematic
data from the upper limb and of EMG from the wrist
extensors and flexors were obtained with the joints
unconstrained and after successively immobilizing
each of the joints. Stiffness and damping values of
each of the joints were obtained as a function of joint
angle, for the shoulder and elbow joints. The wrist
joint was found to have constant stiffness and
damping, and no regulation of these coefficients was
necessary during the gait cycle. The results also
showed how joint immobilization affects the joint
impedance behavior. The EMG results did not
confirm a definite relation between any of the elbow
stiffness or elbow joint angle and the activation of the
flexor and extensor muscles studied. The wide
variability in the impedance results obtained
indicated that the compensatory mechanisms
exercised by each subject to regulate the mechanical
impedance to overcome the joint restriction were
individual, not necessarily indicating to a common
pattern.This study sheds light on the mechanisms of
stabilization of grasped objects during walking and
the results obtained, despite their variability, may be
relevant for the future designing of artificial arms and
robots and for the development of more accurate
control strategies of combined hand grasping and
walking.
REFERENCES
Georgopoulos AP, Grillner S (1989) Visuomotor
coordination in reaching and locomotion. Science
245:1209-1210
Kane TR, Levinson DA (1985) Dynamics: Theory and
Application. McGraw-Hill Book Company, New York
Karniel A, Inbar GF (1999) The use of nonlinear muscle
model in explaining the relatioship between duration,
amplitude, and peak velocity of human rapid
movements. J Motor Behav, 31(3):203-206
Konczak J, Brommann K, Kalveram KT (1999)
Identification of time varying stiffness, damping and
equilibrium position in human forearm movements.
Motor control 3:394-413
Lacqaniti F, Carrozzo M, Borghese NA (1993) Time
varying mechanical behavior of multijointed arm in
man. J Neurophysiol 69(5):1443-1464
Milner TE (2002) Contribution of geometry and joint
stiffness to mechanical stability of the human arm.Exp
Brain Res 143:515-519
Mizrahi, J. (2015) DOI: 10.1007/s40846-015-0014-y
Mechanical Impedance and Its Relations to Motor
Control, Limb Dynamics, and Motion Biomechanics, J.
Med. Biol. Eng., 35 (1):1-20, DOI 10.1007/s40846-
015-0016-9.
Rakheja S, Gurram R, Gouw GJ (1993) Development of
linear and nonlinear hand-arm vibration models using
optimization and linearization techniques. J Biomech
26(10):1253-1260
Rapoport S, Mizrahi J, Kimmel E, Verbitsky O, Isakov E
(2003) Constant and variable stiffness and damping of
the leg joints in human hopping. J Biomech Eng
125:507-514
Roth, N., Seliktar, R. and Mizrahi, J. (2011) Mechanical
Impedance Control in the Human Arm while Manually
Transporting an Open-Top Fluid Filled Dish, Appl.
Bionics and Biomechanics, 8:393-404.
Siegler S, Hillstrom HJ, Freedman W, Moskowits G (1985)
Effect of myoelectric signal processing on the
relationship between muscle force and processed EMG.
American J of Physical Medicine 64(4):130-149
Stroeve S (1999) Impedance characteristics of neuromas-
culoskeletal model of the human arm. I. posture control.
Biol Cybern 81:475-494
Van der Wel RPRD, Rosenbaum DA (2007) Coordination
of locomotion and prehension. Exp Brain Res 176:281-
287
Winter DA. Biomechanics and motor control of human
movement. John Whiley andSons, Inc., Hoboken, NJ;
2009.
Woo SLY, Young EP (1991) Structure and function of
tendons and ligaments. In: Mow VC and Hayes WC
(eds) Basic Orthopedic Biomechanics, 2th edition.
Raven Press, New York, pp199-243
Zajac F E, Winters JM (1990) Modelling muscle system-
joint and body segmental Dynamics’musculoskeletal
actuation, and neuromuscular control. In: Winters JM
and Woo SL-Y (eds) Multiple Muscle Systems:
Biomechanics and Movement Organization. Springer-
Verlag, New York, pp121-148
Modulation of Impedance and Muscle Activation of the Upper Limb Joints while Simultaneously Controlling Manual-grasping and Walking
199
