
Optimal Control of Plug-in Hybrid Electric Vehicle based on
Pontryagin’s Minimum Principle Considering Driver’s Characteristic
Kyusik Park, Hanho Son, Kyunggook Bae, Yoonuk Kim, Hyunhwa Kim,
Jeongseok Yun and Hyunsoo Kim
School of Mechanical Engineering, Sungkyunkwan University, Suwon, Korea
Keywords: Plug-in Hybrid Electric Vehicle (PHEV), Optimal Control, Driver Characteristic.
Abstract: In this study, an optimal control was investigated for a power split type plug-in hybrid electric vehicle (PHEV)
considering the driver’s characteristic. Using the dynamic model of the PHEV powertrain, Hamiltonian was
defined and the optimal co-state was obtained for Pontryagin’s minimum principle (PMP) control. The PMP
control was performed for a normal driver who was selected based on extended driving style questionnaire
(EDSQ), and the battery SOC behaviour and equivalent fuel economy were evaluated. It was found that the
equivalent fuel economy by the PMP control is improved compared with the existing charge depleting/charge
sustaining (CD/CS) control and the battery SOC decreased faster as the sportiness of the driver increased.
1 INTRODUCTION
In plug-in hybrid electric vehicle (PHEV) which uses
the internal combustion engine and motors, the power
distribution between the engine and motors has a
great influence on the vehicle fuel economy (Zhang
and Vahidi, 2012). As a PHEV management strategy,
charge depleting (CD)/charge sustaining (CS) control
is generally used. In CD mode, the vehicle is
propelled only using the electric energy until the
battery SOC reaches to the lower limit. This region is
called, “All Electric Range (AER)”. After AER, the
vehicle is operated in CS mode using the engine and
motor to sustain the SOC. The CD/CS control may
reduce fuel economy because the engine has to be
operated even at low efficiency to maintain the SOC
(Jeong et al., 2016).
To overcome the disadvantage of the CD/CS
control, two types of approach have been used: (1)
rule based control and (2) optimal control.
Rule based control distributes the power by the
rule obtained in advance, using the state of charge
(SOC) of the battery (Sigmund et al., 2014) or wheel
power demand (Pi, 2016). The rule based control has
an advantage to apply to the vehicle in real time.
However, it is heuristic and not optimal. For the
optimal control, dynamic programming (DP) (Wang
et al., 2015), equivalent consumption minimization
strategies (ECMS) (Gao et al., 2017), Pontryagin’s
minimum principle (PMP) (Kim, 2011) were used.
DP provides a global optimal solution (Chen et al.,
2014). However, it only provides the optimal results
for the given route and cannot guarantee the optimal
results when driving cycle is changed. In addition, it
is hardly implementable in real time (Karbowski et al.,
2013). Due to these limitations, DP has been used to
estimate the maximum potential of a given PHEV
configuration (Peng et al., 2017). ECMS and PMP
can be used in real time control since local
optimization is performed at every time step.
However, they cannot guarantee the global
optimization when the constraints such as the final
SOC are not satisfied (Kim, 2011). To implement the
optimal control using ECMS or PMP, it is important
to estimate the optimization variables such as
equivalent factor, co-state that satisfy the constraints
(Wei et al., 2016).
To obtain the appropriate optimization variables,
studies to predict a velocity profile were performed
using Markov chain (Du et al., 2016) and neural
network (Murphey et al., 2013). However, it is very
hard to predict the exact velocity profile due to
uncertain disturbances (Karbowski et al., 2014).
Furthermore, actual driving velocity can be varied
depending on the driver’s characteristic.
Furthermore, in actual driving, the fuel economy
varies depending on the driver’s characteristic, even
if the optimal control is performed (Lee et al., 2015).
Park, K., Son, H., Bae, K., Kim, Y., Kim, H., Yun, J. and Kim, H.
Optimal Control of Plug-in Hybrid Electric Vehicle based on Pontryagin’s Minimum Principle Considering Driver’s Characteristic.
DOI: 10.5220/0006239901510156
In Proceedings of the 3rd International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS 2017), pages 151-156
ISBN: 978-989-758-242-4
Copyright © 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
151
In this study, an optimal control was performed in
real time using PMP. The PMP control was applied
using the optimal co-state that was obtained for a
driver who has normal driving style. PMP control
performance was investigated for various drivers
using the same optimal co-state and the battery SOC
behaviour was evaluated with regard to the driving
style.
2 MODEL OF PLUG IN HYBRID
ELECTRIC VEHICLE
2.1 Vehicle Model
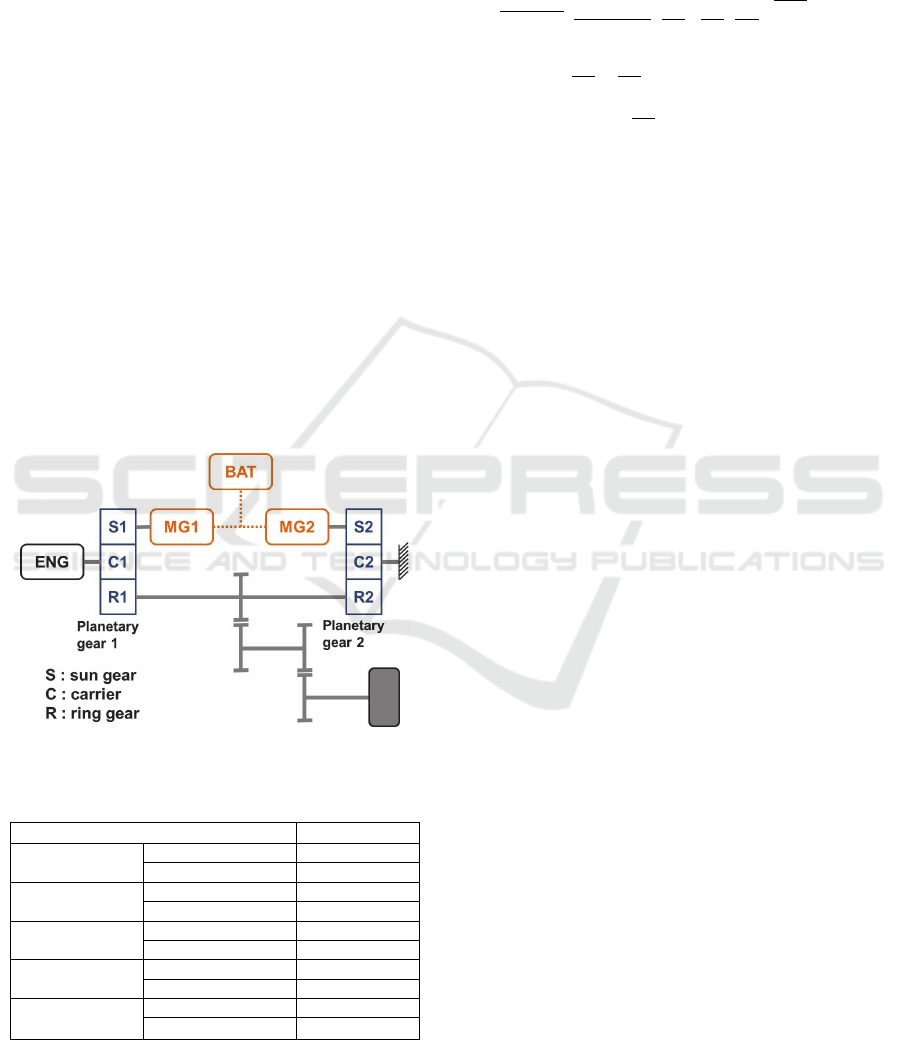
In Figure 1, the target PHEV is shown. In this study,
Toyota Prius Ⅲ were selected as a target PHEV. The
target PHEV consists of one engine, two
motor/generators (MGs) and two planetary gears. The
engine is connected to the carrier of the planetary gear
1. The engine operation is controlled by MG1, which
is connected to the sun gear of the planetary gear 1.
The PHEV can provide two operating modes: (1) EV
and (2) HEV.
Figure 1: Target PHEV configuration.
Table 1: Specifications of target vehicle.
Power split type Specifications
Engine
Max power(kW) 73
Max torque(Nm) 142
MG1
Max power(kW) 42
Max torque(Nm) 153.4
MG2
Max power(kW) 60
Max torque(Nm) 207
Battery
Max power(kW) 27
Capacity(kWh) 4.4
Vehicle
Mass(kg) 1600
Tire radius(m) 0.317
In Table 1, the vehicle specifications are shown.
From the lever analysis of the PHEV
configuration in Figure 1, the torque and speed
equations were derived as follows:
01
∙
∙
1
(1)
1
0
∙
(2)
where T is the torque, ω is the speed, Z is the gear
teeth number and is the gear ratio. The subscripts
1, 2, 1, 1, 2, 2, , , and
represent MG1, MG2, sun gear1, ring gear1, sun
gear2, ring gear2, final reduction gear, required, and
engine, respectively. The required battery power can
be calculated as follows:
P
ŋ
∙T
∙ω
ŋ
∙T
∙ω
(3)
where ŋ
is the efficiency of MG1, ŋ
is the
efficiency of MG2. And is defined as follows:
k
1
1
generating
motoring
(4)
Finally, the required battery power is considered
as a function of the required torque, required speed,
the engine torque, and engine speed.
P
T
,ω
,T
,ω
(5)
3 APPLICATION OF OPTIMAL
CONTROL
3.1 Pontryagin’s Minimum Principle
(PMP)
In this study, an optimal control based on
Pontryagin’s minimum principle (PMP) was used.
PMP is a control method to minimize Hamiltonian at
each time step. Hamiltonian was defined as,
H
t
λ ∙
SOC,
t
(6)
where is the cost function which is the rate of fuel
consumption,
is the state function which is the
rate of SOC,
is the control variable which is the
required power of the battery, and λ is co-state of
PMP.
VEHITS 2017 - 3rd International Conference on Vehicle Technology and Intelligent Transport Systems
152
The rate of fuel consumption can be obtained from
the fuel consumption map for the given engine torque
and speed as,
,
(7)
From Equation (5), the required battery power can
be calculated using the torque and speed of the engine.
,
(8)
Hence, we can determine the rate of fuel
consumption, as the function of the battery power.
(9)
In this study, Coulomb counting method was used
to estimate the battery SOC (Chang, 2013),
1
(10)
where is the battery SOC, is the capacity, is
the current. The subscripts , , , and
represent the initial, battery, current time, initial time,
respectively.
From Equation (10),
can be obtained as
follows:
(11)
The battery current can be expressed as,
(12)
where is the power, is the voltage.
The battery voltage can be calculated using the
open circuit voltage and internal resistance as,
(13)
where is the resistance. The subscripts ,
represent the open circuit, internal, respectively.
From Equation (11), (12), (13),
can be
represented as follows:
1
4
2
(14)
Assuming that the open circuit voltage,
and
internal resistance,
of the battery are the function
of SOC, time derivative of SOC is represented as
gSOC,
t
(15)
In battery model, since
and
do not change
much in usable SOC range, state function,
can
be obtained as only a function of
.
g
,
≅g
(16)
From Equation (16),
is a function of
,
which is independent of SOC. Therefore, time
derivative of co-state is zero.
λ
λ
0
(17)
From Equation (17), it is seen that co-
state, λ is constant.
4 DRIVING DATA
COLLECECTION
4.1 Driver Selection
Through extended driving style questionnaire (EDSQ)
(Lajunen, 2004), various drivers who have different
driving style were selected. In Table 2, drivers’
EDSQ score are shown. Based on the EDSQ score of
the selected driver, driving style was defined as
Sporty, Normal and Eco.
Table 2: EDSQ score of drivers.
Driver# EDSQ Score Driving Style
Driver 1 58 Sporty
Driver 2 49 Sporty
Driver 3 35 Normal
Driver 4 32 Eco
Driver 5 20 Eco
4.2 Route Selection
We chose a route which includes various road styles
such as city, highway and slope ways. Total distance
of the route is 12km and it takes about 20~30 minutes.
To reflect more accurate driving styles of each driver,
the driving data were collected by GPS at 10~12 in
the morning which can avoid other disturbances such
as high traffic congestion.
Optimal Control of Plug-in Hybrid Electric Vehicle based on Pontryagin’s Minimum Principle Considering Driver’s Characteristic
153
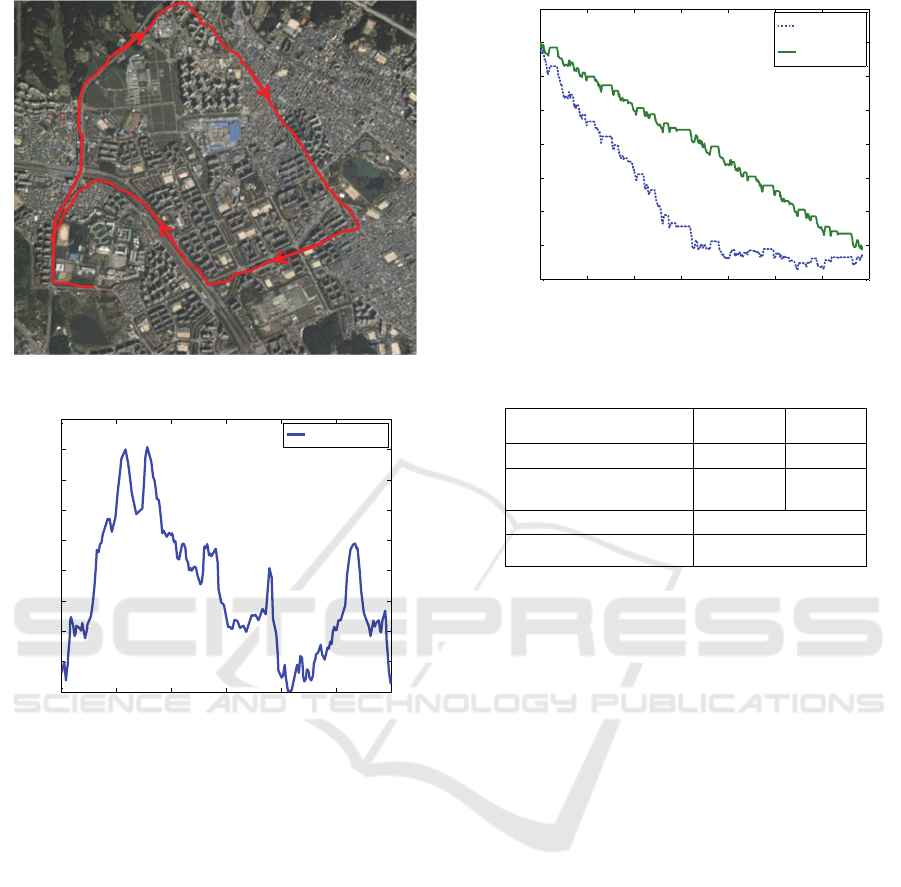
Figure 2: Selected route (12km).
Figure 3: Elevation of the route.
5 SIMULATION RESULTS
5.1 Comparison of PMP and CD/CS
First, simulation was performed for Driver 3 who has
‘Normal’ driving style based on EDSQ. The optimal
co-state was obtained for Driver 3 using the shooting
method.
Since all electric range (AER) of the target PHEV
is 23.4km, the SOC behaviour was investigated when
the vehicle drove the selected route (Figure 2) two
times, which is 24km. In the simulation, the initial
and final SOC were set as 0.6 and 0.3, respectively.
Figure 4: Battery SOC for driver 3.
Table 3: Results of PMP and CD/CS control.
Control PMP CD/CS
Fuel consumption (kg) 0.2711 0.6756
Equivalent fuel
economy (km/l)
27.64 25.31
Improvement (%) 9.21
Co-state (λ)
-1.2484
In Figure 4, the simulation result of the battery
SOC by PMP control was compared with the existing
CD/CS control. In CD/CS control, the vehicle was
driven in EV mode using the electric energy until the
battery SOC reached to 0.3. After that, the vehicle
was operated using the engine and motor for the SOC
balancing.
It is seen that the battery SOC by PMP control
decreased slowly. On the other hand, the battery SOC
by CD/CS control decreased rapidly in CD mode and
was maintained by the SOC balancing in CS mode.
In Table 3, the simulation results were compared.
It is seen that the equivalent fuel economy of the PMP
control is 27.64km/l, which is improved by 9.21%
compared with that of the existing CD/CS control.
5.2 PMP Control for Various Drivers
using the Same Co-State
Now, PMP control was applied to various drivers
using the same co-state (λ=-1.2484) that was obtained
for Driver 3.
0 2000 4000 6000 8000 10000 12000
0
5
10
15
20
25
30
35
40
45
Distance, m
Elevation, m
Elevation
0 500 1000 1500 2000 2500 3000 3500
0.25
0.3
0.35
0.4
0.45
0.5
0.55
0.6
0.65
Time, sec
SOC
CD/CS
PMP
VEHITS 2017 - 3rd International Conference on Vehicle Technology and Intelligent Transport Systems
154

Figure 5: Battery SOC for various drivers.
Table 4: Results of PMP control for various drivers using
the same co-state.
Driver #
Final
SOC
EDSQ
Score
Pearson
correlatio
n
Driver 1 0.2322 58
-0.9418
Driver 2 0.2930 49
Driver 3 0.2979 35
Driver 4 0.3156 32
Driver 5 0.3479 20
Simulation results are shown in Figure 5. It is
noted that the SOC decreased faster as the sportiness
of the driver increased.
In Table 4, the simulation results are compared for
five drivers. The final SOC decreased as EDSQ score
increased, in other words, the sportiness of the driver
increased. This can be proved by Pearson correlation
value, -0.9418, which shows strong negative
relationship. It is also noted that the final SOC
showed some difference from the target final SOC,
0.3.
To meet the SOC constraints, when the PHEV is
operated by a sporty driver, the engine needs to be
turned on more often to charge the battery meanwhile
the battery has to be used more often for an eco-driver.
Since the co-state was obtained for Driver 3, this co-
state cannot satisfy the SOC constraints when the
vehicle is driven by the driver with different
characteristic.
This implies that the optimal co-state needs to be
determined by considering the driver’s characteristic
as well as the vehicle speed profile.
6 CONCLUSIONS
An optimal control was investigated for a power split
type PHEV considering the driver’s characteristic. To
apply the optimal control, dynamic equations of the
target PHEV powertrain were obtained and
Hamiltonian was defined as a function of the rate of
fuel consumption and the rate of the battery SOC.
Representing the rate of SOC as a function of the
battery power, the optimal co-state was obtained for
Pontryagin’s minimum principle (PMP) control.
Driving data were collected for the selected route
which includes city, highway and slope ways. In
addition, driving style was defined as Sporty, Normal
and Eco based on EDSQ.
The PMP control was performed for the normal
driver using the optimal co-state obtained. It was
found from the simulation that the equivalent fuel
economy by PMP control is improved by 9.21%
compared with the existing CD/CS control. It was
also found that the battery SOC by the PMP control
decreased faster as the sportiness of the driver
increased when the same co-state was applied for
various drivers. It was found that the optimal co-state
needs to be determined by considering the driver’s
characteristic as well as the vehicle speed profile.
For future works, a correlation between driver
characteristic and optimal co-state will be obtained
and an algorithm to find out the optimal co-state for a
selected velocity profile will be investigated
considering the correlation factors.
ACKNOWLEDGEMENTS
This material is based upon work supported by the
Ministry of Trade, Industry & Energy(MOTIE,
Korea) under Industrial Technology Innovation
Program. No.10062742, 'Development of Power
Distribution Control for High Fuel Efficiency of
Plug-in Hybrid Electric Vehicle using Route
Information.'
REFERENCES
Chen Zhang, and Vahidi, A. (2012). Route Preview in
Energy Management of Plug-in Hybrid Vehicles. IEEE
Transactions on Control Systems Technology, 20(2),
pp.546-553.
Jeong, J., Karbowski, D., Rousseau, A. and Rask, E. (2016).
Model Validation of the Honda Accord Plug-In. SAE
Technical Paper Series.
0 1000 2000 3000 4000
0.2
0.25
0.3
0.35
0.4
0.45
0.5
0.55
0.6
0.65
Time, sec
SOC
Driver1
Driver2
Driver3
Driver4
Driver5
Sport
y
Optimal Control of Plug-in Hybrid Electric Vehicle based on Pontryagin’s Minimum Principle Considering Driver’s Characteristic
155

Sigmund, D., Lohner, A. and Boh, M. (2014). Simulation-
based development of an energy-management-system
for a drive train of a parallel hybrid electric vehicle.
2014 16th International Power Electronics and Motion
Control Conference and Exposition.
Pi, J., (2016). Development of Route Information Based
Driving Control Algorithm for a Range-Extended
Electric Vehicle. International Journal of Automotive
Technology, Vol. 17, Issue. 6, pp. 1101-1111.
Wang, X., He, H., Sun, F. and Zhang, J. (2015). Application
Study on the Dynamic Programming Algorithm for
Energy Management of Plug-in Hybrid Electric
Vehicles. Energies, 8(4), pp.3225-3244..
Gao, A., Deng, X., Zhang, M. and Fu, Z. (2017). Design
and Validation of Real-Time Optimal Control with
ECMS to Minimize Energy Consumption for Parallel
Hybrid Electric Vehicles. Mathematical Problems in
Engineering, 2017, pp.1-13.
Kim, N., (2011). Optimal Control of Hybrid Electric
Vehicles Based on Pontryagin’s Minimum Principle,
IEEE Trans. Control Syst, Vol 19, Issue. 5, pp.1279-
1287.
Chen, B., Wu, Y. and Tsai, H. (2014). Design and analysis
of power management strategy for range extended
electric vehicle using dynamic programming. Applied
Energy, 113, pp.1764-1774.
Karbowski, D., Smis-Michel, V. and Vermeulen, V. (2013).
Using trip information for PHEV fuel consumption
minimization. 2013 World Electric Vehicle
Symposium and Exhibition (EVS27).
Peng, J., He, H. and Xiong, R. (2017). Rule based energy
management strategy for a series–parallel plug-in
hybrid electric bus optimized by dynamic programming.
Applied Energy, 185, pp.1633-1643.
Wei, H., Chen, Y. and Peng, Z. (2016). Costate Estimation
of PMP-Based Control Strategy for PHEV Using
Legendre Pseudospectral Method. Mathematical
Problems in Engineering, 2016, pp.1-9.
Du, Y., Zhao, Y., Wang, Q., Zhang, Y. and Xia, H. (2016).
Trip-oriented stochastic optimal energy management
strategy for plug-in hybrid electric bus. Energy, 115,
pp.1259-1271.
Murphey, Y., Park, J., Kiliaris, L., Kuang, M., Masrur, M.,
Phillips, A. and Wang, Q. (2013). Intelligent Hybrid
Vehicle Power Control-Part II: Online Intelligent
Energy Management. IEEE Transactions on Vehicular
Technology, 62(1), pp.69-79.
Karbowski, D., Kim, N. and Rousseau, A. (2014). Route-
Based Online Energy Management of a PHEV and
Sensitivity to Trip Prediction. 2014 IEEE Vehicle
Power and Propulsion Conference (VPPC).
Lee, S., Choi, J., Jeong, K. and Kim, H. (2015). A Study of
Fuel Economy Improvement in a Plug-in Hybrid
Electric Vehicle using Engine on/off and Battery
Charging Power Control Based on Driver
Characteristics. Energies, 8(9), pp.10106-10126.
Chang, W. (2013). The State of Charge Estimating Methods
for Battery: A Review. ISRN Applied Mathematics,
2013, pp.1-7.
Lajunen, T., (2004). The Manchester Driver Behavior
Questionnaire: A cross-cultural study. Accident
Analysis and Prevention, Vol. 36, Issue. 2, pp. 231-238.
VEHITS 2017 - 3rd International Conference on Vehicle Technology and Intelligent Transport Systems
156
