
Security Against Collective Attacks of a Modified BB84 QKD Protocol
with Information only in One Basis
Michel Boyer
1
, Rotem Liss
2
and Tal Mor
2
1
D
´
epartement IRO, Universit
´
e de Montr
´
eal, Montr
´
eal (Qu
´
ebec) H3C 3J7, Canada
2
Computer Science Department, Technion, Haifa 3200003, Israel
Keywords:
QKD, Security, Collective Attacks, Error Rate Threshold, Information Bits.
Abstract:
The Quantum Key Distribution (QKD) protocol BB84 has been proven secure against several important types
of attacks: the collective attacks and the joint attacks. Here we analyze the security of a modified BB84
protocol, for which information is sent only in the z basis while testing is done in both the z and the x bases,
against collective attacks. The proof follows the framework of a previous paper (Boyer et al., 2009), but it
avoids the classical information-theoretical analysis that caused problems with composability. We show that
this modified BB84 protocol is as secure against collective attacks as the original BB84 protocol, and that it
requires more bits for testing.
1 INTRODUCTION
Quantum Key Distribution (QKD) protocols take ad-
vantage of the laws of quantum mechanics, and most
of them can be proven secure even against powerful
adversaries limited only by the laws of physics. The
two parties (Alice and Bob) want to create a shared
random key, using an insecure quantum channel and
an unjammable classical channel (to which the ad-
versary may listen, but not interfere). The adversary
(eavesdropper), Eve, tries to get as much information
as she can on the final shared key. The first and most
important QKD protocol is BB84 (Bennett and Bras-
sard, 1984).
Boyer, Gelles, and Mor (BGM09) (Boyer et al.,
2009) discussed the security of the BB84 protocol
against collective attacks. Collective attacks (Biham
and Mor, 1997b; Biham and Mor, 1997a; Biham et al.,
2002) are a subclass of the joint attacks; joint attacks
are the most powerful theoretical attacks. BGM09
improved the security proof of Biham, Boyer, Bras-
sard, van de Graaf, and Mor (BBBGM02) (Biham
et al., 2002) against collective attacks, by using some
techniques of Biham, Boyer, Boykin, Mor, and Roy-
chowdhury (BBBMR06) (Biham et al., 2006) (that
proved security against joint attacks). In this paper,
too, we restrict the analysis to collective attacks, be-
cause security against collective attacks is conjectured
(and, in some security notions, proved (Renner, 2008;
Christandl et al., 2009)) to imply security against joint
attacks. In addition, proving security against col-
lective attacks is much simpler than proving security
against joint attacks.
In many QKD protocols, including BB84, Alice
and Bob exchange several types of bits (encoded as
quantum systems, usually qubits): INFO bits, that are
secret bits shared by Alice and Bob and are used for
generating the final key (via classical processes of er-
ror correction and privacy amplification); and TEST
bits, that are publicly exposed by Alice and Bob (by
using the classical channel) and are used for estimat-
ing the error rate. In BB84, each bit is sent from Alice
to Bob in a random basis (the z basis or the x basis).
In this paper, we extend the analysis of BB84 done
in BGM09 and prove the security of a QKD protocol
we shall name BB84-INFO-z. This protocol is almost
identical to BB84, except that all its INFO bits are in
the z basis. In other words, the x basis is used only for
testing. The bits are thus partitioned into three disjoint
sets: INFO, TEST-Z, and TEST-X. The sizes of these
sets are arbitrary (n INFO bits, n
z
TEST-Z bits, and n
x
TEST-X bits).
We note that, while this paper follows a line of
research that mainly discusses a specific approach of
security proof for BB84 and similar protocols (this
approach, notably, considers finite-key effects and
not only the asymptotic error rate), many other ap-
proaches have also been suggested: see for exam-
ple (Mayers, 2001; Shor and Preskill, 2000; Renner,
2008; Renner et al., 2005).
Boyer, M., Liss, R. and Mor, T.
Security Against Collective Attacks of a Modified BB84 QKD Protocol with Information only in One Basis.
DOI: 10.5220/0006241000230029
In Proceedings of the 2nd International Conference on Complexity, Future Information Systems and Risk (COMPLEXIS 2017), pages 23-29
ISBN: 978-989-758-244-8
Copyright © 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
23

In contrast to the line of research adopted here
(of (Biham and Mor, 1997b; Biham and Mor, 1997a;
Biham et al., 2002; Biham et al., 2006; Boyer et al.,
2009)), in which a classical information-theoretical
analysis caused problems with composability (see
definition in (Renner, 2008)), in this paper we suggest
a method to avoid those problems: we calculate the
trace distance between any two density matrices Eve
may hold, instead of calculating the classical mutual
information between Eve and the final key (as done in
those previous papers). This method is implemented
in this paper for the proof of BB84-INFO-z; it also di-
rectly applies to the BB84 security proof in BGM09,
and it may be extended in the future to show that the
BB84 security proofs of BGM09, BBBGM02, and
BBBMR06 prove the composable security of BB84.
The “qubit space”, H
2
, is a 2-dimensional Hilbert
space. The states |0
0
i, |1
0
i form an orthonormal ba-
sis of H
2
, called “the computational basis” or “the z
basis”. The states |0
1
i ,
1
√
2
[|0
0
i+ |1
0
i] and |1
1
i ,
1
√
2
[|0
0
i − |1
0
i] form another orthonormal basis of
H
2
, called “the x basis”. Those two bases are said
to be conjugate bases.
In this paper, bit strings of some length t are de-
noted by a bold letter (e.g., i = i
1
. . . i
t
with i
1
, . . . , i
t
∈
{0, 1}) and are identified to elements of the t-
dimensional F
2
-vector space F
t
2
, where F
2
= {0, 1}
and the addition of two vectors corresponds to a XOR
operation. The number of 1-bits in a bit string s is de-
noted by |s|, and the Hamming distance between two
strings s and s
0
is d
H
(s, s
0
) = |s +s
0
|.
2 FORMAL DESCRIPTION OF
THE BB84-INFO-Z PROTOCOL
Below we describe the BB84-INFO-z protocol used
in this paper.
1. Alice and Bob pre-agree on numbers n, n
z
, and n
x
(we denote N , n + n
z
+ n
x
), on error thresholds
p
a,z
and p
a,x
, on a linear error-correcting code C
with an r ×n parity check matrix P
C
, and on a
linear key-generation function (privacy amplifica-
tion) represented by an m ×n matrix P
K
. It is re-
quired that all the r + m rows of the matrices P
C
and P
K
put together are linearly independent.
2. Alice randomly chooses a partition P = (s, z, b)
of the N bits by randomly choosing three N-
bit strings s, z, b ∈ F
N
2
that satisfy |s| = n, |z| =
n
z
, |b|= n
x
, and |s+z +b|= N. P thus partitions
the set of indexes {1, 2, ..., N} into three disjoint
sets:
• I (INFO bits, where s
j
= 1) of size n;
• T
Z
(TEST-Z bits, where z
j
= 1) of size n
z
; and
• T
X
(TEST-X bits, where b
j
= 1) of size n
x
.
3. Alice randomly chooses an N-bit string i ∈ F
N
2
,
and sends the N qubit states |i
b
1
1
i, |i
b
2
2
i, . . . , |i
b
N
N
i,
one after the other, to Bob using the quantum
channel. Notice that the INFO and TEST-Z bits
are encoded in the z basis, while the TEST-X bits
are encoded in the x basis. Bob keeps each re-
ceived qubit in quantum memory, not measuring
it yet
1
.
4. Alice publicly sends to Bob the string b =
b
1
···b
N
. Bob measures each saved qubit in the
correct basis (namely, if b
i
= 0 then he measures
the i-th qubit in the z basis, and if b
i
= 1 then he
measures it in the x basis).
The bit string measured by Bob is denoted by i
B
.
If there is no noise and no eavesdropping, then
i
B
= i.
5. Alice publicly sends to Bob the string s. The
INFO bits, used for generating the final key, are
the n bits with s
j
= 1, while the TEST-Z and
TEST-X bits are the n
z
+ n
x
bits with s
j
= 0. The
substrings of i, b that correspond to the INFO bits
are denoted by i
s
and b
s
.
6. Alice and Bob both publish their values of all the
TEST-Z and TEST-X bits, and compare the bit
values. If more than n
z
· p
a,z
of the TEST-Z bits
are different between Alice and Bob or more than
n
x
· p
a,x
of the TEST-X bits are different between
them, they abort the protocol. We note that p
a,z
and p
a,x
(the pre-agreed error thresholds) are the
maximal allowed error rates on the TEST-Z and
TEST-X bits, respectively – namely, in each basis
(z and x) separately.
7. Alice and Bob keep the values of the remaining n
bits (the INFO bits, with s
j
= 1) secret. The bit
string of Alice is denoted x = i
s
, and the bit string
of Bob is denoted x
B
.
8. Alice sends to Bob the r-bit string ξ = xP
T
C
, that is
called the syndrome of x (with respect to the error-
correcting code C and to its corresponding parity
check matrix P
C
). By using ξ , Bob corrects the
errors in his x
B
string (so that it is the same as x).
1
Here we assume that Bob has a quantum memory and
can delay his measurement. In practical implementations,
Bob usually cannot do that, but is assumed to measure in a
randomly-chosen basis (z or x), so that Alice and Bob later
discard the qubits measured in the wrong basis. We assume
that Alice sends more than N qubits, so that N qubits are
finally detected by Bob and measured in the correct basis.
COMPLEXIS 2017 - 2nd International Conference on Complexity, Future Information Systems and Risk
24

9. Alice and Bob compute the m-bit final key k =
xP
T
K
.
The protocol is defined similarly to BB84 (and to
its description in BGM09), except that it uses the gen-
eralized bit numbers n, n
z
, and n
x
(numbers of INFO,
TEST-Z, and TEST-X bits, respectively); that it uses
the partition P = (s, z, b) for dividing the N-bit string
i into three disjoint sets of indexes (I, T
Z
, and T
X
); and
that it uses two separate thresholds (p
a,z
and p
a,x
) in-
stead of one (p
a
).
3 SECURITY PROOF OF
BB84-INFO-Z AGAINST
COLLECTIVE ATTACKS
3.1 Results from BGM09
The security proof of BB84-INFO-z against collective
attacks is very similar to the security proof of BB84
itself against collective attacks, that was detailed in
BGM09. Most parts of the proof are not affected at all
by the changes made to BB84 to get the BB84-INFO-
z protocol (changes detailed in Section 2 of the current
paper), because those parts assume fixed strings s and
b, and because the attack is collective (so the analysis
is restricted to the INFO bits).
Therefore, the reader is referred to the proof in
Section 2 and Subsections 3.1 to 3.5 of BGM09, that
applies to BB84-INFO-z without any changes (except
changing the total number of bits, 2n, to N, which
does not affect the proof at all), and that will not be
repeated here.
We denote the rows of the error-correction parity
check matrix P
C
as the vectors v
1
, . . . , v
r
in F
n
2
, and
the rows of the privacy amplification matrix P
K
as the
vectors v
r+1
, . . . , v
r+m
. We also define, for every r
0
,
V
r
0
, Span{v
1
, ..., v
r
0
}; and we define
d
r,m
, min
r≤r
0
<r+m
d
H
(v
r
0
+1
,V
r
0
) = min
r≤r
0
<r+m
d
r
0
,1
. (1)
For a 1-bit final key k ∈ {0, 1}, we define
b
ρ
k
to be
the state of Eve corresponding to the final key k, given
that she knows ξ. Thus,
b
ρ
k
=
1
2
n−r−1
∑
x
xP
T
C
= ξ
x ·v
r+1
= k
ρ
b
0
x
, (2)
where ρ
b
0
x
is Eve’s state after the attack, given that
Alice sent the INFO bits x encoded in the bases b
0
=
b
s
. We also defined in BGM09 the state
e
ρ
k
, that is a
lift-up of
b
ρ
k
(which means that
b
ρ
k
is a partial trace of
e
ρ
k
).
In the end of Subsection 3.5 of BGM09, it was
found that (in the case of a 1-bit final key, i.e., m = 1)
1
2
tr|
e
ρ
0
−
e
ρ
1
|≤2
s
P
|C
I
| ≥
d
r,1
2
| B
I
= b
0
, s
, (3)
where C
I
is the random variable corresponding to the
n-bit string of errors on the n INFO bits; B
I
is the
random variable corresponding to the n-bit string of
bases of the n INFO bits; b
0
is the bit-flipped string
of b
0
= b
s
; and d
r,1
(and, in general, d
r,m
) was defined
above.
Now, according to (Nielsen and Chuang, 2010,
Theorem 9.2 and page 407), and using the fact that
b
ρ
k
is a partial trace of
e
ρ
k
, we find that
1
2
tr|
b
ρ
0
−
b
ρ
1
| ≤
1
2
tr|
e
ρ
0
−
e
ρ
1
|. From this result and from inequality (3)
we deduce that
1
2
tr|
b
ρ
0
−
b
ρ
1
|≤2
s
P
|C
I
| ≥
d
r,1
2
| B
I
= b
0
, s
. (4)
3.2 Bounding the Differences Between
Eve’s States
We define c , i + i
B
: namely, c is the XOR of the
N-bit string i sent by Alice and of the N-bit string i
B
measured by Bob. For each index 1 ≤ l ≤ N, c
l
= 1
if and only if Bob’s l-th bit value is different from the
l-th bit sent by Alice. The partition P divides the N
bits into n INFO bits, n
z
TEST-Z bits, and n
x
TEST-X
bits. The corresponding substrings of the error string
c are c
s
(the string of errors on the INFO bits), c
z
(the
string of errors on the TEST-Z bits), and c
b
(the string
of errors on the TEST-X bits). The random variables
that correspond to c
s
, c
z
, and c
b
are denoted by C
I
,
C
T
Z
, and C
T
X
, respectively.
We define
f
C
I
to be the random variable corre-
sponding to the string of errors on the INFO bits if
Alice had encoded and sent the INFO bits in the x ba-
sis (instead of the z basis dictated by the protocol). In
those notations, inequality (4) reads as
1
2
tr|
b
ρ
0
−
b
ρ
1
| ≤ 2
s
P
|
f
C
I
| ≥
d
r,1
2
| P
= 2
s
P
|
f
C
I
| ≥
d
r,1
2
| c
z
, c
b
, P
, (5)
using the fact that Eve’s attack is collective, so the
qubits are attacked independently, and, therefore, the
errors on the INFO bits are independent of the errors
on the TEST-Z and TEST-X bits (namely, of c
z
and
c
b
).
As described in BGM09, inequality (5) was not
derived for the actual attack U = U
1
⊗. . . ⊗U
N
ap-
plied by Eve, but for a virtual flat attack (that depends
Security Against Collective Attacks of a Modified BB84 QKD Protocol with Information only in One Basis
25

on b and therefore could not have been applied by
Eve). That flat attack gives the same states
b
ρ
0
and
b
ρ
1
as the original attack U, and gives a lower (or the
same) error rate in the conjugate basis. Therefore, in-
equality (5) also holds for the original attack U. This
means that, from now on, all our results apply to the
original attack U and not the flat attack.
So far, we have discussed a 1-bit key. We will now
discuss a general m-bit key k. We define
b
ρ
k
to be the
state of Eve corresponding to the final key k, given
that she knows ξ:
b
ρ
k
=
1
2
n−r−m
∑
x
xP
T
C
= ξ
xP
T
K
= k
ρ
b
0
x
(6)
Proposition 1. For any two m-bit keys k, k
0
,
1
2
tr|
b
ρ
k
−
b
ρ
k
0
|
≤ 2m
s
P
|
f
C
I
| ≥
d
r,m
2
| c
z
, c
b
, P
. (7)
Proof. We define the key k
j
, for 0 ≤ j ≤m, to consist
of the first j bits of k
0
and the last m− j bits of k. This
means that k
0
= k, k
m
= k
0
, and k
j−1
differs from k
j
at most on a single bit (the j-th bit).
First, we find a bound on
1
2
tr|
b
ρ
k
j−1
−
b
ρ
k
j
|: since
k
j−1
differs from k
j
at most on a single bit (the j-th
bit, given by the formula x·v
r+ j
), we can use the same
proof that gave us inequality (5), attaching the other
(identical) key bits to ξ of the original proof; and we
find that:
1
2
tr|
b
ρ
k
j−1
−
b
ρ
k
j
|
≤ 2
s
P
|
f
C
I
| ≥
d
j
2
| c
z
, c
b
, P
(8)
where we define d
j
as d
H
(v
r+ j
,V
0
j
), and V
0
j
,
Span{v
1
, v
2
, . . . , v
r+ j−1
, v
r+ j+1
, . . . , v
r+m
}.
Now we notice that d
j
is the Hamming distance
between v
r+ j
and some vector in V
0
j
, which means that
d
j
= |
∑
r+m
i=1
a
i
v
i
| with a
i
∈F
2
and a
r+ j
6= 0. The prop-
erties of Hamming distance assure us that d
j
is at least
d
H
(v
r
0
+1
,V
r
0
) for some r ≤ r
0
< r + m. Therefore, we
find that d
r,m
= min
r≤r
0
<r+m
d
H
(v
r
0
+1
,V
r
0
) ≤ d
j
.
The result d
r,m
≤ d
j
implies that if |
f
C
I
| ≥
d
j
2
then
|
f
C
I
| ≥
d
r,m
2
. Therefore, inequality (8) implies
1
2
tr|
b
ρ
k
j−1
−
b
ρ
k
j
|
≤ 2
s
P
|
f
C
I
| ≥
d
r,m
2
| c
z
, c
b
, P
. (9)
Now we use the triangle inequality for norms to find
1
2
tr|
b
ρ
k
−
b
ρ
k
0
|
=
1
2
tr|
b
ρ
k
0
−
b
ρ
k
m
| ≤
m
∑
j=1
1
2
tr|
b
ρ
k
j−1
−
b
ρ
k
j
|
≤ 2m
s
P
|
f
C
I
| ≥
d
r,m
2
| c
z
, c
b
, P
. (10)
The value we want to bound is the expected value
of difference between two states of Eve correspond-
ing to two final keys. However, we should take into
account that if the test fails, no final key is generated,
and the difference between all of Eve’s states becomes
0 for any purpose. We thus define the random variable
∆
(p
a,z
,p
a,x
)
Eve
(k, k
0
) for any two final keys k, k
0
:
∆
(p
a,z
,p
a,x
)
Eve
(k, k
0
|P, ξ, c
z
, c
b
)
,
1
2
tr|
b
ρ
k
−
b
ρ
k
0
| if
|c
z
|
n
z
≤ p
a,z
and
|c
b
|
n
x
≤ p
a,x
0 otherwise
(11)
We need to bound the expected value
h∆
(p
a,z
,p
a,x
)
Eve
(k, k
0
)i, that is given by:
h∆
(p
a,z
,p
a,x
)
Eve
(k, k
0
)i =
∑
P,ξ ,c
z
,c
b
∆
(p
a,z
,p
a,x
)
Eve
(k, k
0
|P, ξ, c
z
, c
b
)
·p(P , ξ , c
z
, c
b
) (12)
Theorem 2.
h∆
(p
a,z
,p
a,x
)
Eve
(k, k
0
)i ≤ 2m
r
P
h
|
f
C
I
|
n
≥
d
r,m
2n
∧
|C
T
Z
|
n
z
≤ p
a,z
∧
|C
T
X
|
n
x
≤ p
a,x
i
(13)
where
|
f
C
I
|
n
is the random variable corresponding to
the error rate on the INFO bits if they had been en-
coded in the x basis,
|C
T
Z
|
n
z
is the random variable cor-
responding to the error rate on the TEST-Z bits, and
|C
T
X
|
n
x
is the random variable corresponding to the er-
ror rate on the TEST-X bits.
Proof. We use the convexity of x
2
, namely, the fact
that for all {p
i
}
i
satisfying p
i
≥ 0 and
∑
i
p
i
= 1, it
holds that (
∑
i
p
i
x
i
)
2
≤
∑
i
p
i
x
2
i
. We find that:
h∆
(p
a,z
,p
a,x
)
Eve
(k, k
0
)i
2
COMPLEXIS 2017 - 2nd International Conference on Complexity, Future Information Systems and Risk
26

=
h
∑
P,ξ ,c
z
,c
b
∆
(p
a,z
,p
a,x
)
Eve
(k, k
0
|P, ξ, c
z
, c
b
)
·p(P , ξ , c
z
, c
b
)
i
2
(by (12))
≤
∑
P,ξ ,c
z
,c
b
∆
(p
a,z
,p
a,x
)
Eve
(k, k
0
|P, ξ, c
z
, c
b
)
2
·p(P , ξ , c
z
, c
b
) (by convexity of x
2
)
=
∑
P,ξ ,
|c
z
|
n
z
≤p
a,z
,
|c
b
|
n
x
≤p
a,x
1
2
tr|
b
ρ
k
−
b
ρ
k
0
|
2
·p(P , ξ , c
z
, c
b
) (by (11))
≤4m
2
·
∑
P,ξ ,
|c
z
|
n
z
≤p
a,z
,
|c
b
|
n
x
≤p
a,x
P
h
|
f
C
I
| ≥
d
r,m
2
| c
z
, c
b
, P
i
·p(P , ξ , c
z
, c
b
) (by (7))
=4m
2
·
∑
P,
|c
z
|
n
z
≤p
a,z
,
|c
b
|
n
x
≤p
a,x
P
h
|
f
C
I
| ≥
d
r,m
2
| c
z
, c
b
, P
i
·p(P , c
z
, c
b
)
=4m
2
·
∑
P
P
h
|
f
C
I
| ≥
d
r,m
2
∧
|C
T
Z
|
n
z
≤ p
a,z
∧
|C
T
X
|
n
x
≤ p
a,x
| P
i
·p(P )
=4m
2
·P
h
|
f
C
I
| ≥
d
r,m
2
∧
|C
T
Z
|
n
z
≤ p
a,z
∧
|C
T
X
|
n
x
≤ p
a,x
i
3.3 Proof of Security
Following BGM09 and BBBMR06, we choose matri-
ces P
C
and P
K
such that the inequality
d
r,m
2n
> p
a,x
+ε is
satisfied for some ε (we will explain in Subsection 3.5
why this is possible). This means that
P
h
|
f
C
I
|
n
≥
d
r,m
2n
∧
|C
T
Z
|
n
z
≤ p
a,z
∧
|C
T
X
|
n
x
≤ p
a,x
i
≤ P
h
|
f
C
I
|
n
> p
a,x
+ ε
∧
|C
T
X
|
n
x
≤ p
a,x
i
. (14)
We will now prove the right-hand-side of (14) to be
exponentially small in n.
As said earlier, the random variable
f
C
I
corre-
sponds to the bit string of errors on the INFO bits if
they had been encoded in the x basis. The TEST-X
bits are also encoded in the x basis, and the random
variable C
T
X
corresponds to the bit string of errors on
those bits. Therefore, we can treat the selection of
the n INFO bits and of the n
x
TEST-X bits as a ran-
dom sampling (after the numbers n, n
z
, and n
x
and the
TEST-Z bits have all already been chosen), and use
Hoeffding’s theorem (that is described in Appendix A
of BGM09).
Therefore, for each bit string c
1
. . . c
n+n
x
that con-
sists of the errors in the n + n
x
INFO and TEST-X
bits if the INFO bits had been encoded in the x ba-
sis, we apply Hoeffding’s theorem: namely, we take
a sample of size n without replacement from the pop-
ulation c
1
, . . . , c
n+n
x
(this corresponds to the random
selection of the INFO bits and the TEST-X bits, as de-
fined above, given that the TEST-Z bits have already
been chosen). Let X =
|
f
C
I
|
n
be the average of the sam-
ple (this is exactly the error rate on the INFO bits, as-
suming, again, the INFO bits had been encoded in the
x basis); and let µ =
|
f
C
I
|+|C
T
X
|
n+n
x
be the expectancy of
X (this is exactly the error rate on the INFO bits and
TEST-X bits together). Then
|C
T
X
|
n
x
≤ p
a,x
is equiva-
lent to (n + n
x
)µ −nX ≤ n
x
· p
a,x
, and, therefore, to
n ·(X −µ) ≥ n
x
·(µ − p
a,x
). This means that the con-
ditions
|
f
C
I
|
n
> p
a,x
+ ε
and
|C
T
X
|
n
x
≤ p
a,x
rewrite
to
X −µ > ε + p
a,x
−µ
∧
n
n
x
·(X −µ) ≥ µ − p
a,x
, (15)
which implies
1 +
n
n
x
(X −µ) > ε, which is equiv-
alent to X −µ >
n
x
n+n
x
ε. Using Hoeffding’s theorem
(from Appendix A of BGM09), we get:
P
"
|
f
C
I
|
n
> p
a,x
+ ε
!
∧
|C
T
X
|
n
x
≤ p
a,x
#
≤ P
X −µ >
n
x
n + n
x
ε
≤ e
−2
n
x
n+n
x
2
nε
2
(16)
In the above discussion, we have actually proved
the following Theorem:
Theorem 3. Let us be given δ > 0, R > 0, and, for in-
finitely many values of n, a family {v
n
1
, . . . , v
n
r
n
+m
n
} of
linearly independent vectors in F
n
2
such that δ <
d
r
n
,m
n
n
and
m
n
n
≤ R. Then for any p
a,z
, p
a,x
> 0 and ε
sec
> 0
such that p
a,x
+ε
sec
≤
δ
2
, and for any n, n
z
, n
x
> 0 and
two m
n
-bit final keys k, k
0
, Eve’s difference between
her states corresponding to k and k
0
satisfies the fol-
lowing bound:
h∆
(p
a,z
,p
a,x
)
Eve
(k, k
0
)i ≤ 2R ne
−
n
x
n+n
x
2
nε
2
sec
(17)
In Subsection 3.5 we explain why this Theorem
guarantees security.
We note that the quantity h∆
(p
a,z
,p
a,x
)
Eve
(k, k
0
)i
bounds the expected values of the Shannon Dis-
tinguishability and of the mutual information be-
tween Eve and the final key, as done in BGM09
Security Against Collective Attacks of a Modified BB84 QKD Protocol with Information only in One Basis
27
and BBBMR06, which is sufficient for proving non-
composable security; but it also avoids composabil-
ity problems: Eve is not required to measure immedi-
ately after the protocol ends, but she is allowed to wait
until she gets more information; and equation (17)
bounds the trace distance between any two of Eve’s
possible states.
3.4 Reliability
Security itself is not sufficient; we also need the key
to be reliable (namely, to be the same for Alice and
Bob). This means that we should make sure that
the number of errors on the INFO bits is less than
the maximal number of errors that can be corrected
by the error-correcting code. We demand that our
error-correcting code can correct n(p
a,z
+ ε
rel
) errors.
Therefore, reliability of the final key with exponen-
tially small probability of failure is guaranteed by the
following inequality: (as said, C
I
corresponds to the
actual bit string of errors on the INFO bits in the pro-
tocol, when they are encoded in the z basis)
P
|C
I
|
n
> p
a,z
+ ε
rel
∧
|C
T
Z
|
n
z
≤ p
a,z
≤ e
−2
n
z
n+n
z
2
nε
2
rel
This inequality is proved by an argument similar to
the one used in Subsection 3.3: the selection of the
INFO bits and TEST-Z bits is a random partition of
n + n
z
bits into two subsets of sizes n and n
z
, respec-
tively (assuming that the TEST-X bits have already
been chosen), and thus it corresponds to Hoeffding’s
sampling.
3.5 Security, Reliability, and Error
Rate Threshold
According to Theorem 3 and to the discussion in Sub-
section 3.4, to get both security and reliability we
only need vectors {v
n
1
, . . . , v
n
r
n
+m
n
} satisfying both the
conditions of the Theorem (distance
d
r
n
,m
n
2n
>
δ
2
≥
p
a,x
+ ε
sec
) and the reliability condition (the ability
to correct n(p
a,z
+ ε
rel
) errors). Such families were
proven to exist in Appendix E of BBBMR06, giving
the bit-rate:
R
secret
,
m
n
= 1 −H
2
(2p
a,x
+ 2ε
sec
)
− H
2
p
a,z
+ ε
rel
+
1
n
(18)
where H
2
(x) , −x log
2
(x) −(1 −x)log
2
(1 −x).
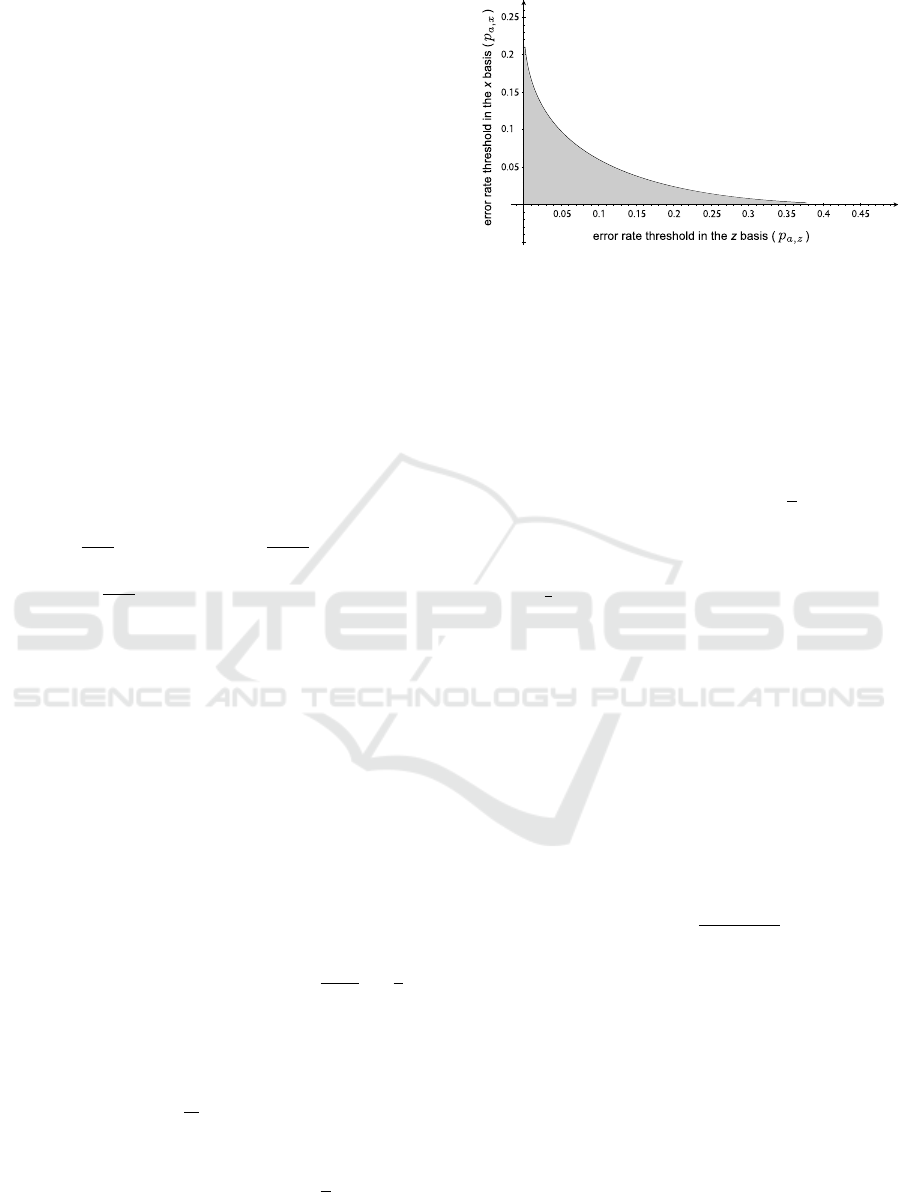
Figure 1: The secure asymptotic error rates zone (below
the curve).
Note that we use here the error thresholds p
a,x
for
security and p
a,z
for reliability. This is possible, be-
cause in BBBMR06 those conditions (security and re-
liability) on the codes are discussed separately.
To get the asymptotic error rate thresholds, we re-
quire R
secret
> 0, and we get the condition:
H
2
(2p
a,x
+ 2ε
sec
) + H
2
p
a,z
+ ε
rel
+
1
n
< 1 (19)
The secure asymptotic error rate thresholds zone
is shown in Figure 1 (it is below the curve), assum-
ing that
1
n
is negligible. Note the trade-off between
the error rates p
a,z
and p
a,x
. Also note that in the
case p
a,z
= p
a,x
, we get the same threshold as BB84
(BBBMR06 and BGM09), which is 7.56%.
4 CONCLUSION
In this paper, we have analyzed the security of the
BB84-INFO-z protocol against any collective attack.
We have discovered that the results of BB84 hold
very similarly for BB84-INFO-z, with only two ex-
ceptions:
1. The error rates must be separately checked to be
below the thresholds p
a,z
and p
a,x
for the TEST-Z
and TEST-X bits, respectively, while in BB84 the
error rate threshold p
a
applies to all the TEST bits
together.
2. The exponents of Eve’s information (security) and
of the failure probability of the error-correcting
code (reliability) are different than in BGM09, be-
cause different numbers of test bits are now al-
lowed (n
z
and n
x
are arbitrary). This implies that
the exponents may decrease more slowly (or more
quickly) as a function of n. However, if we choose
n
z
= n
x
= n (thus sending N = 3n qubits from Al-
ice to Bob), then we get exactly the same expo-
nents as in BGM09.
COMPLEXIS 2017 - 2nd International Conference on Complexity, Future Information Systems and Risk
28

The asymptotic error rate thresholds found in this
paper are more flexible than in BB84, because they
allow us to tolerate a higher threshold for a specific
basis (say, the x basis) if we demand a lower thresh-
old for the other basis (z). If we choose the same er-
ror rate threshold for both bases, then the asymptotic
bound is 7.56%, exactly the bound found for BB84 in
BBBMR06 and BGM09.
We conclude that even if we change the BB84 pro-
tocol to have INFO bits only in the z basis, this does
not harm its security and reliability (at least against
collective attacks). This does not even change the
asymptotic error rate threshold, and allows more flex-
ibility when choosing the thresholds for both bases.
The only drawbacks of this change are the need to
check the error rate for the two bases separately, and
the need to either send more qubits (3n qubits in total,
rather than 2n) or get a slower exponential decrease
of the exponents required for security and reliability.
We thus find that the feature of BB84, that both
bases are used for information, is not very impor-
tant for security and reliability, and that BB84-INFO-
z (that lacks this feature) is almost as useful as BB84.
This may have important implications on the security
and reliability of other protocols that also only use one
basis for information qubits, as done in some two-way
protocols.
We also present a better approach for the proof,
that uses a quantum distance between two states
rather than the classical information. In BGM09,
BBBGM02, and BBBMR06, the classical mutual in-
formation between Eve’s information (after an opti-
mal measurement) and the final key was calculated
(by using the trace distance between two quantum
states); although we should note that in BGM09 and
BBBMR06, the trace distance was used for the proof
of security of a single bit of the final key even when all
other bits are given to Eve, and only the last stages of
the proof discussed bounding the classical mutual in-
formation. In the current paper, on the other hand, we
use the trace distance between the two quantum states
until the end of the proof, which avoids composability
problems that existed in the previous works.
Therefore, this proof makes a step towards making
BGM09, BBBGM02, and BBBMR06 prove compos-
able security of BB84 (namely, security even if Eve
keeps her quantum states until she gets more infor-
mation when Alice and Bob use the key, rather than
measuring them in the end of the protocol). This ap-
proach also applies (similarly) to the BB84 security
proof in BGM09.
ACKNOWLEDGEMENTS
The work of TM and RL was partly supported by the
Israeli MOD Research and Technology Unit.
REFERENCES
Bennett, C. H. and Brassard, G. (1984). Quantum cryptog-
raphy: Public key distribution and coin tossing. In In-
ternational Conference on Computers, Systems & Sig-
nal Processing, IEEE, 1984, pages 175–179.
Biham, E., Boyer, M., Boykin, O. P., Mor, T., and Roy-
chowdhury, V. (2006). A proof of the security of quan-
tum key distribution. J. Cryptol., 19(4):381–439.
Biham, E., Boyer, M., Brassard, G., van de Graaf, J.,
and Mor, T. (2002). Security of quantum key dis-
tribution against all collective attacks. Algorithmica,
34(4):372–388.
Biham, E. and Mor, T. (1997a). Bounds on information
and the security of quantum cryptography. Phys. Rev.
Lett., 79:4034–4037.
Biham, E. and Mor, T. (1997b). Security of quantum cryp-
tography against collective attacks. Phys. Rev. Lett.,
78:2256–2259.
Boyer, M., Gelles, R., and Mor, T. (2009). Security of
the bennett-brassard quantum key distribution proto-
col against collective attacks. Algorithms, 2(2):790–
807.
Christandl, M., K
¨
onig, R., and Renner, R. (2009). Posts-
election technique for quantum channels with appli-
cations to quantum cryptography. Phys. Rev. Lett.,
102:020504.
Mayers, D. (2001). Unconditional security in quantum
cryptography. J. ACM, 48(3):351–406.
Nielsen, M. A. and Chuang, I. L. (2010). Quantum compu-
tation and quantum information. Cambridge univer-
sity press.
Renner, R. (2008). Security of quantum key distribution.
Int. J. Quantum Inf., 6(01):1–127.
Renner, R., Gisin, N., and Kraus, B. (2005). Information-
theoretic security proof for quantum-key-distribution
protocols. Phys. Rev. A, 72:012332.
Shor, P. W. and Preskill, J. (2000). Simple proof of security
of the bb84 quantum key distribution protocol. Phys.
Rev. Lett., 85:441–444.
Security Against Collective Attacks of a Modified BB84 QKD Protocol with Information only in One Basis
29
