Progressive Hedging and Sample Average Approximation for the

Two-stage Stochastic Traveling Salesman Problem

Pablo Adasme

, Janny Leung

and Ismael Soto

Departamento de Ingenier

ıa El

ectrica, Universidad de Santiago de Chile, Avenida Ecuador 3519, Santiago, Chile

Shaw College, The Chinese University of Hong Kong (Shenzhen), 2001 Longxiang Blvd., Longgang District, Shenzhen,

Keywords:

Two-stage Stochastic Programming, Traveling Salesman Problem, Progressive Hedging Algorithm, Sample

Average Approximation Method.

Abstract:

In this paper, we propose an adapted version of the progressive hedging algorithm (PHA) (Rockafellar and

Wets, 1991; Lokketangen and Woodruff, 1996; Watson and Woodruff, 2011) for the two-stage stochastic

traveling salesman problem (STSP) introduced in (Adasme et al., 2016). Thus, we compute feasible solutions

for small, medium and large size instances of the problem. Additionally, we compare the PHA method with the

sample average approximation (SAA) method for all the randomly generated instances and compute statistical

lower and upper bounds. For this purpose, we use the compact polynomial formulation extended from (Miller

et al., 1960) in (Adasme et al., 2016) as it is the one that allows us to solve large size instances of the problem in

short CPU time with CPLEX. Our preliminary numerical results show that the results obtained with the PHA

algorithm are tight when compared to the optimal solutions of small and medium size instances. Moreover, we

obtain signiﬁcantly better feasible solutions than CPLEX for large size instances with up to 100 nodes and 10

scenarios in signiﬁcantly low CPU time. Finally, the bounds obtained with SAA method provide an average

reference interval for the stochastic problem.

1 INTRODUCTION

Most mathematical programming models in the oper-

ations research domain are subject to uncertainties in

problem parameters. There are two well known ap-

proaches to deal with the uncertainties, the ﬁrst one

is known as robust optimization (RO) while the sec-

ond one is known as stochastic programming (SP)

approach (Bertsimas et al., 2011; Gaivoronski et al.,

2011; Shapiro et al., 2009). In this paper, we are

devoted to the latter approach. More precisely, we

deal with the two-stage stochastic traveling sales-

man problem (STSP) introduced in (Adasme et al.,

2016). We propose an adapted version of the pro-

gressive hedging algorithm (PHA) (Rockafellar and

Wets, 1991; Lokketangen and Woodruff, 1996; Wat-

son and Woodruff, 2011) and compute feasible so-

lutions for small, medium and large size instances

of the STSP. Additionally, we compare numerically

the PHA method with the sample average approxima-

tion (SAA) method (Ahmed and Shapiro, 2002) for

randomly generated instances and compute statistical

lower and upper bounds for the problem. For this pur-

pose, we use the compact polynomial formulation ex-

tended from (Miller et al., 1960) in (Adasme et al.,

2016) as it is the one that allows us to solve large size

instances of the problem within a limited CPU time

with CPLEX.

Two-stage SP problems similar as the one we con-

sider in this paper are, for instance the knapsack prob-

lem (Gaivoronski et al., 2011), the maximum weight

matching problem (Escofﬁer et al., 2010), maximal

and minimal spanning tree problems (Flaxman et al.,

2006; Escofﬁer et al., 2010), the stochastic maximum

weight forest problem (Adasme et al., 2013; Adasme

et al., 2015)), to name a few. For the sake of clarity,

the description of the STSP is as follows. We con-

sider the graph G = (V, E

∪ E

) to be a non directed

complete graph with a set of nodes V and a set of

weighted edges E

∪ E

where E

∩ E

0. The sets

and E

contain deterministic and uncertain edge

weights, respectively. We assume that the edges in

the uncertainty set E

can be represented by a set of

K = {1, 2, ··· , |K|} scenarios. The STSP consists of

ﬁnding |K| Hamiltonian cycles of G, one for each sce-

nario s ∈ K, using the same deterministic edges and

440

Adasme P., Leung J. and Soto I.

Progressive Hedging and Sample Average Approximation for the Two-stage Stochastic Traveling Salesman Problem.

DOI: 10.5220/0006241304400446

In Proceedings of the 6th International Conference on Operations Research and Enterprise Systems (ICORES 2017), pages 440-446

ISBN: 978-989-758-218-9

possibly different uncertain edges in each cycle, while

minimizing the sum of the deterministic edge weights

plus the expected edge weights over all scenarios.

Notice that for |K| = 1, the problem reduces to

the classical traveling salesman problem. Our pre-

liminary numerical results show that the results ob-

tained with the proposed PHA algorithm are tight

when compared to the optimal solutions of small and

medium size instances. Additionally, we obtain sig-

niﬁcantly better feasible solutions than CPLEX for

large size instances with up to 100 nodes and 10 sce-

narios in signiﬁcantly low CPU time. Finally, the

bounds obtained with SAA method provide an aver-

age reference interval for the stochastic problem.

Stochastic variants for the traveling salesman

problem have been proposed in (Maggioni et al.,

2014; Bertazzi and Maggioni, 2014) for instance. The

two-stage stochastic problem as presented in this pa-

per can be seen as a particular case of the stochastic

capacitated traveling salesmen location problem with

recourse (Bertazzi and Maggioni, 2014). As far as we

know, PHA and SAA approximation methods for this

new variant of the stochastic traveling salesman prob-

lem have not been studied so far in the literature.

The remaining of the paper is organized as fol-

lows. In Section 2, we present the polynomial two-

stage stochastic formulation of the problem. Then, in

Section 3, we present PHA and SAA methods. Sub-

sequently, in Section 4 we conduct preliminary nu-

merical results in order to compare all the algorithmic

procedures with the optimal solution or best solution

found with CPLEX. Finally, in Section 5 we give the

main conclusions of the paper.

2 TWO-STAGE STOCHASTIC

FORMULATION

In this section, for the sake of clarity we restate

the two-stage stochastic formulation adapted from

(Miller et al., 1960) in (Adasme et al., 2016) for the

traveling salesman problem. For this purpose, let A

and A

represent the sets of arcs obtained from E

and

, respectively where an edge (i, j) is replaced by

two arcs (i, j), ( j, i) of same cost in each correspond-

ing set. This formulation can be written as (Adasme

et al., 2016)

(ST SP

) :

min

{x,y,u}

(

∑

(i, j)∈A

i j

|K|

∑

s=1

∑

(i, j)∈A

i j

)

(1)

subject to:

∑

j:(i, j)∈A

i j

∑

j:(i, j)∈A

i j

= 1, ∀i ∈ V, s ∈ K (2)

∑

i:(i, j)∈A

i j

∑

i:(i, j)∈A

i j

= 1, ∀ j ∈ V, s ∈ K (3)

= 1, ∀s ∈ K (4)

2 ≤ u

≤ |V |, ∀i ∈ |V |, (i 6= 1), ∀s ∈ K (5)

− u

+ 1 ≤

(|V | − 1)(1 − x

i j:(i, j)∈A

− y

i j:(i, j)∈A

∀i, j ∈ V, (i, j 6= 1), s ∈ K (6)

i j

∈ {0, 1}, ∀(i, j) ∈ A

, (7)

i j

∈ {0, 1}, ∀(i, j) ∈ A

, s ∈ K (8)

∈ R

, ∀i ∈ V, s ∈ K (9)

In (STSP

), the parameter p

, ∀s ∈ K in the objective

function (1), represents the probability for scenario

s ∈ K where

∑

s∈K

= 1. Thus, in (1) we minimize

the sum of the deterministic edge weights plus the

expected cost of the uncertain edge weights obtained

over all scenarios. Constraints (2)-(3) force the sales-

man to arrive at and depart from each node exactly

once for each scenario s ∈ K. Next, the constraints (6)

ensure that, if the salesman travels from i to j, then the

nodes i and j are sequentially ordered for each s ∈ K.

These constraints together with (4) and (5) ensure that

each node is in a unique position. Finally, (7)-(9) are

the domain of the decision variables.

In particular, if the variable x

i j

= 1, it means that

the deterministic arc (i, j) ∈ A

is selected in each

Hamiltonian cycle, ∀s ∈ K, otherwise x

i j

= 0. Sim-

ilarly, if the variable y

i j

= 1, the arc (i, j) ∈ A

is se-

lected in the Hamiltonian cycle associated with sce-

nario s ∈ K, and y

i j

= 0 otherwise.

3 PROGRESSIVE HEDGING AND

SAMPLE AVERAGE

APPROXIMATION

In this section, we propose an adapted version of

the progressive hedging algorithm (Rockafellar and

Wets, 1991; Lokketangen and Woodruff, 1996; Wat-

son and Woodruff, 2011) in order to compute feasi-

ble solutions for (ST SP

). Additionally, we present

the sample average approximation method that we

use to compute statistical lower and upper bounds for

the more general case where the two-stage stochastic

Progressive Hedging and Sample Average Approximation for the Two-stage Stochastic Traveling Salesman Problem

441

objective function is treated as a generic expectation

function.

3.1 Progressive Hedging Algorithm

In order to present a PHA procedure, we write for

each scenario s ∈ K, the following subproblem ob-

tained from (ST SP

)

(ST SP

) :

min

{x,y,u}

(

∑

(i, j)∈A

i j

∑

(i, j)∈A

i j

)

subject to:

∑

j:(i, j)∈A

i j

∑

j:(i, j)∈A

i j

= 1,

∀i ∈ V (10)

∑

i:(i, j)∈A

i j

∑

i:(i, j)∈A

i j

= 1,

∀ j ∈ V (11)

= 1 (12)

2 ≤ u

≤ |V |, ∀i ∈ |V |, (i 6= 1) (13)

− u

+ 1 ≤

(|V | − 1)(1 − x

i j:(i, j)∈A

− y

i j:(i, j)∈A

∀i, j ∈ V, (i, j 6= 1) (14)

i j

∈ {0, 1}, ∀(i, j) ∈ A

, (15)

i j

∈ {0, 1}, ∀(i, j) ∈ A

(16)

∈ R

, ∀i ∈ V (17)

Notice that the index “s” is removed from the sec-

ond stage variables in (STSP

). Thus, (ST SP

) has

signiﬁcantly less number of variables than (ST SP

More precisely, the total number of ﬁrst and second

stage variables is of the order of O(|A

|+|A

|) whilst

the total number of variables in (ST SP

) is of the

order of O(|A

| + |A

||K|). Obviously, solving for

each scenario s ∈ K the subproblem (ST SP

) is sig-

niﬁcantly less complex than solving (ST SP

) directly

with CPLEX. In this sense, PHA uses a by-scenario

decomposition approximation scheme in order to ﬁnd

feasible solutions for the complete problem (Watson

and Woodruff, 2011).

The PHA algorithm we adapt for (ST SP

) is de-

picted in Algorithm 3.1 and it can be explained as fol-

lows. First, in step 0 we solve for each s ∈ K, the

subproblem (ST SP

) with CPLEX and save the ﬁrst

stage solution in x

for the iteration t = 0. Next, we

compute the average of the obtained ﬁrst stage solu-

tion sets and save this value in ¯x

. Finally, for each

s ∈ K we compute the values w

where the param-

eter ρ > 0 represents a penalty factor (Watson and

Woodruff, 2011). Subsequently, in step 1 we enter

into a while loop with the stopping condition of

Algorithm 3.1: PHA procedure to compute feasible

solutions for ST SP

Data: A problem instance of (STSP

Result: A feasible solution (x, y) for (ST SP

) with

objective function value z.

Step 0:

t = 0 ;

foreach s ∈ K do

:= argmin

{x,y}



(ST SP

)



¯x

∑

s∈K

;

foreach s ∈ K do

:= ρ(x

− ¯x

)

t = t + 1;

Step 1:

while (t < t

max

and x

6= x

, ∀s, j ∈ K( j 6= s)) do

foreach s ∈ K do

argmin

{x,y}

∑

(i, j)∈A

i j

+ w

t−1

s,i j

i j

− ¯x

t−1

i j

∑

(i, j)∈A

i j

;

s.t. (10)-(17)

¯x

∑

s∈K

;

foreach s ∈ K do

:= w

t−1

+ ρ(x

− ¯x

)

t = t + 1;

Step 2:

if (t = t

max

) then

foreach i ∈ K do

foreach s ∈ K do

:= argmin

{y}



(ST SP

))



Compute a feasible solution of (ST SP

)

with x

and y

, ∀s ∈ K

Save the best solution found as (x

, y

, z

);

else

foreach s ∈ K do

:= argmin

{y}



(ST SP

))



Compute a feasible solution of (ST SP

) with x

and y

, ∀s ∈ K;

Save the feasible solution as (x

, y

, z

)

return (x

, y

, z

);

a maximum number of iteration t

max

while simulta-

neously checking whether the ﬁrst stage solution set

has converged to a unique solution set. The steps in-

side the while loop are exactly the same as those in

step 0, with the difference that now we solve for each

s ∈ K, the subproblem (ST SP

) with the objective

function

∑

(i, j)∈A

i j

+ w

t−1

s,i j

i j

− ¯x

t−1

i j

∑

(i, j)∈A

i j

where the parameters w

t−1

and ρ

penalize the difference in the ﬁrst stage solution sets

within each iteration. Notice that this objective func-

tion uses absolute terms instead of Euclidean terms

as it is performed in (Watson and Woodruff, 2011).

ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems

442

This allows us to formulate the equivalent mixed inte-

ger linear program straightforwardly. Finally, in step

2 we check whether the condition of t = t

max

is satis-

ﬁed, if so it means we have not found convergence

for the ﬁrst stage variables. In this case, we com-

pute a feasible solution for each set of ﬁrst stage vari-

ables and save the best solution. If t < t

max

, it means

we have found a unique set of ﬁrst stage variables

x = x

, ∀s ∈ K. In this case, we simply obtain a fea-

sible solution for (ST SP

) using this set of variables

and save it as best solution found with the algorithm.

3.2 Sample Average Approximation

Method

In this subsection, we brieﬂy sketch the SAA method

used to compute statistical lower and upper bounds

for (ST SP

). It is well known that this method con-

verges to an optimal solution of a continuous two-

stage stochastic linear optimization problem provided

that the sample size is sufﬁciently large (Ahmed and

Shapiro, 2002). For this purpose, we generate several

random samples for the second stage objective func-

tion costs.

We compare the SAA method with the numerical

results obtained with Algorithm 3.1. We remark that

the SAA method allows to obtain only an average ref-

erence interval for the stochastic problem. In other

words, with SAA method we do not solve exactly the

same instances as in the PHA algorithm, since we in-

tend to approximate the expectation function of the

second stage objective function rather than solving for

a particular set of scenarios. The SAA method is de-

picted in Algorithm 3.2.

In step zero of SAA method, we generate

randomly |M| independent samples m ∈ M =

{1, . . . , |M|} with scenario sets N

where |N

| = N.

Subsequently, we generate randomly a reference sam-

ple set N

with sufﬁciently large number of scenarios

where |N

| >> N. Then, in step 1, we solve the re-

ferred two-stage stochastic optimization problem for

each sample m ∈ M where the set K is substituted

by N

. Next in step 2, we compute the average of

the optimal objective function values obtained in step

1. The average is saved as a statistical lower bound

for (ST SP

) (Ahmed and Shapiro, 2002). Similarly,

we solve the referred optimization problem using the

ﬁxed ﬁrst stage solution x

obtained in step 1 for each

m ∈ M , where the set K is substituted by N

. The

latter allows to select the solution x

with the mini-

mum optimal objective function value as the solution

of SAA method. Finally, we generate randomly a ﬁrst

stage solution set x = x

for one sample scenario on

the second stage variables and compute the optimal

Algorithm 3.2: SAA procedure for (ST SP

) with ex-

pectation second stage objective function.

Data: A problem instance of (ST SP

) with

expectation.

Result: Statistical lower and upper bounds for

(ST SP

) with expectation.

Step 0:

Generate randomly |M| independent samples

m ∈ M = {1, . . . , |M|} with scenario sets N

where

| = N ;

Select a reference sample N

to be sufﬁciently large

where |N

| >> N;

Step 1:

foreach m ∈ M do

Solve the two-stage stochastic problem

min

{x,y,u}

(

∑

(i, j)∈A

i j

−1

∑

s=1

∑

(i, j)∈A

i j

)

subject to:(2) − (9)

where the set K is replaced by N

. Save the

sample optimal objective function value v

and

the sample optimal solution x

Step 2:

Compute the average ¯v

|M|

= |M|

−1

∑

|M|

m=1

with the

values obtained in the previous step. Save the average

as a statistical lower bound for (STSP

);

foreach m ∈ M do

Solve the following problem using the ﬁrst stage

solution x

obtained in step 1

min

,y,u}

(

∑

(i, j)∈A

i j

(i j)+

−1

∑

s=1

∑

(i, j)∈A

i j

)

subject to:(2) − (9) for ﬁxed x = x

where the set K is replaced by N

;

Select the solution x

with the minimum optimal

objective function value as the solution of SAA

method.

Generate randomly a ﬁrst stage solution set x = x

with one sample scenario and compute

min

,y,u}

(

∑

(i, j)∈A

i j

(i j)+

−1

∑

s=1

∑

(i, j)∈A

i j

)

subject to:(2) − (9) for ﬁxed x = x

where the set K is substituted by N

;

Save the optimal objective function value as a

statistical upper bound for (ST SP

);

Progressive Hedging and Sample Average Approximation for the Two-stage Stochastic Traveling Salesman Problem

443

objective function value of the referred optimization

problem as a statistical upper bound for (ST SP

). It is

important to note that we compute the SAA solution

as well as the lower and upper bounds for (ST SP

) as-

suming that (ST SP

) has an expectation second stage

objective function.

4 PRELIMINARY NUMERICAL

RESULTS

In this section, we present preliminary numerical re-

sults. A Matlab (R2012a) program is developed using

CPLEX 12.6 to solve (STSP

) and its LP relaxation.

The PHA and SAA methods are also implemented in

Matlab. The numerical experiments have been carried

out on an Intel(R) 64 bits core (TM) with 3.4 Ghz and

8 G of RAM. CPLEX solver is used with default op-

tions.

We generate the input data as follows. The edges

in E

and E

are chosen randomly with 50% of prob-

ability. The values of p

, ∀s ∈ K are generated ran-

domly from the interval [0, 1] such that

∑

s∈K

= 1.

Costs are randomly drawn from the interval [0, 50] for

both the deterministic and uncertain edges. In par-

ticular, the cost matrices c = (c

i j

), ∀(i j) ∈ A

and

= (δ

i j

), ∀(i j) ∈ A

, s ∈ K are generated as input

symmetric matrices.

In Algorithm 3.1, we set the parameter t

max

{7, 12} and save the best run, i.e., the run which al-

lows us to ﬁnd the best feasible solution. The pa-

rameter ρ is calibrated on a ﬁxed value of ρ = 10.

In Algorithm 3.2, we generate randomly |M| = 10

independent samples, each with |N

| = 5 scenarios

for the instances 1-10, whilst for the instances 11-

12, we generate |M| = 10 independent samples each

with |N

| = 2 scenarios since the CPU times become

highly and rapidly prohibitive in this case. Finally,

we generate a reference scenario set with |N

| = 50

scenarios.

In Tables 1 and 2, the instances are the same for

the ﬁrst stage costs. In Table 1, the legend is as fol-

lows. In column 1, we show the instance number. In

columns 2-3, we show the instance dimensions. In

columns 4-5 we present the number of deterministic

and uncertain edges for each instance, respectively.

In columns 6-10, we present the optimal solution of

(ST SP

) or the best solution found with CPLEX in

two hours of CPU time, CPLEX number of branch

and bound nodes, CPU time in seconds, the optimal

solution of the linear relaxation of (STSP

) and its

CPU time in seconds, respectively. In columns 11-

13, we present the best solution found with Algorithm

3.1, its CPU time in seconds and the number of itera-

tions required to ﬁnd the feasible solution. Finally, in

columns 14-15, we present the gaps that we compute

Opt−LP

Opt

∗ 100 and

B.S.−Opt

Opt

∗ 100, respectively.

In Table 1, we solve small, medium and large size

instances ranging from |V | = 10, |K| = 5 to |V | = 100

nodes and |K| = 10 scenarios. From Table 1, ﬁrst

we observe that the number of deterministic and un-

certain edges are balanced. Next, we observe that

(ST SP

) allows to solve to optimality only the in-

stances 1-11 with up to |V | = 30 nodes and |K| = 5

scenarios. For the remaining instances, we cannot

solve to optimality the problem. However, we obtain

feasible solutions for most of them, with the exception

of instance # 15. For this instance, we cannot ﬁnd a

feasible solution with CPLEX in two hours of CPU

time. For the instance # 11, the problem is solved in

3910.61 seconds whilst the instances 1-10 are solved

to optimality in less than 300 seconds. The linear re-

laxation for the instances 1-10 is solved in less than

1 second, while the LP instances 11-20 can be solved

to optimality with CPU times ranging from 1 to 42

seconds. Next, we observe that the gaps for the LP

instances go from 10.55 to 54.14. This clearly shows

that the LP relaxation is not tight and explain the in-

crease in the number of branch and bound nodes. On

the opposite, we observe that the gaps for Algorithm

3.1 are very tight ranging from -66.89% to 11.21%.

Negative gaps mean that the feasible solutions ob-

tained with Algorithm 3.1 are signiﬁcantly better than

those obtained with CPLEX in two hours of CPU

time. Notice that the CPU times required by Algo-

rithm 3.1 are considerably lower than two hours. This

shows the effectiveness of Algorithm 3.1. In particu-

lar, when ﬁnding feasible solutions for large size in-

stances of the problem. Notice that most of the gap

values obtained by Algorithm 3.1 for the instances

which are solved to optimality (e.g., instances 1-10)

are lower than 9% with the exception of instance # 11.

In this case, the gap is 11.21%. Finally, we observe

that the number of iterations required by Algorithm

3.1 is either six or eleven.

In Table 2, the legend is as follows. Columns

1-5 show exactly the same information as in Ta-

ble 1. In columns 6-9, we present statistical lower

bounds, the SAA solution, statistical upper bounds

and CPU time in seconds found by Algorithm 3.2.

Finally, in Columns 10-12 we present gaps that we

compute by



Stat.Lb−Opt

Opt



∗ 100,



SAALb−Opt

Opt



∗ 100 and



Stat.U b−Opt

Opt



∗ 100, respectively where Opt corre-

sponds to the optimal solution or best solution found

in Table 1.

In Table 2, we only solve small and medium size

instances ranging from |V | = 10, |K| = 5 to |V | = 40

ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems

444

Table 1: Numerical results for (ST SP

) using 50% of deterministic edges.

Inst. Dim. # of edges (ST SP

) PHA Algorithm Gaps

|V | |K| |E

| |E

| Opt B&Bn Time (s) LP Time (s) B.S. Time (s) #Iter Gap

Gap

1 10 5 23 22 125.22 115 0.50 112.02 0.32 126.09 22.53 6 10.55 0.69

2 12 5 42 24 101.95 0 0.43 90.95 0.35 103.28 22.05 6 10.78 1.31

3 14 5 41 50 111.90 1655 3.61 81.18 0.35 112.27 23.60 6 27.46 0.33

4 17 5 61 75 131.46 2009 5.61 111.10 0.33 141.41 23.78 6 15.49 7.57

5 20 5 88 102 148.38 15776 108.27 126.52 0.39 150.61 25.57 6 14.73 1.51

6 10 10 30 15 107.78 7 0.64 84.90 0.34 107.78 63.23 6 21.23 0

7 12 10 26 40 147.72 619 1.78 131.11 0.34 149.05 65.17 6 11.25 0.89

8 14 10 43 48 139.45 275 2.07 122.12 0.39 146.99 86.86 11 12.42 5.41

9 17 10 62 74 133.52 37730 238.27 113.30 0.35 138.81 92.22 11 15.14 3.96

10 20 10 93 97 153.02 21294 229.79 133.57 0.46 166.67 73.30 6 12.71 8.92

11 30 5 199 236 115.63 222400 3910.61 82.80 1.37 128.60 45.02 11 28.40 11.21

12 40 5 401 379 147.27 272361 7200 109.89 1.59 147.10 68.49 11 25.38 -0.12

13 60 5 889 881 194.47 60032 7200 114.96 1.82 174.30 164.17 11 40.88 -10.37

14 80 5 1552 1608 243.86 20885 7200 130.76 3.80 186.13 358.81 6 46.38 -23.67

15 100 5 2516 2434 - 6540 7200 122.02 4.31 177.16 739.57 6 - -

16 30 10 221 214 148.56 220674 7200 108.33 2.90 155.46 86.57 6 27.08 4.64

17 40 10 368 412 171.46 83242 7200 117.81 1.91 167.69 118.83 6 31.29 -2.20

18 60 10 844 926 244.26 15384 7200 123.38 4.83 169.16 233.10 6 49.49 -30.74

19 80 10 1549 1611 564.93 7703 7200 135.26 15.86 187.07 673.42 6 76.06 -66.89

20 100 10 2545 2405 275.51 1922 7200 126.35 41.51 186.08 3832.77 6 54.14 -32.46

−

: No solution found with CPLEX in 2 hours.

nodes and |K| = 5 scenarios. We do not solve larger

size instances of the problem as in Table 1, since the

CPU times become rapidly prohibitive in this case.

From Table 2, we mainly observe that the SAA

solution values obtained with Algorithm 3.2 are be-

tween the statistical lower and upper bounds for all

the instances. We compute an average distance for the

lower and upper bounds of 38.74 %, whilst we com-

pute an average distance between the SAA solution

and lower bounds of 27.72 %. Similarly, we compute

an average distance between the upper bounds and

SAA solutions of 11.01 %. We also see that most of

the objective function values obtained in Table 1 are

near the lower and upper bounds obtained with SAA

Algorithm 3.2. Finally, by computing the averages of

columns 10-12 in Table 2, we obtain a minimum of

14.32 units for the column # 11. This suggests that

the SAA solution values are tighter when compared

with the objective function values found in Table 1.

5 CONCLUSIONS

In this paper, we proposed an adapted version of

the progressive hedging algorithm (PHA) (Rockafel-

lar and Wets, 1991; Lokketangen and Woodruff,

1996; Watson and Woodruff, 2011) for the two-stage

stochastic traveling salesman problem (STSP) intro-

duced in (Adasme et al., 2016). Thus, we computed

feasible solutions for small, medium and large size in-

stances of the problem. Additionally, we compared

the PHA method with the sample average approxi-

mation (SAA) method for all the randomly generated

instances and calculated statistical lower and upper

bounds for the problem. For this purpose, we used

the compact polynomial formulation extended from

(Miller et al., 1960) in (Adasme et al., 2016) as it is

the one that allows us to solve large size instances of

the problem within short CPU time with CPLEX. Our

preliminary numerical results showed that the results

obtained with the PHA algorithm are tight when com-

pared to the optimal solutions of small and medium

size instances. Moreover, we obtained signiﬁcantly

better feasible solutions than CPLEX for large size

instances with up to 100 nodes and 10 scenarios in

considerably low CPU time. Finally, the bounds ob-

tained with SAA method provide an average reference

interval for the stochastic problem.

ACKNOWLEDGEMENTS

The ﬁrst and third author acknowledge the ﬁnancial

support of the USACH/DICYT Projects 061413SG,

061513VC DAS and CORFO 14IDL2-29919.

Progressive Hedging and Sample Average Approximation for the Two-stage Stochastic Traveling Salesman Problem

445

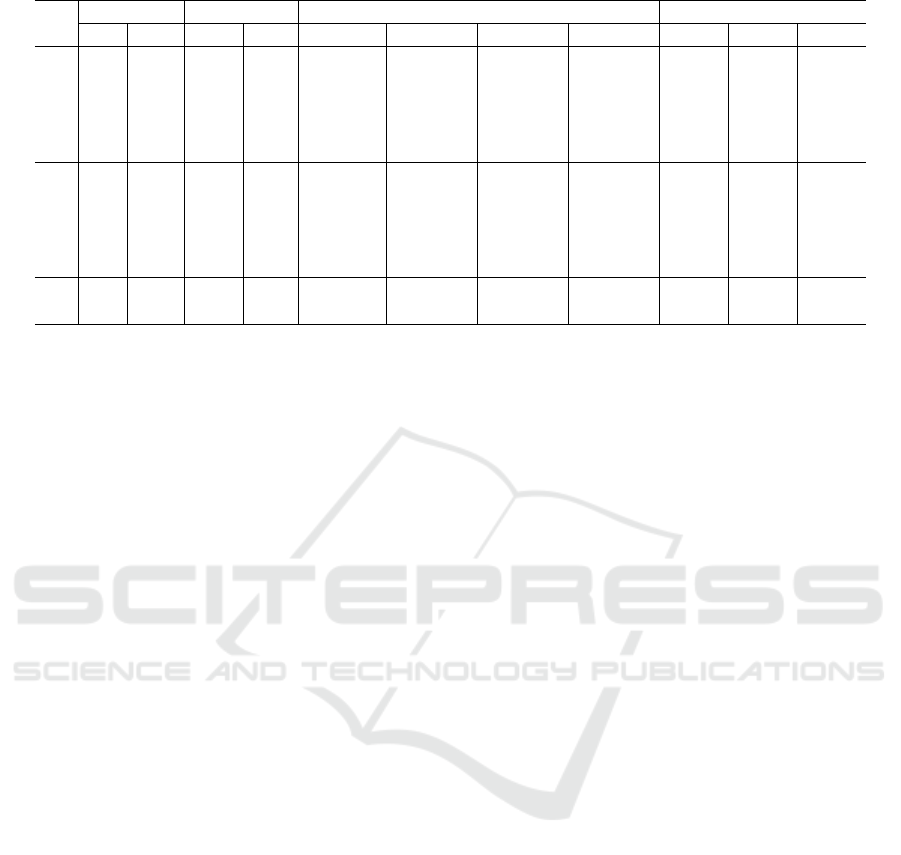
Table 2: Upper and Lower Bounds for the Instances in Table 1 using SAA Algorithm.

Inst. Dim. # of edges SAA Algorithm Gap

|V | |K| |E

| |E

| Stat. Lb SAA Lb Stat. Ub Time (s) Gap

Gap

1 10 5 23 22 108.88 120.29 143.63 8.85 13.05 3.94 14.70

2 12 5 42 24 114.96 141.19 146.70 9.19 12.77 38.49 43.89

3 14 5 41 50 127.02 131.58 144.24 5.39 24.60 29.07 41.49

4 17 5 61 75 127.89 147.79 162.50 43.85 2.72 12.42 23.61

5 20 5 88 102 135.73 156.73 164.87 60.07 8.52 5.63 11.12

6 10 10 30 15 106.84 117.88 136.77 17.27 0.87 9.37 26.89

7 12 10 26 40 133.05 145.32 146.74 28.52 9.93 1.63 0.67

8 14 10 43 48 104.04 133.21 142.80 24.94 25.39 4.47 2.40

9 17 10 62 74 113.52 146.37 153.21 47.30 14.98 9.63 14.75

10 20 10 93 97 118.20 164.43 174.54 100.27 22.76 7.46 14.07

11 30 5 199 236 93.01 145.12 152.34 186.61 19.57 25.50 31.74

12 40 5 401 379 117.18 183.12 196.86 1748.68 20.43 24.34 33.67

REFERENCES

Adasme, P., Andrade, R., Letournel, M., and Lisser, A.

(2013). A polynomial formulation for the stochastic

maximum weight forest problem. ENDM, 41:29–36.

Adasme, P., Andrade, R., Letournel, M., and Lisser, A.

(2015). Stochastic maximum weight forest problem.

Networks, 65(4):289–305.

Adasme, P., Andrade, R., Leung, J., and Lisser, A. (2016).

A two-stage stochastic programming approach for the

traveling salesman problem. ICORES-2016.

Ahmed, S. and Shapiro, A. (2002). The sample average

approximation method for stochastic programs with

integer recourse. Georgia Institute of Technology.

Bertazzi, L. and Maggioni, F. (2014). Solution approaches

for the stochastic capacitated traveling salesmen lo-

cation problem with recourse. J Optim Theory Appl,

166(1):321–342.

Bertsimas, D., Brown, D., and Caramanis, C. (2011). The-

ory and applications of robust optimization. SIAM Re-

views, 53:464–501.

Escofﬁer, B., Gourves, L., Monnot, J., and Spanjaard, O.

(2010). Two-stage stochastic matching and spanning

tree problems: Polynomial instances and approxima-

tion. Eur J Oper Res, 205:19–30.

Flaxman, A. D., Frieze, A., and Krivelevich, M. (2006). On

the random 2-stage minimum spanning tree. Random

Struct Algor, 28:24–36.

Gaivoronski, A., Lisser, A., Lopez, R., and Xu, H. (2011).

Knapsack problem with probability constraints. J

Global Optim, 49:397–413.

Lokketangen, A. and Woodruff, D. L. (1996). Progressive

hedging and tabu search applied to mixed integer (0-

1) multi stage stochastic programming. Journal of

Heuristics, 2(2):111–128.

Maggioni, F., Perboli, G., and Tadei, R. (2014). The multi-

path traveling salesman problem with stochastic travel

costs: a city logistics computational study. Trans-

portation Research Procedia, 1(3):528–536.

Miller, C. E., Tucker, A. W., and Zemlin, R. A. (1960). In-

teger programming formulations and travelling sales-

man problems. J. Assoc. Comput. Mach., 7:326–329.

Rockafellar, R. T. and Wets, R. J. B. (1991). Scenarios and

policy aggregation in optimization under uncertainty.

Mathematics and Operations Research, 16:119–147.

Shapiro, A., Dentcheva, D., and Ruszczynski, A. (2009).

Lectures on stochastic programming: Modeling and

theory. MOS-SIAM Series on Optimization, Philadel-

phia.

Watson, J. P. and Woodruff, D. L. (2011). Progressive hedg-

ing innovations for a class of stochastic mixed-integer

resource allocation problems. Computational Man-

agement Science, 8:355–370.

ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems

446