Post Lasso Stability Selection for High Dimensional Linear Models
Niharika Gauraha
1
, Tatyana Pavlenko
2
and Swapan K. Parui
3
1
Systems Science and Informatics Unit, Indian Statistical Institute, Bangalore, India
2
Mathematical Statistics, KTH Royal Institute of Technology, Stockholm, Sweden
3
Computer Vision and Pattern Recognition Unit, Indian Statistical Institute, Kolkata, India
Keywords:
Lasso, Weighted Lasso, Variable Selection, Stability Selection, High Dimensional Data.
Abstract:
Lasso and sub-sampling based techniques (e.g. Stability Selection) are nowadays most commonly used meth-
ods for detecting the set of active predictors in high-dimensional linear models. The consistency of the Lasso-
based variable selection requires the strong irrepresentable condition on the design matrix to be fulfilled, and
repeated sampling procedures with large feature set make the Stability Selection slow in terms of computation
time. Alternatively, two-stage procedures (e.g. thresholding or adaptive Lasso) are used to achieve consistent
variable selection under weaker conditions (sparse eigenvalue). Such two-step procedures involve choosing
several tuning parameters that seems easy in principle, but difficult in practice. To address these problems
efficiently, we propose a new two-step procedure, called Post Lasso Stability Selection (PLSS). At the first
step, the Lasso screening is applied with a small regularization parameter to generate a candidate subset of
active features. At the second step, Stability Selection using weighted Lasso is applied to recover the most
stable features from the candidate subset. We show that under mild (generalized irrepresentable) condition,
this approach yields a consistent variable selection method that is computationally fast even for a very large
number of variables. Promising performance properties of the proposed PLSS technique are also demonstrated
numerically using both simulated and real data examples.
1 INTRODUCTION
Due to the presence of high dimensional data in most
areas of modern applications (examples include ge-
nomics and proteomics, financial data analysis, as-
tronomy) variable selection methods gain consider-
able interest in statistical modeling and inference. In
this paper, we consider variable selection problems
in sparse linear regression models. We start with the
standard linear regression model
Y = Xβ +ε, (1)
where Y
n×1
is a univariate response vector, X
n×p
is
the design matrix, β
p×1
is the true underlying coeffi-
cient vector and ε
n×1
is an error vector. In particular,
we consider sparse and high dimensional linear mod-
els, where the number of variables (p) is much larger
than the number of observations (n), that is p  n.
Sparsity assumption implies that only a few of the
predictors contribute to the response. We denote the
true active set or the support of β, by S = supp(β).
The goal is to estimate the true active set S from data
(Y,X).
The Lasso (Tibshirani, 1996) has been a popular
choice for simultaneous estimation and variable selec-
tion in sparse high dimensional problems. The Lasso
penalizes least square regression by sum of the ab-
solute value of the regression coefficients, the Lasso
estimator is defined as
ˆ
β
lasso
= arg min
β∈R
p

1
2n
kY −Xβk
2
2
+ λkβk
1

, (2)
where λ ≥ 0 is the regularization parameter that con-
trols the amount of regularization and the `
1
-penalty
encourages the sparse solution. It has been proven
that, under strong conditions (i.e., Irrepresentable
Condition) on the design matrix X, the Lasso cor-
rectly recovers the true active set S with high probabil-
ity, for further details we refer to (Zhao and Yu, 2006),
(Meinshausen and B
¨
uhlmann, 2006) and (B
¨
uhlmann
and van de Geer, 2011). Sampling based procedures
(i.e., Stability Selection and bootstrap Lasso) can be
used as an alternative approach for variable selection,
see (Meinshausen and B
¨
uhlmann, 2010) and (Bach,
2008). Though, the Stability Selection identifies the
most stable features, but repeated sampling proce-
dures make the algorithm very slow specially with the
638
Gauraha, N., Pavlenko, T. and Parui, S.
Post Lasso Stability Selection for High Dimensional Linear Models.
DOI: 10.5220/0006244306380646
In Proceedings of the 6th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2017), pages 638-646
ISBN: 978-989-758-222-6
Copyright
c
 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

large number of predictors. In practice, it is difficult
to satisfy the Irrepresentability Condition, hence the
Lasso does not provide any guarantees on the num-
ber of false discoveries. However, the Stability Selec-
tion has not been widely accepted due to its computa-
tional complexity. When the irrepresentable condition
(IC) is violated, two-stage procedures (e.g. thresh-
olding or adaptive Lasso) are used to achieve consis-
tent variable selection. Such two-step procedures in-
volve choosing several tuning parameters that further
complicates the problem. We propose to combine the
strength of the (adaptively weighted) Lasso and the
Stability Selection for efficient and stable feature se-
lection. In the first step, we apply the Lasso with
small regularization parameter that selects a subset
consisting of small number of features. In the second
step, stability feature selection using weighted Lasso
is applied to the restricted Lasso active set to select
the most stable features. For the weighted `
1
penal-
ization, the weights are computed from the Lasso es-
timator at the first stage such that large effects covari-
ates in the Lasso fit will be given smaller weights and
small effects covariates will be given larger weights.
We call the combination of the two, the Post-Lasso
Stability Selection (PLSS).
Several authors have previously considered two
stage Lasso-type procedures that have better poten-
tial and properties for variable selection than single
stage Lasso, such as adaptive Lasso (Zhao and Yu,
2006), thresholded Lasso (Zou, 2006), relaxed Lasso
(Meinshausen, 2007) and Gauss-Lasso (Javanmard
and Montanari, 2013) to name a few. The Post-Lasso
Stability Selection, is a special case of the two stage
variable selection procedure: (1) Pre-selection stage:
selection of predictors using the Lasso with small tun-
ing parameter; and (2) Selection stage: selection of
the most stable features from preselected predictors
using Stability Selection with weighted Lasso. We
prove that under assumption of Generalized Irrepre-
sentability Condition (GIC) (Javanmard and Monta-
nari, 2013), the initial Lasso active set with small tun-
ing parameter contains the true active set S with high
probability. Then stability feature selection where
base selection procedure is the weighted Lasso, cor-
rectly identifies the stable predictors when applied on
the restricted Lasso active set. The contribution of this
paper is summarized as follows.
1. We briefly review two stage procedures for stable
feature selection and estimation.
2. We propose a new combined approach, namely
the Post Lasso Stability Selection (PLSS): The
Lasso selecting initial active set and the Stabil-
ity Selection using weighted Lasso selecting sta-
ble features from the initial active set.
3. We also utilize the estimation result obtained by
the initial stage Lasso for computing weights of
the selected predictors considered for the next
stage.
4. We prove that under assumption of GIC, the PLSS
correctly identifies the true active set with high
probability.
5. We empirically show that PLSS outperforms the
standard Lasso and the adaptive Lasso in terms of
false positives.
6. We evaluate computational complexity of PLSS,
and show that it is superior than the standard sta-
bility feature selection using the Lasso.
The rest of this paper is organized as follows. In Sec-
tion 2, we provide background, notations, assump-
tions and a brief review of the relevant work. In sec-
tion 3, we define and illustrate the Post Lasso Stability
Selection. In section 4, we carry out simulation stud-
ies and we shall provide conclusion in section 5.
2 BACKGROUND AND
NOTATIONS
In this section, we state notations, assumptions and
definitions that will be used in later sections. We also
provide a brief review of relevant work and our con-
tribution.
2.1 Notations and Assumptions
We consider the sparse high dimensional linear re-
gression set up as in (1), where p  n. We assume
that the components of the noise vector ε are i.i.d.
N(0,σ
2
). The true active set or support of β is denoted
as S and defined as S = {j ∈ {1,..., p} : β
j
6= 0}. We
assume sparsity in β such that s  n, where s = |S | is
the sparsity index. The `
1
-norm and `
2
-norm (square)
are defined as kβk
1
=
∑
p
j=1
|β
j
| and kβk
2
2
=
∑
p
j=1
β
2
j
respectively. For a matrix X ∈ R
n×p
, we use super-
scripts for the columns of X, i.e., X
j
denotes the j
th
column, and subscripts for the rows, i.e., X
i
denotes
the i
th
row. For any S ⊆{1,..., p}, we denote X
S
as the
restriction of X to columns in S, and β
S
is the vector β
restricted to the support S, with 0 outside the support
S. Without loss of generality we can assume that the
first s = |S| variables are the active variables, and we
partition the empirical covariance matrix, C =
1
n
X
T
X,
for the active and the redundant variables as follows.
C =

C
11
C
12
C
21
C
22

(3)
Post Lasso Stability Selection for High Dimensional Linear Models
639

Similarly, the true β is partitioned as

β
1
β
2

.
The weighted Lasso estimator is defined as
β
W L
= arg min
β∈R
p
(
1
2n
kY −Xβk
2
2
+ λ
p
∑
j=1
w
j
|β
j
|
)
,
(4)
where w ∈ R
p
is a known weights vector. We de-
note Λ as the set of considered regularization param-
eters defined as Λ = {λ : λ ∈ (0,λ
max
)}, where λ
max
corresponds to the minimal value of λ for which the
null model is selected. The following two conditions
are assumed throughout the paper. (i)Beta-min con-
dition, the non-zero entries of the true β must satisfy
the condition β
min
≥
cσ
√
n
, for some c > 0. (ii) Condi-
tion on the minimum number of observations, that is
n ≥ s log(p).
2.2 The Lasso Variable Selection
The Least Absolute Shrinkage and Selection Opera-
tor (Lasso), is a penalized least squares method that
imposes an `
1
-penalty on the regression coefficients.
The Lasso does both shrinkage and automatic vari-
able selection simultaneously due to nature of the `
1
-
penalty. The Lasso estimated parameter vector de-
noted as
ˆ
β is defined in (2), and the Lasso estimated
active set denoted by
ˆ
S
lasso
can be given as
ˆ
S
lasso
= {j ∈ {1, ..., p} :
ˆ
β
j
6= 0}. (5)
It is known that Irrepresentable condition is necessary
and sufficient condition for the Lasso to select true
model (see (Zhao and Yu, 2006)), the Irrepresentable
condition is defined as follows.
Definition 1 (Irrepresentable Condition(IC)). The Ir-
representable Condition is said to be met for the set S
with a constant η > 0, if the following holds:
kC
12
C
−1
11
sign(β
1
)k
∞
≤ 1 −η. (6)
In practice, IC on the design matrix X, is quite
difficult to meet. When IC fails to hold, the Lasso
selected active set tends to have many false positive
variables. A substantially weaker assumption than ir-
representability, called Generalized Irrepresentability
Condition was introduced in (Javanmard and Mon-
tanari, 2013). They proved that, such a relaxation
from irrepresentability condition to generalized irrep-
resentability condition allows to cover a significantly
broader set of design matrices. In simple words, under
generalized irrepresentability condition a little noise
is allowed to get selected or the generalized irrepre-
sentability condition can be viewed as irrepresentabil-
ity condition satisfying for some superset of active set
T ⊇ S. In (Javanmard and Montanari, 2013), authors
also derived a suitable choice of λ
0
, such that for the
range (0,λ
0
) the Lasso selects the superset T ⊇S with
high probability.
λ
0
= cσ
r
2log(p)
n
, for some constant c > 1. (7)
2.3 Stability Variable Selection
In this section, we briefly study the stability fea-
ture selection method, which is mainly based on the
concept that a feature is called stable if the proba-
bility of its getting selected is insensitive to varia-
tions in the training set. The Stability Selection, in-
troduced by (Meinshausen and B
¨
uhlmann, 2010), is
an effective method for performing variable selec-
tion in the high-dimensional setting while controlling
the false positive rates. It is a combination of sub-
sampling and high-dimensional feature selection al-
gorithms (i.e., the Lasso). The Stability Selection can
be expressed as a framework for the baseline feature
selection method, to identify a set of stable predictors
that are selected with high probability. The baseline
feature selection method is repeatedly applied to ran-
dom data sub-samples of half-size, and then the pre-
dictors which have selection frequency larger than a
fixed threshold value (usually in the range (0.6, 0.9) )
are selected as stable features.
Though the Lasso does not satisfy the oracle
property and model selection consistency in high-
dimensional data, but it has been proven that the
Lasso selects the true active variables with high prob-
ability for more details we refer to (Meinshausen and
B
¨
uhlmann, 2010). Hence, the Lasso method is com-
monly used as a base feature selection method for Sta-
bility Selection, we call it Stability Lasso. The active
set of variables selected by Stability Lasso is given by
ˆ
S
stab
= {j ∈ {1, ..., p} :
ˆ
Π
j
≥ π
thr
}, (8)
where 0 < π
thr
< 1 is a cut off probability. The vari-
ables with a high selection probability are selected as
stable features. Here the parameter to be tuned is the
exact cut off π
thr
, the influence of π
thr
is very small
usually in the range (0.6,0.9)). Tuning regularization
parameter for the standard Lasso variable selection
can be more challenging than for prediction, since the
prediction optimal (i.e., cross-validated choice) often
includes false positive selections. whereas, the sta-
ble active set does not depend much on the choice
of the Lasso regularization λ, see (Meinshausen and
B
¨
uhlmann, 2010) for more detailed discussion.
ICPRAM 2017 - 6th International Conference on Pattern Recognition Applications and Methods
640

2.4 Review of Relevant work
In this section, we provide a brief review of relevant
work in order to show that how our proposal differs
from other two stage penalized least square methods
for variable selection.
The Lasso variable selection could be inconsis-
tent when IC fails to hold, to overcome this prob-
lem various two stage procedures have been intro-
duced. The adaptive Lasso proposed in (Zou, 2006),
uses adaptive weights for penalizing different coeffi-
cients in the `
1
-penalty as in weighted Lasso (4). The
weights are chosen by an initial model fit, such that
large effects covariates in the initial fit will be given
smaller weights and small effects covariates will be
given larger weights. Mostly, the Lasso is applied
at the initial stage for high dimensional case, to de-
rive the weights for the weighted Lasso at the second
stage, together they are called the Adaptive Lasso.
The adaptive Lasso estimator is defined as follows.
ˆ
β
ada
= arg min
β∈R
p
(
1
2n
kY −Xβk
2
2
+ λ ∗λ
ada
∑
j
|β
j
|
|(
ˆ
β
lasso
)
j
|
)
,
where
ˆ
β
lasso
is computed using the standard Lasso
method (2) as initial fit with initial regularization pa-
rameter λ > 0, and λ
ada
≥ 0 is the regularization pa-
rameter for the second stage. Then the adaptive Lasso
active set can be computed as
ˆ
S
ada
= {j ∈ {1, ..., p} : (
ˆ
β
ada
)
j
6= 0}.
The thresholded Lasso was introduced in (Zhou,
2009), which further reduces the Lasso active set by
eliminating the features having estimated coefficients
below some pre-defined threshold value. More pre-
cisely, in the first stage the initial estimator is obtained
using the Lasso with suitable regularization parameter
λ, and then predictors were selected if their estimated
coefficients are large enough (larger than the thresh-
old value, say
ˆ
β
thr
).
ˆ
S
thr
= {j ∈ {1, ..., p} : |(
ˆ
β
lasso
)
j
| ≥
ˆ
β
thr
},
where
ˆ
β
thr
> 0, is the second tuning parameter for the
thresholded Lasso.
The relaxed Lasso (Meinshausen, 2007) is another
two step procedure, similar to adaptive or thresholded
Lasso. The relaxed Lasso consists of two Lasso steps,
in the first stage the Lasso variable selection is per-
formed for a suitable grid of regularization parame-
ters, say (0,λ
max
) then at the second stage every sub-
model
ˆ
S
λ
is considered and the Lasso with smaller
regularization parameter is used on those sub models.
The relaxed Lasso estimator is given as follows.
β
ˆ
S
(λ,φ) := argmin
β
ˆ
S

1
2n
kY −X
ˆ
S
β
ˆ
S
k
2
2
+ φ ∗λkβ
ˆ
S
k
1

,
where
ˆ
S(λ) is the estimated sub-model from the first
stage.
The above two-stage procedures are proven to be
variable selection consistent under some form of re-
stricted and sparse eigenvalue conditions, see (van de
Geer et al., 2011). But the tuning of regularization pa-
rameters are the main issue in practice. They require
the two dimensional cross-validation (Hastie et al.,
2001) to find the optimal pair of regularization pa-
rameter used at two different stages.
Next, we discuss about the Gauss-Lasso selector
(see (Javanmard and Montanari, 2013)), which is also
a two-stage method that first applies the Lasso, and
then in the second stage it performs ordinary least
squares restricted to the Lasso active set
ˆ
S
lasso
.
ˆ
β
GL
= arg min
β

1
2n
kY −X
ˆ
S
lasso
β
ˆ
S
lasso
k
2
2

Given the sparsity index or number of non-zero co-
efficients s
0
, the Gauss-Lasso selector then finds the
s
th
0
largest entry (in absolute) of
ˆ
β
GL
, denoted by
ˆ
β
s
0
.
Then finally GL active set is given by
ˆ
S
GL
= {j ∈ {1, ..., p} : |(
ˆ
β
GL
)
j
| ≥
ˆ
β
s
0
}
Though, the Gauss-Lasso model selects the correct
model with high probability under GIC which is
weaker than the IC. But, it demands the true sparsity
index s
0
= |S| for selecting s
0
relevant features, but in
practice, the size of active set is not known.
Finally, we mention about the bootstrap Lasso
(Bolasso) which is more close to the Stability Se-
lection. In Bolasso, the Lasso is applied for several
bootstrapped replications of a given sample, then final
active set is given by intersection of the supports of
the Lasso bootstrap estimates. Bolasso is a consistent
variable selection method, that does not assume any
condition on the design matrix X. The Bolasso is not
a preferable choice since it is computationally expen-
sive, as repeatedly applying Lasso on bootstrap sam-
ples specially with large number of predictors makes
it slow.
We propose the Post Lasso Stability Selection as a
computationally fast alternative, which does not need
to be tuned across the two-dimensional grid of tuning
parameters. It is a simple and consistent method for
variable selection even when the irrepresentable con-
dition is violated. We define and discuss PLSS in the
next section.
3 POST LASSO STABILITY
SELECTION
In this section, we introduce a new combined two
stage approach, called Post Lasso Stability Selection.
Post Lasso Stability Selection for High Dimensional Linear Models
641

The first stage involves selecting a super set of the true
active set, using the Lasso with a small regularization
parameter λ
0
(7). Then in the second stage, Stability
Selection using the weighted Lasso is applied on the
Lasso restricted set obtained at the first stage. We also
compute weights from the Lasso estimator from the
first stage to assign different weights to different co-
efficients. On the one hand, the Lasso at the first stage
makes sure the true active set gets selected (along with
some noise) under assumption of the generalized ir-
representability condition on the design matrix X. On
the other hand, the Stability Selection using weighted
Lasso at second stage makes sure that the most stable
predictors finally get selected and the noise features
are eliminated from the final model. aa
Algorithm 1: PLSS Algorithm.
Input: dataset (Y,X,π
thr
)
Output:
ˆ
S:= set of selected variables
Steps: 1. Perform Lasso with
λ
0
=
p
2log(p)/n. Denote the Lasso estimator
as
ˆ
β
lasso
and the Lasso active set as
ˆ
S
lasso
2. Compute weights as w
j
= |(
ˆ
β
lasso
)
j
|.
3. Compute the weighted reduced design
matrix, X
red
= {w
j
∗X
j
: j ∈
ˆ
S
lasso
}.
4. Perform stability feature selection based on
data (Y, X
red
) and obtain the estimated
probabilities π
j
for all j ∈
ˆ
S
lasso
.
Determine the selected active set as
ˆ
S = {j ∈
ˆ
S
lasso
:
ˆ
π
j
≥ π
thr
}
return
ˆ
S
3.1 Consistency of PLSS
We assume that the GIC holds on the design matrix X
for some T ⊆{1,..., p}, and T contains the true active
set S, i.e. T ⊇ S. Without loss of generality we can
assume that the GIC corresponds to the first t = |T |
predictors. In the first stage, then the Lasso active
set contains the true active set with high probability
under GIC assumption. In the second stage, for Sta-
bility Selection with adaptively weighted Lasso, the
bounds on maximal and minimal eigenvalues are re-
quired. As GIC holds for the set T ⊇ S, therefore the
covariance matrix C(T ) is invertible and uncorrelated
with the noise features that implies the minimum and
maximum eigenvalue of sub-matrices of C of size t ×t
are bounded away from 0 and ∞ respectively. Hence,
under GIC assumption the PLSS method is variable
selection consistent.
3.2 Computation Complexity for PLSS
In this section, we discuss the computational com-
plexity of the PLSS. The computation steps are given
in Algorithm (1). Since, the PLSS performs the Lasso
and Stability Selection in two different stages, there-
fore we use the results from those studies. The LARS
(Efron et al., 2004) algorithm is used to compute the
Lasso, the computational cost of LARS is of order
O(np
2
). Computation cost of Stability Selection us-
ing Lasso as a base feature (with 100 sub samples),
is approximately O(25np
2
), where the constant 25 is
due to running 100 simulations on the on sub samples
of size
n
2
, we refer to (Meinshausen and B
¨
uhlmann,
2010) for more details on the derivation of the result.
So, the computational cost of the PLSS for its differ-
ent stages can be given as:
stage one: O(np
2
)
stage two: O(25ns
2
1
), where we assume s
1
is the
size of the Lasso active set and in practice s
1
 p.
Hence, the computation cost of the PLSS is of order
O(np
2
+ 25ns
2
1
).
3.3 Illustration of PLSS
To illustrate the PLSS, we consider a small simulation
example with the following setup.
Data simulation setup
• p = 1000, n = 200 and σ = 1.
• The design matrix X is sampled from a
multivariate normal N
p
(0,Σ), where Σ is
the identity matrix except the left most
5 ×5 sub matrix, which is defined as fol-
lows.





1 0 0 0 ρ
0 1 0 0 ρ
0 0 1 0 ρ
0 0 0 1 ρ
ρ ρ ρ ρ 1





• The active set is defined as S = {1, 2,3, 4},
and for each j ∈ S we set β
j
= 1.
In the above setting, the fifth variable is equally
correlated with all four active predictors. Using the
above setup, we run the following simulation steps to
perform variable selection using Lasso, stability se-
lection and PLSS.
ICPRAM 2017 - 6th International Conference on Pattern Recognition Applications and Methods
642

Simulation steps
1. Construct the design matrix X with ρ =
0.25.
2. Generate an error vector as ε
n×1
∼
N
n
(0,I) and then compute the response
using Eq. (1).
3. Compute the Lasso estimator using the
simulated data set (Y, X) (choose λ using
cross validation) and obtain the Lasso ac-
tive set.
4. Perform Stability Selection on the data set
(Y,X) and obtain the stability path.
5. Perform PLSS (defined later) on the data
set (Y,X), Then compute the stability ac-
tive set and obtain the stability path.
In the following, the results for the above simula-
tion are presented. We remark that, for ρ ≥ 0.25 the
IC is violated by the design matrix X. As a result, the
Lasso always selects the fifth predictor with the first
four relevant predictors and with some other noise
feature as reported by the Lasso active set
ˆ
S
lasso
is
{1,2,3,4,5,239, 265, 326, 374, 469,531,747,794,865,942}.
When applying the Stability Selection using weighted
Lasso, the first four important predictors are selected
with their estimated probabilities close to 1, while
the irrelevant variables are selected with much lower
probability, see Figure (2) for probabilities of features
getting selected.
We also compare the stability paths of the standard
Stability Selection (using Lasso) with the PLSS for
the above example. For each predictor j = {1, ..., p},
the stability path is given by the selection probabilities
{
ˆ
Π
j
(λ) : j = {1, ..., p}, λ ∈ (0,λ
max
)}. From Figures
(1) and (2) (the four important predictors are plot-
ted as red lines, while the paths of noise features are
shown as black lines) , we see that the stability path
of the PLSS is much cleaner or it can be interpreted
as, a lot of computational effort is saved in PLSS as
most of the noise features are getting filtered at the
first stage itself.
Figure 1: Stability Path of the Stability Lasso.
Figure 2: Stability Path of the PLSS.
4 NUMERICAL RESULTS
In this section, we consider simulation settings and
pseudo-real data examples to compare the perfor-
mances of Lasso, Adaptive Lasso, Stability Selection
and PLSS in terms of variable selection. In particular,
we consider the true positive rate and the false dis-
covery rates as a measure of performances, which are
defined as follows.
T PR = |
ˆ
S
\
S|/|S|, and FDR = |
ˆ
S
\
S
c
|/|
ˆ
S| (9)
The Statistical analysis is performed in R3.2.5. We
used, the packages “glmnet” for penalized regression
methods (Lasso, Adaptive Lasso) and the package
“c060” to perform stability feature selection using
Lasso. All mentioned packages are available from
the Comprehensive R Archive Network (CRAN) at
http://cran.r-project.org/.
4.1 Example 1: Simulation
In order to compare the computational cost of the Sta-
bility Selection and the PLSS, we simulated a dataset
with the following details.
Simulation setup for Example 1
• Fix n = 500, and p =
10000, 20000, 30000, 40000, 50000, 100000.
• Set σ = 1, and the design matrix X is sam-
pled from a multivariate normal N
p
(0,I).
• The active set is defined as S = {1, ...,20},
and for each j ∈ S we set β
j
= 1.
The time complexity for both Stability Selection
using the Lasso (using 100 sub samples) and PLSS
on a super computer, are reported in the Table (1).
Post Lasso Stability Selection for High Dimensional Linear Models
643

Table 1: Measure of time complexity (in seconds).
p Stability Selection PLSS
10000 29.070 1.989
20000 53.613 4.654
30000 59.259 5.527
40000 99.986 6.273
50000 202.103 8.762
100000 459.341 28.418
4.2 Example 2: Simulation
We use the following simulation setup for generating
data (Y,X).
Simulation setup for Example 2
• Set p = 1000, σ = 3, and
n = 100, 200, 400.
• Generate the design matrix X from
N
p
(0,Σ), here we consider two different
settings for Σ = {Σ
1
, Σ
2
}, where Σ
1
= I
p
and
Σ
2
(i, j) =

(0.5)
|i−j|
if i 6= j
1 if i = j
,
• The active set is defined as S = {1, ...,20},
and for each j ∈ S we set β
j
= 1.
The performance measures for simulations with
Σ
1
and Σ
2
are reported in Table (2).
Table 2: performance measures for example 2.
n Method Σ
1
Σ
2
TPR FDR TPR FDR
100 Lasso 0.75 0.55 .55 0.71
Ada Lasso 0.75 0.51 .55 0.67
Stab Lasso 0.05 0 0 0
PLSS 0.5 0 .4 0.27
200 Lasso 1 0.65 1 0.66
Ada Lasso 1 0.58 1 0.50
Stab Lasso 0.6 0 0.65 0
PLSS 1 0 1 0
400 Lasso 1 0.54 1 0.53
Ada Lasso 1 0.35 1 0.25
Stab Lasso 1 0 1 0
PLSS 1 0 1 0
4.3 Example 3: Riboflavin Data
We consider Riboflavin data (see (B
¨
uhlmann et al.,
2014)) for the design matrix X with synthetic param-
eters β and simulated Gaussian errors ε ∼ N
n
(0,I).
To fulfil the minimum sample size condition (n ≥
slog(p)) we reduce the dimension to p = 1000, and
the pseudo data generation steps are given as follows.
Data generation for Riboflavin example
• For the design matrix X, select first 1000
covariates which are most associated with
the response.
• Fix s = 10 and for the true active set,
sample ten numbers randomly from the
set {1, ...,50}, and for each j ∈ S we set
β
j
= 1.
• Compute the response using the Equation
(1).
The performance measures are reported in Table
(3), and Figures (3) and (4).
Figure 3: Stability Path of the Stability Lasso for Ri-
boflavin.
Figure 4: Stability Path of the PLSS for Riboflavin.
Table 3: Performance measures for Riboflavin example.
Method TPR FDR
Lasso 0.9 0.57
Ada Lasso 0.9 0.21
Stab Lasso 0.4 0
PLSS 0.9 0
4.4 Example 4: Myeloma Data
Here, we consider the first 1000 highest variance
genes of the real dataset Myeloma (see (Tian et al.,
2003)) for the design matrix X with synthetic param-
eters β and simulated Gaussian errors. The pseudo
data generation steps are similar as the previous ex-
ample (Riboflavine). The performance measures are
reported in Table (4), and Figures (5) and (6).
ICPRAM 2017 - 6th International Conference on Pattern Recognition Applications and Methods
644

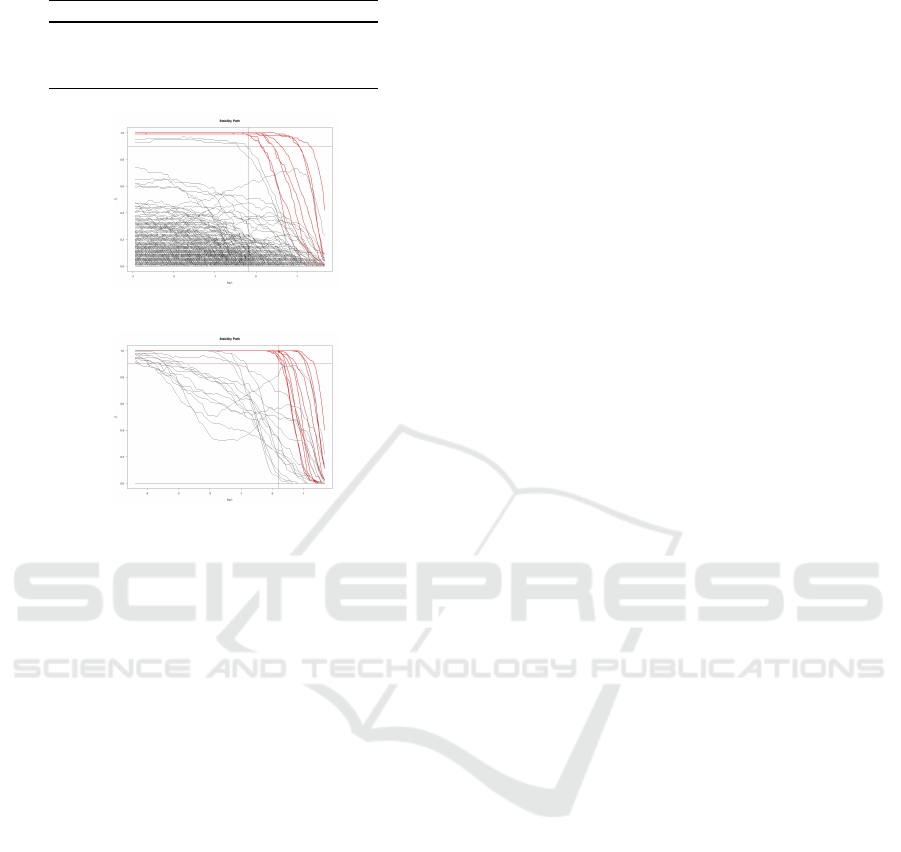
Table 4: Performance measures for Myeloma example.
Method TPR FDR
Lasso 1 0.63
Ada Lasso 1 0.16
Stab Lasso 0.8 0
PLSS 1 0
Figure 5: Stability Path of the Stability Lasso for Myeloma.
Figure 6: Stability Path of the PLSS for Myeloma.
4.5 Empirical Results
It is evident from the results of the simulation and
pseudo real examples that the PLSS method outper-
forms others, the number of false positives selected by
the Lasso and the adaptive Lasso is much larger than
the PLSS (except when the requirement of the mini-
mum number of observations is not met, for n = 100
case in Example 2). The PLSS performs better than
Stability Selection, the Stability Selection misses the
true predictors when the sample size is small, for
n = 200 in Table (2), and for real data case see Tables
(3) and (4), and Figures (3) and (4). From Example 1,
it is apparent that the PLSS outperforms the Stability
Selection in terms of computation complexity.
5 CONCLUSIONS
In this article, we have proposed a two stage vari-
able selection procedure, Post-Lasso Stability Selec-
tion with controlled false positives. At the first stage,
the Lasso is performed with a small regularization pa-
rameter to obtain initial estimator, where small value
of regularization parameter and Generalized Irrepre-
sentable Condition on the design matrix X, ensures
that the Lasso active set contains the true active set
S. At the second stage, Stability Selection using
weighted Lasso is performed on the restricted set,
where the weights are computed from the initial Lasso
estimator. We have shown that the PLSS combines the
strength of the Lasso and the Stability Selection. We
illustrated the method using simulated and real data
examples and our empirical results have shown that
the PLSS compares favorably with other two stage
variable selection techniques. We have also proved
that under GIC assumption on the design matrix, the
PLSS has substantially less false positives than the
Lasso and potentially faster than the Stability Selec-
tion.
ACKNOWLEDGEMENTS
The authors acknowledge the PDC Center for High
Performance Computing at the KTH Royal Institute
of Technology for providing computational resources.
REFERENCES
Bach, F. R. (2008). Bolasso: model consistent lasso esti-
mation through the bootstrap. Proceedings of the 25th
international conference on Machine learning, ACM,
pages 33–40.
B
¨
uhlmann, P., Kalisch, M., and Meier, L. (2014). High-
dimensional statistics with a view towards applica-
tions in biology. Annual Review of Statistics and its
Applications, 1:255–278.
B
¨
uhlmann, P. and van de Geer, S. (2011). Statistics for
High-Dimensional Data: Methods, Theory and Appli-
cations. Springer Verlag.
Efron, B., Hastie, T., Johnstone, I., and Tibshirani, R.
(2004). Least angle regression. Ann. Statist.,
32(2):407–499.
Hastie, T., Tibshirani, R., and Friedman, J. (2001). The Ele-
ments of Statistical Learning; Data Mining, Inference
and Prediction. New York: Springer.
Javanmard, A. and Montanari, A. (2013). Model selec-
tion for high-dimensional regression under the gener-
alized irrepresentability condition. In Proceedings of
the 26th International Conference on Neural Informa-
tion Processing Systems, pages 3012–3020.
Meinshausen, N. (2007). Relaxed lasso. Computational
Statistics and Data Analysis, 52(1):374–393.
Meinshausen, N. and B
¨
uhlmann, P. (2006). High-
dimensional graphs and variable selection with the
lasso. Annals of Statistics, 34:1436–1462.
Meinshausen, N. and B
¨
uhlmann, P. (2010). Stability selec-
tion (with discussion). J. R. Statist. Soc, 72:417–473.
Tian, E., Zhan, F., Walker, R., Rasmussen, E., Ma, Y., Bar-
logie, B., and Shaughnessy, J. J. (2003). The role of
the wnt-signaling antagonist dkk1 in the development
of osteolytic lesions in multiple myeloma. N Engl J
Med., 349(26):2483–2494.
Post Lasso Stability Selection for High Dimensional Linear Models
645

Tibshirani, R. (1996). Regression shrinkage and selection
via the lasso. J. R. Statist. Soc, 58:267–288.
van de Geer, S., Bhlmann, P., and Zhou, S. (2011). The
adaptive and the thresholded lasso for potentially mis-
specified models (and a lower bound for the lasso).
Electron. J. Statist., 5:688–749.
Zhao, P. and Yu, B. (2006). On model selection consis-
tency of lasso. Journal of Machine Learning Re-
search, 7:2541–2563.
Zhou, S. (2009). Thresholded lasso for high dimensional
variable selection and statistical estimation. NIPS,
pages 2304–2312.
Zou, H. (2006). The adaptive lasso and its oracle proper-
ties. Journal of the American Statistical Association,
101(476):1418–1429.
ICPRAM 2017 - 6th International Conference on Pattern Recognition Applications and Methods
646