Mathematical Backdoors in Symmetric Encryption Systems

Proposal for a Backdoored AES-like Block Cipher

Arnaud Bannier and Éric Filiol

Operational Cryptology and Virology Lab, ESIEA, 38 rue des Drs Calmette et Guérin, 53000 Laval, France

Keywords:

Cryptography, Encryption Algorithms, Backdoor, Trapdoor, Cryptanalysis, Block Cipher, AES.

Abstract:

Recent years have shown that more than ever governments and intelligence agencies try to control and bypass

the cryptographic means used for the protection of data. Backdooring encryption algorithms is considered

as the best way to enforce cryptographic control. Until now, only implementation backdoors (at the proto-

col/implementation/management level) are generally considered. In this paper we propose to address the most

critical issue of backdoors: mathematical backdoors or by-design backdoors, which are put directly at the

mathematical design of the encryption algorithm. While the algorithm may be totally public, proving that

there is a backdoor, identifying it and exploiting it, may be an intractable problem. We intend to explain that it

is probably possible to design and put such backdoors. Considering a particular family (among all the possible

ones), we present BEA-1, a block cipher algorithm which is similar to the AES and which contains a math-

ematical backdoor enabling an operational and effective cryptanalysis. The BEA-1 algorithm (80-bit block

size, 120-bit key, 11 rounds) is designed to resist to linear and differential cryptanalyses. A challenge will be

proposed to the cryptography community soon. Its aim is to assess whether our backdoor is easily detectable

and exploitable or not.

1 INTRODUCTION

Despite the fact that in the late 90s/early 2000s, cit-

izens have partially obtained the freedom for using

cryptography, the recent years have shown that more

than ever, governments and intelligence agencies still

try to control and bypass the cryptographic means

used for the protection of data and of private life.

Snowden’s leaks were a ﬁrst upheaval. A tremendous

number of secret projects (from NSA, GCHQ) have

been revealed to the public opinion which proves this

situation.

While the need for the security of everyday life ac-

tivities (for companies, for citizens) requires more and

more cryptography, recent bothering initiatives by po-

litical decision-makers ask for an even stronger con-

trol over cryptography not to say preparing the simple

prohibition or ban of cryptographic application such

as telegram. At the same time, the EU as well as a

number of security agencies (such as French ANSSI,

German BSI) conﬁrmed that it was nonsense and mil-

itate for the mandatory use of end-to-end encryption.

The recurring approaches and attempts consist in

making the implementation of backdoors mandatory.

The simplest and naive approach consists in enforc-

ing key escrowing at the operators’ level. But point-

to-point encryption solutions (which are not equal to

end-to-end encryption) like Telegram or Proton mail

enable to prevent it. A number of different backdoor

techniques are regularly mentioned or proposed.

The most critical aspect in implementation back-

doors lies on the fact that hackers or analysts may ﬁnd

them more or less easily and worse may exploit them.

This is the reason why it is likely that IT operators or

developers are very reluctant to accept backdoors un-

til now. In case of leak, they will inevitably lose users’

conﬁdence and favor the development of trusted ser-

vices abroad. In fact, the backdoor issue arises due

to the fact that only implementation backdoors (at the

protocol/implementation/management level) are gen-

erally considered.

In this paper we address the most critical issue of

backdoors: mathematical or by-design backdoors. In

other words, the backdoor is put directly at the mathe-

matical design of the encryption algorithm. While the

algorithm may be totally public, proving that there is

a backdoor, identifying it and exploiting it, may be an

intractable problem, unless you know the backdoor.

To some extent, the RSA’s Dual_EC_DRBG standard

case falls within this category (Shumow and Fergu-

622

Bannier, A. and Filiol, E.

Mathematical Backdoors in Symmetric Encryption Systems - Proposal for a Backdoored AES-like Block Cipher.

DOI: 10.5220/0006244406220631

In Proceedings of the 3rd International Conference on Information Systems Security and Privacy (ICISSP 2017), pages 622-631

ISBN: 978-989-758-209-7

 2017 by SCITEPRESS – Science and Technology Publications, Lda. All r ights reserved

son, 2007). Other non-public examples are known

within the military cryptanalysis community, and par-

tially revealed to the public thanks to the 1995 Hans

Buehler case (Strehle, 1994). This kind of backdoor

is the most difﬁcult one to address and there is quite

no public work on that topic. It is generally the tech-

nical realm of a few among the most eminent intel-

ligence agencies (namely NSA, GCHQ, SVR/GRU)

which moreover have the ability and power to step in

and to inﬂuence the international standardization pro-

cesses.

We intend to explain that it is probably possible to

design and put such backdoors. Considering a partic-

ular case of mathematical backdoors (among all the

possible ones) based on our previous work (Bannier

et al., 2016), we present a block cipher algorithm

which is similar to the AES and which contains a

mathematical backdoor enabling an operational and

effective cryptanalysis (in other words in a limited

time on a modern desktop computer and with a lim-

ited number of plaintext/ciphertext pairs). This block

cipher algorithm (80-bit block, 120-bit key size, 11

rounds) is designed to resist to linear and differential

cryptanalyses.

This paper is organized as follows. In Section 2

we explore the concept of backdoors and trapdoors

and we identify two main categories, each contain-

ing itself subcategories depending on the nature of

the cipher (stream or block ciphers). This observa-

tion is backed by the personal experience of the sec-

ond author as a military cryptanalyst. We also present

the state-of-the-art, history and previous work regard-

ing backdoors, mostly in symmetric cryptography. In

Section 3, we present our backdoored block cipher

algorithm BEA-1 (standing for Backdoored Encryp-

tion Algorithm 1), based on our work (Bannier et al.,

2016). This is a particular family of trapdoors us-

ing a suitable partition of the plaintext and ciphertext

spaces. In Section 4, we discuss the cryptographic se-

curity of this cipher, with respect to linear and differ-

ential cryptanalyses. We also propose a cryptographic

challenge to the cryptography community

, regarding

the backdoor identiﬁcation and exploitation. We sup-

pose that this backdoor is likely to be detected. Such

a challenge should enable to prove or disprove this

claim. Lastly we conclude in Section 5 and explore

future work.

This challenge will be launched on the Arxiv repository

right after the conference, at the end of February.

2 THE CONCEPT OF BACKDOOR

2.1 Deﬁnition and Classiﬁcation

Proposal

Trapdoors are a two-face, key concept in modern

cryptography. It is primarily related to the concept

of “trapdoor function” — a function that is easy to

compute in one direction, yet difﬁcult to compute

in the opposite direction without special information,

called the “trapdoor”. This ﬁrst “face” relates most

of the time to asymmetric cryptography algorithms.

It is a necessary condition to get reversibility between

the sender/receiver (encryption) or the signer/veriﬁer

(digital signature). The trapdoor mechanism is always

fully public and detailed. The security and the core

principle is based on the existence of a secret infor-

mation (the private key) which is essentially part of

the trapdoor. In other words, the private key can be

seen as the trapdoor.

The second “face” of the concept of trapdoor

relates to the more subtle and perverse concept of

“mathematical backdoor” and is a key issue in sym-

metric cryptography (even if the issue of backdoors

may be extended to asymmetric cryptography; see for

example the case of the DUAL EC_DRBG (Shumow and

Ferguson, 2007), or the case of trapdoored primes ad-

dresses recently in (Fried et al., 2016)).

In this case, the aim is to insert hidden mathemati-

cal weaknesses which enable one who knows them to

break the cipher. If possible, these weaknesses should

be independent of the secret key. Somehow, it consists

to create a hidden asymmetry to the detriment of the

legitimate users of the communication and to the ben-

eﬁt of the eavesdropper. In this context, the existence

of a backdoor is a strongly undesirable property.

In the rest of the present section, we will oppose

the term of trapdoor (desirable property) to that of

backdoor (undesirable property). While the term of

trapdoor has been already used in the very few liter-

ature covering this second face of this problem, we

suggest however to use the term of backdoor to de-

scribe the issue of hidden mathematical weaknesses.

This would avoid ambiguity and maybe would favor

the research work around a topic which is nowadays

mostly addressed by governmental entities in the con-

text of cryptography control and regulations.

Inserting backdoors in encryption algorithms un-

derlies quite systematically the choice of crypto-

graphic standards (DES, AES. . . ). The reason is that

the testing, validation and selection process is always

conducted by governmental entities (NIST or equiv-

alent) with the technical support of secret entities

(NSA or equivalent). So an interesting and critical

Mathematical Backdoors in Symmetric Encryption Systems - Proposal for a Backdoored AES-like Block Cipher

623

research area is: “how easy and feasible is it to design

and to insert backdoors (at the mathematical level) in

encryption algorithms?”. In this paper, we intend to

address one very particular case of this question. It

is important to keep in mind that a backdoor may be

itself deﬁned in the following two ways.

• As a “natural weakness” known — but non

disclosed — only by the tester/validator/ﬁnal

decision-maker (e.g. the NSA as it could have

been the case for the AES challenge). The best

historic example is that of the differential crypt-

analysis. Following Biham and Shamir’s seminal

work in 1991 (Biham and Shamir, 1993), NSA ac-

knowledged that it was aware of that cryptanalysis

years ago (Schneier, 2000). Most of experts esti-

mate that it was nearly 20 years ahead. However a

number of non public, commercial block ciphers

in the early 90s may be weak with respect to dif-

ferential cryptanalysis.

• As an intended design weakness put by the author

of the algorithm. To the authors knowledge, there

is no known cases for public algorithms yet.

As far as symmetric cryptography is concerned,

there are two major families of cipher systems for

which the issue of backdoor must be considered dif-

ferently.

• Stream ciphers. Their design complexity is rather

low since they mostly rely on algebraic primi-

tives (LFSRs and Boolean functions which have

intensely been studied in the open literature). Un-

til the late 70s, backdoors relied on the fact that

quite all algorithms were proprietary and hence

secret. It was then easy to hide non primitive poly-

nomials, weak combining Boolean functions. The

Hans Buehler case in 1995 (Strehle, 1994) shed

light on that particular case.

• Block ciphers. This class of encryption algorithms

is rather recent (end of the 70s for the public part).

They exhibit so a huge combinatorial complexity

that it is reasonable to think to backdoors. As de-

scribed in (Daemen and Rijmen, 2002) for a k-bit

secret key and a m-bit input/output block cipher

there are ((2

)!)

possible such block ciphers.

For such an algorithm, the number of possible in-

ternal states is so huge that we are condemned to

have only a local view of the system, that is, the

round function or the basic cryptographic primi-

tives. We cannot be sure that there is no degen-

eration effect at a higher level. This point has

been addressed in (Daemen and Rijmen, 2002)

when considering linear cryptanalysis. Therefore,

it seems reasonable to think that this combinato-

rial richness of block cipher may be used to hide

backdoors.

Since block ciphers are the most widely used encryp-

tion algorithms nowadays by the general public and

the industry, we will focus on them in the rest of the

paper. Backdoors in stream ciphers have quite never

been exposed to the public.

2.2 Previous Work

One of the ﬁrst trapdoor cipher was proposed in 1997

by Rijmen and Preneel (Rijmen and Preneel, 1997).

The S-boxes are selected randomly and then modiﬁed

to be weak to the linear cryptanalysis. They are ﬁnally

applied to a Feistel cipher such as CAST or LOKI91.

But because of the big size of the S-boxes, the linear

table of such an S-box cannot be computed. However

the knowledge of the trapdoor gives a good linear ap-

proximation of the S-boxes which is then used in a

linear cryptanalysis. As an example, the authors cre-

ated a 64-bit block cipher based on CAST cipher, and

four 8 × 32 S-boxes. If the parameters of the trap-

doors are known, a probabilistic algorithm allows to

recover the key easily. Such a family of trapdoor ci-

phers leads to recover only a part of the key, and the

authors claim that the trapdoor is undetectable. But

in (Wu et al., 1998), Wu and al. discovered a way to

recover the trapdoor if the attacker knows its global

design but not the parameters. They also showed that

there exists no parameter allowing to hide the trap-

door. Nevertheless, it is worthwhile to mention that

in practice, if a real cipher containing a trapdoor is

given, the presence of the trapdoor will certainly not

be revealed.

In (Paterson, 1999), a DES-like trapdoor cipher

exploiting a weakness induced by the round functions

is presented. The group generated by the round func-

tions acts imprimitively on the message space to al-

low the design of the trapdoor. In other words, this

group preserves a partition of the message space be-

tween input and output of the round function. Such a

construction leads to the design of a trapdoor cipher

composed of 32 rounds and using a 80 bits key. The

knowledge of the trapdoor allows to recover the key

using 2

operations and 2

plaintexts. Even if the

mathematical material to build the trapdoor is given,

no general algorithm is detailed to construct such S-

boxes. Furthermore, as the author says, S-boxes using

these principles are incomplete (half of the cipher text

bits are independent of half of the plaintext bits). Fi-

nally, the security against the differential attack is said

not as high as one might expect.

More recently in (Angelova and Borissov, 2013),

the authors created non-surjective S-boxes embedding

a parity check to create a trapdoor cipher. The mes-

ForSE 2017 - 1st International Workshop on FORmal methods for Security Engineering

624

sage space is thus divided into cosets and leads to cre-

ate an attack on this DES-like cipher in less than 2

operations. The security of the whole algorithm, par-

ticularly against linear and differential cryptanalyses

is not given and the authors admit that their attack is

dependent on the ﬁrst and last permutation of the ci-

pher. Finally, the non-surjective S-boxes may lead to

detect easily the trapdoor by simply calculating the

image of each input vector. This problem is natu-

rally avoided in a Substitution-Permutation Network

(SPN) in which S-boxes are bijective by deﬁnition.

In a slightly different context, Caranti and al. an-

swer to Patterson’s question by the afﬁrmative in

(Caranti et al., 2006), by proving that the imprimi-

tivity of the group generated by round functions is ac-

tually related to the cosets of a linear subspace. They

also give some conditions to create such a primitive

group to design a secure cipher that cannot contain

such trapdoor, and ﬁnally show that the AES respects

these conditions. They add in (Caranti et al., 2009)

an algorithm to verify this last condition simply and

show that AES and Serpent S-boxes verify this prop-

erty.

3 DESCRIPTION OF BEA-1

The algorithm BEA-1 (standing for Backdoored En-

cryption Algorithm version 1) is based on our research

work on partition-based trapdoors (Bannier et al.,

2016). This section is intended to describe this cipher

precisely. The cipher operates on 80-bit data blocks

using a 120-bit master key. Our algorithm is directly

inspired by Rijndael (Daemen and Rijmen, 2002), the

block cipher designed by Joan Daemen and Vincent

Rijmen which is now known as the AES (the encryp-

tion standard proposed by the USA, under the haus-

pices of NIST and NSA (NIST, 2000)). Consequently,

our cipher is a Substitution-Permutation Network.

The encryption consists in applying eleven times

a simple keyed operation called round function to the

data block. A different 80-bit round key is used for

each iteration of the round function. Since the last

round is slightly different and uses two round keys,

the encryption requires twelve 80-bit round keys.

These round keys are derived from the 120-bit master

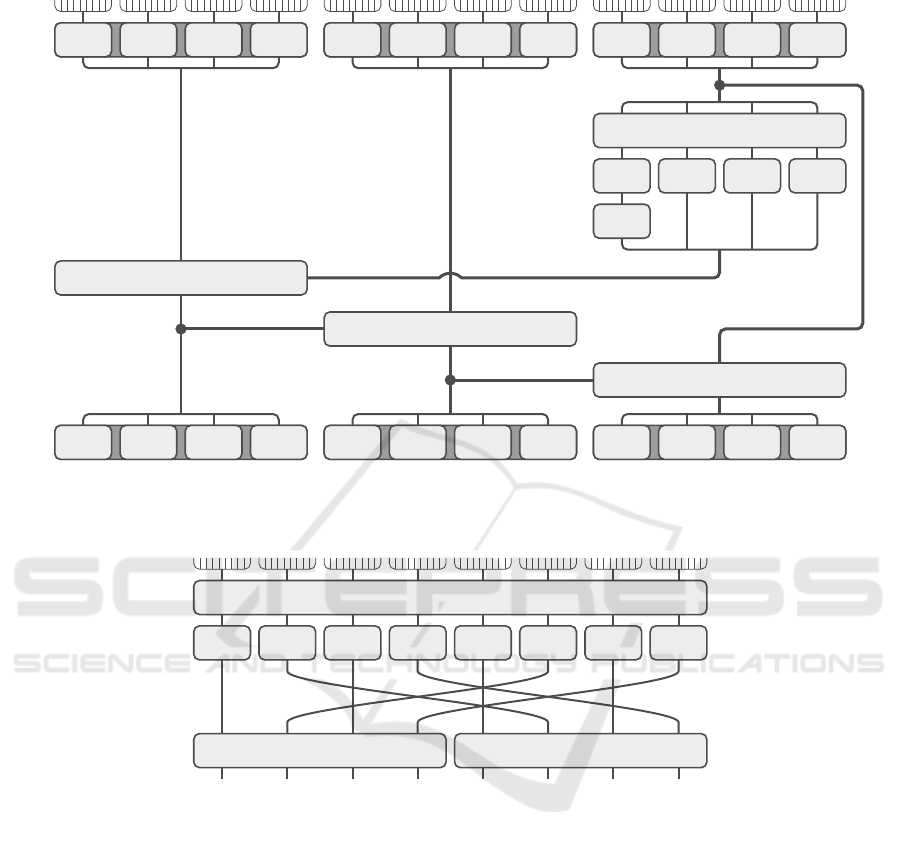
key using an algorithm called key schedule (depicted

in Figure 1).

The round function in Figure 2 is made up of three

distinct stages: a key addition, a substitution layer and

a diffusion layer. The key addition is just a bitwise

XOR between the data block and the round key. The

substitution layer consists in the parallel evaluation

of four different S-boxes and is the only part of the

cipher which is not linear or afﬁne. Following the de-

sign principles of the AES, the diffusion layer comes

in two parts: the ShiftRows and the MixColumns op-

erations.

The decryption is straightforward from the en-

cryption since all the components are bijective. Thus,

to decrypt, we just have to apply the inverse opera-

tions in the reverse order. Remark that the key addi-

tion and the ShiftRows are involutions, therefore the

same operations are used in the decryption process.

In contrast to the AES, the algorithm works with bun-

dles of 10 bits instead of 8 bits. Let F

denote the

Galois Field of order 2. Any 10n-bit block x is seen

as n-tuple of 10-bit bundles (x

, . . . , x

n−1

), thus as an

element of (F

)

. The hexadecimal notation is used

to denote any 10-bit bundle. For example, 37A stands

for 1101111010 in F

The S-boxes S

, S

and S

are four permu-

tations of F

given in Appendix. The linear map

M : (F

)

→ (F

)

processes four 10-bit bundles.

Because of the linearity of this map, M is only deﬁned

on the standard basis of (F

)

. For convenience, its

inverse M

−1

is also given in Appendix.

A pseudo-code for the key schedule is given in Al-

gorithm 1. To provide an overview of its structure, the

ﬁrst step is represented in Figure 1. This representa-

tion also emphasizes the similarities between our key

schedule and the AES one. The pseudo-code for the

encryption and decryption functions are respectively

given in Algorithms 2 and 3. The notation [a k b] de-

notes the concatenation of the vectors a and b. Again,

an overview of the round function is given in Figure 2.

4 CRYPTOGRAPHIC SECURITY

ANALYSIS OF BEA-1

4.1 Differential and Linear

Cryptanalyses

In (Daemen and Rijmen, 2002), Daemen and Rijmen

introduced the differential and the linear branch num-

bers of a linear transformation. With an exhaustive

search, it can be checked that the differential and lin-

ear branch numbers of M are both equal to 5, which

is the maximum. This implies that any 2-round trail

has at least 5 active S-boxes. Thus, a 10-round trail

involves at least 25 active S-boxes.

Note that all the S-boxes are (at most) differen-

tially 40-uniform and linearly 128-uniform. There-

fore, the probability of any 10-round differential trail

is upper bounded by (

1024

)

≈ 2

−116.9

and the abso-

lute bias of a 10-round linear trail is upper bounded

Mathematical Backdoors in Symmetric Encryption Systems - Proposal for a Backdoored AES-like Block Cipher

625

Algorithm 1 - ExpandKey

Input. The 120-bit master key K = (K

, . . . , K

) ∈ (F

)

Output. The twelve 80-bit round keys k

, . . . , k

∈ (F

)

1 (k

, . . . , k

) ← (K

, . . . , K

)

2 For i from 0 to 6 do

3 x ← M(k

12i+8

, . . . , k

12i+11

)

4 x ← (S

))

0≤ j≤3

5 x ← (x

⊕ (3

mod 2

), x

, x

)

6 (k

12i+12

, . . . , k

12i+15

) ← (k

12i+0

, . . . , k

12i+3

) ⊕ x

7 (k

12i+16

, . . . , k

12i+19

) ← (k

12i+4

, . . . , k

12i+7

) ⊕ (k

12i+12

, . . . , k

12i+15

)

8 (k

12i+20

, . . . , k

12i+23

) ← (k

12i+8

, . . . , k

12i+11

) ⊕ (k

12i+16

, . . . , k

12i+19

)

9 For r from 0 to 11 do

10 k

← (k

8r+i

)

0≤i≤7

Algorithm 2 - Encrypt

Input. The 120-bit master key K ∈ (F

)

and the 80-bit plaintext block p ∈ (F

)

Output. The 80-bit ciphertext block c ∈ (F

)

1 k

, . . . , k

← ExpandKey(K)

2 x ← p

3 For r from 0 to 9 do

4 x ← x ⊕ k

AddRoundKey

5 x ← (S

i mod 4

))

0≤i≤7

SubBundles

6 x ← (x

, x

) ShiftRows

7 x ← [M(x

, x

) k M(x

, x

)] MixColumns

8 x ← x ⊕ k

AddRoundKey

9 x ← (S

i mod 4

))

0≤i≤7

SubBundles

10 x ← (x

, x

) ShiftRows

11 x ← x ⊕ k

AddRoundKey

12 c ← x

Algorithm 3 - Decrypt

Input. The 120-bit master key K ∈ (F

)

and the 80-bit ciphertext block c ∈ (F

)

Output. The 80-bit plaintext block p ∈ (F

)

1 k

, . . . , k

← ExpandKey(K)

2 x ← c

3 x ← x ⊕ k

AddRoundKey

4 x ← (x

, x

) InvShiftRows

5 x ← (S

−1

i mod 4

))

0≤i≤7

InvSubBundles

6 x ← x ⊕ k

AddRoundKey

7 For r from 9 to 0 do

8 x ← [M

−1

, x

) k M

−1

, x

)] InvMixColumns

9 x ← (x

, x

) InvShiftRows

10 x ← (S

−1

i mod 4

))

0≤i≤7

InvSubBundles

11 x ← x ⊕ k

AddRoundKey

12 p ← x

by (

128

512

)

= 2

−50

. Consequently, a differential crypt-

analysis of the 10-round version of our cipher would

require at least 2

117

chosen plaintext/ciphertext pairs

and a linear cryptanalysis would require 2

100

known

plaintext/ciphertext pairs.

Even if this is a rough approximation since it does

not take into account the inter-column diffusion pro-

vided by the ShiftRows operation, it sufﬁces to prove

the cipher practical resistance against classical differ-

ential and linear cryptanalyses. In fact, there is only

different plaintext/ciphertext pairs for a ﬁxed mas-

ter key.

4.2 Statistical Analysis of BEA-1

Any cryptographic algorithm must behave as a ran-

dom generator or at least must exhibit enough ran-

domness properties. Therefore, its outputs for differ-

ent classes of inputs must pass all the reference sta-

tistical testings. The most widely used is the NIST’s

Statistical Test Suite (STS) (Rukhin et al., 2001).

We have performed the statistical analysis for

BEA-1 with respect to all the tests which are imple-

mented in STS. Our encryption has passed all the tests

sucessfully. This result is of rather high importance

since

• STS is the tool recommended by the US gov-

ernment to evaluate statistical properties of any

secure encryption algorithm. It is explicitely

mandatory to consider it in the industry.

• The presence of our backdoor remains statistically

undetectable which proves that if statistical prop-

erties are a necessary condition for cryptographic

security it is absolutely not a sufﬁcient property.

It may be bypassed by considering statistical sim-

ulation techniques (Filiol and Josse, 2007). Alge-

ForSE 2017 - 1st International Workshop on FORmal methods for Security Engineering

626

⊕

Bit

Bundle

00–09

10–19

20–29

30–39

40–49

50–59

60–69

70–79

80–89

90–99

100–109

110–119

Figure 1: A diagrammatic representation of the key schedule ExpandKey.

M M

⊕

Bit

Bundle

00–09

10–19

20–29

30–39

40–49

50–59

60–69

70–79

Figure 2: A diagrammatic representation of the round function.

braic or combinatorial weaknesses moreover re-

mains out of reach from statistical analysis.

4.3 Cryptographic Challenge

We propose a cryptographic challenge whose aims is

twofold:

• identifying and explaing what our backdoor con-

sists in,

• exploiting this backdoor in the most efﬁcient way

(in terms of computing time, memory require-

ments, the number of required plaintext/ciphertext

pairs).

We have run our own full cryptanalysis implementa-

tion several times. Each time, we retrieve the 120-bit

key successfully.

This challenge will be ofﬁcially launched right

after the presentation of the present paper, on the

arxiv.org. To take part, participants must send the fol-

lowing data to both authors (prior to any publication):

• the description of the backdoor,

• the description of the attack to exploit the back-

door successfully.

• the relevant source codes. They will help us to

sort the different proposals with respect to, ﬁrst

the number of required plaintext/ciphertext pairs,

second the computing time on our reference com-

puter.

Incentive (non monetary) awards will be awarded to

the three best attacks. Our attack as the reference so-

lution will be presented in at the RusCrypto 2017 con-

Mathematical Backdoors in Symmetric Encryption Systems - Proposal for a Backdoored AES-like Block Cipher

627

ference around end of March 2017. Consequently, the

challenge holds until this date. Moreover the best at-

tack will be considered for publication in the Journal

in Computer Virology and Hacking Techniques.

5 CONCLUSION AND FUTURE

WORK

In this paper, we have proposed an AES-like encryp-

tion algorithm which contains a backdoor at its design

level. This algorithm, named BEA-1, exhibits many

of the desirable properties that any secure algorithm

should. However, it is absolutely unsuitable for ac-

tually protection information. Indeed, we manage to

break it with a rather limited amount of resources suc-

cessfully.

While it is a humble, ﬁrst step in a larger re-

search work, it illustrates the issue of using foreign

encryption algorithms which may contains such hid-

den weaknesses. The very ﬁnal aim of our work is

to prove that it is feasible to embed such undetectable

intended weaknesses. It is consequently a critical is-

sue to have a broader work conducted in this research

area and we hope that other people will also consider

it as such.

The next step will be to consider more sophisti-

cated combinatorial structures.

REFERENCES

Angelova, V. and Borissov, Y. (2013). Plaintext recovery

in des-like cryptosystems based on s-boxes with em-

bedded parity check. Serdica Journal of Computing,

7(3):257p–270p.

Bannier, A., Bodin, N., and Filiol, E. (2016). Partition-

based trapdoor ciphers. Cryptology ePrint Archive,

Report 2016/493. http://eprint.iacr.org/2016/493.

Biham, E. and Shamir, A. (1993). Differential cryptanalysis

of the data encryption standard, volume 28. Springer.

Caranti, A., Dalla Volta, F., and Sala, M. (2009). On some

block ciphers and imprimitive groups. Applicable al-

gebra in engineering, communication and computing,

20(5-6):339–350.

Caranti, A., Volta, F. D., Sala, M., and Villani, F. (2006).

Imprimitive permutations groups generated by the

round functions of key-alternating block ciphers and

truncated differential cryptanalysis. arXiv preprint

math/0606022.

Daemen, J. and Rijmen, V. (2002). The design of Rijndael.

Springer Verlag.

Filiol, E. and Josse, S. (2007). A statistical model for unde-

cidable viral detection. Journal in Computer Virology,

3(2):65–74.

Fried, J., Gaudry, P., Heninger, N., and Thomé, E. (2016).

A kilobit hidden snfs discrete logarithm computa-

tion. Cryptology ePrint Archive, Report 2016/961.

http://eprint.iacr.org/2016/961.

NIST (1998–2000). Advanced encryption standard archive.

http://csrc.nist.gov/archive/aes/.

Paterson, K. G. (1999). Imprimitive permutation groups and

trapdoors in iterated block ciphers. In Fast Software

Encryption, pages 201–214. Springer.

Rijmen, V. and Preneel, B. (1997). A family of trapdoor

ciphers. In Fast Software Encryption, pages 139–148.

Springer.

Rukhin, A., Soto, J., Nechvatal, J., Barker, E., Leigh, S.,

Levenson, M., Banks, D., Heckert, A., Dray, J., Vo,

S., Rukhin, A., Soto, J., Smid, M., Leigh, S., Van-

gel, M., Heckert, A., Dray, J., and Iii, L. E. B. (2001).

A statistical test suite for random and pseudorandom

number generators for cryptographic applications.

Schneier, B. (1998–2000). The nsa’s cryptographic capa-

bilities. http://csrc.nist.gov/archive/aes/.

Shumow, D. and Ferguson, N. (2007). On the possibility of

a back door in the nist sp800-90 dual ec prng. In Proc.

Crypto, volume 7.

Strehle, R. (1994). Verschlüsselt: der Fall Hans Bühler.

Werd.

Wu, H., Bao, F., Deng, R. H., and Ye, Q.-Z. (1998). Crypt-

analysis of rijmen-preneel trapdoor ciphers. In Ad-

vances in Cryptology—Asiacrypt’98, pages 126–132.

Springer.

APPENDIX

The present appendix contains the different tables for

the S-boxes (Figures 5, 6, 7 and 8), the linear map M

(Figure 3) and its inverse M

−1

(Figure 4). They can

be copied and pasted for a practical implementation

of the encryption algorithm.

ForSE 2017 - 1st International Workshop on FORmal methods for Security Engineering

628

x 7→ M(x)

(001, 000, 000, 000) 7→ (112, 1BC, 36C, 0C5)

(002, 000, 000, 000) 7→ (344, 394, 342, 165)

(004, 000, 000, 000) 7→ (23F, 15B, 0C7, 0A7)

(008, 000, 000, 000) 7→ (215, 11F, 1E0, 2E7)

(010, 000, 000, 000) 7→ (2D9, 10A, 0C4, 095)

(020, 000, 000, 000) 7→ (231, 120, 322, 016)

(040, 000, 000, 000) 7→ (3C6, 010, 0EC, 261)

(080, 000, 000, 000) 7→ (32C, 199, 2C5, 07A)

(100, 000, 000, 000) 7→ (35C, 13E, 212, 110)

(200, 000, 000, 000) 7→ (13E, 20F, 253, 0BC)

(000, 001, 000, 000) 7→ (237, 252, 004, 0F8)

(000, 002, 000, 000) 7→ (0CC, 32A, 01A, 2DB)

(000, 004, 000, 000) 7→ (13B, 2FA, 328, 38C)

(000, 008, 000, 000) 7→ (022, 37D, 08D, 3D4)

(000, 010, 000, 000) 7→ (1F4, 1C5, 1FF, 31D)

(000, 020, 000, 000) 7→ (39A, 062, 38C, 2EB)

(000, 040, 000, 000) 7→ (006, 131, 32E, 12B)

(000, 080, 000, 000) 7→ (15E, 0BF, 1E2, 04F)

(000, 100, 000, 000) 7→ (17E, 011, 198, 3C5)

(000, 200, 000, 000) 7→ (0E6, 0ED, 314, 289)

(000, 000, 001, 000) 7→ (075, 380, 371, 2E9)

(000, 000, 002, 000) 7→ (38B, 1A6, 221, 260)

(000, 000, 004, 000) 7→ (019, 08E, 280, 1A7)

(000, 000, 008, 000) 7→ (0DC, 0B1, 061, 3DE)

(000, 000, 010, 000) 7→ (189, 2AB, 1A6, 39D)

(000, 000, 020, 000) 7→ (1B2, 0A7, 178, 208)

(000, 000, 040, 000) 7→ (269, 2CC, 27E, 1CD)

(000, 000, 080, 000) 7→ (09A, 1DD, 336, 34B)

(000, 000, 100, 000) 7→ (2D5, 29F, 072, 04D)

(000, 000, 200, 000) 7→ (009, 175, 254, 3ED)

(000, 000, 000, 001) 7→ (28D, 172, 3EA, 24E)

(000, 000, 000, 002) 7→ (058, 044, 3A0, 281)

(000, 000, 000, 004) 7→ (22D, 1C8, 221, 18B)

(000, 000, 000, 008) 7→ (370, 1D0, 3CD, 07F)

(000, 000, 000, 010) 7→ (256, 130, 382, 067)

(000, 000, 000, 020) 7→ (37F, 282, 3A4, 3D8)

(000, 000, 000, 040) 7→ (165, 3BA, 19B, 0F7)

(000, 000, 000, 080) 7→ (1C7, 259, 17E, 0BE)

(000, 000, 000, 100) 7→ (38E, 3D2, 2CD, 21C)

(000, 000, 000, 200) 7→ (099, 176, 3BC, 031)

Figure 3: Speciﬁcation of M.

x 7→ M

−1

(x)

(001, 000, 000, 000) 7→ (10B, 221, 09D, 398)

(002, 000, 000, 000) 7→ (1AE, 1E9, 2CB, 245)

(004, 000, 000, 000) 7→ (1AB, 11E, 05F, 3A4)

(008, 000, 000, 000) 7→ (08D, 04D, 016, 34C)

(010, 000, 000, 000) 7→ (0AD, 337, 3C5, 2D4)

(020, 000, 000, 000) 7→ (322, 3FD, 3D5, 0E5)

(040, 000, 000, 000) 7→ (002, 246, 2E2, 380)

(080, 000, 000, 000) 7→ (1E9, 3FE, 238, 329)

(100, 000, 000, 000) 7→ (0F5, 1BD, 210, 210)

(200, 000, 000, 000) 7→ (2D8, 209, 353, 243)

(000, 001, 000, 000) 7→ (07D, 2BB, 037, 3C8)

(000, 002, 000, 000) 7→ (055, 128, 25A, 17F)

(000, 004, 000, 000) 7→ (0EB, 2FD, 3C3, 176)

(000, 008, 000, 000) 7→ (3D1, 236, 09D, 2F1)

(000, 010, 000, 000) 7→ (06D, 1BE, 3EB, 0BE)

(000, 020, 000, 000) 7→ (3D9, 069, 21B, 11B)

(000, 040, 000, 000) 7→ (3AA, 29E, 239, 1C0)

(000, 080, 000, 000) 7→ (0BD, 1B1, 18E, 2AB)

(000, 100, 000, 000) 7→ (2D7, 1F4, 378, 157)

(000, 200, 000, 000) 7→ (395, 295, 38D, 129)

(000, 000, 001, 000) 7→ (15E, 23B, 378, 376)

(000, 000, 002, 000) 7→ (0D0, 34D, 18C, 354)

(000, 000, 004, 000) 7→ (084, 128, 167, 20B)

(000, 000, 008, 000) 7→ (1C7, 3F1, 063, 33C)

(000, 000, 010, 000) 7→ (141, 222, 031, 28A)

(000, 000, 020, 000) 7→ (009, 1D9, 3CC, 131)

(000, 000, 040, 000) 7→ (169, 1A1, 02D, 39B)

(000, 000, 080, 000) 7→ (0C8, 111, 34B, 38E)

(000, 000, 100, 000) 7→ (263, 36C, 361, 369)

(000, 000, 200, 000) 7→ (0A6, 050, 36D, 016)

(000, 000, 000, 001) 7→ (015, 371, 2DC, 0E2)

(000, 000, 000, 002) 7→ (04A, 1EC, 1B6, 3B4)

(000, 000, 000, 004) 7→ (2BE, 1DD, 223, 1FA)

(000, 000, 000, 008) 7→ (322, 319, 244, 300)

(000, 000, 000, 010) 7→ (19A, 0E6, 364, 0F2)

(000, 000, 000, 020) 7→ (13C, 355, 058, 07F)

(000, 000, 000, 040) 7→ (211, 2D9, 1B2, 362)

(000, 000, 000, 080) 7→ (14F, 3D2, 0E2, 1C7)

(000, 000, 000, 100) 7→ (005, 38F, 215, 2DF)

(000, 000, 000, 200) 7→ (03D, 208, 27E, 249)

Figure 4: Speciﬁcation of M

−1

Mathematical Backdoors in Symmetric Encryption Systems - Proposal for a Backdoored AES-like Block Cipher

629

..0 ..1 ..2 ..3 ..4 ..5 ..6 ..7 ..8 ..9 ..A ..B ..C ..D ..E ..F

00. 0BA 026 0A0 1E1 183 3DB 1A4 083 110 350 085 2E5 3B4 195 359 2E6

01. 33A 26B 209 217 1CE 2E3 0C0 136 129 0C8 3D6 054 040 3F2 09F 322

02. 11B 07F 139 07D 2CF 02A 268 227 246 1C5 12B 3B6 16C 20D 1E7 35B

03. 313 0CD 11E 1E6 117 355 182 0E6 094 1B9 19C 28C 2B9 336 0AF 19D

04. 2BC 1A9 31B 02E 282 2AE 272 2E9 3AA 1DD 013 2D3 30F 35A 159 1BB

05. 11C 12A 248 3C7 28B 191 025 173 018 38D 1A1 185 007 156 378 312

06. 0C9 143 05D 3FA 038 3DE 081 0F9 2D1 3FB 1C7 3E0 1DC 16A 2D8 23F

07. 030 1EB 3AF 311 36D 3BD 3C9 348 261 1AF 071 3EE 3BA 3AB 1B8 3CA

08. 22B 118 279 0F6 3FF 122 1B2 360 1D6 1B6 3D4 3BB 3B3 0EA 097 308

09. 3A9 086 0AE 15A 253 058 0BB 3D5 01D 1A3 23E 053 35D 277 384 0E2

0A. 233 2B8 2AF 0D0 1B1 105 0B3 215 2A2 27F 2DB 17E 12C 3A2 18E 2AC

0B. 321 09C 294 04C 036 2F1 3D2 18D 188 349 128 069 198 2F4 3DC 370

0C. 138 324 23C 1FD 082 247 005 0A3 0F0 273 152 17B 1A0 1C8 04E 34C

0D. 12F 0CC 075 10E 290 021 1AE 211 3E6 17A 276 289 3B5 123 01F 048

0E. 201 08F 29A 002 179 32E 120 1AC 1E3 109 079 37C 297 096 12D 323

0F. 165 0AC 18B 0AB 1FF 230 25B 3D3 111 07E 21C 1BE 187 30E 34A 318

10. 269 343 29F 395 1AD 1D2 023 2DE 1B3 35E 2D7 044 206 3F1 310 0A7

11. 287 3C3 2A5 213 3E4 3DA 0FD 140 38E 2C2 154 254 15F 02C 1FB 1ED

12. 1C6 051 062 090 214 14B 190 15D 0A1 186 032 0B9 1DA 239 3D1 383

13. 331 06D 02D 009 2FC 3AD 2AA 363 1EF 38F 39A 2DC 3BF 106 39B 31F

14. 03E 0DE 1BC 067 0CF 155 2CE 240 05E 0E8 0C4 149 08C 3E5 2A1 150

15. 1D1 228 3DF 0E0 3F6 193 19B 27D 2B0 35C 0E3 171 180 022 00E 358

16. 161 0EE 365 15B 0C3 2CD 3E1 06C 119 283 0F1 3B9 212 226 076 382

17. 38C 1D3 15C 0B2 22C 314 056 216 364 3DD 1E9 020 176 389 2F2 073

18. 06F 27E 027 14E 177 26D 1BA 0EC 25A 194 3C6 2F9 221 0E1 3F4 0B7

19. 14F 293 144 0FB 2F0 3ED 0F4 1CC 0C6 065 028 315 3E2 2DD 274 0FA

1A. 0D3 041 080 2C5 072 08D 339 2A3 1F1 1DF 2F5 267 015 0B1 275 21B

1B. 091 03F 259 18F 1C3 27B 319 153 0D2 0BD 2D0 064 000 379 2F6 2A9

1C. 142 0F5 3EF 03B 3F8 344 3BC 265 0E7 334 238 08E 347 174 18C 162

1D. 112 1D0 01C 292 2C0 0E9 2B6 301 0C1 30D 369 1C0 1E4 1F7 08A 2FA

1E. 3CB 34D 2BE 28F 09A 39D 232 262 333 2F8 397 2C4 06E 27A 317 017

1F. 327 26C 325 167 05B 36C 362 004 3F7 0F7 20B 22D 222 2D2 0CA 196

20. 33F 3B2 17D 302 146 170 367 18A 1DE 0B5 099 3BE 2C1 0BC 2A0 01B

21. 11D 010 342 169 366 2EC 088 361 291 131 2FF 199 1CA 3B0 00D 24F

22. 2B7 063 3EB 281 0A5 070 1CB 07B 270 2CC 398 32B 1C1 396 278 39E

23. 160 0FF 1A2 0D4 024 24B 178 1BD 326 2EF 28D 392 21F 24A 10B 042

24. 141 256 229 218 0EB 260 145 050 035 0E5 300 3AE 1E2 34E 223 20A

25. 164 02F 0C5 210 1A6 258 3F5 32D 1B4 2EA 1C4 3D0 381 371 2D9 101

26. 3C8 3F3 1F2 10F 0D1 1BF 2D6 320 390 25E 249 341 33B 203 087 23A

27. 09E 095 2C8 3A6 0F2 263 108 307 3E8 3C4 2BB 14C 36E 13E 2C9 376

28. 014 00F 0DA 133 163 05C 0AA 1E5 019 37D 043 1FC 184 07A 3FE 03D

29. 0FE 25F 26E 3B7 135 2E8 3B1 1B7 012 2CA 0C2 113 001 271 1D8 01A

2A. 16F 1C9 0AD 236 299 3CF 3EC 24E 3F0 1D4 3CC 2BF 2C3 338 1B5 25C

2B. 181 052 243 1F3 11F 2EE 332 32C 034 3A8 2B4 34F 031 305 006 124

2C. 13F 13C 19E 3A0 17C 2E2 3CE 345 3CD 0EF 205 31A 23D 06B 059 19F

2D. 1E0 3D8 3F9 103 337 0DB 14D 353 127 0CE 385 114 107 3D7 057 288

2E. 04F 2B2 2CB 039 234 2B5 2E1 32A 2FB 115 116 37B 3A5 092 373 17F

2F. 21E 2AB 37F 2FD 2ED 2BA 1EA 125 208 16E 33C 0A9 2F3 3C2 3C1 21D

30. 11A 0A4 3EA 047 157 25D 1D9 10A 16D 20E 098 2B1 340 22E 241 078

31. 1F5 0ED 31E 298 3A7 30C 1CF 05F 351 0E4 335 046 151 24C 1EE 235

32. 12E 2A6 1A5 061 3A1 29C 011 066 093 03A 38A 1F8 1F0 084 134 356

33. 225 20C 3D9 2E4 0A8 0BE 1FE 0FC 0C7 377 2F7 07C 074 045 1E8 05A

34. 36B 36F 37E 375 04D 1FA 257 13B 089 220 399 00B 158 2D5 068 280

35. 357 0DD 0BF 1B0 2A7 23B 255 3FC 00A 330 2A4 200 016 008 126 0A6

36. 09B 37A 284 2D4 0F3 28E 237 31D 0DF 368 386 060 374 31C 033 26A

37. 100 394 1F9 04B 391 39F 30B 00C 077 2EB 3E3 231 29B 049 202 224

38. 132 2DA 2A8 286 06A 189 130 13D 1EC 29D 104 387 32F 316 207 137

39. 0DC 02B 1D7 21A 354 39C 0B6 329 285 3A4 0D9 245 2B3 0D6 33E 252

3A. 0CB 1DB 172 296 192 04A 244 250 1F6 2AD 2C6 346 09D 388 328 3A3

3B. 2C7 3E7 29E 3C0 0D5 22A 1F4 168 3FD 242 102 3C5 0F8 251 264 2DF

3C. 27C 029 003 38B 10C 380 10D 295 303 197 1CD 219 13A 306 166 304

3D. 175 19A 0D8 28A 0A2 26F 3B8 1C2 148 30A 0B8 24D 1A7 121 15E 372

3E. 0B4 266 22F 2FE 0B0 055 01E 3AC 14A 2E0 34B 1D5 3E9 393 2E7 037

3F. 20F 0D7 1A8 1AB 16B 36A 352 204 2BD 08B 147 1AA 35F 03C 309 33D

Figure 5: Speciﬁcation of the S-box S

..0 ..1 ..2 ..3 ..4 ..5 ..6 ..7 ..8 ..9 ..A ..B ..C ..D ..E ..F

00. 021 09B 37A 3AB 0DF 016 1FE 004 07C 3BE 141 397 300 185 00C 1A7

01. 2FA 3AA 235 0B9 003 3CF 14A 18F 356 363 173 2E4 168 0CF 373 379

02. 2CA 326 16B 393 283 2E0 2B9 3E9 12F 247 3D8 07B 288 146 30F 267

03. 15C 01F 22C 0F8 10F 35D 367 343 1EC 047 008 062 2CF 3D6 36B 148

04. 0B4 2E3 25E 234 0D2 1F8 184 2FF 2EB 2BB 3A1 34F 312 10B 2EA 04D

05. 1B1 2FE 084 229 216 337 0D4 08D 21F 035 164 32A 1AA 182 24B 1BF

06. 245 257 01E 34E 375 197 292 1DD 14D 190 27E 13D 137 3A3 228 392

07. 010 34C 389 114 3B9 28B 325 210 1E7 30B 388 1A1 094 088 038 1C2

08. 305 38E 112 0AA 01B 260 3C1 104 30E 3D4 0EF 079 347 382 22E 09D

09. 1E6 087 278 20D 25B 060 215 2C6 3E0 055 3F9 179 252 1B5 105 368

0A. 029 1E9 2C4 2C5 037 233 204 133 3BD 20B 37D 1AE 03D 116 1B2 2F3

0B. 266 333 08F 050 1B9 328 26F 1EA 1A9 0E6 291 2ED 05E 162 1EE 362

0C. 15B 351 20F 17D 08B 2D5 259 271 14F 2F5 011 3E7 14B 391 248 0B2

0D. 119 3CD 160 23E 06A 0D0 3C3 01C 171 3D3 349 061 16F 0FB 1DF 342

0E. 082 068 218 2E9 3B3 225 2F9 230 020 223 151 0C5 2A9 0FE 096 045

0F. 0F2 0DA 03A 015 049 370 14C 255 369 193 38A 20E 0B1 3A6 039 387

10. 24C 030 315 3CA 0A1 0C6 02C 203 107 115 3FE 244 26C 264 1C6 1C9

11. 123 090 36F 28F 1A3 19D 0BE 317 19B 25C 117 0ED 395 0BF 37E 3E4

12. 04C 3FB 103 2E6 3C8 11E 3D1 279 316 38C 277 286 081 074 213 1F7

13. 3C5 095 2FC 09F 2B5 332 05C 31F 324 09E 2DD 3FC 19F 111 2A7 2B0

14. 091 329 106 10E 012 273 2EC 341 080 174 2DB 1C7 102 2D3 2EE 1B0

15. 03F 2D4 364 131 0A6 275 00A 386 052 3DC 339 11A 211 02A 27F 0DD

16. 318 27B 17B 2D7 1E4 285 0AC 269 3F4 1EF 093 3BB 307 08E 3B0 0EB

17. 209 2CB 0BB 3A5 129 1CA 027 028 3E6 064 221 125 159 2B7 0F9 37C

18. 054 32D 3F6 031 053 29F 23C 2A1 0D9 237 336 232 1B3 1C1 380 2C1

19. 1DA 360 30C 265 34A 17F 296 3E1 20C 0A2 1F6 207 0F1 040 1D5 026

1A. 200 121 134 2AB 2FB 272 0D7 07E 001 262 27A 1FF 299 3EB 1FA 39F

1B. 253 006 128 36E 14E 289 0F6 3A8 3D2 261 178 3E5 2C0 0B7 303 181

1C. 097 22A 32E 166 306 0FC 139 138 3BF 1AC 1FD 29B 0AF 041 2CC 0CA

1D. 23B 1F2 25D 0EC 314 20A 03C 120 3C6 0C0 158 28C 3E8 21E 06E 263

1E. 0C4 085 1BD 051 3E2 153 013 0F3 2B6 1A8 17C 2DC 2C7 3B7 33C 29E

1F. 0B5 27C 3F2 398 194 099 0A9 320 35A 366 2C2 05D 1F9 226 098 04E

20. 05A 3AC 33E 0E8 0A7 186 1D8 17E 126 32B 110 05F 1A5 390 3CE 1FC

21. 11F 019 3D5 13C 2BD 251 355 065 1F5 3DF 152 07A 086 1B6 308 188

22. 0DC 124 15F 075 2E7 39E 046 302 32C 2CE 3CC 3AF 208 066 394 12B

23. 06D 371 2AF 12A 378 319 24D 1D7 37F 3A2 21D 157 31A 3FF 3B2 2DA

24. 071 31B 256 3F3 33D 280 144 08C 21C 058 1CD 2D6 165 3A0 077 354

25. 022 32F 359 2BC 374 1EB 30A 192 1CF 1BA 06B 0A0 177 183 28E 2A8

26. 29C 130 323 122 331 201 3B1 0BC 25A 0D8 34B 11B 24F 2E8 1F1 3F5

27. 31C 254 346 376 11C 000 243 0C8 381 0E9 22D 01A 161 3D0 07F 1E0

28. 295 175 04F 3C4 1AF 2A2 191 2F7 34D 36C 2E2 3D7 0F7 18B 0F5 2F6

29. 0C1 30D 025 1F3 01D 1D3 06C 13B 109 2DF 38B 2E5 18C 0E1 231 10D

2A. 36D 3DB 377 1DB 16D 09C 024 242 072 39B 31D 2C9 149 0F0 089 0A3

2B. 0EA 057 250 2CD 38F 2A0 0B3 169 12D 309 2D8 2AD 358 3F1 1C8 043

2C. 268 2A3 1D6 28A 3EC 18D 2AA 02F 1DE 3C7 0D3 274 147 219 02D 2B2

2D. 0CC 13F 383 3DA 3ED 26A 0AE 1DC 301 2A4 350 2F2 0AB 2A6 39A 014

2E. 2D2 352 108 0E3 270 3E3 02E 29D 1BE 06F 002 059 0A4 198 23A 044

2F. 0CB 258 348 39C 176 2B4 007 3C2 33F 217 287 073 238 15E 03B 167

30. 2B8 2D0 340 0F4 0BD 2F0 353 100 18A 29A 399 246 1CB 02B 1A2 2E1

31. 3F0 212 1B7 032 281 357 3AD 048 322 3A9 3B6 33A 196 1BB 1FB 19A

32. 1E2 0AD 101 033 22F 227 0B6 345 0C2 220 07D 298 3EF 0B8 2F1 0DE

33. 304 0E4 202 0D1 21B 005 12C 0EE 13A 0C7 092 00D 05B 009 37B 365

34. 0DB 2AC 27D 39D 3A7 214 338 1AD 335 2DE 1D9 1E5 1C0 3DE 140 24A

35. 2B3 26B 1F0 3C0 3A4 04A 0A8 2C3 0BA 078 1D4 1E3 16A 145 170 2C8

36. 00B 35B 1AB 127 2BF 16E 2BE 241 1E1 063 334 2B1 136 3EE 3B8 1C5

37. 23D 2D1 042 372 3BA 1ED 0FA 327 0C9 018 1C3 396 3F8 26E 1BC 187

38. 034 3FD 310 118 1D1 076 22B 143 38D 33B 0E5 0D5 3B4 199 3C9 3B5

39. 0E2 195 10A 284 156 150 11D 155 3DD 15D 0CD 163 1A0 0C3 10C 35C

3A. 180 1A6 321 00E 276 03E 25F 0D6 189 206 1D0 1CC 26D 205 17A 3FA

3B. 35E 036 35F 2F8 067 2BA 2A5 16C 3D9 2FD 297 18E 113 0FD 313 0E7

3C. 15A 1B8 08A 239 04B 384 083 385 2F4 19C 12E 017 3BC 224 135 290

3D. 09A 311 240 13E 0A5 24E 069 3CB 0FF 236 36A 1A4 344 3AE 1E8 31E

3E. 132 23F 222 070 2AE 3EA 249 023 293 0B0 330 21A 28D 1CE 154 172

3F. 1F4 056 00F 2EF 361 1D2 0E0 1C4 19E 282 1B4 3F7 294 142 2D9 0CE

Figure 6: Speciﬁcation of the S-box S

ForSE 2017 - 1st International Workshop on FORmal methods for Security Engineering

630

..0 ..1 ..2 ..3 ..4 ..5 ..6 ..7 ..8 ..9 ..A ..B ..C ..D ..E ..F

00. 12E 38B 18E 131 039 10D 2DE 246 286 2BE 315 384 21D 142 06D 0CA

01. 2A2 2CE 264 085 374 3BB 3B9 1B7 3E6 3BC 207 002 392 1B5 0BA 318

02. 39C 2EE 1DA 125 019 063 27E 126 19A 082 305 0E3 206 0A0 009 3C6

03. 100 3F3 2AD 199 102 108 1DB 2F0 310 245 0A8 116 022 3C1 028 332

04. 1E1 2E7 0DA 2B7 0CB 07C 2A0 240 150 165 258 2C8 0C4 334 36B 2D1

05. 1E0 138 39A 0FF 1A7 10C 353 19B 171 038 3BD 000 3A2 1B8 282 2EB

06. 1D4 3D4 20F 23C 0D7 154 012 0DF 3A8 237 09E 155 2E2 189 2F2 136

07. 1B4 381 273 123 052 12C 158 033 2D2 3D3 23B 3B8 2F7 160 341 124

08. 337 1E6 3BE 327 1D3 045 2E4 107 1C2 263 2A4 2CF 244 196 36A 16D

09. 0A1 2C3 004 049 209 3A3 221 361 01E 1B0 05D 319 21B 249 2B2 399

0A. 198 26A 080 1B1 340 28A 33C 316 0FC 37F 1A8 134 17F 3DF 34F 3E5

0B. 2D9 32A 34A 1D1 09D 3FB 0BE 3EA 383 036 3B6 222 22E 2B6 3A6 0FA

0C. 1C1 0B2 113 3E8 129 34C 153 333 07E 01F 01D 213 299 0F8 130 1B9

0D. 182 0A2 1A1 3D5 119 10F 24C 020 097 3F0 280 112 04C 14D 1EB 307

0E. 386 0AE 322 2FE 0C5 3D7 1AF 345 05B 3F5 110 1C8 03C 1C5 35A 0C0

0F. 3F1 15B 338 1CB 0F4 2B4 00F 3A1 242 03D 29D 1B3 003 114 3FA 313

10. 35F 217 261 2C1 15D 28F 390 1C9 1DD 3C7 14F 11D 066 04D 03B 0E9

11. 2BA 2FD 347 191 044 0B8 194 148 256 360 326 257 1AE 396 09B 2CD

12. 1E7 3CD 1FF 269 040 3E7 08A 216 0C9 33B 3D9 1BC 2B1 325 11B 16F

13. 053 22A 186 180 27D 11F 2A9 13E 3E1 0D4 24E 1D2 2FC 3C9 1FB 31A

14. 3DE 1D7 025 372 339 2C7 2ED 25F 0A7 098 2EF 247 0E8 2D3 105 09F

15. 2CC 36D 31F 24B 1D8 241 068 211 2AF 0AA 355 35C 026 2BD 238 0EF

16. 35B 233 05A 1BE 291 368 137 035 298 140 26B 1E4 379 07F 3EB 164

17. 20B 12D 375 1BF 12F 1AA 18B 268 3F4 364 0F7 1CC 0B9 3C5 060 19D

18. 22B 17C 11C 0B1 23A 3B4 05F 2F5 219 224 0E5 042 06F 39D 218 023

19. 1DE 177 190 395 274 359 0E2 2E9 397 0F1 010 099 17D 08E 314 317

1A. 0DC 03F 1AC 1A6 132 152 195 3AD 3E9 3C2 1BB 0F0 0CD 074 178 174

1B. 184 3E0 389 2FB 1A9 0B7 250 27B 06C 13B 0FB 296 297 30F 350 14E

1C. 007 10E 19C 055 351 034 175 103 272 02D 2C0 21C 047 20D 0EA 29B

1D. 13F 1DF 162 376 0BF 1CA 3EC 2B9 3FE 388 133 0A9 33A 304 1FE 059

1E. 13D 0BD 294 02B 127 1E8 275 07B 14C 018 031 1C6 0A3 0EC 27C 087

1F. 38D 3B0 284 1FA 1F5 00A 3E2 02E 228 285 34B 311 075 2F1 1C4 094

20. 3FF 202 27F 2F9 30D 135 33F 301 3D8 2C6 3D2 309 057 073 1F1 289

21. 3B5 3CE 111 0B4 20E 1BA 1F7 24A 394 157 366 336 39B 017 25C 3C4

22. 1EC 2BC 144 1E9 193 16A 33D 344 295 079 027 2D4 38A 17A 292 0AC

23. 0F2 35E 1EF 0BB 106 071 2DA 3F7 084 037 2AB 330 0B0 2DB 07A 22D

24. 00C 149 0AF 290 2E0 122 283 32E 3AE 3C3 1D9 2E5 37B 0BC 265 32D

25. 089 2CB 115 081 18A 255 05C 1A3 287 0D0 276 32C 0C3 30B 226 1C0

26. 2F3 0A5 121 2AA 210 091 208 3EE 230 320 385 28E 21E 3F9 11E 05E

27. 159 281 0C8 37C 0DD 188 04F 26E 33E 2F8 3A0 3B3 3C8 227 1A2 3AA

28. 302 36E 38F 19E 212 13C 24D 0B3 141 3EF 1CE 262 145 362 346 176

29. 1E3 14B 3A9 3DD 093 3F8 070 0D3 1EA 3BA 248 146 201 243 1F6 205

2A. 1CD 20A 2F6 00E 267 26D 2A7 1FC 2D0 0D1 38E 006 30A 3E3 2C5 28B

2B. 2D5 3A7 1D5 3A4 101 2D7 34E 2B5 072 26C 090 1F8 1F9 3AF 1F0 0C2

2C. 2C2 21A 06A 0AB 1EE 109 16B 15E 161 38C 156 271 279 369 342 1D6

2D. 01A 016 352 173 34D 354 181 185 1A5 23F 16C 030 215 1C3 2EA 0CF

2E. 0DE 078 18D 01B 117 393 3F2 39E 37D 1BD 24F 18C 29A 0A4 08D 187

2F. 015 065 0C1 251 00D 348 014 21F 001 008 2CA 321 1B2 1B6 043 147

30. 223 0B6 054 1AB 0FD 373 31E 323 20C 151 10B 288 2DF 041 349 2E3

31. 32F 0ED 277 179 278 3F6 23E 252 077 04A 120 200 308 300 312 04B

32. 1ED 048 30C 183 0D2 39F 3B7 0AD 3FD 204 050 1C7 197 3BF 046 04E

33. 1F3 343 051 1F2 169 266 25A 26F 0F3 2B0 095 17B 31B 0F6 0E6 2DC

34. 225 36C 377 253 058 0E1 021 31C 3D6 1AD 167 2AC 06B 23D 398 032

35. 35D 2FA 00B 391 239 0F5 335 02C 083 143 02A 29E 36F 214 104 14A

36. 0E4 096 19F 2E1 1FD 30E 28D 07D 11A 0EE 0EB 370 358 1DC 163 056

37. 367 03A 2D6 363 229 3DA 08B 1E5 270 2E8 2FF 168 10A 2AE 170 28C

38. 2A3 08C 1CF 076 3D1 32B 2EC 2A5 2C9 2A6 29C 3ED 09C 0CC 2A8 203

39. 0FE 293 29F 2F4 0E7 232 0CE 3AB 13A 011 3DB 220 0D8 1F4 22F 236

3A. 062 1A4 27A 128 329 324 067 365 024 2B8 3E4 0D6 3AC 3A5 172 306

3B. 16E 0DB 3C0 25B 088 2D8 303 380 259 2A1 1E2 0B5 02F 029 356 2BF

3C. 2C4 03E 2BB 3B1 17E 3CC 01C 25E 2B3 069 0A6 15C 0D5 3DC 118 2E6

3D. 2DD 235 18F 371 064 260 0C7 0E0 0C6 1D0 254 0D9 37A 387 3CB 234

3E. 3D0 15F 3B2 08F 15A 013 331 328 06E 25D 0F9 092 166 378 31D 139

3F. 005 09A 12B 061 231 1A0 3CF 3CA 382 192 086 357 22C 12A 3FC 37E

Figure 7: Speciﬁcation of the S-box S

..0 ..1 ..2 ..3 ..4 ..5 ..6 ..7 ..8 ..9 ..A ..B ..C ..D ..E ..F

00. 200 084 1B5 30A 25A 151 174 3F9 113 3B4 35B 291 332 170 021 31E

01. 00E 2FC 023 0B0 3A9 259 2BC 378 031 050 0D0 1FF 26C 0D5 214 23E

02. 1AB 0AB 3AC 036 0E2 2F6 07A 0EA 2CB 0FE 24E 280 138 073 219 3EA

03. 2E2 27C 032 162 285 13C 0B6 1ED 0B3 2F5 2C6 34B 335 1EF 26E 37A

04. 273 17E 30F 2E7 14B 3BC 1CE 039 315 01A 144 1C4 20A 17B 362 10D

05. 235 1D9 2F9 0A4 052 0E3 0BD 061 02C 140 0E1 156 10E 250 288 1BE

06. 07C 2B8 05D 242 192 0A8 3B0 0DB 129 2AF 063 3AF 3D1 0C8 0A6 029

07. 2B9 3B8 0D2 078 2A2 06E 2CF 3CF 0EF 0E7 019 1F1 07E 1BB 2C7 251

08. 36A 2CA 076 216 2E5 0E6 1DD 2FE 390 277 1D2 394 2C5 022 05A 396

09. 0F4 265 0FD 150 057 111 2EC 29C 3DF 11F 13A 158 388 1D3 3C8 386

0A. 38B 279 064 1A4 028 22F 1D5 352 2C8 257 3C4 355 104 322 2C1 382

0B. 1DF 1A9 137 3DC 015 096 2AA 2A4 3F6 1A3 3DA 086 2E8 343 233 11A

0C. 0A5 38D 328 348 292 132 3F4 059 31C 1AC 1C6 3BF 1C2 36D 1D8 0ED

0D. 191 3D3 3D4 3DE 0E8 373 034 23C 224 3C5 11E 393 00B 308 2DA 00F

0E. 209 230 19D 184 1B8 339 360 2D7 011 305 17A 324 344 128 3F0 0F3

0F. 317 0B4 08D 18E 035 0C9 345 0D3 37D 3CA 284 3EF 00D 197 36B 06B

10. 08B 10B 18A 218 046 32A 2CC 0AE 254 3FC 066 246 24D 232 0A2 145

11. 2DB 199 37F 1E1 392 3F3 1C8 1CD 136 2D0 325 27B 068 1F5 077 22D

12. 12F 2F4 0B2 2E9 3CC 296 2EA 116 30D 276 02D 266 09C 25E 157 195

13. 3A1 3F2 3D7 130 258 227 0D4 26B 027 1EA 379 329 179 2D5 0C4 09F

14. 39E 09E 1FD 15B 126 2B3 15E 012 21A 372 356 154 042 017 217 19B

15. 1F8 261 3ED 14A 1FB 110 037 1B7 079 045 3C9 0EE 2B6 107 3CB 302

16. 19E 21D 1E5 205 25F 3BD 196 198 337 069 32E 0DF 3EE 201 0BC 3C2

17. 01D 37B 3C0 0A3 22E 123 2A9 0DE 2A7 2FF 3A5 05B 38F 047 1B4 350

18. 0CB 0A1 29D 1FC 024 29B 3A3 2A1 3BE 215 09A 37E 2A0 0C2 377 0B1

19. 149 33B 323 365 3D6 2E3 082 35A 38C 0D7 134 3D0 36E 336 334 1F6

1A. 1DC 3B2 2B1 213 3F1 1FA 380 06C 020 211 033 28D 0DA 34C 20C 1A8

1B. 28F 369 349 3F5 2FB 1CF 383 387 35E 08F 29A 135 3A7 2B0 346 30E

1C. 163 33C 32F 093 0FA 125 244 226 1C1 1EE 1A2 252 1E9 3A0 146 3D8

1D. 148 353 0FF 37C 09D 2C0 268 048 117 1E3 2A6 003 11B 0AD 1D7 313

1E. 072 18D 297 39A 0C7 12D 016 222 056 1CB 287 095 366 293 3E0 354

1F. 13E 299 190 10F 25B 183 080 1B6 361 3AA 3E1 318 2BA 15C 0D8 1DB

20. 342 2EE 1AE 04F 1A7 2CD 2F8 03A 06A 0BA 188 090 2B7 1E4 16F 0C5

21. 1B0 2D2 1CC 3B9 267 153 24B 1E7 20B 0FC 2E6 0F7 3BB 376 1C7 0D9

22. 00C 271 0AA 1C5 357 1E8 01E 3FE 081 245 314 294 164 13F 212 340

23. 141 1B9 120 02E 34F 0E4 092 26A 171 249 22B 206 0C0 001 0A0 23F

24. 02B 2BB 06F 05E 275 20E 3B3 12A 28A 100 2AC 22A 263 0F9 1C0 21B

25. 203 303 35C 295 088 008 3E5 0DD 307 105 121 185 0A7 3EC 11C 347

26. 094 39D 1B2 02A 3B1 204 114 312 167 131 304 290 231 3E7 2D3 3D2

27. 2C2 32C 3E6 04A 009 10C 327 1BD 2D1 1BA 2FD 35D 253 2EF 282 3D9

28. 338 14F 1B1 28B 330 2F0 18C 175 12E 169 2D9 223 2F3 255 0C3 13D

29. 398 15F 16D 2DC 2BD 0FB 3FA 2ED 147 161 01B 04B 17D 28C 058 3C1

2A. 1A6 21F 1DA 0E9 124 2BF 39C 005 054 35F 143 3CE 19A 043 36F 1F3

2B. 0CF 286 18B 243 006 106 333 152 1BF 3FF 3B7 1EC 30B 098 08E 1D1

2C. 089 3CD 1F0 210 2EB 309 2F7 13B 20D 3AD 02F 0EC 11D 06D 3A8 38E

2D. 311 1E6 3FB 0AF 2E1 12B 220 03D 0F1 2FA 208 16C 28E 181 33A 119

2E. 109 10A 0CA 2A5 010 31F 3BA 0B7 3B5 2DD 193 2AD 283 085 00A 32B

2F. 2A8 3AB 1D0 2F1 0EB 2DF 298 1DE 065 17C 18F 364 33E 0B8 2CE 1F2

30. 289 142 2B2 0D6 3E2 24C 101 24A 39B 09B 097 1A0 229 375 320 062

31. 33D 118 3EB 03C 15A 281 1A1 207 3C7 331 319 27A 127 34E 07B 239

32. 23A 300 0B5 01C 2B5 1E0 39F 180 321 133 26F 371 1B3 363 26D 0F5

33. 0C6 165 0F6 19C 070 0E0 367 002 247 389 053 27F 2D6 2B4 3DB 29E

34. 30C 1AD 0E5 22C 15D 2E0 013 236 2A3 228 0BB 14D 018 278 155 1C9

35. 178 0CD 370 07D 3A6 23B 049 2D4 397 0BF 1BC 21E 399 3F8 0AC 004

36. 34A 055 04D 14C 33F 1F7 301 05C 3A2 112 2DE 075 3F7 391 040 326

37. 2D8 000 0DC 0D1 041 14E 067 160 166 168 051 0A9 31B 0CC 16E 172

38. 1CA 2C4 3C3 1E2 03F 173 27E 08A 25D 1F9 014 17F 044 16B 2F2 176

39. 31D 3E9 108 139 2C9 04C 187 071 29F 381 316 038 0CE 2C3 34D 1AA

3A. 122 225 1C3 04E 368 351 202 38A 102 189 194 306 026 0F0 248 08C

3B. 05F 19F 2BE 270 060 083 186 3DD 2AE 0C1 23D 272 241 0F8 1EB 01F

3C. 374 177 3E4 358 1FE 099 2AB 1D4 3A4 310 030 1AF 1F4 0BE 074 16A

3D. 274 1D6 21C 3FD 3C6 238 234 262 3D5 31A 395 27D 3E8 240 1A5 087

3E. 32D 359 341 25C 0B9 115 237 0F2 2E4 12C 103 025 20F 260 3AE 269

3F. 07F 03B 03E 007 182 159 091 3B6 3E3 384 264 385 36C 256 221 24F

Figure 8: Speciﬁcation of the S-box S

Mathematical Backdoors in Symmetric Encryption Systems - Proposal for a Backdoored AES-like Block Cipher

631