Enterprise Level Security with Homomorphic Encryption

Kevin Foltz and William R. Simpson

Institute for Defense Analyses, 4850 Mark Center Drive, Alexandria, VA 22311, U.S.A.

Keywords: Enterprise, Database, System Design, Confidentiality, Integrity, Enterprise Level Security, Homomorphic

Encryption, Application Security, Security, Cloud Services, End-to-End Encryption, Key Management,

Database Security.

Abstract: Enterprise Level Security (ELS) is an approach to enterprise information exchange that provides strong

security guarantees. It incorporates measures for authentication, encryption, access controls, credential

management, monitoring, and logging. ELS has been adapted for cloud hosting using the Virtual

Application Data Center (VADC) approach. However, a key vulnerability in placing unprotected data in the

cloud is the database that stores each web application’s data. ELS puts controls on the end-to-end

connection from requester to application, but an exploit of the back-end database can allow direct access to

data and bypass ELS controls at the application. In a public cloud environment the data and web application

may be vulnerable to insider attacks using direct hardware access, misconfiguration, and redirection to

extract data. Traditional encryption can be used to protect data in the cloud, but it must be transferred out of

the cloud and decrypted to perform processing, and then re-encrypted and sent back to the cloud.

Homomorphic encryption offers a way to not only store encrypted data, but also perform processing directly

on the encrypted values. This paper examines the current state of homomorphic encryption and its

applicability to ELS.

1 INTRODUCTION

Enterprise Level Security (ELS) provides a way to

secure access to web resources (Chandersekaran,

2008; Chandersekaran, 2012; Foltz, 2016a; Foltz,

2016b; Foltz, 2016c; Simpson, 2011; and Simpson,

2016). It provides end-to-end authentication,

confidentiality, and integrity from web browser to

web resource provider. When combined with an

external solution for availability, it promises a

comprehensive enterprise solution for security of

web resources.

Most web service providers are partitioned into a

front-end web application and back-end stored data.

ELS provides secure communication to the web

application, and the Virtual Application Data Center

(VADC) model extends this to cloud hosting (Foltz

and Simpson, 2016b). However, ELS extends only

from requester to application, and it does not include

the stored data. This data is often the enterprise’s

most valuable digital asset, and the boundary of ELS

between the application and database provides a

potential access path that bypasses ELS protections.

To maintain ELS security levels in a cloud

environment, some means of protecting the data is

required.

In addition to the data, the web application may

be vulnerable to attacks in a public cloud. Cloud

operators may have access to all data in the cloud,

and through virtual machine managers they may also

gain visibility into the application code running on

the servers.

Homomorphic encryption provides a way to

manipulate encrypted data to perform computations

without decrypting the data. This is useful for the

ELS stored data problem because it allows a web

application’s stored data to remain encrypted at all

times, even during data operations. An attacker at

the stored data has no access to plaintext values.

Homomorphic encryption also addresses the web

application problem because the web application

code can be recompiled to operate on homomorphic

encrypted data. Attackers viewing the web

application cannot extract computational process

information or unencrypted data from the

computation.

When implementing an ELS system on a private

data center there is an implicit safe zone where data

and applications can be run. The machines remain

under physical control, and the people working on

Foltz, K. and Simpson, W.

Enterprise Level Security with Homomorphic Encryption.

DOI: 10.5220/0006245901770184

In Proceedings of the 19th International Conference on Enterprise Information Systems (ICEIS 2017) - Volume 1, pages 177-184

ISBN: 978-989-758-247-9

177

them are part of the enterprise. When moving to the

cloud, this safe zone is replaced by a potentially

hostile or compromised environment, which

threatens to expose sensitive data. Homomorphic

encryption offers a way to reclaim this safe zone

while maintaining many of the benefits of cloud

hosting.

This paper discusses the methods and issues in

using homomorphic encryption within an ELS

architecture. The following sections describe ELS

and homomorphic encryption, discuss integrating

homomorphic encryption into ELS, and provide an

analysis of the security and performance

implications.

2 ENTERPRISE LEVEL

SECURITY

The ELS design addresses five security principles:

 Know the Players – enforce bi-lateral end-to-end

authentication;

 Maintain Confidentiality – maintain end-to-end

unbroken encryption between data requester and

provider;

 Separate Identity from Access and Privilege –

use separate authentication and authorization

credentials;

 Maintain Integrity – validate that what was

received is exactly what was sent;

 Require Explicit Accountability – monitor and

log transactions.

2.1 Know the Players

In ELS, the identity credential is an X.509 Public

Key Infrastructure (PKI) certificate (DoDI, 2011;

RSA, 2012). This identity is required for all active

entities, both person and non-person, as shown in

Figure 1. PKI credentials are verified and validated.

Ownership is verified by a holder-of-key check.

Supplemental authentication factors may be required

from certain entities, such as biometric data

(Chandersekaran and Simpson, 2008).

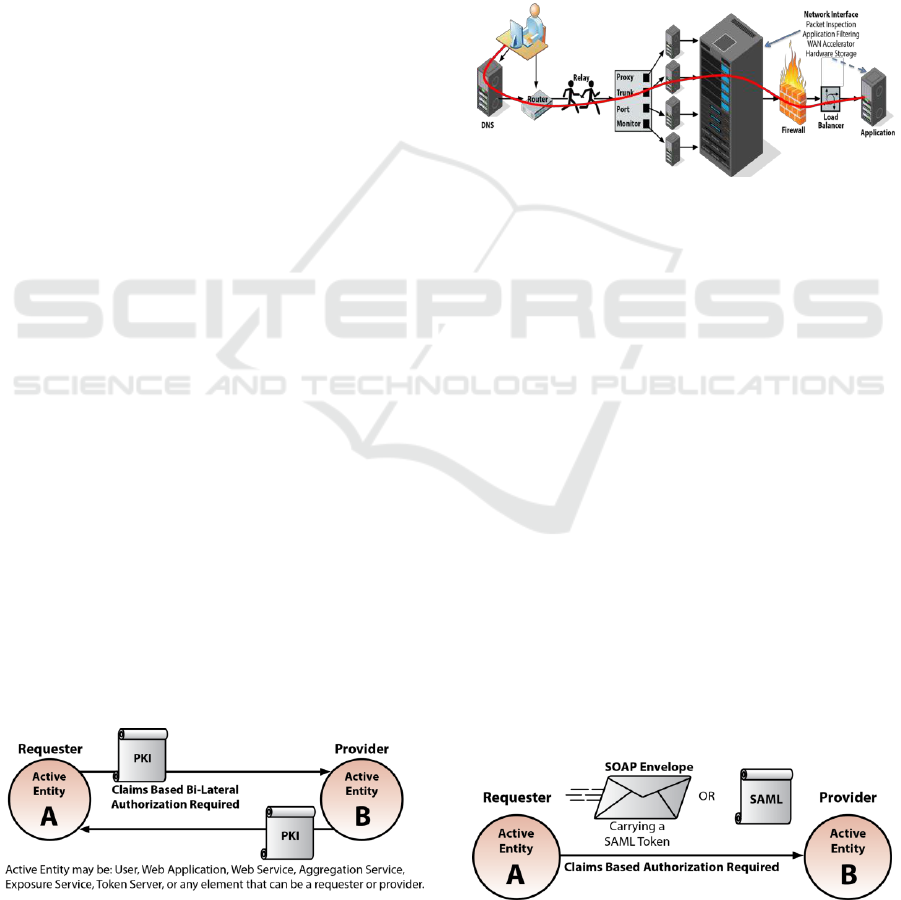
Figure 1: Bi-lateral Authentication.

2.2 Maintain Confidentiality

Figure 2 shows how ELS establishes end-to-end

Transport Layer Security (TLS) encryption through

the numerous intermediaries that may route, scan, or

process data between requester and application

(W3C, 2008). The red line indicates the path of

encrypted data from end to end through routers,

relays, proxies, firewalls, and load balancers, which

may view and manipulate the encrypted content.

ELS end-to-end encryption ensures they are not able

to view or modify the raw unencrypted content

without triggering an error at the endpoints.

Figure 2: End-to-End Encryption.

2.3 Separate Access and Privilege from

Identity

ELS can accommodate changes in location,

assignment, and other attributes by separating the

use of associated attributes from the identity.

Whenever changes to attributes occur, access claims

are recomputed based on new associated attributes,

allowing immediate access to required mission

information. As shown in Figure 3, access

credentials use the Security Assertion Markup

Language (SAML) (Ragouzis et al., 2008). SAML

authorization tokens used with ELS differ from the

more commonly used single-sign-on (SSO)

authentication tokens (Chandersekaran and Simpson,

2012). Authentication is performed through TLS

using PKI credentials. This separation prevents a

compromised SAML token from providing

immediate access. The credential for access and

privilege is bound to the requester by ensuring a

match of the distinguished name used in both

authentication and authorization credentials.

Figure 3: Claims-Based Authorization.

ICEIS 2017 - 19th International Conference on Enterprise Information Systems

178

2.4 Maintain Integrity

Integrity is implemented by end-to-end TLS

message authentication codes (MACs), as shown in

Figure 4. Chained integrity, in which trust is passed

on transitively from one entity to another, is not used

because it is not as strong as employing end-to-end

integrity. At the application layer, packages (SAML

tokens, etc.) are signed by the sender, and signatures

are verified and validated by the receiver.

Figure 4: Integrity Measures.

2.5 Require Explicit Accountability

As shown in Figure 5, ELS monitors specified

activities for accountability and forensics. The

monitor files are formatted in a standard way and

stored locally. For enterprise files, a monitor sweep

agent reads, translates, cleans, and submits records

to an enterprise database for recording log records

periodically or on-demand. Local files are cleaned

periodically to reduce overall storage and to provide

a centralized repository for help desk, forensics, and

other activities (Simpson and Chandersekaran,

2011). However, the principle of accountability

requires unambiguous identification of the entity

performing these actions. This means that proxies,

go-betweens, and impersonators acting “on behalf

of” other entities are not allowed.

By abiding with the tenets and principles

discussed above, ELS allows users access without

accounts by computing targeted claims for the

enterprise. ELS has been shown to be a viable,

scalable alternative to current access control

schemas. A complete description of ELS basics is

provided in (Foltz and Simpson, 2016b).

Figure 5: Accountability through Centralized Monitoring.

3 HOMOMORPHIC

ENCRYPTION

Homomorphic encryption refers to methods of

encryption that allow operations on the ciphertext to

map to corresponding operations on the underlying

plaintext. For example, raw, unpadded RSA

encryption is performed as follows to compute

ciphertext c from plaintext message m:

c = ENC(m) = m

(mod n).

(1)

The product of two encrypted values

= ENC(m

)

(2)

and

= ENC(m

)

(3)

∙ c

= m

∙ m

(mod n)

(4)

= (m

∙ m

)

(mod n)

(5)

= ENC(m

∙ m

)

(6)

The product of the encrypted values is just the

encrypted product of the corresponding plaintext

values.

Different homomorphic encryption schemes have

different operations, and the ciphertext and plaintext

operations can differ. Paillier encryption, for

example, has the property:

ENC(m

+ m

) = ENC(m

) ∙ ENC(m

(7)

In this case, multiplication of ciphertext

corresponds to addition of plaintext.

For both RSA and Paillier, only a single

operation is possible. In 2009, Gentry published his

thesis describing an encryption scheme that allows

both addition and multiplication (Gentry, 2009).

With these two operations it is possible to compute 1

+ (-1) ∙ (a ∙ b) for two inputs a and b. If a and b are

binary values, this is the computation of the NAND

function, which can be used to build a logical circuit

that can perform any computation. Therefore, such a

homomorphic encryption method allows the

Enterprise Level Security with Homomorphic Encryption

179

computation of any function on encrypted data. This

is called Full Homomorphic Encryption (FHE).

Methods, such as RSA and Paillier, that allow

some computation but not arbitrary functions are

called Partial Homomorphic Encryption (PHE).

Another class of homomorphic encryption allows

the computation of any function on encrypted data,

like FHE, but only for a limited number of

executions of an operation. For example, it may

allow any number of additions, but only up to n

multiplications for some number n. These Somewhat

Homomorphic Encryption (SWHE) methods are

often related to FHE methods. In particular, Gentry’s

FHE method builds on SWHE and removes the limit

on the number of multiplications through

bootstrapping.

Even FHE has its limitations for providing

security. Although confidentiality is maintained by

keeping data encrypted at all times, integrity

requires additional work. An operation on

homomorphic data does not leak the value of the

data, but the result of such a computation in the

cloud has no method of verification. The cloud

provider could, for example, replay results of

previous computations or encrypt its own chosen

results using known public keys.

A solution that provides verifiable computing is

presented in (Gennaro, Gentry, and Parno, 2010).

The representation of the circuit that computes the

function is garbled in a way that the entity doing the

computation does not know what is being computed.

This method builds on homomorphic encryption to

monitor the integrity of results.

This integrity check is critical to ELS cloud

hosting. Because the homomorphic encryption

approach provides confidentiality and integrity, it

extends ELS security properties into a hostile cloud

environment.

4 HOMOMORPHIC

ENCRYPTION WITH ELS

This section discusses the integration of

homomorphic encryption into an ELS architecture.

However, before examining homomorphic

encryption, we first examine the limitations of

standard encryption.

4.1 No Homomorphic Encryption

One approach using standard encryption is to host

the application locally and store encrypted data in

the cloud. The browser and application are outside

the cloud in a controlled environment, and the

database is inside the cloud. The application

encrypts data before sending it to the cloud database

and decrypts it after retrieval. The cloud is simply a

place to store data. All computation occurs on local,

trusted machines. Cryptographic keys are

maintained by the local application.

This scenario maintains confidentiality, since

only encrypted content is sent to the cloud.

However, all processing of data requires retrieving

it, decrypting it, and performing the computation

locally. If the results of the computation are to be

stored, they must be encrypted and sent back to the

cloud. Such a model for cloud security works well

for all data set sizes, but the size of data that is

retrieved and sent must be small and the

computation must be quick. In such a case, the main

resource requirement is the storage, and the network

transmissions and local computation are relatively

minor. This could be the case for a forensics archive,

in which large amounts of data are stored for

potential use but only small portions are actually

ever used.

The problem with traditional encryption comes

when a computation requires access to all of the

data, such as computation of an average or

maximum value. In such a case, all of the encrypted

data must be retrieved and decrypted, and then the

computation can take place on the decrypted values.

With limited network bandwidth and potentially

limited requester computation resources the

traditional approach has significant overhead.

Homomorphic encryption, in contrast, only requires

encrypting the request and decrypting the response.

The computation is performed on the encrypted

values.

The following discussion covers solutions that

use homomorphic encryption.

4.2 FHE with Full Application in

Cloud

The most desirable implementation for security is to

place the application and data in the cloud, each with

homomorphic encryption, and use verifiable

computation for the application logic. Figure 6

provides the basic concept. This provides

confidentiality and integrity of the data and

computation results even when hosting in a hostile

environment. The requester would need a way to

encrypt request data to the application and decrypt

encrypted responses from the application.

ICEIS 2017 - 19th International Conference on Enterprise Information Systems

180

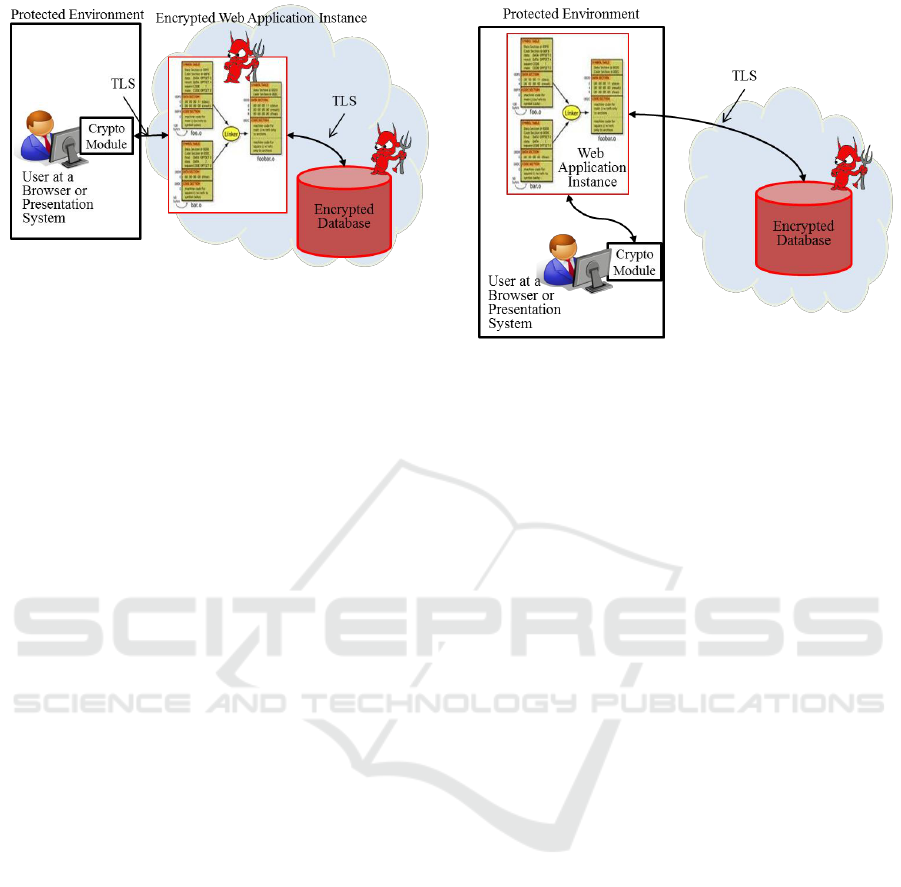
Figure 6: Full Homomorphic Concept.

One approach is for the requester browser to manage

this encryption and decryption, along with the key

generation and management. However, this requires

rewriting the browser. A simpler approach is to have

a separate module that is attached to the browser and

modifies outgoing and incoming traffic to encrypt

and decrypt content, respectively. This enables the

browser functionality and cryptography to be

modular so that browser updates do not break

cryptography and changes in cryptography do not

require rewriting browser code.

To the browser, nothing has changed. The

cryptographic module handles translation of

plaintext requests to homomorphic encrypted

requests. The server code is recompiled to operate

on encrypted data with verifiable computing. No

homomorphic keys are stored in the cloud, and any

server keys for encryption, signatures or other

operations remain encrypted under homomorphic

encryption. The browser cryptographic module takes

the responsibility of managing and using

homomorphic encryption keys.

4.3 FHE with Only Data in Cloud

Recompiling applications to operate on

homomorphic encrypted data is not always

desirable. In these cases the application can be

hosted locally while the data is hosted in the cloud.

The data itself is encrypted for homomorphic

operation. This concept is shown in Figure 7.

There are two possibilities for how the database

is hosted in the cloud. It can be recompiled for

homomorphic encrypted operation or it can remain

as-is and only the data is encrypted. The case in

which the database code is recompiled is identical to

the case in which the application is recompiled,

except that the cryptographic module now attaches

to the application calling the database instead of the

browser calling the application.

Figure 7: Protected Application Homomorphic Concept.

For the encrypted data in the unmodified database,

there are some additional considerations. For

homomorphic encryption in which the operations on

the plaintext and ciphertext differ, the database

commands may need to be rewritten to account for

this difference. For example, if addition of plaintext

values is accomplished by multiplying ciphertext

values, then all database requests to add values must

be changed to multiplication requests.

Even if the operations are the same, the data

types and sizes of plaintext and ciphertext may be

different. The necessary types and sizes for the

ciphertext must be available in the database.

The main advantage of this method over placing

the full application data and logic in the cloud is that

the application and database code require no

changes. The only change is the addition of the

cryptographic module to the application to translate

database commands into homomorphic encrypted

commands.

4.4 Performance Considerations

Homomorphic encryption solves many of the

security problems for ELS cloud hosting, but this

security comes at a cost. Homomorphic encryption

algorithms are a small subset of possible encryption

algorithms, and all of the currently available

homomorphic algorithms are slower than traditional

encryption algorithms.

However, the comparison is not that simple.

Traditional encryption has only two operations:

encryption and decryption. Homomorphic

encryption has these two as well as operations on the

data itself. Typically, addition and multiplication are

the plaintext operations, but the operations on the

ciphertext may be more complicated operations or

Enterprise Level Security with Homomorphic Encryption

181

similar operations on larger data values, both of

which can incur performance penalties. To assess

the performance of homomorphic encryption, it is

important to understand how the fundamental

operations of encryption, decryption, addition, and

multiplication are used. These different operations

often have different performance, which must be

combined or averaged to provide an overall

performance assessment.

There are two generic use cases for

homomorphic encryption in the cloud. The first is a

bulk load of existing plaintext data and applications.

This requires encrypting all the data and

applications. This is an infrequent event, but for

large data sets or applications, it can be very

resource-intensive. It is often highly parallelizable,

so the main issue is throughput. The time taken will

depend on the size of the data set, the available

resources, and the computation requirements of

encryption. For this first use case, the baseline for

comparison is encrypting the data with the

Advanced Encryption Standard (AES) encryption

algorithm.

The second use case for encryption is user access

to encrypted data. If individual users perform the

encryption and decryption of requests and responses

in a distributed way, the performance of the requests

is unlikely to be significantly affected. Unless large

data sets are transferred, the encryption or

decryption of data will incur only a small latency

based on local encryption or decryption of requests

and responses.

If a central server manages keys and performs

cryptographic operations, this frees users from key

management, but it creates a central bottleneck for

performance. The central server must do all

encryption and decryption, which may require

dedicated computing resources to manage the

throughput.

Addition and multiplication are used to

manipulate data in the cloud. Such operations do not

decrypt or encrypt data, so performance depends

only on the performance of the ciphertext operations

that are used to implement the additions and

multiplications on the underlying plaintext.

If the application itself is encrypted, the code will

involve different additions and multiplications in

order to do computation. This is another area where

the specific application will influence performance.

The operational model for an application will be

some mix of additions, multiplications, uploads, and

downloads. As a result, it is not possible to

determine the performance penalty of using

homomorphic encryption without knowledge of the

application itself. We examine instead the individual

operations, which enable further analysis for specific

applications.

To track the degradation in performance, a

sample data base was used with both plaintext and

homomorphic searches as a model in (Gligor, 2014).

Real-world testing of various homomorphic

encryption methods (Gentry, Halevi, and Smart,

2012; Cheon et al., 2013; Doroz, Hu, and Sunar,

2014; Lauter, Naehrig, and Vaikuntanathan, 2011;

and Joppe et al., 2013) shows that FHE encryption

incurs a performance penalty of a factor of about

compared to AES encryption. For example, a 1-

microsecond AES encryption would take about 3

hours using FHE. This is prohibitively slow, and

there is no indication that this will become feasible

for real-world applications in the near future.

SWHE methods can be orders of magnitude

faster than corresponding FHE methods. Encryption

can be roughly 10

2.5

times slower than AES, which

is approaching feasibility for specific use cases.

However, encryption for operations on data are

much slower. Encryption for homomorphic addition

is 10

3.8

times slower, and encryption for

multiplication is 10

7.5

times slower. These factors

make current and near-future adoption unlikely.

An important consideration for real-world

performance is the actual time taken, not just the

factor above the non-homomorphic operation, since

encryption, addition, and multiplication, although all

very fast, have different performance. For the

current numbers, however, the message is clear that

homomorphic encryption retains significant

performance penalties and little or no probability

that improvements in commodity hardware will be

able to reduce these penalties to acceptable levels.

The few options available for FHE and SWHE are

more like existence proofs than performance-

optimized standards. As a result, performance

suffers significantly compared to the highly

optimized symmetric encryption methods like AES

that are in use today.

4.5 A Possible Compromise

Full Homomorphic Encryption enables arbitrary

computations on encrypted data. This allows any

functions on any data to be computed. However,

many use cases are more restricted in their

computations and this full generality is not always

needed. At the other extreme of full generality is a

case in which a simple comparison operation is all

that is needed.

For example, a database stores a list of values,

ICEIS 2017 - 19th International Conference on Enterprise Information Systems

182

and the only operations on the data are to add new

values, delete values, or ask whether a particular

value already exists. In this case, any deterministic

encryption algorithm is sufficient. To add or delete,

just add or delete the encrypted value. To query a

value, just encrypt it and ask whether that encrypted

value is present. This is again a very narrow use case

in which traditional encryption is sufficient.

Methods, such as RSA, Paillier, and other PHE

methods may offer a good compromise between

FHE and traditional encryption. These PHE methods

allow some computation beyond simple comparisons

with traditional encryption while being orders of

magnitude faster than FHE or SWHE (Gligor, 2014).

The smaller performance penalty might make it

feasible for specialized applications for which PHE

operations provide sufficient data manipulation

capabilities.

Recent simulations with PHE suggest a

manageable performance overhead when restricted

to standard SQL queries. This approach was initiated

by CryptDB (Akin and Sunar, 2015; Dayıoğlu et al.,

2015; Naveed, Kamara, and Wright, 2015; Popa et

al., 2012; Wang, Agrawal, and Abbadi, 2012). This

suggests that ELS with PHE at the database may be

a promising future direction for investigation.

5 CONCLUSIONS

Homomorphic encryption shows promise as a

solution to ELS cloud security issues. FHE allows

data and processing to be protected in the cloud for

confidentiality. With some modification to the

application, it is also possible to provide integrity.

However, real-world implementation is not likely to

be feasible in the near future due to the performance

overhead of current FHE implementations. PHE

shows promise for current use. The functions and

architectures that can be used are limited, but

performance overhead is relatively small. More

work is needed to investigate exactly which

functions can be implemented with PHE and

whether such functions can operate with adequate

performance.

ACKNOWLEDGEMENTS

The authors wish to acknowledge the assistance of

Virgil Gligor for his deep insights and broad

knowledge in homomorphic encryption and related

areas. The authors wish to acknowledge Coimbatore

Chandersekaran for initiating this project in

homomorphic encryption. Although he is no longer

with us to inspire this research, his intellect and

advice is a part of this work. The authors also would

like to thank Frank Konieczny and SAF/A6 for

funding the work. These acknowledgements imply

neither endorsement nor agreement by the

individuals or their agencies with any of the results

cited.

REFERENCES

Akin, I. H., and Berk S. 2015. “On the Difficulty of

Securing Web Applications using CryptDB,”

International Association for Cryptologic Research.

Available at https://eprint.iacr.org/2015/082.

Chandersekaran, C. and Simpson, W. R. 2008. “The Case

for Bi-lateral End-to-End Strong Authentication.”

World Wide Web Consortium (W3C) Workshop on

Security Models for Device APIs. London, England.

Chandersekaran, C. and Simpson, W. R., 2012. “A

Uniform Claims-Based Access Control for the

Enterprise.” International Journal of Scientific

Computing, Vol. 6, No. 2, ISSN: 0973-578X, pp. 1–

23.

Cheon, J. H., Coron, J., Kim, J., Lee, M. S., Lepoint, T.,

Tibouchi, M., and Yun, A. 2013. “Batch fully

homomorphic encryption over the integers.” In:

Johansson, T., Nguyen, P.Q., eds. EUROCRYPT

2013. LNCS, vol. 7881. Heidelberg: Springer, pp.

315–335.

Dayıoğlu, Z. N. et al. 2015. “Secure Database in Cloud

Computing: CryptDB Revisited,” International

Journal of Information Security Science, Vol. 3, No. 1,

pp. 129–147.

U.S. Department of Defense. 2011. DoDI 8520.2, Public

Key Infrastructure (PKI) and Public Key (PK)

Enabling.

Foltz, K. and Simpson, W. R. 2016. “The Virtual

Application Data Center.” In: Proceedings of

Information Security Solutions Europe (ISSE) 2016.

Paris, France.

Foltz, K. and Simpson, W. R. 2016. “Enterprise Level

Security – Basic Security Model.” In: Proceedings of

the 20th World Multi-Conference on Systemics,

Cybernetics and Informatics: WMSCI, Volume I,

WMSCI 2016. Orlando, FL.

Foltz, K. and Simpson, W. R. 2016. “Federation for a

Secure Enterprise.” In: Proceedings of The Twenty-

first International Command and Control Research and

Technology Symposium (ICCRTS 2016). London,

UK.

Gennaro, R., Gentry, C., and Parno, B. 2010. “Non-

interactive verifiable computing: outsourcing

computation to untrusted workers.” In: Proceedings of

the 30th annual conference on Advances in

cryptology. Santa Barbara, CA, USA.

Enterprise Level Security with Homomorphic Encryption

183

Gentry, C. 2009. “A Fully Homomorphic Encryption

Scheme.” Doctoral thesis. Stanford University.

Available at https://crypto.stanford.edu/craig/craig-

thesis.pdf.

Gentry, C., Halevi, S., and Smart, N. 2012.

“Homomorphic evaluation of the AES circuit.” In:

Advances in Cryptology - CRYPTO 2012. Springer,

pp. 850-8.

Gligor, V. 2014. “Homomorphic Computations in Secure

System Design,” Final Report. Pittsburgh, PA:

Carnegie Mellon University.

Joppe, W., Lauter, K., Loftus, J., and Naehrig, M. 2013.

“Improved Security for a Ring-Based Fully

Homomorphic Encryption Scheme.” In: Lecture Notes

in Computer Science, PQCrypto. Springer. pp. 45–64.

Lauter, K., Naehrig, M., and Vaikuntanathan, V. 2011.

“Can homomorphic encryption be practical?” In: C.

Cachin, and Ristenpart, T., eds. CCSW ’11, ACM. pp.

113–124.

Naveed, M., Kamara, S., and Wright, C. V. 2015.

“Inference Attacks on Property-Preserving Encrypted

Databases.” In: CCS’15, Denver, CO.

Popa, R. A., Redfield, C. M.S., Zeldovich, N., and

Balakrishnan, H. 2012 “CryptDB: Processing Queries

on an Encrypted Database,” Comm. ACM, vol. 55, no

9, Sept. 2012 (also Proc. of 23rd ACM SoSP, Sept.

2011).

Ragouzis, N. et al. 2008. “Security Assertion Markup

Language (SAML) V2.0 Technical Overview.”

OASIS Committee Draft, March 2008.

RSA Laboratories. 2012. “Public Key Cryptography

Standard, PKCS #1 v2.2,” RSA Cryptography

Standard, Oct 27, 2012.

Simpson, W. R. 2016. Enterprise Level Security –

Securing Information Systems in an Uncertain World.

Boca Raton, FL: CRC Press, p. 397.

Simpson, W. R. and Chandersekaran, C. 2011. “An Agent

Based Monitoring System for Web Services.” In:

CCCT2010, Volume II. Orlando, FL. pp. 84–89.

World Wide Web Consortium. 2008. “The Transport

Layer Security (TLS) Protocol Version 1.2.” RFC

5246.

Wang, S., Agrawal, D., and Abbadi, A. E. 2012. “Is

homomorphic encryption the holy grail for database

queries on encrypted data?” Technical report,

Department of Computer Science, University of

California Santa Barbara.

Doroz, Y., Hu, Y., and Sunar. B. 2014. “Homomorphic

AES evaluation using NTRU.” In: Cryptology ePrint

Archive, Report 2014/039.

ICEIS 2017 - 19th International Conference on Enterprise Information Systems

184