Triangular Curvature Approximation of Surfaces

Filtering the Spurious Mode

Paavo Nevalainen

, Ivan Jambor

, Jonne Pohjankukka

, Jukka Heikkonen

and Tapio Pahikkala

Dept. of Information Tech., Univ. of Turku, FI-20014 Turku, Finland

Dept. of Diagnostic Radiology, Univ. of Turku, FI-20014 Turku, Finland

{ptneva, ivjamb, jonne.pohjankukka, jukhei,tapio.pahikkala}@utu.ﬁ

Keywords:

Curvature Spectrum, Parameterless Filtering, Irregular Triangulated Networks, Discrete Geometry.

Abstract:

Curvature spectrum is a useful feature in surface classiﬁcation but is difﬁcult to apply to cases with high noise

typical e.g. to natural resource point clouds. We propose two methods to estimate the mean and the Gaussian

curvature with ﬁltering properties speciﬁc to triangulated surfaces. Methods completely ﬁlter a highest shape

mode away but leave single vertical pikes only partially dampened. Also an elaborate computation of nodal

dual areas used by the Laplace-Beltrami mean curvature can be avoided. All computation is based on trian-

gular setting, and a weighted summation procedure using projected tip angles sums up the vertex values. A

simpliﬁed principal curvature direction deﬁnition is given to avoid computation of the full second fundamental

form. Qualitative evaluation is based on numerical experiments over two synthetical examples and a prostata

tumor example. Results indicate the proposed methods are more robust to presence of noise than other four

reference formulations.

1 INTRODUCTION

Wide-scale point clouds have become accessible to

analysis everywhere. The point cloud surface regis-

tration typically has an approximate or accurate De-

launay triangular or tetrahedral mesh generation as a

preliminary step. The surface models are called irre-

gular triangularized networks (TIN) for historical re-

asons. The application domains can be roughly di-

vided to three categories by the target environment:

built environment, natural resource data and medical

3D imaging.

The ratio 0 ≤ σ

/r ≤ 0.3 of the perpendicular

noise component σ

and the nominal surface radius r

describe the difﬁculty of curvature registration. The

built environment data has usually high point den-

sity and small noise ratio compared to the natural re-

source data (Mitra and Nguyen, 2003). Built surfa-

ces are usually solid, curvature values change slowly

over distance, and it is desirable to be able to detect

the local curvature accurately. A typical mean curva-

ture method for such data is based on the Laplace-

Beltrami (L-B) operator (Meyer et al., 2003; Mes-

moudi et al., 2012).

Other two application domains have

the noise ratio much higher, approximately

/r = 10

−2

...10

−1

(Schaer et al., 2007). Sur-

Figure 1: The voluminous highest noise component ari-

ses either from the scanning process (LiDAR point clouds,

left), or from the voxel granularity (right). Neither case

should require any parameters to ﬁlter. Occasional anoma-

lies (circles) should be transferred intact to pattern recogni-

tion phase.

faces, e.g. the terrain surface, are porous, covered

with vegetation or mathematically undeﬁned. Natural

resource data is gatherer by aerial light detection

and ranging (LiDAR) or by spatial photogrammetry.

Natural resource data has shape recognition tasks

where the point samples per target ratio reaches

one (Nevalainen et al., 2016), i.e. one single elevated

hit is a possible target (e.g. a surface stone), see

Fig. 1. Detection of an individual target is naturally

uncertain in the presence of noise, but one can cluster

larger areas e.g. to stony or non-stony ones using

e.g. the curvature spectrum (Nevalainen et al., 2015).

On the other hand, there is a natural frequency limit

deﬁned by the nominal mesh length. Excitation of

this frequency over a large area (see Fig. 1 left side) is

684

Nevalainen, P., Jambor, I., Pohjankukka, J., Heikkonen, J. and Pahikkala, T.

Triangular Curvature Approximation of Surfaces - Filtering the Spurious Mode.

DOI: 10.5220/0006249206840692

In Proceedings of the 6th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2017), pages 684-692

ISBN: 978-989-758-222-6

usually a numerical artifact which should be ﬁltered

at some point of the processing.

Medical 3D applications, especially magnetic re-

sonance imaging (MRI), often have non-isotropic

voxels causing excitation at the frequency limit, see

right part of the Fig. 1. Numerical methods should be

resilient to effect of noise, low sampling and discreti-

zation patterns.

Surface registration is reminiscent of interpola-

tion, whereas noise reduction is ﬁltering. Typically,

these two operations can be performed in any order, or

combined together. Spatial ﬁltering requires several

parameters, and it is worthwhile to seek curvature re-

gistration methods, which would handle the highest

frequency as depicted in Fig. 1:

1. leaving single pikes to be handled by later pattern

recognition and ﬁltering steps.

2. eliminating automatically large excitations of the

highest frequency.

Naturally, if such a behaviour is squarely against

the needs of a speciﬁc application, there is an abun-

dant supply of existing curvature registration met-

hods, which should be employed instead. Alternative

methods have several opposing properties for discrete

differential operators (Wardetzky et al., 2007) used as

building blocks for curvature analysis. If a new appli-

cation ﬁeld arises, one has to be aware of the trade-

offs between different properties.

The Gaussian and mean curvature completely de-

ﬁne the local curvature of any continuous surface. It

is the consensus of the current research that the local

Gaussian curvature is best estimated on TIN models

by so called angle deﬁcit (see e.g. (Crane et al., 2013),

and the result is robust to noise. This reference met-

hod is named as vertex Gaussian in this paper.

This paper uses the classical differential geometric

deﬁnition of the average Gaussian curvature (Press-

ley, 2010): it is the ratio of the total orientation change

over a surface area, a TIN triangle in this case. It is

pointed out in Sec. 3.1 that this simple deﬁnition leads

to a triangular Gaussian curvature estimation on ver-

tices, which ﬁlls the requirements 1 and 2 mentioned

before.

The mean curvature is numerically more difﬁcult

target than Gaussian curvature. One starting point for

computation has been neglected in the literature thus

far. It is possible to deﬁne the mean curvature by the

local rate of change of the surface area when the sur-

face is mapped towards the direction of its unit nor-

mal (Pressley, 2010). This deﬁnition is related to the

theory of minimal surfaces and it can be applied di-

rectly to the triangulated surface with deﬁned vertex

normals. Also this novel mean curvature formulation

has the earlier mentioned properties 1 and 2, as rumi-

nated in Sec. 3.1.

The rest of the paper has the following struc-

ture: Section 2 introduces the triangular Gaussian and

mean curvatures, and a collection of competing deﬁ-

nitions. Also the problem of ﬁnding the principal cur-

vature direction has been addressed there. Section 3

has a practical example (prostata tumor), and two

synthetical test cases to verify the properties 1 and 2

of the proposed method. Section 4 brings in the con-

clusions.

2 TRIANGULAR CURVATURE

The following notation will be used throughout the

presentation. The set of cloud points P ⊂ R

is gi-

ven. A triangle t = (a,b,c), a, b, c ∈ T ⊂ P

is de-

ﬁned by three vertex points which can be referred in

cyclic fashion in counterclockwise order (with three

possible combinations considered identical). To shor-

ten the notation, the vertex membership a ∈ t and

the geometric insidence q ∈ t have the same nota-

tion, when the intended meaning is clear from the

context. A vertex p has a set of surrounding triang-

les T

= {t ∈ T |p ∈ t} ⊂ T . The edge neighborhood

= ∪

t∈T

t \{p} is a counterclockwise cyclically or-

dered set of points connected to p by a triangle edge.

The triangle t = {a, b,c} has a unique face normal

(oriented outwards) and an area A

= (b − a) × (c − a)

= kN

k/2 (1)

= N

, (2)

where N

is a temporary cross product term and vec-

tor power v

= v/kvk of a vector v denotes the vector

normalization.

Your Paper

You

November 15, 2016

Abstract

Your abstract.

References

Figure 2: Triangle concepts: tip angles φ

t p

are indexed by

vertices p of triangles t. Also the vertex normal n

and face

normal n

depicted.

The local curvature state of the surface is comple-

tely deﬁned after ﬁnding out both mean curvature H

and the Gaussian curvature G. Sections 2.1- 2.7 pre-

sent the curvature quantities both in a triangle t and at

a vertex p.

Triangular Curvature Approximation of Surfaces - Filtering the Spurious Mode

685

2.1 Triangular Gaussian Curvature

The tangential orientation change ∆α over a length l

deﬁnes κ, the average of the curvature of a 2D curve

over the same length: κ = ∆α/l. Analogous to this,

the average of the Gaussian curvature of a smooth sur-

face S ⊂ R

can be deﬁned (Pressley, 2010, p.166-

168) as the ratio G

= ω

, where A

is the surface

area of S and ω

is the solid angle of which the sur-

face normal n(q),q ∈ S traces. This deﬁnition can be

applied to a triangle t = {a,b,c} with vertex normals

with the exception that the accurate surface

S is not known and the triangle area A

is a lower

bound approximation of the hypothetical smooth area

meas(S

). Ramiﬁcations of this fact will be addressed

in Sec. 3.1.

The solid angle ω

in Eq. 3 is the total trace of

normal n(q), q ∈ t and, assuming a barycentric inter-

polation scheme, it equals the solid angle of a vec-

tor tri-blade n

, n

(van Oosterom and Strackee,

1983):

tan(ω

/2) =

·n

×n

1+n

·n

(3)

= ω

. (4)

The numerator in Eq. 3 equals zero when at least two

vertex normals are parallel, which results in require-

ments 1 and 2 of Sec. 1 to be fulﬁlled as far as trian-

gular Gaussian G

of Eq. 4 is concerned. This will be

elaborated further in Sec. 3.1.

2.2 Triangular Mean Curvature

Considering a triangle t = (a,b,c) and the associa-

ted surface normal approximants n

at verti-

ces a,b,c, and a barycentric dependency of normals

n(q),q ∈ t in the triangle t, one can deﬁne a nor-

mal mapped parallel triangle t

= {q + u n(q)|q ∈ t}.

Using a deﬁnition of (an averaged) mean curvature

in (Pressley, 2010, p. 207), one gets:



u=0



−n

)×(c−a)+(b−a)×(n

−n

)

· n

. (5)

Note that triangular mean curvature H

≡ 0 when all

the vertex unit normals are parallel i.e. n

= n

This leads to requirements 1 and 2 of Sec. 1 to be

fulﬁlled.

2.3 Projective Tip Angles as Weights

The vector angle function acos() and the projected

vector angle function acos

() simplify the upcoming

presentation. The projection angle φ

is the angle φ

between vectors v

and v

when seen from direction

n. See the right part of the Fig. 3. A projection matrix

P(n) = I − n

is used to deﬁne acos

(.):

acos(v

) = cos

−1

· v

) (6)

= P(n)v

, i = 1,2

acos

) = acos(v

). (7)

Note that acos(v

) ≡ acos

×v

Your Paper

You

November 21, 2016

Abstract

Your abstract.

References

Figure 3: Left: the angle φ

between two vectors v

and

the projected angle φ

between projected vectors v

Right: Deﬁnition of the edge angles φ

and φ

of an edge

(p,q).

The projective tip angles φ

t p

are used systemati-

cally to average all triangular quantities X

, t ∈ T to

corresponding vertex quantities X

, p ∈ P :

= acos

(p − a, b − a) ( See Fig. 3) (8)

∑

t∈T

t p

(9)

∑

t∈T

t p

/φ

. (10)

This weighting procedure of a quantity X will be de-

noted as: X

→ X

in the rest of the text.

Good numerical properties of tip angle weighting

pointed us to amortize the computational costs by ap-

plying it to produce the following vertex properties:

normals n

, triangular mean curvature H

, triangu-

lar Gaussian G

and principal curvature direction v

Another beneﬁt was the uniﬁed handling of the boun-

dary points, since the angle sums φ

≤ φ

≤ 2π give

an excellent weighting at the boundary. This is impor-

tant because e.g. the natural resource data is prune to

have missing values and holes in the point cloud, and

the boundary points are thus common. When a point

p is not in the border, the sum of projected angles

equals: φ

≡ 2π. There are other weighting schemes

in the literature, these are being discussed in Secti-

ons 2.5 and 2.6.

2.4 Vertex Gaussian

Since the projected tip angles have been introduced,

it is possible to deﬁne an alternative vertex Gaussian

using the spherical excess (Crane et al., 2013) formu-

lation. The vertex Gaussian of Eq. 12 serves as a re-

ICPRAM 2017 - 6th International Conference on Pattern Recognition Applications and Methods

686

ference method:

∑

t∈T

t p

(11)

= (φ

− φ

)/(A

/3). (12)

2.5 Vertex Normals

Vertex normals n

are weighted from triangle normals

using the generic scheme of projected tip weighting

deﬁned in Eq. 10: n

→ n

. There are several other

possible deﬁnitions. Vertex normals can be conside-

red pointing towards the new altered vertices after the

local surface is varied, or they somehow represent a

continuous but unknown reference positions. The al-

ternatives satisfying DDG convergence requirements

listed in (Crane et al., 2013) are reproduced here for

discussion. The vertex normal can be:

1. The vector area: n



∑

t∈T



2. The area (or volume) gradient n

= (dA

/d p)

when one vertex p is varied in R

3. The normal of a sphere which inscribes vertex p

and its edge-neighborhood points N

. See (Max,

1999; Crane et al., 2013).

Such a sphere ﬁtting required by the alternative 3 is

impossible with usual point clouds, but just applying

the deﬁnition from a case of a perfect sphere ﬁt to any

general triangle neighborhood, the resulting normal

vector n

behaves smoothly:





∑

t=(a,p,b)∈T

kb − pkka − pk





According to (Jin et al., 2005), versions 1 and 2 are

simple but prune to noise, projected tip angle weig-

hting (our choice) is reliable and simple, and version

3 is rather good but also somewhat expensive.

2.6 Other Mean Curvature Deﬁnitions

This short survey omits all methods based on a local

ﬁt of a smooth interpolant, see e.g. (Yang and Qian,

2007). These methods show resilience to noise, but

tend to have an uncontrollable loss of high frequen-

cies and are usually computationally more expensive

than the methods presented in the following.

The mean curvature through the discrete Laplace-

Beltrami (also known as the cotan-Laplace) operator

has been documented in (Mesmoudi et al., 2012). It

is one of the best methods according to (Mesmoudi

et al., 2012). The mean curvature H

at a vertex p

becomes:

∑

b∈N

(

tanφ

)(b − p)k, (13)

where triangles t

∈ T

have a common edge (p, b)

with opposite vertex angles φ

,φ

. See Fig. 3. The

vertex speciﬁc area A

≈ A

/3 is the area of so called

mixed Voronoi cell. Using A

instead of A

/3 reduces

the area contribution of possible obstuse angles φ

t p

a way, which is detailed in (Mesmoudi et al., 2012).

The exact value of A

depends on the geometry of

the triangle set T

but is always rather close to the

above given expected average. The variance in A

adds numerical stability of the estimates of the vertex

mean curvature H

but is rather costly to calculate.

Your Paper

You

November 15, 2016

Abstract

Your abstract.

References

Figure 4: The edge angle β

is positive when the edge

folds downwards (or inwards in case of tumors).

The concentrated Gaussian curvature by (Mes-

moudi et al., 2012) equals Eq. 12. The concentrated

mean curvature by (Mesmoudi et al., 2012) is re-cast

to the notation in this paper as:

sgn(t

) = −sgn((b − p) · n

) (14)

= acos(n

)sgn(t

) (15)

= 2π −

∑

∈T

(16)

(2π − ω

), (17)

where the edge angles β

are depicted in Fig. 4,

the angle sum ω

is the inwards opening solid angle

at vertex p, and the summation is done over edges

(p,q), q ∈ N

The sign of the edge angle β

is determined by a

vector blade handedness sign (a determinant sign) of

an edge (p,q) = t

∩t

between triangles t

= (a, p,q)

and t

= (q, p,b), see Eq. 14. Note that the edge sign

is positive for pikes (the situation depicted in Fig. 4)

and symmetric: sgn(t

) = sgn(t

). The normals

are a result of earlier stages of the computational

process.

Also the solid angle ω

in Eq. 17 is already avai-

lable from the preceding solid angle ﬁltering (SAF),

which can be done to reduce the noise level of the

point cloud or for ﬁltering out the foliage signal (Ne-

valainen et al., 2016), or before any shape classiﬁca-

tion via curvature spectrum. Availability of spatial an-

gles ω

makes this method computationally the chea-

pest one.

Triangular Curvature Approximation of Surfaces - Filtering the Spurious Mode

687

In some applications like tumor detection in elec-

tron magnetic resonance (EMR) imaging, the orienta-

tion of the surface normal n

is completely free (but

outwards from the tumor). That is why the edge sig-

num refers only to two adjoined triangles t

and t

which are both oriented outwards. The signum in

Eq. 15 requires one vector operation (saxpy, see (Go-

lub and Van Loan, 1996)) of R

vectors.

Barycentric interpolation (Theisel et al., 2004) is

based on normalized linear change of the normal n

over the triangle t from where a generic expression

for Gaussian and mean curvature can be deduced. For

our purposes only the mean curvature H

t p

of triangle

t = (a,b,c) at a vertex point p ∈ {a, b,c} needs to

be considered. The Eq. 18 is adapted to our notation

from (Theisel et al., 2004; Nevalainen et al., 2015):

h = n

× (c − b) + n

× (a − c) + n

× (b − a)

t p

= (n

· h)/(2n

· N

) (18)

t p

→ H

, (19)

where h is a temporary vector multiplicant.

There is also a triangular approximation of the se-

cond fundamental form (Crane et al., 2013; Rusinkie-

wicz, 2004), which is used in (Rusinkiewicz, 2004)

to derive the principal curvatures, mean and Gaussian

curvature principal and directions directly. This met-

hod requires iteration of a least squares problem, and

it seems to be computationally more expensive than

the methods covered here.

There are other possible interpolation schemes

over a triangle, e.g. using radial basis or by applying

the well-known Rodriguez rotation formula (Dorst

et al., 2007) twice (ﬁrst over one edge, then between

edge and a vertex of interest). Preliminary tests indi-

cate that these options seem to lead to more complex

formulas yet the numerical results stay very close to

the schemes included to this study. This holds to both

the triangular and the vertex values.

2.7 Principal Curvature Orientation

The curvature eigenvalues κ

and κ

of a triangle t

are the curvature extremals when tracing a continuous

surface S through point p by a perpendicular plane:

= H

− G

,l = 1,2 (20)

Object and shape recognition may use any subset of

the four curvature characteristics G,H,κ

,κ

The barycentric surface normal map t → t

was

used to derive Eq. 5. By applying it again, but this

time to ﬁnd a trajectory with most drastic curvature

effect per traversed arc length on a triangle t, one gets

the principal curvature direction v

of a triangle t. This

is a direction with the largest curvature (eigenvector

of κ

). The second eigenvector is not of interest, since

it will be dictated by the ﬁrst eigenvector. Another

Figure 5: Averaging principal curvature direction v

from

triangles (above) to vertices v

(below).

way to express v

is based on constraining the second

fundamental form to be diagonal and solving the prin-

cipal direction from this constraint at Eq. 21. This is

different from (Rusinkiewicz, 2004), where whole the

second fundamental form is solved by least squares

ﬁtting a set of linear constraints. Below are the equa-

tions leading to the eigenvalue problem:

= P(b − c)(a − c) (before scaling)

= P(a − c)(b − c) (before scaling)

·(a−c)

·(b−c)

= (n

− n

+ (n

− n

P(n

= λv

, (21)

where

are constituents of a constant

matrix D

= dn

/dq, the rate of change of the normal

at triangle t. Note that eigenvalue λ is not proportional

to principal curvature, since the barymetric mapping

does not preserve the unity of the normals.

The weighted summation scheme v

→ v

Eq. 10 is not directly applicable, since the principal

directions ±v

are deﬁned by the orientation only, wit-

hout a coherent sign. The summation must take this

into account. The following heuristics relies on the

monotonic nature of the vector summation of the non-

unit cumulative vector ˆv

ˆv

(S) = P(n

)

∑

t∈T

t p

sgn

t p

∗

= argmax

k ˆv

(S)k

= ( ˆv

∗

))

, (22)

where S is the set of signums S = {sgn

t p

}

t∈ T

, which

can be found performing O(|T

|) scalar products

ICPRAM 2017 - 6th International Conference on Pattern Recognition Applications and Methods

688

ˆv

p current

· v

by a single enumeration and reversing a

subset of signums if necessary.

The weighting scheme in Eq. 22 relies on the pro-

jected tip angle weights φ

t p

, which have multiple ap-

plications and thus can be amortized from computa-

tional cost. The weighting scheme in (Rusinkiewicz,

2004) uses triangular contributions of the vertex spe-

ciﬁc area A

. This weighting scheme has not been

tested by us. Overall, avoiding the least squares ﬁt

and area weighting makes our method less expensive

computationally.

3 NUMERICAL EXPERIMENTS

Two synthetical models and a visual inspection of

a practical problem have been covered, see Secti-

ons 3.1- 3.3. The following mean curvature methods

have been compared:

1. triangular average mean curvature (our method)

2. L-B (Meyer et al., 2003)

3. concentrated mean curvature (Mesmoudi et al.,

2012)

4. barycentric interpolation of the normal (Theisel

et al., 2004)

Two Gaussian curvatures have been compared, trian-

gular average Gaussian (our method, Eq. 4), and ver-

tex Gaussian (Crane et al., 2013). Since there are 3

vertex normal deﬁnitions, 2 weighted summation po-

licies, 4 mean curvature and 2 Gaussian curvature de-

ﬁnitions, results of only the most interesting combi-

nations have been provided.

3.1 A Local Pike

This model demonstrates the different character of

each methods with respect to noise in the surface nor-

mal direction. Especially the two noise modes presen-

ted in Fig. 1 are modelled. The case 1 in Fig. 6 is an

apex of a larger regular formation. The case 2 is a sin-

gle pike which can be either noise or a useful feature.

The case 3 demonstrates a large noise ﬁeld at the hig-

hest possible frequency dictated by point cloud den-

sity. The geometrical mean

|G| = κ

derived from

the Gaussian curvature G is used for the comparisons,

since it has the same physical dimension (inverse of

radius) as the mean curvature.

The abscissa value h is the height of point p.

When h → 0, it is the planar special case with nominal

radius r → ∞ and κ r → 1.

The barycentric method exaggerates curvature at

large h values, which are likely to be noise. The bary-

centric mean curvature and the triangular curvatures

a local pike, cases 1,2,3

-1

-2

-2 -1 0 1 2

-0.5

0.5

1.5

case 1

triang. H

L-B H

concen. H

baryc. H

vertex G

triang. G

-2 -1 0 1 2

-0.5

0.5

1.5

case 2

-2 -1 0 1 2

-0.5

0.5

1.5

case 3

Figure 6: Four mean curvature methods and two Gaussian

curvature methods compared in various settings with one

point protruding out. The square root of the Gaussian cur-

vature is used for comparison. The analysis point at height

h has been circled.

(our methods, both G and H) tend to dampen a sin-

gular pike (case 2). The barycentric method is losing

its dampening tendency at high values of h, which are

more likely to be noise.

The output value of the vertex mean and Gaussian

curvatures (and barycentric mean curvature) is scaled

downwards (dampened) by a ratio w, value of which

depends on the case. The cases 1, 2,3 have dampe-

ning ratios w = 1, 1/3, 0. A singular pike (case 2) has

dampening factor 1/3 which is still adequate to con-

tribute in the curvature spectrum or to be detected by

later pattern recognition phase.

The egg cell pattern of case 3 gets completely

dampened by triangular curvatures G and H, and by

the barycentric method. The vertex normals deﬁned

by Eqs. 2 and 10 become parallel, which then cau-

ses the triangular curvatures of the involved triangles

t to be zero, see Eqs. 5 and 4. This can be a use-

ful property in some applications, e.g. in stone de-

tection (Nevalainen et al., 2016), or in reducing the

granularity effect produced by voxels.

The concentrated curvature, vertex Gaussian, and

Laplace-Beltrami are closely related in all cases. The

behaviour of all six methods is rather similar to each

other in the hyperbolical case (a saddle point) and this

case has not been included in this presentation.

3.2 A Torus

A torus of radii r = 1, R = 2.5 has been used. This is

a classical test case, since the curvature aspects of the

ideal shape are analytical, yet both elliptic and hyper-

Triangular Curvature Approximation of Surfaces - Filtering the Spurious Mode

689

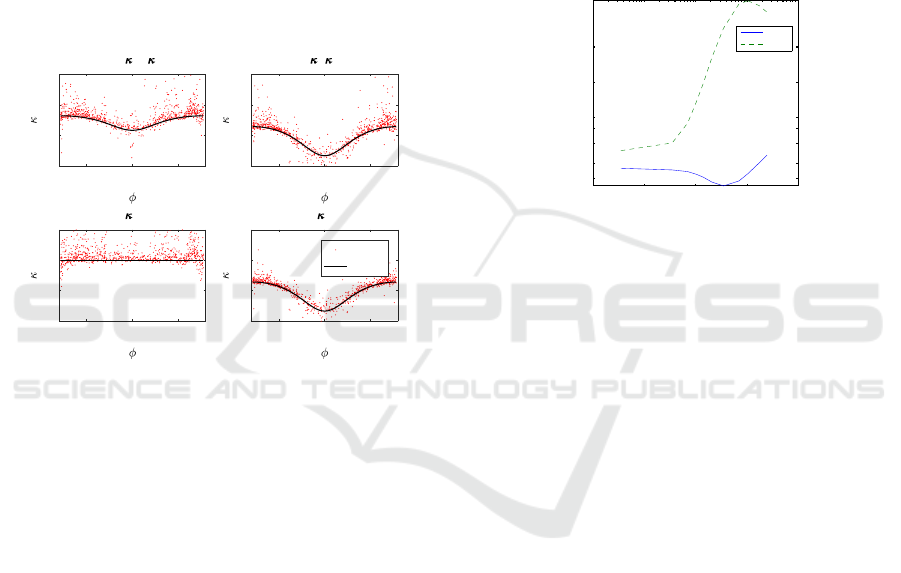
bolic local surface metrics occurs.

Two torii, a dense one with |P | = 820 and a sparse

one with |P | = 220 were used. Fig. 7 shows the sparse

torus with uniform local height distribution. A uni-

form distribution is used also on the tangential mani-

fold metrics. The height noise concerns point loca-

tions and the tangential noise concerns triangulation

irregularity. The height noise std. was varied between

0 ≤ σ

≤ 0.3r. The upper end of the noise is typi-

cal to many LiDAR applications. The height noise

distributions from real LiDAR data are not uniform

nor Gaussian. The main curvature spectrum seems to

depend mainly on the std of the uniform or natural

height distribution, not from the choice between the

two.

-2 0 2

-1

0.5*(

)

-2 0 2

-1

1 2

-2 0 2

-1

-2 0 2

-1

triang.

ideal

Figure 7: The triangular mean curvature and triangular

Gaussian curvature and two curvature eigenvalues on a to-

rus as a function of the angle φ associated with the smaller

radius. The height noise is at the maximum σ

/r = 0.3.

3.3 A Prostate Tumor

The main difﬁculty with MRI point clouds arises from

the anisotropy of the point cloud. The voxels are

elongated 2.75 × 0.48 × 0.48 mm

and this demands

a lot from the curvature analysis methods. Informa-

tion about the curvature spectrum of the tumor has

been applied to e.g. breast cancer classiﬁcation (Lee

et al., 2015). It is possible that the curvature spectrum

will be an important feature alongside spatial texture

patterns, 3D Fourier transform, overall size and loca-

tion of the tumor for clustering algorithms. The Gaus-

sian curvature and principal curvature direction can

help in e.g. descriptor based vectorization (Vranic

and Saupe, 2001). Fig. 10 depicts a prostate lesion,

which shows a typical developable shape: the lesion

could be spread back to planar (its Gaussian curvature

is approximately zero).

3.4 Results

Our method, when referred, means triangular mean

and Gaussian (Eqs. 5, 4, 10) and the principal curva-

tures derived from them. Tests reach the high noise

amplitude range σ

/r = 0.3 typical to the natural re-

source data, see Fig. 7. Effects of noise ﬁltering of L-

B and our method have been depicted in Fig. 8. L-B

is bound by its ﬁdelity to local geometry. Difference

at smooth surface (the left part of the abscissa) is due

to the irregularity of the triangles, which brings some

advantage to an averaging method like ours.

−4

−3

−2

−1

0.3

0.4

0.6

0.8

RMSE(H)

Effect of height noise to mean curvature error

triang.

Figure 8: The root mean square error of the mean curva-

ture H estimation error under different perpendicular noise

levels σ

(std.) on a torus with radii r and R.

Fig. 9 has curvature spectrae based on L-B and

our method. Other methods were inferior at the noisy

end and had to be excluded. The presence of noise

spreads the detected spectrum from the ideal smooth

case. L-B manages the task only if the triangulariza-

tion is rather regular and the height noise almost zero.

Our method captures two-thirds of the mean curva-

ture distribution, yet suffers from the spectrum spread

caused by the noise, which is inevitable. Both Gaus-

sian approximations perform as well enabling e.g. the

curvature spectrum classiﬁcation to be possible under

wide range of noise levels. Other two methods (con-

centrated and barycentric) perform worse than L-B.

Fig. 10 depicts the prostate lesion with the Gaus-

sian curvature close to zero everywhere meaning its

surface is mostly developable (a so called ruler sur-

face). This is an artifact caused by a combination of

the elongated voxels and the method used for trian-

gularization. The surface has high energy noise com-

ponent caused by the voxel granularity. Our methods

dampen this highest geometric noise component au-

tomatically. Also concentrated and barycentric mean

curvatures performs surprisingly well. L-B suffers

from its ﬁdelity to the highest shape frequency com-

ponent.

The computational cost of the barycentric method

is too high when compared to its performance, see

ICPRAM 2017 - 6th International Conference on Pattern Recognition Applications and Methods

690

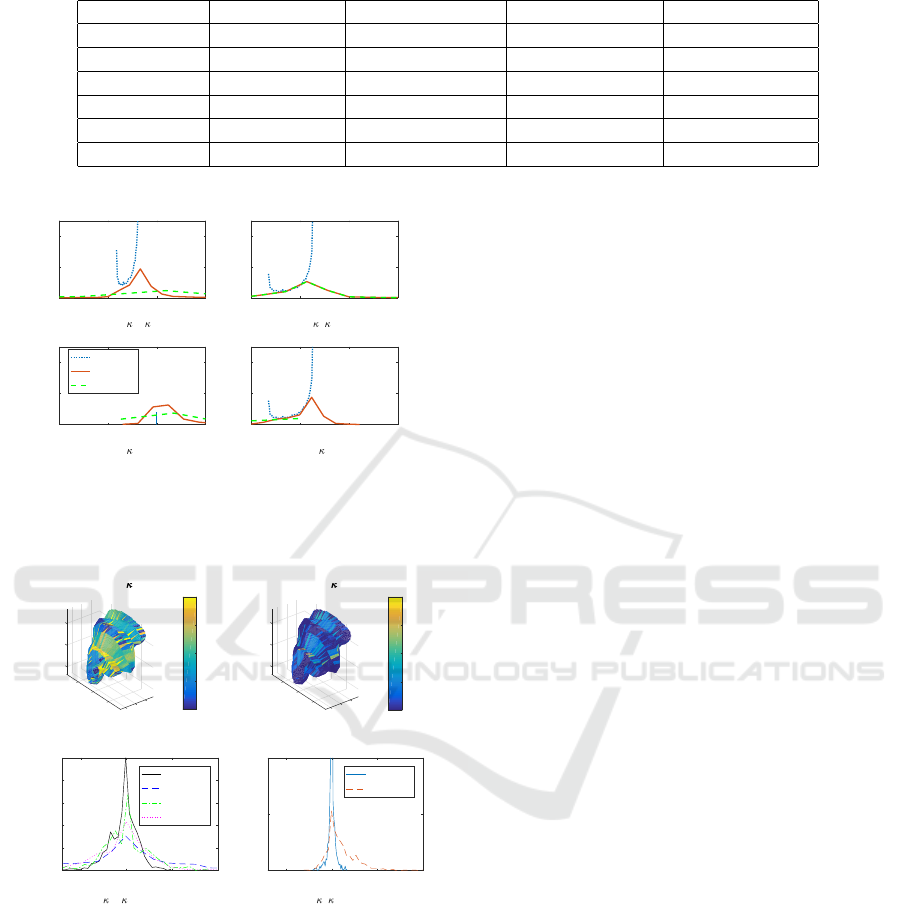
Table 1: Evaluation of the mean curvature methods. Proposed methods in boldface.

Method Vector opers/t Spectrum quality Singular noise w Massive noise w

vertex G 15 good 1 1

triangular G 15 good 1/3 0

triangular H 15 good 1/3 0

LB 18 average 1 1

concentrated 2 poor 1 1

barycentric 32 poor 1/3 0

-1 0 1 2

0.5*(

)

-1 0 1 2

1 2

-1 0 1 2

ideal

triangular

L-B

Figure 9: The ideal curvature spectra of a torus with r = 1,

and Laplace-Beltrami and triangular approximations. The

effect of height noise σ

/r = 0.1 spreads out the approxi-

mated spectrae.

160

170

180

x,y,z (mm)

160

triangul.

150

-0.1

0.1

0.2

0.3

-1

160

170

180

x,y,z (mm)

160

triangul.

150

-0.1

0.1

0.2

0.3

-1

-0.5 0 0.5 1

(

)/2 (mm

-1

)

mean curvature H

triangular

L-B

concentr

barycentr

-0.5 0 0.5 1

1 2

(mm)

-2

Gaussian curvature G

triangular

vertex

Figure 10: Upper row: the principal curvature components.

Lower row: Distributions of the mean and Gaussian curva-

tures by different methods.

Table 1. L-B has the best accuracy when the perpen-

dicular noise is small and the triangulation is rather

regular, but fails when the perpendicular noise is high.

The spectrum quality is given a qualitative judgement.

See the deﬁnition of the dampening ratio w at Sec. 3.1.

4 CONCLUSIONS

The proposed method (triangular mean and Gaussian

curvature) has about the same computational demand

as the reference method (LB mean and vertex Gaus-

sian curvature) in case where the vertex speciﬁc area

of the mixed Voronoi cell is computed exactly as

recommended in (Mesmoudi et al., 2012). Based on

the good performance under height noise, it seems

that the triangular method should be used in such na-

tural resource data applications, where the curvature

spectrum is required, and the spectral range should

reach near the highest shape frequency, but excluding

the large excitations of the mentioned frequency.

The above deﬁnition may seem contrived, but e.g.

a typical rasterization process is lossy and tuning the

ﬁltering process requires a lot of parameters, which

concern the highest shape frequency naturally contai-

ned with the methods proposed here. Further valida-

tion is necessary with e.g. track analysis of forestry

harvesters (Pierzchala et al., 2016).

Principal orientation computation presented in

Sec. 2.7 is closely related to other two methods pre-

sented, e.g. it uses the same projected tip angle weig-

hts. One has to inspect in the future how useful the

principal orientations are in micro-topographic analy-

sis. It may be that a multi-scale approach for produ-

cing several TIN models with coherent curvature and

principal orientation information is needed.

There is a huge bulk of raster analysis methods

and a lot of experience in applying these methods for

e.g. height raster data analysis. Emerging triangular

analysis tools based on DDG will not outdate these

methods, but in some cases there seems to be potential

to improve the curvature spectrum range closer to the

theoretical limit dictated by the point cloud sample

density and the known sample accuracy.

ACKNOWLEDGEMENTS

This work was supported by the funding from the

Academy of Finland (Grant 295336). Kevin R. Vixie

Triangular Curvature Approximation of Surfaces - Filtering the Spurious Mode

691

and Otis Chodosh brought up the intuitive view to

mean curvature on Math Overﬂow site on 2012.

REFERENCES

Crane, K., de Goes, F., Desbrun, M., and Schr

oder, P.

(2013). Digital geometry processing with discrete ex-

terior calculus. In ACM SIGGRAPH 2013 Courses,

SIGGRAPH ’13, pages 7:1–7:126, New York, NY,

USA. ACM.

Dorst, L., Fontijne, D., and Mann, S. (2007). Geometric

Algebra for Computer Science: An Object-Oriented

Approach to Geometry. Morgan Kaufmann Publishers

Inc., San Francisco, CA, USA, 1st edition.

Golub, G. H. and Van Loan, C. F. (1996). Matrix Com-

putations (3rd Ed.). Johns Hopkins University Press,

Baltimore, MD, USA.

Jin, S., Lewis, R., and West, D. (2005). A comparison of

algorithms for vertex normal computation. The Visual

Computer, 21:71–82.

Lee, J., Nishikawa, R. M., Reiser, I., Boone, J. M., and

Lindfors, K. K. (2015). Local curvature analysis for

classifying breast tumors: Preliminary analysis in de-

dicated breast ct. Medical Physics, 42(9).

Max, N. (1999). Weights for computing vertex normals

from facet normals. Journal of Graphics Tools, 4(2).

Mesmoudi, M. M., De Floriani, L., and Magillo, P. (2012).

Discrete curvature estimation methods for triangula-

ted surfaces. In Applications of Discrete Geometry

and Mathematical Morphology, pages 28–42. Sprin-

ger.

Meyer, M., Desbrun, M., Schr

oder, P., and Barr, A. H.

(2003). Visualization and Mathematics III, chapter

Discrete Differential-Geometry Operators for Trian-

gulated 2-Manifolds, pages 35–57. Springer Berlin

Heidelberg, Berlin, Heidelberg.

Mitra, N. J. and Nguyen, A. (2003). Estimating surface

normals in noisy point cloud data. In Proceedings of

the Nineteenth Annual Symposium on Computational

Geometry, SCG03, pages 322–328, New York, NY,

USA. ACM.

Nevalainen, P., Middleton, M., Kaate, I., Pahikkala, T., Su-

tinen, R., and Heikkonen, J. (2015). Detecting stony

areas based on ground surface curvature distribution.

In 2015 International Conference on Image Proces-

sing Theory, Tools and Applications, IPTA 2015, Orle-

ans, France, November 10-13, 2015, pages 581–587.

Nevalainen, P., Middleton, M., Sutinen, R., Heikkonen, J.,

and Pahikkala, T. (2016). Detecting terrain stoniness

from airborne laser scanning data . Remote Sensing,

8(9):720.

Pierzchala, M., Talbot, B., and Astrup, R. (2016). Mea-

suring wheel ruts with close-range photogrammetry.

Forestry, 89(4):383–391.

Pressley, A. (2010). Elementary Differential Geometry.

Springer Undergraduate Mathematics Series. Springer

London.

Rusinkiewicz, S. (2004). Estimating curvatures and their

derivatives on triangle meshes. In Symposium on 3D

Data Processing, Visualization, and Transmission.

Schaer, P., Skaloud, J., Landtwing, S., and Legat, K. (2007).

Accuracy Estimation for Laser Point Cloud Including

Scanning Geometry. In Mobile Mapping Symposium

2007, Padova.

Theisel, H., R

ossl, C., Zayer, R., and Seidel, H. P. (2004).

Normal based estimation of the curvature tensor for

triangular meshes. In In PG04: Proceedings of the

Computer Graphics and Applications, 12th Paciﬁc

Conference on (PG2004), pages 288–297. IEEE Com-

puter Society.

van Oosterom, A. and Strackee, J. (1983). A solid angle of a

plane triangle. IEEE Trans. Biomed. Eng., 30(2):125–

126.

Vranic, D. V. and Saupe, D. (2001). 3d shape descriptor

based on 3d fourier transform. In Fazekas, K., edi-

tor, 3D Shape Descriptor Based on 3D Fourier Trans-

form In Proceedings of the EURASIP Conference on

Digital Signal Processing for Multimedia Communi-

cations and Services (ECMCS 2001), pages 271–274.

Wardetzky, M., Mathur, S., Kaelberer, F., and Grinspun, E.

(2007). Discrete laplace operators: No free lunch. In

Belyaev, A. and Garland, M., editors, Geometry Pro-

cessing. The Eurographics Association.

Yang, P. and Qian, X. (2007). Direct computing of surface

curvatures for point-set surfaces. In SPBG’07, pages

29–36.

ICPRAM 2017 - 6th International Conference on Pattern Recognition Applications and Methods

692