Brain Tumor Segmentation Based on Non Negative Matrix Factorization
and Fuzzy Clustering
Ujjwal Baid
1
, Shubham Talbar
2
and Sanjay Talbar
1
1
Department of Electronics and Telecommunication Engineering,
Shri Guru Gobind Singhji Institute of Engineering and Technology, Nanded, India
2
Department of Biologically Inspired System Sciences, Indian Institute of Technology, Jodhpur, Rajasthan, India
Keywords:
Brain Tumor Segmentation, Non-negative Matrix Factorization, Fuzzy Clustering.
Abstract:
The problem of computational brain tumor segmentation has attracted researchers over a decade because of
its high clinical relevance and challenging nature. Automatic and accurate detection of brain tumor is one
of the major areas of research in medical image processing which helps radiologists for precise treatment
planning. Magnetic Resonance Imaging (MRI) is one of the widely used imaging modality for visualizing and
assessing the brain anatomy and its functions in non-invasive manner. In this paper a novel approach for brain
tumor segmentation based on Non-Negative Matrix Factorization(NMF) and Fuzzy clustering is proposed.
Proposed algorithm is tested on BRATS 2012 training database of High Grade and Low Grade Glioma tumors
with clinical and synthetic data of 80 patients. Various evaluation parameters like Dice index, Jaccard index,
Sensitivity, Specificity are evaluated. Comparison of experimental results with other state of the art brain tumor
segmentation methods demonstrate that proposed method outperforms existing segmentation techniques.
1 INTRODUCTION
Gliomas are the most frequent p rimary brain tumors
in adults and account for 70% of adult malignant
primary brain tumo rs with average survival time of
one year. Glioma arises from glial cells and infiltra-
tes the surrounding tissues such as white matter fiber
tracts with very rapid growth [Menze et al., 2015].
Axial slice of T1 weighted, T2 weighted and Fluid-
attenuated inversion recovery(FLAI R) magnetic reso-
nance images are shown with Glioblastoma tumor in
fig. 1. On the right side, different heterogeneous regi-
ons of the brain tumor i.e. edema, active and necrotic
regions are shown. Accurate segmentation of brain
tumor tissues from Brain MRI images is of profound
importance in many clinical applications such as sur-
gical planning and image-guided interventions.
Brain tumor segmentation is challenging task be-
cause o f its non-rigid and complex shape, variation in
size and position from patient to patient which make
classical segmentation techniques, su c h as threshol-
ding, edge detection, region g rowing, classification
and clustering ineffective at accurate delineation of
complex bound aries between tumor and healthy tis-
sues. Brain tumor segmentatio n methods are broadly
classified into four categories as: Threshold based,
Region based, Pixel classification based and Mo del
based techniques with pros and cons over each ot-
her [Gordillo et al., 2013]. Baue r e t al. [S. Bauer and
Reyes, 2012] pro posed brain tumor segmentation ap-
proach based on integrated hierarchical classification
and regulariz a tion in an energy minimization scheme.
Geremia et al. [E. Geremia and Ayache, 2012 ] pre-
Figure 1: L eft: Axial slice of MRI with T1, T2, FLAIR mo-
dalities and Right: intra-tumor tissues parts. [Corso et al.,
2008].
134
Baid U., Talbar S. and Talbar S.
Brain Tumor Segmentation Based on Non Negative Matrix Factorization and Fuzzy Clustering.
DOI: 10.5220/0006250701340139
In Proceedings of the 10th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2017), pages 134-139
ISBN: 978-989-758-215-8
Copyright
c
 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Figure 2: Proposed block diagram for Brain Tumor segmentation from MRI i mages.
sented automatic segmentation of gliomas in 3D MR
images with ra ndom decision fo rest framework which
gives a voxel-wise probabilistic classification. Many
approa c hes to brain tumor segmentation h ave been
implemented over decades but there is no winning
theory.
Non-negative Matrix Factorization (NMF) is di-
mensionality reduction tool used in machine lear-
ning with wide range of applications in data mining.
Non-negative Matrix Factorization (NMF) can c luster
complex data with extracting features. These features
can learn characteristics of data classes. This signifi-
cance o f NMF is of great use in ima ge segmentation.
In NMF segmentation features are extracted in a new
space obtained by decomposing input data into basis
matrix W and coefficient matrix H. Vectors of coeffi-
cient matrix H represent the degree of association o f
each data point to the basis feature [Lee and Seung,
2000]. There are very few approaches for medical
image segmentation using NMF. Xie et al. [Xie et al.,
2011] proposed a method for segmentation which ex-
tracts the basis tenso r images from the diffusion ten-
sor images DTI data.
This DTI data is factorised using NMF and
then segmen ted. Sandler et al. [Sandler and Lin-
denbaum, 2011] propo sed a segmentation ap proach
where image is divided into several regions and his-
togram of each region is factorized using NMF. Hos-
seini [Hosseini-asl et al., 2014] proposed lung seg-
mentation in CT images based on NMF with visual
appearance mo delling. Lung voxels were separated
from chest voxels ba sed on extracted model and k-
means clustering. Dera et al. [Dera, 2015] propo-
sed segmentation algorithm for brain MRI using le-
vel set and NMF. Number o f distinct regions in image
and and their local distribution is evaluated which is
incorporated into energy function of Level set met-
hod. Though some researcher s have proposed NMF
for segmentation, applying NMF in M RI images is
still challenging.
2 PROPOSED METHOD
In this paper a novel framework is proposed for Brain
tumor segmentation . The block diagram for the pro-
posed framework is shown in fig. 2 com prising seven
steps. I n first step MRI volume of FLAIR images is
pre-processed with anisotropic filter. Data matrix(V)
is generated in second step while decomposition of
data matrix(V) in to b a sis matrix(W) and coefficient
matrix(H) is achieved in next step. The fourth step
is u sed to cluster the coefficient matrix(H) with fuzzy
C-means clustering which segments whole tumor in
FLAIR slice. Step 5, step 6 and step 7 gives Necrotic
tumor segmentation in T2 slices. The above steps are
discussed below in detail.
2.1 Preprocessing on MRI Volume
Pre-proc essing operations like de-noising, skull strip-
ping and intensity normalization have direct impact
on brain tumor segmentation. FLAIR and T2 MRI vo-
lume is pre-processed with anisotropic diffusion filte-
Brain Tumor Segmentation Based on Non Negative Matrix Factorization and Fuzzy Clustering
135

ring for de-noising. Bias field normalization is carried
out with ITK N3 from [Tustison and Gee, 2010].
2.2 Construction of Data Matrix V
The idea behind the construction of data matrix is
to incorporate the contextual information pre sent in
inter-slices of MRI image volume for better segmen-
tation. Every pixel in the slice to be segmented is re-
presented by 27 pixels. These 27 pixels comprised of
9 pixels from the slice to be segmented, 9 pixels from
the previous slice and 9 pixels from the next slice i.e.
(3 ×3 × 3) win dow as shown in step 2 of fig. 2. Thus,
for every pixel a voxel of 27 elements is obtained. All
voxels are concatenated to form data m a trix(V).
2.3 Decomposition of Data Matrix (V )
As each pixel is represented by 27 pixels, size of
the data ma trix (D) is increased significantly and we
need dimensionality reduc tion to overcome this pro-
blem. To decompose multi-dimensional matrix, Non-
negative Ten sor Decomposition( NTD) was proposed
[Cichocki et al., 2009]. However, in this method large
matrices are computed using iterative steps of multi-
dimensional matrix product and division which is
computationally complex. Hence, NMF is preferred
over NTD to overcome this pro blem. NMF compu-
tes a lower rank approximation with non-subtractive
combinations of non-negative basis vectors. Consi-
der data matrix V ∈ R
m×n
and desired rank is p ≪
min(m,n). The data matrix V can be decomposed
into basis m atrix W ∈ R
m×p
and coefficient matrix
H ∈ R
p×n
as shown in eq. 1. The coefficient matrix
can also be termed a s feature ma trix.
V ≈ W H (1)
where, W and H are non-negative. W is basis ma-
trix and H is coefficient matrix which can be obtained
by reformu la ting the optimization problem in e q 2.
min
W,H
F(W,H) ≡k V − W H k
F
, s.t. W,H > 0, (2)
To optimize eq 2. several algorithms have been
developed like Multiplicative Alternate Least Squ a-
res (ALS), Projected Gradient Descent (PGD) [Ber ry
et al., 2007] . In our approach Alternate Non-negative
Least Square Algorithm b ased on active set (ANLS-
AS) is used [Kim and Park, 2008] . Cost function mi-
nimization ( Co nvergence) is w ith less iterations and
faster in ANLS-AS compare to other optimizing met-
hods which is desirable. I n ANLS eq. 3 is iterated till
the co nvergence criteria is satisfied. While iterating
in eq. 3 H is fixed whereas in eq. 4, W is fixed.
min
W ≥0
k H
T
W
T
−V
T
k
2
F
(3)
min
H≥0
k W H −V k
2
F
(4)
Generalised cost function for ANLS-AS algo-
rithm is given in eq. 5
min
G≥0
k BG −Y k
2
F
(5)
where, B ∈ R
p×q
and Y ∈ R
p×l
and we need to
optimize G. Eq. 5 c an be decomposed into l inde-
pendent NLS equations with m ono right hand side as
given in eq. 6
min
G≥0
k BG −Y k
2
F
→ min
g
1
≥0
k Bg
1
− y
1
k
2
2
, ...
... min
g
l
≥0
k Bg
l
− y
l
k
2
2
(6)
where, G = [g1, ...,g
l
] ∈ R
q×l
and Y = [y1,...,y
l
] ∈
R
p×l
Eq. 3 and eq. 4 are solved alternatively at each
iteration and c onverted to the form of eq. 5. Afte r the
convergence criteria is fulfilled, ea ch colum n of W re-
presents basis vector and each column of H represents
coefficient vector which is shown in step 2 of fig. 2.
2.4 Segmentation with FCM
In this step coefficient matrix H is segmented with
fuzzy c-means clustering algorithm to cluster voxels.
With region growing algorithm, whole tumor is seg-
mented in FLAIR image and whole tumor mask is
created. Af te r this step whole tumor is segmented i. e.
Edema and Necrotic part together.
2.5 Segmentation of Necrotic Tumor
Tumor ma sk which was obtained by region growing
segmentation in FLAIR slice is multiplied with cor-
respond ing T2 slice. It is observed that necrotic cells
differs from Edema in T2 slice. Step two, three and
four are repeated with the output of step five. Again
with region growing algorithm necrotic part is seg-
mented in T 2 slice. In fina l step, segmentation out-
put of necrotic tumor is overlayed on segmentation o f
whole tumor.
3 RESULTS AND DISCUSSION
In order to evaluate the accuracy of the proposed seg-
mentation approach, we assess its performance on the
BIOIMAGING 2017 - 4th International Conference on Bioimaging
136

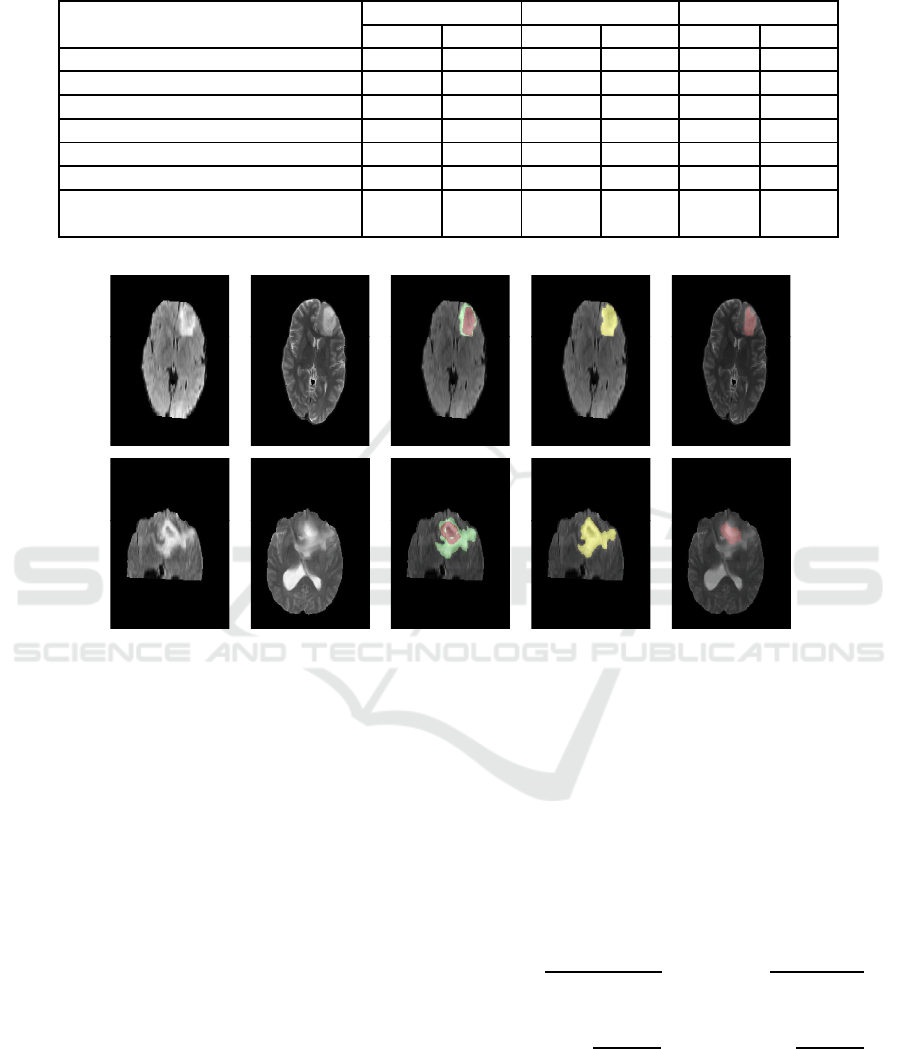
Table 1: Comparison between proposed method and other approaches in terms of dice similarity coefficient. Note that the
results of our segmentation algorithm are obtained (3 × 3 × 3) window.
Dataset
High Grade Real Low Grade Real Average
Edema Tumor Edema Tumor Edema Tumor
[Zikic et al., 2012] 0.70 0.71 0.44 62
[S. Bauer and Reyes, 2012] 0.61 0.62 0.35 0.49 0.59 0.73
[E. Geremia and Ayache, 2012] 0.56 0.68 0.29 0.52 – –
[Hamamci and Unal, 2012] 0.56 0.73 0.38 0.71 – –
[Menze et al., 2012] 0.69 0.70 0.49 0.23 – –
[T. Riklin Raviv and Menze, 2012] 0.60 0.58 0.35 0.32 – –
Proposed
Method
0.77 0.72 0.80 0.76 – –
(a) FLAIR slice (b) T2 slice (c) Ground
Truth
(d) Whole
Tumor Segmen-
tation
(e) Necro-
tic Tumor
Segmentation
Figure 3: Segmentation results of L ow Grade Glioma Tumor (Real).
BRATS 2012 challenge dataset. BRATS 2012 trai-
ning dataset consists of fully an notated 20 High Grade
Glioma (Real), 10 Low Grade Glioma(Real), 25 High
Grade Glioma (Synthetic) and 25 Low Grade Glioma
(Synthetic) patients [Menze et al., 2 015]. Real data
images are obtained from various hospitals an d synt-
hetic images are generated using TumorSim software
with gro und-truth. MRI volume in the 2012 data-
set contains skull-stripped m ultimodal MR image vo-
lume of 80 patients. For each patient, T1, T2, T1c,
FLAIR MR images are available with ground truth
marked by clinicians as edema, necrotic and whole
tumor.
All volumes are skull stripped and linearly co-
registered using affine registration and interpolated to
1mm isotropic resolution. We have segmented the vo-
lume into Whole tumor, edema and necrotic/c ore clas-
ses with proposed algorithm. Let, T
0
and T
1
be the
normal tissue and tumor tissue marked in the ground
truth. Similarly, P
0
and P
1
be the p redicted normal tis-
sue an d tumor tissue segmented with the algorithms.
Va rious performanc e parameters like Dice coefficient,
Jaccard co efficient, Sensitivity, Specificity are evalua-
ted for comparison. Dice and Jaccard coefficients are
widely used as evaluation tool to find segmentation
accuracy between segmented image and ground truth
and given in eq. 7 and eq. 8
Dice =
|P
1
∧ T
1
|
(|P
1
| + |T
1
|)/2
Jaccard =
|P
1
∧ T
1
|
(|P
1
| ∪ |T
1
|)
(7)
Sensitivity =
|P
1
∧ T
1
|
|T
1
|
Speci f icity =
|P
0
∧ T
0
|
|T
0
|
(8)
Segmentation resu lts with the proposed alg orithm
are shown in fig. 5, fig. 3, and fig. 4 for High Grade
Real, Low Grade Real and synthetic tumors respecti-
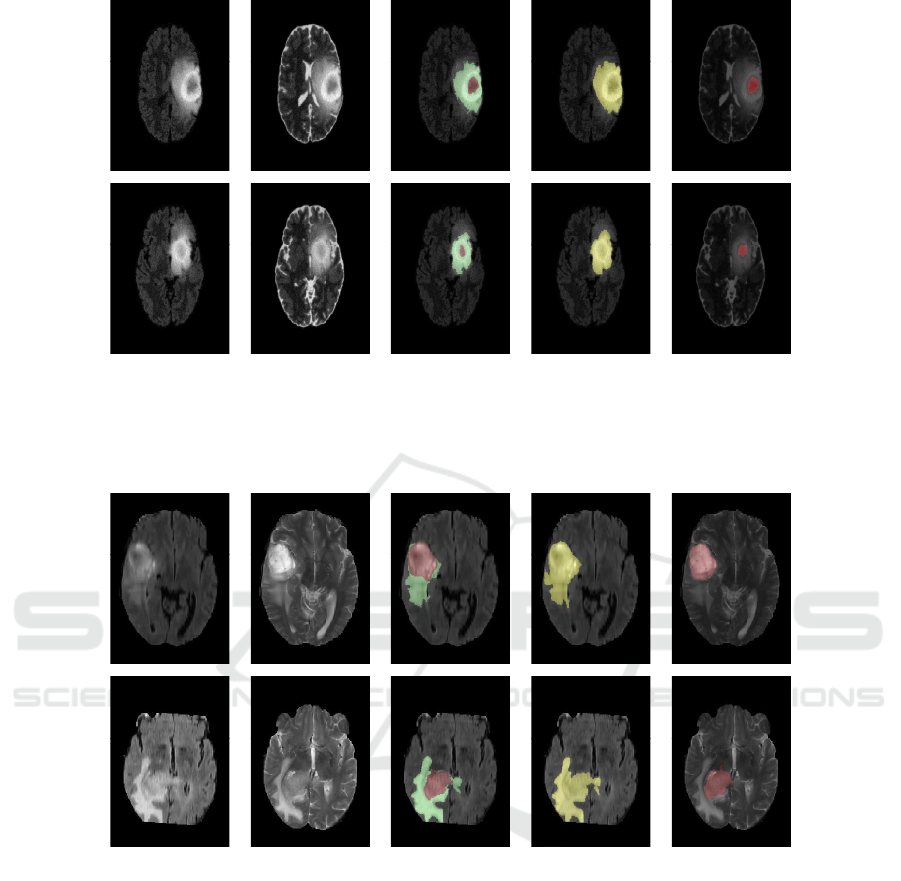
vely. Each row represents (from left to rig ht) FLAIR
slice, T2 slice, Gr ound Truth, Whole tumor segmenta-
tion in FLAI R slice, Necrotic tumor segmentation in
Brain Tumor Segmentation Based on Non Negative Matrix Factorization and Fuzzy Clustering
137

(a) FLAIR slice (b) T2 slice (c) Ground
Truth
(d) Whole
Tumor Segmen-
tation
(e) Necro-
tic Tumor
Segmentation
Figure 4: Segmentation results of Synthetic High Grade Gl ioma Tumor (1st row ) and Synthetic Low Grade Glioma Tumor(2nd
row).
(a) FLAIR slice (b) T2 slice (c) Ground
Truth
(d) Whole
Tumor Segmen-
tation
(e) Necro-
tic Tumor
Segmentation
Figure 5: Segmentation results of High Grade Glioma Tumor (Real).
T2 slice. The proposed method a chieves mean Dice
Similarity Coefficient as 0.77 for tum or and 0.81 for
edema for (3 × 3 × 3) window. T he detailed experi-
mentation results with d ice similarity coefficient, sen-
sitivity, specificity and Hausdorff distance are listed
in Table 1.
Comparison with the existing segmenta tion
techniques is shown in Table 1 which demonstrate
that our method pe rforms better in terms of dice simi-
larity coefficient. Proposed algorithm is furthe r evalu-
ated on different window sizes (5 ×5 ×3), (7 ×7 ×3)
and (9 × 9 × 3). It is found that (3 × 3 × 3) window
outperforms over other sizes. Also, for the larger win-
dow sizes the dimension of the voxel increases wh ic h
in turn increases co mputation complexity for factori-
zation of data matrix (V ).
4 CONCLUSION
A new method for brain tumor segmen ta tion has been
proposed based on Non Negative matrix factoriza-
tion(NMF) and fuzzy c-means clustering. Segmenta-
tion accuracy in terms of dice similarity coefficient is
BIOIMAGING 2017 - 4th International Conference on Bioimaging
138

improved by incorporating pixel info rmation present
in p revious slice and next slice in MRI volume d ata.
The performance of our method is evaluated on 80
patients of BRATS 20 12 training dataset and comp a-
red with other existing segmentation techniques. The
results demonstrate tha t our method outperfor ms the
other brain tumor segmentation algorithm. The per-
formance of the proposed algorithm is also compared
by varying window sizes i. e. voxel with different di-
mensions and it can be conclu ded that best results are
obtained for (3 × 3 × 3) wind ow. In future, segmen-
tation accuracy can be improved by delineating mor e
accurate boundary using T1c MRI volume data which
differentiates tumor boundary with non tumor tissue.
ACKNOWLEDGEMENTS
This research work ha s been suppor te d by Visvesva-
raya PhD sche me of Ministry of Electronics & Infor-
mation Technology, Government of India.
REFERENCES
Berry, M. W., Browne, M., Langville, A. N., Pauca, V. P.,
and Plemmons, R. J. (2007). Algorithms and appli-
cations for approximate nonnegative matrix factori-
zation. Computational Statistics and Data Analysis,
52(1):155–173.
Cichocki, A., Zdunek, R., Phan, A. H., and Amari, S. I.
(2009). Nonnegative Matrix and Tensor Factoriza-
tions: Applications to Exploratory Multi-Way Data
Analysis and Blind Source Separation.
Corso, J. J., Sharon, E., Dube, S., El-Saden, S., Sinha,
U., and Yuille, A. (2008). Efficient multilevel brain
tumor segmentation wit h integrated bayesian model
classification. IEEE Transactions on Medical Ima-
ging, 27(5):629–640.
Dera, D. (2015). Level Set Segmentation using Non-
Negative Matrix Factorization of Brain MRI Images.
E. Geremia, B. M. and Ayache, N. (2012). Spatial decision
forests for glioma segmentation in multi-channel mr
images. Proc.MICCAI-BRATS, pages 14–18.
Gordillo, N., Montseny, E., and Sobrevilla, P. (2013). State
of the art survey on MRI brain tumor segmentation.
Magnetic Resonance Imaging, 31(8):1426–1438.
Hamamci, A. and Unal, G. (2012). Multimodal brain tumor
segmentation using the ”tumor-cut” method on the
brats dataset. Proc.MICCAI-BRATS, pages 19–23.
Hosseini-asl, E., Zurada, J. M., and El-baz, A. (2014). Lung
Segmentation Based on Nonnegative Matrix Factori-
zation Electrical and Computer Engineering Depart-
ment , University of Louisville , Louisville , K Y
, USA . Bioengineering Department , University of
Louisville , Louisville , KY , USA . Information Tech.
(502):877–881.
Kim, H . and Park, H. (2008). N onnegative matrix factori-
zation based on alternating nonnegativity constrained
least squares and active set method. SIAM Journal on
Matrix Analysis and Applications, 30(2):713–730.
Lee, D. D. and Seung, H. S. (2000). 401788a0. 401(October
1999):788–791.
Menze, B . H., Jakab, A., Bauer, S., Kalpathy-Cramer, J.,
Farahani, K., Kirby, J., Burren, Y., Porz, N., Slot-
boom, J., Wiest, R., Lanczi, L., Gerstner, E., Weber,
M. A., Arbel, T., Avants, B. B., Ayache, N., Buendia,
P., Collins, D. L., Cordier, N., Corso, J. J., Criminisi,
A., Das, T., Delingette, H., Demiralp, ., Durst, C. R.,
Dojat, M., Doyle, S., Festa, J., Forbes, F., Geremia,
E., Glocker, B., Golland, P., Guo, X., Hamamci, A.,
Iftekharuddin, K. M., Jena, R., John, N. M., Konu-
koglu, E., Lashkari, D., Mariz, J. A., Meier, R., Pe-
reira, S., Precup, D., Price, S. J., Raviv, T. R., Reza,
S. M. S., Ryan, M., Sarikaya, D., Schwartz, L., S hin,
H. C., Shotton, J., Silva, C. A., Sousa, N., Subbanna,
N. K., Szekely, G., Taylor, T. J., Thomas, O. M., Tus-
tison, N. J., Unal, G., Vasseur, F., Wintermark, M.,
Ye, D. H., Zhao, L., Zhao, B., Zikic, D., Prastawa,
M., Reyes, M., and Leemput, K. V. (2015). The
multimodal brain tumor i mage segmentation bench-
mark (brats). IEEE Transactions on Medical Imaging,
34(10):1993–2024.
Menze, B. H., Leemput, K. V., Lashkari, D., Weber, M. A.,
Ayache, N., and Golland, P. (2012). Segmenting gli-
oma in multi-modal images using a generative model
for brain lesion segmentation. Proc.MICCAI-BRATS,
pages 49–55.
S. Bauer, T. Fejes, J. S. R. W. L. P. N. and Reyes, M.
(2012). Segmentation of brain tumor images based
on integrated hierarchical classification and regulari-
zation. Proc.MICCAI-BRATS, pages 10–13.
Sandler, R. and Lindenbaum, M. (2011). Nonnegative ma-
trix factorization with earth mover’s distance metri c
for image analysis. IEEE Transactions on Pattern
Analysis and Machine Intelligence, 33(8):1590–1602.
T. Riklin Raviv, K. V. L. and Menze, B. H. (2012). Multi-
modal brain tumor segmentation via latent atlases.
Proc.MICCAI-BRATS, pages 64–73.
Tusti son, N. and Gee, J. (2010). N4itk: Nick’s n3 itk imple-
mentation for mri bias field correction.
Xie, Y., Ho, J., and Vemuri, B. C. (2011). Nonnegative
factorization of diff usion tensor images and its appli-
cations. LNCS, 6801:550–561.
Zikic, D., Glocker, B., Konukoglu, E., Shotton, J., Crimi-
nisi, A., Ye, D. H., Demiralp, C., Thomas, O. M., Das,
T., Jena, R., and Price, S. J. (2012). Context-sensitive
classification forests for segmentation of brain tumor
tissues. Proc.MICCAI-BRATS, pages 1–9.
Brain Tumor Segmentation Based on Non Negative Matrix Factorization and Fuzzy Clustering
139