Dynamic Indexing for Incremental Entity Resolution in Data
Integration Systems
Priscilla Kelly M. Vieira
1,2
, Bernadette Farias Lóscio
1
and Ana Carolina Salgado
1
1
Federal University of Pernambuco, Center of Informatics, Recife, Pernambuco, Brazil
2
Federal Rural University of Pernambuco, Recife, Pernambuco, Brazil
Keywords: Data Integration, Entity Resolution, Data Matching, Duplicate Detection, Indexing.
Abstract: Entity Resolution (ER) is the problem of identifying groups of tuples from one or multiple data sources that
represent the same real-world entity. This is a crucial stage of data integration processes, which often need to
integrate data at query time. This task becomes even more challenging in scenarios with dynamic data sources
or with a large volume of data. As most ER techniques deal with all tuples at once, new solutions have been
proposed to deal with large volumes of data. One possible approach consists in performing the ER process on
query results rather than the whole data set. It is also possible to reuse previous results of ER tasks in order to
reduce the number of comparisons between pairs of tuples at query time. In a similar way, indexing techniques
can also be employed to help the identification of equivalent tuples and to reduce the number of comparisons
between pairs of tuples. In this context, this work proposes an indexing technique for incremental Entity
Resolution processes. The expected contributions of this work are the specification, the implementation and
the evaluation of the proposed indexes. We performed some experiments and the time spent for storing,
accessing and updating the indexes was measured. We concluded that the reuse turns the ER process more
efficient than the reprocessing of tuples comparison and with similar quality of results.
1 INTRODUCTION
In the last years, companies and government
organizations around the world increased their
production of digital data. In general, these data are
stored in multiple data sources, which can be
heterogeneous and dynamic. To access and analyze
these data in a uniform and integrated fashion, data
integration strategies are needed. The aim of data
integration is to combine heterogeneous and
autonomous data sources for providing a single view
to the user (Gruenheid et al, 2014). One of the main
steps of the data integration process is the Entity
Resolution (ER) (Christen, 2012).
The ER process aims to identify tuples from one
or multiple data sources referring to the same real-
world entity. This problem has been the focus of
several works (Christen, 2012) and it is known by a
variety of names: Record Linkage, Entity Resolution,
Object Reference, Reference Linkage, Duplicate
Detection or Deduplication. In this paper, we adopt
the term Entity Resolution (Christen, 2012).
Given a large volume of data, ER can be a very
costly and time-consuming process. In general, the
most cost-demanding task of the ER process is the
tuple pair comparison, which requires the comparison
of every pair of tuples to calculate the corresponding
similarity. To reduce costs, ER can be performed in
an incremental way. In this case, just a subset of the
available tuples, i.e., an increment, is processed and
compared at each iteration of the ER process.
Additionally, results of previous iterations can be
reused during the comparison of new tuples. Doing
this, the volume of classified tuples increases
incrementally reducing the costs of the overall ER
process.
In this paper, we focus on an incremental ER
approach over query results. This means that the
increment is the query result and the ER should be
performed at query execution time. Given that we are
dealing with large volumes of data, performing the
ER at query time is even more challenging. Among
the solutions proposed in the literature to deal with
this challenge, we are interested on the use of
indexing techniques (Christen, 2012).
To reduce the costs of performing ER at query
execution time, we propose a dynamic indexing
technique. The dynamic indexes are available in main
memory, reducing the costs of disk access, and can be
Vieira, P., Lóscio, B. and Salgado, A.
Dynamic Indexing for Incremental Entity Resolution in Data Integration Systems.
DOI: 10.5220/0006251801850192
In Proceedings of the 19th International Conference on Enterprise Information Systems (ICEIS 2017) - Volume 1, pages 185-192
ISBN: 978-989-758-247-9
Copyright © 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
185

updated to reflect the new results of the incremental
ER process. In the following, we summarize the main
contributions of this paper:
 To the best of our knowledge, this is the first work
that proposes and formalizes an indexing
technique for incremental ER over query results;
 We propose two dynamic indexes: Similarity
Index and Cluster Index. The first one is used to
index the similarity values between each pair of
tuples being compared. The second one indexes a
list of clusters of tuple identifiers;
 We show that reusing the results of previous
iterations turns the ER process significantly faster
and with results of similar quality compared with
traditional approaches.
The remainder of the paper is organized as
follows. Section 2 describes some important
theoretical concepts related to ER and indexing
techniques. Section 3 describes our proposal for
dynamic indexes. Section 4 presents some
experimental results. Section 5 discusses related
work. Finally, Section 6 concludes the paper.
2 BACKGROUND
In general, the traditional ER process includes five
steps (Christen, 2012): (i) Data pre-processing:
ensures that the attributes used for the comparison
have the same structure, and their content follows the
same format. (ii) Indexing: reduces the quadratic
complexity of the ER process using data structures
that facilitate the efficient and effective generation of
candidate pairs of tuples that likely correspond to the
same real-world entity. (iii) Tuple pair comparison:
calculates the similarity value (Christen, 2012)
between each candidate pair of tuples. (iv)
Classification: defines if a pair of tuples is a match or
not. (v) Evaluation: assess the quality of result of the
ER process.
However, other approaches, like the incremental
ER (Gruenheid et al., 2014) and the query-based ER
(Bhattacharya and Getoor, 2007; Altwaijry et al.,
2013; Su et al., 2010), can have additional steps in
order to reduce the costs of the overall process. The
incremental approach, for example, has additional
steps to allow the reuse of previous ER iterations
during the record pair comparison step (Whang and
Garcia-Molina, 2014).
This paper focus on indexing step for incremental
ER. Different indexing techniques are proposed in the
literature, like the standard blocking (Christen, 2012;
Christen, 2012a; Ramadan et al., 2015). This
technique segregates tuples into blocks according to
a certain criteria, called blocking key, whose values
are calculated based on one or more attributes that
describe the tuple. Doing this, just tuples belonging to
the same block will be compared during the record
pair comparison step.
Most of the indexing techniques deals with the
problem of traditional ER (offline processing of static
databases). In this case, all the available tuples are
indexing once. A limited number of research aims
real-time ER or ER for dynamic databases.
The dynamic indexes can be updated to reflect the
new results of the incremental ER process. In this
case, just a subset of the available tuples are inserted
or searched at query-time.
3 APPROACH FOR DYNAMIC
INDEXING FOR ENTITY
RESOLUTION
In this section, we present our dynamic indexing
approach for incremental ER over query results.
Initially, we present an overview of our approach for
incremental ER and next we define the dynamic
indexes proposed in this work.
As mentioned earlier, the ER process is
essentially a clustering problem, in which each cluster
contains tuple identifiers that represent a single real-
world entity. If we consider the ER problem in
multiple data sources, each tuple can be from a
different source.
In the following, consider S = {s
1
, s
2
, ..., s
m
}, a set
of data sources and Q = {q
1
, q
2
, ..., q
n
}, a set of queries
running on S. Given a query q
d
, a data integration
system (Gruenheid et al., 2014) reformulates the
query into queries that can be executed over each data
source belonging to S, q
d
= {s
1
.q
d1,
s
2
.q
d2
, …, s
m
.q
dm
},
where s
i
.q
di
is the query q
d
reformulated over the data
source s
i
. Each data source has a set of concepts L
denoted by s
i
.L = {l
1
, l
2
, ..., l
o
}, which represent
concepts from the real-world. For example, Author or
Person. Considering that our approach is based on
query results, in the following we present a definition
for query result and tuple.
Definition 1 (Query Result). A query result,
denoted by q
d
.r, is a set q
d
.r = {s
1
.q
d1
.r
1,
s
2
.q
d2
.r
2
, …,
s
m
.q
dm
.r
m
}, where s
i
.q
di
.r
i
is the result of the query q
d
reformulated over the data source s
i
. Each s
i
.q
di
.r
i
has
a set of tuples (T).
Definition 2 (Tuple). Each tuple t
k
belonging to
T has a data source identifier, denoted s
k
.Id, that
represents the data source the tuple belongs to,
and a
set of pairs,



,


,



,


,…,

,

, where a
x
denotes an attribute of a concept and v
x
denotes its
ICEIS 2017 - 19th International Conference on Enterprise Information Systems
186

value. A tuple t
k
has a pair

,

), that represents a
single identifier of t
k
(t
k
.Id).
In this work, we make the following three
assumptions:
 The mapping between schemas was resolved in
the schema matching step of the data integration
process (Gruenheid, 2014);
 All the tuples that answer a query were retrieved,
utilizing a search engine (Bhattacharya and
Getoor, 2007; Su et al., 2010);
 All the clusters were created considering a single
concept, for example clustering by Author,
Affiliation or Address. This allows better reuse of
clusters. For example, if a query requires
information about Author and Address concepts,
and to identify an author it is necessary to
disambiguate the Address, the two concepts are
clustered separately and the ER process combines
the results. In other moment, if a query needs only
information about Address concept, the previous
clusters of the Address can be reused. To simplify
matters, we assume that all queries in the
experiments are related to a single real-word
concept.
3.1 Overview of the ER Approach over
Query Results
Our proposal for an incremental ER approach over
query results is presented in Figure 1. Consider as
input a set of tuples obtained as the result of a query
q
d
. The first step is the Dynamic Indexing (step 1),
which consists of creating blocks of tuple pairs that
are candidate to correspond to the same real-world
entity. For each tuple of each block, a blocking key
(or search key) (Christen, 2012) is created, whose
values are generated based on the values of either a
single or several attributes. As an example, consider
the Figure 2, which shows blocking key values
created using the Double-Metaphone function
(Christen, 2012) over the attribute Name.
Next, previous indexes are analyzed to be reused
(Analysis of Previous Indexes, step 2) in order to
reduce the execution time of the ER process. For this
purpose, we propose two indexes: Cluster Index (CI)
and Similarity Index (SI). The first one indexes a list
of clusters of tuple identifiers. The second one
indexes similarity values between pairs of tuples.
More details about these indexes are presented in the
next sections. At the end of this step, tuples that were
not previously processed, denoted by new tuples, are
sent as input to the Tuple Pair Comparison step (step
3). Additionally, information about existing clusters
is sent as input to the Local Clustering step (step 4).
Figure 1: Entity resolution over query results.
Figure 2: Query result over Author concept. The last
column shows the generated blocking keys.
During the Tuple Pair Comparison step, the
similarity values between each pair of new tuples
from q
d
.r is calculated. At the end of this step, the
similarity values are sent as input to the Local
Clustering step (step 4). Next, the new tuples are
classified considering tuples from existing clusters.
Doing this, existing clusters will grow incrementally
with the addition of new similar tuples or new clusters
will be created. At the end of the process, the
duplicated tuples are identified and the dynamic
indexes are updated (step 5).
In the next section, we
define the dynamic indexes and we present how they
are created
3.2 Cluster Index
A Cluster Index (CI) indexes a list of clusters of tuple
Dynamic Indexing for Incremental Entity Resolution in Data Integration Systems
187

identifiers and is defined as follows.
Definition 3 (Cluster Index). A cluster index is
defined by a list of pairs, CI = [(key
1
, Clus
1
), (key
2
,
Clus
2
), …,(key
n
, Clus
n
)], where key
i
is a blocking key
to access the index and Clus
i
is a list of triples, defined
by Clus
i
= {(s
1
.Id, t
1
.Id
,
ClusterId
1
), (s
2
.Id, t
2
.Id,
ClusterId
2
),
…,
{(s
m
.Id, t
m
.Id, ClusterId
m
)}, where s
k
.Id
denotes the data source identifier of the tuple
identified by t
k
.Id and ClusterId
k
is the identifier of the
cluster that t
k
.Id belongs to.
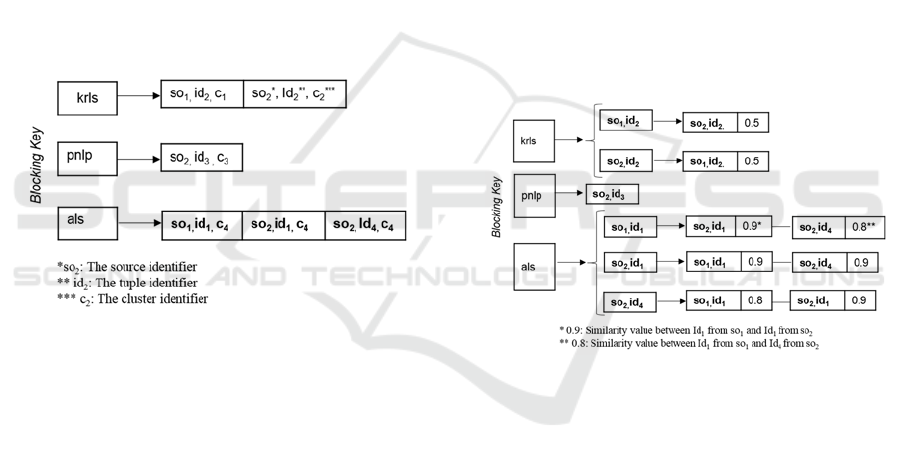
Figure 3 shows the CI corresponding to the tuples
of Figure 2. Each blocking key corresponds to an
entry in the cluster index, which points to a list of
tuple identifiers together with their corresponding
data source and cluster identifiers. For example, the
tuple with id
2
from so
1
and the tuple with id
2
from so
2
will have the same blocking key value (e.g. krls) and
therefore will be on the same list pointed by als.
However, those tuples belong to different clusters, c
1
and c
2
respectively.
Figure 3: The Cluster Index created from the tuples in
Figure 2.
During the Analysis of Previous Indexes, a search
is performed on the CI in order to find tuples that were
previously indexed. For each tuple t
k
from q
d
.r, a
blocking key is generated. If there is a corresponding
entry in the CI for this key and t
k
.Id was previously
indexed, i.e, the identifier of t
k
is in the list of
identifiers of key, then the corresponding ClusterId is
retrieved. When a tuple was not previously indexed,
then it should be compared with other tuples from q
d
.r
in order to obtain the similarity values between them.
Finally, during the Local Clustering step, existing
clusters will be updated or new clusters will be
created based on those similarity values.
3.3 Similarity Index
To identify if a tuple is duplicated regarding a set of
tuples (if they belong to the same cluster), it is
necessary to make comparisons between this tuple
and each one of the others. For this purpose, similarity
functions are commonly used.
The Similarity Index (SI) indexes the similarity
values between pairs of tuples. At each new query
result, similarity values are retrieved from SI or
inserted into SI. Doing this, we can reduce the cost of
calculating tuple similarity values at query time,
which significantly reduces the time needed for the
overall ER process (see Section 5). The Similarity
Index is defined as follows.
Definition 4 The Similarity Index (SI) is defined
by a list of pairs, SI = [(key
1
, Lis
1
), (key
2
, Lis
2
), …,
(key
n
, Lis
n
)], where key
i
is a blocking key value and
Lis
i
is defined by a list of pairs, Lis
i
= [(s
1
.Id, t
1
.Id),
(s
2
.Id, t
2
.Id), …, {(s
m
.Id, t
m
.Id)], where s
k
.Id denotes
the data source identifier and t
k
.Id is the tuple
identifier that share the same blocking key value.
Each pair (s
k
.Id, t
k
.Id) is related to a list of triples, Sim
k
= [(s
1
.Id, t
1
.Id
,
simValue
1
), (s
2
.Id, t
2
.Id
,
simValue
2
),…,
(s
p
.Id, t
p
.Id
,
simValue
p
)], where simValue
l
is the
similarity value between the tuple t
k
.Id from s
k
.Id and
the tuple t
1
.Id from s
l
.Id.
Figure 4: The SI created from the tuples of Figure 2.
Figure 4 shows the SI corresponding to the tuples
of Figure 2. Each blocking key corresponds to an
entry in the similarity index, which index a list of
similarities values between pair of tuples together
with their corresponding data source identifier (s
k
.Id).
For example, the similarity value between the tuple
id
1
from so
1
and the tuple id
1
from so
2
, that have the
same blocking key (als), is 0.9. Also the similarity
value between the tuple id
1
from so
1
and the tuple id
4
from so
2
, with the same blocking key (als), is 0.8. The
similarity function used in the example was
Levenshtein (Christen, 2012) over the attribute name.
During the Analysis of Previous Indexes, a search
is performed on the SI in order to find similarity
values that were previously indexed. For each pair of
tuples t
i
and t
j
from q
d
.r, a blocking key is generated.
After that, the process access the previous SI to
retrieve the similarity value between t
i
and t
j
. If there
ICEIS 2017 - 19th International Conference on Enterprise Information Systems
188

is a corresponding entry in the SI for the key value,
t
i
.Id and t
j
.Id were previously indexed, i.e, the
similarity value between t
i
and t
j
is already in SI.
Then, the corresponding similarity value is retrieved.
When the similarity between a pair of tuples was not
previously indexed, then the tuples should be
compared in order to obtain the similarity value
between them.
4 EXPERIMENTAL
EVALUATION
In this section, we present the results of an
experimental evaluation performed on real-world
datasets. The results show that our dynamic indexing
proposal is likely to succeed in an incremental ER
process. Additionally, we show that the incremental
ER has a better performance than traditional ER,
without compromising the quality of results.
4.1 Experiment Setup
Dataset: The experiments used the CDDB (CDDB,
2016) dataset, which is composed by tuples
describing CDs. This dataset includes 9763 tuples
randomly extracted from freeDB (FreeDB, 2016),
with 298 duplicates. These duplicates are in a gold
standard file that shows all duplicate pair of tuples.
We created a set of random samples of tuples from
CDDB to simulate a set of query results. The samples
size varies according to the purpose of each
experiment. The tuples were indexed using the
Double-Metaphone function (Christen, 2012) and the
Levenshtein string similarity function (Christen,
2012) was used for pairwise similarity computation.
It is important to note that we ignored edges with a
similarity value below 0.9. This value was chosen
experimentally. The threshold is increased by 0.01 in
every iteration, from 0.7 value of threshold up to 1.0.
Implementation: To determine the effectiveness
of our dynamic indexing proposal, we implemented
the following batch algorithms and its respective
incremental clustering algorithms:
 Hill – Climbing (HC) (Guo et al., 2010): An ideal
clustering should have a high cohesion within
each cluster and a low correlation between
different clusters. Several objective functions
have been proposed for clustering (Tan et al.,
2006). The choice of this function is orthogonal to
our technique; here we adopt the cohesion, where
the high values of cohesion are better than low
values.
 Single-Link (SL) (Bhattacharya and Getoor,
2007a): adopts a hierarchical clustering approach,
where in each step of the clustering process, the
clusters whose two closest members have the
smallest distance are merged.
We have chosen these algorithms because they
were previously used for ER and are evaluated as
good algorithms for scenarios with a large volume of
data (Tan et al., 2006; Gruenheid et al., 2014). The
algorithms were implemented in Java and the
experiments were performed on a Windows machine
with Intel Core i5 (2.2GHz).
Measures: We measured the efficiency and
quality of the results from the incremental ER process
using the proposed indexes. For efficiency, we
repeated the experiments 100 times and reported the
average execution time. For quality, we reported the
F-measure (Christen, 2012), given that we have the
gold standard. To calculate the F-measure, it is
necessary to calculate Precision and Recall measures.
The precision measure indicates, among the pairs of
records that are clustered together, how many of them
are correct; the recall measures, among the pairs of
records that refer to the same real-world entity, how
many of them are clustered together; and the F-
measure is computed as
∙∙

.
Objective: The goal of the experiments is two-
fold. First, we want to show that the proposed indexes
are suitable for a dynamic environment because of
performance improvement. Second, we will show
that results of the incremental Entity Resolution using
the proposed indexes have the quality similar to
traditional Entity Resolution with batch algorithms.
4.2 Experiment to Measure Efficiency
To measure the efficiency, we created a set of random
samples from CDDB to simulate a set of query
results. For example, in Figure 5, we start with 70%
of tuples from the query result indexed and the other
30% are new tuples, i.e., tuples not previously
indexed. The percentage of duplicated tuples is
decreased from 70% to 10%. For each sample, we
repeated the experiment 100 times. The result was the
average of values in all executions. The same
interpretation should be used to Figure 6 - Figure 8.
Dynamic Indexing for Incremental Entity Resolution in Data Integration Systems
189

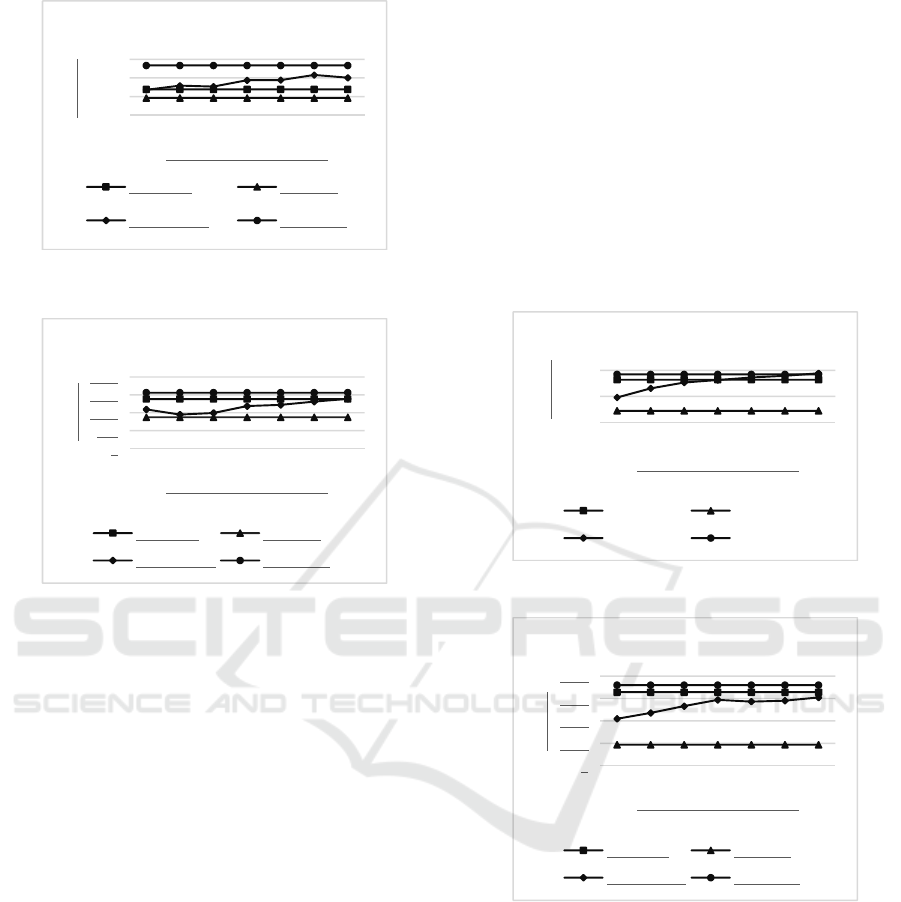
Figure 5: Time execution for naive SI using HC Algorithm.
Figure 6: Time execution for modified SI using HC
Algorithm.
It is important to highlight that the random
samples allow the configuration of the indexes to be
different for each execution, representing samples of
tuples with different characteristics. For example,
scenarios with sparse indexes or dense indexes.
We considered four cases in each experiment
(Figure 5 – Figure 8): (i) Traditional: uses a batch
algorithm. (ii) Best-Case: uses an incremental
algorithm, assuming that all tuples from the query
result were indexed. (iii) Average-Case: uses an
incremental algorithm, assuming that a percentage of
tuples from the query result were indexed and another
percentage is new. (iv) Worst-Case: assumes that all
tuples from the query result are new and they were
not indexed.
Additionally, we considered two scenarios: i)
Naive SI: all the similarity values calculated during
the ER process are indexed in the SI, independently
of a threshold (Figure 5 and Figure 7). ii) Modified
SI: only the similarity values above a threshold are
indexed in the SI (Figure 6 and Figure 8). Each
scenario was executed with Hill-Climbing (Figure 5
and Figure 6) and Single-Link (Figure 7 and Figure
8) algorithms.
We observed that the size of the SI influences the
performance of the ER process. Because of naive SI
cost, we concluded that a modified SI is more
efficient than naive SI for the incremental ER over
query results. The incremental ER using modified SI
shows a better performance than traditional ER.
We observed in the Average-Case, with Hill-
Climbing algorithm, that in the best case the
incremental ER over query results is approximately
31.4% more efficient than traditional ER. The lower
gain was approximately 5.2%. The time in Figure 6
decreases as more indexes are reused, reducing the
number of comparisons between pairs of tuples at
query time.
Figure 7: Time execution for naive SI using SL Algorithm.
Figure 8: Time execution for modified SI using SL
algorithm.
Also, we observed in the Average-Case, with
Single-Link algorithm, the same behavior that Hill-
Climbing algorithm. In the best case the incremental
ER over query results is approximately 36.2% more
efficient than traditional ER. The lower gain was
approximately 7.2%.
Additionally, to evaluate the time of access on
main memory and the scalability of the proposed
indexes, we generate a dataset, which has 130k tuples,
by Febrl tool (Christen, 2008). We analyzed the
average access time, considering a search for a
random value in the indexes. In this case, the search
0
1000
2000
3000
70% 60% 50% 40% 30% 20% 10%
Time (ms)
Percentage of indexed tuples
CDDB Hill-Climbing - Naive SI
Traditional Best-Case
Average-Case Worst-Case
0
500
1000
1500
2000
70% 60% 50% 40% 30% 20% 10%
Time (ms)
Percentage of indexed tuples
CDDB Hill-Climbing - Modified SI
Traditional Best-Case
Average-Case Worst-Case
0
2000
4000
70% 60% 50% 40% 30% 20% 10%
Time (ms)
Percentage of indexed tuples
CDDB Single Link - Naive SI
Traditional Best-Case
Average-Case Worst-Case
0
1000
2000
3000
4000
70% 60% 50% 40% 30% 20% 10%
Time (ms)
Percentage of indexed tuples
CDDB Single-Link - Modified SI
Traditional Best-Case
Average-Case Worst-Case
ICEIS 2017 - 19th International Conference on Enterprise Information Systems
190

was performed in indexes of different sizes and the
value to be searched could be in any position or be
non-existent.
For this experiment, random samples were
extracted from the Febrl dataset. These samples were
clustered by single-link algorithm. The generated
clusters were inserted in the CI and the similarity
value between pairs of tuples were inserted in the SI.
The indexes size was increased by approximately
10k, from 1k up to 100k. For each index size, we
repeated the experiment 500 times.
Figure 9: CI access time.
Figure 10: SI access time.
For the CI, for each sample generated and
processed, we searched randomly a tuple from Febrl
dataset. Figure 9 shows an average of times measured
in each case. It is important to note that the variation
of CI access time in relation to the indexed data
volume is small. However, in the first case (1k tuples)
we observed a time out of line. This happened
because the random tuples chosen to be searched in
the CI were almost never found, since the Febrl
dataset has 130K tuples and only approximately 0.7%
were indexed. This scenario can represent a real
scenario, where we do not have much information
about the data.
For the SI, for each sample generated and
processed, we extracted randomly a pair of tuples and
searched its similarity value in the SI. Figure10 shows
the time average measured in each case.
It is important to note that, in the same way as in
the CI, the variation of SI access time in relation to
the indexed data volume is small and in the first case
(1k tuples) we observed a time out of line. This case
represented often executions the worst-case, where
the similarity value is not retrieved.
4.3 Experiment to Measure Quality
For measuring the quality of the results of the ER
process, we calculated the average of F-measure over
a set of runs of the previous experiments. We
considered two cases: i) The quality of the result
when batch algorithms (Hill-Climbing and Single-
Link) were used, without indexes. ii) The quality of
the result when an incremental algorithm (Hill-
Climbing and Single-Link adapted) was used together
with the proposed indexes. We measured the result of
average execution 100 times. For each execution, we
considered the same configuration of previous
experiments. Initially, a query result has 70% of tuple
indexed, then 60%, and so on.
Figure 11: F-measure of HC algorithm.
Figure 12: F-measure of SL algorithm.
We evaluated the F-measure of ER with Hill –
Climbing (Figure11) and Single – Link (Figure12)
algorithms. In both cases, we observed that the F-
measure with incremental algorithm is very close to
the ER with batch algorithm. In the Hill-Climbing
algorithm, we observed that the highest difference
between the ER F-measure with batch and
incremental algorithm was 0.105 and the smallest
0
0,02
0,04
0,06
0,08
0,1
Time (ms)
Number of tuples inserted in CI
Febrl Cluster Index (CI)
0
0,2
0,4
0,6
Time (ms)
Number of similarity values inserted in SI
Febrl - Similarity Index (SI)
0
0,5
1
70% 60% 50% 40% 30% 20% 10%
F-measure
Percentage of indexed tuples
CDDB Hill-Climbing
Incremental Algorithm Batch Algorithm
0,6928
0,693
0,6932
0,6934
70% 60% 50% 40% 30% 20% 10%
F-measure
Percentage of indexed tuples
CDDB Single-Link
Incremental Algorithm Batch Algorithm
Dynamic Indexing for Incremental Entity Resolution in Data Integration Systems
191

difference was 0.016. In the Single-Link algorithm
(Figure 12), we did not observe relevant difference
among the quality results.
5 RELATED WORK
Recent researches have focused on the use of queries,
indexing techniques or both to reduce the volume of
data to be processed (Bhattacharya and Getoor, 2007;
Altwaijry et al., 2013; Christen, 2012a; Ramadan et
al., 2015; Vieira, 2016). Different indexing
techniques are summarized in (Christen, 2012a).
However, most of these techniques are focused on
traditional ER process, with batch algorithms and just
few researches focus on incremental ER (Gruenheid
et al., 2014; Whang et al., 2013; Altowin et al., 2014;
Whang and Garcia-Molina, 2014).
In (Bhattacharya and Getoor, 2007; Altwaijry et
al., 2013), a query-time ER is proposed, but the
indexing to reuse previous classifications was not
considered. In (Whang et al., 2013; Gruenheid et al.,
2014), an incremental ER approach is proposed, but
the indexing is static and the ER is not query-driven.
In (Ramadan et al., 2015) dynamic indexes are
proposed. Both papers focused on information
retrieval and not on data integration process
(Christen, 2012). Besides that, just attribute and
similarity values are indexed and not clusters of
tuples that refer to the same real-world entity.
Our indexes are different in three aspects. First,
our focus is the data integration process and an
incremental ER over query results. Second, our
proposal is to index tuple identifiers, and not attribute
values. In scenarios with a large volume of data, using
multiple attributes for similarity index functions can
be very costly and time-consuming (Christen, 2012;
Ribeiro et al, 2016). Third, we propose to index
similarity values and previous ER of tuples from
multiple data sources.
6 CONCLUSIONS
In this paper, two indexes for incremental ER over
query results were presented, Cluster Index and
Similarity Index. The quality and the efficiency of the
ER process were evaluated, as well as the impact of
the Similarity Index size on the incremental ER
process was investigated. We showed, on a real
dataset, that our indexes are suitable for the
incremental ER process. The incremental ER had the
same quality of traditional processes, without
indexes, but was more efficient. As future work, we
intend to analyze the indexes with other datasets, as
well as to evaluate other ER incremental algorithms.
REFERENCES
Altowim, Y., Kalashnikov, D. V., Mehrotra, S. (2014).
Progressive Approach to Relational Entity Resolution.
In: VLDB. Hangshou, China.
Altwaijry, H., Kalashnikov, D. D., Mehrotra, S. (2013).
Query-Driven Approach to Entity Resolution. In:
VLDB. Trento, Italy.
Bhattacharya, I., Getoor, L. (2007). Query-time Entity
Resolution. Journal of Artificial Intelligence Research.
V 30 , issue 1, pp 621-657.
Bhattacharya, I.; Getoor, L. (2007a). Entity Resolution In
Graphs. In: Mining Graph Data. John Wiley & Sons,
Inc.
CDDB (2016). Available in: http://hpi.de/naumann/
projects/repeatability/datasets/cd-datasets.html.
Christen, P. (2008). Febrl – An Open Source Data Cleaning,
Deduplication and Record Linkage System with a
Graphical User Interface. In: KDD. Las Vegas, USA.
Christen, P. (2012). Data Matching: Concepts and
Techniques for Record Linkage, Entity Resolution, and
Duplicate Detection. Springer.
Christen, P. (2012a). A Survey of Indexing Techniques for
Scalable Record Linkage and Deduplication. In: TKDE.
V 24, issue 9, pp 1537-1555.
FreeDB (2016). Available in: http://www.freedb.org/
Gruenheid, A.; Dong, X. L.; Srivastava, D. (2014).
Incremental Record Linkage. In: VLDB. Hangzhou,
China.
Guo, S.; Dong, X.; Srivastava, D.; Zajac, R. (2010). Record
linkage with uniqueness constraints and erroneous
values. In: PVLDB. Singapore.
Ramadan, B. et al. (2015). Dynamic Sorted Neighbourhood
Indexing for Real-Time Entity Resolution. In: Journal
of Data and Information Quality. V 6, issue 4, nº 15.
Ribeiro, L. A. et al. (2016). SJClust: Towards a Framework
for Integrating Similarity Join Algorithms and
Clustering. In: ICEIS. Rome, Italy.
Su, W., Wang, J., Lochovsky, F, H. (2010). Record
Matching Over Query Results from Multiple Web
Databases. In: TKDE. V 22, issue 4, pp 578-589.
Tan, P.; Steinbach, M.; Kumar, V. (2006). Introduction to
Data Mining. Pearson.
Vieira, P. K. M.; Salgado, A. C.; Lóscio, B. F. (2016). A
Query-driven and Incremental Process for Entity
Resolution. In: AMW. Panama City, Panama.
Whang, S. E.; Marmaros, D.; Garcia-Molina, H. (2013).
Pay-As-You-Go Entity Resolution. In: TKDE. V 25,
issue 5, pp 1111-1124.
Whang, S. E.; Garcia-Molina, H. (2014). Incremental entity
resolution on rules and data. In VLDB Journal. V 23,
issue 1, pp 77- 102.
ICEIS 2017 - 19th International Conference on Enterprise Information Systems
192