Enhancing Pigeon-Hole based Encoding of Boolean Cardinality

Constraints

Soukaina Hattad, Said Jabbour, Lakhdar Sais and Yakoub Salhi

CRIL - CNRS UMR 8188, University of Artois, Lens, France

Keywords:

Satisﬁability, Linear inequalities, Cardinality Constraints.

Abstract:

In this paper, we propose to deal with the encoding of cardinality constraints

∑

i=1

> b into conjunctive

normal form. We consider the one proposed recently (Jabbour et al., 2014) based on pigeon-hole problem.

Then, we show that even if the number of clauses of the CNF based encoding is in O(b ×(n−b)) , the number

of literals of resulting formula can be much more higher: O(b(n − b)

). To decrease the complexity in terms

of number of literals, we propose a compact representation of some clauses of the encoding. Our approach

allows to have a quadratic encoding in terms of literals while maintaining the same complexity in terms of

clauses and additional variables. An experimental evaluation is performed to show the competitiveness of the

new encoding.

1 INTRODUCTION

Today, Boolean satisﬁability (SAT) has gained a con-

siderable audience with the advent of a new gener-

ation of solvers able to solve large instances encod-

ing real-world problems. In addition to the traditional

applications of SAT to hardware and software for-

mal veriﬁcation, this impressive progress led to in-

creasing use of SAT technology to solve new real-

world applications such as planning, bioinformatics,

cryptography, and data mining. Encoding applica-

tions as formulas in CNF became now a usual prac-

tice. One of the most important ﬂaws of CNF or

Boolean representation in general rises in the difﬁ-

culty to deal with counting constraints, among them

the cardinality constraint and its more general form

the pseudo Boolean constraint. Indeed, several appli-

cations involve counting arguments expressed as car-

dinality or pseudo Boolean constraint. This kind of

constraints arises frequently out of the encoding of

real-world problems such as radio frequency assign-

ment, time tabling and product conﬁguration prob-

lems to cite a few. For the above reasons, several

authors have addressed the issue of ﬁnding an efﬁ-

cient encoding of cardinality (e.g. (Warners, 1996),

(Bailleux and Boufkhad, 2003), (Sinz, 2005), (Silva

and Lynce, 2007), (As

ın et al., 2009)) and pseudo

Boolean constraints (e.g. (E

en and S

orensson, 2006;

Bailleux et al., 2009)) as a CNF formula. Efﬁciency

refers to both the compactness of the representation

(size of the CNF formula) and to the ability to achieve

the same level of constraint propagation (generalized

arc consistency) on the CNF formula.

In this paper, we present an enhancement of the

pigeon-hole based encoding of the cardinality con-

straint into CNF. We provide a new encoding allow-

ing a compact representation leading to a reduction in

terms of the number of literals of the original one.

The rest of this paper is organized as follows. Af-

ter some preliminary deﬁnitions and technical back-

ground, we recall the Pigeon-Hole based CNF encod-

ing of the cardinality constraint. Then, we present

our approach to enhance this encoding by provid-

ing a more compact representation in terms of num-

ber of literals. An experimental evaluation on Partial

MaxSAT instances is performed to demonstrate the

competitiveness of our proposal. We conclude with

some interesting and general perspectives.

2 TECHNICAL BACKGROUND

AND PRELIMINARY

DEFINITIONS

2.1 Preliminary Deﬁnitions and

Notations

A Boolean formula F in Conjunctive Normal Form

(CNF) is a conjunction of clauses, where a clause is

Hattad S., Jabbour S., Sais L. and Salhi Y.

Enhancing Pigeon-Hole based Encoding of Boolean Cardinality Constraints.

DOI: 10.5220/0006252502990307

In Proceedings of the 9th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2017), pages 299-307

ISBN: 978-989-758-220-2

299

a disjunction of literals. A literal is a positive (x) or

negated (¬x) propositional variable. The two literals

x and ¬x are called complementary. We denote by

l the complementary literal of l. More precisely, if

l = x then

l = ¬x, otherwise

l = x. The variable as-

sociated to a literal l is denoted by |l|. Let us recall

that any Boolean formula can be translated to CNF

using linear Tseitin’s encoding (Tseitin, 1968). The

size of the CNF F is deﬁned as

∑

c∈F

|c|, where |c| is

the number of literals in c. A unit clause is a clause

containing only one literal (called unit literal), while

a binary clause contains exactly two literals. A Horn

(resp. reverse Horn) clause is a clause with at-most

one positive (resp. negative) literal. A positive (resp.

negative) clause is a clause whose literals are all pos-

itive (resp. negative). An empty clause, denoted ⊥, is

interpreted as false (unsatisﬁable), whereas an empty

CNF formula, denoted >, is interpreted as true (satis-

ﬁable).

The set of variables occurring in F is denoted V

and its associated set of literals L

= ∪

x∈V

{x,¬x}

. A set of literals is complete if it contains one lit-

eral for each variable in V

, and fundamental if it

does not contain complementary literals. A literal l

is called monotone or pure if

l does not appear in F .

An interpretation ρ of a Boolean formula F is a func-

tion which associates a truth value ρ(x) ∈ {0,1} (0 for

false and 1 for true) to some of the variables x ∈ V

ρ is complete if it assigns a value to every x ∈ V

, and

partial otherwise. An interpretation is alternatively

represented by a complete and fundamental set of lit-

erals. A model of a formula F is an interpretation ρ

that satisﬁes the formula, denoted ρ |= F . A formula

G is a logical consequence of a formula F , denoted

F |= G, iff every model of F is a model of G.

Let c

and c

be two clauses such that c

= (x ∨ α)

and c

= (¬x ∨ β), η[x,c

] = (α ∨ β) denotes the

resolvent on x between c

and c

. A resolvent is called

tautological when it contains complementary literals.

F |

denotes the formula obtained from F by as-

signing x the truth-value true. Formally F |

= {c | c ∈

F , {x, ¬x} ∩ c =

0} ∪ {c\{¬x} | c ∈ F ,¬x ∈ c}.

This notation is extended to interpretations: given

an interpretation ρ = {x

,. . . ,x

}, we deﬁne F |

(.. . ((F |

). . . |

∗

denotes the formula F closed under unit prop-

agation, deﬁned recursively as follows: (1) F

∗

= F

if F does not contain any unit clause, (2) F

∗

=⊥ if

F contains two unit-clauses {x} and {¬x}, (3) other-

wise, F

∗

= (F |

)

∗

where x is the literal appearing in

a unit clause of F .

Let c

and c

be two clauses of a formula F . We

say that c

(respectively c

) subsume (resp. is sub-

sumed) c

(resp. by c

) iff c

⊆ c

. If c

subsume c

then c

|= c

(the converse is not true).

Let c ∈ F such that x ∈ c, the literal x of c

is called blocked if ∀c

∈ F such that ¬x ∈ c

and

c 6= c

, η[x,c, c

] is a tautology. A clause c ∈ F is a

blocked clause if it contains a blocked literal (Kull-

mann, 1997). A blocked clause c ∈ F can be deleted

from F while preserving satisﬁability.

2.2 Pigeon-Hole Principle

The pigeon-hole based encoding is based on the

Pigeon-Hole principle widely used in proof complex-

ity. It asserts that there is no injective mapping from

b pigeons to n holes as long as b > n. Stephen A.

Cook proved that the propositional formula encod-

ing the Pigeon-Hole problem have polynomial size

proof in extended resolution proof system (Cook,

1976). A polynomial proof is also obtained by Kr-

ishnamurthy (Krishnamurthy, 1985) using resolution

with symmetry. The Pigeon-Hole principle PHP

can

be expressed as a propositional formula in conjunc-

tive normal form. The variables of PHP

are p

i j

with

1 6 i 6 b, 1 6 j 6 n; the variable p

i j

is intended to

denote the condition that pigeon i is sitting in hole j.

The CNF formula encoding PHP

can be stated as

follows:

j=1

i j

, 1 6 i 6 b (1)

16i<k6b

(¬p

i j

∨ ¬p

k j

), 1 6 j 6 n (2)

The ﬁrst equation (1) expresses that any pigeon

must be put in at least one hole, while the equation (2)

constrains each hole to contain at most one pigeon.

2.3 Symmetries in SAT

As the Pigeon-Hole based encoding heavily exploit

symmetries (Krishnamurthy, 1985), we brieﬂy recall

the symmetry breaking framework in SAT. For more

details on symmetry, we refer the reader to some but

not exhaustive list of works in SAT (Benhamou and

Sais, 1992), (Benhamou and Sais, 1994), (Crawford

et al., 1996; Aloul et al., 2003) and CSP (Puget, 1993;

Gent et al., 2006).

First, let us introduce some deﬁnitions on group

theory. A group (G,◦) is a ﬁnite set G with an asso-

ciative binary operation ◦ : G × G → G admitting a

neutral and an inverse element. The set of all permuta-

tion P over a ﬁnite set E associated to the composition

operator ◦, denoted (P ,◦), forms a group. Further-

more, each permutation σ ∈ P can be represented by a

set of cycles {c

.. . c

} where each cycle c

is a list of

ICAART 2017 - 9th International Conference on Agents and Artiﬁcial Intelligence

300

elements of E (l

.. . l

) s.t. ∀1 6 k < n

,σ(l

) = l

k+1

and σ(l

) = l

Let F be a CNF formula, and σ a permutation

over L(F ). We can extend the deﬁnition of the per-

mutation σ to F as follows: σ(F ) = {σ(c)|c ∈ F }

and σ(c) = {σ(l)|l ∈ c}.

Deﬁnition 1. Let F be a CNF formula and σ a per-

mutation over the literals of F , σ is a symmetry of F

if it satisﬁes the following conditions:

• σ(¬x) = ¬σ(x), ∀x ∈ L

• σ(F ) = F

From the deﬁnition above, a symmetry σ deﬁnes

an equivalence relation over the set of possible assign-

ments. We need to consider only one assignment from

each equivalence class. Breaking symmetries consist

in eliminating all symmetric assignments except one

in each equivalence class. The most used approach

to break symmetries consists in adding new clauses

- called symmetry breaking predicates (SBP) or lex

leader constraints - to the original formula (Crawford,

1992; Crawford et al., 1996; Aloul et al., 2003; Walsh,

2006).

Before introducing the general deﬁnition of SBP,

let us illustrate the main idea behind this technique

using a simple example. Let σ = (x

) be a sym-

metry of a CNF formula F with only one cycle. Sup-

pose that F admits m = {x

,¬y

.. .} as a model, then

σ(m) = {¬x

,. . .} is also a model of F . To break

this symmetry, it is sufﬁcient to lay down an order-

ing on the values of x

and y

. For example, adding

conjunctively the constraint x

6 y

, which can be ex-

pressed by the clause c = (¬x

∨ y

), to the formula

F , leads to a new formula Φ = F ∪ {c} while pre-

serving satisﬁability. The model m of F is eliminated

as it is not a model of Φ. All other models of F not

satisfying the added binary clause are also eliminated.

This idea is generalized in deﬁnition 3 to a symmetry

containing arbitrary number of cycles.

Deﬁnition 2. Let σ = (x

),. . . ,(x

) be a sym-

metry of F . σ is called lexicographically ordered

iff ∀i(1 6 i 6 n − 1) |x

| < |x

i+1

| and ∀i(1 6 i 6 n)

| < |y

| holds.

Deﬁnition 3 (SBP (Crawford et al., 1996)). Let F be

a CNF and σ = (x

)(x

). . . (x

) a symmetry

of F . Then the symmetry breaking predicates, called

sbp

, associated to a lexicographically ordered sym-

metry σ is deﬁned as the conjunction of the following

constraints:

• (x

6 y

)∧

• (x

= y

) → (x

6 y

)∧

• . . . ∧

• (x

= y

)∧(x

= y

). . . (x

n−1

= y

n−1

) → (x

6 y

)

Similarly, in order to break a set of symmetries

one need to add conjunctively symmetry breaking

predicates associated to each individual symmetry.

The following property shows that symmetry

breaking predicates approach preserves the satisﬁa-

bility between the original formula and the generated

one.

Proposition 1 ((Crawford et al., 1996)). Let F be a

CNF formula and σ a symmetry of F . Then F and

(F ∧ sbp

) are equivalent w.r.t. satisﬁability.

In order to limit the combinatorial explosion of the

clausal transformation of these predicates, one has to

add one variable α

per cycle (x

) to express the

equality between x

and y

. However, one of the major

drawbacks of this approach is that the size of the sym-

metry breaking predicates is exponential in the worst

case. Recently, interesting reductions in the size of

the SBP has been obtained in (Aloul et al., 2006) us-

ing non redundant generators concept.

3 PIEGON-HOLE BASED

ENCODING OF CARDINALITY

CONSTRAINTS

∑

i=1

> b such that x

is propositional variable (x

∈

{0,1}), for 1 6 i 6 n, is a well known cardinality con-

straint. As mentioned by Joot P. Warners in (Warn-

ers, 1996), this kind of constraints and its generalized

form

∑

i=1

> b (where a

are positive integers) can

be polynomially encoded as a propositional formula

in CNF. The ﬁrst polynomial CNF expansion of cardi-

nality constraint is proposed by Hooker in an unpub-

lished note (see also (Warners, 1996)). The authors

start from the encoding formulated of the constraint

∑

i=1

> b as it is was described in (Warners, 1996)

(page 12):

(¬z

∨ x

), 1 6 i 6 n, 1 6 k 6 b (3)

i=1

, 1 6 k 6 b (4)

(¬z

∨ ¬z

), 1 6 i < j 6 n, 1 6 k 6 b (5)

In (Warners, 1996) the author mentions that the

formula (3) says that x

is true if some z

is true, while

formula (4) combined with formula (5) say that for

each k exactly one z

must be true.

However this formulation is clearly wrong. Let

us give a counter example. Suppose that x

= 0 for

1 6 i 6 n−(b−1). In such a case, the cardinality con-

straint

∑

i=1

> b is unsatisﬁable as one needs to set

Enhancing Pigeon-Hole based Encoding of Boolean Cardinality Constraints

301

b variables to true among the set of remaining unas-

signed variables R = {x

n−(b−2)

n−(b−3)

,. . . ,x

}. In-

deed, this is clearly impossible as the number of unas-

signed variables is n − (n − (b − 2)) + 1 = b − 1. On

the contrary, the CNF formula made of (3), (4) and

(5) is satisﬁable. One can set the remaining variables

of R to true and for each k (1 6 k 6 b) set exactly one

to true for (n − (b − 2) 6 i 6 n).

Despite of the importance of the Warners’ paper

and its precursory nature on the subject, to our knowl-

edge, this error in the formulation of the ﬁrst transla-

tion of the cardinality constraint to CNF reported by

Warners was never raised.

Based on the description above, Jabbour et al. pro-

posed in (Jabbour et al., 2014) the correct reformula-

tion of the CNF representation of the cardinality con-

straint

∑

j=1

> b, denoted P

in the sequel:

k=1

(¬p

∨ x

), 1 6 i 6 n (6)

i=1

, 1 6 k 6 b (7)

16k<k

(¬p

∨ ¬p

), 1 6 i 6 n (8)

Let us mention that the two equations (7) and (8)

encode the well-known pigeon hole problem PHP

where b is the number of pigeons and n is the num-

ber of holes (p

expresses that pigeon k is in hole i).

The mapping between the models of PHP

and those

∑

i=1

> b are obtained thanks to the equation (6).

Indeed, the propositional variable x

is true if the hole i

contains one of the pigeons k for 1 6 k 6 b. If we take

again the previous counter example, the CNF formula

becomes unsatisﬁable as it encodes an unsatisﬁ-

able Pigeon-Hole problem PHP

b−1

In this original polynomial transformation, the

number of variables is n + b × n and the number of

clauses required is n × b + b + n ×

b×(b−1)

. The over-

all complexity is in O(b × n) variables and O(n × b

)

clauses.

Unfortunately, checking the satisﬁability of a

Pigeon-Hole formula is computationally hard except

if we use resolution with symmetry or extended reso-

lution proof systems. In the following, we show how

to improve the efﬁciency of this Pigeon-Hole based

encoding of the cardinality constraint. By efﬁciency,

we mean enhancing the propagation capabilities (unit

propagation) of the obtained CNF. To this end, we

show in the next section, how symmetries of the this

Pigeon-Hole formulation can be used to enhance this

ﬁrst version of our encoding.

3.1 Symmetry Breaking on the

Pigeon-Hole based Encoding

An enhancement of Pigeon-Hole Based Encoding is

proposed using symmetry breaking predicates and

used to reduce the size of Pigeon-Hole based encod-

ing of the cardinality constraint while ensuring unit

propagation.

For clarity reason, and to better visualize the re-

ductions on the previous encoding P

, we use the fol-

lowing matrix representation for the CNF formula (7).

Each row represents a positive clause of (7).







·· · [p

·· · p

]

·· · [p

2(b−1)

·· · p

2(n−1)

] p

·· · p

b(n−(b−1))

] ·· · p







Efﬁcient Encoding. The enhanced CNF Pigeon-

Hole based encoding, called phP

, of a cardinality

constraint is deﬁned as:

¬p

(b−k+1)(i+k−1)

∨ x

(i+k−1)

, 1 6 i 6 n − b + 1,

1 6 k 6 b

(9)

n−b+1

i=1

(b−k+1)(i+k−1)

, 1 6 k 6 b (10)

(b−k+1)k

∨ · · · ∨ p

(b−k+1)(i+k)

∨ ¬p

(b−k)(i+k+1)

0 6 i 6 n − b − 1,1 6 k 6 b − 1

(11)

This efﬁcient phP

encoding is obtained from P

en-

coding using sophisticated reductions. Before illus-

trating how such reductions are performed, let us de-

scribe brieﬂy this encoding. The formula (10) cor-

responds to the reduction of (7) to only the sub-

clauses represented in brackets (see the previous ma-

trix). These sub-clauses are obtained by deducing that

the literals belonging to the upper-left corner triangle

and to the lower-right corner triangle of the previous

matrix must be assigned to false. For instance, the

clause p

∨ ··· ∨ p

b(n−(b−1))

∈ (11) is obtained for

k = 1, corresponding to the last clause in brackets of

the previous matrix. Moreover, the formula (9) cor-

responds to the restriction of (6) to the variables ap-

pearing in (10). Finally, the formula (11), called stair-

implications, link successive rows in the matrix from

the bottom to the top. With these implications the set

of negative binary clauses (8) are made redundant and

ICAART 2017 - 9th International Conference on Agents and Artiﬁcial Intelligence

302

then can be dropped. One can see that the number of

clauses of (11) is smaller than that of (8).

From phP

, one can deduce that the overall complex-

ity of our encoding is in O(b × (n − b)) variables and

clauses.

3.2 phP

Encoding: Algorithm

In this section, we provide an algorithm to help the

user to generate CNF Pigeon-Hole Based encoding

in a simple way. Let us ﬁrst consider the following

example.

Example 1. Let x

≥ 5 a

cardinality constraint. The following matrix, is given

in order to better visualise how the CNF Pigeon-Hole

Based encoding is derived.







↓ ↓ ↓ ↓ ↓ ↓ ↓







The rows of the matrix allow us to derive the positive

clauses of (10):

∨ p

The binary clauses of (9) are obtained as follows:

for each column j of the matrix, we generate the

binary clauses connecting the literals of the column j

with the variables x

¬p

∨ x

¬p

∨ x

¬p

∨ x

¬p

∨ x

¬p

∨ x

¬p

∨ x

¬p

∨ x

¬p

∨ x

¬p

∨ x

¬p

∨ x

¬p

∨ x

¬p

∨ x

¬p

∨ x

¬p

∨ x

¬p

∨ x

The last category of clauses corresponds to

(11). The clauses express a relation between two

successives lines in the matrix representation. Such a

relation can be easily derived by a simple observation

on the above matrix.

∨ ¬p

∨ p

∨ ¬p

∨ p

∨ ¬p

∨ p

∨ ¬p

∨ p

∨ ¬p

In the sequel we present a transformation proce-

dure (Algorithm 1) allowing us to derive phP

from

a given cardinality constraint. Algorithm 1 starts by

creating the matrix p(b × n − b + 1) with b rows and

n − b + 1 columns, where each element p

i j

(0 ≤ i <

b,0 ≤ j < n − b + 1) corresponds to the propositional

variables set by the function newVar() (line 4). In

line 5, we generate the positive clauses of (10). The

initialization of the matrix p of variables together with

the generation of the positives clauses of (10) are done

in lines 1-8. From line 9 to line 20, the algorithm build

all the clauses of (11) and (9). Note that by inverting

the rows and columns of the matrix, the clauses of

(9) are generated as (x

i+ j−1

∨¬p

i j

) (line 18) which is

clearly more simple.

Algorithm 1: Pigeon-Hole-Based CNF encoding.

Require: A cardinality constraint

∑

i=1

> b

1: for (i = 1; i ≤ b; i + +) do

2: c =

3: for ( j = 1; j ≤ (n − b + 1); j + +) do

4: p

i j

= newVar()

5: c ← c ∪ p

i j

6: end for

7: F ← F ∪ c

8: end for

9: for (i = 1; i ≤ b; i + +) do

10: c =

11: for ( j = 1; j ≤ (n − b + 1); j + +) do

12: c ← c ∪ p

i j

13: if (i ≤ b − 1 && j ≤ n − b) then

14: c ← c ∪ ¬p

(i+1) j

15: F ← F ∪ c

16: c ← c \ {¬p

(i+1) j

};

17: end if

18: F ← F ∪ {¬p

i j

i+ j−1

}

19: end for

20: end for

21: return F

4 ENHANCING PHP

REDUCING THE SIZE OF THE

CNF IN TERMS OF LITERALS

In this section we propose an enhancement of the pre-

vious encoding in order to reduce the size of the CNF

i.e. the total number of literal occurrences. Indeed,

until now we considered the complexity w.r.t. the

number of variables and clauses needed to encode the

cardinality constraint into CNF. In the sequel, we pro-

pose an interesting enhancement of our encoding by

reducing the size of the CNF. The following proposi-

Enhancing Pigeon-Hole based Encoding of Boolean Cardinality Constraints

303

tion states the number of literals occurrences needed

to obtain phP

Proposition 2. |phP

| is in O(n

)

Proof. The pigeon-hole encoding is obtained through

three set of clauses (9), (10) and (11). The number

of literals of (9) is equals to (b − 1) × (2 + . . . + (n −

b + 1)) = (b − 1) × ((n − b + 1) × (

n−b+2

) − 1). For

(10) the size of the clauses is b × (n − b + 1). Finally

the total size of the clauses of (11) is 2× b × (n − b +

1). By considering the worst case, where b =

, we

deduce that the size of phP

is in O(n

According to Proposition 2, the number of literal

occurrences is in O(b × (n − b)

) in the worst case.

Consequently, for b near

and for large values of n,

the encoding leads to huge CNF formula. Further-

more, as many clauses of (10) and (11) are of large

size, this will slow down the unit propagation pro-

cess. To overcome this drawback, we propose a more

compact representation of (10) and (11) allowing to

reduce the complexity in terms of literal occurrences

from O(n

) to quadratic in the worse case. To this

end, we propose to make use of the mining based

compression approach of CNF formulae proposed in

(Jabbour et al., 2013). The compression approach is

obtained using an original combination of data min-

ing techniques with the well known Tseitin’s encod-

ing (Tseitin, 1968). The proposed approach called

Mining4CNF uses itemset mining techniques to de-

tect hidden structures in the CNF and use them to re-

duce the size of the CNF formula. More precisely,

the approach allows to derive frequent (appearing

many times in the formula) sub-clauses. Such sub-

clauses are then substituted by a fresh variable, while

adding a new boolean function representing such sub-

clauses (Tseitin encoding). Also, in (Jabbour et al.,

2013), the authors show that this compression tech-

nique achieves signiﬁcant compression rate on many

CNF instances including some specialized constraints

such as the AtMostOne Constraint (

∑

i=1

6 1). To

illustrate such approach, let us consider the following

example.

Example 2. Let Φ be the formula containing the fol-

lowing 10 clauses:

∨ ¬x

, x

∨ ¬x

, x

∨ ¬x

¬x

∨ ¬x

, ¬x

∨ ¬x

, ¬x

∨ ¬x

¬x

∨ x

¬x

∨ x

¬x

∨ x

Mining4CNF ﬁrst enumerates some interesting

(or frequent) sub-clauses, and use them to compress

the CNF formula in the second step. Suppose that

∨ x

) is a frequent sub-clause, the formula Φ

can be rewritten as:

∨ ¬x

, x

∨ ¬x

, x

∨ ¬x

¬x

∨ ¬x

, ¬x

∨ ¬x

, ¬x

∨ ¬x

¬x

∨ x

∨ y

¬x

∨ x

∨ y

¬x

∨ x

∨ y

¬y ∨ x

∨ x

As we can remark, an implication y → x

∨ x

∨

is sufﬁcient, as the sub-clause (x

∨ x

) oc-

curs with positive polarity. This enhancement is in-

troduced by Plaisted and Greenbaum that essentially

produces a subset of Tseitin’s representation (Plaisted

and Greenbaum, 1986).

In this simple example, the original formula contains

31 literals, while the new formula involves only 27

literals. As the compression process is based on the

Tseitin encoding, the transformation preserves satis-

ﬁability.

Before presenting how Mining4CNF can be

adapted to compress our Pigeon-Hole based encod-

ing of cardinality constraints, let us recall the clauses

encoded in (11) and (10). Equation 11 expresses a

relation between two successives rows in the matrix

representation. In order to simplify its representation

the indices are then changed below since some literals

are proved to be false. The clauses of (11) present a

staircase form.

Let us ﬁx k = (n − b) to simplify the new matrix

representation as follows:







.. . p

b(n−b)

b(k+1)

→ p

.. . p

2(k+1)

→ p

.. . p

1(k+1)

↓ ↓ ↓ ↓ ↓ ↓ ↓

.. . .. . .. . .. . x







The clauses linking the two rows pointed by ar-

rows in the above matrix are:

∨ ¬p

∨ p

∨ ¬p

∨ p

∨ ¬p

∨ p

∨ . . . ∨ p

∨ ¬p

So such clauses form a triangle. Note that the

clauses of (10) corresponds to the rows of the ma-

trix. For the compression purposes, we add to each

triangle one positive clause (in bold font) from (10)

as follows:

ICAART 2017 - 9th International Conference on Agents and Artiﬁcial Intelligence

304

∨ ¬p

∨ p

∨ ¬p

∨ p

∨ ¬p

∨ p

∨ . . . ∨ p

∨ ¬p

∨ p

∨ . . . ∨ p

∨ p

1(k+1)

∨ ⊥

To obtain the set of all clauses encoded by (10) and

(11), we add conjunctively all the triangles (clauses)

that can be generated from each two successives rows

of the matrix. As we can observe, the number of tri-

angles is b − 1 while the number of rows (positive

clauses) is b. By adding one positive clause of (10)

to its corresponding triangle, the following positive

clause (p

∨ . . . ∨ p

b(k+1)

) remains.

Based on this sets of clauses (in the form of tri-

angles), we can observe that there they contain many

frequent sub-clauses. For example, the sub-clauses

c = (p

∨ p

∨ ... ∨ p

k+1

) appears (k + 1)/2

times. For the simplicity of the presentation, we

consider k an odd number. Applying Mining4CNF

approach leads to the substitution each sub-clause in

all clauses where it appears with a new variable α.

To preserve satisﬁability, we have to add the clause

∨ p

∨ . . . ∨ p

k+1

∨ ¬α). This process allows to

substitute (

k+1

)

literals with (

k+1

+1) literals.

Consequently, the size reduction in terms of number

of literals is (

k+1

)

− (

k+1

+ 1) =

−

literals. After replacing such sub-clause and adding

the new clause, one can remark that the new derived

formula can be divided into the two following

formulae:

∨ ¬p

∨ p

∨ ¬p

∨ p

∨ ¬p

∨ p

∨ .. . ∨ p

∨ ¬p

∨ p

∨ .. . ∨ p

∨ p

k+1

∨ ¬α

and

α ∨ ¬p

k+1

α ∨ p

k+3

∨ ¬p

k+3

α ∨ p

k+3

∨ p

k+5

∨ ¬p

k+5

α ∨ p

k+3

∨ p

k+5

∨ p

k+7

∨ .. . ∨ p

∨ ¬p

α ∨ p

k+3

∨ p

k+5

∨ ¬p

k+7

∨ .. . ∨ p

∨ ¬p

1(k+1)

∨ ⊥

Interestingly, partitioning the original formula (trian-

gle) as two formulae (triangles) allows us to deﬁne a

recurrence relation that we describe later.

In the following, we formally describe how to

compact the equations (10) and (11), using the sets of

clauses (in the form of triangles). Let us ﬁrst deﬁne

the function f as follows:

f (x

,. . . ,x

,. . . ,y

) =

i=1

(¬y

∨

j=1

)

It is straightforward to conclude that the clauses

linking two rows in the matrix can be expressed using

the function f . For rows number 1 and 2 (with arrows

on the left hand side of the matrix), it can be deﬁned as

f (p

,. . . , p

1(k+1)

, p

,. . . , p

,⊥). Each application

of f corresponds to a triangle of clauses (see above).

Then the clauses of equations (10) and (11) can be

rewritten using f as:







∨ .. . ∨ p

b(k+1)

) ∧

b−1

i=1

f (p

,.. ., p

i(k+1)

, p

(i+1)1

,.. ., p

(i+1)k

,⊥)







Then, the general CNF formula of phP

can be

deﬁned as:







∨ .. . ∨ p

b(k+1)

) ∧

b−1

i=1

f (p

,.. ., p

, p

(i+1)1

,.. ., p

(i+1)k

,⊥) ∧

i+ j=k+1

∨ ¬p

i j

)







Algorithm 2 describes how to compress

f (x

,. . . ,x

,. . . ,y

). It apply a greedy ap-

proach to replace frequent sub-clauses by choosing

the one allowing to maximize the reduction rate.

Note that, when n is less than 5 (line 1), compacting f

do not leads to any improvement in terms of number

of literals.

Algorithm 2: f (x

,.. ., x

,.. ., y

1: if n ≤ 5 then

2: return

i=1

(¬y

∨

j=1

)

3: end if

4: k = (int) (n / 2)

5: α ← newVar()

6: return f (x

,. . . ,x

k−1

,. . . ,y

k−1

,¬α) ∧

f (α,x

k+1

,. . . ,x

,. . . ,y

)

Proposition 3. Using Mining4CNF compression ap-

proach, |phP

| is in O(n

Proof. Let us now show the complexity of our new

encoding after the applications of the compression ap-

proach. Note that the number of literals occurrences

encoded in f (p

,. . . , p

i(k+1)

, p

(i+1)1

,. . . , p

(i+1)k

,⊥)

is in O(k). Indeed, let us denote by L(n) the number

Enhancing Pigeon-Hole based Encoding of Boolean Cardinality Constraints

305

of literal occurrences of f (x

,. . . ,x

,. . . ,y

). Ac-

cording to Algorithm 2, L(n) satisﬁes the following

recurrence equation:

L(n) = 2 × L(

) (12)

L(5) = 20. (13)

It is clear that L(n) is in O(n). Then, using such

algorithm, the number of literal occurrences of f is re-

duced from quadratic to linear. As in phP

, f is used

(b − 1) times, then the complexity of phP

in term of

number of literal occurrences becomes quadratic, i.e.,

O(b × (n − b)).

Let us note that the compression approach in-

creases the number of fresh variables and clauses.

However, the complexity of our Pigeon-Hole based

encoding phP

in term of additional clauses and lit-

erals remains the same. Indeed, the number of new

variables and clauses added using Algorithm 2 does

not exceed n. Then the complexity of phP

is in

O(b × (n − b)) variables and O(b × (n − b)) clauses.

5 EXPERIMENTS

In this section, we carried out an experimental eval-

uation of the performance of our enhanced Pigeon-

Hole based encoding of the cardinality constraint.

The primary goal is to assess the competitiveness

of our proposal. For this purpose, we compared

the performances using QMaxSAT

solver used to

solve MaxSAT instances. Let us recall that QMaxSAT

uses the encoding deﬁned in (Bailleux and Boufkhad,

2003). It is also based on minsat

solver. We use

the last version of minisat. We denote by QMaxSAT-

PHP the version of QMaxSAT where the encoding

(Bailleux and Boufkhad, 2003) is substituted with

the enhanced pigeon-holed based encoding. We con-

sidered the instances of Partial MaxSAT competition

2015

. All the experiments are done on a cluster In-

tel Xeon quad-core avec 32GB of RAM et 2.66 Ghz.

The time out is ﬁxed to 30 minutes.

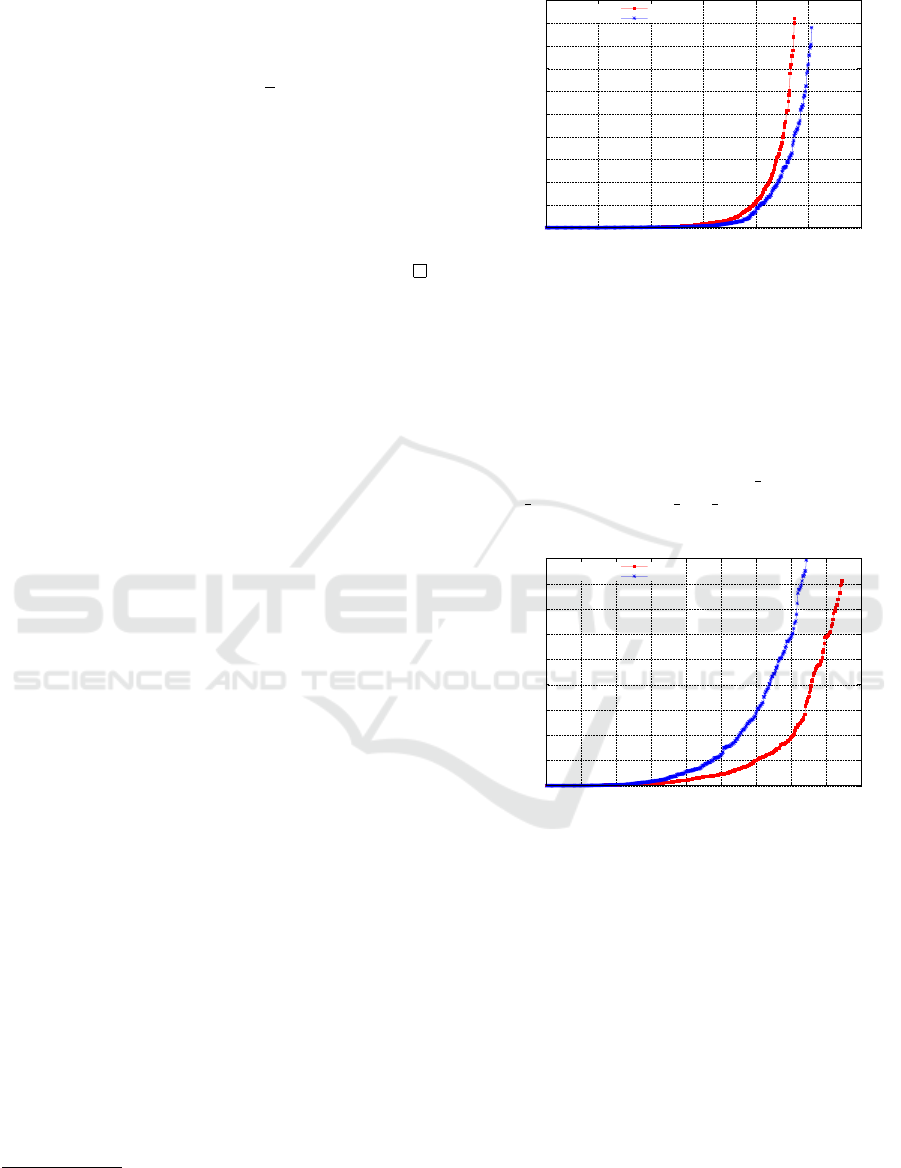
Figure 1 represents the results obtained on in-

stances encoding partial MaxSAT problems belong-

ing to crafted category. Each dot (x, y) represents the

number of instances x solved in less than y seconds.

As we can see, QMaxSAT-PHP is more efﬁcient than

classical QMaxSAT. It solves 32 instances more. Fur-

thermore, there exists some classes of instances where

our approach is clearly the best e.g., AES*, s38584*.

https://sites.google.com/site/qmaxsat/

http://minisat.se/

http://www.maxsat.udl.cat/15/

200

400

600

800

1000

1200

1400

1600

1800

2000

0 100 200 300 400 500 600

time (seconds)

#instances

QMaxSAT

QMaxSAT-PHP

Figure 1: Results on crafteds instances.

Figure 2 represents the results obtained on in-

stances encoding partial MaxSAT problems be-

longing to application category. In contrast to

crafted instances, here classical QMaxSAT out-

performs our solver. It solves 51 instances

more. Furthermore, as for crafted case, there

exists a set of classes where QMaxSAT is the

best e.g., splitedReads*, b20 C-mbd14-0202*,

b20-s PathRelaxation Set FS*. However, there

exists classes where our solver is better e.g., atcoss*.

200

400

600

800

1000

1200

1400

1600

1800

0 50 100 150 200 250 300 350 400 450

time (seconds)

#instances

QMaxSAT

QMaxSAT-PHP

Figure 2: Results on applications instances.

6 CONCLUSION AND FUTURE

WORKS

In this paper, we proposed an enhancement of

the Pigeon-Hole based encoding of cardinality con-

straints into CNF. The new encoding is competitive

as it remains in O(b(n − b)) variables and clauses. In-

terestingly, we demonstrate that mining-based com-

pression techniques can achieve substantial reduction

in the size of the encoding. This opens a promising

perspective on how to extend the reasoning applied in

this paper to other kinds of constraints (e.g. global

constraints). Experimental results shows that our new

encoding is competitive on crafted instances.

ICAART 2017 - 9th International Conference on Agents and Artiﬁcial Intelligence

306

The generalization of our reasoning to encode

general pseudo Boolean constraint to CNF is also a

short term perspective. Finally, we plan to conduct

an experimental evaluation of our Pigeon-Hole based

encoding w.r.t. the well-known encodings.

REFERENCES

Aloul, F. A., Ramani, A., Markov, I. L., and Sakallah, K. A.

(2003). Solving difﬁcult instances of boolean satisﬁ-

ability in the presence of symmetry. IEEE Trans. on

CAD of Integrated Circuits and Systems, 22(9):1117–

1137.

Aloul, F. A., Sakallah, K. A., and Markov, I. L. (2006).

Efﬁcient symmetry breaking for boolean satisﬁability.

IEEE Trans. Computers, 55(5):549–558.

ın, R., Nieuwenhuis, R., Oliveras, A., and Rodr

ıguez-

Carbonell, E. (2009). Cardinality networks and their

applications. In 12th International Conference on

Theory and Applications of Satisﬁability Testing (SAT

2009), pages 167–180.

Bailleux, O. and Boufkhad, Y. (2003). Efﬁcient cnf encod-

ing of boolean cardinality constraints. In 9th Interna-

tional Conference on Principles and Practice of Con-

straint Programming (CP 2003), pages 108–122.

Bailleux, O., Boufkhad, Y., and Roussel, O. (2009). New

encodings of pseudo-boolean constraints into cnf. In

SAT’2009, pages 181–194.

Benhamou, B. and Sais, L. (1992). Theoretical study of

symmetries in propositional calculus and applications.

In 11th International Conference on Automated De-

duction (CADE’1992), volume 607 of Lecture Notes

in Computer Science, pages 281–294. Springer.

Benhamou, B. and Sais, L. (1994). Tractability through

symmetries in propositional calculus. Journal of Au-

tomated Reasoning, 12(1):89–102.

Cook, S. A. (1976). A short proof of the pigeon hole

principle using extended resolution. SIGACT News,

8(4):28–32.

Crawford, J. (1992). A theorical analysis of reasoning by

symmetry in ﬁrst order logic. In Proceedings of Work-

shop on Tractable Reasonning, AAAI, pages 17–22.

Crawford, J. M., Ginsberg, M. L., Luks, E. M., and Roy,

A. (1996). Symmetry-breaking predicates for search

problems. In KR, pages 148–159.

en, N. and S

orensson, N. (2006). Translating pseudo-

boolean constraints into sat. JSAT, 2(1-4):1–26.

Gent, I. P., Petrie, K. E., and Puget, J.-F. (2006). Chapter 10

symmetry in constraint programming. In F. Rossi, P.

v. B. and Walsh, T., editors, Handbook of Constraint

Programming, volume 2 of Foundations of Artiﬁcial

Intelligence, pages 329 – 376. Elsevier.

Jabbour, S., Sa

ıs, L., and Salhi, Y. (2014). A pigeon-hole

based encoding of cardinality constraints. In Interna-

tional Symposium on Artiﬁcial Intelligence and Math-

ematics, ISAIM 2014, Fort Lauderdale, FL, USA, Jan-

uary 6-8, 2014.

Jabbour, S., Sais, L., Salhi, Y., and Uno, T. (2013). Mining-

based compression approach of propositional formu-

lae. In CIKM, pages 289–298.

Krishnamurthy, B. (1985). Shorts proofs for tricky formu-

las. Acta Informatica, 22:253–275.

Kullmann, O. (1997). On a generalization of extended res-

olution. Discrete Applied Mathematics, 34:73–95.

Plaisted, D. A. and Greenbaum, S. (1986). A structure-

preserving clause form translation. Journal of Sym-

bolic Computation, 2(3):293–304.

Puget, J. (1993). On the satisﬁability of symmetrical con-

straint satisfaction problems. In proceedings of ISMIS,

pages 350–361.

Silva, J. P. M. and Lynce, I. (2007). Towards robust cnf

encodings of cardinality constraints. In 13th Interna-

tional Conference on Principles and Practice of Con-

straint Programming (CP 2007), pages 483–497.

Sinz, C. (2005). Towards an optimal cnf encoding of

boolean cardinality constraints. In 11th International

Conference on Principles and Practice of Constraint

Programming (CP 2005), pages 827–831.

Tseitin, G. (1968). On the complexity of derivations in the

propositional calculus. In Slesenko, H., editor, Struc-

tures in Constructives Mathematics and Mathematical

Logic, Part II, pages 115–125.

Walsh, T. (2006). General symmetry breaking con-

straints. In 12th International Conference on Prin-

ciples and Practice of Constraint Programming (CP

2006), pages 650–664.

Warners, J. P. (1996). A linear-time transformation of linear

inequalities into conjunctive normal form. Informa-

tion Processing Letters.

Enhancing Pigeon-Hole based Encoding of Boolean Cardinality Constraints

307