Educating Computer Science Educators Online

A Racket MOOC for Elementary Math Teachers of Finland

Tiina Partanen

, Pia Niemel

, Linda Mannila

and Timo Poranen

Tampere City, Tampere, Finland

Pervasive Computing, Tampere University of Technology, Tampere, Finland

Abo Academi University, Turku, Finland

Computer Sciences, University of Tampere, Kalevantie 4, 33100 Tampere, Finland

Keywords:

Computer Science Education, K-12 Education, Teacher Training, MOOC, Racket, Teacher Professional

Development (TPD), Math-integrated Computer Science.

Abstract:

Many countries all over the world are in the process of introducing programming into their K-12 curricula.

New Finnish Curriculum includes programming mentioned especially in accordance with mathematics and

crafts. Consequently, Finland needs to train teachers to teach programming at elementary school level. In

this paper, we describe how elementary math teachers were educated online to teach programming using the

Racket programming language. The aim of the course was to increase both content knowledge (CK) and

technological pedagogical content knowledge (TPACK). By analyzing the course feedback, questionnaires

and exercise data, we present the teachers’ views on the course and effects on their professional development

(TPD). Finally, we describe development ideas for future online courses.

1 INTRODUCTION

Our society is becoming increasingly digitalized,

which has also given rise to a global discussion on the

role of computer science in education. As a conse-

quence, a number of countries all over the world have

introduced computational thinking, programming or

computer science in their K-9 curricula. Since 2014,

for instance students in England have learned to com-

pute starting at the age of ﬁve. In Finland, program-

ming has been part of the national curriculum ef-

fective since autumn 2016. It was introduced as a

cross-curricular addition, but integrated in particular

into the syllabi of crafts (grades 3-9) and mathemat-

ics (grades 1-9).

Integrating programming into the basic education

was a remarkable change, to which Finnish teacher

training departments have not yet fully adapted.

Henceforth, both pre- and in-service teachers need

to learn to program and obtain an understanding of

the core elements of computational thinking. Adding

curriculum requirements of this kind retrospectively

changes the job description of a teacher signiﬁcantly.

The employer is responsible for taking care of the

teachers’ training and providing time for sufﬁcient

professional development. In addition to new require-

ments, rapid technological disruptions – especially

within information and communication technology

(ICT) – necessitate the continuous professional devel-

opment of teachers in order to ensure frictionless ca-

reer moves in future. By choosing courses that enable

them to fulﬁll curriculum requirements, thus enhanc-

ing employability, teachers aim at maximizing their

market value. Hence, they are willing to put their own

effort into studying.

Although this training need is recognized by the

government, in-service training resources are insufﬁ-

cient. Against this background, all voluntary train-

ing initiatives are warmly welcome. In this paper,

we present the Racket track of Koodiaapinen MOOC,

a project initiated informally by a group of volun-

teer teachers to respond to the gap in formal train-

ing. After the voluntary start, the Ministry of Edu-

cation is currently sponsoring the MOOC by offering

the organizers funding according to the number of in-

service teachers completing the course. The goals of

the course are two-fold: to educate math teachers to

learn programming in the ﬁrst instance, and secondly,

to function as a tool in the search for best practices to

teach programming.

Partanen, T., Niemela, P., Mannila, L. and Poranen, T.

Educating Computer Science Educators Online - A Racket MOOC for Elementary Math Teachers of Finland.

DOI: 10.5220/0006257800470058

In Proceedings of the 9th International Conference on Computer Supported Education (CSEDU 2017) - Volume 1, pages 47-58

ISBN: 978-989-758-239-4

1.1 Theoretical Background

Teachers now ﬁnd themselves in a situation where

they need to upgrade their skills and knowledge re-

lated to technology, programming and digital com-

petence. This can be seen as a type of transforma-

tion, although, it does not fully match ’transforma-

tive learning’ as deﬁned by Mezirow (1997). As an

initiator, Mezirow depicts a ’disorienting dilemma’,

but the way in which he describes the process can be

seen as too intimidating: during disorientation, fear,

anger and shame are listed as the driving forces. Con-

sequently, we chose to speak about the ’reorienting

dilemma’ of teachers instead. In the current reorien-

tation, the most dominant motivation is the external

pressure caused by changes in the curriculum and the

consequent demands to educate students accordingly.

Emotionally, reorientation is also less engaging than

disorientation.

Fortunately in Finland, teachers commonly ex-

hibit several types of internal motivation, e.g., their

own personal willingness to develop. Teachers con-

sciously build and develop their technological knowl-

edge and expertise as agents of their professional de-

velopment. In order to attain a better view on mo-

tivational factors, we refer to the self-reinforcement

and self-efﬁcacy theories of Bandura (2006), where

self-efﬁcacy is an important predictor in successful

professional development, even more than the actual

achievements. On a global scale, the self-efﬁcacy of

Finnish teachers is considered high and boosted by

excellent PISA results, which teachers strive to main-

tain. In addition, they are aware of the new standards

set by the education authorities as a response to the

rapid technological development.

The change in perceived self-efﬁcacy is one metric

for assessing the MOOC course learning outcomes.

Kennedy (2016) talks about enactment problems in

bringing new programming skills into the classroom

context after attending a professional development

course. She highlights the gap between the course set-

up and the actual teaching context of the real class-

room. Good self-efﬁcacy in math is anticipated to

lower this threshold and foster the transfer. In this

study, we wish to focus in particular on teaching math

and programming together, and examine how math

teachers adapt to the change.

1.2 Research Questions

• What has been learned about organizing a pro-

gramming MOOC for teachers?

• How did the teachers evaluate the Racket course?

• How did the teachers describe the effect of the

course on their professional development and self-

efﬁcacy in teaching programming?

2 RELATED WORK

2.1 Digital Competence in the Finnish

Curriculum

In December 2014, a new curriculum for Finnish

basic education (grades 1-9) was accepted by the

Finnish National Board of Education. This curricu-

lum has been in effect since August 2016 and empha-

sizes digital competence as an interdisciplinary skill

throughout all grades. The curriculum excerpts below

mention programming explicitly in the objectives of

two subjects, mathematics and crafts:

Grades 1-2

Digital competence: ”Students get and share expe-

riences about digital media and programming in an

age-appropriate manner.”

Mathematics: ”Students get acquainted with the pro-

gramming basics by creating step-by-step instruc-

tions, which are also tested.”

Grades 3-6

Digital competence: ”Students learn to program and

become aware of how technology depends on deci-

sions made by humans.”

Mathematics: ”Students plan and implement pro-

grams using a visual programming language.”

Crafts: ”Students practice programming robots

and/or automation.”

Grades 7-9

Digital competence: ”Programming is practised as

part of various other subjects.”

Mathematics: ”Students should develop their algo-

rithmic thinking and learn to solve problems using

math and programming. In programming, students

should practise good coding conventions.”

Crafts: ”Students use embedded systems, plan, and

apply programming skills in order to create prod-

ucts.”

As the curriculum stipulates that programming is to

be taught integrated with math, we start by examin-

ing how best to exploit the expected synergy bene-

ﬁts. Compared with programming, math has a well-

established syllabus that has evolved into its current

state since the very dawn of the educational system.

Despite certain minor syllabus areas being dropped

from, or reintroduced to, the curriculum, the core con-

tent of the math syllabus has remained much the same

for decades. In order to ensure smooth transition, the

CSEDU 2017 - 9th International Conference on Computer Supported Education

strong math core should be exploited in order to intro-

duce the analogous and logically progressive steps for

programming. It is tentatively assumed that integrat-

ing programming into math will move the center of

gravity of the syllabus towards computational think-

ing.

Computational thinking has gained traction since

the seminal article by Wing (2006) on the topic.

There is no absolute consensus on the deﬁnition

of the term computational thinking, but many start

from Wing’s (2011) observation, “[t]he thought pro-

cesses involved in formulating problems and their so-

lutions so that the solutions are represented in a form

that can be carried out by an information-processing

agent.” Several operational deﬁnitions have been sug-

gested, for instance one presenting a set of corner-

stones of computational thinking including data col-

lection, analysis and representation, problem decom-

position, abstraction, algorithms, automation, parallel

code and simulation (Barr and Stephenson, 2011). Pa-

pert (1996) has stated, ”Computer science develops

students’ computational and critical thinking skills

and shows them how to create, not simply use, new

technologies. This fundamental knowledge is needed

to prepare students for the 21st century, regardless of

their ultimate ﬁeld of study or occupation”.

Math is at the very core of programming that re-

quires algebraic, logic and problem solving skills.

Synergy implies mutual beneﬁt between two entities,

and although the beneﬁts that a good understanding

about math and perceived self-efﬁcacy confer on the

learning of computational skills are clear (Lent et al.,

1991; Zeldin and Pajares, 2000), the transfer in the

other direction, from programming to math, may not

be that obvious. In a successful transfer, however, a

student should be capable of ﬁnding the common un-

derlying conceptual bases of different topics (Jarvis

and Pavlenko, 2008). Finding such analogies requires

a certain level of intellectual maturity and that a stu-

dent has elaborated on the learning material concep-

tually in order to reach a deeper understanding.

In general, successful transfer correlates with al-

ready acquired expertise: the greater the expertise,

the more well-rounded one is skill-wise and the more

ﬂexible one’s mental models are for adopting new

knowledge (Bransford et al., 2000). An expert ﬁnds

correspondences and analogies by exploiting the pre-

viously constructed knowledge. The expert can easily

and without extraneous effort identify the signiﬁcant

features of the new material and is hence able to eas-

ily learn in new situations. A novice, on the other

hand, can become bogged down by the amount of

data and may concentrate on irrelevancies. In deﬁn-

ing the concept of expertise, the Gestalt psychologists

(e.g. K

ohler, 1970) refer to the insight experience that

helps learners ﬁnd the right solutions intuitively and

enables them to predict the outcomes in new situa-

tions.

Transfer may happen either laterally or vertically

(Gagn

e, 1965), near or far or by the low road or

the high road (Perkins and Salomon, 1988) imply-

ing a certain hierarchy of learning. In addition, Rich

et al. (2013) state that one of the two complemen-

tary subjects tends to be interpreted in learners’ minds

in a more abstract manner while the other encour-

ages to focus on application. In the case of math

and programming, math is more abstract, while pro-

gramming is understood as applied math (Dijkstra,

1982). In math, educators have long talked about

conceptual and procedural knowledge (Gray and Tall,

1994): conceptual knowledge comprises a full pos-

session of the appropriate concepts and the ability

to link them together, i.e., the high road to knowl-

edge transfer, while procedural knowledge consists of

well-internalized mathematical routines on the low-

road. Practicing math routines is anticipated to pro-

vide one appropriate affordance for programming in-

terventions.

Transfer between math and programming will be

streamlined by bridging the current math syllabus

with corresponding programming topics. In addition

to students, we note the value of transfer to in-service

teachers: the similarity between math and program-

ming of the Racket MOOC is expected to motivate

math teachers to learn programming.

2.2 Examples of K-12 Computer

Science Elsewhere

To get a better grasp of the current situation of pro-

gramming or computer science education EU-wide,

European Schoolnet carried out a review of the state

of computer science education in 2015 (Heintz et al.,

2016). The majority of European countries (17 out of

21) had already introduced or were in the process of

introducing computer science concepts in their K-12

curriculum (Balanskat and Engelhart, 2014). Some

countries, such as the UK, introduced computer sci-

ence as a separate subject (English Department for

Education, 2013), while others decided to integrate it

with other subjects, for instance, Finland (Finnish Na-

tional Board of Education, 2014). The length of the

syllabi varies from K-9 to K-12, and a few countries

only include computer science in the upper grades

(10-12). However, integrating computer science with

math seems risky. For instance, an OECD report has

suggested that the higher the degree of computer us-

age in math lessons, the poorer are the results (OECD,

Educating Computer Science Educators Online - A Racket MOOC for Elementary Math Teachers of Finland

2015). Thus the need for developing and evaluating a

suitable pedagogy for the integration is palpable.

In determining the role of computer science in

education, there are various metaphors used, e.g.

computer science as literacy, a maker mind-set, or

grounded math (Burke and Burke, 2016). If the lit-

eracy metaphor is used, then programming as digital

literacy emphasizes the same logical skills as are ap-

plied in constructing linguistically correct sentences,

that is, using e.g. and/or/not in order to get the internal

logic of the sentence expressed. From a ’maker mind-

set’ perspective, the programming language should be

as productive as possible, with a low learning curve,

which suggests visual programming languages, such

as Scratch. Some studies have, however, questioned

the beneﬁts of Scratch in enhancing problem solving

skills and good programming practices (G

ulbahar and

Kalelioglu, 2014; Meerbaum-Salant et al., 2011). The

grounded math approach highlights the links between

programming and math: the transfer between math

and programming seems closest to the functional pro-

gramming paradigm. For example, learning functions

in algebra can be practised using functional program-

ming languages.

Combining functional programming with math is

not new. Historically, attempts range from the early

use of LOGO (Futschek, 2006; Kulik, 1994) to re-

cent experiments employing Racket and Haskell (Ale-

gre and Moreno, 2015). While results from the

LOGO initiatives varied (Kulik, 1994), Racket eval-

uations have consistently been positive and stable

(Felleisen et al., 2014; Felleisen and Krishnamurthi,

2009; Schanzer et al., 2015; Schanzer, 2015). The

amount of research and the positive results reported

convinced our course organizers to choose Racket for

the teacher training MOOC.

2.3 Teaching Programming using

Racket

The Racket programming language http://racket-

lang.org) is a multi-paradigm language, which also

supports functional programming. Being a Scheme

dialect previously known as PLT Scheme, it has been

developed further as an open source project (Flatt and

Findler, 2012). Racket includes a programming IDE,

DrRacket, designed especially for teaching purposes

(Felleisen and Krishnamurthi, 2009). In contexts

where DrRacket cannot be installed, a web-based en-

vironment called WeScheme (Yoo et al., 2011) can

be used. WeScheme also enables online sharing and

remixing of programs.

DrRacket has built-in support for the so-called stu-

dent languages starting with Beginning Student and

ending up with Advanced Student Language. Each

of these Student Languages gradually introduces new

programming primitives and concepts. Simpliﬁed

syntax and semantics help beginners grasp the core

concepts of function design, such as composition and

calling. Tool creators have also deﬁned more precise

error messages in order to assist novices in debugging

and analyzing code (Marceau et al., 2011).

DrRacket comes with graphics and anima-

tion libraries (2htdp/image, 2htdp/universe) that

are especially apt for beginner level program-

ming. These libraries were developed for more

than a decade in the Program by Design project

http://www.programbydesign.org/). Along with these

libraries, the guide book ”How to Design Programs”

was written by Felleisen et al. (2014) for high school

and college level programming courses. The book

emphasizes the advantages of functional program-

ming and introduces Design Recipe to systematize

problem solving by dividing it into a chain of smaller

decisions. The Recipe also instructs how to construct

a program by composing functions and encourages

writing tests before an actual function implementation

(Felleisen et al., 2014).

To preserve the purity of the functional paradigm,

the imperative features of Racket are pushed back.

For instance, an assignment operation (set!) and other

functions causing side effects (display, read) are not

introduced until the student reaches Advanced Stu-

dent Language level. In the most recent version of

”How to Design Programs”, these imperative features

were removed altogether (Felleisen et al., 2014).

The Program by Design project provides a sepa-

rate program for middle school called Bootstrap. Its

mission is to introduce computer science by teaching

algebra by programming a video game using Racket.

This algebraic approach has been proved to improve

understanding about math concepts, such as variables

and functions (Wright et al., 2013). Racket also en-

ables passing numbers, strings and images as pa-

rameters. Using images in calculations justiﬁes the

description of Racket as ”arithmetic with images”

(Felleisen and Krishnamurthi, 2009).

A number of articles promote DrRacket as a

prominent way of learning algebra (Lee et al., 2011;

Schanzer, 2015), especially when special care is taken

of the valid instructions and purposefully planned ex-

ercises and pedagogical models, such as the Cycle

of Evaluation (Schanzer, 2015). The use of design

recipes turned out to foster the right order of opera-

tions and composition of nested functions. Felleisen

and Krishnamurthi (2009) boldly suggests that Boot-

strap (functional programming) provides the strongest

evidence of the favorable effects of programming

CSEDU 2017 - 9th International Conference on Computer Supported Education

on math skills, along with the fact that researchers

have long viewed programming as a promising do-

main where to practise math concepts (Papert, 1996;

Resnick et al., 2009). Bootstrap arranges professional

training workshops for middle school math teachers

in the USA. In addition, Racket was utilized in the

professional training of math teachers in Israel (Levy,

2013). This training was based on the principles of

Program by Design, emphasizing test-ﬁrst develop-

ment and the featured “algebra of images”.

3 METHOD

The idea for Koodiaapinen MOOC was introduced in

2015 by Tarmo Toikkanen and Tero Toivanen during

the annual Interactive Technology in Education con-

ference in H

ameenlinna, Finland. The initial idea was

to help teachers learn programming with material that

has been prepared especially for them by their peers,

for instance, more experienced teachers.

Design based research aims at linking theory and

practice in the discipline of education (Reimann,

2011). It stipulates the use of several iterations and re-

designs of an educational artifact based on feedback

and experience. The beta version of the course was

developed and executed without funding, and four

voluntary MOOC administration members worked in

their spare time. According to the principles of DBR,

the course and its content would then be improved

course-by-course based on the feedback received.

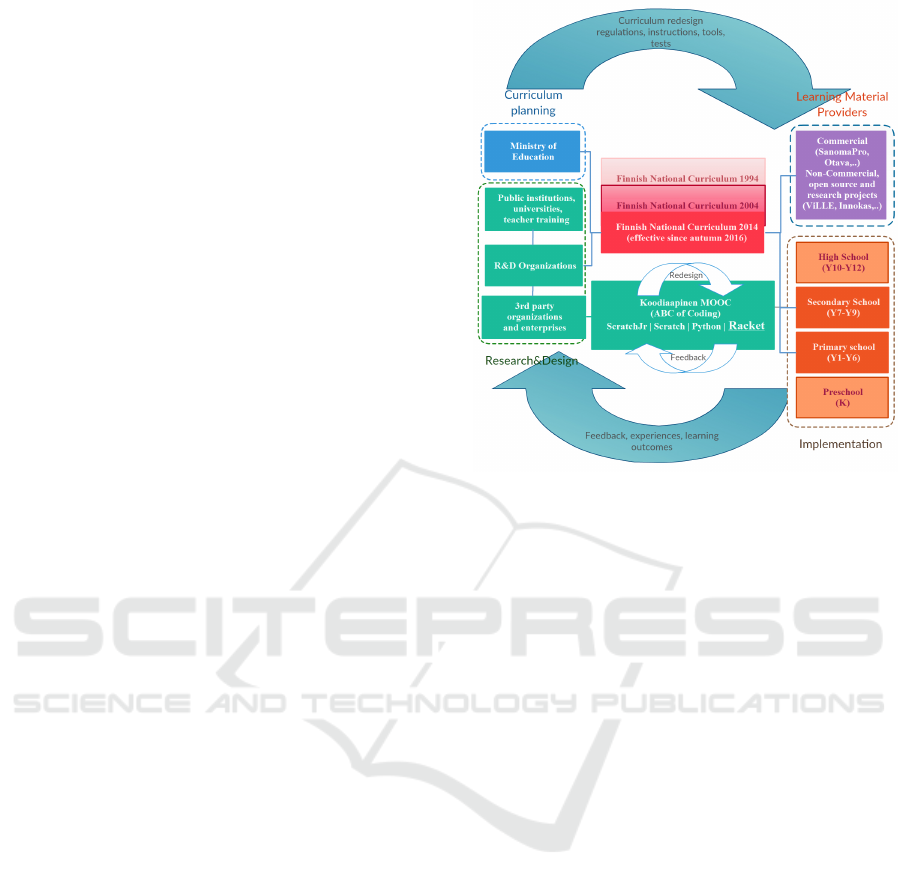
Figure 1 illustrates the process of two nested de-

sign cycles: the outer cycle is the process of cur-

riculum planning that takes place once a decade,

while the inner one is the iterative process of de-

veloping the ’Coding at School’ Racket material

http://racket.koodiaapinen.ﬁ. Development proceeds

in cycles, where different stakeholders give feedback.

Based on the customers, in-service teachers in the

present study, the artifact is redesigned together with

researchers, whose research interests lie in integrating

computational thinking with math education.

First three tracks of the Koodiaapinen course

(ScratchJr, Scratch, Racket) targeted at a number of

general goals: promoting creativity; presenting pro-

gramming as a tool for creating something new and

inspiring; sharing pedagogical ideas and artifacts dur-

ing the course; using exercises directly applicable in

a classroom context in order to make it easier for

teachers to get started; offering course participants

sufﬁcient content knowledge so that they would not

limit themselves to applying ready-made program-

ming materials but also be able to create their own

programming exercises; and enabling peer-support by

Figure 1: Nested DBR cycles of curriculum updates (up-

date/10yrs) and Coding at School courses (2 updates/yr).

urging participants to help each other on discussion

forums. The use of these peer-support channels was

crucial, given the lack of resources.

The very core of the ’Coding at School’ Racket

material is to reveal the nature of programming as

a sort of applied mathematics and show how math-

ematics can be taught through programming. The ap-

proach is designed to motivate math teachers to adopt

programming in their teaching, and to show that pro-

gramming lessons are not time wasted.

After the course, its potential effects on the partic-

ipating teachers’ content knowledge (CK) and tech-

nological pedagogical content knowledge (TPACK)

were evaluated (Voogt et al., 2013). TPACK measures

the efﬁciency of teachers in exploiting technology in

their teaching, and this evaluation required suitable

rubrics. However, the ﬂuent use of technology dur-

ing math lessons is not the core goal of the MOOC.

Instead, the study aims at building on the existing

math foundation and fully exploiting and transfering

this knowledge as programming skills in order to cre-

ate the positive feelings of self-efﬁcacy from the very

beginning. Consequently, in this study, the TPACK

model has been exploited in an attempt to ﬁll the

newly-created space between math and computer sci-

ence, by focusing in particular on a smooth transfer

between these two disciplines.

Educating Computer Science Educators Online - A Racket MOOC for Elementary Math Teachers of Finland

3.1 MOOC Platform Selection

Eliademy, the free Finnish platform, was

selected for the autumn 2015 MOOC

https://eliademy.com/catalog/koodiaapinen.html).

Eliademy comprises such basic features as course

editing and management tools, a discussion forum,

assignment systems for returning ﬁles and support

for quizzes. At that time, the platform did not include

peer-review. In addition, sharing artifacts and ideas

was not functional in Eliademy, and as a result the

course was transferred to Padlet (http://padlet.com),

an online notice board system instead.

While Padlet worked nicely for sharing images

and code via WeScheme links and essays via Google

Drive or OneDrive, an integrated grading system was

missing. This lack caused manual work for the in-

structor. In addition, Padlet did not allow the in-

structor to contact participants, which prevented her

from giving personal feedback on, for instance, their

programming style and essays. Hence, an integrated

learning environment would have been preferable.

For the spring 2016 MOOC

(https://plus.cs.hut.ﬁ/aapinen-racket/K2016/),

the course platform was switched to A+

(https://plus.cs.hut.ﬁ/ developed by Aalto Uni-

versity and used in the university’s own programming

courses. In the beginning, A+ did not support

showcasing of returned artifacts. As this was found

crucial for the Koodiaapinen MOOC, the Rubyric

team added the feature.

After this change, Rubyric’s peer-review func-

tionality was used to minimize the workload of the

course personnel. The new system enabled the in-

structor to deﬁne grading rubrics and points, so the

peer-review was as easy as selecting an appropriate

description for the code quality among given options.

Peer-reviews were conducted anonymously without

using the Padlet-style review wall. Code to be re-

viewed was allocated randomly to reviewers. Ex-

ercises that were not peer-reviewed were put on the

Padlet-style wall with the participants’ names so that

peers could comment on their work, as shown in Fig-

ure 2. Piazza http://piazza.com was used as the dis-

cussion platform. These services were integrated us-

ing IMS-LTI protocol.

3.2 Course Design Principles

The implementation of the Racket track was inspired

by the Systematic Program Design online course of-

fered by edx.org (Kiczales, 2015). Similarly to that

course, the Racket MOOC contained weekly exer-

cises with the following introductory material:

Figure 2: Topic 1 artifacts on the Padlet-style wall (Spring-

2016.)

1. Short motivational video, in which the lecturer in-

troduced the contents and the purpose of the ex-

ercise. Some videos also responded to feedback

received during the previous week.

2. Tutorial screen capture videos introduced the core

concepts. The lecturer used DrRacket for show-

ing programming examples that demonstrated the

concepts to be learned during that week. The step-

per tool was used extensively in order to explain

the evaluation rules. Some written notes were

added online, but the course content was mainly

delivered in video format. The idea was that the

course participants could test the programming

examples themselves while watching the videos.

3. The Design Recipe was used to demonstrate the

principles of function design, see Figure 3. By

using the recipe, a user can solve one detail at a

time and proceed step-by-step until the function is

ready. One of its noteworthy features is the deﬁni-

tion of test cases before implementing the actual

function body.

Figure 3: Design recipe presented as a staircase that helps

to design a function step-by-step.

4. Exercises and their solutions were delivered as

both DrRacket and WeScheme ﬁles and used as

self-tests of the course content presented in the

video tutorials.

5. Hands-on exercises differed from the System-

atic Program Design exercises as neither peer-

review nor multiple choice quizzes were used to

CSEDU 2017 - 9th International Conference on Computer Supported Education

check how well the material had been understood.

Lastly, Koodiaapinen had an essay about the ped-

agogical aspects instead of a programming project

as in Systematic Program Design.

The programming exercises and their so-

lutions were taken from the Coding at

School material and the Coder’s handbook

http://racket.koodiaapinen.ﬁ/manuaali/), which

contains documentation for the graphics and ani-

mation libraries (2htdp/image and 2htdp/universe),

Beginning Student Language primitives, and new

library additions of Racket Turtle and display-read.

4 RESULTS

The ﬁrst Racket track was carried out on a weekly

basis. At the end of each week, feedback was col-

lected ﬁrst using Google Forms and later Grader, an

online survey tool developed at Aalto University. The

feedback was saved and analyzed in order to improve

the next course. Open-ended textual feedback for the-

ory and exercises was solicited, as well as a time es-

timate about the workload of a week. In this chapter,

we introduce our results in chronological order, ﬁrst

the Autumn-2015 results and corresponding lessons

learned, followed by the Spring-2016 results.

4.1 Autumn-2015

Promisingly, up to 369 teachers attended the beta ver-

sion of the Racket track of Koodiaapinen MOOC. The

Racket track turned out to be signiﬁcantly more dif-

ﬁcult in comparison with the other tracks (ScratchJr,

Scratch), thus preventing participants from maintain-

ing the same pace. Based on the feedback, the

course had too much weekly content: the target was 2

h/week, but the actual workload was notably higher,

3-4 h/week. As a result, the MOOC team decided to

slow down the Racket track. To complete the course,

80% of the coursework had to be returned, as 140 out

of the 369 participants did (completion rate 38%).

The autumn course proceeded in the order of

functions-logic-loops. All in all, too many concepts

were introduced simultaneously and teachers started

to struggle with learning, which in turn resulted in

an excessive amount of questions in the discussion

area. On the other hand, experienced programmers

still lacked a few crucial tools needed in the exercises,

e.g., a conditional structure. Lesson learned: Topics

need to be organized based on their difﬁculty: sim-

ple things ﬁrst and then proceeding to more advanced

techniques in a widening spiral. Exercises must be

synced with the introduced topics.

Coupling a function with the design recipe caused

confusion: participants did not see the need for test

cases and stubs. Lesson learned: These topics need

to be introduced separately, ﬁrst functions and man-

ual testing in an interactive window. After this, tests

may be automated with check-expect and re-used in

designing new functions. Automatic tests will help in

understanding how functions should be implemented

and in checking that functions behave as expected. A

similar order is also used in the guide ’How to Design

Programs’ (Felleisen et al., 2014).

No major problems due to DrRacket and

WeScheme were reported. However, check-

expect supported images in DrRacket but not in

WeScheme, thus examples worked differently, which

left WeScheme users puzzled. In addition, some in-

teroperability issues arose due to a few functions in-

troduced in Racket-lang documents, yet the Finnish

Coder’s handbook was restricted only to primitives

functional in both.

Due to time constraints, some important concepts

were left out from the autumn course, e.g., recur-

sion, local variables and more advanced usage of lists.

However, these skills were needed when implement-

ing the quiz application in a good programming style

without repetition. Lesson learned: The quiz was

found highly motivating and applicable for school,

however, the corresponding lesson is to be comple-

mented with the needed advanced topics.

The ﬁnal essay worked as expected: teachers

found it both motivating and useful. Postponing ped-

agogical and curriculum considerations to the end of

the course was a deliberate design decision: one needs

to understand relevant programming and computa-

tional thinking ideas as well as challenges involved

in teaching before adjusting the curriculum. The es-

say aimed at highlighting TPACK issues and summa-

rizing the ideas evolved during the course. The main

TPACK threads of this MOOC were to ponder how

to apply the course exercises to STEM subjects, es-

pecially math, and foster creativity, culminating with

the ﬁnal essay. In addition, the accomplished self-

designed artifacts were one step towards advancing

self-efﬁcacy and enactment.

The course material for Spring-2016 was revised

and rearranged and new material was developed based

on the lessons learned from Autumn-2015. The style

of the beta version was retained: introductory and tu-

torial videos, PowerPoint slides, exercises with solu-

tions and the programming artifacts to be returned

and reviewed. Three returned artifacts were peer-

reviewed, and therefore they had ﬁxed return and re-

view deadlines. For all other artifacts, the deadline

was the end of the course.

Educating Computer Science Educators Online - A Racket MOOC for Elementary Math Teachers of Finland

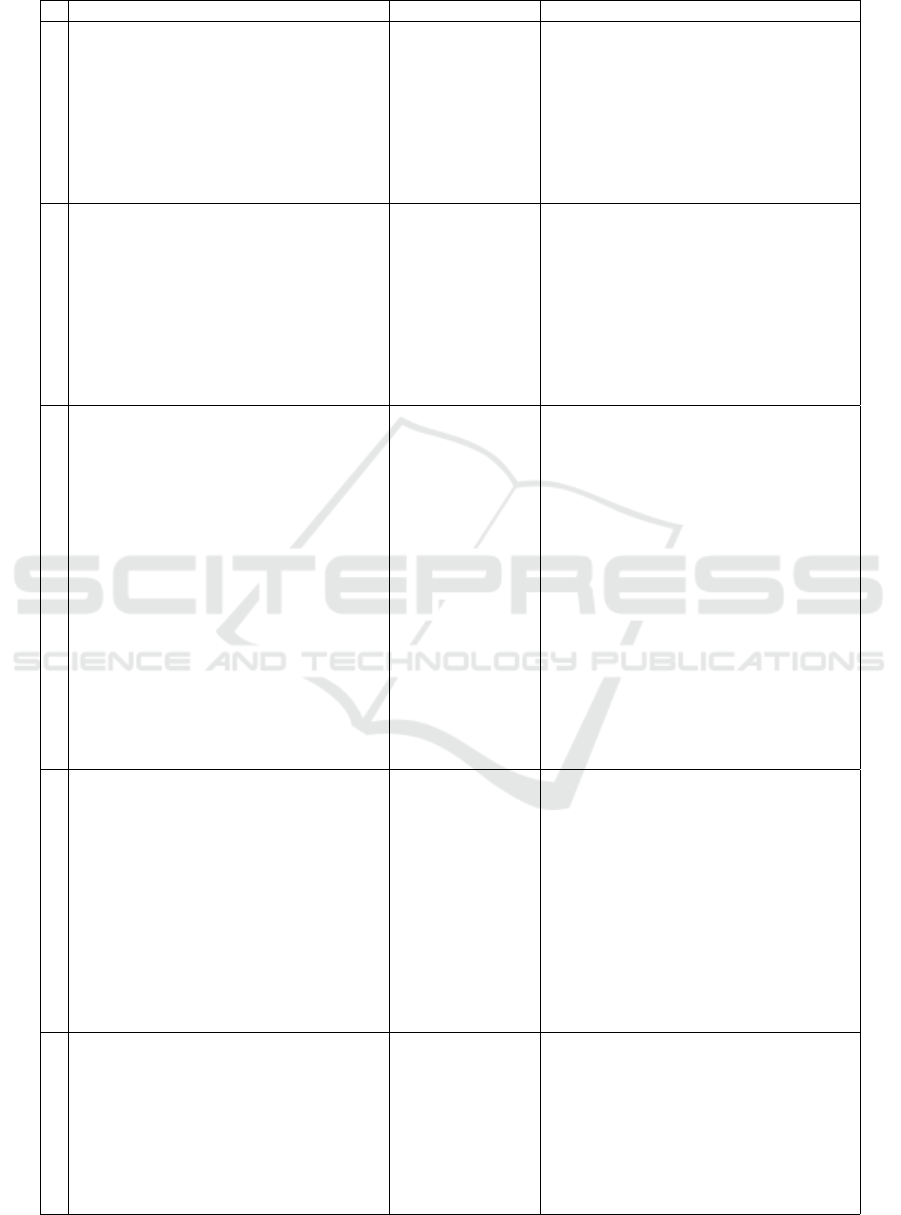
Table 1: Two iterative Racket track development cycles based on the feedback (Autumn-2015/Spring-2016).

w Autumn-2015 Lessons Learned Spring-2016

1 Introduction to Racket programming using

images (2htdp/image library), problem de-

composition, variables as global constants.

Artifact: An image shared by participants

The image created

positive feelings

of achievement:

using simple

geometric shapes

familiarized the

teachers with the

tool and enabled

creativity.

t1: The same exercise as in autumn

2 Using functions and parameters to solve

problems (abstraction), the design recipe

as a scaffold.

Artifact: Deﬁnition of a function (screen

capture images). The 1st exercise focused

on purpose of the function, its signature,

a stub and test cases, i.e. on demonstrating

the design recipe process. The 2nd exercise

was to implement the actual function body

and the minimum of two function calls.

Contents from

weeks 2-4 from

autumn 2015 were

divided into topics

2-5 and new con-

tent on recursion

and broader usage

of lists was added.

t2: Earlier introduction: how to use

true/false, comparison operators, predi-

cates and conditional structure (if) to con-

trol code execution, how to test functions

in an interaction window and by writing

unit tests (check-expect)

Artifact: Deﬁnition of a function, which

uses if-expression, including the purpose,

signature and test cases for all code

branches. Peer-reviewed by 3 participants

Boolean operators (and, or, not), compar-

isons, predicates, and conditional struc-

tures (if, else) to control code execution.

The animation engine (2htdp/universe),

reading a user input (display-read library)

familiarizing with WeScheme.

Artifact: WeScheme code with condi-

tional structures, the result could be an

animation, a simple quiz or an automated

calculator for some math formulas. Shared

with the group

*) Time for the autumn material of

week 3 was doubled (week 3 became

weeks 3 - 4)

More code skele-

tons provided for

t3-5, so the course

participants did

not need to create

applications from

scratch.

t3: The design recipe for functions. Writ-

ing tests ﬁrst, Boolean operators and

conditional structure for more complex

logic, animation engine (2htdp/universe),

WeScheme to share code

Artifact: No changes to the animation and

the simple mouse app. The quiz and the

calculator postponed.

t4: Helper and recursive functions, reading

user input (display-read library), blocks

with side-effects (user interaction), local

variables for storing the input

Artifact: Deﬁning multiple functions (at

least one recursive) i.e. a purpose, a sig-

nature and test cases. The end result could

be an image, recursive calculation or a sim-

ple calculator that asks an input in a loop.

Peer-reviews by 3 course participants

5 Looping using higher order functions

(map, foldl, foldr) and lists, usage of

Racket Turtle library to draw geometric

shapes.

Artifact: Shared image, which uses a

looping structure and either:

1. higher order functions + 2htdp/image

2. higher order functions/loops with re-

peat + Racket Turtle

As similar ex-

ercises were

already done in

accordance with

the recursion,

only Racket Tur-

tle option was

maintained and

foldl/foldr were

left out.

t5: Lists to store a set of values, iterating a

list recursively and producing new lists or

one result value, how to use image ﬁles in

DrRacket and WeScheme applications

Artifact: WeScheme code, which imple-

ments a simple list based quiz using a re-

cursive list-eater function, shared with oth-

ers.

t6: Looping using lists and higher order

functions (map), usage of Racket Turtle li-

brary to draw geometric shapes

Artifact: Shared image, drawn using

Racket Turtle library

6 Requirements of the Finnish curriculum

for the programming, algorithmic think-

ing/computational thinking, and how to

teach and integrate it with other subjects.

Artifact: Either a.) an essay (1-2 pages)

reﬂecting the challenges of teaching pro-

gramming b.) design of a new exercise

c.) a syllabus for integrating programming

into one’s own subject

Participants felt

that this exercise

was particularly

applicable for

their work and

hence found it

motivating.

t7: The same exercise as in autumn, except

peer-reviews were added

CSEDU 2017 - 9th International Conference on Computer Supported Education

Some participants complained that it was difﬁcult

to create programs from scratch and preferred exer-

cises with given code skeletons. Thus, such skele-

tons were provided as a scaffold for writing a program

in order to support a learning path with distinct use-

modify-create steps (Lee et al., 2011).

4.2 Spring-2016

The course syllabus for Spring-2016 was designed

so that different aspects of algorithmic thinking (ab-

straction, logic, repetition) were introduced side by

side starting from the easier ideas and progressing to

more advanced ideas. The course content was di-

vided into seven topics, each scheduled to take 10-

14 days. Three topics were almost identical to those

in Autumn-2015: topic 1, topic 6 (previously 5) and

topic 7 (previously 6), i.e., the ﬁnal essay was left un-

changed. Table 1 illustrates an overview of the course

content and exercises, and how the course developed

according to the feedback.

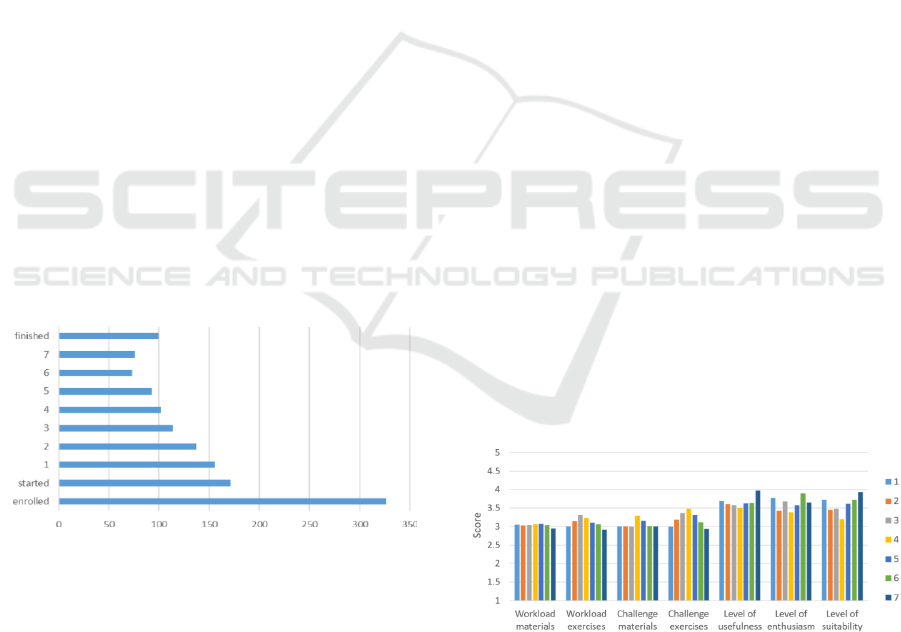
The Spring-2016 version of the Racket track had

fewer participants (171) than the beta version, as it

was competing for the same target group with a newly

introduced Python track. Of these 171 participants

who started the Racket track, 100 ﬁnished, resulting

in a 58% completion rate (80% of the coursework was

required to pass). The completion rate was 31%, tak-

ing into account all teachers (325) who had enrolled

on the MOOC. The number of teachers, whose re-

turned coursework was accepted for topics t1 - t7, is

illustrated in Figure 4.

Figure 4: Number of accepted coursework for topics 1-7.

4.2.1 Pre-course Survey

We conducted a pre-course survey to get background

information about the participants (N=137) using

Grader, which was also used for lesson feedback.

Based on the survey, most participants had some pre-

vious experience in programming: only 26% had

none, and as many as 45% had used more than one

programming language/environment. In the order of

popularity, the languages mentioned were Scratch,

34%, C/C++ 30 %, Java 26 %, Pascal 22 % , Basic

20 %, Python 15 %, Visual Basic 14 %, JavaScript 10

%, FORTRAN 9 %, LOGO 8 % and C# 3 %. The

greatest number of participants were among the 25-

to-35 age group (42%) and the majority of them were

female (78%). Almost 90% of the course participants

were math teachers and a similar proportion (91%)

taught in grades 7-9. Almost two thirds (61%) re-

ported that they had never used programming in their

teaching.

Compared to Autumn-2015, notably fewer pro-

gramming questions were asked on the discussion

forum. Consequently, the peer support that proved

so important during Autumn-2015, was almost non-

existent during Spring-2016. The same phenomenon

was noted in all four tracks of Koodiaapinen. One

possible reason is that the Piazza was too difﬁcult to

use, another might be that the joint discussion area of

all tracks was laborious to follow and hence distanc-

ing. In addition, discussions generated email notiﬁ-

cations to all participants, which was found annoy-

ing. Moreover, while Autumn-2015 was advertised to

everyone, Spring-2016 was marketed mainly to math

teachers, who are anticipated to be more ﬂuent with

technology by default, thus asking less questions.

4.2.2 Course Feedback

The teachers’ feedback on their level of experienced

enthusiasm, suitability and usefulness of the seven

topics covered was above average on a scale of 1-

5 (1: not at all, 2: a bit, 3: reasonably, 4: a lot, 5:

very much). The highest enthusiasm was created by

programming images (t1,6) and animations (t3). The

ﬁnal essay (t7) scored the highest on the suitability

and usefulness due to its pedagogical and curriculum

reﬂections, whereas recursion (t4) scored the lowest.

Overall, however, the scores did not differ remark-

ably, see Figure 5:

Figure 5: Spring-2016 feedback for topics 1-7.

The course feedback indicated a medium difﬁ-

culty level for most lessons, but recursion was consid-

ered the most difﬁcult in all aspects. In similar vain,

the workload of most topics scored in the middle,

where the exercises using more complex logic and

the animation library resulted in the highest workload

scores. The actual hours used per topic are shown in

Educating Computer Science Educators Online - A Racket MOOC for Elementary Math Teachers of Finland

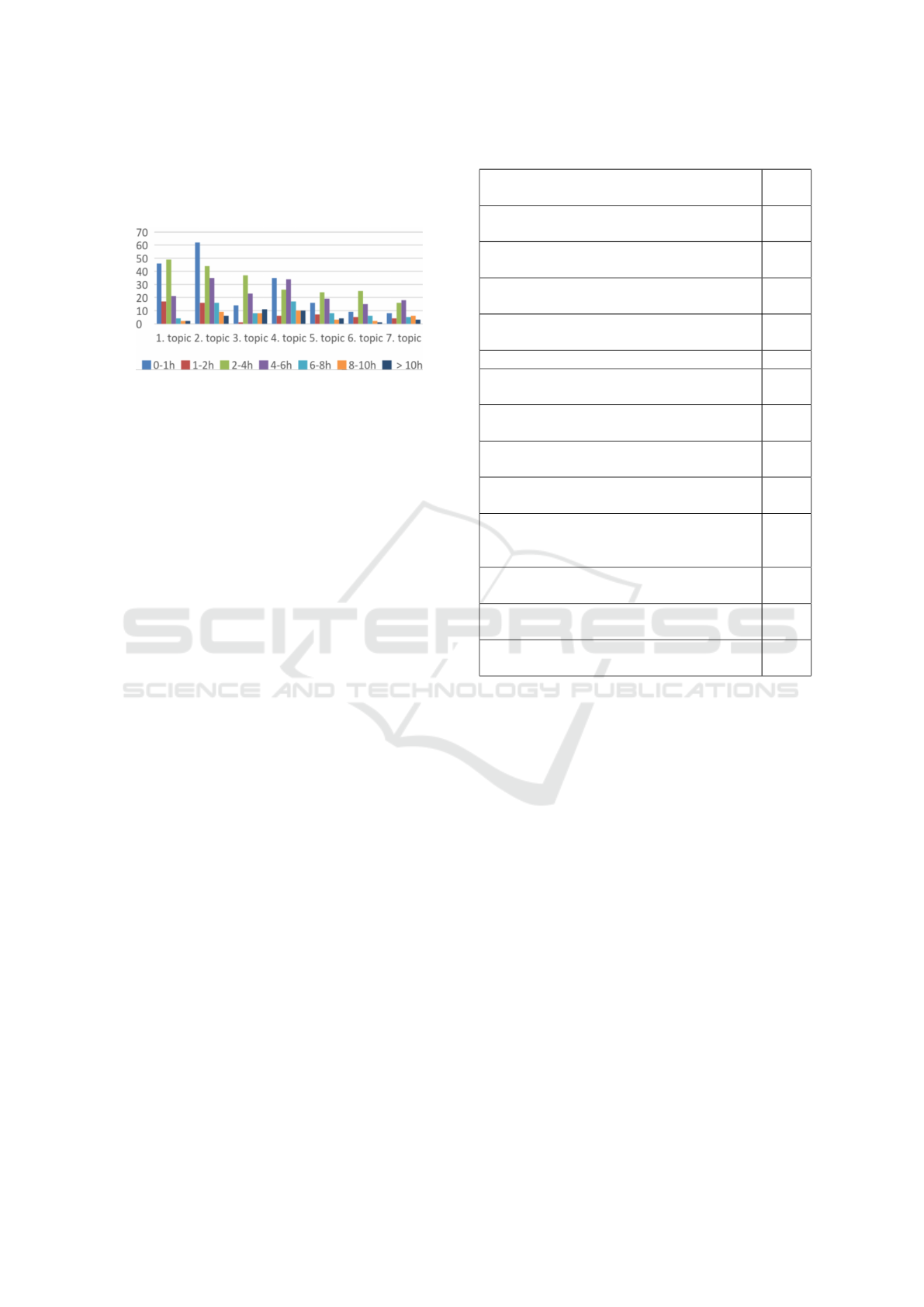
Figure 6. The target for Spring-2016 was 3-4 hours of

work per topic, and in fact most participants used 2-6

hours. Hence, the target was reasonably close to the

realization.

Figure 6: Amount of participants as a function of workload

grouped by topics.

4.2.3 Post-course Surveys for the Course

Development

At the end of the course, the course setup was evalu-

ated by the participants, but the survey gain was no-

tably low at that iteration: only 12 participants an-

swered, out of which 11 completed the course. The

teachers were asked, for example, to list aspects that

helped in completing the course, the top three reasons

being:

1. the tutorial videos of the course

2. the importance of the subject

3. concrete programming exercises

Table 2 and 3 illustrate the claims that the par-

ticipants agreed on either ’strongly’ or ’to a certain

extent’. The rejected claims were ’The course did

not support my development in becoming a teacher

of programming’ (1.75) and ’The course did not of-

fer sufﬁcient knowledge of teaching programming’

(2.25). Most improvement ideas related to the course

schedule and the difﬁculty of the exercises:

1. Only peer-reviewed exercises had deadlines while

the rest had to be completed before the course

end. This made it possible to complete tasks in

the wrong order, causing difﬁculties. Setting ped-

agogically adjusted deadlines would improve this.

2. For some topics, the video examples were simpler

than the real exercises. This can be remedied ei-

ther by having the material cover more complex

examples, or making the exercises easier to match

the difﬁculty level of the videos.

3. Although the video tutorials were considered

helpful and clear, a few teachers would preferred

written material: after watching a video, ﬁnding

speciﬁc information caused problems.

Table 2: Claims that participants agreed on.

Feature Score

[1..5]

MOOC-style courses are well suited for

professional development

4.5

The course provided skills needed for

teaching programming

4.4

The course increased my knowledge on

how to teach programming

4.3

The course provided methods for teaching

programming

4.3

The course worked well for as a MOOC 4.3

The course gave me concrete ideas (tips)

for my work as a teacher

4.3

The teaching methods applied enhanced

my learning

4.1

The course increased my conﬁdence in

programming as a teacher

3.9

I was committed to learning actively by

myself during this course

3.9

I will promote the contents that I learned

during this course to the other teachers in

my school district and my own school

3.6

The course made me excited about pro-

gramming

3.6

The course increased my interest in learn-

ing more about teaching programming

3.6

I received sufﬁcient support during the

course

3.6

4. To complete the course, 6 out of 7 topics were

required, thus a few participants did not return the

ﬁnal essay. It, however, was considered the most

important topic, in particular more important than

those covered in topics 5 and 6. Consequently,

the teachers suggested that the ﬁnal topic should

be compulsory and either 5 or 6 elective.

The course material and exercises were spread on

multiple platforms, such as A+, Eliademy, Rubyric

and Piazza, which was found confusing. Moreover,

A+ and Eliademy required separate accounts, which

led into problems e.g. when opening solution ﬁles

in Eliademy. In order to ﬁnd the exercises more

easily, the teachers suggested direct links to be at-

tached to the material. Due to the variety of plat-

forms, following the course execution was also prob-

lematic. The status of a delivery was shown in several

places, thus getting an overview of each assignment

was cumbersome, which hampered the recognition of

pending peer-reviews. Only a sufﬁcient number of

peer-reviews granted a credit and because of pending

reviews a number of credits were missing. Credits

were delayed also because the course set-up required

CSEDU 2017 - 9th International Conference on Computer Supported Education

the instructor to accept each return separately. Yet

another source of annoyance was Piazza by sending

participants an excessive amount of email notiﬁca-

tions. Consequently, the teachers proposed a daily or

weekly digest instead.

These improvement ideas were taken into account

in the later versions of the Racket course; the devel-

opment of the course is meant to be continuous. Af-

ter implementing a few of these improvements, mul-

tiple beneﬁts could already be listed regarding the

new platform and course syllabus. First, reviewing

and grading of returned artifacts was much easier us-

ing the new Padlet-style wall. Also peer-reviewing

decreased the amount of work, since the instructor

needed to manually review only the cases that were

unclear. Secondly, code reviews provided a new

learning opportunity and clariﬁed the requirements of

good programming style, for instance, why appropri-

ate naming and written purpose statements for func-

tions are important and why code needs to be tested.

Thirdly, the new course syllabus and schedule seemed

to work better and the workload for the course partic-

ipants and the instructor was more balanced.

5 CONCLUSIONS

We have developed an online programming course for

elementary school teachers, emphasizing the linkage

between mathematics and programming, and facili-

tating creativity and sharing. As the ﬁrst result, we

found that teachers were willing to learn program-

ming and appreciated the pedagogical considerations

in particular: the ﬁnal exercise of writing the es-

say scored highest of all exercises on both suitabil-

ity and usefulness. The previous programming exer-

cises aimed at enhancing the content knowledge. As

such, the programming exercises were tailored to be

ﬁt for teaching in authentic classroom settings, but in

conjuncture with learning to program teachers were

called to reﬂect on the exercises and come up with

new aspects and brand new tasks as well.

Secondly, the teachers’ feedback from the Spring-

2016 course iteration was more positive than from the

ﬁrst beta trial, which indicated that the level of difﬁ-

culty and workload were becoming reasonable. The

contents of the course were perceived both suitable

and useful. In addition, the course seemed to cre-

ate a fair amount of enthusiasm, making this type

of programming MOOC a motivating and interest-

ing form of professional development for in-service

teachers. In the effort to provide effective in-service

training, the improvement of the learning platform

and ﬁne-tuning the course material should be contin-

uous. Consequently, the course will be incrementally

improved based on the participants’ feedback: these

two subsequent Racket courses prove that this type of

agile course development is feasible.

Thirdly, the positive course feedback and reﬂec-

tions in essays seem to suggest that professional de-

velopment and self-efﬁcacy of the participants in-

creased. However, future research should observe the

long-term effects of the course, e.g., how many partic-

ipants actually started using the learned material and

skills in their work. As Kennedy (2016) points out,

real enactment in the school context is the ﬁnal test.

Further studies should also examine more thor-

oughly the suitability of the material for elementary

math and the question whether the course gave a sat-

isfactory enough insight into computational thinking.

For the purpose, the ﬁnal essays provide a plethora of

data to review. Systematic research and executing var-

ious learning experiments will enable determining the

best practices for developing computational thinking

and enhancing math syllabus, thus fulﬁlling the new

requirements of the Finnish Curriculum 2014.

ACKNOWLEDGMENTS

We thank the Aalto University A+ and Rubyric teams

for their efforts for the Koodiaapinen MOOC. We ex-

press our gratitude to Emmanuel Schanzer for modi-

fying WeScheme to suit our material and to Technol-

ogy Industries of Finland Centennial Foundation for

funding the development of the Koodiaapinen MOOC

in Spring 2016. Last but not least, thanks to Tarmo

Toikkanen for coordination.

REFERENCES

Alegre, F. and Moreno, J. (2015). Haskell in Middle and

High School Mathematics. In TFPIE vol. 1,.

Balanskat, A. and Engelhart, K. (2014). Computing our

future: Computer programming and coding-Priorities,

school curricula and initiatives across Europe. European

Schoolnet.

Bandura, A. (2006). Guide for constructing self-efﬁcacy

scales. Self-efﬁcacy beliefs of adolescents 5.

Barr, V. and Stephenson, C. (2011). Bringing computational

thinking to K-12: what is Involved and what is the role

of the computer science education community? ACM

Inroads 2, 48–54.

Bransford, J. D., Brown, A. L. and Cocking, R. R. (2000).

How people learn.

Burke, Q. and Burke, Q. (2016). Mind the metaphor: chart-

ing the rhetoric about introductory programming in K-12

schools. On the Horizon 24, 210–220.

Educating Computer Science Educators Online - A Racket MOOC for Elementary Math Teachers of Finland

Dijkstra, E. W. (1982). How do we tell truths that might

hurt? In Selected Writings on Computing: A Personal

Perspective pp. 129–131. Springer.

English Department for Education (2013). National Cur-

riculum in England Computing programmes of study.

Felleisen, M., Findler, R., Flatt, M. and Krishnamurthi, S.

(2014). How to Design Programs, Second Edition. MIT-

Press.

Felleisen, M. and Krishnamurthi, S. (2009). Viewpoint

Why computer science doesn’t matter. Communications

of the ACM 52, 37–40.

Finnish National Board of Education (2014). Finnish Na-

tional Curriculum 2014.

Flatt, M. and Findler, R. (2012). PLT - The Racket guide 1.

Futschek, G. (2006). Algorithmic thinking: the key for un-

derstanding computer science. In International Confer-

ence on Informatics in Secondary Schools-Evolution and

Perspectives pp. 159–168, Springer.

Gagn

e, R. M. (1965). The Conditions of Learning. New

York: Holt, Rinehart and Winston.

Gray, E. M. and Tall, D. O. (1994). Duality, ambiguity,

and ﬂexibility: A proceptual view of simple arithmetic.

Journal for research in Mathematics Education , 116–

140.

ulbahar, Y. and Kalelioglu, F. (2014). The effects of teach-

ing programming via Scratch on problem solving skills:

A discussion from learners’ perspective. Informatics in

Education-An International Journal 13.1, 33–50.

Heintz, F., Mannila, L. and F

arnqvist, T. (2016). A Re-

view of Models for Introducing Computational Think-

ing, Computer Science and Computing in K-12 Educa-

tion. Frontiers in Education October.

Jarvis, S. and Pavlenko, A. (2008). Crosslinguistic inﬂuence

in language and cognition. Routledge.

Kennedy, M. (2016). How does professional development

improve teaching? Review of Educational Research .

Kiczales, G. (2015). UBCx: SPD1x Systematic Program

Design - Part 1 (version 1, summer 2015).

Kulik, J. A. (1994). Meta-analytic studies of ﬁndings on

computer-based instruction vol. 1, of Technology assess-

ment in education and training pp. 9–34. Psychology

Press.

ohler, W. (1970). Gestalt psychology: An introduction

to new concepts in modern psychology. WW Norton &

Company.

Lee, I., Martin, F., Denner, J., Coulter, B., Allan, W., Erick-

son, J., Malyn-Smith, J. and Werner, L. (2011). Compu-

tational thinking for youth in practice. ACM Inroads 2,

32–37.

Lent, R. W., Lopez, F. G. and Bieschke, K. J. (1991). Math-

ematics self-efﬁcacy: Sources and relation to science-

based career choice. Journal of counseling psychology

38, 424.

Levy, D. (2013). Racket Fun-ﬁctional Programming to

Elementary Mathematics Teachers. In TFPIE2013 TF-

PIE2013.

Marceau, G., Fisler, K. and Krishnamurthi, S. (2011). Mea-

suring the effectiveness of error messages designed for

novice programmers. In Proceedings of the 42nd ACM

technical symposium on Computer science education pp.

499–504, ACM.

Meerbaum-Salant, O., Armoni, M. and Ben-Ari, M. (2011).

Habits of programming in scratch. In Proceedings of the

16th annual joint conference on Innovation and technol-

ogy in computer science education pp. 168–172, ACM.

Mezirow, J. (1997). Transformative learning: Theory to

practice. New directions for adult and continuing educa-

tion 1997, 5–12.

OECD (2015). Students, Computers and Learning.

Papert, S. (1996). An exploration in the space of mathemat-

ics educations. International Journal of Computers for

Mathematical Learning 1, 95–123.

Perkins, D. N. and Salomon, G. (1988). Teaching for trans-

fer. Educational leadership 46, 22–32.

Reimann, P. (2011). Design-based research pp. 37–50.

Methodological choice and design. Springer.

Resnick, M., Maloney, J., Monroy-Hern

andez, A., Rusk,

N., Eastmond, E., Brennan, K., Millner, A., Rosenbaum,

E., Silver, J. and Silverman, B. (2009). Scratch: pro-

gramming for all. Communications of the ACM , 52,

60–67.

Rich, P. J., Leatham, K. R. and Wright, G. A. (2013). Con-

vergent cognition. Instructional Science , 41, 431–453.

Schanzer, E., Fisler, K., Krishnamurthi, S. and Felleisen,

M. (2015). Transferring skills at solving word prob-

lems from computing to algebra through Bootstrap. In

Proceedings of the 46th ACM Technical symposium on

computer science education, pp. 616–621, ACM.

Schanzer, E. T. (2015). Algebraic Functions, Computer Pro-

gramming, and the Challenge of Transfer .

Voogt, J., Fisser, P., Roblin, N. P., Tondeur, J. and van

Braak, J. (2013). Technological pedagogical content

knowledge–a review of the literature. Journal of Com-

puter Assisted Learning 29, 109–121.

Wing, J. M. (2006). Computational thinking. Communica-

tions of the ACM 49, 33–35.

Wing, J. M. (2011). Computational thinking. In VL/HCC

p. 3, csta.acm.org.

Wright, G., Rich, P. and Lee, R. (2013). The inﬂuence of

teaching programming on learning mathematics. In So-

ciety for Information Technology & Teacher Education

International Conference vol. 2013, pp. 4612–4615, ed-

itlib.org.

Yoo, D., Schanzer, E., Krishnamurthi, S. and Fisler, K.

(2011). WeScheme: the browser is your programming

environment. In Proceedings of the 16th annual joint

conference on Innovation and technology in computer

science education pp. 163–167, ACM.

Zeldin, A. L. and Pajares, F. (2000). Against the odds:

Self-efﬁcacy beliefs of women in mathematical, scien-

tiﬁc, and technological careers. American Educational

Research Journal 37, 215–246.

CSEDU 2017 - 9th International Conference on Computer Supported Education