
Concept and Realization of a Diagnostic System for Smart Environments
Eric Heiden
1
, Sebastian Bader
2
and Thomas Kirste
2
1
University of Southern California, Los Angeles, U.S.A.
2
Institute of Computer Science, University of Rostock, Rostock, Germany
Keywords:
Automatic Diagnosis, Diagnostic Engine, Non-monotonic Reasoning, Model-based Diagnosis.
Abstract:
Automatically diagnosing a complex system containing heterogeneous hard- and software components is a
challenging task. To analyse the problem, we first describe different scenarios a diagnostic engine might be
confronted with. Based on those scenarios, a concept and an implementation of a semi-automatic diagnostic
system are presented and some first benchmarks are shown.
1 INTRODUCTION
Imagine you enter a smart conference room, connect
your laptop with the first available HDMI-port and
the system automatically switches on the main pro-
jector. Smart Environments like this allow the user
to seamlessly interact with an ensemble of intercon-
nected devices. Sensors and actuators are combined
to provide an unobtrusive environment in which the
user’s intentions are inferred to facilitate multimedia-
enabled conferences or lectures. Immediately the first
slide of your presentation appears on the screen and
you can start your talk. But suddenly the projected
display turns blank and you have to interrupt the pre-
sentation. What could possibly have happened? The
green power indicating LED of the projector is still
glowing and your laptop indicates it is duplicating its
screen via the HDMI connection, too. Perhaps the
display signal connection is broken? But after having
manually checked the firmness of every cable on the
way from your notebook to the projector the symptom
still persists. Finally you see no other option than ask-
ing the facility manager to look after the problem. A
short while later she finds the source of the error: the
projector’s lamp has exceeded its lifespan. Her expert
knowledge helped her diagnose the problem.
This contrived scenario gives rise to several ques-
tions: How could this situation be handled better?
What if we had expert knowledge immediately avail-
able without always having to seek out technicians to
identify and troubleshoot malfunctions? Which au-
tomatic methods do exist for the diagnosis of error
sources?
In this paper, we present an approach for a diag-
User
Knowledge
Diagnostic Engine
Middleware
System
description
Diagnosis
Observations
Observations
Figure 1: Context of the Diagnostic Engine.
nostic engine and its realization in our smart meet-
ing room. Figure 1 shows the context of a diagnos-
tic engine. The engine has predefined knowledge of
the environment, i.e. the system of interconnected
components to be diagnosed. Provided with a symp-
tomatic observation, the engine reasons about possi-
ble sources of the encountered malfunction. To im-
prove these explanations, further observations can be
gathered using the middleware to retrieve status infor-
mation from the system’s components. As not every
detail is observable through the middleware, the en-
gine can also ask the user to provide observations.
First, we present a number of scenarios with in-
creasing difficulty in Section 2. We review different
approaches for diagnostic systems in Section 3. In
Section 4, we present our concept for a diagnostic en-
gine and describe our implementation in Section 5.
Finally, we present some preliminary benchmark-
results in Section 6.
318
Heiden E., Bader S. and Kirste T.
Concept and Realization of a Diagnostic System for Smart Environments.
DOI: 10.5220/0006257903180329
In Proceedings of the 9th International Conference on Agents and Artificial Intelligence (ICAART 2017), pages 318-329
ISBN: 978-989-758-220-2
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

2 DIAGNOSTIC SCENARIOS
In the following, several exemplary scenarios are de-
scribed to demonstrate different aspects of failure di-
agnosis. Scenarios are grouped by their difficulty from
a diagnostic engine’s perspective ranging from prob-
lems which can be detected by a single automatic
step, up to unsolvable issues which cannot be diag-
nosed, not even in cooperation with the user. The
analysis of problem classes furthermore allows to nar-
row down the diagnosis problem to only some sub-
systems which can be effectively treated by semi-
automatic diagnosis.
Scenarios are described by first indicating what
the diagnostic engine knows about the system. This
a-priori knowledge consists of a wiring diagram rep-
resenting the system description, and the user’s ob-
servations on the state of the involved components. If
we are confronted with a diagnosis problem, these ob-
servations should contain symptomatic descriptions
which differ from the normal system behavior.
The omniscient perspective explains holistically
the actual system configuration and true causes for
the occurring issues. If the diagnostic engine were
to know these facts, the proper diagnosis would be
calculable instantaneously. Subsequently, the partial
view of the system from the diagnostic engine’s per-
spective is examined to derive all possible diagnoses
the system can infer based on the observations and
its understanding of the system. If the diagnosis is
too vague to be useful for troubleshooting, the engine
makes further observations or asks the user to perform
these in order to gain more detailed information on the
true causes of symptoms.
These scenarios are contrived and are meant to fa-
cilitate a more lucid view on the general idea of di-
agnostic reasoning and probable pitfalls of automatic
diagnosing.
2.1 Automatically Identifiable Problems
This category contains scenarios which the diagnostic
engine can identify completely autonomously without
cooperating with the user, i.e. solely based on infor-
mation accessible through the middleware.
2.1.1 Complete Observations
The user tries to display content from laptop L on pro-
jector P but the screen remains blank. The user has
already observed that P is switched off and that all
involved devices and connections work as expected
without any problems.
Omniscient Perspective:
• All components work correctly.
• All involved cables are in proper condition.
• The projector is switched off.
Possible Error Sources:
• The projector is switched off.
This scenario represents the special case where the
provided observations are detailed enough to account
for a precise diagnosis. No further knowledge is re-
quired to infer that the powered off projector is the
single error source because it is given that all compo-
nents function.
2.1.2 Automatic Observations
The user tries to display content from laptop L on
projector P but the screen remains blank. L and the
control server S work as expected, and L provides an
HDMI video signal. All connections are stable. All
devices are switched on.
Omniscient Perspective:
• All components work correctly.
• All involved cables are in proper condition.
• S configured P to use the wrong input port.
Possible Error Sources:
• P is defect (e.g. projector lamp burned out, firmware
error, overheating, serious physical damage).
• S configured the wrong input on P.
• P ignores the configuration carried out by S and hence
uses the wrong input.
The diagnostic engine is now confronted with an am-
biguous situation where multiple diagnosis candidates
compete. Here, a tie-breaking observation is neces-
sary. Let us assume that the engine asks S which in-
put configuration has been set on P. S now requests
status information from P and reports P’s input con-
figuration. This automatic observation reveals that P
is using the VGA port instead of HDMI to which L is
connected to. From this knowledge it can be inferred
that P is not defect (for simplicity we assume that if P
can be accessed via Ethernet it is completely ok) and
only S made the wrong input configuration. Without
the need of human cooperation the engine could diag-
nose the symptom completely automatically. And the
system could subsequently fix the problem automati-
cally by reconfiguring P.
2.2 Semi-automatically Identifiable
Problems
Scenarios in which problems can only be diagnosed
in cooperation with the user belong to this category.
Concept and Realization of a Diagnostic System for Smart Environments
319

2.2.1 Non-automatically Observable System
Properties
Laptop L and projector P are switched on but P does
not show any output. The HDMI connection between
L and P is stable.
Omniscient Perspective:
• L works correctly.
• The HDMI connection between L and P is stable.
• The projector lamp in P has burned out.
Possible Error Sources: Let us assume that in this sce-
nario we have a more detailed model of projector P than
in the previous scenarios:
• P has a firmware bug.
• The projector lamp of P has burned out.
• The configured resolution of L is too high.
While the latter hypothesis can be discarded by per-
forming an automatic test if L’s resolution is greater
than the maximum resolution supported by P, the
ambiguity between the first two diagnosis candidates
remains. In this case the user needs to check the
projector-related properties.
It can be argued that those two observations can
only be carried out by technicians and therefore the
true cause of error is still hard to retrieve. On the
other hand, the problem could be clearly limited to
projector P by the diagnostic engine so that in a real
world scenario the projector could just be replaced as
an immediate retaliatory action.
2.2.2 Multiple Simultaneous Faults
Both laptops, L
1
and L
2
, the server S and the projector
P are switched on and are in proper condition. How-
ever, P does not display anything.
Omniscient Perspective:
• All components work correctly.
• The HDMI cable between L
1
and P, and the VGA
cable between L
2
and P are broken.
• P is configured to use the VGA port as input source.
Possible Error Sources:
• The HDMI cable between L
1
and P is broken.
• The VGA cable between L
2
and P is broken.
• The HDMI cable between L
1
and P and the VGA ca-
ble between L
2
and P are broken.
First, the diagnostic engine should determine which
input has been selected by P. Therefore, S is commis-
sioned to request information on the input configura-
tion of P. This returns V GA as the active input port
and thus it can be reasoned that the VGA connection
between L
2
and P is broken.
Now that we are certain about one component of
our diagnosis it would also be helpful to know if there
might be any more faults in the system. Let us now
assume that P’s input configuration is read-only so
that S cannot alter the setting automatically. How-
ever, in order to check whether the HDMI connection
between L
2
and P is broken, we need to test if P also
does not show anything if HDMI is selected as in-
put. Thus, the diagnostic engine has to ask the user to
carry out this diagnostic action and then tell whether
P shows something or not. The user reports that the
screen is still blank after HDMI has been defined as
input. Ultimately, the diagnostic engine concludes
the following: both the HDMI connection between
L
2
and P as well as the HDMI connection between L
1
and P are broken.
If the user was unable to perform the diagnostic
step of altering the system’s configuration to provide
a new observation, it would not be decidable whether
the HDMI connection between L
1
and P was broken
or not. A common approach to handle this knowl-
edge gap would be to assume that everything is work-
ing correctly unless we have concrete evidence to re-
tract such assumption (e.g. by observing a symptom).
Below we shall see how this type of so-called non-
monotonic reasoning is handled from a logical per-
spective.
2.2.3 Disconnected Subsystems
Until now, we have assumed that our diagnostic en-
gine somehow can instruct system-inherent compo-
nents, e.g. servers, to perform observations or alter
the system configuration. In reality however, the di-
agnostician itself is a device or a software running on
network-attached hosts which might fail or loose con-
nection – just like any other component. To examine
this property in detail, let us assume the following sce-
nario: Laptop L, the diagnostic engine D und the NAS
(Network-Attached Storage) are connected to switch
S via Ethernet. While all devices are working as ex-
pected, L cannot connect to NAS.
Omniscient Perspective:
• All components work correctly.
• The Ethernet between D and S is broken.
• The Ethernet connection between NAS and S is bro-
ken.
Possible Error Sources:
• The Ethernet connections D – S and NAS – S are bro-
ken.
• The Ethernet connections D – S and L – S are broken.
• The Ethernet connections D – S, L – S and NAS – S
are broken.
The diagnostic engine cannot perform further obser-
vations automatically because it is disconnected from
the subsystem B = {NAS, L, S}. Therefore, all non-
empty permutations of broken Ethernet connections
between components c
1
, c
2
∈ B, together with the fact
that Ethernet connection D – S is broken, are valid
ICAART 2017 - 9th International Conference on Agents and Artificial Intelligence
320

diagnoses. This ambiguity can only be resolved if D
gets access to S or by asking the user to check all con-
nections.
2.3 Unidentifiable Problems
This class comprises diagnostic scenarios where the
diagnostic engine is unable to diagnose the symptoms
– not even in cooperation with a human user.
2.3.1 Hidden Interactions
After switching on a lamp, all lamps and projectors
are suddenly powered off.
Omniscient Perspective:
• All components work correctly.
• The lamps and projectors are connected to power
sources which share the same fuse.
• Due to power overload of too many connected de-
vices, this fuse was tripped and caused the power out-
age for all projectors and lamps.
Possible Error Sources: N/A
The engine cannot propose any diagnoses since it is
not aware of the interaction between projectors and
lamps. The fact that their power sources share the
same fuse might not be indicated in the wiring plan.
The engine cannot even ask the user to check the fuses
because it can only reason about facts which are pro-
vided as system knowledge.
Several approaches exist to handle hidden interac-
tions (see (B
¨
ottcher, 1995; Kuhn and de Kleer, 2010)).
If we observe a malfunction which affects completely
unrelated parts of the system like in the given sce-
nario, it can be assumed that hidden, unintended in-
teractions have occurred.
2.3.2 Intermittent Abnormalities
In this scenario, the diagnostic engine runs directly on
the user’s laptop L.
The switch S intermittently becomes unavailable.
Laptop L is working correctly and the Ethernet con-
nection between L and S is stable.
Omniscient Perspective:
• Laptop L is working correctly.
• The Ethernet connection from L to S is stable.
• Switch S is congested sometimes when the user wants
to access it.
Possible Error Sources: N/A
Imagine that coincidentally, every time the diagnos-
tician tries to access S, the switch responds immedi-
ately. This observation contradicts with the user’s ob-
servation and in contrast shows no symptoms. There-
fore, it can only be reasoned that S is working cor-
rectly despite the apparent malfunction.
This problem could be addressed by letting the di-
agnostic engine constantly observe every network ac-
cess L is making. This kind of online diagnosis would
then experience – just like the user – the symptomatic
timeouts. However, during the course of this paper
only offline scenarios are considered in which a mal-
function has occurred and the user subsequently re-
quests an explanation of the observed symptoms.
2.3.3 Wrong Observations
Laptop L and projector P are switched on but P does
not show any output (cf. Scenario 2.1.1).
Omniscient Perspective:
• All components work correctly.
• The projector is configured to select its HDMI port as
input source.
• The observation provided by the user is wrong, i.e. P
indeed displays content from L.
Possible Error Sources:
• P is broken.
This diagnosis (that P is broken) is wrong because the
diagnostician trusted the user-provided observation
and does not have any automatic verification methods
for given observations. Observations (human-made
or automatic) do not need to be invalid only because
of human deceit, often technical devices themselves
report false status information if they are broken, i.e.
they are behaving abnormally. This problem could be
tackled by assigning quantifying the degree of belief
when dealing with arbitrary inputs. A diagnostic the-
ory of involving probabilistic reasoning to deal with
uncertainty is given by (Lucas, 2001).
3 PRELIMINARIES
Before introducing two main concepts of diagnostic
reasoning, namely consistency-based and abductive
diagnosis, this section covers the general notion of di-
agnosis in the real-world context and its development
to an A.I. discipline.
While the term diagnosis can also mean the pure
decision whether a system is working or not, this pa-
per is based on the definition of diagnosis as a method
to identify the causes of observed system faults as pre-
cisely as possible.
Similar to real world diagnosis where experts are
asked to find those parts in complex systems, like cars
or powerhouses, which account for the observed mal-
function, diagnosis as a subfield in artificial intelli-
gence similarly provides techniques to identify causes
of observed symptoms – especially for applications
which require significant expert knowledge. This task
Concept and Realization of a Diagnostic System for Smart Environments
321

requires observations of the actual, possibly unex-
pected system behavior as well as knowledge of the
problem domain sufficient enough to infer meaning-
ful conclusions.
Diagnostic Engines first emerged during the late
1960’s to early 1970’s in the form of rule-based ex-
pert systems (Angeli, 2010). Causal representations
of symptoms and faults were explicitly written as
hard-coded or compiled knowledge as an attempt to
mimic human expert behavior. These systems had
major drawbacks when applied to non-static domains
were properties evolve and affect the causal relation-
ships between observed problems and underlying er-
ror sources. Knowledge engineers were required to
cooperate with human experts in order to manually
update the knowledge base.
In contrast to these heuristic approaches, model-
based diagnosis which emerged during the 1980’s, al-
lowed for an estimation of system behavior which can
be compared to the observed outcomes in order to de-
tect abnormalities. These systems showed a higher
degree of robustness compared to rule-based systems
because they could better handle unexpected cases.
Current trends in diagnostic systems present the
coupling of classical model-based diagnosis with
other AI techniques like neural networks or genetic
algorithms (Angeli, 2010) to improve knowledge ac-
quisition and diagnose complex and dynamic systems
more effectively.
Model-based diagnosis is a commonly used
framework that works by modelling a system consist-
ing of interacting components or subsystems via log-
ical formulas. While it possible to define fault mod-
els, during the course of this paper only the system’s
expected behavior is modelled as in (Reiter, 1987;
de Kleer, 1986; Lucas, 2001). Conversely, the out-
puts of the real-world implementation of the system
are measured and the observations are as well logi-
cally formalized. The discrepancies between the ob-
servations and the predicted behavior are finally used
to diagnose faulty components whose behavior con-
tradict the model’s behavior.
Reiter proposed in (Reiter, 1980) a logic for de-
fault reasoning called default logic which extends
first-order logic by allowing to perform default as-
sumptions. While in standard logic it can only be
stated that something is either TRUE or FALSE, de-
fault logic can express facts that are typically TRUE
only with a few exceptions.
For example, the fact that almost all projectors
have a VGA port can be represented as follows in de-
fault logic:
PROJECTOR(x) : M HAS-VGA(x)
HAS-VGA(x)
Here M stands for it is consistent to assume so that
this default rule can be read as: given the fact that x
is a projector (prerequisite) and it is consistent to be-
lieve that x has a VGA port (justification), then one
may assume that x has a VGA port (conclusion). To
specify the notion of this consistency requirement, the
semantics of default logic is described in the follow-
ing.
A default theory is defined as a pair (W, D), where
D is a set of default rules and W is the set of logical
formulas which define our background theory. If the
prerequisite of a given default D is entailed from our
theory W and every justification is consistent with W
than we can add the conclusion to the theory.
Since the consequence relation is not monotonic,
default reasoning is a kind of non-monotonic reason-
ing.
First-order logic is monotonic, i.e. given two sets
A and B of first-order formulas where A ` w, then
every model of A ∪ B is also a model of A so that
A ∪ B ` w. If we assume B to be newly discovered in-
formation, the addition of B to our existing knowledge
A does not affect the outcome w of A ∪ B with respect
to the models of A. That means, if later discoveries
reveal contradictions to formerly assumed rules they
cannot be retracted.
However, in any reasoning method were assump-
tions or beliefs are made, like default reasoning or
abductive reasoning (Section 3.2), it is necessary to
retract an assumption in order to avoid inconsisten-
cies with newly gained evidence. Adding knowledge
to the theory which contradicts the assumptions shall
invalidate them and thus reduce the set of conclu-
sions that can be derived from the theory. The notion
that further evidence does not monotonically grow the
set of derivable propositions describes the property of
non-monotonic reasoning.
3.1 Consistency-based Diagnosis
The theory by Reiter on Diagnosis from First Princi-
ples (Reiter, 1987) is a model-based approach which
conjectures about faulty components by only select-
ing hypotheses which are consistent with the sys-
tem’s model and the observations. This approach laid
an important foundation for the automatic identifica-
tion of problems not only in electric circuitry as in
the early days of automatic diagnosis, but universally
across many different domains. In the following, di-
agnosis from first principles will be used to present
the concept of consistency-based diagnosis.
In this model-based approach the only informa-
tion available to explain discrepancies between the
observed and correct system are first principles, i.e.
ICAART 2017 - 9th International Conference on Agents and Artificial Intelligence
322

wor ks ( l ) :− n ot ab ( l ) .
wor ks ( p ) :− n ot ab ( p ) .
sh o ws ima ge ( p ) :− works ( l ) , works ( p ) ,
no t ab ( b ) , n ot ab ( hdmi ) .
Figure 2: Prolog implementation of a simple diagnosis ex-
ample.
the model of the system’s expected behavior repre-
sented using logical formulas. Reiter’s theory is ap-
plicable to any logic L which fulfills the following
criteria:
1. Binary semantics so that every sentence of L has
value TRUE (>) or FALSE (⊥).
2. {∧, ∨, ¬} are supported logical operators which
have their usual semantics in L .
3. denotes semantic entailment in L.
4. A sound, complete and decidable theorem prover
exists for L.
In general, first-order logic (FOL) is only semide-
cidable, i.e. the question whether an arbitrary formula
f is logically valid (a theorem) in L can always be an-
swered correctly whereas a negative or no answer at
all will be given if f is not valid in L. To still fulfill the
last criterion, we will from now on define a decidable
subset of FOL as the logic L to be used for diagnosis.
This is established by requiring L to be a FOL with
finite domain of discourse D (Herbrand universe) and
finite Herbrand base.
Definition 1 (System). The system is defined as a pair
(SD, COMPONENTS) consisting of SD, the system de-
scription which contains rules of logic L describing
the system’s normal behavior, and COMPONENTS, the
finite set of constants representing the components.
Components can be devices, connections, subsys-
tems, or any entity that could be (partially) respon-
sible for the system’s malfunction and should there-
fore be included in the diagnosis. The system descrip-
tion makes use of AB(c)-predicates which express for
component c ∈ COMPONENTS that c is behaving ”ab-
normally”. Thus, when modelling the intended sys-
tem behavior these abnormal-predicates only occur in
its negated form.
For a running example let us revisit our first fully
automatically diagnosable scenario. In addition to the
system properties described before, let us also assume
that projector P’s lamp B is a component which can
burn out preventing P to show anything.
We could represent this scenario using the follow-
ing system description SDas a set of definite Horn
clauses shown in Figure 2 Similarly to SD, the obser-
vations are given as a finite set of logical formulas
in L as well. A diagnostic problem is defined as the
triple (SD, COMPONENTS, OBS). For this example, let
OBS = {¬ IMAGE(P), WORKS(L)} be the set of our
observations, i.e. we observed that P did not show an
image and L was working.
A diagnosis for the problem
(SD, COMPONENTS, OBS) is defined as the minimal
set (under set inclusion) ∆ ⊆ COMPONENTS where
SD ∪ OBS ∪ {AB(c) | c ∈ ∆} ∪ {¬AB(c) | c ∈
COMPONENTS\∆} is consistent.
Generally, a valid diagnosis would be the trivial
solution that all components are faulty, since we are
following the model-based approach were only the
expected behavior is known. Therefore, the Principle
of Parsimony has been established in (Reiter, 1987)
and advocates the minimal diagnosis. To find minimal
diagnoses it helps to reformulate the aforementioned
definition of ∆ in terms of conflict sets.
A conflict set for (SD, COMPONENTS, OBS) is de-
fined as C = {c
1
, . . . , c
2
} ⊆ COMPONENTS such that
SD ∪OBS ∪{¬AB(c
1
), . . . , ¬AB(c
n
)} is inconsistent. A
conflict set C is minimal iff no subset C
0
⊂ C exists
that is also a proper conflict set satisfying the equa-
tion.
Consistency-based diagnosis interprets the consis-
tency requirement by the semantics of classical logic
where a logical formula f ∈ L is consistent if f
has model, i.e. an interpretation or assignment of
variables of f to the domain of discourse D so that
the meaning of f is TRUE. Therefore, we can as-
sume the unresolved consistency terms WORKS(P)
and ¬WORKS(P) to be TRUE since a model exists
for SD ∪ OBS ∪ {AB(c) | c ∈ ∆} ∪ {¬AB(c) | c ∈
COMPONENTS\∆} ∪ {WORKS(P)} and another model
exists for SD ∪ OBS ∪ {AB(c) | c ∈ ∆} ∪ {¬AB(c) | c ∈
COMPONENTS\∆} ∪ {¬WORKS(P)}. As we will later
see, this consistency definition of non-stable models
marks the fundamental difference to abductive rea-
soning (cf. Section 3.2). The following two conflict
sets can be found:
C
1
= {AB(B), AB(P), AB(HDMI)}
C
2
= {AB(B), AB(L), AB(P), AB(HDMI)}
Hence we have the minimal conflict set is C
1
=
{AB(B), AB(P), AB(HDMI)}.
For a collection S of sets, a hitting set H for C is a
set H ⊆
S
S∈C
such that ∀S ∈ C : H ∩ S 6=
/
0. A hitting
set is minimal if no proper subset of it is a hitting set.
Reiter uses this definition to reformulate the charac-
terization of diagnoses: ∆ ⊆ COMPONENTS is a diagno-
sis for (SD, COMPONENTS, OBS) iff ∆ is a minimal hit-
ting set for the collection of minimal conflict sets for
(SD, COMPONENTS, OBS). For our example, three mini-
mal hitting sets can be found which represent our min-
imal diagnoses ∆
1
= {AB(B)}, ∆
2
= {AB(P)}, ∆
3
=
{AB(HDMI)}.
Concept and Realization of a Diagnostic System for Smart Environments
323

3.2 Abductive Diagnostic Reasoning
Abductive reasoning is a form of logical inferenc-
ing that hypothesizes explanations for a given ob-
servation, and is viewed as a competing concept to
consistency-based diagnosis. As a powerful concept
to handle commonsense reasoning, it has been applied
in the diagnosis domain (Eiter and Gottlob, 1995).
Abduction became a powerful reasoning method
to Artificial Intelligence especially in the field of di-
agnosis which is considered by (Christiansen, 2005)
as one of the most representative and best understood
application domains for abductive reasoning. It has
further served as a basis for other types of expert sys-
tems, e.g. in the medical domain, and apart from di-
agnosis in areas such as planning, natural language
understanding and machine learning (Christiansen,
2005).
Abduction is a logical reasoning method that gen-
erates, given a logical theory or domain knowledge
T and a set of observations O, explanations (= hy-
potheses) E which explain O according to T such that
T ∪E O, and T ∪E is consistent. Abductive reason-
ing is a type of non-monotonic reasoning since hy-
potheses E which have been made given theory T and
observations O might become obsolete due to new ob-
servations O
0
which require the reasoning system to
retract those explanations which do not meet the two
constraints from above. Therefore, default reasoning
can be based on abduction instead of non-monotonic
logics so that defaults are represented as hypotheses
to be made or retracted instead of deriving conclu-
sions within non-monotonic logics (cf. (Eshghi and
Kowalski, 1989)).
An abductive theory is a triple (P, IC, A), where
P is a logic program defining the domain knowledge,
IC is a set of integrity constraints (logical formulas)
which define constraints on the abduced predicates,
and A is a set of abducible ground atoms.
We can now define express (P,IC, A) in terms of
the diagnosis domain in order to identify faulty com-
ponents ∆ ⊆ COMPONENTS in a malfunctioning system
in the same way as finding the best explanations for
given symptoms. A system (SD,COMPS) is formal-
ized as follows: SD is the system definition, as de-
fined by P, and COMPS is the set of system components
which can be possible sources of errors, as defined by
A.
The integrity constraints IC can be used to ad-
ditionally constrain the generated diagnose, e.g. by
stating that certain components A
0
⊆ A cannot be di-
agnosed as faulty.
When diagnosing a system, one needs to observe
the malfunction and represent these symptomatic ob-
servations as a set of logical formulas OBS. The diag-
nosis problem (SD, COMPS, OBS) is solved through ab-
duction by retracting some of the ¬AB-assumptions.
The resulting set ∆ ⊆ A is a valid diagnosis if it ex-
plains all of the observed symptoms.
To meet the goal of providing useful diagnoses
which do not contain any, for the fault explanation
insignificant components, the Principle of Parsimony
advocates minimal diagnoses. Hence, a diagnosis
for (SD, COMPS, OBS) is according to (Ray and Kakas,
2006) a minimal set ∆ ⊆ A such that SD ∪∆ OBS∩IC.
We will use implementations of abductive reason-
ing in the form of logic programming and answer
set programming. These systems follow the stable
model semantics which was motivated by formalizing
the behavior of SLDNF resolution (selective, linear,
definite resolution with negation as failure), a com-
mon resolution strategy for logic programming sys-
tems like Prolog.
For any set M of atoms from Π, let Π
m
be the
program (reduct) generated from Π by removing
1. each rule that has a negative literal ¬l in its body
where l ∈ M, and
2. all negative literals in the bodies of the remaining
rules.
Since Π
M
is now negation-free, it has a unique mini-
mal Herbrand model. If this model is equal to M, then
M is a stable set of Π (Gelfond and Lifschitz, 1988).
Answer Set Programming (ASP) is a form of
declarative programming which is primarily ad-
dressed to solving NP-hard search problems. It has
its roots in Reiter’s theory of default reasoning and in
the generation of stable models.
In ASP, search problems are first ground-
instantiated by so-called grounders like LPARSE
which are front-ends accepting logic programs. In
the next step, ASP solver like SMODELS or DLV
solve these computable search problems by calculat-
ing all stable models of the grounded programs. Un-
like SLDNF-employing reasoning tools like Prolog,
ASP solvers always terminate (Lifschitz, 2008). In
addition, the performance of current ASP solvers is
comparable to highly efficient SAT solvers because
similar algorithms are used.
Consistency-based and abductive diagnosis both
represent techniques for identifying the error sources
of a malfunctioning system. Although these methods
can be applied to the same task, the results that are
calculated sometimes differ. In contrast, abductive di-
agnosis is more restrictive on the selection of diagnos-
tic explanations: the diagnosis ∆ in conjunction with
the system description SD must have a stable model
which logically entails the observations.
ICAART 2017 - 9th International Conference on Agents and Artificial Intelligence
324

One difference between consistency-based and
abductive diagnosis is that the former applies a
weaker criterion on valid diagnoses, because it uses
the consistency formula in the traditional FOL seman-
tic.
4 CONCEPT
The following section presents the conceptual ideas
and algorithm behind the implemented diagnostic en-
gine.
4.1 Refining Hypotheses
The diagnosis ∆ is a set of hypotheses which ex-
plain the system’s malfunction based on the given
knowledge as logic program P and observations OBS.
Although can already calculate minimal diagnoses
which only select as few components as possible us-
ing consistency-based or abductive reasoning, there
are often too many explanations given to efficiently
isolate the true causes of the problem. In fact, model-
based diagnosis is often criticized for not being able
to ‘pinpoint a failing component from the available
symptom information’ (Koseki, 1989).
Therefore, further observations are necessary to
refine the diagnosis. Let us assume that P is given
by the set of Horn clauses and our logic program sup-
ports negation as failure to be interpretable within sta-
ble model semantics.
What could be a further observation? Con-
sider our running example and its system description
shown as logic program in Figure 2. In the context
of semiautomatic diagnosis it is assumed that the user
does not know the true source of errors, i.e. faulty
components represented by AB-predicates. Based on
the observation of not shows
image(p) we can only
propose to observe works(l) or works(p) as these
two predicates belong to rules in P which further con-
tain AB-predicates. After the initial observation of
not shows image(p) the set of minimal diagnoses
would be {{l}, {p}, {b}, {hdmi}}. If the user would
observe works(l), then according to stable model se-
mantics the diagnostic engine would retract {l} from
the diagnosis. This refinement of the diagnosis ex-
emplifies non-monotonic reasoning where additional
knowledge leads to the retraction of assumptions.
Starting from the initial, non-empty diagnosis ∆
0
which has been computed by at least a single obser-
vation of the system’s symptoms (otherwise ∆
0
=
/
0
since P is consistent) the diagnostic engine proposes
predicates G ⊆ P\(OBS ∪ {¬l | l ∈ OBS}) which have
not yet been observed (neither negated nor positive).
If the user or an automatic middleware system can ob-
serve the predicate p ∈ G, p or ¬p is added to our
observations OBS, depending on what was observed
about p. If p or ¬p are not observable, the diagnostic
engine should propose a new predicate for observa-
tion, if available. Otherwise, no more observations
can be proposed.
Algorithm 1 FINDABDUCIBLES(p, T, OBS) calcu-
lates the set of abducibles ⊆ ABDUCIBLES which can
be abduced from T ∪{p} in case p is observed. Here,
a reasoning system, e.g. ASP system is required in
order to calculate the stable models of the current the-
ory.
Algorithm 1: Finding abducibles.
procedure FINDABDUCIBLES(p, T, OBS)
R ←
/
0
// CSM = CalculateStableModels
for all A ← CSM(T ∪ OBS{p}, ABDUCIBLES) do
R ← R ∪ A
end for
return R
end procedure
Note that we are unifying the minimal diagnoses
which possibly consist of multiply components which
together must be faulty in order to explain the given
symptom. Instead of having sets of sets of possibly
faulty entities, the set representation of all candidates
allows us to quantify for each diagnosis step the utility
of an observation.
4.2 Proposing Observations
The information which abducibles can be eliminated
from the diagnosis ∆ if we observe that a predicate
p or its negation is true can then be used to propose
such p which maximally reduces ∆. Thanks to the Al-
gorithm 1 we can calculate which diagnosis (or any)
would result from observing p or ¬p so that we can
select a p which would result in the smallest possible
diagnosis 6=
/
0.
4.3 Interactive Diagnosis
The diagnosis process as defined in Algorithm 3 starts
with the knowledge base, i.e. program, P and a symp-
tomatic observation OBS which is a set of positive
or negated predicates occurring in P. The diagno-
sis ∆ is calculated by accumulating all abducibles
∈ A = {AB(. . . )} which explain the given observation
OBS. Using further, proposed observations as from
Algorithm 2, the diagnosis is refined or assured: Ab-
ducibles contradicting ∆ will be used to reduce ∆ by
removing the negations of these abducibles.
Concept and Realization of a Diagnostic System for Smart Environments
325

Algorithm 2: Selecting the optimal observation.
Require: ∆ 6=
/
0 ∧ OBS 6=
/
0 ∧ ∆
f
⊂ ∆ ∧ ∀p ∈ P :
OBSERVINGCOST(p) > 0
procedure PROPOSEOBSERVATION(P, ∆, ∆
f
, OBS)
O ←
/
0
for all p ∈ P\(OBS ∪ {¬l | l ∈ OBS}) do
p
AB+
← FINDABDUCIBLES(p, P, OBS)
p
AB−
← FINDABDUCIBLES(¬p, P, OBS)
v ← min{p
AB+
, p
AB−
}
// if abducibles can be calculated.
O[p] ← v
end for
if O 6=
/
0 then
return argmin
p∈P\OBS
O[p]
else
return ⊥
end if
end procedure
Abducibles which confirm ∆ will be added to the fixed
diagnosis ∆
f
. ∆
f
is reflected during the diagnos-
tic reasoning process using the Integrity Constraints
IC. These constraints limit the calculated set of ab-
ducibles by only allowing abducibles which do not
conflict with ∆
f
. The diagnosis finishes if no further
observation can be proposed or if ∆ is small enough
so that the user can troubleshoot the problem.
5 IMPLEMENTATION
The implemented diagnostic system covers the full
workflow from extracting knowledge of semistruc-
tured wiring information to interactively providing
the user with diagnoses. This section first covers the
general architecture of the implemented system and
then describes the necessary implementation steps in
detail from start to finish of the diagnosis workflow.
5.1 Architecture
The module for knowledge extraction takes as input
wiring information from a CSV (comma-separated
ProLogICA: abduce
dlv: diagnosis frontend
User
Diagnosis
Diagnostic Engine
Automatic observations as
additional LP Rules
Middleware
Logic Programming Rules
(Prolog, dlv)
Knowledge
Wiring information in CSV Empirical Knowledge
Device Mechanics
Device Interactions
Rules, facts, constraintsKnowledge
Diagnosis
sufficient or
empty
Calculate diagnosis
Observation
is automatable
Propose observation
yes
Observations
Observable property
no
Observations
Observable
property
yes
no
Knowledge Extraction
(Python)
Disjunctive Datalog
Abductive Logic Program
GraphViz
Figure 3: Architecture of the implemented Diagnostic Sys-
tem.
values) table and is further provided with device-
related code to model the behavior of different devices
as well as the interaction between them. This knowl-
edge can be represented via disjunctive datalog and
abductive logic programs. By formulizing the wiring
graph in DOT (a graph description language) it can
be visualized by graph drawing tools like dot or neato
from the Graphviz package.
Algorithm 3: The complete diagnosis process.
Require: P 6=
/
0 ∧ OBS 6=
/
0
Require: ABDUCE(G, P, IC, A) queries the Abductive Rea-
soner given the theory (P, IC, A) and goal G, and subse-
quently yields all minimal solutions ⊆ P (A) which ex-
plain G.
procedure DIAGNOSE(P, OBS)
∆ ←
/
0
∆
f
←
/
0
while (∆ not refined enough and
∃p ∈ P : p 6∈ OBS and ¬p 6∈ OBS and
(({p} ∪ OBS ∪ P ∪∆
f
consistent) or
({¬p} ∪ OBS ∪ P ∪∆
f
consistent))) do
∆ ←
S
ABDUCE(OBS, P, ∆
f
, {AB(. . . )})
β ← PROPOSEOBSERVATION(P, ∆, ∆
f
, OBS)
if β = ⊥ then
return ∆
No more observations can be proposed
end if
if β is observable then
(p
AB+
, p
AB−
) ←
FINDABDUCIBLES(β, P, ∆, ∆
f
, OBS)
if β is observed as false then
OBS ← OBS ∪ {¬β}
∆ ← ∆\{¬l | l ∈ p
AB−
}
∆
f
← ∆
f
∪ p
AB−
else
OBS ← OBS ∪ {β}
∆ ← ∆\{¬l | l ∈ p
AB+
}
∆
f
← ∆
f
∪ p
AB+
end if
end if
end while
return ∆
end procedure
The formal description as a logic program can then
be used via ProLogICA to find diagnoses by perform-
ing abductive reasoning or DLV to diagnose using an-
swer set programming. The implemented Diagnostic
Engine uses DLV to generate diagnoses if provided
with an initial observation by the user. An interactive
loop has been implemented to refine the calculated di-
agnosis based on automatic observations by querying
the middleware (e.g. publish-subscribe infrastructure)
or by instructing the user to conduct observations of
non-automatically observable system properties.
The interactive diagnosis session finishes once the
user accepts the diagnosis as refined enough to trou-
ICAART 2017 - 9th International Conference on Agents and Artificial Intelligence
326

bleshoot the symptoms, or if there are no further ob-
servable (neither by a human nor the middleware) sys-
tem properties which could improve the diagnosis.
5.2 Knowledge Representation and
Reasoning
Diagnostic reasoning heavily depends on the provided
information of the implemented system and thus can
be seen as a discipline belonging to knowledge repre-
sentation and reasoning (KR).
The logical representation of a system and its di-
agnosis using logical reasoning has several advan-
tages over other diagnosis approaches:
• Logical formulae to describe the system structure
can be extracted easily from existing system data,
e.g. wiring diagrams or technical manuals.
• The logical rules are human-interpretable so the
user can comprehend and, if necessary, reproduce
the diagnostic reasoning.
• Only normal behavior needs to be modeled allow-
ing for smaller (human) effort to define the system
since no fault definitions are required.
• It is ensured that the calculated diagnosis is mini-
mal, i.e. the minimal set of possible sources of er-
ror is returned. This reduces further troubleshoot-
ing efforts.
Because of the pecularities of the two target plat-
forms, ProLogICA and DLV, two separate modules
have been implemented to formalize wiring informa-
tion as logic programs, namely Abductive Logic and
Datalog Programs. This decision was enforced for the
following reasons:
• ProLogICA relies on the non-declarative (linear)
semantic of python so that transitive connections
cannot be defined recursively (in contrast to DLV)
as
conn(A,C) : −conn(A, B), conn(B,C).
but instead must be stated using a helping predi-
cate rconn which handles the recursion so that
rconn(A,C) : −conn(A, B), rconn(B,C).
• ProLogICA exhibits poor performance on too
many nested and especially non-grounded rules.
Thus, connections between all devices have been
resolved via depth-first search.
• Not-AB-statements cannot be written as
not(ab(...)) but only not ab(...) in DLV while the
latter syntax was not supported on the used SWI
Prolog implementation.
• DLV requires AB-statements to be grounded,
while this leads to cryptic constants in Prolog.
5.3 Available Implementations
The diagnostic engine has been realized using two
different implementations: the answer set program-
ming environment DLV and the abductive reasoning
tool ProLogICA.
DLV stands for DataLog with Disjunction (where
V represents the logical operator ∨) and is a disjunc-
tive logic programming system. Rules can be written
in disjunctive datalog (function-free) of the form
a
1
∨ ·· ·∨ a
n
← b
1
, . . . , b
k
, ¬b
k+1
, . . . , ¬b
k+m
.
which allows DLV as an ASP system to solve prob-
lems whose complexity lies beyond the solvable
scope of non-disjunctive programming. DLV imposes
a safety condition on variables in rules such that a rule
is logically equivalent of its Herbrand instances.
DLV provides a diagnosis front-end for Abduc-
tive Diagnostic Reasoning as well as for Consistency-
Based Diagnosis. As described in (Eiter and Gottlob,
1995), a diagnostic problem represented by the set of
observations OBS, the system description SD and the
set of AB-atoms can be rewritten in disjunctive data-
log so that every stable model which the ASP solver
finds represents a diagnosis. The input programming
language for this front-end however does not support
disjunctive datalog and instead falls back to tradi-
tional datalog (function-free logic programming).
ProLogICA is an implementation of Abductive
Logic Programming (ALP) in Prolog. It allows the
user to define in a single file the abductive theory
(P, IC, A), where P represents the set of rules to de-
scribe the domain knowledge, IC is a set of integrity
constraints, and A declares the abducible predicates
(Ray and Kakas, 2006).
In contrast to competing implementations of ab-
ductive reasoning, ProLogICA allows the occurrence
of negated abducibles so that the formalization of nor-
mal system behavior can be made as described in Re-
iter’s Theory.
5.4 Semi-Automatic Diagnosis
Human-machine cooperation is realized via propos-
ing system properties to the user which would im-
prove the diagnosis. This section presents the im-
plementation of this fundamental aspect of semi-
automatic diagnosis.
Given a scenario as logic program which repre-
sents the system description, and a file of hypoth-
esis declarations which describe the possible AB-
predicates to be assumed as a diagnosis, the user first
needs to provide an initial observation. Then, a di-
agnosis is calculated. If this calculation fails, the ob-
servations contain a contradiction or no hypotheses
Concept and Realization of a Diagnostic System for Smart Environments
327
0
5
10
15
20
25
10
−2
10
0
10
2
Number of abducible predicates
Time in seconds
FD
FDsingle
FR
FRsingle
FRmin
Figure 4: Benchmark Results of the DLV Diagnosis Fron-
tend.
could be found. In order to simulate automatic ob-
servations, an additional file can be provided which
contains non-abducible predicates either negated (us-
ing not) or non-negated. If the ranking of possible
observations returns predicates that are automatically
observable, these observations are added to the set of
current assumptions. If there are no automatic ob-
servations, the user is asked to perform a proposed
observation. These observations help to refine the di-
agnosis so that |∆
n+1
| ≤ |∆| for every loop of the in-
teractive diagnosis.
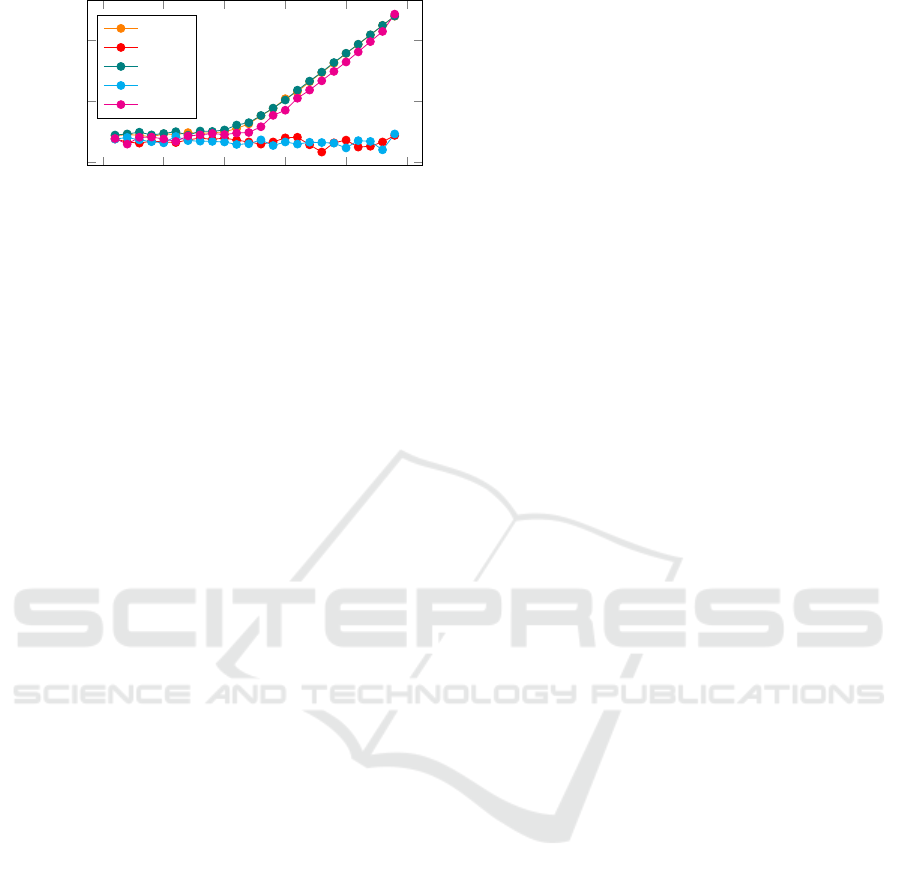
6 RESULTS
The results show that it is unfeasible for DLV to cal-
culate minimal diagnoses under the subset-relation.
Even for 24 possible faults in the given scenario, it
took more than 12 minutes to calculate a diagnosis.
However, single fault diagnosis and non-minimal di-
agnosis showed the vast performance gain which ASP
systems can provide. Thanks to grounding of the
given program and an efficient solver, DLV is able
to handle complex scenarios and logic programs with
(in our case more than 1500 lines of code) efficiently.
ProLogICA did exhibit no such problems as DLV
when calculating minimal diagnoses. Although the
number of abducible predicates does not seem to con-
siderably influence its calculation performance, the
type of knowledge representation played a crucial role
whether ProLogICA was able to find a solution, or
to not terminate. Especially rules which were highly
nested, or with non-grounded variables constantly in-
hibited ProLogICA from terminating or finding useful
solutions.
7 SUMMARY
The implemented diagnostic engine provides an in-
teractive environment where in cooperation with the
user a sufficient diagnosis can be found. The paper
provided a theoretical background, discussed several
approaches and the algorithmic framework to realize
semi-automatic diagnosis in smart environments.
However, several qualifications must be imposed
in order to guarantee useful and timely diagnoses.
With the current implementation, either single faults
can be detected efficiently despite a complex system
description, or the system’s model needs to simpli-
fied. This can be done by avoiding deep nesting in the
system description or by limiting the set of possible
fault candidates.
The diagnostic engine could be improved by fur-
ther implementing context knowledge of the compo-
nents to be diagnosed. Heuristics could be applied to
automatically limit the set of faulty components. If
the model-based diagnostic engine would have em-
pirical information available to not treat every com-
ponent equally as a potential source of malfunction,
the selection of diagnosis candidates could be greatly
accelerated. Heuristic knowledge would also provide
the user with better explanations from the beginning
since empirical information on probable faults can be
used. These symptom-failure association rules could
be learned from experience (cf. (Koseki, 1989)) to
better mimic the expertise of a human diagnostician.
Performance improvements could be made over pure
model-based diagnosis due to the caching of rules.
REFERENCES
Angeli, C. (2010). Diagnostic Expert Systems: From Ex-
perts Knowledge to Real-Time Systems. Advanced
Knowledge Based Systems: Model, Applications &
Research, 1:50–73.
B
¨
ottcher, C. (1995). No Faults in Structure? How to Diag-
nose Hidden Interaction. Proceedings of the Interna-
tional Joint Conference on Artificial Intelligence (IJ-
CAI’95), pages 1728–1735.
Christiansen, H. (2005). Abductive reasoning in Prolog and
CHR. Science, pages 1–18.
de Kleer, J. (1986). An assumption-based TMS. Artificial
Intelligence, 28(2):127–162.
Eiter, T. and Gottlob, G. (1995). The complexity of logic-
based abduction. Journal of the ACM, 42(1):3–42.
Eshghi, K. and Kowalski, R. a. (1989). Abduction Com-
pared with Negation by Failure. Proceedings of the
Sixth International Conference on Logic Program-
ming, (JANUARY):234–254.
Gelfond, M. and Lifschitz, V. (1988). The stable model
semantics for logic programming. In 5th International
ICAART 2017 - 9th International Conference on Agents and Artificial Intelligence
328

Conf. of Symp. on Logic Programming, pages 1070–
1080.
Koseki, Y. (1989). Experience Learning in Model-Based
Diagnostic Systems. Proc. IJCAI, pages 1356–1362.
Kuhn, L. and de Kleer, J. (2010). Diagnosis with Incom-
plete Models: Diagnosing Hidden Interaction Faults.
Proceedings of the 21st International Workshop on
Principles of Diagnosis, pages 1–8.
Lifschitz, V. (2008). What Is Answer Set Programming?
23rd AAAI Conf. on Artificial Intelligence2, pages
1594–1597.
Lucas, P. J. F. (2001). Bayesian model-based diagno-
sis. International Journal of Approximate Reasoning,
27(2):99–119.
Ray, O. and Kakas, A. (2006). ProLogICA: a practical sys-
tem for Abductive Logic Programming. Workshop on
Non-Monotonic Reasoning.
Reiter, R. (1980). A logic for default reasoning. Artificial
Intelligence, 13(1-2):81–132.
Reiter, R. (1987). A theory of diagnosis from first princi-
ples. Artificial Intelligence, 32(1):57–95.
Concept and Realization of a Diagnostic System for Smart Environments
329
