
Evaluation of Talents’ Scientific Research Capability
based on Rough Set Fuzzy Clustering Algorithm
Yan Xia, Xinlin Wu and Hui Feng
Shanghai Joint Laboratory for Discipline Evaluation, Shanghai Education Evaluation Institute, Shanghai, China
Keywords: Rough Set, Fuzzy Clustering, Talent Evaluation, Scientific Research Capability.
Abstract: Scientific research is one of the main functions of universities and colleges. The scientific research level of
universities and colleges depends on talents’ scientific research capability. The evaluation of scientific
research capability of talents is one of the effective methods to check their scientific research level. This
paper presents a method to evaluate talents’ scientific research capability based on rough set fuzzy
clustering. The method introduces how to use domain rough set theory and generalized fuzzy C-means
clustering algorithm to cluster and evaluate research capability of talents, combining with evaluation
indicator system of scientific research capability. An automatic system to cluster and evaluate scientific
research capability is implemented, verifying the method and analyzing data from a university in Shanghai.
It provides advice and guidance for scientific research management and development strategy in order to
promote the overall level of scientific research in universities and colleges.
1 INTRODUCTION
Research talents can support the development of
national and regional economy. They are the core
competitive power in universities and colleges. The
scientific research level and potential development
of universities and colleges depend on the scientific
research capability of talents in them. The
characteristic of talents’ scientific research
capability, such as diversity and comprehensive,
requires the talent management more humanized,
scientific and adaptive in universities and colleges
(Gao, 2005). Currently it is mainly replies on
experience, performance deduction and traditional
theory of human resources in talent management,
which is lacking of the effective support of
information technology. Thus it can’t meet the need
of current situations of quantity growth and
diversification in talent management. It has become
a hotspot in higher education field how to establish a
trustable evaluation system of talents’ scientific
research capability in universities and colleges based
on objective data. With its help, the talent echelon
and specialized troop will be partitioned more
properly, and measures in line with the development
of talent team can formulated more appropriately.
Therefore the educational administrative department
can promote the development of higher education in
China healthily and rapidly.
This paper proposes an evaluation method of
talents’ scientific research capability based on rough
set fuzzy clustering algorithm in order to meet the
requirement of talent management and to solve the
existing problems in traditional evaluation methods.
The method introduces domain rough set theory and
generalized fuzzy C-means clustering algorithm to
cluster and evaluate research capability of talents,
combining with evaluation indicator system of
scientific research capability (Maji and Pal, 2007).
An automatic system to cluster and evaluate
scientific research capability is implemented, which
makes use of data mining technology. The function
modules are designed according to the
characteristics of scientific research data.
2 RELATED WORKS
At present, evaluation of talents’ scientific research
capability in universities and colleges is usually
carried out in a way combining objective calculation
of data and peer review from the performance
perspective. However the scientific research activity
is dynamic and comprehensive. The traditional
method is complicated in process and is easily
Xia, Y., Wu, X. and Feng, H.
Evaluation of Talents’ Scientific Research Capability based on Rough Set Fuzzy Clustering Algorithm.
DOI: 10.5220/0006261603590366
In Proceedings of the 9th International Conference on Computer Supported Education (CSEDU 2017) - Volume 2, pages 359-366
ISBN: 978-989-758-240-0
Copyright © 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
359

influenced by the subjectivity and so on. The data
mining technology is widely used to meet the
requirement of talent management in new period,
such as the evaluation method based on analytic
hierarchy process (AHP) and Delphi (Wu and Xia,
2000), the comprehensive evaluation model based
on grey system (Liu et al., 2010), the evaluation
method based on data envelopment analysis (DEA)
(Jahanshahloo, et al., 2004), the evaluation model
based on probabilistic neural network (PNN) (Hoya,
2003), evaluation model based on discrete Hopfield
and BP neural network (Lee, 1999), and so on.
However the evaluation indicator system of
scientific research capability is complicated. There’s
interaction between each indicator. It is difficult to
use certain mathematical model to evaluate.
In order to solve the existing problems in
evaluation of talents’ scientific research capability,
this paper proposes a new evaluation method based
on rough set fuzzy clustering algorithm. An
automatic clustering and evaluation system is
implemented, verifying the method and analyzing
data from a university in Shanghai. It provides
advice and guidance for scientific research
management and development strategy in
universities and colleges.
3 EVALUATION METHOD OF
TALENTS’ SCIENTIFIC
RESEARCH CAPABILITY
BASED ON ROUGH SET
FUZZY CLUSTERING
ALGORITHM
The evaluation method of talents’ scientific research
capability is based on Rough Set Fuzzy Clustering
Algorithm. The theory of rough set and fuzzy
clustering algorithm is introduced firstly (Maji and
Pal, 2007). The method is then described in details.
3.1 Basic Definitions
The rough set theory begins with the notion of an
approximation space.
Definition 1
,UR
is a pair, where U is nonempty
set, the universe of discourse, and
R
is an
equivalence relation on
U .
R
is reflexive,
symmetric, and transitive. The relation
R
decomposes the set U into disjoint classes with two
elements x and y in same class if and only if
(, )
x
yR
. Let
/UR
denote the quotient set of U
by
R
, which is defined as (1).
i
X
is an equivalence
class of
R
,
1,2,...,im
. If the two elements x and
y in
U belongs to the same equivalence class
/
i
X
UR
, x and y are indistinguishable.
12
/{ }, ,...,
m
UR XX X
(1)
Definition 2 The equivalence classes of
R
and the
empty set
are the elementary sets in
approximation space
,UR
. Given an arbitrary set
2
U
X
, in general, it may not be possible to
precisely describe
X
in
,UR
.
X
by a pair of
lower and upper approximations are defined as (2).
The lower approximation
()XR
is the union of all
the elementary sets which are subsets of
X
, and the
upper approximation
()RX
is the union of all the
elementary sets which have nonempty intersection
with
X
.
() ()
ii
ii
XX XX
XRXandRXX
(2)
Definition 3 The interval which is defined as (3) is
the representation of an ordinary set in the
approximation space
,UR
, and is simply called
the rough set of
X
. Furthermore a set of
X
is said
to be definable in
,UR
if and only if
() ()RX RX
.
(),[()]XXRRX
(3)
The traditional clustering belongs to hard partition.
Each pending object will be assigned to a definite
class with a clear boundary. However most objects
in real world are appropriate for soft partition with
fuzzy clustering since they are not so strictly
defined. Fuzzy C-means algorithm (FCM) is a well-
known clustering algorithm. It obtains the final
clustering result by optimizing the objective
function.
Definition 4 Let
1
{, , , }
j
n
Xx x x
be the set of
n objects and
1
{, , , }
ic
Cv v v
be the set of c
centroids. The FCM provides a fuzzy function which
is defined as (4). It partitions a set of n patterns
X
into c clusters by minimizing the objective function.
1
1,m
is the fuzzifier.
i
v is the i
th
centroid
corresponding to the i
th
cluster
i
.
[0,1]
ij
u
is the
probabilistic membership of the pattern
j
x
to
i
.
CSEDU 2017 - 9th International Conference on Computer Supported Education
360

.
is the distance norm.
i
v and
ij
u
is defined as (4-1)
and (4-2).
1
2
11
()
m
nc
ij j i
ji
J uxv
(4)
1
1
()
()
n
m
ij j
j
i
n
m
ij
j
x
(4-1)
1
1
2
1
2
1
1
m
ji
ij
c
m
ji
i
x
x
the condition
11
1
cn
ij
ij
(4-2)
Rough set theory and fuzzy clustering algorithm
is combined in the generalized fuzzy C-means
clustering algorithm.
Definition 5 Let
()
i
A
and
()
i
A
be the upper and
lower approximations of cluster
i
. Let
(){() ()}
iii
BAA
denote the boundary region
of cluster
i
. The object function
R
FP
J
is defined as
(5).
1
A
and
1
B
are defined as (5-1) and (5-2).
Proportional parameter
is defined as (5-3). The
parameter
corresponds to the relative importance
of lower and boundary regions. The constants
,, ,ab
defined the relative importance of
probabilistic and possibilistic memberships.
12
,1,mm
are the fuzzifiers. The value of
can be adjusted in the process of algorithm
optimization.
11
1
1
(1 ) , ( ) , ( )
() ,()
() ,()
ii
RFP ii
ii
ABifAB
JA ifA B
BfAB
(5)
2
12
2
1
1() 1 ()
{( ) ( ) } (1 )
ii ii
cc
m
mm
ij ij j i i ij
ixA i xA
A abvxv v
(5-1)
2
12
2
1
1() 1 ()
{( ) ( )} (1 )
ii ii
cc
m
mm
ij ij j i i ij
ixB i xB
Bvxvv
(5-2)
2
2
2
1
1
()
()
n
m
ij j i
j
i
n
m
ij
j
x
(5-3)
Definition 6 Considering the different weight of
each indicator in evaluation indication system of
scientific research capability, the object function
with weight is defined as
WRFP
J in (6), together with
1w
A
and
1w
B in (6-1) and (6-2).
11
1
1
(1 ) , ( ) , ( )
() ,()
() ,()
wwii
WRFP w i i
wii
ABifAB
JA ifA B
BfAB
(6)
2
12
2
1
1() 1 ()
{[( ) ( ) ]} (1 )
ii ii
cc
m
mm
wijijjiiij
ixA i xA
A abvxv v
(6-1)
2
12
2
1
1() 1 ()
{[ ( ) ( ) ]} (1 )
ii ii
cc
m
mm
wijijjiiij
ixB i xB
Bvxvv
(6-2)
3.2 Workflow
The work flow of Evaluation Method of Talents’
Scientific Research Capability is shown as Method 1
according to the above definition.
Method 1: EMTSRC-RSFC (Evaluation Method of
Talents’ Scientific Research Capability based on Rough
Set Fuzzy Clustering)
Input: Samples (the set of talent samples), Attributes-C
(the number of clusters)
Output: The clusters with the number of Attributes-C
Workflow:
EMTSRC-RSFC (Samples, Attributes-C)
Begin:
1) Initialize affiliation matrix
ij
u
;
2) Select objects with the number of Attributes-C as
centroids randomly;
Repeat
3) Scan all of the samples, and assign to
corresponding centroid;
4) Calculate affiliation matrix
ij
u
according to the
formula (4-2);
5) Calculate each centroid according to the formula
(4-1);
6) Adjust centroids, calculate and optimize the
objective function according to the formula (6);
Until objective function
WRFP
J
is obtained the
optimal solution;
End
The recursive step of method EMTSRC-RSFC
stops when it meets with the condition of optimal
objective function.
The time complexity of method EMTSRC-RSFC
is
2
()
O Samples Log SamplesAttributes C
.
Samples is the cardinal number of the set of talent
samples.
It is necessary to seek with global optimum
instead of local one when seeking optimal solution
of objective function in EMTSRC-RSFC.
Evaluation of Talents’ Scientific Research Capability based on Rough Set Fuzzy Clustering Algorithm
361

4 APPLICATION OF
EVALUATION METHOD OF
TALENTS’ SCIENTIFIC
RESEARCH CAPABILITY
4.1 Evaluation Indicator System of
Scientific Research Capability
This paper uses the fourth round of evaluation
indicators from Discipline Evaluation Indicator
System for reference, which is promulgated by
China Academic Degrees and Graduate Education
Development Center (CDGDC, 2016). The content
of Evaluation Indicator System of Scientific
Research Capability is shown in Table 1. The
Evaluation Indicator System is composed of 3
primary indicators, including Scientific Research
Achievement, Scientific Research Award, and
Scientific Research Projects. Each primary indicator
is composed of several secondary indexes, 11
secondary indicators in all. Each secondary indicator
contains a number of observation points with
different weight, which can be considered as tertiary
indicators. For example, Scientific Research
Achievement, one of the primary indicators,
contains 4 secondary indicators. There are 10
observation points in quality of academic papers,
one of the secondary indicators, such as the number
of highly cited papers in ESI, the number of papers
published in domestic and international
representative journals, the number of papers
published in domestic and international conference
and so on.
The weight of the primary indicator is
i
,
,,iABC . The weight of the secondary indicator
is
j
i
,
1, 2,...,jm
The
m
is the cardinal number
of corresponding secondary indicator. The weight of
the tertiary indicator is
k
j
i
,
1, 2,...,kn .
n
is
the cardinal number of corresponding tertiary
indicator. The records in database map to the tertiary
indicator. The weight of the evaluation attribute
k
j
i
Table 1: Evaluation Indicator System of Scientific Research Capability.
Primary Secondary
Observation Points
A. Scientific
Research
Achievement
A1. Quality of Academic
Papers
Number of highly cited papers in ESI, Number of papers published in
domestic and international representative journals, the number of papers
published in domestic and international conference, Number of academic
reports invited in domestic and international conference, Number of
international cooperation papers, etc
A2.Academic Monographs
Number of academic monographs published in the past five years, etc
A3.Teaching Materials
Number of teaching materials on national level in the past five years, etc
A4. Patents
Number of international patents, Number of patents transformed,
Number of decision-making counsel reports, etc
B. Scientific
Research
Award
B1. National Awards
Number of national natural science awards, Number of technology
invention awards, Number of science and technology progress awards,
etc
B2. Ministry of Education
Awards
Number of research achievement awards of Ministry of Education
(Science and technology disciplines, humanities and social science
disciplines), etc
B3. Provincial and
Ministerial Awards
Number of provincial natural science awards, Number of provincial
technology invention awards, Number of provincial science and
technology progress awards, Number of provincial philosophy,
humanities and social science awards, etc
B4. International Awards
Number of art creation awards, Number of architectural design awards,
etc
C. Scientific
Research
Projects
C1. National Projects
Number of national major foundation projects, Number of 973 projects,
Number of national natural science projects, Number of national social
science foundation projects, Number of national education planning
projects, etc
C2. Ministry of Education
Projects
Number of ministry of education social science foundation projects,
Number of ancient committee projects, etc
C3. Provincial and
Ministerial Projects
Number of provincial and major special research projects, etc
CSEDU 2017 - 9th International Conference on Computer Supported Education
362

is defined as
jj
k
ijk i i i
.
This paper use principal component analysis
method (Yang and Feng, 2012) to analyze the
relationship between each evaluation indicator and
calculate the coefficient value. If the value is larger
than the threshold, the indicators are assumed
associated, and will be combined with other
indicator or be deleted. Non-redundant indicator
system is recorded in database.
4.2 Data Selection
To ensure authenticity, reliability and authority, the
original data related to the Evaluation Indicator
System of Scientific Research Capability can be
obtained from databases of the educational
administrative department, databases of universities
and colleges, and the third party electronic literature
databases. They are focusing on tertiary indicators.
The data are integrated into the basic information
table of talents in the database. The table structure is
shown in Table 2, which defines 38 evaluation
indicator attributes. The table of weight needs setting
to keep weight of each evaluation indicator
attributes. The table of relationship needs setting to
keep associated evaluation indicator attributes.
We shall do some preprocessing works, such as
cleaning, data integration, data transformation, data
reduction and so on since data from source databases
are incomplete, inconsistent, and redundant (Carlo,
2010).
Table 2: Table Structure of Basic Information of Talents in Universities and Colleges.
No Field Meaning Field Name Field Type
Field
Length
Primary
Key
Empty
Default
Value
1 University or College ID DWDM char 6 No No NULL
2 University or College Name DWMC varchar 30 No No NULL
3 Identification ZJH char 20 Yes No NULL
4 Name XM varchar 30 No No NULL
5 Date of Birth CSNY datetime 6 No Yes NULL
6 Position ZW varchar 30 No Yes NULL
7 Title ZC varchar 30 No Yes NULL
8
Number of Highly Cited Papers in
ESI
ESIGBYLW mediumint 6 No Yes NULL
9
Number of papers in SSCI, AHCI &
CSSCI, CSCD
SACLW mediumint 6 No Yes NULL
10
Fellow in International Academic
Organization
ZYGJXSZZF mediumint 6 No Yes NULL
11
Number of Papers published in
International Representative
Journals
GJDBLW mediumint 6 No Yes NULL
12
Number of Academic Reports
invited in International Conference
GJHYBG mediumint 6 No Yes NULL
13
Number of International
Cooperation Papers
GJHZLW mediumint 6 No Yes NULL
14 Number of Academic Monographs XSZZ mediumint 6 No Yes NULL
15
Number of National Natural
Science awards
GJZRKXJ mediumint 6 No Yes NULL
16
Number of National Major
Foundation Projects
GJZRKXJJ mediumint 6 No Yes NULL
17
Number of Provincial and Major
Special Research Projects,
SBJXM mediumint 6 No Yes NULL
… … … … … … …
42 H index LWHZS mediumint 6 No Yes NULL
43 Number of International Patents GJZL mediumint 6 No Yes NULL
44 Number of Patents Transformed ZLZH mediumint 6 No Yes NULL
45
Number of Decision-making
Counsel Reports
JCBG mediumint 6 No Yes NULL
Evaluation of Talents’ Scientific Research Capability based on Rough Set Fuzzy Clustering Algorithm
363
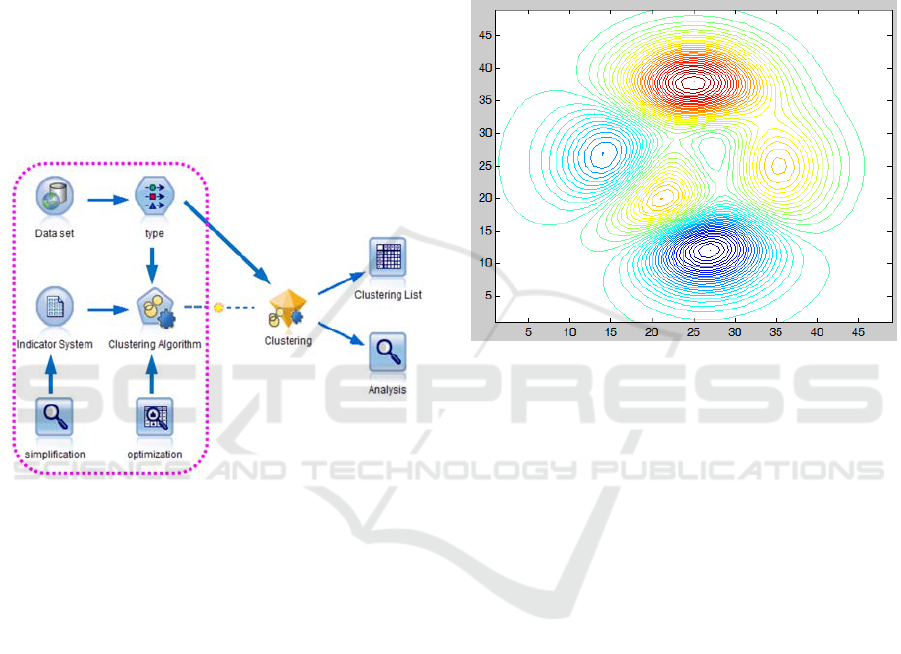
4.3 Automatic Clustering and
Evaluation System
4.3.1 System Structure
The system structure of automatic system to cluster
and evaluate scientific research capability based on
rough set fuzzy clustering algorithm is shown in
figure 1. The process is as follows.
1. Create model: Cluster the talent data by evaluation
method of talents’ scientific research capability.
Generate cluster list.
2. Optimize model: Adjust parameters smoothly,
such as the proportional parameter, etc.
3. Apply model: Apply the optimized model to
cluster talent data.
Figure 1: System structure of automatic system to cluster
and evaluate scientific research capability.
4.3.2 Create Sample Dataset
This paper focuses on evaluation of talents’
scientific research capability in universities and
colleges of Shanghai. It makes clustering and
evaluation of talents’ scientific research capability of
first-class disciplines from a university in Shanghai.
The type of talents’ scientific research capability is
set to 4 categories, outstanding, excellent, potential
and general. Therefore the number of clusters is set
as 4 in database.
The sample of dataset is shown in Table 3. 312
candidates from 8 disciplines in a university of
Shanghai are selected as samples in dataset.
,1,2,,38Ai i
are defined as evaluation
indicator attributes in Table 2. Then evaluation
method of talents’ scientific research capability
based on rough set fuzzy clustering is applied to
cluster the dataset.
4.3.3 Create Cluster Model of Talents’
Scientific Research Capability
When running the automatic system to cluster and
evaluate scientific research capability, the cluster
model does some preprocessing works to simplify
the evaluation indicator system, and cluster the data
by the evaluation method. Figure 2 shows parts of
the clusters that are partitioned by age.
Figure 2: Clusters of talents’ scientific research capability
in a university that are partitioned by age.
4.3.4 Analyze and Optimize Cluster Model
of Talents’ Scientific Research
Capability
How to evaluate the method of talents’ scientific
research capability based on rough set fuzzy
clustering is important. Significance test can be used
to analyze the method. Corresponding parameters is
fine-tuned, such as the fuzzifiers
12
,mm ,
proportional parameter
,
relative importance of
probabilistic and possibilistic memberships
,, ,ab
,
etc. After the method is optimized, the optimal
clusters will be obtained. It is effective if our scheme
can achieve about 80% accuracy in forecasts.
4.4 Use Automatic Clustering and
Evaluation System to Do Dynamic
Evaluation
The automatic system to cluster and evaluate
scientific research capability based on rough set
fuzzy clustering algorithm clusters talents’ scientific
research capability according to objective data
instead of subjective assumption. It establishes
CSEDU 2017 - 9th International Conference on Computer Supported Education
364
Table 3: Samples of dataset of talents’ scientific research capability.
No
Evaluation Indicator Attributes
… A5 A6 A7 A8 … A21 A22 A23 A24 A25 …
1 … >8 4.3 >5 9 … high 5 yes 0 excellent …
2 … <=2 0 5..10 11 … medium 6 yes 0 excellent …
3 … 2..5 0 >10 470 … medium 53 yes 47.7 good …
4 … 5..8 0 5..10 74 … medium 20 yes 17.1 good …
5 … <=2 0 <5 111 … low 17 no 6.1 fair …
6 … 2..5 0 5..10 43 … high 14 yes 30.3 poor …
7 … 5..8 5.4 >10 0 … medium 0 yes 40 excellent …
8 … <=2 2.4 <5 0 … high 0 no 33.3 fair …
9 … 2..5 0 5..10 37 … medium 14 no 4.8 fair …
10 … <=2 6.3 >10 169 … low 30 no 27.8 fair …
11 … 2..5 0 5..10 2 … medium 1 no 6.3 excellent …
12 … >8 4.1 <5 159 … medium 28 yes 20.8 poor …
13 … 2..5 6.7 5..10 43 … medium 10 no 18.5 fair …
14 … >8 0 >10 170 … high 24 yes 8.3 good …
15 … 5..8 3.3 5..10 9 … medium 5 yes 0 excellent …
… … … … … … … …
310 2..5 1.3 5..10 26 1 yes 30.4 fair
311 … <=2 0 5..10 47 … medium 27 no 15.8 fair …
312 … 2..5 1.3 >10 42 … medium 16 yes 15 good …
foundation for the objective scientific research
capability evaluation system. Figure 3 shows parts of
the evaluation results of talents’ scientific research
capability in a university in Shanghai after analyzing
the clusters in Figure 2. It initializes and monitors
the talents’ scientific research capability
dynamically. The educational administrative
department and the university can easily understand
the characteristics and status of talents. It provides
advice and guidance for scientific research
management and development strategy in order to
promote the overall level of scientific research.
Figure 3: Evaluation results of talents’ scientific research
capability by age.
5 DISCUSSION AND
CONCLUSIONS
This paper proposes a method of talents’ scientific
research capability based on rough set fuzzy
clustering algorithm on the basis of extensive
investigation and careful analysis of the existing
evaluation methods. An automatic system is
established to cluster and analyze talents’ scientific
research capability in universities and colleges of
Shanghai. The study and application of the method is
helpful to reveal the development tendency of
scientific research capability. It predicts the progress
and breakthrough of talents’ scientific research
capability in the future. Meanwhile it provides basis
for the educational administrative department to
develop a new round strategy.
In the future, we will take further research on
parameter optimizing in rough set fuzzy clustering
according to the characteristics of talents’ scientific
research capability. Evaluation result will be
deduced more scientifically and reasonably.
0
50
100
150
29‐40 41‐50 51‐60 >60
Outstanding
Excellent
Potential
General
Evaluation of Talents’ Scientific Research Capability based on Rough Set Fuzzy Clustering Algorithm
365

ACKNOWLEDGEMENTS
This work is supported by the Young Scholar in
University Cultivation Fund of Shanghai Municipal
Education Commission (Grant Nos: ZZPGY14002)
and ISTIC-THOMSON REUTERS Joint
Scientometrics Laboratory Open Fund. The Open
Fund is set up by Institute of Scientific and
Technical Information of China and company of
Thomson Reuters. The authors thank Jie Yang
(Professor in Graduate School of Education at
Shanghai Jiao Tong University) and Zhongping
Zhang (Professor in School of Information Science
and Engineering at Yanshan University) for helpful
discussions. Finally, we thank the reviewers for
helpful suggestions leading to an improved
manuscript.
REFERENCES
Carlo, Batin, 2010. The book, Data Quality: Concepts,
Methodologies and Techniques, 1
st
edition.
CDGDC, 2016. The fourth round of discipline evaluation
indicator system and related instructions. 2016,
http://www.chinadegrees.cn/xwyyjsjyxx/sy/syzhxw/28
1741.shtml.
Gao, Yan, 2005. The review of studies on human resource
management theory, Journal of Northwest University
(Philosophy and Social Sciences Edition, vol. 35.
Hoya, T., 2003. On the capability of accommodating new
classes within probabilistic neural networks, IEEE
Transaction on Neural Network, vol. 14.
Jahanshahloo, GR., Lotfi, FH., Shoja, N., Tohidi, G.,
Razavyan, S., 2004. Input estimation and identification
of extra inputs in inverse DEA models, Applied
Mathematics and Computation, vol.156.
Lee, DL., 1999. New stability conditions for Hopfield
neural network in partial simultaneous update mode,
IEEE Transaction on Neural Network, vol. 10.
Liu, Danping, Zhou, Jiangfang, Wu, Jie, 2010. The
synthesis evaluation model of college teacher’s ability
in scientific research based on grey system, Science
and Technology Management Research, vol. 21.
Maji, P., Pal, SK, 2007. Rough set based generalized fuzzy
C-means algorithm and quantitative indices, IEEE
Trans. on Systems, Man, and Cybernetics, Part B:
Cybernetics, vol. 37.
Wu, Yingyu, Xia, Bing, 2000. Index assessment system
about synthetic achievements and solutions analysis of
scientific research institutes in Jiangsu provinces,
Science Research Management, vol. 21.
Yang, Xue, Feng, Hui, 2012. An evaluation on the input-
output performance of universities based on principal
component analysis, Shanghai Management Science,
vol. 34.
CSEDU 2017 - 9th International Conference on Computer Supported Education
366
