Frequency Stabilization of an Adaptive Self-phase-conjugated

Passively Q-switched Laser using Volume Bragg Grating on the

Photo-thermo-refractive Glass

S. A. Ivanov

, A. P. Pogoda

, N. V. Nikonorov

, A. V. Fedin

and A. A. Sergeev

ITMO University, Birzhevaya line, 4, St. Petersburg, Russia

Baltic State Technical University, St. Petersburg, Russia

Keywords: Frequency Stabilization, Volume Bragg Grating, PTR Glass, Passive Q-switch, Self-phase-conjugated.

Abstract: In conclusion, we successfully demonstrated laser frequency stabilization of an adaptive self-phase-

conjugated passively Q-switched laser by mean of the transmitting volume Bragg grating on the photo-

thermo-refractive glass. Application of such grating inside the cavity provides desired pulse to pulse

frequency stability and reduce bandwidth of the radiation from 18 to 4 pm with outstanding output parameters

such as pulse energy of 100mJ, peak power of 10MWt and beam quality of M

=1.15. We assume that the key

factor of wavelength stabilization in our case is angular selectivity of the grating. But this kind of selection

operates only with feedback mirror. These results have shown that transmitting volume Bragg gratings on

photo-thermo-refractive glass are great candidate for stabilization of pulsed laser systems.

1 INTRODUCTION

A recent interest in powerful pulsed solid-state lasers

with high spatial brightness and narrow bandwidth is

caused by many possibilities of its applications, for

example, in the remote monitoring (Boreysho et al.

2005), the laser-induced breakdown spectroscopy

(Lebedev et al. 2011), and the ultra-hard material

processing (Basiev et al. 2007).

A high-brightness, high-beam-quality laser

radiation can be achieved by mean of self-adaptive

laser cavity based on self-pumped four-wave mixing

directly inside laser medium. It provides phase

conjugate self-compensation of laser beam oscillation

distortions (Bel’dugin et al. 1989; Damzen et al.

1992). Increasing of phase conjugation efficiency via

the number of feedback loops leads to a simultaneous

increase in energy of the free-running trains and beam

quality. Improvement of spatial characteristics is

provided by the increasing contrast of gain gratings in

the active medium. Increasing feedback efficiency

leads to self-Q-switching. Furthermore, mode

competition leads to the spectral selection and a

single-frequency pulse with a bandwidth of about 300

MHz. However, the frequency of the radiation varies

from pulse to pulse within the gain bandwidth. This

instability substantially limits the applications of such

laser.

Figure 1: Absorption spectra of photo-thermo-refractive

glass.

A promising way to solve this problem is an

implementation of additional selective element such

as volume Bragg grating on photo-thermo-

refractive(PTR) glass. PTR glass is very promising

optical material for recording of highly efficient

volume phase holograms operating in red visible and

near IR spectral range (700-2500nm) (Dubrovin, et

al., 2016; Dotsenko, et al., 1998; Efimov, et al., 1999;

Ivanov S., Pogoda A., Nikonorov N., Fedin A. and Sergeev A.

Frequency Stabilization of an Adaptive Self-phase-conjugated Passively Q-switched Laser using Volume Bragg Grating on the Photo-thermo-refractive Glass.

DOI: 10.5220/0006262403230327

In Proceedings of the 5th International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS 2017), pages 323-327

ISBN: 978-989-758-223-3

323

Ivanov, et al., 2014). This glass is a multicomponent

photosensitive sodium-zinc-aluminosilicate glass

doped with fluorine, antimony, cerium, and silver.

UV exposure followed by thermal treatment leads to

precipitation of nano-crystalline phase of NaF

(NikonorovN V, et al., 2010) in glass host which is

responsible for refractive index change. Such

mechanism opens a way of manufacturing different

kinds of holographic optical elements with high

uniformity and diffraction efficiency, spectral and

angular selectivity. Moreover, since the sizes of

nanocrystals are relatively small (10-20 nm), that is

why PTR glasses exhibit rather a low level of

scattering. Also this glass has no absorption band in

visible and NIR spectral regions (Fig.1) which makes

it great candidate for high energy laser optical

elements fabrication. Laser-induced damage

threshold of PTR glass is of 10 J/cm2 (1 ns pulse at

1.06 μm) (Efimov et al. 1999).

In this paper, we discuss laser frequency

stabilization of an adaptive self-phase-conjugated

passively Q-switched laser by mean of the volume

Bragg grating on the photo-thermo-refractive glass.

2 EXPERIMENTAL

In this study we have used volume Bragg grating

recorded in PTR glass. Grating was recorded with He-

Cd laser (325nm) with period of 1167nm. Grating had

15mm aperture, 1.2mm thickness and diffraction

efficiency of 90%. Angle of diffraction at operating

wavelength of 1064 was calculated to be θ

= 27.1

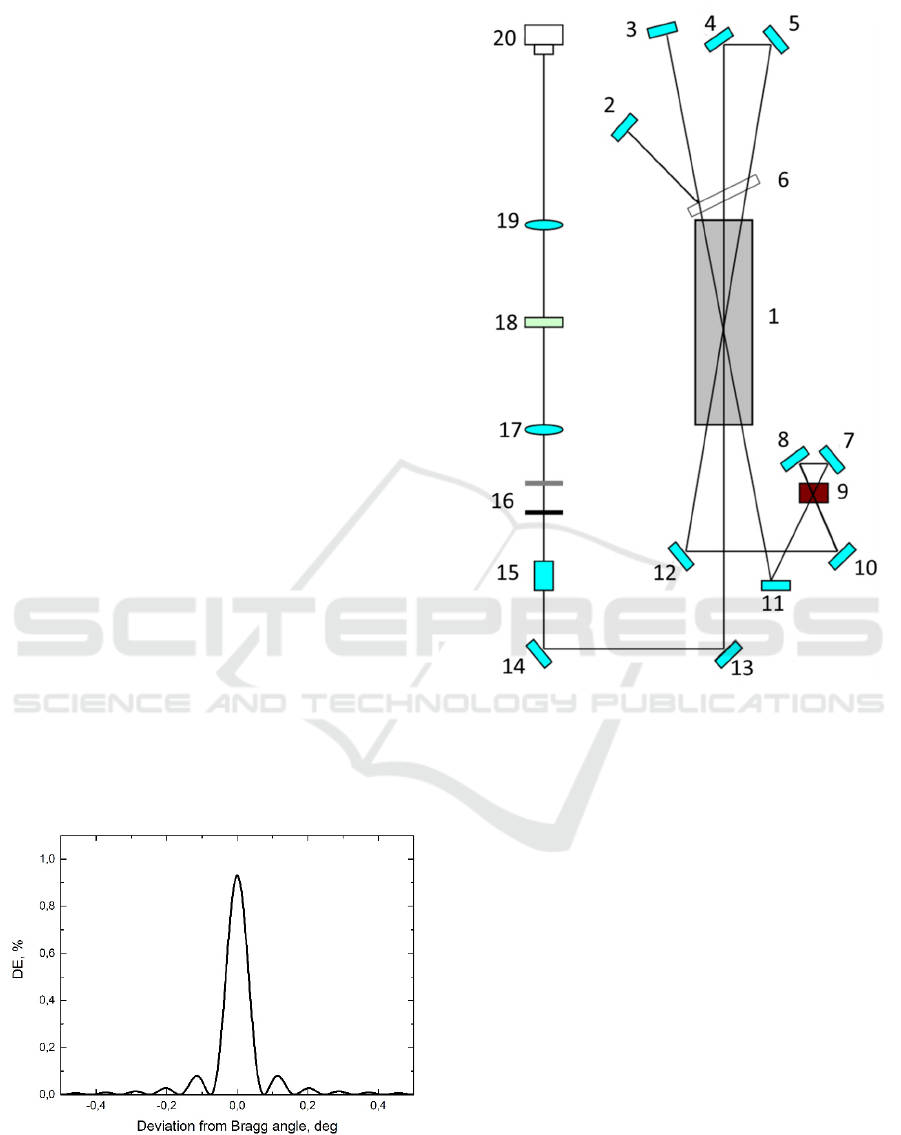
Angular selectivity of this grating was measured to be

δ = 0.07

(Fig.2).

Figure 2: Angular dependence of the first order of

diffraction.

Figure 3: Experimental setup. 1 – active element, 2 –

grating feedback mirror 3-5,7,810-12 – cavity mirrors, 6 –

volume Bragg grating, 9 -

LiF:F

crystal,

13,14 –

rotational mirrors, 15 – KTP crystal, 16 – filters, 17-18 –

projection lenses, 18 – Fabry-Perot etalon, 20 – CCD

camera.

To study the lasing properties laser head with a

cylindrical active element of Nd: YAG (1.1 at.% Nd

) with rod size of Ø 6.3 × 100 mm was used.

Transverse four-side pumping was carried out with

twelve arrays of laser diodes such as SLM 3-2 with

the size of the emitting area of 5 × 25 mm and a peak

power of up to 2 kW per stack. The maximum pump

energy was Ep = 10.3 J. For the passive Q-switch LiF:

crystal with initial transmission T

= 14% was

used. Results are obtained at the optimal length of the

cavity L = 55cm. Spectral composition of the

radiation was measured in the second harmonic

generation mode obtained with nonlinear KTP

crystal. The second harmonic radiation passing

through the infrared and the neutral filters was

directed at the Fabry-Perot interferometer with a free

spectral range of 28 pm. The resulting interference

PHOTOPTICS 2017 - 5th International Conference on Photonics, Optics and Laser Technology

324

pattern was projected by a lens on the CCD camera

Ophir-Spiricon. Next the interference pattern was

analyzed with Fiji software. Experimental setup is

shown on fig. 3.

Due to the high angular selectivity grating

placed in 3 beams was operating only for one

fulfilling Bragg condition. Unfortunately for rest

beams it was acting as losses which naturally

decreased output power of the system. Grating was

placed on a holder which allowed to switch it on and

off replacing it with equal thickness PTR glass slab.

We had to replace grating with equal PTR glass

sample to maintain generation conditions. Mirror 2

was providing feedback for the radiation diffracted on

the grating.

3 RESULTS AND DISCUSSIONS

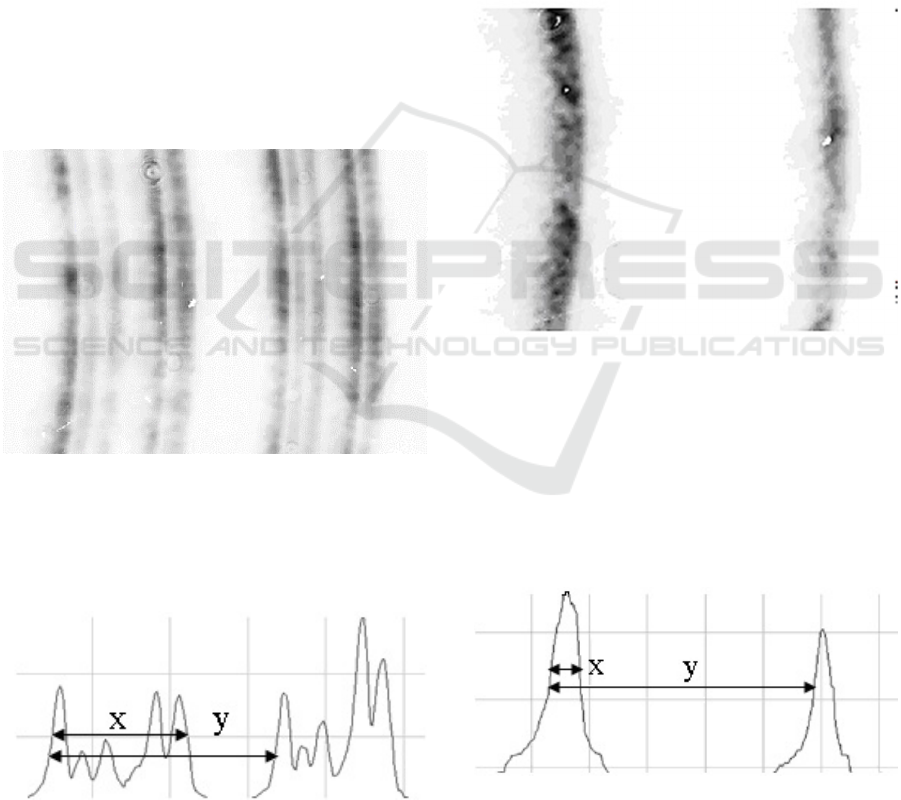
Fig. 4 present interference pattern of the laser

radiation while no grating is present in the setup.

Figure 4: Interference patter of the laser radiation without

volume Bragg grating.

As one can see interferogram consists of up to six

rings in the one order of diffraction which mean that

corresponding number of longitudal modes is present.

Figure 5: Cross section of interference fringe.

Analysis of the fringe cross section (Fig. 5)

obtained with CCD camera was made using folowing

relation between free spectral range (FSR) interaval

of Fabry-Perrot etalon and line bandwidth:

  / ∗  (1)

Where x – bandwidth in pixels, y – free spectral range

in pixels, FSR – free spectral range of etalon (28pm).

Calculations shows that total bandwidth of laser

radiation in this case is about 18pm. Fig. 6 presents

interference patter of the laser radiation with volume

Bragg grating inside the cavity. One can see that in

this case there is only one ring is present in each

difraction order which means that with our grating

laser operates on single logitudal mode.

Figure 6: Interference pattern of the laser radiation with

volume Bragg grating.

Cross section (Fig.7) analysis shows that in this case

laser radiation has a bandwidth of a 4pm which is

almost 5 times lower that without grating. Moreover,

in our experiment we observed that slight rotation of

the grating can adjust output wavelength. Due to the

high angular selectivity of the grating adjustment can

be done very precise.

Figure 7: Cross section of interference fringes.

Worth noting that in case of transmitting volume

Bragg grating its spectral selectivity is not so high as

Frequency Stabilization of an Adaptive Self-phase-conjugated Passively Q-switched Laser using Volume Bragg Grating on the

Photo-thermo-refractive Glass

325

expected. For instance, in this work grating spectral

selectivity was just 0.7nm which is exceeding

neodymium gain bandwidth. Therefore, we assume

that parameter which plays key role in frequency

stabilization is angular selectivity of the grating.

Placing the grating inside the cavity provide strict

conditions on the radiation direction of propagation.

This conditions so strong that only one wavelength in

the cavity can fulfill it during spontaneous

luminescence. And thus this wavelength has a better

feedback and lower threshold in comparison with

other frequencies. Thus this results in narrowing the

emission spectra of the laser. But in terms of stability

it still unclear why application of transmitting volume

Bragg grating locks pulse to pulse frequency. We

presume that combination of high angular selectivity

and mirror 2 position in our setup defines the

wavelength. Their relative orientation determines the

optical path inside the cavity and the only frequency

which can travel through this path considering Bragg

condition is start to rise. In confirmation of this

speculation we build up a single loop cavity in which

loop was made by 3 cavity mirrors and transmitting

Bragg grating (Fig. 8).

Figure 8: Single loop cavity with transmitting VBG. 1 –

active element, 2-4 – cavity mirrors, 5 – volume Bragg

grating, 6,7 – output coupler.

This setup differs from what we used before but in

this case we also achieved frequency stabilization and

narrowing with transmitting volume Bragg grating in

presence of any of output couplers (OC). But if we

remove both mirrors 6 and 7 we obtain a narrow line

pulses with no stability in pulse to pulse frequency.

Interesting fact that there is no difference if mirror 6

or 7 is in cavity, any of them in combination with

volume Bragg grating provides frequency

stabilization. Thus we assume that in this kind of

setup optical path of a beam inside the cavity depends

from wavelength and in the absence of OC operating

frequency is undetermined. But as soon as we apply

any of OC we induce additional selection to the

cavity. As before there is plenty of optical paths with

different wavelength exist in the cavity but now only

one of them fulfill Bragg condition and receive

feedback from OC which decrease its threshold. In

addition, we could adjust operating frequency by

slight rotation of either grating or OC itself. This can

serve as a proof of our ideas about wavelength

stabilization.

4 CONCLUSIONS

In present work we successfully demonstrated laser

frequency stabilization of an adaptive self-phase-

conjugated passively Q-switched laser by mean of the

transmitting volume Bragg grating on the photo-

thermo-refractive glass. As expected this grating

provides desired pulse to pulse frequency stability.

Moreover, our investigation shows that

implementation of the volume Bragg grating in the

multiloop cavity reduce the bandwidth of the

radiation from 18 to 4 pm with outstanding output

parameters such as pulse energy of 100mJ, peak

power of 10MWt and beam quality of M

=1.15. We

assume that the key factor of wavelength stabilization

in our case is angular selectivity of the grating. But it

operates only with feedback mirror.

ACKNOWLEDGEMENTS

This work was financially supported by Russian

Scientific Foundation (Agreement # 14-23-00136)

REFERENCES

Boreysho A. S., Konyaev M. A., Morozov A. V., Pikulik A.

V., Savin A. V., Trilis A. V., Chakchir S. Ya., Boiko N.

I., Vlasov Yu. N., Nikitaev S. P., and Rozhnov A. V.,

2005 Mobile multiwave lidar complexes Quantum

Electron., 35, pp.1167-1178.

Lebedev V. F., and Shestakov A. A., 2011 Fast LIBS

identification of solids during the laser ablation process.

Proc. SPIE Int. Soc. Opt. Eng., 7822, p. 78220V.

Basiev T.T., Garnov S.V., Klimentov S.M., Pivovarov

P.A., Gavrilov A.V., Smetanin S.N., Solokhin S.A., and

Fedin A.V., 2007. High-speed ablation of ultradeep

channels by a phase-conjugate dynamically controlled

passively Q-switched Nd:YAG laser Quantum

Electron., 37, pp. 956-960.

Bel’dugin I.M., Berenberg V.A., Vasil’ev A.E., Mochalov

I.V., Petnikova V.M., Petrovskii G.T., Harchenko

M.A., and Shuvalov V.V., 1989. Solid-state lasers with

PHOTOPTICS 2017 - 5th International Conference on Photonics, Optics and Laser Technology

326

self-pumped phase-conjugate mirrors in an active

medium. Sov. J. Quantum electron., 19, pp. 740-742.

Damzen M. J., Green R. P. M., Crofts G. J., 1992. High-

reflectivity four-wave mixing by gain saturation of

nanosecond and microsecond radiation in Nd:YAG.

Optics letters, v. 17, No. 19, pp.1331-1333.

Dotsenko, A., Glebov, L. & Tsekhomsky, V., 1998. Physics

and chemistry of photochromic glasses, CRC Press.

Dubrovin, V.D., Ignatiev, A.I. & Nikonorov, N.V., 2016.

Chloride photo-thermo-refractive glasses. Optical

Materials Express, 6(5), pp.1701–1713.

Efimov, O.M., Glebov, L.B., Grantham, S. & Richardson,

M., 1999. Photoionization of silicate glasses exposed to

IR femtosecond pulses. Journal of Non-Crystalline

Solids, 253(1–3), pp.58–67.

Ivanov, S.A., Angervaks, A.E. & Shcheulin, A.S., 2014.

Application of photo-thermo-refractive glass as a

holographic medium for holographic collimator gun

sights. Proceedings of SPIE, 9131, p.91311B.

Nikonorov, N., Aseev, V. & Ignatiev, A., 2010. New

polyfunctional photo-thermo-refractive glasses for

photonics applications. In ODF’10. pp. 209–210.

Efimov O.M., Glebov L.B., Papernov S., Schmid A.W.,

1999 Laser-induced damage of photo-thermo-refractive

glasses for optical-holographic-element writing. Laser-

Induced Damage in Optical Materials. Proc. SPIE

3578, pp.554-575.

Frequency Stabilization of an Adaptive Self-phase-conjugated Passively Q-switched Laser using Volume Bragg Grating on the

Photo-thermo-refractive Glass

327