A Lower Bound on the Number of Nodes with Multiple Slots in Wireless

Sensor Networks with Multiple Sinks

Sain Saginbekov

, Arshad Jhumka

and Yerzhan Mademikhanov

Department of Computer Science, School of Science and Technology, Nazarbayev University, Astana, 010000, Kazakhstan

Department of Computer Science, University of Warwick, Coventry CV4 7AL, U.K.

Keywords:

Wireless Sensor Networks, Multiple Sinks, Data Aggregation Scheduling, Lower Bound, Many-to-many

Communication, Routing.

Abstract:

Wireless Sensor Networks (WSNs) once deployed, are left unattended for extended periods of time. During

this time, the network can experience a range of faulty scenarios. If a sink node fails, data gathered by sensor

nodes may not be delivered to a destination. One way to increase the reliability of such WSNs is to deploy with

more than one sink. In this paper, we formalise the problem of many-to-many data aggregation scheduling in

WSNs with multiple sinks and establish a lower bound on the number of nodes with multiple slots.

1 INTRODUCTION

Typically, WSNs, once deployed, are left unattended

for extended periods of time. During this time, the

network can experience a range of faulty scenarios:

(i) any sensor node may fail due to energy exhaus-

tion, (ii) links may fail due to interference or (iii) the

sink may fail to communicate due to some reasons

such as link failures, node and sink failures. For ex-

ample, in (Paritosh et al., ), the authors observe that 4

of the 7 correctly working nodes had communication

failure with the sink over time, furthermore, they ob-

serve sink outage due to power failure. In a deploy-

ment (Polastre et al., 2004), a crash of the database

running on the sink node resulted in the complete

loss of data for two weeks. Likewise, in a deploy-

ment (Tolle et al., 2005), two weeks of data were lost

due to a sink outage. In (Szewczyk et al., 2004), au-

thors observed a sink outage due to harsh weather. In

such situations, as mentioned, the loss of the single

sink results in the loss of the network.

One way to increase the reliability of such WSNs

is to deploy with more than one sink. Moreover, de-

ploying more than one sink may improve network

throughput and prolong network lifetime by balanc-

ing energy consumption, and may address fault tol-

erance issues (Lee et al., 2005; Valero et al., 2012;

Sitanayah et al., 2012).

A number data aggregation scheduling (DAS) al-

gorithms have been proposed for WSNs with a sin-

gle sink. There also exist DAS algorithms for WSNs

with multiple sinks. For example, DAS algorithms

for a WSN with multiple sinks have been presented

in (Kawano and Miyazaki, 2008; Bo and Li, 2011).

However, those works present DAS algorithms where

many nodes send data to only one sink, whereas

this paper considers the problem of data aggregation

scheduling where many nodes send to many sinks.

In (Saginbekov et al., 2016), the authors focused

on the same problem. However, their proposed algo-

rithm performs data aggregation from many nodes to

two sinks. Their algorithm also works for more than

two sinks, but in sub-optimal ways. The main idea

of that algorithm was to develop a backbone that con-

nects two sinks and then schedule nodes transmission.

The same idea, i.e., building a backbone can

be used in WSNs with multiple sinks, which is di-

rectly related to the problem of developing a Steiner

tree (Gilbert and Pollak, 1968). We are interested in

developing a minimum Steiner tree, which is known

to be NP-complete (Karp, 1972), as it reduces the

number of nodes with multiple slots.

In this context, we make the following novel con-

tributions:

• We formalise the problem of DAS scheduling in a

WSN with multiple sink.

• We prove a lower bound for solving a variant of

DAS called weak DAS.

The rest of the paper is organized as follows. In

Section 2, we present an overview of related work.

202

Saginbekov S., Jhumka A. and Mademikhanov Y.

A Lower Bound on the Number of Nodes with Multiple Slots in Wireless Sensor Networks with Multiple Sinks.

DOI: 10.5220/0006263502020206

In Proceedings of the 6th International Conference on Sensor Networks (SENSORNETS 2017), pages 202-206

ISBN: 421065/17

In Section 3, we formalise the problem of Data Ag-

gregation Scheduling (DAS) in a WSN with multiple

sinks. Then, in Section 4, we show a lower bound for

solving a variant of DAS called weak DAS. Finally,

in Section 5, we discuss future work and conclude the

paper.

2 RELATED WORK

Communication protocols that have been developed

for WSNs with multiple sinks can be found in (Mot-

tola and Picco, 2011; Kawano and Miyazaki, 2008;

Bo and Li, 2011; Thulasiraman et al., 2007; Tuy-

suz Erman and Havinga, 2010; Hui Zhou and Xu,

2012). A data collection protocol that tries to decrease

the number of redundant transmissions has been pro-

posed in (Mottola and Picco, 2011). This protocol

uses information about the neighbourhood nodes to

reduce transmissions while collecting data from many

nodes to many sinks.

In (Thulasiraman et al., 2007), the authors propose

an algorithm that builds two node-disjoint paths from

every node to two different sinks. If one path fails, the

other is used to route the data. In (Tuysuz Erman and

Havinga, 2010), the authors propose a routing pro-

tocol with hexagon-based architecture. Nodes in the

network are grouped into hexagons according to their

locations. A routing protocol proposed in (Hui Zhou

and Xu, 2012), is based on trees. In this protocol, dif-

ferent trees rooted at different sinks are used to for-

ward data.

The schemes that have been proposed in (Kawano

and Miyazaki, 2008; Bo and Li, 2011) have more rel-

evance to our work. In (Kawano and Miyazaki, 2008),

the authors propose two algorithms: an algorithm that

builds shortest path trees rooted at each root and a

scheduling algorithm that exploits a graph colouring

algorithm to allow nodes to forward their messages to

their closest sink without message collisions. The au-

thors of (Bo and Li, 2011), propose two data aggre-

gation scheduling algorithms for multiple-sink sen-

sor networks. The ﬁrst algorithm is Voronoi-based

scheduling where the sensing area is divided into re-

gions forming k forests, one forest for each sink. Then

the algorithm assigns slots to nodes. The second al-

gorithm is Independent scheduling which differs from

the ﬁrst one in forest construction. However, in both

of these algorithms different portions of sensor nodes

send their data to a single different sink, i.e., many-

to-one communication, whereas we consider the case

where many nodes send their data to many sinks.

3 PROBLEM FORMULATION

We present the following deﬁnitions that we will use

in this paper.

Deﬁnition 1 (Schedule) A schedule S : V → 2

is a

function that maps a node to a set of time slots.

Deﬁnition 2 (DAS-label) Given a network G =

(V, E), a sink ∆, a schedule S and a path γ = n ·

m.. . ∆, we say that n is DAS-labeled under S on γ

for ∆ if ∃t ∈ S (n) · ∃t

∈ S (m) : t

> t.

We call the node m on γ the ∆-parent of n and γ

the DAS-path for n.

Deﬁnition 3 (Strong and Weak schedule) Given a

network G = (V, E), a sink ∆ ∈ V and a schedule S,

S is said to be a strong DAS schedule for ∆ for a node

n ∈ V iff ∀ path γ

= n · m

. .. ∆, n is DAS-labeled un-

der S on γ

for ∆. S is a weak DAS schedule for ∆ for

n if ∃ path γ = n · m

. .. ∆ such that n is DAS-labeled

under S on γ for ∆.

A schedule S is strong DAS (resp. weak DAS) for

G iff ∀n ∈ V , S is strong DAS schedule (resp. weak

DAS schedule) for ∆ for n.

A strong schedule, which is impossible to de-

velop (Jhumka, 2010), in essence, is resilient to prob-

lems that occur in the network such as radio links not

working or node crashes during deployment. On the

other hand, a weak schedule is not resilient and, any

problem happening, will entail that a message from

node n to m will be lost.

Given a network with n sinks ∆

, ∆

,··· , ∆

wish to develop a weak schedule for all sinks. There

are different ways to achieve this. In general, to de-

velop a weak schedule, several works have adopted

the approach whereby a tree is ﬁrst constructed,

rooted at the sink, and then slots assigned along the

branches to satisfy the data aggregation constraints.

A trivial solution is to construct n trees, each rooted

at a sink, and then to assign slots to nodes along the

trees. This means that nodes can have n slots, i.e.,

meaning that nodes may have to do n transmissions

for the same message. Thus, to reduce the number of

transmissions, we want to reduce the number of slots

for nodes to transmit in.

3.1 DAS Scheduling

We model our problem as follows:

We capture slots assignment with a set of decision

variables.



1 t ∈ S(n)

0 otherwise

A set value assignment to these variables represent

a possible schedule. The number of slots used, which

A Lower Bound on the Number of Nodes with Multiple Slots in Wireless Sensor Networks with Multiple Sinks

203

equates to the number of transmission by nodes, has

to be reduced for extending the lifetime of the net-

work.

We capture the number of nodes with multiple

slots as follows:



1 |S(n)| > 1

0 otherwise

However, such a schedule may not assign a slot to

a given node, so we need to rule out some schedules

with a constraint:

∀n ∈ V · ∃t : t

= 1

The above constraint means that all nodes in the

network will be assigned at least one slot. We also

rule out schedules S that assign the same slot to two

nodes that are in the two-hop neighbourhood, i.e,

∀m, n ∈ V : t

= 1 ∧t

= 1 ⇒ ¬2HopN(m, n)

Nodes can get information about slots assigned to

nodes of two-hop neighbourhod by exchanging mes-

sages. Finally, we require to generate weak DAS

schedules S, i.e.,

∀i ∈ N, ∀m ∈ V · ∃n ∈ V, (m · n . . . ∆

) : t

= 1 ⇒ ∃τ >

t : τ

= 1

Thus, there are different ways to generate a collision-

free weak DAS schedule for all sinks. For instance,

one may want to minimise numSlots to reduce the

number of slots during which nodes transmit. An-

other way is to reduce the number of times any node

can transmit, in some sort of load balancing. Thus,

our goal is to solve the following problem, which we

call the EECF-N-DAS problem (for energy-efﬁcient

collision-free N-sinks DAS):

EECF-N-DAS problem: Obtain an S such that

minimise

∑

∀t

∑

∀n∈V

subject to

1. ∀n ∈ V · ∃t : t

6= 0

2. ∀i ∈ N, ∀m ∈ V · ∃n ∈ V, (m · n . . . ∆

) : t

1 ⇒ ∃τ > t : τ

= 1

3. ∀m, n ∈ V : t

= 1 ∧ t

= 1 ⇒

¬2HopN(m, n)

The EECF-N-DAS problem consists of two subprob-

lems: (i) The ﬁrst two conditions amount to what

we call the weak DAS problem and (ii) the fourth

condition ensures that any weak DAS schedule is

collision-free. Collision freedom is guaranteed by

ensuring that no two nodes in a 2-hop neighbourhood

share the same slot.

4 THEORETICAL

CONTRIBUTIONS

In (Saginbekov et al., 2016), authors proved that it is

impossible to have a weak schedule in a network with

more than one sink where all nodes have only one slot.

Therefore, there should be a certain number of nodes

that require at least two slots.

In this section, we investigate how small can the

number of nodes with multiple slots be to generate

an energy efﬁcient collision-free weak schedule in a

network with multiple sinks.

4.1 All Nodes Have Multiple Slots

(

∑

∀n∈V

= |V |)

A trivial solution to this is as follows: generate k trees,

each rooted at a different sink, where k is the number

of sinks. For sink ∆

, starting with slot |V |, assign,

in decreasing order, slots to nodes using Breadth-ﬁrst

search algorithm (BFS) (Cormen et al., 2001). The

same process is repeated with other trees rooted at

∆

i≤k

, except they start with slot i ∗ |V |. This sets

an upper bound for collision-free weak schedules for

WSNs.

4.2 Towards Minimizing the Number of

Nodes with Multiple Slots (

∑

∀n∈V

)

One way of building a network that solves the weak

DAS problem is to assign two slots to the nodes on a

tree that connects all ∆

1≤i≤k

, and assign one slot to all

other nodes like shown in Figure 1(a).

The scheme works as follows: Initially, the

scheme builds a backbone tree that connects all sinks.

Then one node on the backbone tree is selected as a

super virtual root (shaded node in Figure 1(a)). Then,

the scheme starts to build trees rooted at each node,

called a virtual root, on the backbone tree (ﬁlled cir-

cles in Figure 1(a)). There exist many tree-building

algorithms. For example, BFS algorithm can be used

to build such trees. After building trees rooted at the

virtual roots, nodes that are not on the backbone tree

(circles in Figure 1(a)) forward their data to their vir-

tual root. On the way towards a virtual root, each

node aggregates received data from its children. After

receiving aggregated data, each virtual root forwards

data to the super virtual root. The super virtual root,

in turn, aggregates received data and sends the ﬁnal

aggregated data to the sinks using the backbone tree.

In other words, only virtual roots forward the data to-

wards the sinks. Thus, in this scheme, only the nodes

that are on the backbone tree send twice, except the

super node. The super node sends only once.

SENSORNETS 2017 - 6th International Conference on Sensor Networks

204

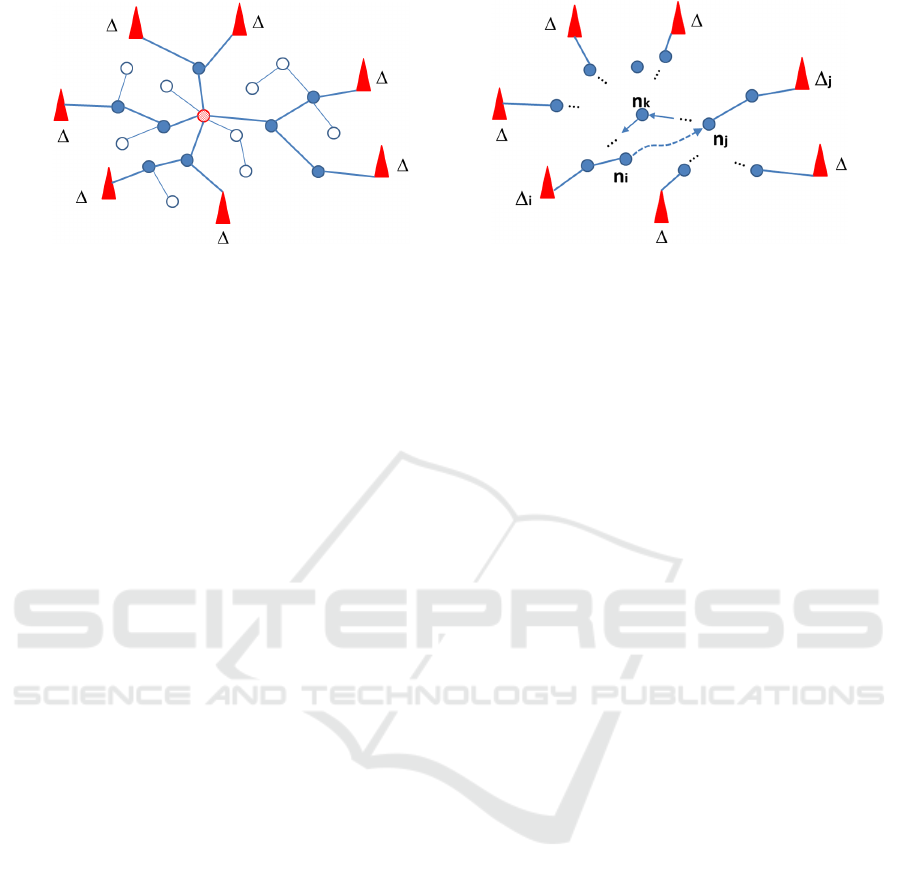
(a) (b)

Figure 1: (a) An example of network that solves weak DAS. Tree (bold lines) shows the backbone in which the nodes (virtual

roots) have at least two slots. (b) An illustration of the proof of Theorem 1.

Now, the question is does the scheme above mini-

mize the number of nodes that send the same message

more than once? In other words, does the scheme

reduce the number of nodes with multiple slots? In

the scheme above, the number of nodes with multiple

sinks is equal to the number of nodes on the backbone

tree minus one (the number of virtual roots except the

super root ). Can we reduce it further? The answer is

no, if the backbone tree is Steiner minimal tree.

Corollary 1 Given a network G = (V, A) with k sinks

∆

, ∆

, . . ., ∆

, where k ≥ 2, and a Steiner minimal

tree, with m nodes, that connects all k sinks, then there

exists a weak DAS S for G,

∑

∀n∈V

= m − 1.

Since we know that it is possible to obtain a weak

DAS schedule S that assigns two or more slots to at

most m − 1 nodes, the objective is to determine the

minimum number of such nodes with at least two

slots. This is captured in the following result (The-

orem 1):

Theorem 1 Given a ﬁnite network G = (V, A) with k

sinks ∆

, ∆

, . . ., ∆

, where k ≥ 2, and a Steiner min-

imal tree T , with m nodes, that connects all k sinks.

Then, there exists no weak DAS schedule S for G such

that

∑

∀n∈V

≤ m − 2.

From Corollary 1, we know that it is possible to

have a weak DAS schedule with at most m − 1 nodes

that assigned more than two slots. Now, we prove that

it is impossible to have such a schedule with less than

m − 1 nodes.

Proof.

We assume that there exists a weak DAS S for ﬁnite

network G such that

∑

∀n∈V

≤ m − 2 under S, and

show a contradiction.

Let T ⊂ G be a Steiner minimal tree which spans

all sinks in G ∆

, ∆

, . . ., ∆

. Since there are only m −

2 nodes in G that have more than one slot, there exist

at least two nodes in T that have only one slot, say n

and n

with, without loss of generality, S(n

) < S(n

Note that, as T is a tree, a path P

i j

between n

and n

connects at least two sinks, say ∆

and ∆

. Assume

that n

is closer to ∆

than to ∆

(See Figure 1(b) for

illustration).

Now, as n

should send its packet to ∆

and cannot

use P

i j

to deliver its packet to ∆

(as S(n

) < S(n

)),

there should exist a node n

(See Figure 1(b)), other

than n

, such that S(n

) < S(n

). If n

is assigned

more than one time slot, then we are done, as the num-

ber of nodes with more than one slot becomes m − 1.

Otherwise, as n

has only one slot and S(n

) < S(n

there should exist another node n

such that S(n

) <

S(n

) to deliver the packet of n

to ∆

. If n

is assigned

more than one time slot, then we are done. It contin-

ues like this until there exists a node with at least two

time slots. However, if there is no such a node, then

as G is ﬁnite, it is impossible to have a weak DAS

schedule for G that has m − 2 nodes with at least two

time slots.



5 CONCLUSIONS AND FUTURE

WORK

In this paper, we formalised the problem of data ag-

gregation scheduling in WSNs with multiple sinks.

We then established a lower bound on the number of

nodes with multiple slots. We proved that the num-

ber of nodes that send one message more than once

cannot be less than the number of nodes in minimal

Steiner tree that connects all sinks. As a future work

we plan to develop an approximation algorithm that

solves the DAS problem in WSNs with multiple sinks,

and conduct simulation and testbed experiments to

evaluate its performance.

A Lower Bound on the Number of Nodes with Multiple Slots in Wireless Sensor Networks with Multiple Sinks

205

REFERENCES

Bo, Y. and Li, J. (2011). Minimum-time aggregation

scheduling in multi-sink sensor networks. In SECON,

pages 422–430. IEEE.

Cormen, T. H., Stein, C., Rivest, R. L., and Leiserson, C. E.

(2001). Introduction to Algorithms. McGraw-Hill

Higher Education, 2nd edition.

Gilbert, E. N. and Pollak, H. O. (1968). Steiner minimal

tree. SIAM Journal on Applied Mathematics, 16:1–

29.

Hui Zhou, Dongliang Qing, X. Z. H. Y. and Xu, C. (2012).

A multiple-dimensional tree routing protocol for mul-

tisink wireless sensor networks based on ant colony

optimization. 2012.

Jhumka, A. (2010). Crash-tolerant collision-free data ag-

gregation scheduling for wireless sensor networks. In

SRDS 2010, pages 44–53.

Karp, R. M. (1972). Reducibility among combinatorial

problems. In Proceedings of a symposium on the Com-

plexity of Computer Computations, pages 85–103.

Kawano, R. and Miyazaki, T. (2008). Distributed data ag-

gregation in multi-sink sensor networks using a graph

coloring algorithm. AINA, pages 934–940.

Lee, H., Klappenecker, A., Lee, K., and Lin, L. (2005).

Energy efﬁcient data management for wireless sensor

networks with data sink failure. IEEE MASS, 0:210.

Mottola, L. and Picco, G. P. (2011). Muster: Adaptive

energy-aware multisink routing in wireless sensor net-

works. IEEE Trans. Mob. Comput., 10(12):1694–

1709.

Paritosh, P., Kirk, M., Alistair, R., Ong, H., and Hart,

J. Glacial environment monitoring using sensor net-

works. In Real-World Wireless Sensor Networks,

Stockholm, Sweden, 20 - 21 Jun 2005.

Polastre, J., Szewczyk, R., Mainwaring, A., Culler, D., and

Anderson, J. (2004). Wireless sensor networks. chap-

ter Analysis of Wireless Sensor Networks for Habitat

Monitoring, pages 399–423. Kluwer Academic Pub-

lishers, Norwell, MA, USA.

Saginbekov, S., Jhumka, A., and Shakenov, C. (2016). To-

wards energy-efﬁcient collision-free data aggregation

scheduling in wireless sensor networks with multiple

sinks. In SENSORNETS 2016 - Proceedings of the

5th International Confererence on Sensor Networks,

pages 77–86.

Sitanayah, L., Brown, K. N., and Sreenan, C. J. (2012).

Multiple sink and relay placement in wireless sen-

sor networks. In WAITS 2012 (Workshop on AI in

Telecommunications and Sensor Networks).

Szewczyk, R., Polastre, J., Mainwaring, A. M., and Culler,

D. E. (2004). Lessons from a sensor network expedi-

tion. In EWSN, pages 307–322.

Thulasiraman, P., Ramasubramanian, S., and Krunz, M.

(2007). Disjoint multipath routing to two distinct

drains in a multi-drain sensor network. In INFOCOM,

pages 643–651. IEEE.

Tolle, G., Polastre, J., Szewczyk, R., Culler, D., Turner, N.,

Tu, K., Burgess, S., Dawson, T., Buonadonna, P., Gay,

D., and Hong, W. (2005). A macroscope in the red-

woods. In Proceedings of the 3rd international confer-

ence on Embedded networked sensor systems, SenSys

’05, pages 51–63, New York, NY, USA. ACM.

Tuysuz Erman, A. and Havinga, P. (2010). Data dissem-

ination of emergency messages in mobile multi-sink

wireless sensor networks. In Med-Hoc-Net 2010,

pages 1–8.

Valero, M., Xu, M., Mancuso, N., Song, W.-Z., and Beyah,

R. A. (2012). Edr

: A sink failure resilient approach

for wsns. In ICC 2012. IEEE.

SENSORNETS 2017 - 6th International Conference on Sensor Networks

206