Appliance Usage Prediction for the Smart Home with an Application to

Energy Demand Side Management

And Why Accuracy is not a Good Performance Metric for this Problem

Marc Wenninger

, Jochen Schmidt

and Toni Goeller

Department of Computer Science, Rosenheim University of Applied Sciences, Rosenheim, Germany

MINcom GmbH, Rosenheim, Germany

Keywords:

Real Time Pricing (RTP), Household Appliance Usage Prediction, Demand Side Management.

Abstract:

Shifting energy peak load is a subject that plays a huge role in the currently changing energy market, where

renewable energy sources no longer produce the exact amount of energy demanded. Matching demand to supply

requires behavior changes on the customer side, which can be achieved by incentives such as Real-Time-Pricing

(RTP). Various studies show that such incentives cannot be utilized without a complexity reduction, e. g., by

smart home automation systems that inform the customer about possible savings or automatically schedule

appliances to off-peak load phases. We propose a probabilistic appliance usage prediction based on historical

energy data that can be used to identify the times of day where an appliance will be used and therefore make

load shift recommendations that suite the customer’s usage proﬁle.

A huge issue is how to provide a valid performance evaluation for this particular problem. We will argue why

the commonly used accuracy metric is not suitable, and suggest to use other metrics like the area under the

Receiver Operating Characteristic (ROC) curve, Matthews Correlation Coefﬁcient (MCC) or

-Score instead.

1 INTRODUCTION

With renewable energy sources, electric grid operators

face a variety of new challenges. One being the highly

variable amount of power produced, e. g. by wind tur-

bines or photovoltaic systems. In order to guarantee

the stability of the grid, the amount of energy in the

grid has to be just right. Hence, supply and demand

must match. Up to now, unexpected power ﬂuctuations

emerged on the demand side only (in particular indus-

trial plants and private households), which could be

balanced for example by gas engines. A wind turbine,

however, generates energy in windy weather condi-

tions, but not necessarily when the power is required

on the demand side. In windless phases (or cloudy

ones in terms of photovoltaic systems), the result is an

undersupply of power in the grid. As power cannot be

stored very efﬁciently, over-production is also a major

problem for grid operators. Therefore, the problem to

be solved is to balance demand and supply. One step

in this direction is the smoothing of load peaks through

load shifting, i. e., shifting parts of power consumption

to other time periods, in which less power is used.

Our aim is to develop solutions for optimal load

shifting for private consumers using artiﬁcial intelli-

gence, and Real-Time-Pricing (RTP) as an incentive

to integrate the customer into the balancing of supply

and demand (see (Hassan et al., 2016) for a discussion

of methodologies to assist grid operators in designing

incentives for consumer participation in demand re-

sponse management taking into account inconvenience

for participating users). RTP are tariffs, in which elec-

tricity cost varies over time (e. g., the price changes

every 15 min) (S.a., 2005a). Studies suggest that RTP

models require a complexity reduction in order to be

accepted by the end-user (S.a., 2005b), as well as that

customers will respond with shaving instead of shifting

of their peak demand (Schleich and Klobasa, 2013).

We therefore combine such tariffs with the knowledge

of a household’s typical power consumption, which

form the basis for an intelligent demand side manage-

ment system. The system is then capable of shifting

loads to better suited time periods through measures

speciﬁcally tailored to user behavior. Simulations have

already shown that such systems can effectively re-

duce the peak-to-average ratio (Mohsenian-Rad and

Leon-Garcia, 2010). We aim to reduce the system’s

complexity sufﬁciently, in order to enable technically

unversed persons to make use of it as well.

Smart meters are used for metering and billing;

Wenninger, M., Schmidt, J. and Goeller, T.

Appliance Usage Prediction for the Smart Home with an Application to Energy Demand Side Management - And Why Accuracy is not a Good Performance Metric for this Problem.

DOI: 10.5220/0006264401430150

In Proceedings of the 6th International Conference on Smart Cities and Green ICT Systems (SMARTGREENS 2017), pages 143-150

ISBN: 978-989-758-241-7

143

Tariff Server

Billing Component

Actuator / Switch

Information System

Home Automation

Billing System

Headend System

Smart-Meter

Smart-Meter Infrastructure

Customer

Provider

Gateway

Real-Time-Pricing

Tariffs

Figure 1: The big picture: the system for transmission and

evaluation of tariff information is decoupled from the smart

meter infrastructure. The customer has full control over the

home automation gateway, therefore no privacy issues arise.

This article’s focus is on exploiting RTP tariffs on the home

automation side using AI methods.

these devices are digital electricity meters that connect

to the utility company over a communication network.

The design of a system for residential smart grid appli-

cations is discussed, e. g., in (Viswanath et al., 2016).

As shown in Fig. 1, the system being developed in

our project for transmission and evaluation of tariff

information is decoupled from the smart meter infras-

tructure. The evaluation of tariffs in the home automa-

tion gateway may be augmented by a large variety of

additional information, for example: historical energy

consumption data of single appliances or the entire

household; the presence or absence of residents; or

weather forecasts. With this data, using artiﬁcial in-

telligence methods, behavior patterns can be detected;

combined with tariff information the optimal use of

household appliances can be computed. Based on the

results of these computations, appliances can be con-

trolled directly using the home automation system. A

main challenge is to avert that power cost minimization

has negative consequences for the user. This requires

appliance usage proﬁling.

Appliance usage proﬁling and prediction is al-

ready discussed in various publications, where, e. g.,

ON/OFF probabilities are used to build a non-

homogeneous Markov Chain to model end-use energy

proﬁles on appliance level (Kang et al., 2014); (Chang

et al., 2013) propose a daily pattern based probability

model. Decision trees and Bayesian network-based

prediction are utilized in (Arghira et al., 2012) to dis-

cover behavior patterns within sequential data; (Heier-

man and Cook, 2003) propose using the ED (Episode

Discovery) data-mining algorithm for this purpose.

(Hawarah et al., 2010) predict the user behavior with

bayesian networks and (Basu et al., 2013) compare the

performance of different classiﬁers such as bayesian

networks, decision trees and decision tables for predict-

ing the future 24h power consumption of an appliance.

In this paper, as a ﬁrst step, we present an approach

for predicting appliance usage (e. g., for dishwashers,

washing machines etc.), which allows the automation

system to either control the appliances directly, or to

give recommendations to the residents in which time

period using the appliance would result in lower energy

costs, based on the users’ normal behavior patterns,

which are learned from historical data automatically.

This requires some kind of energy load prediction.

Our prediction model is based on the appliance’s us-

age cycles, thus requiring the extraction of appliance

operation cycles (start/end time) from its electricity

metering data (Stephen et al., 2014).

2 PREDICTION METHOD

Probabilistic Model.

There are basically two main

factors that need to be taken into account when com-

puting the probability that an appliance will be used:

The time elapsed since it was used last and the time

of day it is usually used. For example, a dishwasher

will typically be switched on in more or less regular

intervals and only at certain times of day (e. g., nor-

mally not at 2 a. m.). We model these separately as

probability distribution functions (PDFs), where in the

following

will denote the event elapsed time and

the event time of day. To give recommendations to the

user, the combined probability of these two events has

to be calculated and must be above a deﬁned threshold

to initiate a recommendation:

P(E ∩ D) = P(E | D)P(D)

if independent

= P(E)P(D) .

(1)

Statistical independence of

and

is assumed here;

although strictly speaking not necessary, as the condi-

tional probability

P(E | D)

can be computed from the

data if a sufﬁcient amount of representative data are

available. As this is quite often not the case (cf. Sect. 4

for details on typical data sets), the independence as-

sumption results in more stable estimates of

P(E ∩ D)

That independence is valid can be checked on the data

set by computing the product on the right and middle

of (1), and checking that equality holds.

The probability

P(E)

that the appliance is not used

for a time period

(here measured in minutes) is mod-

eled by an exponential distribution:

P(E) = P(E ≤ t) =

(

1 − e

−λt

t ≥ 0

0 t < 0

. (2)

A maximum likelihood estimate of the parameter

can be obtained from a sufﬁciently large data set by

SMARTGREENS 2017 - 6th International Conference on Smart Cities and Green ICT Systems

144

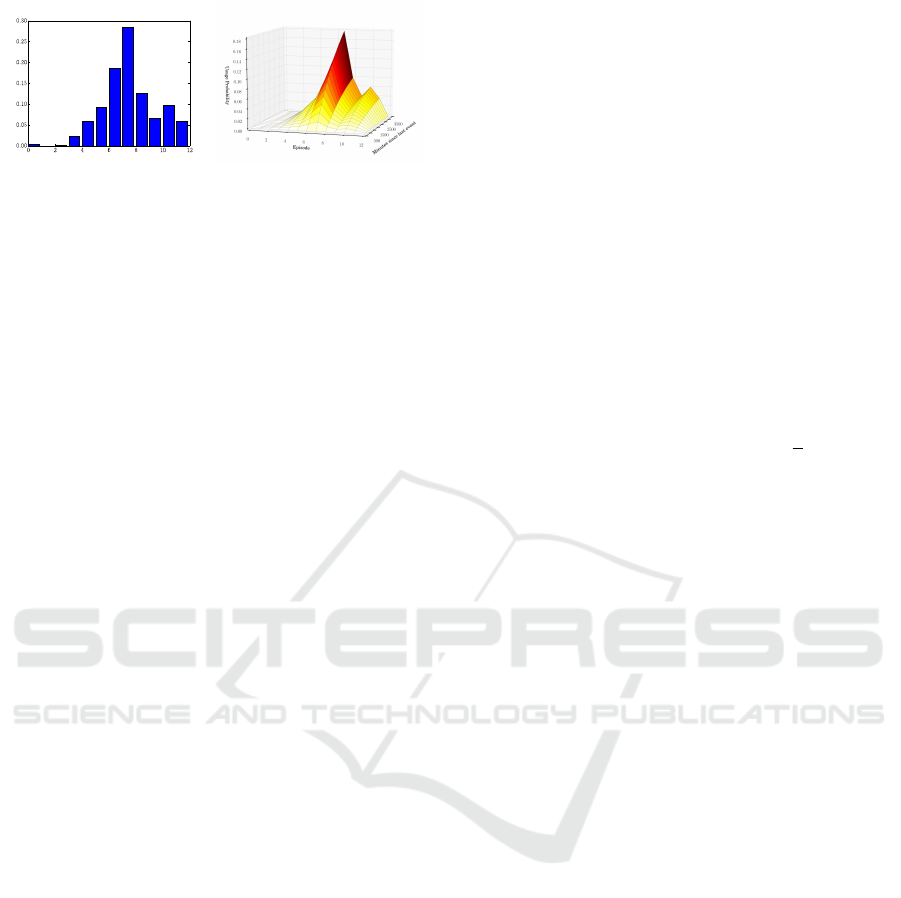
Figure 2: Example of estimates for

P(D)

(discrete density of

appliance usage throughout the day, left) and the combined

cumulative distribution

P(E ∩ D)

(right). Episode length is

2h, resulting in 12 episodes per day.

computing the mean value of the time periods between

consecutive appliance-switch-on events. A good es-

timate of

will be obtained when the time between

usage is fairly regular, resulting in a small value for

the variance of the time periods.

In contrast to using a continuous distribution for

, a discrete PDF for the event

is estimated from

the sample data by computing relative frequencies of

appliance usage viewed over the 24 hour time period

of a day. This period has to be divided into discrete

intervals, which we will call episodes in the follow-

ing. An episode must be sufﬁciently large, so that

statistically valid relative frequencies (which are an

estimate of the probability that the appliance is used

in a particular episode) can be obtained. On the other

hand, it has to be small enough to be of practical use.

We found episodes having a length of 1h to 2h to be

a good compromise. To avoid issues with episodes

where no samples are contained in the data set, leading

to density values of zero, the Parzen window approach

(Parzen, 1962; Duda et al., 2000) can be applied, which

is basically an interpolation and smoothing method,

typically using Gaussians. Figure 2 shows an example

of a discrete PDF computed from the GREEND data

set (Monacchi et al., 2014).

Inactivity Detection.

Most household appliances

with non-homogeneous distribution in electricity con-

sumption require the user’s presence when starting

the appliance. Thus, the prediction of a household

appliance usage is often accompanied by a prediction

of the home’s occupancy; in some cases an appliance

might even be directly linked to the presence of a spe-

ciﬁc person. Without ground truth on the occupancy,

a strong indication that can be found in the historical

electricity data is the usage of such appliances in the

recent history. We therefore add knowledge of the

events that occurred in recent history to the prediction

by lowering the probability in case no appliance was

used in recent episodes. We found that the past 12h to

24h are of speciﬁc interest and improve the prediction

signiﬁcantly. This approach may be replaced by more

sophisticated occupancy detection algorithms, which

are not the focus of this paper.

Threshold Estimation.

Now that the usage proba-

bility can be computed at any time of day, a threshold

has to be set that determines whether the home au-

tomation system turns on the appliance (or gives a

recommendation to the user to do so). Note, that the

absolute values of

P(E ∩ D)

depend heavily on the

time interval chosen as episode duration. Obviously,

longer episodes result in higher probabilities for appli-

ance usage during this period; e. g., using 2h instead of

1h episodes would approximately double the probabil-

ities (exactly for uniform distribution, less so for uni-

/multi-modal densities). We propose to compute the

threshold automatically from the training data by cal-

culating

P(E ∩ D)

for each episode of the training set.

Let

be the predicted probability at the

-th turn-on

event of a total of

that occurs in the data, the thresh-

old

is computed as the mean:

∑

N−1

i=0

. If

extreme outliers are expected or more control over the

threshold is desired, the Median or any other quantile

may be used instead.

Extended Model.

The model described above

works well when appliances are typically used in fairly

regular intervals, like dishwashers. There are scenar-

ios, however, where it fails; e. g., a household may

use the washing machine every Saturday, but not only

for a single washing cycle but two or three times in a

row. While the estimate for

P(D)

will still be valid,

the parameter

of the exponential distribution will be

invalid. This issue can be overcome by introducing an

additional discrete random variable

, describing how

many times an appliance has been used during the past

episodes. The parameter

can be adjusted to the

appliance at hand; e. g., for a washing machine a 10h

period may sufﬁce. Generalization of (1) gives:

P(E ∩ D) =

∞

∑

i=0

P(E ∩ D | U = i)P(U = i)

∑

i=0

P(E ∩ D | U = i)P(U = i)+

P(E ∩ D | U > n

)P(U > n

) ,

(3)

where

is an upper limit for the number of times an

appliance is used that can be derived from the training

data (a washing machine may be switched on 3 or

4 times in a 10h interval, but not 20 times); from a

certain value of

onwards, all probabilities

P(U = i)

will usually be zero.

Appliance Usage Prediction for the Smart Home with an Application to Energy Demand Side Management - And Why Accuracy is not a

Good Performance Metric for this Problem

145

3 ACCURACY IS NOT A GOOD

PERFORMANCE METRIC

In many publications on appliance usage prediction or

energy load disaggregation the performance metric ac-

curacy is chosen to evaluate the proposed classiﬁcation

methods. The accuracy

is deﬁned as the proportion

of data that has been classiﬁed correctly:

A =

+ T

, (4)

where

is the total number of events,

is the num-

ber of positive events and

is the number of nega-

tive events that have been classiﬁed correctly (True

Positives and True Negatives, respectively). For the

problem at hand we get a true positive if the algorithm

predicts that an appliance is running during a given

time period and the appliance is actually doing so. In

the same manner, for a true negative the prediction is

that the appliance is off and this is truly the case. The

denominator n is then the total number of episodes.

The main issue with this commonly chosen metric

is that it is not meaningful for rare events; this is known

as the accuracy paradox (Zhu and Davidson, 2007;

Valverde-Albacete and Peláez-Moreno, 2014). Rare

events, however, are in most

cases the standard when

looking at the problem of appliance usage prediction!

Consider, for instance, a dishwasher: this appliance

is normally used quite regularly, say every other day,

where it takes about 2h to ﬁnish its cycle. This means,

though, that in 96% of the total time the dishwasher is

off. Even if it is used twice as often, i. e., every day, it

will still be off 92% of the time. Publications making

use of accuracy, such as (Heierman and Cook, 2003;

Barbato et al., 2011; Basu et al., 2013; Lee et al., 2013;

Lachut et al., 2014), could therefore easily be outper-

formed for rare events by simply always predicting no

occurrence (i. e., a Negative), which will result in an

accuracy of 96% for the dishwasher example above.

The issue of selecting an appropriate metric has

been addressed before by several authors from vari-

ous ﬁelds (Cook, 2007; Hand, 2009; Powers, 2011;

Makonin and Popowich, 2015). The overall perfor-

mance of a binary classiﬁer is usually captured using

the Receiver Operating Characteristic (ROC), which

is a plot of the true positive rate (TPR, also called sen-

sitivity, recall, or detection rate) vs. false positive rate

(FPR). These are given by:

TPR =

, FPR =

, (5)

where

is the number of negative events that have

been classiﬁed incorrectly as positive ones,

is the

The possible exception being appliances like fridges or

freezers.

total number of positive and

the total number of

negative events, with

n = P + N

. Examples of ROC

plots are shown in the experiments section in Fig. 4.

A perfect classiﬁer would show a rectangular curve,

while the main diagonal indicates complete random-

ness. Any point on the curve can be selected for classi-

ﬁcation by choosing the classiﬁer’s parameters appro-

priately. Every point results in a different value for the

accuracy

calculated as shown in

(4)

. In publications,

where only accuracy is presented, this will usually be

the point on the ROC curve where the maximum value

is obtained.

This is similar for the following two metrics, the

-Score and the Matthews Correlation Coefﬁcient

(MCC):

= 2 ·

PREC · TPR

PREC + TPR

, PREC =

+ F

, (6)

where

PREC

is called precision, and

TPR

is the true

positive rate (recall) from (5).

MCC =

− F

PN(T

+ F

)(F

+ T

)

, (7)

with

and

being the number of false and true

negatives, respectively.

ranges from

, the

MCC, being a correlation coefﬁcient, ranges from

−1

. In both cases zero indicates total randomness

and one perfect classiﬁcation. While the

-Score also

suffers from a bias when sample sizes for positive and

negative data are different, the MCC balances these. It

is therefore much better suited for measuring classiﬁer

performance in cases, where events are rare.

In contrast to all these metrics, which measure per-

formance for a single point on the ROC curve, the Area

Under Curve (AUC) tries to capture the quality of the

whole ROC in single numerical value by computing

the area under the ROC:

AUC =

ROC dFPR. (8)

For a correctly evaluated classiﬁer, the AUC will range

from

0.5

(total randomness) to

(perfect). Although

reducing two dimensions to a single one without los-

ing information is not feasible, AUC is still a valid

metric for overall performance, and much better suited

than accuracy. Extensions of AUC can be found in

literature, e. g. (Hand, 2009), who suggests a weighted

AUC.

Unfortunately, knowledge regarding evaluation

metrics does not seem to be widely spread in the en-

ergy usage prediction and disaggregation community.

This has been criticized before by several authors like

(Kim et al., 2011; Makonin and Popowich, 2015), alas

with apparently little effect. We propose using AUC,

, and MCC, and will give results for all three metrics

in this paper’s experiments section.

SMARTGREENS 2017 - 6th International Conference on Smart Cities and Green ICT Systems

146

4 EXPERIMENTAL RESULTS

Evaluating the proposed prediction method requires

high resolution power consumption measurements of

individual appliances. A few publicly available data

sets already exists, usually containing the whole house

and appliance level energy consumption data (see Ta-

ble 1). We selected homes from the GREEND data

set (Monacchi et al., 2014) to evaluate our prediction

model. This set was chosen as it provides enough mea-

surements to enable statistical analysis of events and

is of sufﬁcient data quality. Other data sets, such as

REDD (Kolter and Johnson, 2011) or ECO (Beckel

et al., 2014), do not provide enough data or the re-

quired quality (e. g., there are often long periods where

data is missing). The GREEND data set provides mea-

surements of eight homes with a varying amount of

appliances and measuring periods ranging from 134 to

500 days. The data are sampled with a rate of 1 Hz and

provide the power consumption in Watts per appliance.

Comparing our results to previous usage prediction

publications proved to be infeasible as the results are

not comparable due to the chosen data set or evaluation

metric. Evaluations using artiﬁcially generated data

(Heierman and Cook, 2003; Barbato et al., 2011) are

not comparable as the amount of introduced random-

ness will dictate the result, especially for rare events

such as dishwasher usage. We do not consider these

evaluations as valid. Publications evaluating appli-

ance usage prediction on short data sets, e. g. REDD

(Truong et al., 2013a; Truong et al., 2013b), are also

not comparable due to the insufﬁcient amount of data

in the set. REDD contains data for only up to 19 days,

a duration that we consider totally inadequate for train-

ing and evaluation of rare events such as dishwasher

usage.

Extracting Events.

As the prediction is based on

event occurrences, where an event is deﬁned by the

start and end of an appliance’s usage cycle, in a ﬁrst

pre-processing step the events must be extracted from

the continuous power consumption data stream. As the

start and end of an event are not provided by any of the

data sets listed in Table 1, the performance of the event

extraction cannot be measured against ground truth.

We ﬁrst aggregate the data to

1/60

Hz by averaging

the power consumption. The start and stop of an event

are deﬁned by the rising and falling edge of the signal,

which allows using a threshold method. In case an

appliance’s power consumption falls below the thresh-

old during an event, this event will be partitioned, thus

(incorrectly) generating multiple usage cycles instead

of a single one. For the method proposed in this paper,

the partitioning will not be an issue for computing the

discrete estimate of

P(D)

(1)

; however, the estimate

of the exponential distribution

P(E)

(2)

would

be distorted. We overcome this problem by deﬁning an

individual threshold for each type of appliance, which

minimizes the partitioning, and then only use events of

sufﬁcient length. Table 2 gives a statistical overview

of the extracted events for appliances selected from

the GREEND data set.

Results.

The extracted events were split into two

disjoint parts,

60%

for training and

40%

for evalu-

ation. The training set is used to estimate

(2)

by calculating the mean value between consecutive

appliance-switch-on events. As an example,

for the

dishwasher in house 3 is 2274 minutes (

≈ 1.6

days).

An episode length of 360 minutes was chosen, which

divides the day into four partitions. A smaller episode

length leads to a more time precise prediction task, and

vice versa. As we do not require high time precision,

but rather a recommendation window that suites the

user’s behavior patterns, four partitions per day give a

reasonable recommendation window.

The probability

P(D)

from

(1)

for each episode is

calculated by binning the appliance-switch-on event

duration into the corresponding episode-bin. Figure 3

shows

P(E ∩ D)

for the dishwasher in house 3. It

clearly shows the characteristics of

P(D)

: The appli-

ance is not likely to be used in the morning, very likely

during midday and medium in the evening. With this

information we can deﬁne the user’s preferred usage

window and only recommend load shifts within this

window. It also shows the effect of

P(E)

on the com-

bined probability, as the probability drops immediately

after the appliance is switched on. This respects the

mean duration between events, hence no load shift rec-

ommendation must be made until a signiﬁcant proba-

bility is reached in the successive episodes.

For usage prediction performance comparison be-

tween the appliances in different homes we calculate

the ROC and the area under the ROC curve (AUC) by

changing the threshold probability at which the predic-

tion will consider the appliances as being used; also

the

-Score and MCC. The results are highly depen-

dent on the house and appliance (cf. Table 2) The worst

prediction result is obtained for the fridge in house 1,

a MCC of 0.029, which is complete randomness. The

reason is insufﬁcient data: Table 2 shows that there

were only 15 events available in the whole data set,

therefore good performance cannot be expected.

Although very good results can typically be

achieved for fridges, these are not ideal for load shift-

ing; dishwashers, washing machines and dryers on

the other hand are of special interest, as they are well

suited for this purpose. ROC curves for these appli-

Appliance Usage Prediction for the Smart Home with an Application to Energy Demand Side Management - And Why Accuracy is not a

Good Performance Metric for this Problem

147

Table 1: Publicly available appliance and whole house energy consumption data sets.

Data set Reference Location

Duration/

house

# of

houses

Appliance

sample intvl

Aggregate

sample intvl

REDD (Kolter and Johnson, 2011) MA, USA 3–19 days 6 3 sec 1 sec & 15 kHz

Smart* (Barker et al., 2012) MA, USA 3 months 3 1 sec 1 sec

AMPds 2 (Makonin et al., 2016) BC, Canada 2 years 1 1 min 1 min

UK-DALE

(Kelly and Knottenbelt, 2015)

London, UK 3–26 months 5 6 sec 1–6 sec & 16 kHz

ECO (Beckel et al., 2014) Switzerland 8 months 6 1 sec 1 sec

GREEND (Monacchi et al., 2014) Italy & Austria 12 months 9 1 sec –

Dataport (Pecan Street Inc., 2014) TX, USA 0–2.75 years 824 1 min 1 min

DRED (Uttama Nambi et al., 2015) Netherlands 2 months 1 1 sec 1 sec

Table 2: Statistics of extracted events of the GREEND data

set, providing the days between ﬁrst and last events as well

as the total events count for six different homes. Also shown

are resulting performance metrics using an episode length of

360 minutes.

H# Appliance Days Events AUC F

MCC

0 coffee maker 308 676 0.703 0.708 0.498

0 dishwasher 306 143 0.684 0.389 0.348

0 fridge freezer 309 7353 0.999 0.999 0.972

0 lamp 307 215 0.701 0.524 0.344

0 television 117 445 0.567 0.852 0.251

0 washing mach. 309 256 0.591 0.378 0.190

1 bedside light 473 456 0.859 0.704 0.580

1 dishwasher 472 248 0.651 0.335 0.213

1 dryer 473 405 0.859 0.811 0.763

1 fridge 454 15 0.550 0.017 0.029

1 washing mach. 467 166 0.839 0.415 0.390

2 coffee maker 494 512 0.580 0.333 0.180

2 dishwasher 495 477 0.856 0.654 0.553

2 dryer 495 424 0.828 0.596 0.499

2 television 497 1446 0.770 0.786 0.618

2 washing mach. 497 794 0.809 0.728 0.634

3 coffee maker 456 250 0.719 0.397 0.349

3 dishwasher 456 211 0.843 0.414 0.394

3 fridge 460 1100 0.917 0.909 0.818

3 television 461 849 0.827 0.783 0.652

3 washing mach. 457 279 0.789 0.392 0.329

4 fridge freezer 282 137 0.802 0.471 0.451

4 television 280 2242 0.753 0.675 0.543

4 television 2 280 1657 0.657 0.706 0.332

4 washing mach. 263 81 0.641 0.198 0.168

5 fridge freezer 418 13054 0.734 0.985 0.665

5 lamp 416 322 0.627 0.420 0.193

5 television 417 1297 0.867 0.880 0.710

5 television 2 417 677 0.582 0.561 0.247

5 washing mach. 415 521 0.624 0.396 0.229

ances are shown in Fig. 4. The best prediction results

for this type of appliance were achieved for the dryer

in house 1 with an AUC of 0.859 and MCC of 0.763.

The home with the most predictable dishwasher and

washing machine usage is house 2, with AUC 0.856,

MCC 0.553 (dishwasher), and AUC 0.809, MCC 0.634

(washing machine). On the other hand, the results for

house 0 are AUC 0.684, MCC 0.348 (dishwasher) and

AUC 0.591, MCC 0.190 (washing machine). The rea-

0 0 0 3 06 09 12 15 18 2 1 0 0

0.00

0.05

0.10

0.15

0.20

0 0 0 3 06 09 12 15 18 2 1 0 0

0.00

0.05

0.10

0.15

0.20

0 0 0 3 06 09 12 15 18 2 1 0 0

0.00

0.05

0.10

0.15

0.20

0 0 0 3 06 09 12 15 18 2 1 0 0

0.00

0.05

0.10

0.15

0.20

0 0 0 3 06 09 12 15 18 2 1 0 0

0.00

0.05

0.10

0.15

0.20

0 0 0 3 06 09 12 15 18 2 1 0 0

0.00

0.05

0.10

0.15

0.20

Figure 3: Usage probability prediction and real occurrence

for each day of a dishwasher during 2015/2/1 to 2015/2/6

(l.r.t.b). The gray area marks the time the appliance is

switched on, the curve the probability of the device being

switched on at each minute. For a clearer demonstration, we

chose an episode length of 120 minutes; the x-axis is labeled

by the hour of the day.

son for the performance difference compared to other

homes lies in behavior changes of the inhabitants of

house 0, which can be shown by comparing the proba-

bility distribution

P(D)

for training and evaluation data

(see Fig. 5). While in the dishwasher’s training data

the ﬁrst episode of a day has a probability of 0.37, in

the evaluation data it is 0.08. The probability densities

show that the events where moved to the last episode

of the day, an episode with a low probability in the

training data. The changes, represented as the mean

square error (MSE), between training and evaluation

are 0.0462 for house 0 and 0.0033 for house 2. Thus,

the preconditioned behavior consistency is no longer

given in house 0, a problem which could be overcome

by analyzing recent behavior changes and adapting

P(D) accordingly. This is a topic for future research.

SMARTGREENS 2017 - 6th International Conference on Smart Cities and Green ICT Systems

148

(a) H#0 – dishwasher (b) H#1 – dishwasher

(e) H#2 – dishwasher (f) H#2 – washing machine

(g) H#3 – dishwasher (h) H#3 – washing machine

Figure 4: Examples of ROC curves of the prediction al-

gorithm on the GREEND data set. Dishwasher, washing

machine, and dryer were selected as these appliances are par-

ticularly suited for load shifting. A perfect classiﬁer would

show a rectangular curve, while the main diagonal indicates

complete randomness.

(a) training data (b) test data

Figure 5:

P(D)

of the dishwasher in house 0 shows signiﬁ-

cant difference between (a) training and (b) evaluation.

5 CONCLUSION

We presented probabilistic models for appliance usage

prediction based on historical energy data. The appli-

cation we have in mind is to give recommendations to

the user (or home automation system), whether switch-

ing an appliance on would result in lower energy costs

whilst taking into account the appliance’s typical us-

age pattern in the particular household. An important

topic for future work is to investigate how to handle

long term behavior changes like those found in house

0 of the GREEND data set for the dishwasher, and

how to adapt the model over time. The results on the

GREEND data set look promising; there are currently

no publications available providing results for this kind

of application that we could use as a benchmark, as the

evaluation method is often invalid due to the accuracy

paradox, or the amount of data used for training is

insufﬁciently low to provide reliable results. At the

moment, it is not yet clear what the best and most

meaningful performance evaluation metric for this sort

of prediction problem would be, as in contrast to usual

classiﬁcation problems, the goal is not to predict the

exact time an appliance is used, but rather give a rec-

ommendation at convenient times. We presented our

results using the AUC,

and MCC metrics to provide

a comparable benchmark for future publications.

ACKNOWLEDGEMENTS

This work was funded by the German Federal Ministry

of Education and Research (BMBF), grant 01LY1506.

REFERENCES

Arghira, N., Hawarah, L., Ploix, S., and Jacomino, M. (2012).

Prediction of appliances energy use in smart homes.

Energy, 48(1):128–134. 6th SDEWES Dubrovnik Con-

ference SDEWES 2011.

Barbato, A., Capone, A., Rodolﬁ, M., and Tagliaferri, D.

(2011). Forecasting the usage of household appliances

through power meter sensors for demand management

in the smart grid. In IEEE Intern. Conf. SmartGrid-

Comm, 2011, pages 404–409.

Barker, S., Mishra, A., Irwin, D., Cecchet, E., Shenoy, P.,

and Albrecht, J. (2012). Smart*: An Open Data Set

and Tools for Enabling Research in Sustainable Homes.

In Proceedings of SustKDD, Beijing, China.

Basu, K., Hawarah, L., Arghira, N., Joumaa, H., and Ploix,

S. (2013). A prediction system for home appliance

usage. Energy and Buildings, 67:668 – 679.

Beckel, C., Kleiminger, W., and Cicchetti, R. (2014). The

eco data set and the performance of non-intrusive load

monitoring algorithms. In Proceedings of the 1st ACM

Intern. Conf. BuildSys 2014, pages 80–89.

Chang, C., Verhaegen, P.-A., Duﬂou, J. R., Drugan, M. M.,

and Nowe, A. (2013). Finding days-of-week represen-

tation for intelligent machine usage proﬁling. Journ. of

Industrial and Intelligent Information, 1(3):148–154.

Appliance Usage Prediction for the Smart Home with an Application to Energy Demand Side Management - And Why Accuracy is not a

Good Performance Metric for this Problem

149

Cook, N. R. (2007). Use and Misuse of the Receiver Operat-

ing Characteristic Curve in Risk Prediction. Circula-

tion, 115(7):928–935.

Duda, R. O., Hart, P. E., and Stork, D. G. (2000). Pattern

Classiﬁcation (2nd Edition). Wiley-Interscience.

Hand, D. J. (2009). Measuring classiﬁer performance: a

coherent alternative to the area under the ROC curve.

Machine Learning, 77(1):103–123.

Hassan, N. U., Khalid, Y. I., Yuen, C., Huang, S., Pasha,

M. A., Wood, K. L., and Kerk, S. G. (2016). Frame-

work for minimum user participation rate determina-

tion to achieve speciﬁc demand response management

objectives in residential smart grids. International Jour-

nal of Electrical Power & Energy Systems, 74:91–103.

Hawarah, L., Ploix, S., and Jacomino, M. (2010). User

behavior prediction in energy consumption in housing

using bayesian networks. In Proc. of the 10th ICAISC,

pages 372–379, Berlin, Heidelberg. Springer-Verlag.

Heierman, III, E. O. and Cook, D. J. (2003). Improving

home automation by discovering regularly occurring

device usage patterns. In Proc. of the Third IEEE

Intern. Conf. on Data Mining, ICDM ’03, pages 537–

540, Washington, DC, USA. IEEE Computer Society.

Kang, Z., Jin, M., and Spanos, C. J. (2014). Modeling

of end-use energy proﬁle: An appliance-data-driven

stochastic approach. In The 40th Annual Conf. of the

IEEE Industrial Electronics Society, Dallas, TX, USA,

pages 5382–5388.

Kelly, J. and Knottenbelt, W. (2015). The UK-DALE

dataset, domestic appliance-level electricity demand

and whole-house demand from ﬁve UK homes. Sci.

Data, (2):150007.

Kim, H., Marwah, M., Arlitt, M., Lyon, G., and Han, J.

(2011). Unsupervised Disaggregation of Low Fre-

quency Power Measurements. In Proceedings of the

2011 SIAM, pages 747–758.

Kolter, Z. and Johnson, M. J. (2011). REDD: A public data

set for energy disaggregation research. In Proc. of

SustKDD.

Lachut, D., Banerjee, N., and Rollins, S. (2014). Predictabil-

ity of energy use in homes. In IGCC, pages 1–10.

Lee, S., Ryu, G., Chon, Y., Ha, R., and Cha, H. (2013).

Automatic standby power management using usage

proﬁling and prediction. IEEE Transactions on Human-

Machine Systems, 43(6):535–546.

Makonin, S., Ellert, B., Bajic, I. V., and Popowich, F. (2016).

Electricity, water, and natural gas consumption of a res-

idential house in Canada from 2012 to 2014. Scientiﬁc

Data, 3(160037):1–12.

Makonin, S. and Popowich, F. (2015). Nonintrusive load

monitoring (NILM) performance evaluation. Energy

Efﬁciency, 8(4):809–814.

Mohsenian-Rad, A.-H. and Leon-Garcia, A. (2010). Optimal

residential load control with price prediction in real-

time electricity pricing environments. IEEE Trans.

Smart Grid, 1(2):120–133.

Monacchi, A., Egarter, D., Elmenreich, W., D’Alessandro,

S., and Tonello, A. M. (2014). GREEND: An energy

consumption dataset of households in Italy and Austria.

In IEEE Int. Conf. SmartGridComm, pages 511–516.

Parzen, E. (1962). On Estimation of a Probability Den-

sity Function and Mode. The Annals of Mathematical

Statistics, 33(3):1065–1076.

Pecan Street Inc. (2014). Dataport.

https://dataport.pecanstreet.org/.

Powers, D. M. W. (2011). Evaluation: From Precision,

Recall and F-Measure to ROC, Informedness, Marked-

ness & Correlation. Journal of Machine Learning

Technologies, 2(1):37–63.

S.a. (2005a). Beneﬁts of demand response in electricity

markets and recommendations for archiving them. U.S.

Department of Energy.

S.a. (2005b). Demand response program evaluation - Final

report. Quantum Consulting Inc. and Summit Blue

Consulting, LLC Working Group 2 Measurement and

Evaluation Committee, California Edison Company.

Schleich, J. and Klobasa, M. (2013). How much shift in

demand? Findings from a ﬁeld experiment in Ger-

many. In Lindström, T., editor, Rethink, renew, restart.

ECEEE 2013 Summer Study. Proc., pages 1919–1925.

European Council for an Energy-Efﬁcient Economy.

Stephen, B., Galloway, S., and Burt, G. (2014). Self-learning

load characteristic models for smart appliances. IEEE

Transactions on Smart Grid, 5(5):2432–2439.

Truong, N. C., McInerney, J., Tran-Thanh, L., Costanza,

E., and Ramchurn, S. D. (2013a). Forecasting multi-

appliance usage for smart home energy management.

In Proc. of the Twenty-Third Int. Joint Conf. on Artiﬁ-

cial Intelligence (IJCAI), pages 2908–2914. AAAI.

Truong, N. C., Tran-Thanh, L., Costanza, E., and Ramchurn,

S. D. (2013b). Towards appliance usage prediction

for home energy management. In Proc. of the Fourth

Intern. Conf. on Future Energy Systems, e-Energy ’13,

pages 287–288, New York, NY, USA. ACM.

Uttama Nambi, A. S., Reyes Lua, A., and Prasad, V. R.

(2015). LocED: Location-aware Energy Disaggrega-

tion Framework. In Proc. of the 2nd ACM Int. Conf.

on Embedded Systems for Energy-Efﬁcient Built Envi-

ronments, BuildSys, pages 45–54, New York, USA.

Valverde-Albacete, F. J. and Peláez-Moreno, C. (2014).

100% Classiﬁcation Accuracy Considered Harmful:

The Normalized Information Transfer Factor Explains

the Accuracy Paradox. PLOS ONE, 9(1):1–10.

Viswanath, S. K., Yuen, C., Tushar, W., Li, W. T., Wen, C. K.,

Hu, K., Chen, C., and Liu, X. (2016). System Design

of Internet-of-Things for Residential Smart Grid. IEEE

Wireless Communications, 23(5):90–98.

Zhu, X. and Davidson, I. (2007). Knowledge Discovery and

Data Mining: Challenges and Realities. Information

Science Reference, Hershey, New York.

SMARTGREENS 2017 - 6th International Conference on Smart Cities and Green ICT Systems

150