Initial Results of a Method for the Generation of Triangle Meshes

Representing Bone Fragments using a Spatial Decomposition

F´elix Paulano-Godino and Juan J. Jim´enez-Delgado

Department of Computer Science, University of Ja´en, Campus Las Lagunillas s/n, Ja´en, Spain

Keywords:

Bone Fragments, 3D Reconstruction, Spatial Decomposition, Triangle Mesh.

Abstract:

The generation of a virtual representation of the bones and fragments is an artiﬁcial step required in order

to obtain helpful models to work with in a simulation. Nowadays, the Marching Cubes algorithm is a de

facto standard for the generation of geometric models from medical images. However, bone fragments models

generated by Marching Cubes are huge and contain many unconnected geometric elements inside the bone

due to the trabecular tissue. The development of new methods to generate geometrically simple 3D models

from CT image stacks that preserve the original information extracted from them would be of great interest.

In order to achieve that, a preliminary study for the development of a new method to generate triangle meshes

from segmented medical images is presented. The method does not modify the points extracted from CT

images, and avoid generating triangles inside the bone. The aim of this initial study is to analyse if a spatial

decomposition may help in the process of generating a triangle mesh by using a divide-and-conquer approach.

The method is under development and therefore this paper only presents some initial results and exposes the

detected issues to be improved.

1 INTRODUCTION AND

BACKGROUND

Computer-assisted fracture reduction procedures usu-

ally require the generation of 3D models represent-

ing bone fragments. Although the generated models

could be point clouds or volumes, most of the times

these models are meshes, since computer-assisted

techniques require geometric algorithms (Jim´enez

et al., 2016). In particular, interactive environments

usually require triangle meshes in order to apply col-

lision detection strategies. Computed Tomography

(CT) is the most appropriate and accessible data ac-

quisition techniquefor distinguishing bone from other

tissues and thus, for generating 3D bone fragment

models (Egol et al., 2010). This type of image stores

at each pixel the radio-density obtained during the CT

scan as intensity values in the image. The morphol-

ogy of bone fragments makes the generation of trian-

gle meshes difﬁcult, since the shape of the segmented

regions is very irregular because trabecular tissue ap-

pears in the outer part of the bone fragment due to

the fracture. These features inﬂuence the choice of a

method for generating meshes.

Nowadays, the Marching Cubes (MC) algorithm

(Lorensen and Cline, 1987) is a de facto standard for

slice i

slice i+1

Figure 1: Simpliﬁed representation of the case in which

contours from two consecutive slices do not have a one-to-

one correspondence. Left, zoomed area showing the difﬁ-

culty of deciding which points should be sewed together in

3D.

generating triangle meshes representing bone frag-

ments to be used in computer-assisted procedures

(Jim´enez et al., 2016). The MC algorithm has been

utilized to generate meshes that represent acetabu-

lar fractures (Fornaro et al., 2008)(Fornaro et al.,

2010a), fractured pelvic bones (Fornaro et al., 2010b)

(Lee et al., 2012) and proximal humerus fractures

(F¨urnstahl et al., 2012). This algorithm has also been

used to generate fragment models to represent highly

fragmented bone fractures (Willis et al., 2007) and

to provide models for a virtual orthopaedic surgery

simulator (Tsai et al., 2001). The size of the models

generated by these methods depends on the resolution

of the medical images and the complexity of the seg-

mented bone structures; hence models generated by

MC are usually huge and contain unconnected geom-

298

Paulano-Godino F. and JimÃl’nez-Delgado J.

Initial Results of a Method for the Generation of Triangle Meshes Representing Bone Fragments using a Spatial Decomposition.

DOI: 10.5220/0006266302980305

In Proceedings of the 12th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2017), pages 298-305

ISBN: 978-989-758-224-0

etry inside the bone due to the morphology of trabec-

ular tissue (Paulano et al., 2015). Therefore, gener-

ated meshes commonly need to be post-processed to

improve their features. An alternative approach con-

sists of generating a 3D model by triangulating ex-

ternal contours of the bone fragments extracted from

medical images. However, this approach involves the

resolution of some complex problems, such us decid-

ing which points should be sewn together in 3D, or

managing sewing when the contours are subdivided

in consecutive slices (Figure 1). The use of spatial de-

compositions (Samet, 2010) allows dividing the point

cloud into small sets of points, reducingthe mesh gen-

eration problem to smaller sub-problems.

In this paper, an initial study for the development

of an alternative method to generate triangle meshes

from medical images using a spatial decomposition

is presented. In this study, we decided to use a spa-

tial decomposition named tetra-tree (Jim´enez et al.,

2006), since conducted studies demonstrated that it

presents several advantages for interactive environ-

ments with regards to other data structures based on

rectangular cells such as the octree (Chen and Huang,

1988). Mainly, the tetra-tree makes the selection of

related triangles easier, being able to select inacces-

sible parts without the use of complementary algo-

rithms (Jim´enez et al., 2011). Section 2 describes the

main stages of the proposed method. Then Section

3 discusses the main advantages of using a tetra-tree

to generate triangle meshes and analyses the issues to

improve in the proposed method.

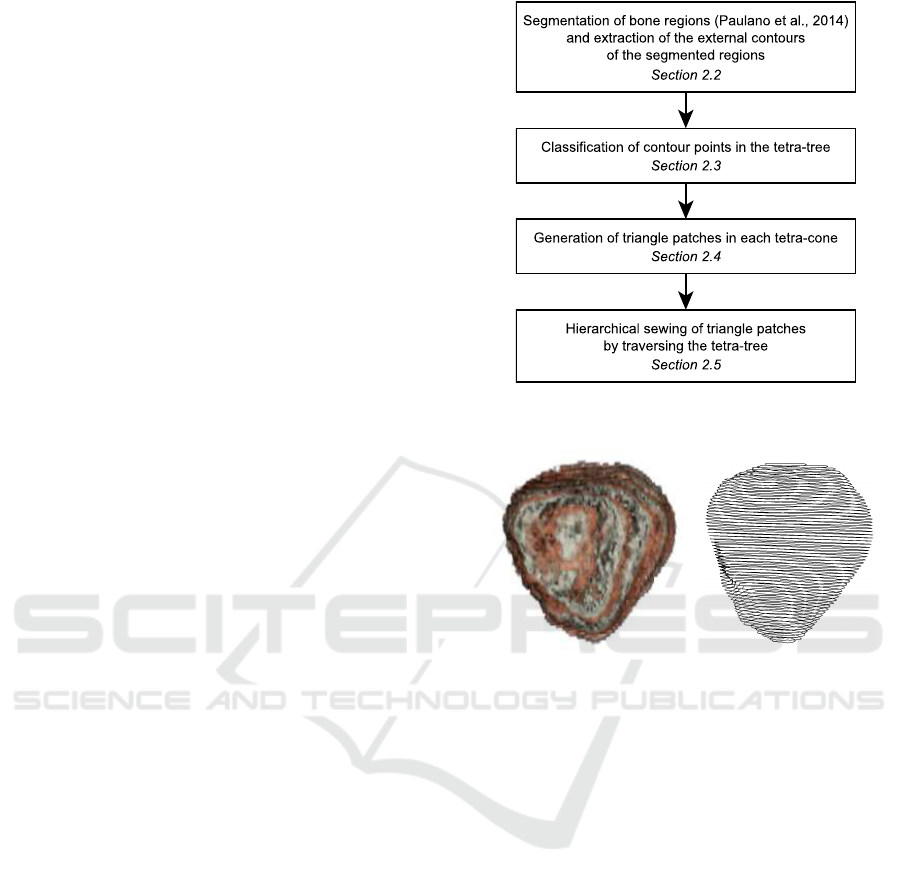
2 PROPOSED METHOD

2.1 Overview

The ﬁrst stage of the proposed mesh generation

method consists of extracting contour points from

medical images. Then, a spatial decomposition

named tetra-tree (Jim´enez et al., 2006) recursively di-

vides the space into tetrahedra with a shared origin

named tetra-cones, so that these tetra-cones cover the

whole space without overlapping. As the tetra-tree

is built, the contour points are classiﬁed in the tetra-

cones. After that, triangle patches are generated using

the points classiﬁed in each tetra-cone. Finally, tri-

angle patches are hierarchically sewn in order to ob-

tain the reconstructed model. Figure 2 summarizes

the stages of the proposed method.

With the aim of easing the understanding of the

proposed algorithms, a simple model representing a

patella (Figure 3) will be used to exemplify the pro-

cess in the following subsections.

Figure 2: Overview of the proposed mesh generation

method.

Figure 3: Left, volume visualization of a patella segmented

from CT images. Right, external contours extracted from

the segmentation results.

2.2 Segmentation and Extraction of

External Contours

The input of our mesh generation method is a point

cloud representing the outer part of bone fragments.

These point clouds must be extracted from the infor-

mation available in medical images.

In a ﬁrst step, all the bone fragments are seg-

mented from CT scans. For that purpose, the segmen-

tation algorithm described in (Paulano et al., 2014)

is used. The algorithm generates a region for each

bone fragment in each slice (Figure 3, left). Unlike

other approaches, this algorithm is able to separate

wrongly joined bone fragments during the segmenta-

tion process. Then the external contour of each seg-

mented region is extracted. With that aim, an ap-

proach similar to the proposed in (Pulido et al., 2014)

is applied. First, the Marching Squares algorithm is

utilized in order to generate contours from the seg-

mented regions (Ho et al., 2005). This algorithm can

be considered as a 2D adaptation of MC. The algo-

Initial Results of a Method for the Generation of Triangle Meshes Representing Bone Fragments using a Spatial Decomposition

299

Figure 4: Left, a tetra-tree associated to the contour points.

Right, points belonging to each tetra-cone are shown in a

different colour.

rithm does not ensure that the generated contours are

closed, but this is not relevant in this case since the

ﬁnal goal is to generate point clouds. Due to the noise

present in the regions because of trabecular tissue, in-

ner contours may be obtained. These inner contours

are removed using the point-in-polygon algorithm by

Feito and Torres (Feito and Torres, 1997); hence only

the outer contour of each fragment is extracted in each

slice. After removing internal contours, the vertices

of each external contour are grouped in order to form

the point cloud used as input by the mesh generation

algorithm (Figure 3, right).

2.3 Classiﬁcation in the Spatial

Decomposition

A tetra-tree (Jim´enez et al., 2006) is a spatial decom-

position technique that recursively divides the space

into tetra-cones with a common origin, so that these

tetra-cones cover the entire space without overlapping

among them (Figure 5, left). As the tetra-tree is built,

the points are classiﬁed in the generated tetra-cones

(Figure 4, right). Then the tetra-tree is adapted in or-

der to ﬁt the classiﬁed geometric elements. For that

purpose, the enveloping tetrahedron associated with

each tetra-cone is calculated. The enveloping tetrahe-

dron of a given tetra-cone is the smallest tetrahedron

that shares the origin and the lateral faces with that

tetra-cone, and contains all the points that are classi-

ﬁed into it (see Figure 5, right). Since a tetra-cone

is deﬁned by three planes that intersect in a point,

the top cover of each tetrahedron is a triangle. This

top cover is perpendicular to the segment that goes

from the centroid of the model to its incircle. The dis-

tance from the centroid of the model to the top cover

is established by the point classiﬁed in the tetra-cone

which is furthest to the centroid. Figure 4 (left) shows

an adapted tetra-tree associated with the point cloud

representing the patella.

Figure 5: Left, a representation of the subdivision of a tetra-

cone. Right, a schema that represents the bounding tetra-

hedra associated with a tetra-cone (Jim´enez and Segura,

2008).

2.4 Generation of Patches

The classiﬁcation of all the contour points in the tetra-

tree enables the execution of a divide-and-conquerap-

proach, so that the points classiﬁed in each tetra-cone

are triangulated in order to generate patches. Nev-

ertheless, not all the points classiﬁed in a tetra-cone

must be triangulated together. In order to avoid gen-

erating incorrect triangles, the points are clustered be-

fore being triangulated. A Euclidean cluster extrac-

tion algorithm has been used to group the points that

must be triangulated together. With this algorithm,

the points are grouped whenever they can be con-

nected by points closer than a pre-deﬁned threshold.

In the case of the patella that we use as example, only

one cluster is generated for each tetra-cone.

Once the clusters have been generated, the points

belonging to each cluster are used to generate patches.

The proposed method triangulates points belonging

to consecutive contours. In order to perform the tri-

angulation, the connectivity information of the con-

tours is used. First, the contour points are sorted and

grouped by slices. Then the contours of each slice are

divided into connected polylines. After that, the poly-

lines belonging to consecutive slices are triangulated.

Depending on the number of polylines in which each

contour has been divided, three different triangula-

tion cases are considered: one-to-one, one-to-two and

two-to-two. Any other case is discarded and thus not

triangulated during this stage of the algorithm. De-

pending on each case, a different triangulation algo-

rithm is applied.

2.4.1 One-to-One Triangulation

The easiest case occurs when both contours are com-

posed by only one polyline. In this case new trian-

gles are generated, minimizing the number of trian-

gles with large sides and small angles. Given the ﬁrst

two points of each polyline A

, A

, B

, the algo-

rithm ﬁrst computes the distance from A

to B

and

the distance from B

to A

. The smaller of these two

GRAPP 2017 - International Conference on Computer Graphics Theory and Applications

300

n-1

Figure 6: Top, example of a one-to-one triangulation of

polylines using the proposed algorithm. Bottom, obtained

triangles.

distances deﬁnes the segment which is used to gen-

erate the triangle. In Figure 6, the red coloured trian-

gle A

is discarded since the distance between B

and A

is bigger than the distance from A

to B

. This

step is repeated until all the points belonging to one of

the polylines have been triangulated. Finally, the last

point of the already sewn polyline is used to gener-

ate triangles with the remaining points of the opposite

polyline. Considering that all the points of B have

been triangulated and A

is the next point in A to be

triangulated, the algorithm tries to generate new tri-

angles until the distance from A

to B

is greater than

twice the average distance between A and B. This

constraint provides a better triangle distribution and

avoids degenerated triangles. In Figure 6, the purple

coloured triangle A

n−1

is discarded because the

distance from B

to A

is bigger than twice the aver-

age distance between A and B.

2.4.2 One-to-Two Triangulation

If one of the contours is composed by two sub-

polylines - A and B -, these must be sorted before

being sewn. Then the sub-polylines are sequentially

sewn to the polyline C of the opposite contour. Since

the two sub-polylines are sewn using the same pro-

cess, the algorithm to sew a single sub-polyline A to

a polyline C is explained for simplicity. Firstly, the

polyline point C

closest to the ﬁrst point of A is cal-

culated. In Figure 7, the closest point to A

is coloured

in purple. After that, the one-to-one algorithm is ap-

plied but starting from the closest point previously

calculated. Using that algorithm, new triangles are

generated until all the points of A have been triangu-

lated. Then the last point of A is used to generate

new triangles. The main difﬁculty consists of decid-

ing when to stop sewing a sub-polyline and to start

the next one. Being C

the next point of the polyline

to be triangulated, the algorithm stops sewing the sub-

polyline A when the distance from the last point of A

to C

is greater than twice the average distance be-

tween A and C and it is also bigger than the distance

from the ﬁrst point of B to C

. As in the one-to-one

case, these constraints provide a better triangle distri-

bution and avoid degenerate triangles. Once the ﬁrst

sub-polyline A has been sewn, the same procedure is

repeated for the second sub-polyline B. In Figure 7,

the closest point to B

is coloured in blue. Being C

the next point of C to be triangulated, in this case

new triangles are generated until the distance from

the last point of B to C

is larger than twice the av-

erage distance between B and C or all the points have

been triangulated. In Figure 7, the red coloured trian-

gle C

l−1

is discarded because the distance from

to C

is bigger than twice the average distance be-

tween B and C.

Closest

point to A

Closest

point to B

Figure 7: Top, example of a one-to-two triangulation of

polylines using the proposed algorithm. Bottom, obtained

triangles.

2.4.3 Two-to-Two Triangulation

The two-to-two case requires deciding which sub-

polylines haveto be sewn together. Two sub-polylines

are sewn if the average distance between them is less

than a pre-deﬁned threshold. This value is manually

set and mainly depends on the distance between slices

in the source medical images. The order in which the

sub-polylines are sewn is also determined by the dis-

tance between them. Firstly, the system tries to sew

together the two closest sub-polylines, and then the

two remaining sub-polylines. In both cases, the one-

to-one algorithm (Figure 6) is used in order to sew the

two sub-polylines.

The triangulation algorithm described above must

be repeated in order to generate patches for each clus-

ter. Figure 8 shows the triangle patches generated by

the triangulation algorithm in the case of the patella.

2.5 Sewing Triangle Patches

The triangulation algorithm generates one or more tri-

angle patches for each tetra-cone. In order to close the

mesh, these patches need to be sewn together. For that

purpose, the tetra-tree hierarchy is traversed in post-

order. For each node of the hierarchy, the patches

stored in its 4 children nodes that are closer than a

Initial Results of a Method for the Generation of Triangle Meshes Representing Bone Fragments using a Spatial Decomposition

301

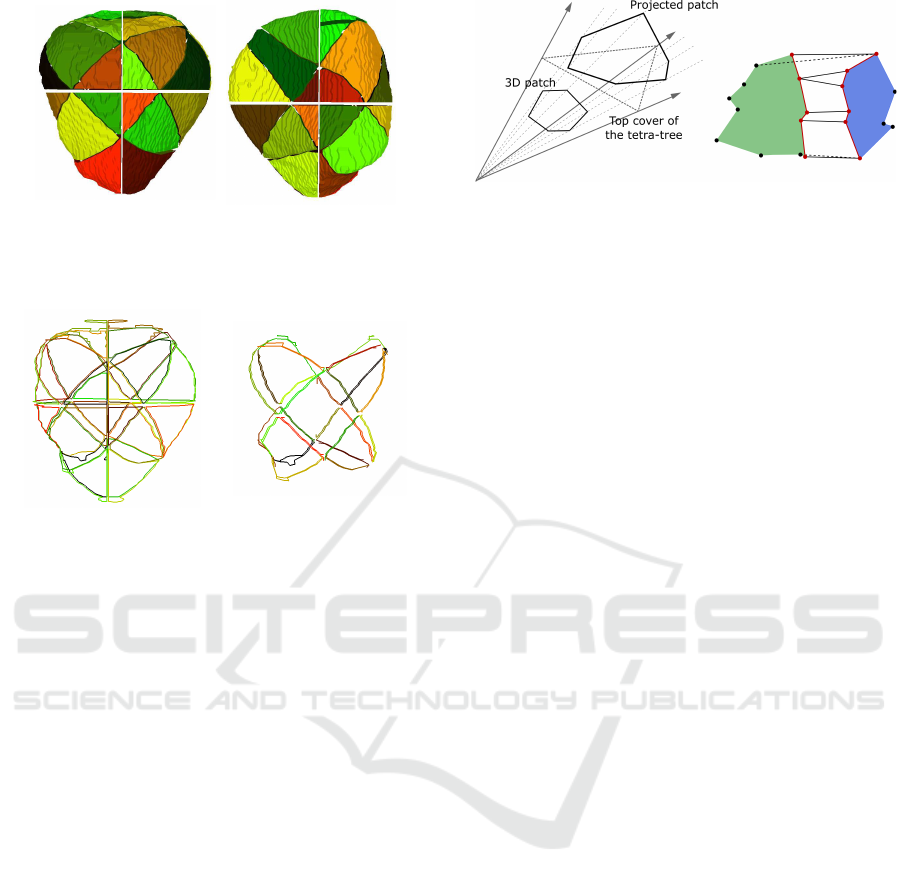
Figure 8: From left to right: front and back views of the

triangle patches generated by applying the triangulation al-

gorithm to each cluster in the leaf nodes of the hierarchy.

Each patch is displayed in a different colour.

Figure 9: Left, external contours of the triangle patches gen-

erated in each leaf tetra-cone. The external contour of each

patch is displayed in a different colour. Right, pairs of poly-

lines that are triangulated together in the last level of the

tetra-tree. Each pair is displayed in the same colour.

previously deﬁned threshold are sewn. As occurs in

the patch generation algorithm, this threshold value is

manually chosen and depends on the point distribu-

tion, and thus on the distance between slices and the

resolution of the source medical images. The order in

which the patches are sewn is deﬁned by the distance

between patches and closer patches have priority.

The algorithm proposed to sew two patch contours

starts with the identiﬁcation of the points to be sewn.

For that purpose, the external edges of each patch are

calculated (Figure 9, left) as the edges that only be-

long to one triangle. Then these edges are projected

onto the plane deﬁned by the top cover of the tetra-

cone containing them. In order to avoid overlapping

of the projection of the two patches, the patches are

separated by the displacing them the distance between

the centroids of both patches, in the direction deﬁned

by both centroids. In 2D, the edges to be sewn are

deﬁned as those whose points can be connected to a

point belongingto the other patch without intersecting

any of the two patches (Figure 10). Figure 9 (right)

shows the polylines to be sewn between every two

patches in the last level of the tetra-tree for the case of

the patella. Finally, new triangles are generated using

the one-to-one method to sew two polylines already

described in Section 2.4.

This sewing procedure is repeated in each node of

Figure 10: Left, schema that represents the linear projec-

tion of the external contours of a triangle patch onto the

plane deﬁned by the top cover of its associated tetra-cone.

Right, schema representing the selection of the edges to be

sewn between two patches. Solid lines connect points of

edges that belong to the group of edges to be sewn group

since they do not intersect with any patch. Dotted lines in-

tersect with the patch, and therefore their associated edges

are discarded.

the hierarchy. Once all the nodes of a level have been

processed, the generated patches are transferred to the

parent node and the sewing algorithm is repeated at

the upper level. The process is repeated until reach-

ing the root node of the tetra-tree. The top image of

Figure 11 shows the patches generated in each of the

tetra-cones belonging to the top level of the tetra-tree.

At the top level, the parent node receives the

patches generated in its eight children nodes. These

patches have to be sewn together in order to close the

mesh. In this step of the algorithm, patches are sewn

two by two in a sequential process. Figure 11 sum-

marizes the three stages of this process.

At the ﬁrst two stages of the process (Figure 11,

top and middle), the criteria used to select the points

to be sewn is that each point must be sewn to its clos-

est patch. Given a pair of patches, P

and P

, the

points to be sewn in P

are those whose closest patch

is P

. The points to be sewn in P

are calculated us-

ing the same procedure. Then patches are sewn using

the one-to-one algorithm previously described to sew

polylines. Due to the holes associated with the ﬁrst

and the last slices of the stack, two sub-polylines may

be obtained when calculating the edges to be sewn in

some cases. To deal with the sewing in these cases,

the two-to-two algorithm is applied.

At the last stage of the process (Figure 11, bot-

tom), only two patches are remaining. At this stage,

all the external edges of both patches belong to the

polylines to be sewn, and therefore, the algorithm

to extract external contours is applied to get them.

Since the polylines representing the external contours

are closed, the one-to-one sewing algorithm requires

being adapted to properly join the two patches. As

mentioned above, the generated model contains two

holes associated with the contours in the ﬁrst and the

last slices of the stack. Nevertheless, these two holes

GRAPP 2017 - International Conference on Computer Graphics Theory and Applications

302

Patches

External edges

Polylines

to be sewn

Stage 1

Stage 2Stage 3

Figure 11: Left, triangle patches received as input in each of the three stages carried out at the top level of the tetra-tree.

Centre, external edges of those patches. Right, calculated polylines to be sewn at each of the three stages.

Figure 12: Front and back views of a mesh generated using

the proposed procedure in the case of the patella.

do not affect to the application of the algorithm, and

can be ﬁlled at the end. Figure 12 shows the results

obtained by applying the method in the case of the

patella.

3 DISCUSSION AND

CONCLUSIONS

In this paper, a preliminary study for the develop-

ment of a new method to generate triangle meshes

representing bone fragments from medical images has

been presented. This method uses a spatial decom-

position to implement a divide-and-conquer approach

that allows simplifying the problems that arise when

triangulating the contours extracted from consecutive

slices. Since the presented method is under develop-

ment, only initial results have been shown. Next para-

graphs discuss the main advantages of using a tetra-

tree instead of other spatial decompositions, as well as

the main aspects that should be improved in order to

apply the proposed method in the generation of more

complex bone fragment models.

The use of a tetra-tree provides additional prop-

erties to the generated model that encourage its uti-

Initial Results of a Method for the Generation of Triangle Meshes Representing Bone Fragments using a Spatial Decomposition

303

lization in interactive environments (Jim´enez et al.,

2011). This spatial decomposition enables the visu-

alization of the triangles that either take part or are

close to taking part in an interaction, enabling the ac-

cessibility to far or non-visible parts of the generated

model without having to use additional algorithms

such as ray-triangle or ray-box intersection tests. Ad-

ditionally, the tetra-tree provides a smooth transition

when changing the level of detail during interaction.

In contrast to other widely used spatial decomposi-

tions like the octree (Chen and Huang, 1988), the

tetra-tree is object-centred; hence the classiﬁcation of

the geometry is invariant to rotations. Moreover, the

construction cost is lower and the interaction times

are faster than using an octree (Jim´enez et al., 2011).

Although the developed algorithm produces

promising results in the generation of bone fragment

models, some cases in which the algorithm does not

perform well have been detected. Firstly, the classiﬁ-

cation of points in the tetra-tree is not always optimal,

and hinders the generation of patches in the more ir-

regular areas, especially in the case of long bones. In

addition, the classiﬁcation of points often generates

triangulation cases that cannot be solved using the al-

gorithms described in Section 2.4. Finally, in the case

of models with several concavities, the linear projec-

tion proposed in Section 2.5 in order to ﬁnd the edges

to be triangulated for sewing two patches may not be

the best option.

Regarding the classiﬁcation of the point cloud, the

tetra-tree does not provide a homogeneous classiﬁca-

tion of the points in the case of long bone fractures. In

these cases, the more detailed area, which is usually

the fracture zone, is located at the ends of each bone

fragment; hence the tetra-tree should be further sub-

divided in those areas. The research of a new spatial

decomposition that ﬁts better the shape of any bone

fragment would be proﬁtable. For that purpose, the

new spatial decomposition could use additional infor-

mation such as the intensity value or the estimated

curvature at each point.

During the generation of patches from contours,

we detected that two special triangulation cases are

not resolved. On the one hand, some isolated points

can be classiﬁed into one tetra-cone because of the

location of the centroid and the orientation of the

tetra-tree. These points divide polylines into two sub-

polylines, and thus a hole is obtained duringtriangula-

tion. Furthermore, isolated points may cause that the

triangulation algorithm described in Section 2.4 gen-

erates incorrect triangles. In order to solve this case,

two different approaches could be used: developing a

new triangulation algorithm that is not affectedby iso-

lated points, or reclassifying the points of the affected

tetra-cone avoiding isolated points.

On the other hand, a closed small contour can be

completely classiﬁed in a single tetra-cone. There-

fore, that closed contour must be triangulated with the

polyline extracted from the next slice. The one-to-

one triangulation algorithm described in Section 2.4

is not able to properly generate triangles in that case.

To address this case, two different strategies could

be utilized: reclassifying the points in the tetra-tree

avoiding the classiﬁcation of entire contours in a sin-

gle tetra-cone, or developing a new triangulation al-

gorithm with the purpose of dealing with this case.

Once patches havebeen generated in the leaf tetra-

cones, these are hierarchically sewn as described in

Section 2.5. In order to calculate the edges to be tri-

angulated, patches are linearly projected onto the top

plane of their associated tetra-cone. This projection

obtains good results in some of the testes cases. How-

ever, the linear projection of the patches onto the top

plane of the tetra-tree does not work well if the bone

fragments have various concavities, such as the case

of femoral condyles. In order to deal with these cases,

a different type of projection should be used.

In the future, new methods will be developed in

order to solve the special cases detected when sewing

consecutive contours. In addition, the method could

be extended to work with alternative spatial decompo-

sitions that ﬁt better the shape of any bone fragment.

For that purpose, these spatial decompositions could

use not only the position of the points, but also the

intensity and the estimated curvature at each point, in

order to adjust them better to the bone fragment in the

more detailed areas like the fracture zone. Finally, a

new strategy to correctly calculate edges to be sewn

when a linear projection does not perform well will

be developed

ACKNOWLEDGEMENTS

This work has been partially supported by the Min-

isterio de Econom´ıa y Competitividad and the Euro-

pean Union (via ERDF funds) through the research

project DPI2015-65123-R.

REFERENCES

Chen, H. H. and Huang, T. S. (1988). A survey of construc-

tion and manipulation of octrees. Computer Vision,

Graphics, and Image Processing, 43(1):112–113.

Egol, K. A., Koval, K. J., and Zuckerman, J. D. (2010).

Handbook of Fractures. Lippincott Williams &

Wilkins.

GRAPP 2017 - International Conference on Computer Graphics Theory and Applications

304

Feito, F. R. and Torres, J. C. (1997). Inclusion test for gen-

eral polyhedra. Computers & Graphics, 21(1):23–30.

Fornaro, J., Harders, M., Keel, M., Marincek, B., Trentz,

O., Szekely, G., and Frauenfelder, T. (2008). Interac-

tive visuo-haptic surgical planning tool for pelvic and

acetabular fractures. Studies in health technology and

informatics, 132(Figure 1):123–5.

Fornaro, J., Keel, M., Harders, M., Marincek, B., Sz´ekely,

G., and Frauenfelder, T. (2010a). An interactive sur-

gical planning tool for acetabular fractures: initial re-

sults. Journal of orthopaedic surgery and research,

5(50):1–8.

Fornaro, J., Sz´ekely, G., and Harders, M. (2010b). Semi-

automatic segmentation of fractured pelvic bones for

surgical planning. Biomedical Simulation, 5958:82–

89.

F¨urnstahl, P., Sz´ekely, G., Gerber, C., Hodler, J., Snedeker,

J. G., and Harders, M. (2012). Computer assisted re-

construction of complex proximal humerus fractures

for preoperative planning. Medical image analysis,

16(3):704–20.

Ho, C.-c., Fu-che, W., Bing-yu, C., and Ouhyoung, M.

(2005). Cubical marching squares: Adaptive feature

preserving surface extraction from volume data. Com-

puter Graphics Forum, 24:2005.

Jim´enez, J. J., Feito, F. R., and Segura, R. J. (2011). Tetra-

trees properties in graphic interaction. Graphical

Models, 73(5):182–201.

Jim´enez, J. J., Feito, F. R., Segura, R. J., and Og´ayar,

C. J. (2006). Particle Oriented Collision Detection us-

ing Simplicial Coverings and Tetra-Trees. Computer

Graphics Forum, 25(1):53–68.

Jim´enez, J. J., Paulano, F., Pulido, R., and Jim´enez, J.

(2016). Computer assisted preoperative planning of

bone fracture reduction: simulation techniques and

new trends. Medical Image Analysis, 30:30–45.

Jim´enez, J. J. and Segura, R. J. (2008). Collision detection

between complex polyhedra. Computers & Graphics,

32(4):402–411.

Lee, P.-Y., Lai, J.-Y., Hu, Y.-S., Huang, C.-Y., Tsai, Y.-

C., and Ueng, W.-D. (2012). Virtual 3D planning

of pelvic fracture reduction and implant placement.

Biomedical Engineering: Applications, Basis and

Communications, 24(03):245–262.

Lorensen, W. E. and Cline, H. E. (1987). Marching cubes:

A high resolution 3D surface construction algorithm.

ACM Siggraph Computer Graphics, 21(4):163–169.

Paulano, F., Jim´enez, J. J., and Jim´enez, J. (2015). Sur-

face reconstruction of bone fragments: A comparative

study. In Tavares, J. M. R. S. and Jorge, R. N., editors,

Computational Vision and Medical Image Processing

V, chapter 51, pages 321–326. CRC Press.

Paulano, F., Jim´enez, J. J., and Pulido, R. (2014). 3D seg-

mentation and labeling of fractured bone from CT im-

ages. The Visual Computer, 30(6-8):939–948.

Pulido, R., Paulano, F., and Jim´enez, J. J. (2014). Recon-

struction & Interaction with3D Simpliﬁed Bone Mod-

els. In WSCG 2014 Communication Papers Proceed-

ings, pages 321–327.

Samet, H. (2010). Sorting in space: multidimensional, spa-

tial, and metric data structures for computer graph-

ics applications. In SA ’10 ACM SIGGRAPH ASIA

2010 Courses, pages 1–52, Seoul, Republic of Korea.

ACM.

Tsai, M.-D., Hsieh, M.-S., and Jou, S.-B. (2001). Virtual

reality orthopedic surgery simulator. Computers in Bi-

ology and Medicine, 31(5):333–351.

Willis, A., Anderson, D., Thomas, T., Brown, T., and

Marsh, J. L. (2007). 3D reconstruction of highly frag-

mented bone fractures. In Medical Imaging 2007: Im-

age Processing. Proceedings of the SPIE, page 65121.

Initial Results of a Method for the Generation of Triangle Meshes Representing Bone Fragments using a Spatial Decomposition

305