3D Human Shapes Correspondence using the Principal Curvature Fields

on a Local Surface Parametrization

Ilhem Sboui, Majdi Jribi and Faouzi Ghorbel

CRISTAL Laboratory, GRIFT Research Group, National School of Computer Sciences, La Manouba University,

La Mannouba, Tunisia

ilhem.sboui@gmail.com, majdi.jribi@ensi.rnu.tn, faouzi.ghorbel@ensi.rnu.tn

Keywords:

3D Human Shapes, Correspondence, Darcyan Coordinates System, Principal Curvatures, Symmetry.

Abstract:

In this paper, we address the problem of the correspondence between 3D non-rigid human shapes. We propose

a local surface description around the 3D human body extremities. It is based on the mean of principal

curvature ﬁelds values on the intrinsic Darcyan parametrization constructed around these points. The similarity

between the resulting descriptors is, then, measured in the sense of the L

distance. Experiments on a several

human objects from the TOSCA dataset conﬁrm the accuracy of the proposed approach.

1 INTRODUCTION

Non-rigid three-dimensional shapes matching has

been an active research topic in computer vision over

the last years. It is a key task in many applications

such as space-time reconstruction, motion tracking

and recognition, shape retrieval and videos indexing.

The goal of non rigid shape matching is to ﬁnd a map

f : S → T between points on one surface S to their

equivalent points on a second surface T.

The problem of establishing a correspondence be-

tween non-rigid shapes remains challenging and par-

ticularly tough since the correspondence involves sur-

faces representing differentposes of an articulated ob-

jects and generally highly deformed surfaces.

In this context, several methods have been proposed

for ﬁnding a correspondence between non-rigid 3D

shapes in the state-of-the-art. A detailed survey on

3D shapes matching methods was proposed by (Van

Kaick et al., 2010). Two categories of 3D non-rigid

correspondence can be distinguished according to the

resolution of the matched points: sparse and dense.

Various approaches have addressed the sparse corre-

spondence which aims to map a small set of points on

a given surface. The most common ones consist on

extracting local shape descriptors at a set of feature

points. (Zhang et al., 2008) proposed a method which

is robust to the symmetry problem and consists on

deforming a given shape to have alignment between

feature points and then minimizing resulting distor-

tion. Later, (Zheng et al., 2013) proposed a shape de-

scriptor based on iso-lines of harmonic ﬁelds between

shape extremal points to establish a correspondence.

Then, they, demonstrated the effectivenessof their de-

scriptor to intrinsic reﬂectional symmetry. (Yaron and

Thomas, 2009) proposed a method for only nearly-

isometric surfaces using the Mobius transform. A de-

scriptor based on fuzzy geodesics to ﬁnd correspon-

dences between sparse sets of points on shapes differ-

ing by extreme deformations was presented by (Sun

et al., 2010). On the other hand, (Ovsjanikov et al.,

2010) proposed an approach which relies on match-

ing feature points in a space of a heat kernel for a

given point on a surface and then the correspondence

is obtained by searching the most similar heat kernel

maps . Moreover, (Yusuf Sahillio˘glu, 2014) proposed

an algorithm relying on the dynamic programming to

match shape extremities which was unable to com-

pletely alleviate the symmetrical ﬂip problem.

One of the alternatives centered around the notion of

minimum distortion correspondence is the method of

(Bronstein et al., 2006). They introduced the gener-

alized multidimensional scaling (GMDS) which al-

lows ﬁnding the minimum distortion embedding of

one surface onto another using an approximation to

the Gromov-Hausdorff distance.

Various prominent methods in the literature seek

to ﬁnd dense correspondence between 3D non-rigid

shapes. One of the notable approaches is proposed by

(Kim et al., 2011) consisting on combining multiple

low-dimensional intrinsic maps to produce a blended

map. They, then, associated conﬁdence and consis-

tency weights to each map and ﬁnd the best blending

to establish a ﬁnal correspondence. An other alterna-

tive, introduced also by (Bronstein et al., 2009) was

Sboui I., Jribi M. and Ghorbel F.

3D Human Shapes Correspondence using the Principal Curvature Fields on a Local Surface Parametrization.

DOI: 10.5220/0006266606310636

In Proceedings of the 12th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2017), pages 631-636

ISBN: 978-989-758-225-7

631

based on the diffusion distance instead of the geodesic

one in the GromovHausdorff framework. Some at-

tempts to ﬁnd dense correspondence based on embed-

ding the shapes onto a spectral domain like the ap-

proach of (Jiang et al., 2013) using a non-rigid vari-

ant of the ICP (Iterative Closest Point) algorithm and

(Aalo et al., 2013) who proposed a spectral formu-

lation for the generalized multidimensional scaling

method denoted as spectral GMDS.

Within this context, (Taylor et al., 2012) focused on

matching human shapes in various poses using an ef-

ﬁcient learned regression function for the articulated

shapes correspondences.

Very recently, (Wei et al., 2015) developeda newdeep

learning approach using a convolutional neural net-

work architecture for ﬁnding dense correspondences

between human bodies.

In this paper, we propose a novel approach to ﬁnd a

sparse correspondence between deformed shapes of

type 3D human body. Our proposal consists on an

intrinsic local description of the human surfaces ex-

tremities. It is based on the construction of a lo-

cal discrete representation known by Darcyan Coor-

dinates System. Then, principal curvatures ﬁeld are

computed for each discrete representation around the

extracted extremities. Matched points are obtained by

measuring the similarity between their correspondent

local representations in the sense of the L

distance.

Thus, this paper will be structured as follows: In the

second section, we describe the proposed descriptor

construction process. For the next section, we repre-

sent our 3D human bodies correspondence approach.

The fourth section is devoted to the experimental re-

sults on 3D human objects from the TOSCA dataset

and our proposed solution to handle the problem of

the symmetry.

2 HUMAN SHAPES

CORRESPONDENCE

We intend to establish a sparse correspondence be-

tween 3D human body objects with different non rigid

deformations. We propose to make a correspondence

between these shapes extremities since they give a

good description of human body structure. The pro-

posed approach is based on an intrinsic description

of the extreme points neighborhood using the darcyan

representation and the principal curvature ﬁeld. We

present, in this section, all the steps of the construc-

tion of the novel local description around the extrem-

ities points.

2.1 Extremities Extraction

In this section, we intend to extract extremities over

the human body shapes applying the robust approach

proposed by (Julien et al., 2006) which results a set

of interest points invariant to the human pose. This

approach is described below:

Let x

and x

be the farthest vertices on a surface mesh

M in the sense of the geodesic distance. We denote by

dist

(x, y) the geodesic distance between x and y two

vertices on M.

We consider g

and g

two scalar functions associated

to each vertex x of M. g

and g

are deﬁned as follow:

= g

dist

(x, x

) and g

= g

dist

(x, x

)

We denote by E

and E

the sets of the local extrema

of, respectively, g

and g

. The set of extremities,

denoted by E, is deﬁned by the intersection of E

and

E = E

Figure 1 illustrates the resulting extreme points on 3D

human surfaces.

Figure 1: 3D human shapes extremeties.

2.2 Darcyan Coordinates System

Representation

After the extraction of the extreme points, local de-

scription around these points must be performed in

order to ensure the good correspondence between dif-

ferent shapes. But, for the same 3D object, different

meshes may exist. In fact, each mesh depends on its

initial parametrization. For this reason, we propose

to use the well known Darcyan Coordinates System,

introduced by D’Arcy Thompson (Thompson, 1917).

Such parametrization is well adapted to our context

since it is constructed around a reference point.

Here, we, brieﬂy, recall the construction process of

the Darcyan representation.

This parametric representation materialized by coor-

dinates system relatively to a given point on a sur-

face is, in fact, obtained by the superposition of the

geodesic level curves around the reference point and

the radial lines coming from the same point.

Thus, let S be a two dimensional differential mani-

fold, and let consider U

the geodesic potential ﬁeld

VISAPP 2017 - International Conference on Computer Vision Theory and Applications

632

coming from a reference point r on S.

This function U

: S → R

computes for any point p

on S the length of the geodesic curve joining it to the

reference point r. This function is well deﬁned, since

a geodesic curve between two points of a 2D differ-

ential manifold exists (Cohen and Kimmel, 1997).

A geodesic level curve of value equal to λ around a

reference point r on the surface S can be formulated

as follows:

= {p ∈ S;U

(p) = λ} (1)

is materialized by the set of all points on S having

the same geodesic distance λ from r. Therefore, the

surface S can be approximately reconstructed by all

these geodesic level curves, so that, S ≈ ∪

We remind as well as the process of radial lines curves

construction from a reference point r of the surface S.

Like mentioned in (Gadacha and Ghorbel, 2013), the

radial curves represent a solution of the followingsys-

tem :







dP(t)

= −∇U

(P)

P(0) = r

dP(t)

t=0

= α

(2)

Where P(t) is the geodesic path emanating from r and

following the opposite gradient ∇ direction onU

. Ra-

dial lines curves, denoted by C

, are therefore gener-

ated according to the angular direction α which can

be arbitrary taken. Similar to geodesic level curves, a

reconstruction of the surface S can be approximated

by ∪

Here we deﬁne Darcyan representation D as the su-

perposition of both n geodesic level curves and m ra-

dials lines curves relatively to a given point r.

k,l

(r) =



λk

αl

, 1 ≤ k ≤ n, 1 ≤ l ≤ m



Figure 2 shows the steps of the Darcyan coordinate

system construction.

Figure 2: Darcyan system reconstruction: (a)-geodesic level

curves, (b)-Radial curves. (c) The superposition of both sys-

tem of curves.

Consequently, the Darcyan coordinates system is

obtained by the superposition of both these sets of

curves emanating from a reference point. We pro-

pose to extract the intersection points between these

two kinds of curves. The resulting discrete paramet-

ric points are ordered since each point is indexed by

the level of geodesic curve and the radial line it be-

longs to.

2.3 Principal Curvature Computation

Let S be a given surface. X : (u, v) ∈ D ⊂ R

→

(x(u, v), y(u, v), z(u, v)) ∈ S ⊂ R

is a parametric rep-

resentation of S.

At a point p = X(x

, x

) on S, let consider the tangent

plane according to the basis (u, v).

The normal vector to S at p is denoted by N(p) =

∧x

respecting a chosen orientation.

Thus, the curvature formulation is given using the fol-

lowing coefﬁcients:

E = x

, F = x

, G= x

, L = x

→

, M = x

→

and N = x

→

LN−M

EG−F

EN−2FM+GL

2(EG−F

)

E, F and G denote the ﬁrst fundamental coefﬁcients,

while L, M, N are the second ones.

and K

represent, respectively, the Gaussian cur-

vature and the Mean curvature p = X(x

, x

Therefore, the principal curvatures are deducted

from these formulations K

= k

max

min

and K

max

min

)

max

and k

min

deﬁne the principal maximal and mini-

mal curvatures respectively.

2.4 Darcyan Principal Curvature Fields

Descriptor

Relying on the Darcyan representation and the prin-

cipal curvature ﬁelds computation on this local

parametrization recalled above, we deﬁne a novel 3D

shape descriptor, based on intrinsic geometric prop-

erty, which is invariant under Euclidean motions.

We propose to compute the mean of both

principal maximal and minimal curvatures on the

intersection points of each geodesic level curve.

We denote

max

and k

min

the mean of, respec-

tively, k

max

and k

min

for the i

geodesic level

curve. Hence the novel descriptor is deﬁned by

max

, k

min

, .., k

max

, k

min

, ..., k

max

, k

min

1≤i≤m

. Here,

m indicates the number of geodesic level curves. The

proposed descriptor is illustrated in Figure 3.

Figure 3: Illustration of the proposed descriptor: (a) the

Darcyan representation construction around a reference

point, (b) the vector of curvature ﬁels computation and the

obtained intersection points(in red color).

3D Human Shapes Correspondence using the Principal Curvature Fields on a Local Surface Parametrization

633

Figure 4: 3D human shapes matching approach.

2.5 3D Human Shapes Extremities

Matching

In order to establish non-rigid correspondence be-

tween human surface objects, we compute the pro-

posed descriptor around each extreme point. The gen-

erated vectors consist on the mean of principal curva-

ture ﬁeld values over the parametric discrete points.

Thereafter, We search for the minimal distance L

be-

tween all the pairs of the resulting vectors to ﬁnd the

most similar ones.

The targeted matching is then acquired by ﬁnding the

similarity between the resulting descriptors. This pro-

cess is also illustrated in Figure 4.

3 EXPERIMENTATION

In this section, we present the experimental results in

order to test the effectiveness of our approach. We

have conducted the experiments on several 3D human

objects in different poses from the TOSCA database

(Bronstein and Bronstein, 2008) which contains 3D

objects undergoing non-rigid deformations.

We ﬁrst of all present the approximation of the pro-

posed description steps on the 3D meshes.

3.1 Approximation on 3D Meshes

A 3D object is assumed to be a 2D differential mani-

fold. In practice, it is materialized by a 3D mesh. It

is, therefore, necessary to approximate the proposed

approach on the 3D meshes. The computation of the

geodesic paths and distances on the triangle meshes

is achieved by the use of the Fast Marching algorithm

(Kimmel and Sethian, 1998). While for the principal

curvature computation, we rely on the algorithm of

(Meyer et al., 2002). Figure 5 illustrates the Darcyan

intrinsic parametric representation around the extrem-

ities of a 3D human body mesh.

Figure 5: Darcyan representation around a human body ex-

tremities from the TOSCA dataset.

VISAPP 2017 - International Conference on Computer Vision Theory and Applications

634

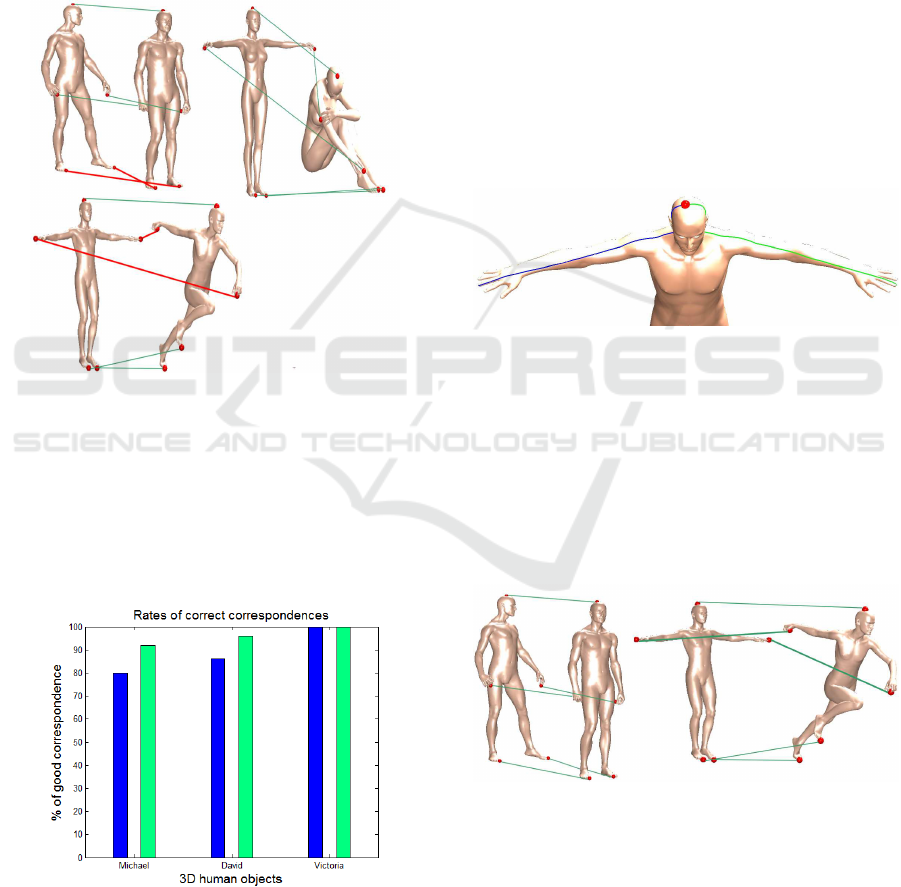
3.2 The Correspondence Results

We evaluate our matching approach on different hu-

man objects of the TOSCA database (David, Victoria

and Michael). We have chosen for each object the

same number of poses. After the normalization of

these shapes, we have extracted the extremities for

all these body shapes. We have, then, constructed

our proposed descriptor around these selected points.

Figure 6 shows some results of our correspondence

method.

Figure 6: Correspondence results for various human mod-

els from the TOSCA dataset, green lines indicate correct

matches.

The obtained correct correspondence percentages

range from 80% to 100% for the three human models

in the chosen poses. The bars colored in blue, in Fig-

ure 7, show the correct matching rates. We deem that

our approach seems to be able of handling 3D human

shapes with various poses.

Figure 7: The Correspondence rates for human models from

the TOSCA dataset, the blue and green colors indicate, re-

spectevely, the percentage of the correct matches and the

obtained ones allevating the problem of the symmetry.

The resulting correspondences show, in some

cases, a confusion in the human sides. Hence, a left

hand or a left foot may be matched to a right one of

another object. This confusion is due to the symmet-

ric structure of the human shape.

To alleviate the problem of the symmetry, we propose

to add another geometrical property that could distin-

guish the right part from the left one of the human

body. For this type of shapes, the top of the head is

the unique extreme point that has not a symmetrical

equivalent.

Thus, we propose to compute the sign of the angle

between the two vectors V

and V

: the vector V

a reference one. It corresponds to the tangent to the

geodesic curve at the top of the head and joining this

point to the tip of the noise. For the vector V

, it cor-

responds to the tangent at the top of the head to the

geodesic curve joining this last point and the other se-

lected extremities (Figure 8).

Figure 8: Geodesic curves joining the top of the head and

the hand extremities.

The computed angle for the right part of the hu-

man body has an opposite sign comparing with the

one of the left part. This process allows to raise

up the correspondence results as shown in Figure 9.

For the object David the percentage of correct corre-

spondence increases from 86% to 96% for the object

David and from 80% to 92% for the object Michael.

The green bars in Figure 7 show the new percentages.

Figure 9: Correspondence after the symmetry correction.

4 CONCLUSIONS

In this paper, we have proposed a novel approach to

establish the correspondencebetween 3D human bod-

ies undergoing non-rigid deformations. We have pre-

sented a novel intrinsic description based on a princi-

3D Human Shapes Correspondence using the Principal Curvature Fields on a Local Surface Parametrization

635

pal curvatures computation on a local parametrization

using the Darcyan coordinates system. We have also

proposed a solution for the problem of the symmetri-

cal extremities. The obtained results show the perfor-

mance of our proposed method for studying the 3D

human body matching.

In future works, we intend to achieve the optimal res-

olution of the local Darcyan representation by ﬁnd-

ing the suitable number of the geodesic levels and the

radial lines curves. We propose also to perform the

experimentation on others 3D human databases with

different properties and to test the robustness of the

intrinsic descriptor to the noise.

REFERENCES

Aalo, Y., Dubrovina, A., and Kimmel, R. (2013). Spectral

generalized multi-dimensional scaling. pages 380–

392.

Bronstein, A. and Bronstein, M. (2008). Regularized partial

matching of rigid shapes. In European Conference on

Computer Vision, pages 143–154. Springer.

Bronstein, A. M., Bronstein, M. M., and Kimmel,

R. (2006). Generalized multidimensional scal-

ing: a framework for isometry-invariant partial

surface matching. Proceedings of the National

Academy of Sciences of the United States of America,

103(5):1168–1172.

Bronstein, A. M., Bronstein, M. M., Kimmel, R., Se-

ries, I. M. a. P., Hall, L., and E, C. S. S. (2009).

A Gromov-Hausdorff Framework with Diffusion Ge-

ometry for Topologically-Robust Non-rigid Shape

Matching. pages 612–626.

Cohen, L. and Kimmel, R.(1997). Global Minimum for Ac-

tive Contour Models. International Journal on Com-

puter Vision, 24(1):57–78.

Gadacha, W. and Ghorbel, F. (2013). A stable and accurate

multi-reference representation for surfaces of R3: Ap-

plication to 3D faces description. IEEE International

Conference on Automatic face and Gesture Recogni-

tion (FG2013), Shanghai- China.

Jiang, L., Zhang, X., and Zhang, G. (2013). Partial

shape matching of 3D models based on the Laplace-

Beltrami operator eigenfunction. Journal of Multime-

dia, 8(6):655–661.

Julien, T., Mohamed, D., and Jean-Philippe, V. (2006).

Invariant highlevel reeb graphs of 3d polygonal

meshes. International Symposium on 3D Data Pro-

cessing, Visualization, and Transmission (3DPVT),

page 105?112.

Kim, V. G., Lipman, Y., and Funkhouser, T. (2011).

Blended intrinsic maps. ACM Transactions on Graph-

ics, 30(4):1.

Kimmel, R. and Sethian, J. a. (1998). Computing geodesic

paths on manifolds. Proceedings of the National

Academy of Sciences of the United States of America,

95(15):8431–8435.

Meyer, M., Desbrun, M., Schr¨oder, P., and Barr, A. H.

(2002). Discrete Differential-Geometry Operators for

Triangulated 2-Manifolds. International Workshop on

Visualization and Mathematics.

Ovsjanikov, M., M´erigot, Q., M´emoli, F., and Guibas, L.

(2010). One point isometric matching with the heat

kernel. Eurographics Symposium on Geometry Pro-

cessing, 29(5):1555–1564.

Sun, J., Chen, X., and Funkhouser, T. A. (2010). Fuzzy

geodesics and consistent sparse correspondences for:

eformable shapes. 29(5):1535–1544.

Taylor, J., Shotton, J., Sharp, T., and Fitzgibbon, A. (2012).

The vitruvian manifold: Inferring dense correspon-

dences for one-shot human pose estimation. pages

103–110.

Thompson, D. (1917). On growth and form. University

press in Cambridge, Cambridge, MA.

Van Kaick, O., Zhang, H., Hamarneh, G., and Cohen-Or, D.

(2010). A Survey on Shape Correspondence. Com-

puter Graphics Forum, xx:1–23.

Wei, L., Huang, Q., Ceylan, D., Vouga, E., and

Li, H. (2015). Dense human body correspon-

dences using convolutional networks. arXiv preprint

arXiv:1511.05904.

Yaron, L. and Thomas, F. (2009). M¨obius voting for surface

correspondence. 28(3):72.

Yusuf Sahillio˘glu, Y. Y. (2014). Multiple shape correspon-

dence by dynamic programming. 33(7):121–130.

Zhang, H., Sheffer, A., Cohen-Or, D., Zhou, Q., Van Kaick,

O., and Tagliasacchi, A. (2008). Deformation-driven

shape correspondence. Eurographics Symposium on

Geometry Processing, 27(5):1431–1439.

Zheng, Y., Tai, C.-L., Zhang, E., and Xu, P. (2013). Pair-

wise harmonics for shape analysis. IEEE transactions

on visualization and computer graphics, 19(7):1172–

1184.

VISAPP 2017 - International Conference on Computer Vision Theory and Applications

636