Segmentation of the LV Wall with Trabeculations
Cl
´
ement Beitone
1,2
, Christophe Tilmant
1,2
and Fr
´
ed
´
eric Chausse
1,2
1
Universit
´
e Clermont Auvergne, Institut Pascal, BP 10448, F-63000 Clermont-Fd, France
2
CNRS, UMR 6602, Institut Pascal, F-63171 Aubi
`
ere, France
Keywords:
Semi Automatic Cardiac Segmentation, Threshold, Level Set, Legendre Moments.
Abstract:
The evaluation of cardiac functional parameters for heart disease diagnosis requires to have an accurate seg-
mentation result. We propose a method to efficiently and reliably segment both the endocardial and the epi-
cardial borders of the left ventricle. We use MR short axis images acquired in SSFP mode. Our framework
combines a threshold-based approach to produce an estimation of the shape of the cardiac wall and a level
set approach that refine it. We assessed our method on two databases built for two MICCAI challenges. Our
results would have positioned us at the third place of the 2009 challenges.
1 INTRODUCTION - STATE OF
THE ART
According to the World Health Organization in 2012,
cardiovascular diseases were responsible for 30% of
the total number of deaths. Systolic function impair-
ment and especially the left ventricle (LV) is one of
the main characteristics reflecting that the heart is
damaged. Quantitative analysis provides important
cardiac functional parameters for heart disease diag-
nosis, for example the strain measure showed is a re-
liable prognostic value.
The evaluation of these parameters requires to
have an accurate segmentation result. This step has
been the subject of a large number of studies: a re-
view and an evaluation of segmentation methods ap-
plied to MR images can be found in (Petitjean and
Dacher, 2011).
Among all the methods, threshold-based have
proven their efficiency. For example, the procedure
proposed by Jolly (Jolly, 2009) combines a multi-
seeded fuzzy connectedness approach and a registra-
tion algorithm to segment the wall of the left ventricle
in sequences of MR images. This work was ranked as
one of the best at the MICCAI 09 challenge for car-
diac MR left ventricle segmentation. Nevertheless,
one of the weakness of these strategies is that they
are generally designed for a unique purpose. They
tend to fail if the subject strays too far from the nomi-
nal value. Hence, they generally require an additional
stage to refine their results.
The deformable models are another major cate-
gory in cardiac segmentation. In particular, the level
set framework has been extensively used to tackle this
problem as it is convenient to implement specific con-
straints. For example, in (Feng et al., 2013) the au-
thors represent the cardiac wall with two specified
level contours of a level set function. These con-
tours are maintained separated by a geometric con-
straint. More recently in (Ngo et al., 2016), the au-
thors have mixed a deep learning approach with a
level set method to segment the left ventricle in MR
sequences. Here, the level set is used as a fine tun-
ing method that completes the work produced by the
deep learning algorithm. The drawback of the level
set approaches is their need to be initialized close to
the final solution in order to work properly.
In this article, we propose a method to efficiently
and reliably segment both the endocardial and the epi-
cardial borders of the left ventricle in MR short axis
images acquired in SSFP mode. Unlike the work pro-
posed in (Beitone et al., 2015) where the aim of the
authors was to extract an endocardial border encom-
passing only the blood pool, we try here to follow the
Figure 1: Overview of the proposed framework.
Beitone C., Tilmant C. and Chausse F.
Segmentation of the LV Wall with Trabeculations.
DOI: 10.5220/0006270903010305
In Proceedings of the 12th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2017), pages 301-305
ISBN: 978-989-758-225-7
Copyright
c
 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
301

classical guidelines of the clinicians. Therefore, we
integrate as much as possible the trabeculations in-
side the region enclosed by the endocardial border.
Our framework mixes a threshold-based algorithm to
produce an estimation of the shape of the cardiac wall
and a level set method to refine it. This framework is
very fast in terms of computation time. The figure 1
illustrates this pipeline. We have assessed our strategy
on two databases published at the MICCAI 09 and 11
challenges.
2 PROPOSED FRAMEWORK
Our aim is to retrieve a shape homeomorphic to a ring:
the wall of the left ventricle. For that we combine two
different approaches. First a threshold-based segmen-
tation builds a first shape close to the solution. Then, a
level set segmentation refines it and produces the final
result.
After analysing several manual segmentations, we
have extracted some criteria which characterize the
expectations of the experts. The contour produced by
the algorithm must be relatively smooth. The endo-
cardial contour must integrate the blood pool, the pil-
lars and all the trabeculations along the edge. Build-
ing up an algorithm able to satisfy those constraints
requires an analysis of the impulse responses of the
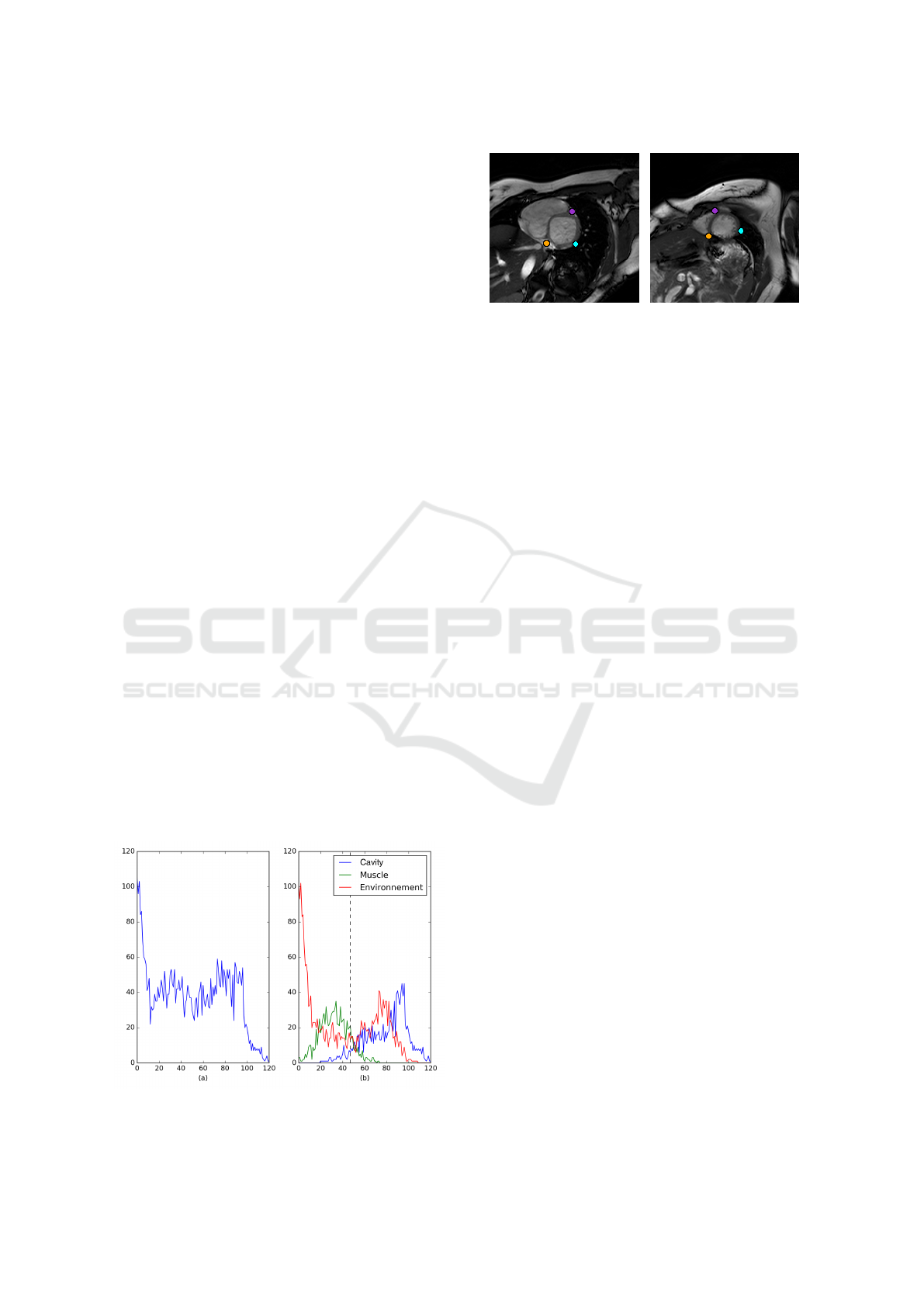
tissues. The figure 2(a) presents the distributions of
the blood pool, the cardiac muscle and the environ-
ment of the heart. This histogram is based on the la-
bels produced by an expert.
It shows that the parts corresponding to the blood
pool and to the muscle share a small range of values
on the histogram. This is a direct consequence of the
integration into the blood pool of the pillars and the
trabeculations. This last integration raises some dif-
ficulties. The gray levels of the trabeculations corre-
Figure 2: The histogram of the different tissues is based on
expert segmentation.
Figure 3: Manual initialization on the basal slice (left) and
propagation on the apical slice (right).
spond to a transition between two modes in the his-
togram and it is also a spatial transition between two
regions. Our aim is to integrate as much trabecula-
tions as possible in the blood pool, in order to pro-
duce a contour close to what the experts expect. As
we use a threshold-based method, we have to find an
algorithm that determines a reliable threshold.
2.1 Semi Automatic ROI Detection
To initialize our method the expert, have to select
three points on the basal slice. Two of these points
are on each side of the shared border between the ven-
tricles. More precisely, these locations correspond to
the intersection between the anteroseptal and anterior
regions and between the inferoseptal and inferior re-
gions. The last point is located on the free wall of the
mycoardium at the intersection between the anterolat-
eral and the inferoseptal region. These points are then
automatically propagated from the base to the apex
using a block matching algorithm. The result of our
initialization procedure is illustrated on the figure 3.
2.2 Threshold-based Segmentation
Our approach is a specialization of the optimal algo-
rithm proposed by Otsu (Otsu, 1975). This method
computes the optimal threshold T
Otsu
which splits
an histogram in two modes. Unfortunately, our his-
tograms are not exactly bimodal: they are biased by
the distribution of the pixel associated to the environ-
ment. Hence, the threshold given by Otsu is shifted
from the optimal position for our problem. For exam-
ple, on the figure 2(b) the Otsu threshold (black line)
is closer to the green mode than to the blue one. This
bias might have a significant impact on the quality of
the segmentation. In extreme situations, like the one
presented on the figure 5(c), it can lead to the creation
of a connection between the two ventricles.
We look for a factor f
re f
as f
re f
× T
Otsu
gives a
segmentation that contains only the blood pool and
little or no trabeculations. We call this surface S
re f
.
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
302

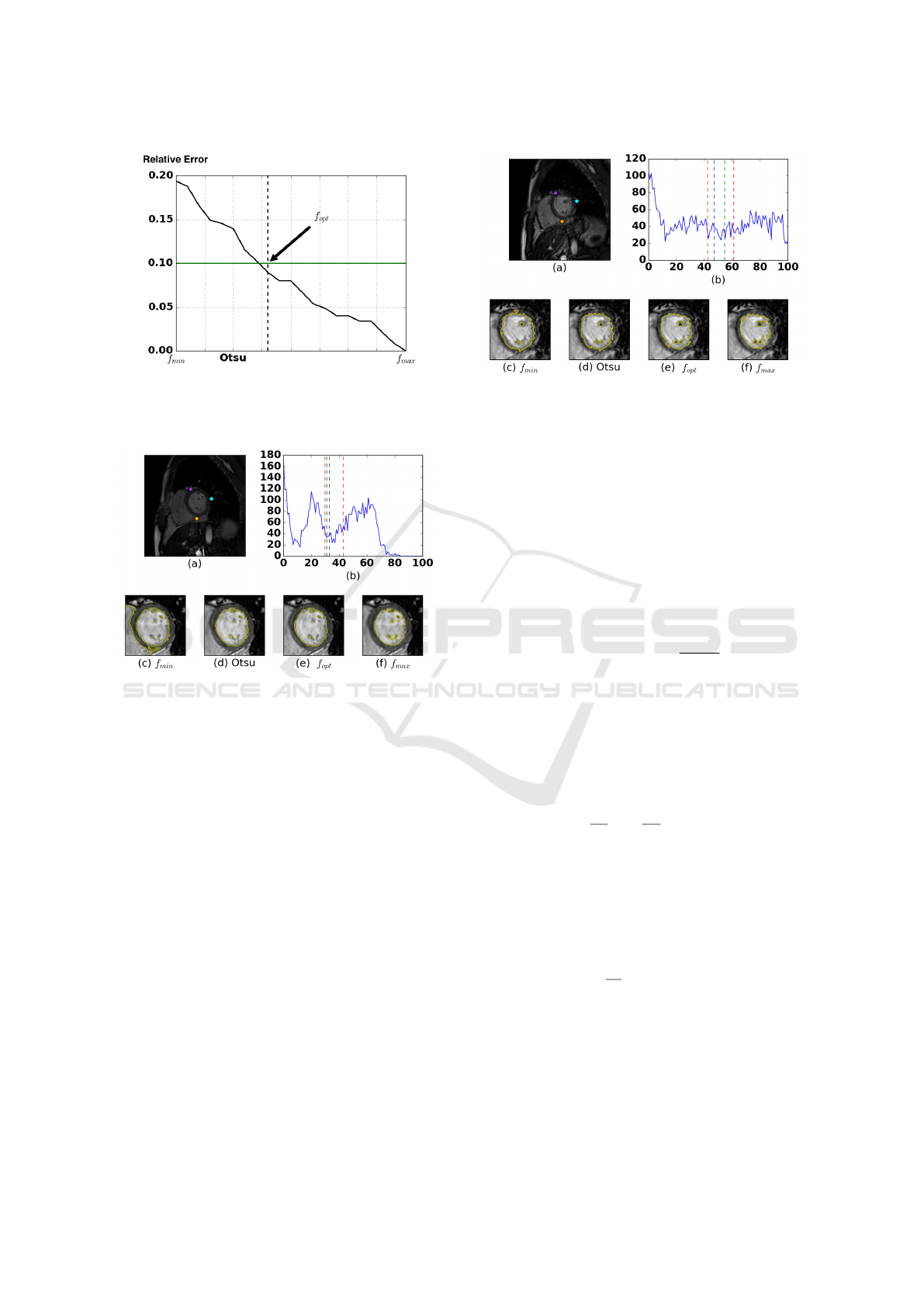
Figure 4: Example of relative error to the surface of S
re f
.
The line in green is the desired error corresponding to a
relative difference of 10%. The vertical line in dashed black
is the optimal threshold selected by our method.
Figure 5: Illustration of the threshold-based segmentation.
(a) The original image. (b) The histogram associated to the
ROI in (a). (c-f) The results of the segmentation obtained
by applying factors to the Otsu threshold T
Otsu
.
Then, we iteratively compute the relative errors be-
tween S
re f
and the surfaces of the segmentations ob-
tained by applying factors inferior to f
re f
to the value
T
otsu
. Using these errors values, we compute a curve
similar to the one presented on the figure 4. Accord-
ing to the expert segmentation, the trabeculations oc-
cupy 10 percent of the surface of the endocardium.
We used this value to set our stopping criterion.
Experimentally, we have found that setting f
re f
to
1.3 gives reliable results. The figures 5 and 6 show
that the selected T
opt
= f
opt
× T
Otsu
leading to S
opt
may be on the left or on the right of the value T
Otsu
depending on the dynamic range of the images.
Finally, we compute the convex hull of S
opt
to in-
clude the pillars. We obtained our first representation
of the wall S
w
by computing the external morpholog-
ical gradient of S
opt
with a dilation equal to 7.5mm.
This value corresponds to the lower boundary of the
average thickness of the cardiac wall. We also store a
thicker gradient image S
tw
with a thickness of 8.5mm.
Figure 6: Illustration of the threshold-based segmentation.
(a) The original image. (b) The histogram associated to the
ROI in (a). (c-f) The results of the segmentation obtained
by applying factors to the Otsu threshold T
Otsu
.
This image is used as a shape reference in our level set
model.
2.3 Level Set-based Segmentation
2.3.1 Deformable Model Framework
The variational formulation of the segmentation prob-
lem by means of a deformable model is stated as:
S = argmin
S
∗
∈F
S
E(S
∗
) ⇔
δE(S )
δS
= 0 (1)
In our case S corresponds to the final shape of our
model. This shape is taken from a family of solu-
tions F
S
, by minimizing the energetic functional E.
This optimization problem is solved by means of a
descent method on an artificial temporal parameter
t. The model is put into motion, it is a deformable
model:
∂S
∂t
= −
δE
δS
= V n (2)
This problem is equivalent to a front propagation
where the variation is homogeneous to a speed V onto
the normal n. The calculus of variations on E can be
computed using shape derivative tools (Aubert et al.,
2003). In the level set framework, Sethian (Sethian,
1999) showed that this problem can be stated as:
∂φ
∂t
= V |∇φ|, (3)
where φ, the level representation, is a higher order
function and φ
−1
(0) = S .
2.3.2 Proposed Model
As our threshold-based method produces an initial
shape very close to the solution, the level set is used to
Segmentation of the LV Wall with Trabeculations
303

fine-tune the final contour. Our model combines three
terms as:
E = αE
LCV
+ (1 −α)E
LM
+ βE
RC
(4)
where the term E
LCV
is the local version (Foulonneau
et al., 2003) of the well known Chan & Vese func-
tional (Chan and Vese, 2001). Global methods pro-
vide more energy but are meaningful only if the distri-
bution over the considered object follows a stationary
process. As our images present some non-stationarity
over the myocardium and over its neighbourhood, the
local evaluation of the averages ensures that the mis-
labelling along the perimeter is fixed. This term is
stated as:
E
LCV
(φ) =
Z
Ω
x
δφ
Z
Ω
y
B(x, y) · F (I(y), φ(y)) dydx
(5)
where I is the current cardiac image and B is the ball
used to extract the local neighborhood along the cur-
rent contour at each location x. Here, F stands for the
Chan & Vese model.
The term E
LM
is the shape constraint applied to the
segmentation. This functional relies on the Legendre
moments as it was introduced by Lankton (Lankton
and Tannenbaum, 2008). It ensures that the global
shape is correct and homeomorphic to a ring. The
shape reference is set to S
tw
. This term is stated as:
E
LM
(S , S
re f
) =
N−1
∑
i=0

λ
i
− λ
re f
i

2
(6)
where the Legendre moments λ
i
are the results of the
decomposition of the shapes S and S
re f
over a basis
of Legendre polynomials. The order of the decompo-
sition is linked to the quality of the description. This
decomposition is invariant to the scale and the trans-
lation.
Finally the regularization term E
RC
ensures that
the contour remains relatively smooth and is based on
the length of the contour. Our model is initialized with
S
w
.
3 RESULTS
In order to quantitatively evaluate the detected endo-
cardial and epicardial contours we used a local and
a global measure. The global measure is the Dice
metric which evaluates the overlap between the expert
surface and the computed one. The local measure is
the average perpendicular distance from the automat-
ically segmented contour to the corresponding manu-
ally drawn expert contour, averaged over all contour
points.
3.1 Evaluation on the Database
MICCAI09
The database built for the MICCAI 09 challenge for
the segmentation of the left ventricle contains 45 pa-
tients. For each patient a SSFP sequence in short axis
acquired on a 1.5T GE Signa is given along with a
segmentation of the cardiac wall done by an expert.
All the images have been acquired in apnoea (10 to 15
seconds) with a temporal resolution of 20 images per
cycle. Between 6 to 12 SAX slices are given to cover
the myocardium from the base to the apex. Each slice
has a thickness of 8mm and the distance between two
slices is 8mm. The spatial resolution is 1.25mm in the
short axis plan.
This database is split in three parts: Online,
Training and Validation. We get respectively an
average value for the Dice metric of 0.89(±0.04),
0.91(±0.04) and 0.90(±0.04). For the average per-
pendicular distance between the manual segmen-
tation and our contour, we get an average equal
to 2.39(±1.64), 2.31(±1.78) and 2.24(±1.51)mm.
These results position us virtually at the third place
of the challenge.
3.2 Evaluation on the Database
MICCAI11
We have also used the multimodal database built for
the MICCAI 2011 challenge: Motion Tracking Chal-
lenge (MTCdb). This database contains the exams of
15 patients. The SSFP images were acquired on a 3T
Philips Achieva System with a temporal resolution of
30 images in short axis per cycle. The spatial resolu-
tion is between 1.15 and 1.25mm for each slice and
the space between two slices is equal to 8mm. About
9 to 14 slices are necessary to capture the heart from
the base to the apex.
On that database, we get an average Dice metric
of 0.94(±0.04) and an average perpendicular distance
equal to 1.46(±1.54)mm. The figure 7 illustrates the
quality of the contours we obtained. As expected the
endocardial border encompass the trabeculations and
the contours are smooth.
4 CONCLUSION
We have presented a segmentation framework to effi-
ciently and reliably segment the endocardial and the
epicardial borders in MR images. Our aim was to en-
compass as much as possible the trabeculations in-
side the endocardial border to follow the guidelines
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
304

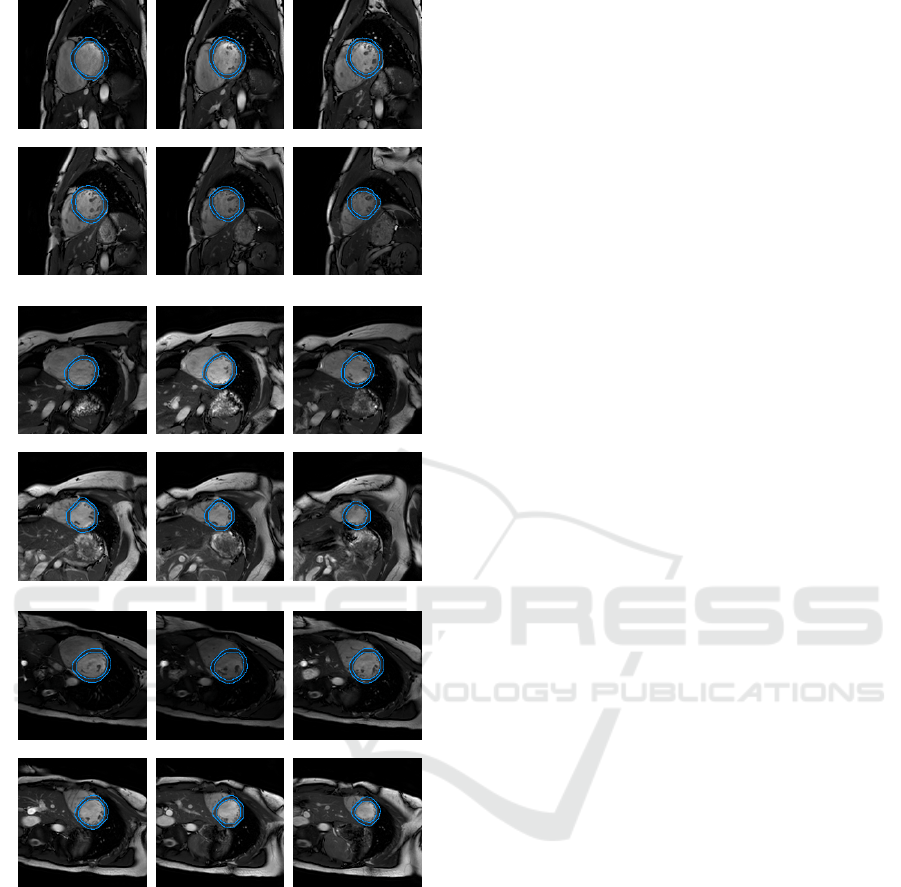
(a) Patient 1
(b) Patient 2
(c) Patient 3
Figure 7: Illustration of the segmentation results for some
patients. Slices from the base to apex.
of the experts. We have evaluated our approach on
two databases and have obtained results that virtually
positioned us at the third place of a challenge. Our re-
sults are similar to those obtained with a deep learning
algorithm. Nevertheless, we obtain them in a fraction
of the computational time required by this approach.
REFERENCES
Aubert, G., Barlaud, M., Faugeras, O., and Jehan-Besson,
S. (2003). Image segmentation using active contours:
Calculus of variations or shape gradients? SIAM Jour-
nal on Applied Mathematics, 63(6):2128–2154.
Beitone, C., Tilmant, C., and Chausse, F. (2015). Fully
automatic deformable model integrating edge, texture
and shape-application to cardiac images segmenta-
tion. In VISAPP (1), pages 517–522.
Chan, T. F. and Vese, L. A. (2001). Active contours with-
out edges. IEEE Transactions on image processing,
10(2):266–277.
Feng, C., Li, C., Zhao, D., Davatzikos, C., and Litt, H.
(2013). Segmentation of the left ventricle using dis-
tance regularized two-layer level set approach. In In-
ternational Conference on Medical Image Computing
and Computer-Assisted Intervention, pages 477–484.
Springer.
Foulonneau, A., Charbonnier, P., and Heitz, F. (2003). Ge-
ometric shape priors for region-based active contours.
In Image Processing, 2003. ICIP 2003. Proceedings.
2003 International Conference on, volume 3, pages
III–413. IEEE.
Jolly, M. (2009). Fully automatic left ventricle segmenta-
tion in cardiac cine mr images using registration and
minimum surfaces. The MIDAS Journal-Cardiac MR
Left Ventricle Segmentation Challenge, 4.
Lankton, S. and Tannenbaum, A. (2008). Localizing region-
based active contours. IEEE transactions on image
processing, 17(11):2029–2039.
Ngo, T. A., Lu, Z., and Carneiro, G. (2016). Combining
deep learning and level set for the automated segmen-
tation of the left ventricle of the heart from cardiac
cine magnetic resonance. Medical Image Analysis.
Otsu, N. (1975). A threshold selection method from gray-
level histograms. Automatica, 11(285-296):23–27.
Petitjean, C. and Dacher, J.-N. (2011). A review of seg-
mentation methods in short axis cardiac mr images.
Medical image analysis, 15(2):169–184.
Sethian, J. A. (1999). Level set methods and fast marching
methods: evolving interfaces in computational geom-
etry, fluid mechanics, computer vision, and materials
science, volume 3. Cambridge university press.
Segmentation of the LV Wall with Trabeculations
305