Hex-utils: A Tool Set Supporting HexASCII Hexagonal rasters

ıs Moreira de Sousa and Jo

ao Paulo Leit

Eawag - Swiss Federal Institute of Aquatic Science and Technology,

Uberlandstrasse 133, 8600 D

ubendorf, Switzerland

Keywords:

HexASCII, Hexagonal raster, Hexagonal Mesh, Hex-utils.

Abstract:

The advantages of hexagonal meshes over squared grids in discretising spatial variables have been known

for long. Notwithstanding, the raster data formats used in geo-spatial disciplines to this purpose are still

today almost exclusively reliant on squared grids. The HexASCII ﬁle format is a core element in an attempt

to introduce hexagonal rasters to mainstream GIS, deﬁning a simple vehicle to store and share such data

structures. This article describes the hex-utils tool-kit, an Application Programming Interface (API) and a

set of command line tools enabling the use of HexASCII rasters. Basic operations are supported: creation

of new hexagonal rasters from different inputs and transformation into ﬁle formats readable by desktop GIS

programmes. The API sets a framework for the development of further functionality.

1 INTRODUCTION

In Geographic Information Systems (GIS), the raster

data structure provides a straightforward mean to cap-

ture real world phenomena, by discretising spatial

variables into tessellations of samples. Rasters divide

the cartographic plane regularly into small areas of

the same shape, inside which the spatial variable in

question is assumed to be constant. This is possible

only with three regular geometric shapes (i.e., hav-

ing all sides of equal length): the equilateral triangle,

the square and the hexagon. Raster grids used in GIS

have been predominantly organised in squared pat-

terns in which the space between each row and each

column of samples is constant; to a good extent this is

a consequence of spatial data acquisition methods.

However, hexagonal rasters yield two essential

advantages over square grids that are relevant in GIS.

In ﬁrst place is the higher spatial resolution pro-

vided by hexagonal meshes of equal area (Mersereau,

1979); or conversely, the lower number of cells re-

quired by a hexagonal raster to match the resolu-

tion of a squared counterpart. In second place is the

isotropy of the hexagonal neighbourhood; in a square

grid each cell has four neighbours to which it shares

an edge and four with which it shares only a vertex.

In a hexagonal raster each cell shares an edge with

each of its six neighbours, and all their cell centroids

are at the same distance.

On the downside, hexagons yield the distinc-

tive characteristic of not being dividable into smaller

hexagons, and neither forming a larger hexagon when

agglomerated. This issue has been addressed in dif-

ferent ways, such as that proposed with the Gener-

alised Balanced Ternary cell index system (Gibson

and Lucas, 1982). Moreover, raster cell aggregation

is not a frequent operation in spatial analysis pro-

cesses.

The shortcomings of square grids became evident

early in the history of Computer Science, motivat-

ing suggestions for a shift to hexagonal meshes al-

ready in 1960s (Golay, 1969). But in spite of further

theoretical developments and other advantages iden-

tiﬁed, this shift never fully materialised. Likewise in

the GIS ﬁeld, neither hexagonal raster ﬁle formats,

nor supporting tools were ever fully developed. Scant

work with hexagonal sampling schemes or hexagonal

meshes is conducted on vector topologies.

These were the motivations leading to the speciﬁ-

cation of the HexASCII ﬁle format (HASC for short),

an open formalism to store and port hexagonal rasters

as text ﬁles (de Sousa and Leit

ao, In review). This

speciﬁcation sets the minimum information required

to capture cell geometry, mesh dimensions and loca-

tion, plus the cell data themselves.

A prototype application is presented in this article,

a set of tools developed to provide basic functional-

ity for HexASCII rasters. It comprises an Applica-

tion Programming Interface (API) and a set of com-

mand line tools demonstrating the creation of Hex-

ASCII rasters and their integration with existing GIS

software. These assets intend to be a step towards the

Sousa, L. and Leitão, J.

Hex-utils: A Tool Set Supporting HexASCII Hexagonal rasters .

DOI: 10.5220/0006275801770183

In Proceedings of the 3rd International Conference on Geographical Information Systems Theory, Applications and Management (GISTAM 2017), pages 177-183

ISBN: 978-989-758-252-3

177

adoption of hexagonal rasters in GIS and spatial anal-

ysis practice.

These tools are gathered in a project called

hex-utils released under an open source licence and

made available at GitHub

. They can also be installed

from a PyPi repository

This article starts with a brief overview of the Hex-

ASCII ﬁle format in Section 2; Section 3 describes

the API underlying the tool-kit and Section 4 goes

through the various command line tools developed to

date; Section 5 summarises the article and points to

future work.

2 OVERVIEW OF THE HexASCII

FILE FORMAT

An HexASCII raster is a text ﬁle composed by two

parts: an opening metadata section and a string of cell

values. The metadata section describes cell and mesh

geometry and positions the raster in the cartographic

domain. The metadata is described with a set of seven

key and value pairs, of which ﬁve are mandatory and

two are optional:

• ncols: number of columns;

• nrows: number of rows;

• xll: x coordinate of the lower left cell centroid;

• yll: y coordinate of the lower left cell centroid;

• side: cell side length;

• angle: mesh rotation angle (optional);

• no data: string representing null or missing val-

ues (optional).

Listing 1 presents the HexASCII ﬁle for the

hexagonal raster depicted in Figure 1. The full spec-

iﬁcation of this ﬁle format, as well as the reasoning

leading to its structure, is available in (de Sousa and

Leit

ao, In review).

Listing 1: Example of an HexASCII ﬁle.

ncols 4

nrows 3

xll 3.1

yll 2.2

side 2

angle 15

no_da t a 9999

11 21 31 41

12 22 32 42

13 23 33 43

https://github.com/ldesousa/hex-utils

https://pypi.python.org/pypi/hex-utils

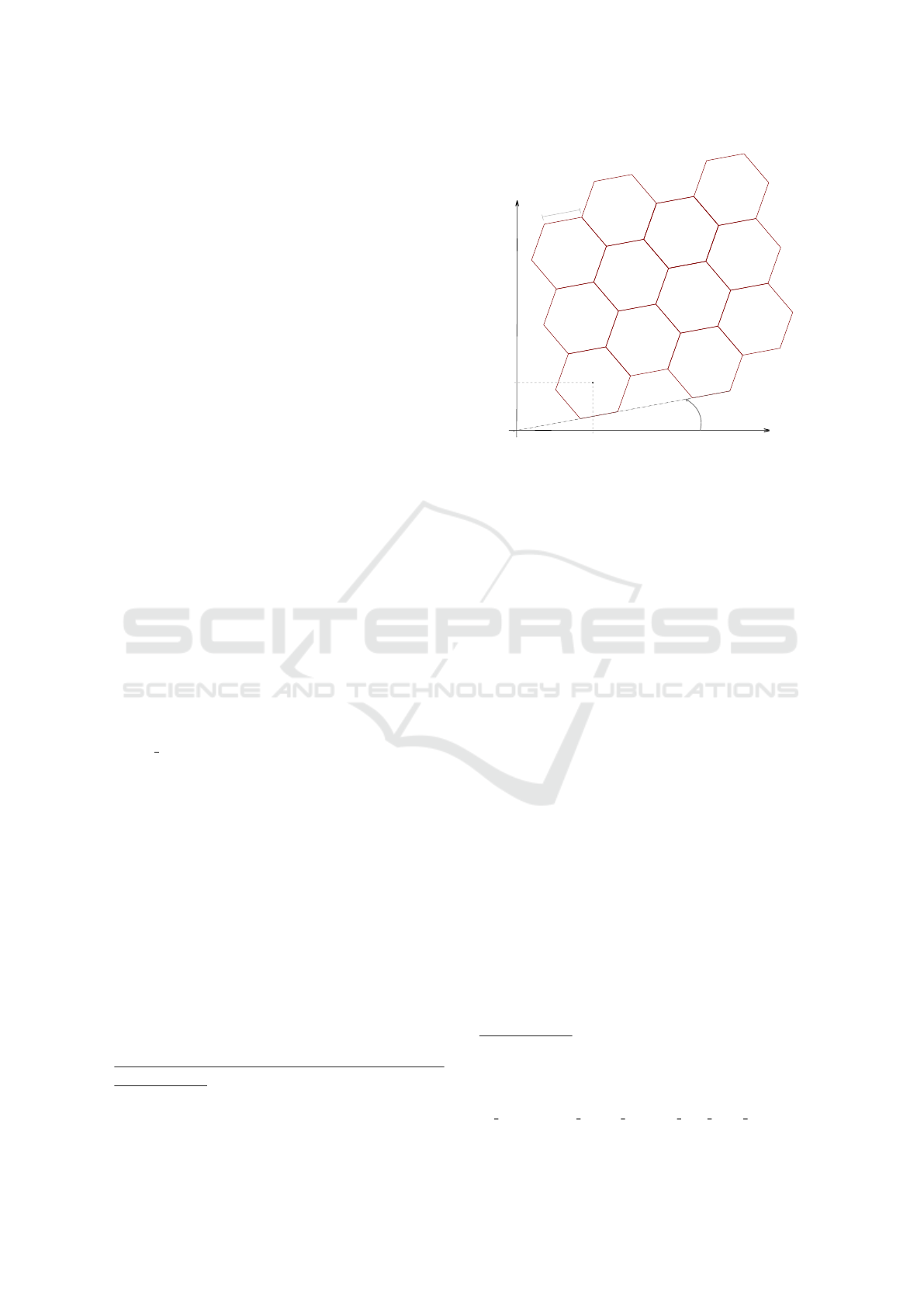
132.2

3.1

15º

Figure 1: The hexagonal raster described by the HASC ﬁle

in Listing 1.

3 THE HexASCII APPLICATION

PROGRAMMING INTERFACE

(API)

The tools enabling the HexASCII ﬁle format were de-

veloped in the Python programming language (Sanner

et al., 1999). This language was chosen in ﬁrst place

for its versatility, as useful to ad hoc scripting as to

high level object-oriented programming. Python also

facilitates the manipulation of spatial data through a

number of libraries such as GDAL/OGR (Warmer-

dam, 2008) OWSLib

, Shapely

or GeoPandas

granting it growing popularity among geo-spatial pro-

grammers.

The prototype command line tools rely on the do-

main model depicted in Figure 2, describing rasters

in general and then speciﬁc ﬁle formats. This domain

model is the blueprint for the API implemented in the

Python programming language. Both the HexASCII

format and the ASCII squared raster format speciﬁed

by ESRI

are included in this model. The latter is one

of the data sources for the creation of new hexagonal

rasters.

The model starts with the abstract class Grid that

encloses various aspects of a raster. This class can be

seen as a template for the minimum metadata, data

and functionality required for a raster grid format.

https://geopython.github.io/OWSLib/

https://pypi.python.org/pypi/Shapely

http://geopandas.org/

http://resources.esri.com/help/9.3/arcgisdesktop/com/

gp toolref/spatial analyst tools/esri ascii raster format.htm

GISTAM 2017 - 3rd International Conference on Geographical Information Systems Theory, Applications and Management

178

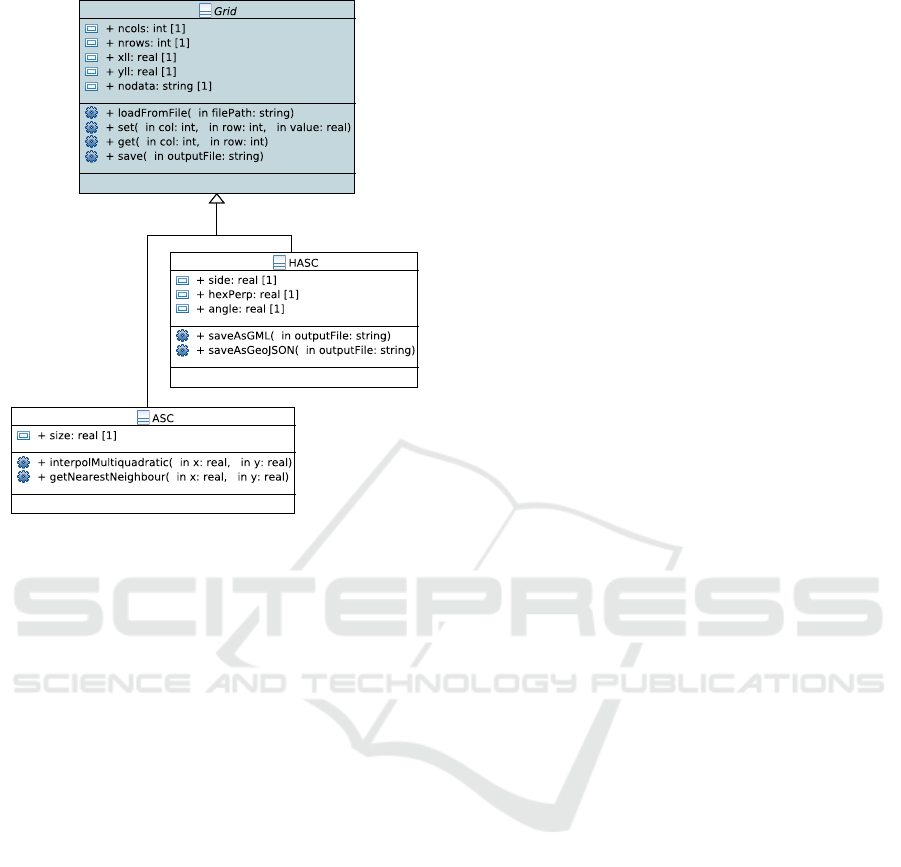
Figure 2: The domain model underlying the tools support-

ing the HASC ﬁle format.

These include: number of columns (ncols), number

of rows (nrows), coordinates positioning the grid in

the cartographic space (xll and yll) and an identi-

ﬁer for empty or null values (nodata). The data is

stored internally as a two-dimensional array, that can

not be directly assessed (it is a protected property).

The init() method initialises the properties de-

scribed above in a child instance of the Grid class.

To assign a new value to a grid cell there is the set()

method, that takes as arguments a column number, a

row number and a new value. Conversely, to retrieve

the value of a cell, there is the get() method, tak-

ing as arguments a column and a row number. The

loadFromFile() method provides the functionality

to read the raster metadata and data from an existing

ﬁle. Finally, the save() method is available to cre-

ate a persistent ﬁle on disk with the current data and

metadata of the instance, according to the format sub-

scribed to by the child class.

The ASC class is a concrete implementation of the

Grid type, representing the ESRI ASCII raster for-

mat. Beyond the properties inherited from Grid, this

class adds the size property, another metadata ele-

ment determining the width and height of each grid

cell. The init() method is redeﬁned to allow the set

up of this additional property. Two new methods are

introduced in this class, both concerning the interpo-

lation of data values: (i) getNearestNeighbour(),

that simply returns the value of the cell whose cen-

troid is nearest to the given coordinates, and (ii)

interpolMultiquadratic(), that for a given pair

of coordinates applies the multi-quadratic interpola-

tion technique (Chaplot et al., 2006) with the values

of the nine nearest cells. These methods are used to

interpolate grid values for a resulting HexASCII type

grid.

Lastly there is the HASC class, the concrete imple-

mentation of the HexASCII ﬁle format. It adds three

properties: (i) side - the length of an hexagonal cell

side; (ii) hexPerp - the distance between two paral-

lel sides of a cell; and (iii) angle - the angle of ro-

tation of the grid. The hexPerp property is required

in various calculations (e.g. cell area, cell centroids),

thus it keeps the value at hand avoiding its constant

computation. An important difference from the ESRI

ASCII raster ﬁle format to HexASCII is grid posi-

tioning. While in the HexASCII format the positional

coordinates (the xll and yll properties) refer to the

centre of the lower left cell, in the ESRI format these

coordinates refer to the lower left corner of the lower

left cell.

The HASC class also introduces a few meth-

ods. The init() method is again redeﬁned

to set up the class speciﬁc properties. The

getCellCentroidCoords() method returns the car-

tographic location of a cell, given its discrete coordi-

nates (column and row). The saveAsGML() method

persists the mesh instance as a vector ﬁle using

the Geography Markup Language (GML) (Burggraf,

2006), a standard maintained by the Open Geospatial

Consortium (OGC). This method creates an hexag-

onal polygon for each grid cell, to which is as-

signed an attribute named value with the respec-

tive cell value. A similar output is produced by the

saveAsGeoJSON() method, but producing a vector

ﬁle using the GeoJSON language (Butler et al., 2008).

4 COMMAND LINE TOOLS

Using the API described above, a number of com-

mand line tools are made available with hex-utils to

perform basic operations with HexASCII grids; each

one is detailed below.

4.1 asc2hasc

This tool provides a simple mean to create an hexag-

onal raster from an existing square raster. It

calculates the geometry of the resulting hexagonal

mesh and uses either the nearest neighbour or the

multi-quadratic interpolation techniques to calculate

Hex-utils: A Tool Set Supporting HexASCII Hexagonal rasters

179

its values (using the getNearestNeighbour() and

interpolMultiquadratic() methods of the ASC

class).

The asc2hasc tool functions in two distinctive

modes: either preserving cell area (using the -a ﬂag)

or preserving spatial resolution (-r ﬂag). In the ﬁrst

mode the resulting hexagonal cells are conceived to

have the same area of the original squares; this means

a larger number of cells in the resulting hexagonal

mesh. In the -r mode the resulting hexagonal cells

are 13.4% larger than the original squares. This last

mode does not preserve entirely the same spatial res-

olution, since the interpolation itself induces a certain

loss of signal detail. From this hexagonal cell area pa-

rameter is derived the hexagonal cell side (S

), a key

element in the ensuing calculations.

The following step is the computation of the num-

ber of columns and rows in the resulting mesh. The

number of columns is calculated as the minimum

number that can entirely cover the horizontal span of

the grid, as given in the following expression:





(1)

Where C

is the number of columns in the hexag-

onal grid, C

the number of columns in the square

grid, S

the side of the input square cells and S

the

side of the resulting hexagonal cells. 3S

/2 is the dis-

tance between two opposite vertices of the hexagonal

cell. The application of the ceiling operation guaran-

tees that all square cells are covered in the horizontal

sense.

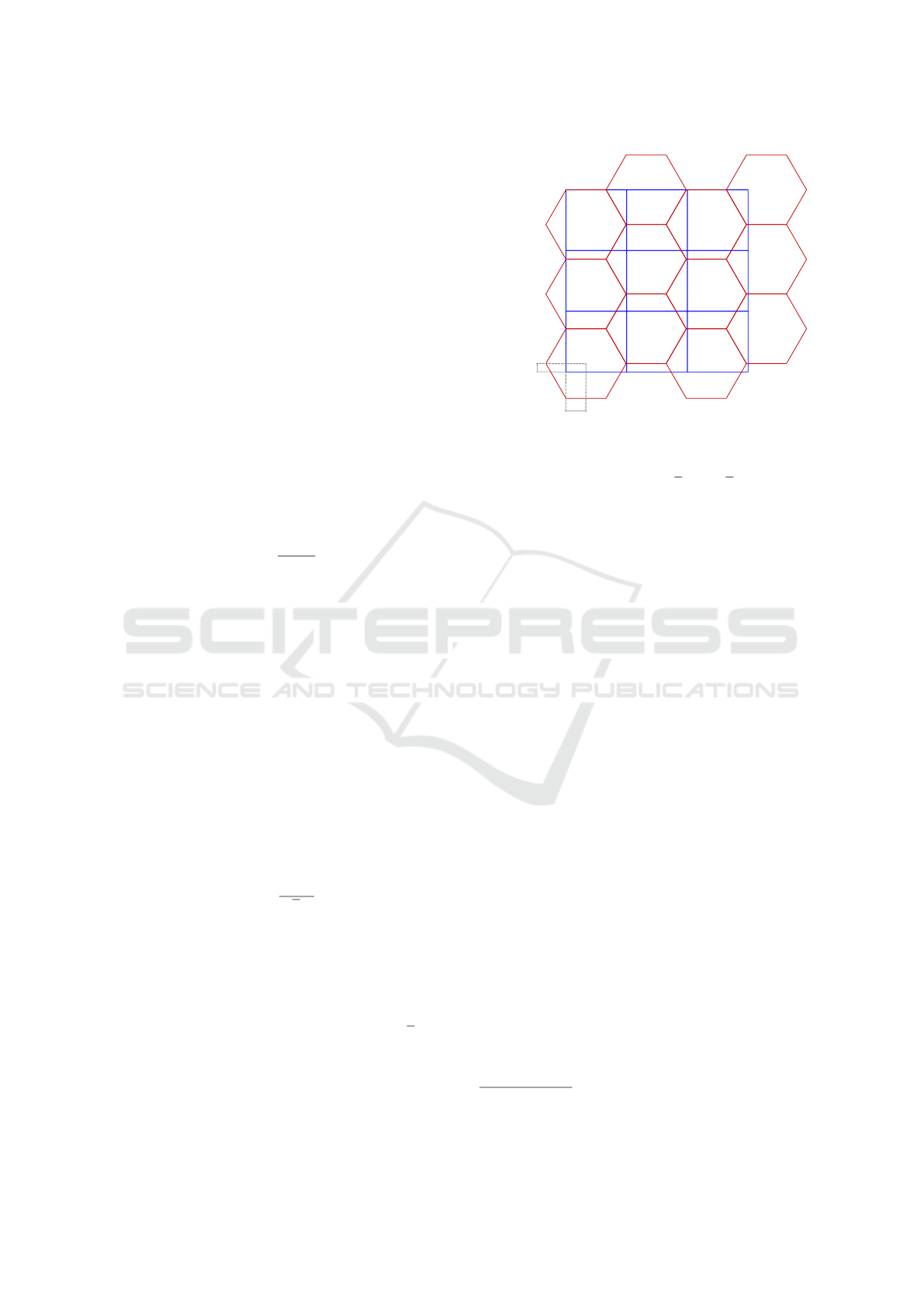
This computation is not as straightforward for the

number of rows, since there is a vertical displace-

ment of 3S

/2 between two consecutive columns in a

North-South hexagonal grid (where two sides of each

hexagon are parallel to the xx axis). To save space, the

option in this case is to cover only partially the input

square cells at the bottom row; the number of rows is

thus calculated as follows:



√



(2)

Where R

is the number of rows in the hexagonal

mesh and R

the number of rows in the square grid.

The resulting mesh is positioned in space with the

number of rows in mind. Even columns are set in

order to cover exactly the top square row; odd rows

thus miss partially the bottom square row. This bot-

tom sleave uncovered by odd rows is at most

√

in height. The concrete coordinates of the lower left

hexagonal centroid are thus computed as:

= x0

+ S

/2 (3)

Rs Ss -

Rh √3 Sh +

√3 Sh / 2

Sh / 2

Figure 3: Positioning of an HASC grid relative to the square

grid of origin.

= y0

+ R

−R

√

/2 (4)

Where the pair (x0

,y0

) are the coordinates of the

lower left corner of the square grid and (x0

,y0

) the

centroid coordinates of the lower left hexagonal cell.

Figure 3 exempliﬁes these calculations.

The resulting hexagonal mesh covers as much

as possible of the original square without exceed-

ing exaggeratedly the original extent. This option

“by excess” means extra extents along the margins

of the original grid. The top half of the top cells in

odd columns and part of the bottom of cells in even

columns lay beyond the extent of the original grid

The leftmost column can exceed the original extent

by as much as 3S

/2.

Beyond the arguments determining cell dimen-

sions, the asc2hasc tool takes also the -m ﬂag deﬁn-

ing which interpolation technique to use. Two options

are available: mq for multi-quadratic interpolation and

nn for the nearest neighbour. Finally, the ﬂags -i and

-o provide the paths to the input ESRI ASCII square

raster and the output HexASCII ﬁle. An example of

use:

asc2hasc -r -m mq -i /path/to/input.asc

-o /path/to/output.hasc

4.2 csv2hasc

This tool creates a new HexASCII raster from a set of

point samples. This is a common operation in GIS, in

which users extrapolate a regular mesh over a region

of interest from a collection of sparsely located ob-

servations. Spatial variables subject to such treatment

may be temperature, rainfall, altitude, soil quality, etc.

Note that grid indexing starts with zero, e.g. the left-

most cell columns in Figure 3 are even.

GISTAM 2017 - 3rd International Conference on Geographical Information Systems Theory, Applications and Management

180

The basic input to the tool is a comma separated

values (CSV) ﬁle (Shafranovich, 2005), structured

in three columns representing in succession: easting

coordinate, northing coordinate and observed value.

Each row corresponds to an individual observation.

Listing 2 provides an example.

Listing 2: Example of a CSV ﬁle input to csv2hasc.

1002.5 , 845.2 ,57.3 ,

1005.1 , 850.7 ,66.2 ,

998.6 ,841.9 , 4 2 . 7 ,

1007.2 , 852.4 ,38.9 ,

The user must also declare an area of interest to

be covered by the resulting raster. This is particularly

useful if the observations do not cover exactly the re-

gion under study. Additionally, the desired cell geom-

etry must be speciﬁed too. These inputs are provided

to the tool through a set of arguments:

-x : the bottom x coordinate of the area of interest.

-y : the left y coordinate of the area of interest.

-X : the top x coordinate of the area of interest.

-Y : the right y coordinate of the area of interest.

-s : the length of the cell side in the resulting grid.

-i : path to the input CSV ﬁle.

-o : path to the output HASC raster ﬁle.

The output hexagonal mesh is dimensioned and

positioned in the Cartographic space using the same

process described in Section 4.1 and exempliﬁed in

Figure 3. The values of the new HexASCII raster

are interpolated using the multi-quadratic method, ap-

plied to the ﬁve samples closest to each cell centroid.

An example of usage:

csv2hasc -x 0 -y 0 -X 2000 -Y 2000

-s 0.62 -i input.csv -o output.hasc

4.3 surface2hasc and

surface2asc

In order to assess the comparative performance of

hexagonal and square rasters of similar spatial res-

olution two tools where developed that sample di-

rectly a given continuous surface. With these tools

a same method or process can be applied on equiv-

alent rasters to investigate different results between

hexagons and squares. Sampling directly a continu-

ous surface avoids the signal losses that would occur

interpolating from an existing raster or from a set of

sparse observations.

As their name imply, surface2hasc produces an

HexASCII raster and surface2asc an ESRI ASCII

grid. They require a series of inputs that declare the

spatial extent to sample, the geometry of the resulting

mesh and identify the location of the surface function.

Each of these inputs is provided with a speciﬁc argu-

ment:

-x : the bottom x coordinate of the extent to sample.

-y : the left y coordinate of the extent to sample.

-X : the top x coordinate of the extent to sample.

-Y : the right y coordinate of the extent to sample.

-s : the length of the cell side in the resulting grid.

-m : the Python module containing the surface func-

tion.

-f : the name of the surface function.

-o : path to the output raster ﬁle.

The tool starts by calculating cell geometry and

then positions a mesh overlapping the extent declared.

In the hexagonal case the same “by excess” approach

employed in the asc2hasc tool is applied. The sur-

face function is then imported; it is assumed it resides

in a reachable Python module, declared with the -m

argument. The function is assumed to take in two ar-

guments, the easting and northing coordinates, and to

return a numerical value

. Figure 4 presents an exam-

ple surface and the resulting HexASCII grid produced

with the following command:

surface2hasc -x 0 -y 0 -X 2000 -Y 2000

-s 19.6 -m surfaces.surfaceGaussian

-f fun -o output.hasc

4.4 hasc2gml and hasc2geojson

The hasc2gml tool creates a GML ﬁle representing

the input HexASCII raster. For each cell of the raster

a polygon feature is created in the GML ﬁle with its

exact geometry. To each feature is assigned an at-

tribute named value containing the value of the corre-

sponding HexASCII cell. The resulting GML ﬁle is

usually thirty times larger than the original HexAS-

CII, stressing the usefulness of the latter as a portable

ﬁle format.

hasc2gml uses directly the loadFromFile() and

saveAsGML() methods of the HASC class. It takes no

additional arguments, beyond the paths to the input

and output ﬁles. The following exempliﬁes its use:

hasc2gml /path/to/input.hasc

/path/to/output.gml

A few surface examples are available at the GitHub

repository, in the surfaces package.

Hex-utils: A Tool Set Supporting HexASCII Hexagonal rasters

181

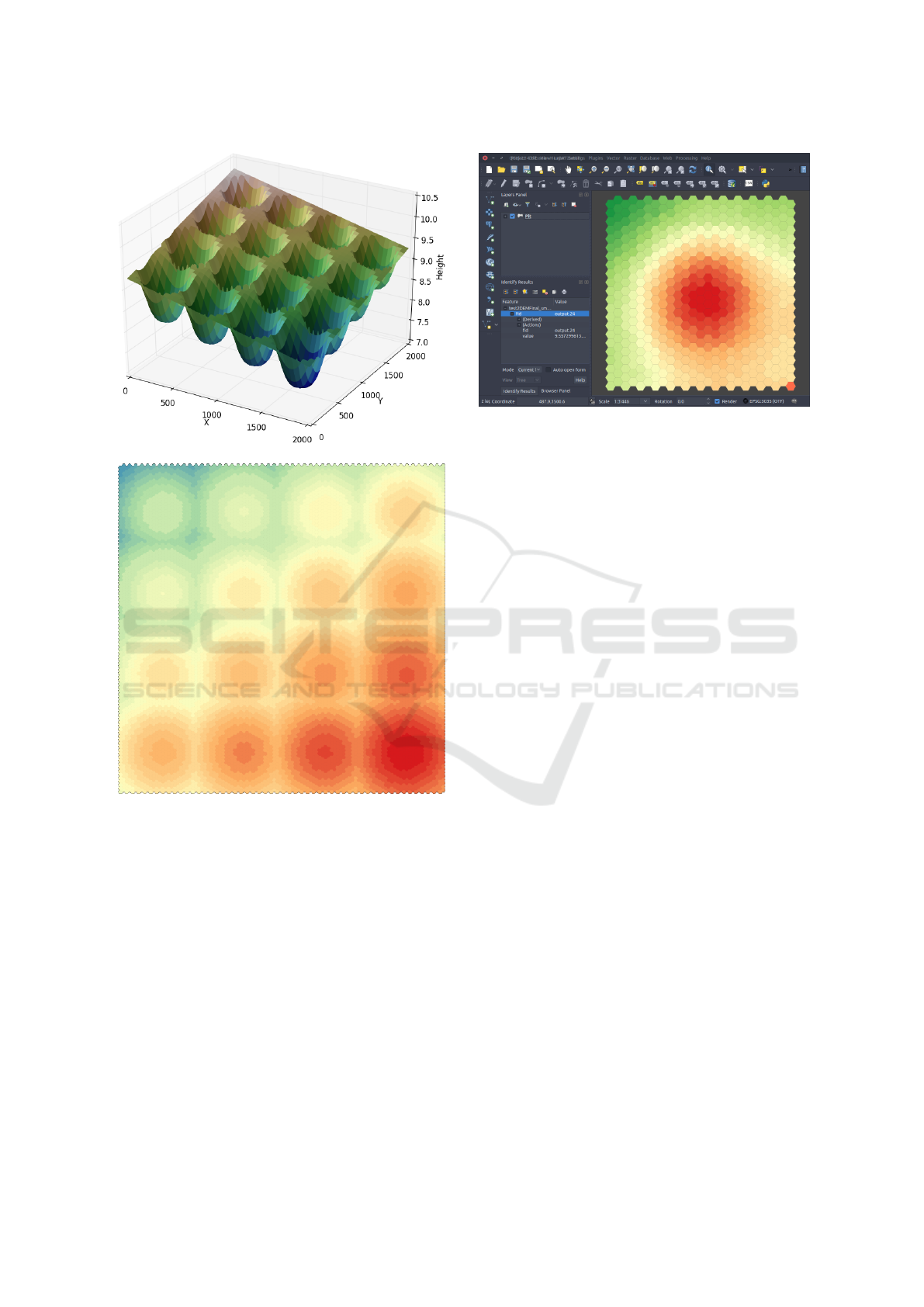
(a) Continous surface.

(b) HASC displayed as a GML layer in QGIS.

Figure 4: A sample surface and the resulting HASC grid

displayed in QGIS.

The hasc2geojson tool is in all similar, with

the difference being the output data format, GeoJ-

SON (Butler et al., 2008) in this case. This data for-

mat requires in general one third less disk space than

GML; still it requires some twenty times the space

used by the original HexASCII.

hasc2geojson /path/to/input.hasc

/path/to/output.json

The purpose of these tools is to facilitate the

visualisation of HexASCII grids in traditional GIS

desktop software. The resulting GML or GeoJSON

ﬁles can be seamlessly loaded into one of such pro-

grammes and there be subject to styling with choro-

Figure 5: An HASC raster displayed through a GML layer

in QGIS.

pleths, feature selection, feature inquiring, geometri-

cal assessment and so forth. Figure 5 portraits a GML

ﬁle created from an HexASCII raster displayed in

QGIS (Team et al., 2013).

5 SUMMARY AND FUTURE

WORK

In spite of their well known advantages over tradi-

tional square grids, hexagonal rasters are yet to be

adopted as a common data structure in GIS. Such

evolution is unlikely to happen without tools facili-

tating the use of this space partitioning pattern. The

hex-utils tool-kit is a ﬁrst step in this direction, to-

wards the ultimate goal of making hexagonal meshes

as easy to use as their squared counterparts in GIS.

The hex-utils tool-kit comprises a basic API

and a set of command line tools providing essential

functionality to manipulate HexASCII rasters. They

make possible the creation of hexagonal rasters and

their visualisation in desktop GIS software. The API

can be the basis for the development of further soft-

ware supporting hexagonal rasters.

The next steps towards a simpliﬁed use of hexago-

nal rasters will have to address data acquisition, with

mechanisms to translate other common spatial data

sources into hexagonal rasters. Tools to transform

LiDAR point clouds or to discretise vectors into Hex-

ASCII rasters are therefore natural extensions to the

hex-utils tool-kit. Another step concerns the devel-

opment of hexagonal map algebra tools; a prototype

previously developed in the C# language (de Sousa,

2006) is a candidate to be integrated into the tool-kit.

Modern GIS software has become increasingly

easy to evolve and extend. The development of ad-

GISTAM 2017 - 3rd International Conference on Geographical Information Systems Theory, Applications and Management

182

vanced tools and data structures, such as hex-utils

and the HexASCII ﬁle format, is today not only sim-

pler, but also easier to reach by a wide range of poten-

tial users. All elements seem to be in place for hexag-

onal rasters to ﬁnally start entering the mainstream

GIS.

REFERENCES

Burggraf DS. 2006. Geography markup language. Data Sci-

ence Journal. 5:178–204.

Butler H, Daly M, Doyle A, Gillies S, Schaub T,

Schmidt C. 2008. The geojson format speciﬁcation.

URL: http://wwwgeojsonorg/geojson-spechtml/ (ac-

cessed 29-11-2016).

Chaplot V, Darboux F, Bourennane H, Legu

edois S, Sil-

vera N, Phachomphon K. 2006. Accuracy of interpo-

lation techniques for the derivation of digital elevation

models in relation to landform types and data density.

Geomorphology. 77(1):126–141.

de Sousa LM. 2006.

Algebra de Mapas em Grelhas Hexag-

onais [master’s thesis]. Universidade T

ecnica de Lis-

boa.

de Sousa LM, Leit

ao JP. In review. HexASCII: a ﬁle for-

mat for cartographical hexagonal rasters. International

Journal of Geographic Information Science.

Gibson L, Lucas D. 1982. Spatial data processing using

generalized balanced ternary. In: Proceedings of the

IEEE Conference on Pattern Recognition and Image

Processing. p. 566–571.

Golay MJE. 1969. Hexagonal parallel pattern transforma-

tions. IEEE Transactions on Computers. 18(8):733–

740.

Mersereau R. 1979. The processing of hexagonally sampled

two-dimensional signals. In: Proceedings of the IEEE;

Vol. 67. p. 930–949.

Sanner MF, et al. 1999. Python: a programming lan-

guage for software integration and development. J

Mol Graph Model. 17(1):57–61.

Shafranovich Y. 2005. Common format and mime

type for comma-separated values (csv) ﬁles. URL:

https://2rfcnet/4180 (accessed 13-02-2017).

Team QD, et al. 2013. Qgis geographic information sys-

tem. Open Source Geospatial Foundation Project

http://qgis osgeo org.

Warmerdam F. 2008. The geospatial data abstraction li-

brary. In: Open source approaches in spatial data han-

dling. Springer; p. 87–104.

Hex-utils: A Tool Set Supporting HexASCII Hexagonal rasters

183