Constraint Analysis based on Energetic Reasoning Applied to the
Problem of Real Time Scheduling of Workflow Management Systems
Flávio Félix Medeiros
1
and Stéphane Julia
2
1
Institute of Computation, Federal Institute of Mato Grosso do Sul - IFMS, Hilda Streat 203, Naviraí, Brazil
2
Computer Science Department, Federal University of Uberlandia - UFU, Uberlândia, Brazil
Keywords:
Workflow Management System, Petri Nets, Constraint Programming, Energetic Reasoning.
Abstract:
The objective of this paper is to propose a constraint analysis applied to the problem of real time scheduling in
workflow management systems. The adopted model is a p-time Workflow net with a hybrid resource allocation
mechanism. The approach considers time constraint propagation techniques for the different types of routings
that exist in workflow processes. Different types of resources, discrete and continuous, are then incorporated
into the model and an approach based on energetic reasoning is applied. Energetic reasoning can identify
unacceptable schedulings due to the energetic inability of the involved resources in the implementation of
the related activities. An update of the temporal constraints is then produced in order to eliminate the dates
inconsistent with the set of scheduling solutions. Considering the set of modified constraints, a specialized
inference mechanism called token player is then applied, which has the purpose of obtain in real time an
admissible scenario corresponding to a specific sequence of activities that respects the time constraints.
1 INTRODUCTION
The purpose of a workflow management system
(Aalst and Hee, 2004) is to run workflowprocesses. A
workflow process represents a sequence of activities
of an organization that must execute a specific case in
order to achieve a specific goal (treat a specific case).
Over recent years, Business Process Management has
become important in order to raise service quality and
a company’s performance (Hofstede et al., 2010).
According to (Aalst and Hee, 2004), the use of
Petri nets for the modeling of workflow processes has
many advantages, as in the fact of forcing a precise
process definition in enterprise systems.
Some models based on Petri nets were defined ex-
clusively for workflow representation as the workflow
Nets defined by Aalst (Aalst and Hee, 2004). The
workflow Net has only a Start place and only one End
place. A token in a Start place represents a case that
needs to be handled and a token in a End place rep-
resents a case that has been handled. Every task is
associated with a transition and every condition is as-
sociated with a place. In addition, every task and con-
dition must be on a path between the Start place and
the End place.
The workflow Nets are also used as an abstrac-
tion of the workflow process that is used to check the
soundness property. This property guarantees the ab-
sence of deadlocks and other anomalies that can be
detected without domain knowledge (Aalst and Hee,
2004).
The scheduling problem (Lee and DiCesare,
1994) aims to organize in time a sequence of activ-
ities, taking into consideration some time constraints
(timeslots) and restrictions shared resources used in
the implementation of the activities. Considering the
real-time system case, many scenarios (many cases in
a workflow management system) can be run simulta-
neously and conflict for shared resources, that must be
solved in real time (without backtrack mechanisms),
may occur if any non-preemptive resource is called
at the same time to execute activities that belong to
different scenarios.
The fundamental difference between the tradi-
tional scheduling problem of production systems and
the scheduling problem in workflow management sys-
tems is the nature of the resources involved in the
execution of activities. For production systems, the
resources represent physical equipment and are re-
presented by simple tokens (discrete type resources)
in the places. For workflow management systems
(WFMS), resources can represent physical equipment
as well as human resources. For example, we can al-
locate a nurse in a hospital to take care of several pa-
Medeiros, F. and Julia, S.
Constraint Analysis based on Energetic Reasoning Applied to the Problem of Real Time Scheduling of Workflow Management Systems.
DOI: 10.5220/0006275903730380
In Proceedings of the 19th International Conference on Enterprise Information Systems (ICEIS 2017) - Volume 3, pages 373-380
ISBN: 978-989-758-249-3
Copyright © 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
373

tients at the same time during her working day. In this
situation, a nurse cannot be seen as a single discrete
token. As a direct consequence, a model based on an
ordinary Petri net is not appropriate to represent all
the features that exist in workflow management sys-
tems.
Another problem is the uncertainty associated
with the behavior of human resources. This problem
makes it impossible to compute a predictable schedul-
ing solution for processes commonly found in manu-
facturing systems (Lee and DiCesare, 1994).
In this paper, a method of analysis under cons-
traints that aims to building a constraint knowledge
base system that can be integrated into a real time
scheduling strategy, is presented. In particular, the
main approach will consider a kind of energetic rea-
soning applied on resource constraints that exist in
workflow management systems.
2 TIME WORKFLOW NET WITH
HYBRID RESOURCE
ALLOCATION MECHANISM
The model proposed in this paper is the same model
adopted in (de Oliveira et al., 2008). It is a p-time
Petri net with hybrid resource allocation mechanisms.
The control structure follows the same as that used in
a classic workflow Net (Aalst and Hee, 2004), with a
Start place, a End place and with the main routings
that exist in workflow processes. The main defini-
tions and concepts related to the workkflow Net are
presented following in sections 2.1 and 2.2, respec-
tively.
2.1 Workfow Nets
• It has only one source place, named Start and only
one sink place, named End. These are special
places such that the Start place has only outgoing
arcs and the End place has only incoming arcs.
• A token in Start represents a case that needs to be
handled and a token in End represents a case that
has been handled.
• Every task t (transition) and condition p (place)
should be on a path from Start place to End place.
The formal definition of workflow Net is pre-
sented in the following.
Definition 1 (Workflow Net). A Petri net P N
= {P,T,F} is a workflow Net if, and only if,
1. There is one source place i ∈ P such that •i = φ,
2. There is one sink place o ∈ P such that o• = φ,
3. Every node x ∈ P∪T is on a path from i to o.
A workflow Net has one input place (i) and one
output place (o) due to the fact that any case handled
by the process represented by the workflow Net is cre-
ated when it enters the WFMS and is deleted once it
is completely handled by the WFMS, i.e., the work-
flow Net specifies the life-cycle of a case. Finally, the
third requirement in Definition 1 has been added to
avoid "dangling tasks and / or conditions", i.e., tasks
and contitions that do not contribute to the processing
of cases (Aalst and Hee, 2004).
As previously mentioned, a workflow Net has a
soundness property. This property is a correctness cri-
terion related to its dynamic behavior.
2.2 Soundness
A workflow Net is Sound if, and only if, the follow-
ing requirementes are satisfied (Aalst and Hee, 2004)
(Soares Passos and Julia, 2013).
• For each token put in the Start place, one and only
one token appears in End place.
• When the token appears in End place, all the other
places are empty for this case.
• For each transition (task), it is possible to move
from the initial state to a state in which that tran-
sition is enabled, i.e. there are no dead transitions.
The formal definition of soundness is presented
in the following:
Definition 2 (Soundness). A process modelled
by a workflow Net P N = {P,T,F} is sound if, and
only if:
1. For every state M reachable from state i, there ex-
ists a firing sequence leading from state M to state
o.
Formally,
∀
M
(i
∗
−→ M) ⇒ (M
∗
−→ o)
2. State o is the only state reachable from state i with
at least one token in place o. Formally,
∀
M
(i
∗
−→ M∧ M ≥ o) ⇒ (M = o)
3. There are no dead transitions in (PN,i). Formally,
∀
t∈T
∃
M,M
′
i
∗
−→ M
∗
−→ M
′
An activity can be associated to a transition in a
workflow Net. However, as presentend in (Leiliane
et al., 2016), in order to explicitly indicate the begin-
ning and the end of each activity in execution, two
sequencial transitions plus a place to model an activiy
ICEIS 2017 - 19th International Conference on Enterprise Information Systems
374

is used. The first transition represents the beginning
of the activity, the place represents the activity, and
the second transition represents the end of the activity
(Wang and Rosca, 2009) .
In this work, instead of associating tasks to transi-
tions, tasks are associated with specific places. Thus,
the resource allocation mechanisms can be easily
viewed on tasks.
In the following the main features of this model
are presented.
2.3 Routing Constraints
The handle complaints process presented in (Aalst
and Hee, 2004) will be used to illustrate the various
types of routings studied in this work. In this process,
a complaint needs to be initially registered. Then the
customer, who made the complaint, and the depart-
ment affected by the complaint are contacted. The
customer is contacted in order to obtain more infor-
mation. The department is informed about the com-
plaint and it is asked to take an initial action. These
two activities should be executed in parallel (paral-
lel routing). After that, the information is collected,
and in sequence, a decision must be taken (sequential
routing). Depending on the decision that was taken,
a payment is made or a letter is sent to the customer
(alternative routing). Finally the complaint is filed.
Figure 1 illustrates the different types of routings
on the handle complaints process. The places E
j
with
j=0 to 10 represent waiting places between activities.
The activities are associated with the places A
i
with
i=1 to 8. In particular, the places E0 and E10 represent
the Start and the End of the process. The token in E0
represent a case to be handled.
2.4 Time Constraints
Usually, the time required to execute an activity in
a workflow process is non-deterministic. According
to (de Oliveira et al., 2008), explicit time constraints
existing in systems with real-time characteristics can
be formally specified using a p-time Petri net model,
corresponding to a static time interval associated to
each place of the model.
The dynamic behavior of p-time Petri net depends
on the marking of the network and also of the tokens
temporal situation that is given by the visibility in-
terval (de Oliveira et al., 2008). A visibility interval
[(δ
p
)min, (δ
p
)max] associated with a token in a place
p of a p-time Petri net specified the minimum date
((δ
p
)min) at which a token is available in p to trig-
ger an output transition of p (earliest start date of an
activity), and the maximum date after which the to-
Figure 1: Handle complaints process.
ken becomes unavailable (dead) and cannot be used
to trigger any transition (latest start date of the cor-
responding activity).
2.4.1 Static Interval
The static definition of a p-time Petri net is based on
static intervals that represent the permanency inter-
val of the tokens in the places from the point of view
of the activities duration. The static definition of a
p-time Petri net can be shown in (de Oliveira et al.,
2008).
Figure 1 shows static intervals related to the activ-
ities of the handle complaints process. For each ac-
tivity A
i
, there exists a static interval that specifies its
minimum and maximum duration. In particular, the
static intervals associated with the tasks collect in A4
and file in A8 are [0, 0]s because their durations hold
no valeu when compared to other tasks of the handle
complaints process.
2.4.2 Visibility Interval
According to (de Oliveira et al., 2008) the dynamic
behavior of p-time Petri net depends on the marking
of the net and on the time situation of the tokens,
which is given by the visibility intervals whose
definition is the following one:
Definition 3 (Visibilit Interval of a p-time
Petri Net). A visibility interval [(δ
p
)
mim
, (δ
p
)
max
]
Constraint Analysis based on Energetic Reasoning Applied to the Problem of Real Time Scheduling of Workflow Management Systems
375

associated with a token in a place p of a p-time Petri
net defines:
• the earliest date (δ)
min
when the token in p be-
comes available for the firing of an output transi-
tion of p;
• the latest date (δ)
max
after which the token be-
comes non-available (dead) and cannot be used
for the firing of any transition.
2.5 Resource Constraints
Some of the resources used in workflow management
systems can be considered of discrete types and can
be represented by simple tokens. It is generally the
resources which represent physical equipment such as
a printer, for example. Other resources can be repre-
sented by continuous resources. It is generally the
case of human type resources. These resources are
represented by a real number that shows the availabil-
ity of a human resource.
According to (David, 2010) a discrete resource
allocation mechanism and a continuos resource
mechanism can be defined as following:
Definition 4 (Discrete Resource Allocation
Mechanism). A discrete resource mechanism can
be defined by the marked ordinary Petri net model
(David, 2010)
C
DR
= h A
DR
, T
DR
, Pre
DR
, Pos
DR
, M
DR
i with:
• A
DR
=
S
N
DR
α=1
A
α
∪ {R
D
} where R
D
represents the
discrete resource place, A
α
an activity place and
N
DR
the number of activities which are connected
to the discrete resource place R
D
.
• T
DR
=
S
N
DR
α=1
T
in
α
∪
S
N
DR
α=1
T
out
α
where T
in
α
rep-
resents the input transtion of the activity A
α
and
T
out
α
represents the output transtion of the activity
A
α
.
• Pre
DR
: A
DR
× T
DR
→ {0,1} the input inci-
dence application, such as Pre
DR
(R
D
, T
in
α
) = 1
and Pre
DR
(A
α
, T
out
α
) = 1 (other combinations of
place/transition are equal to zero).
• Pos
DR
: A
DR
× T
DR
→ {0,1} the output inci-
dence application, such as Pos
DR
(R
D
, T
out
α
) = 1
and Pos
DR
(A
α
, T
in
α
) = 1 (other combinations of
place/transition are equal to zero).
• M
DR
: R
D
→ R the initial marking application,
such as M
DR
(R
D
) = m
D
the number os discrete
resources of the same type.
Definition 5 (Continuous Resource Allocation
Mechanism). A continuous allocation mechanism
can be defined by the marked hybrid Petri net model
(David, 2010)
C
C
CR = h A
CR
, T
CR
, Pre
CR
, Pos
CR
, M
CR
i whith:
• A
CR
=
S
N
CR
α=1
A
α
∪ {R
C
} where R
C
represents the
continuous resource place, A
α
an activity place
and N
CR
the number of activities which are con-
nected to the continuous resource place R
C
.
• T
CR
=
S
N
CR
α=1
T
in
α
∪
S
N
CR
α=1
T
out
α
where T
in
α
repre-
sents the discret input transtion of the activity A
α
and T
out
α
represents the discrete output transtion
of the activity A
α
.
• Pre
CR
: A
CR
× T
CR
→ R
+
the input incidence ap-
plication, such as Pre
CR
(R
C
, T
in
α
) = X
α
and X
α
in
R
+
and Pre
CR
(A
α
, T
out
α
) = 1 (other combinations
of place/transition are equal to zero).
• Pos
CR
: A
CR
× T
CR
→ R
+
the output inci-
dence application, such as Pos
CR
(R
C
, T
out
α
) = X
α
and Pos
CR
(A
α
, T
in
α
) = 1 (other combinations of
place/transition are equal to zero).
• M
CR
: R
C
→ R
+
the initial marking application,
such as M
CR
(R
C
) = m
C
the availability (in percent-
age) of the continuous resource.
3 CONSTRAINT PROPAGATION
TECHNIQUE
3.1 Time Constraint Propagation on
Routings
The time constraint propagation technique on rout-
ings proposed in this paper was originally presented
in (de Oliveira et al., 2008). The visibility intervalsas-
sociated with the waiting places E
j
between the activ-
ities of the workflow Net are calculated using classica
techniques of constraint propagation based on graphs
without circuits (de Oliveira et al., 2008), and setting
the beginning date of a case as well as its maximum
duration to be completed.
Figure 2 illustrates the application of the time con-
straint propagation mechanism over the routes of the
handle complaints process, considering four cases to
be treated.
In figure 2 (A), the minimum borders of visibility
intervals associated with the place E0 represent the
start date of four cases to be treated by the workflow
process. The maximum borders of visibility inter-
vals associated with the place E10 represent the ex-
pected end dates of the four cases, knowing that the
maximum duration to treat each case is 105 units of
time. Since the minimum and maximum durations of
ICEIS 2017 - 19th International Conference on Enterprise Information Systems
376

Figure 2: Example of time constraint propagation mecha-
nism on routings.
each activity (static intervals)are knownas well as the
workflow process routings, we can apply constraints
propagation mechanisms to obtain the waiting times
between the activities (visibility intervals associated
with waiting places Ei. Figure (2 (B)) shows the re-
sulting visibility intervalsafter applying the constraint
propagation techniques for each one of the four cases.
For example, the visibility interval V1 associated with
the place E7 means that the activity pay associated
with case 1 can be started between the earliest date
45 and the latest date 90.
3.2 Energetic Reasoning for Resource
Constraints
The time constraint propagation mechanism that con-
siders the resources availability takes into account an
approach based on a kind of energetic reasoning pro-
posed initially by Artigues and Lopez (Artigues and
Lopez, 2015). Such an approach was used to treat the
problem of task scheduling in manufacturing systems
using a model based on graphs with activities on arcs.
Energetic reasoning shows the relationship that exists
between the energy provided by the resources and the
energy consumed by the activities.
Considering the context of workflow management
systems, each activity i can be characterized by its
minimum (Pmin
i
) and maximum (Pmax
i
) durations
and must be executed within a time window [r
i
, d
i
]
with r
i
representingthe earliest date of the activity and
d
i
representing the latest delivery date of the activity.
3.2.1 Global Consistency Study
According to (Artigues and Lopez, 2015) the max-
imum available energy that a resource can provide
in a given time window ∆ =[F
∆
, S
∆
] is defined as:
W
∆
= A.(F
∆
− S
∆
) where A is an energy intensity
value that the resource in question provides to execute
the activities that use it.
Considering an activity i, that starts at date S
i
and
finishing at date F
i
, considering also the energy inten-
sity A
i
that it requires from the resource and a given
time window ∆, two situations can occur to define the
energy required by i in ∆:
If ([S
i
, F
i
] ∩ ∆) 6=
/
0 then
W
∆
i
= a
i
.[min(F
i
, F
∆
) − max(S
i
, S
∆
)].
If ([S
i
, F
i
] ∩ ∆) =
/
0 then W
∆
i
= 0, where W
∆
i
is the
energy required by i in ∆. More generally, we can say
that
W
∆
i
= a
i
.max[0, min(F
i
, F
∆
) − max(S
i
, S
∆
)].
Since S
i
(earliest date of activity i) is a variable,
W
∆
i
is also a variable, therefore, we can derive some
minimum values taking into account the time interval
[r
i
, d
i
].
The minimum energy required by an activ-
ity i over the time window ∆, which is called
W
∆
i
, is obtained by the position of the activity
i that least overlaps the time window ∆: W
∆
i
=
a
i
.max[0, min(Pmin
i
, F
∆
− S
∆
, r
i
+ Pmin
i
− S
∆
, F
∆
−
d
i
+ Pmin
i
)].
ConsideringW
∆
, an energy providedby a resource
on a given time window ∆, and
∑
n
i=1
W
∆
i
, the energy
required by the activities that will use it in the same
time window ∆, we can derive a global consistency
condition which must be respected by any scheduling
at any interval ∆,
∀∆,
∑
n
i=1
W
∆
i
≤ W
∆
(1)
The formula in (1) means that the sum of the en-
ergy spent for the activities that use the same resource
in a time interval ∆ has to be smaller than the total
energy produced by the resource. In particular, from
condition (1), the following proposition can be drawn.
If ∃∆ such that
∑
n
i=1
W
∆
i
> W
∆
, then there exists
no admissible scheduling.
Figure 3 illustrates a conflict situation for the
shared resource R2 (Complaints employee) of the
handle complaints process illustrated in Figure 5(A).
This resource will be involved in the execution of
Constraint Analysis based on Energetic Reasoning Applied to the Problem of Real Time Scheduling of Workflow Management Systems
377

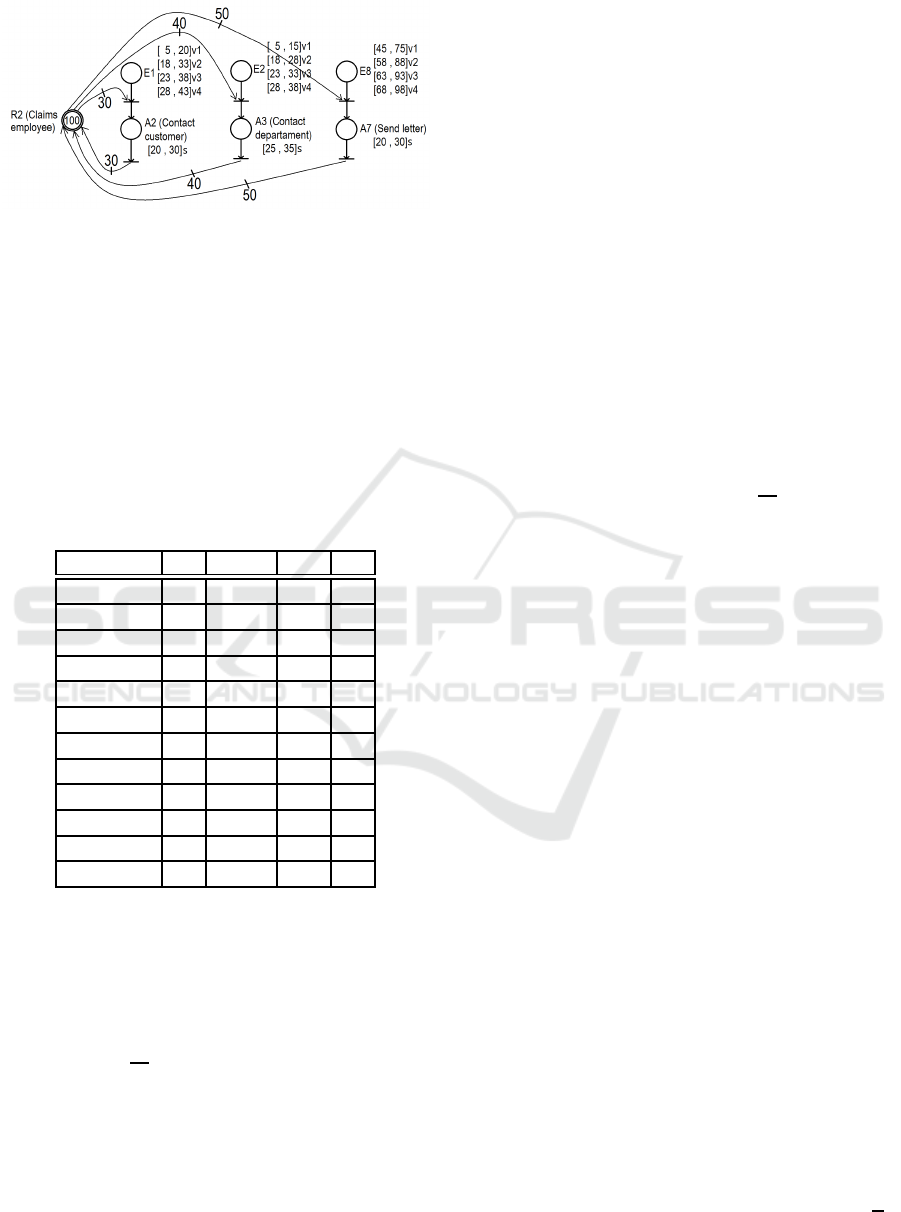
Figure 3: Continuous resource allocation mechanism.
twelve different activities. Table 1 presents these ac-
tivities with their respective time constraints [r
i
, d
i
],
their minimum durations (Pmin
i
) and their energy in-
tensities (a
i
). The time restriction r
i
is given by the
minimum bounds of visibility intervals, Pmin
i
by the
minimum bounds of static intervals, d
i
by the sum of
minimum bounds of visibility intervals and the max-
imum bounds of the static intervals, and a
i
by the
weights associated to the archs of the continuous re-
source R2.
Table 1: Data of the activities involved with resource R2.
i r
i
Pmin
i
d
i
a
i
A2 Case 1 5 20 50 30
A2 Case 2 18 20 63 30
A2 Case 3 23 20 68 30
A2 Case 4 28 20 73 30
A3 Case 1 5 25 50 40
A3 Case 2 18 25 63 40
A3 Case 3 23 25 68 40
A3 Case 4 28 25 73 40
A7 Case 1 45 20 105 40
A7 Case 2 58 20 118 40
A7 Case 3 63 20 123 40
A7 Case 4 68 20 128 40
For example, considering the activity A3, related
to Case 4, an interval ∆ that covers the entire exe-
cution window [S
∆
, F
∆
] = [r
i
, d
i
] must be chosen. In
this case, ∆=[S
∆
= 28, F
∆
= 73]. Adding up the min-
imum energy needed for the complete execution of
each of the twelve activities, within the considered ∆,
we obtain
∑
n
i=1
W
∆
i
= 3830. This value is less than
the energy that the resource R2 can provide during
this studied interval (W
∆
=4500). This ensures that in
the interval ∆, the resource R2 can provide the mini-
mum energy required to execute the 12 activities com-
pletely.
In the example of the handle complaints process,
it can be verified that for the 12 activities using the
resource R2, the global consistency condition is satis-
fied. A situation where condition (1) is not respected
would imply in the impossibility of finding an ac-
ceptable scheduling without relaxing some of the time
constraints.
Energetic reasoning also takes into account a set S.
This set denotes constraint variables that represent the
starting dates of the activities consistent with [r
i
, d
i
]
and with the resource restrictions involved in the exe-
cution of the activities. The global consistency condi-
tion does not allow for the direct updating of the vari-
ables in set S. For this, a local consistency condition
can be considered.
3.2.2 Local Consistency Study
When considering an activity i, the global consistency
condition (1) can be rewritten as follows,
∀i, ∀∆,W
∆
i
≤ W
∆
−
∑
n
j=1, j6=i
W
∆
j
Considering the maximum value of the right side
of the condition above, we can derive the maximum
value for its left side.
The term A
∆
i
= W
∆
−
∑
n
j=1, j6=i
W
∆
j
is called the
maximum energy available left by other activities in
the interval ∆, for the execution of the activity i. Any
starting date S
i
of the activity i, that leads to a higher
energy consumption than the maximum energy avail-
able to it, must be modified.
The constraint propagation mechanisms that are of
interest in this work aim to remove inconsistent val-
ues of certain activities in order to reduce the set of
possible solutions.
As previously mentioned, the set S denotes
constraint variables, which represent the starting
dates of the activities consistent with [r
i
, d
i
] and with
the resource restrictions involved in the execution of
the activities. At this point the formal definition of
the set S can be presented as follows.
Definition 6 (Constraint Variables of the Set
S). A starting date S
i
of an activity i will be part of
the set S if, and only if the following three conditions
are satisfied,
1. S
i
∈ [r
i
, d
i
],
2. ∀∆,
∑
n
i=1
W
∆
i
≤ W
∆
,
3. ∀i, ∀∆,W
∆
i
≤ W
∆
−
∑
n
j=1, j6=i
W
∆
j
.
According to (Artigues and Lopez, 2015), a way
to locally verify that the resource used by a particular
activity provides sufficient energy for its full comple-
tion taking into account the value of A
∆
i
(maximum
energy available for the activity i) is to perform the
calculation of the maximum equivalent duration
p
∆
i
.
This duration represents the maximum duration of the
ICEIS 2017 - 19th International Conference on Enterprise Information Systems
378

resource availability to execute the activity i respect-
ing the minimum energy expenditure of others activi-
ties that use the same resource in the interval ∆. Thus
p
∆
i
is given by the ratio between A
∆
i
and the energy
intensity that i requires from the resource: p
∆
i
=
A
∆
i
a
i
.
For example, considering the activity A3 of case 4
on figure 3 it can be verified that by adopting an inter-
val ∆, which covers exactly the minimum duration of
the activity execution,
∆ = [S
∆
= ((δ
p
)min), F
∆
= ((δ
p
)min) + Pmin
i
], that
is [S
∆
= 28, F
∆
= 28 + 25 = 53] (figure 4) and con-
sidering the maximum energy available A
∆
i
=970 for
this activity in this interval ∆, the obtained value of
p
∆
i
=24.25 is less than the value of Pmin
i
=25. In this
particular case, the value of
p
∆
i
=24.25 means that the
resource R2 can supply energy to the activity A3 on
case 4 during 24.25 time units. Since the minimum
duration of the activity corresponds to 25 time units,
there exists a local inconsistency as the resource du-
ration availability is less than the minimum necessary
to execute the corresponding activity. In order to find
a time range within the time interval [r
i
, d
i
] where the
duration p
∆
i
is greater or equal to Pmin
i
, a displace-
ment of the interval ∆ on the right can be applied.
Figure 4: Displacement of the delta time interval.
The interval ∆, after the displacement on the right,
in accordance to the subtraction between (Pmin
i
) and
(
p
∆
i
) (25 - 24.25 ≈ 0.8), is equal to [S
∆
= 28 +
0.8, F
∆
=53+0.8] = [S
∆
=28.8 ,F
∆
=53.8]. By perform-
ing the calculation of the maximum equivalent dura-
tion, taking into account this new interval ∆, we ob-
tain
p
∆
i
=24.4. Since the maximum equivalentduration
is still smaller than the minimum duration of the ac-
tivity A3 associated to case 4 (Pmin
i
=25), there still
exists a local inconsistency corresponding to the ear-
liest starting date of this activity. Thus, it is necessary
to continue producing a right displacement of ∆ until
a local consistency condition is verified.
By moving the interval ∆ for nine times on the
right, a new inteval ∆ =[S
∆
=34.1 ,F
∆
=59.1] is pro-
duced (figure 4). By performing the calculation of
the maximum equivalent duration, taking into account
this final interval ∆, we obtain
p
∆
i
=25.5, with p
∆
i
>
Pmin
i
. Then, the earliest starting date of the activity
A3 associated to case 4 becomes 34.1 ≈ 34, as shown
in figure 5 (B).
In fact, if this activity starts between the dates 28
Figure 5: Application of the energy reasoning approach on
the handle complaints process.
and 34 (visibility interval obtained after applying the
time constraint propagation technique on the routings
of the process and before applying energetic reason-
ing on the resource involved in the activity execution),
we are sure that an inconsistency will happen and as a
consequence a schedule that respects all the time con-
straints will not be found.
The moving of the latest starting dates of any ac-
tivity of the workflow process can be performed in a
similiar way considering left displacements of maxi-
mum bounds of ∆ intervals.
After the upgrade of the visibility interval V4 in
E2, related to activity A3 associated to case 4 (figure
5 (B)), the same propagation technique must be ap-
plied to the other activities of the handle complaints
process. The final result is show in Figure 5(B).
4 GENERAL PRINCIPLE FOR
REAL TIME SCHEDULING
A possible technique for allowing the dynamic exe-
cution of a p-time Petri nets (real time scheduling)
is the p-time Petri net token player algorithm presen-
tend in (de Oliveira et al., 2008). In particular, when
the model of the workflow process is based on a p-
time Petri net model, the algorithm of the token player
Constraint Analysis based on Energetic Reasoning Applied to the Problem of Real Time Scheduling of Workflow Management Systems
379

must allows to solve in real time conflicts for shared
resources.
The main purpose of the scheduling technique is
then to find a sequence of activities, from Start place
to End place, which respect the set of time constraints
given by the visibility intervals associated to each ac-
tivity of the process.
The token player has a calendar of events (mini-
mum and maximum bounds of the visibility intervals
for each case) scheduled over time. Each time a min-
imum bound is reached, a token becomes available.
If this token enables a transition and if there is no
actual conflict for a shared resource, the transition is
fired; otherwise the conflict is isolated and a decision-
making mechanism is activated to verify if the tran-
sition can be fired at the minimum date indicated on
its visibility interval. If a transition is fired, a new
marking is produced and new visibility intervals are
computed; otherwise, the next event of the calendar
is treated. The decision-making mechanism is based
on the generation of class graphs and was presented
in (de Oliveira et al., 2008). If a maximum date of a
visibility interval is reached, then the death of a token
happens and a time constraint is violated. In this case,
there is no guarantee that deadliness of the process
will be respected.
5 CONCLUSIONS
The major contribution of this work concerns the im-
provement of a knowledge base system that defines a
set of time constraints that a token player must respect
during the execution of a real-time scheduling tech-
nique. The main objective is to produce for each case
of a workflow Net a sequence of activities that respect
a set of temporal constraints, given by a set of visibil-
ity intervals (date intervals that fix the starting dates
of the activities). In particular, the filtering technique
based on a kind of energetic reasoning and on global
and local conditions ensures that the existing incon-
sistent time windows will be removed and reallocated
in different dates in order to create favorable condi-
tions for the existence of an admissible scheduling so-
lution. Applying a kind of intelligent token player al-
gorithm with decision making mechanism to the new
knowledge base obtained after applying the energetic
reasoning, the quality of the produced scheduling so-
lutions (in particular the respect of deadlines associ-
ated to the cases of the process) will then be increased,
in particular if compared with basic strategies of the
type FIFO (First in First Out), which are generally the
ones applied to this kind of business systems.
A prototype of the presented approach was imple-
mented in Visual Prolog programming language.
As a future work proposal, a real time scheduling
strategy based on a kind of token player similiar to the
one presented in (Freitas et al., 2016) will be imple-
mented and validated on the Colored Petri net model-
ing and simulation tool known as CPN Tolls (Jensen
et al., 2007)
REFERENCES
Aalst, W. V. D. and Hee, K. V. (2004). Workflow Manage-
ment: Models, Methods and Systems. MIT Press.
Artigues, C. and Lopez, P. (2015). Energetic reasoning for
energy-constrained scheduling with a continuous re-
source. Journal of scheduling, 18(3):225 – 241.
David, R., A. H. (2010). Discrete, Continuous, and Hybrid
Petri Nets. 2nd edn. Springer Publishing Company,
Incoporated.
de Oliveira, F. F., Julia, S., and Valette, R. (2008). Real time
scheduling of workflow management systems based
on a p-time petri net model with hybrid resources.
Simulation Modelling Practice and Theory 16, pages
462–482.
Freitas, J. C. J., Julia, S., and Rezende, L. P. (2016). Mod-
eling a fuzzy resource allocation mechanism based on
workflow nets. 18th International Conference on En-
terprise Information Systems, pages 559 – 566.
Hofstede, A., Aalst, W., Adams, M., and Russell, N. (2010).
Modern Business Process Automation: YAWL and its
Support Environment. Springer-Verlag, Berlin.
Jensen, K., Kristensen, M., and Wells, L. (2007). Coloured
petri nets and cpn tools for modelling and validation
of concurrent modeliling. International Journal on
Software Tools for Technology Transfer, pages 213 –
254.
Lee, D. and DiCesare, F. (1994). Scheduling flexible manu-
facturing systems using petri nets and heuristic search.
In IEEE transactions on Robotics and Automation,
pages 123–132.
Leiliane, P. R., Julia, S., and Cardoso, J. (2016). Uncer-
tain marking for dealing with partial parallelization in
business processes. In Proceedings of the 18th Inter-
national Conference on Enterprise Information Sys-
tems, pages 118–125.
Soares Passos, L. M. and Julia, S. (2013). Qualitative anal-
ysis of interorganizational workfflow nets using linear
logic: Soundness verification. Procedings of the 2013
IEEE 25th International Conference on Tools with Ar-
tificial Intelligence, pages 667–673.
Wang, J., T. W. and Rosca, D. (2009). Emergency response
workflow resource requirements modeling and analy-
sis. IEEE Transactions on SMC, Part C, 39:270-283.
ICEIS 2017 - 19th International Conference on Enterprise Information Systems
380