
Feature Model Composition Assisted by Formal Concept Analysis
Jessie Carbonnel
1
, Marianne Huchard
1
, Andr
´
e Miralles
2
and Cl
´
ementine Nebut
1
1
LIRMM, CNRS and Universit
´
e de Montpellier, 161 rue Ada, 34095, Montpellier Cedex 5, France
2
TETIS, IRSTEA, 500 rue Jean-Franois Breton, 34093, Montpellier Cedex 5, France
Keywords:
Software Product Line, Feature Model, Feature Model Composition, Formal Concept Analysis.
Abstract:
In the domain of software product lines, Feature Models (FM) play a central role in variability modeling, com-
pleted by configuration collections (from concrete software product lines), logical representations, constraint
programming or conceptual structures, coming from the field of Formal Concept Analysis (FCA). The devel-
opment of feature models may take several forms, including their synthesis from configuration collections or
their design in several steps (by several teams or with different concerns). FM composition (merge) operators
are part of that design activity as they assist their iterative building. In this paper, we describe an approach,
based on two main merging semantics (intersection and union), which assists designers in merging several
FMs. This approach benefits from the help of FCA to represent all the FMs with the same configuration set
through a canonical form. We describe the implementation of our approach and present a set of concrete
examples.
1 INTRODUCTION
Software Product Lines have been introduced to re-
duce the cost and the time needed for producing soft-
ware systems, while increasing their quality and di-
versity (Pohl et al., 2005). The design of a software
product line can be achieved in different ways, de-
pending on the context. It has two main phases, do-
main engineering, where commonality and variability
are captured and application engineering, which fo-
cuses on the software product derivation. In domain
engineering, requirement models are defined, includ-
ing more specifically feature models that are widely
used (Kang et al., 1990). Feature models (FM) de-
scribe the commonalities and the variability of a soft-
ware product line based on a hierarchical decomposi-
tion of the system features, provided with annotations
and logical formulas. An FM defines the acceptable
set of configurations, a configuration being a set of
features. As any design process, defining an FM is not
straightforward, as several concerns have to be taken
into account, several actors can participate and differ-
ent sources of information can be used, depending if
the FM is defined using real-word product lines (a set
of concrete products already exists and the FM has to
synthesize their configurations) or is defined during
requirement analysis (Krueger, 2002).
Merging several FMs or simply analyzing their
differences takes part in this design activity and has
been studied thoroughly in the literature (Acher et al.,
2010). These activities require in particular to com-
pute intersection and union of FMs. However, there
is an inherent divergence between structural intersec-
tion/union and the intersection/union of the config-
uration sets. Indeed, one main semantics of a fea-
ture model is its configuration-semantics (She et al.,
2011), given by the set of configurations defined by
the feature model. An issue which has to be addressed
is the fact that FMs are not canonical forms, in the
sense that a set of configurations (sets of features) of-
ten can be represented by several FMs (Czarnecki and
Wasowski, 2007). This is the same for alternative
representations as propositional formulas and con-
straints (in Constraint Problem solving approaches).
The originality of our approach is to base the merging
of feature models on a canonical structure obtained
through the application of Formal Concept Analysis,
using the configuration-semantics of feature models.
In the domain of software product lines, when the
configuration set of a product collection was the pri-
mary artifact, other approaches have been tried, that
rely on Formal Concept Analysis and several of its
associated representations. The conceptual structures
mix features and configurations. They have limits re-
lated to the need of enumerating the configurations
and to the loss of ontological knowledge (as proposi-
tional formulas). As a counterpart, they are canoni-
cal and have graphical representations, that show re-
Carbonnel, J., Huchard, M., Miralles, A. and Nebut, C.
Feature Model Composition Assisted by Formal Concept Analysis.
DOI: 10.5220/0006276600270037
In Proceedings of the 12th International Conference on Evaluation of Novel Approaches to Software Engineering (ENASE 2017), pages 27-37
ISBN: 978-989-758-250-9
Copyright © 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
27

lations between configurations, between features, and
between features and configurations.
In this paper, we propose an approach, based
on FCA, for understanding and assisting the fea-
ture model composition (intersection and union), also
known as feature model merging, and provide assis-
tance to designers during this activity. This work can
also be used to extract a representation (with or with-
out a feature model) for aligning two sets of prod-
uct configurations, as in the case of two organisms (or
vendors) that would propose or analyze a unified rep-
resentation of their products.
Section 2 explains how the FCA framework al-
lows us to build canonical forms for variability in a
configuration set, in the sense that they encode all the
feature models that have the same configuration set.
Section 3 recalls the definition of main merge opera-
tors by (Acher et al., 2010) and describes the way con-
ceptual structures may be used to understand and to
guide the merge operations (intersection and union).
Section 4 describes a process that implements the ap-
proach, gives some illustrations of its application and
investigates the scope of applicability. Section 5 de-
tails the related work. Section 6 concludes the docu-
ment with some perspectives.
2 FCA FOR VARIABILITY
REPRESENTATION
There are several means for representing feature-
based variability, from configuration set, proposi-
tional logic, set of constraints (in Constraint Satis-
faction Problem paradigm), to graph-based, or Fea-
ture Models (FMs) that can be considered a standard
representation. Here we consider the FODA model
(Kang et al., 1990), that is the most widely-used in
the litterature.
2.1 Running Example
To illustrate the rest of the paper, we use the example
of grid-based medical imaging services proposed in
(Acher et al., 2010). The original feature model is
denoted FM1 and we also introduce a variation of this
feature model denoted FM1v, both feature models are
presented in Figure 1.
Let us consider the FM1. It represents a service
for medical imaging. The set of features is orga-
nized in a tree where the features are the nodes and
the edges indicate various dependencies between fea-
tures. The medical imaging service (MI) requires a
modality (Mo) and a format (F). This mandatory rela-
tion is indicated through an edge ending with a black
disk. The format (F) optionally needs a header (H),
indicated by an edge ending with a white circle. The
children of a feature may also be grouped into xor
groups (if the parent feature belongs to a configura-
tion, exactly one child feature of the group is also
present) or into or groups (if the parent feature be-
longs to a configuration, one or more child features
of the group are also present). An xor group is indi-
cated by a black line connecting the edges going from
the parent to the children. An or group (not present
in this example) is indicated by a black filled zone
connecting the edges going from the parent to the
children. In this FM, the modality (Mo) imposes to
choose exactly one image acquisition technique (xor
group) among magnetic resonance imaging (MRI) or
X-ray computed tomography (CT).
In another FM that appears later in the paper, an-
other image acquisition technique, namely positron
emission tomography (PET), will be proposed. The
format (F) requires the anonymizing service and op-
tionally a service for header addition (H). The header
may be written using exactly one (xor group) of the
medical image exchange standards: Digital Imaging
and Communication in Medicine (DICOM) or Neu-
roimaging Informatics Technology Initiative (Nifti).
2.2 Applying Formal Concept Analysis
The two feature models of Figure 1 admit the same
set of configurations, which is denoted by [[FM1]]=
[[FM1v]]. This configuration set is shown in Table 1
in which we have a column per feature and a line per
configuration and in which a cross for column c and
line l means that configuration l owns the feature c. In
the FCA framework, such a table is called a Formal
Context.
Table 1: Formal context of the configuration set associated
with FM1 and FM1v.
MI1
A
CT
D
F
H
MI
MRI
Mo
N
MI1c0 × × × × × × ×
MI1c1 × × × × × × ×
MI1c2 × × × × ×
MI1c3 × × × × ×
MI1c4 × × × × × × ×
MI1c5 × × × × × × ×
Definition 1 (Formal Context). A formal context K
is a 3-tuple (G, M, I), where G is an object (configura-
tion) set, M an attribute (feature) set, and I ⊆ G×M
is a binary relation which associates objects (config-
urations) with attributes (features) they own. For a
context K = (G, M, I), for g ∈ G we will denote by I(g)
the set of features of g, i.e. the set {m ∈ M|(g, m) ∈ I}.
ENASE 2017 - 12th International Conference on Evaluation of Novel Approaches to Software Engineering
28
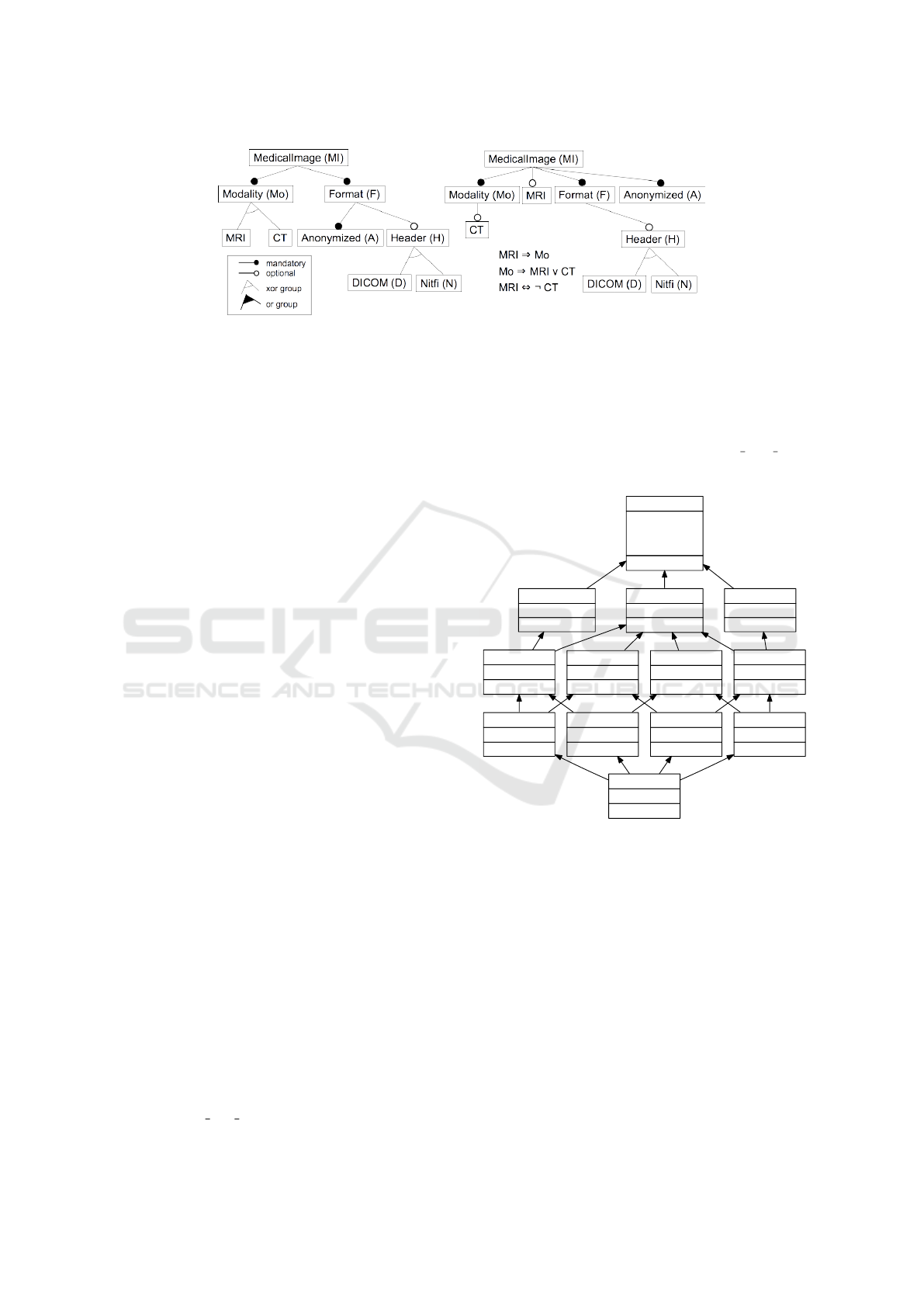
Figure 1: Left-hand-side: Feature Model FM1 from (Acher et al., 2010) (for a medical imaging service); Right-hand-side:
one equivalent variation FM1v (with same set of configurations).
From the formal context, specialized algorithms
from FCA framework extract formal concepts. A for-
mal concept is a maximal group of objects associated
with the maximal group of attributes they share. It can
be read in the table of the context as a maximal rect-
angle of crosses (modulo permutations of rows and
columns).
Definition 2 (Formal Concept). Given a formal con-
text K = (G, M, I), a formal concept associates a max-
imal set of objects with the maximal set of attributes
they share, yielding a set pair C = (Extent(C),
Intent(C)) such that:
• Extent(C) = {g ∈ G|∀m ∈ Intent(C), (g, m) ∈ I}
is the extent of the concept (objects covered by the
concept).
• Intent(C) = {m ∈ M|∀g ∈ Extent(C), (g, m) ∈ I}
is the intent of the concept (shared attributes).
For example, ({MI1c1, MI1c5}, {MI, Mo, F, A,
MRI, H}) is the concept that groups configurations
MI1c1 and MI1c5 (concept extent) that share the fea-
tures MI, Mo, F, A, MRI and H (concept intent).
The formal concepts are ordered using inclusing
of their extent. Given two formal concepts C
1
=
(E
1
, I
1
) and C
2
= (E
2
, I
2
) of K, the concept specializa-
tion/generalization order
C
is defined by C
2
C
C
1
if
and only if E
2
⊆ E
1
(and equivalently I
1
⊆ I
2
). C
2
is
a specialization (a subconcept) of C
1
. C
1
is a gener-
alization (a superconcept) of C
2
. Due to these defini-
tions, C
2
intent inherits (contains) the attributes from
C
1
intent, while C
1
extent inherits the objects from C
2
extent.
Definition 3 (Concept Lattice) . If we denote by C
K
the set of all concepts of K, L
K
=(C
K
,
C
), is the con-
cept lattice associated with K.
The graphical representation of the concept lattice
exploits the inclusion property (see Figure 2) to avoid
representing in the concepts the top-down inherited
features and the bottom-up inherited configurations.
A concept is represented in this document in a three-
part box. The top part contains the concept identifier
(e.g. Concept MI1 10), the middle part contains the
features of the intent that are introduced by this con-
cept (e.g. CT), the bottom part contains the configu-
rations of the extent that are introduced by this con-
cept (e.g. MI1c2). With inherited features, and con-
figurations the whole concept is Concept MI1 10 =
({MI1c2, MI1c0, MI1c4}, {MI, Mo, F, A, CT }).
Figure 2: Concept lattice associated with Table 1.
Specific suborders can be isolated in the concept
lattice, as the AOC-poset which contains only the con-
cepts introducing at least one object (configuration),
or at least one attribute (feature) (or both, see Figure
3 (a)), or the AC-poset which contains only the con-
cepts introducing at least one attribute (feature) (see
Figure 3 (b)). In the AOC-poset (as in the concept
lattice) a configuration (resp. a feature) appears only
once, thus we have a maximal factorization of con-
figurations and features. In the AC-poset, one con-
figuration (e.g. MI1c4) may appear several times, but
features remain maximally factorized revealing a sim-
plified structure.
Furthermore, if the formal context is exactly the
set of valid configurations of an FM, conceptual struc-
Feature Model Composition Assisted by Formal Concept Analysis
29
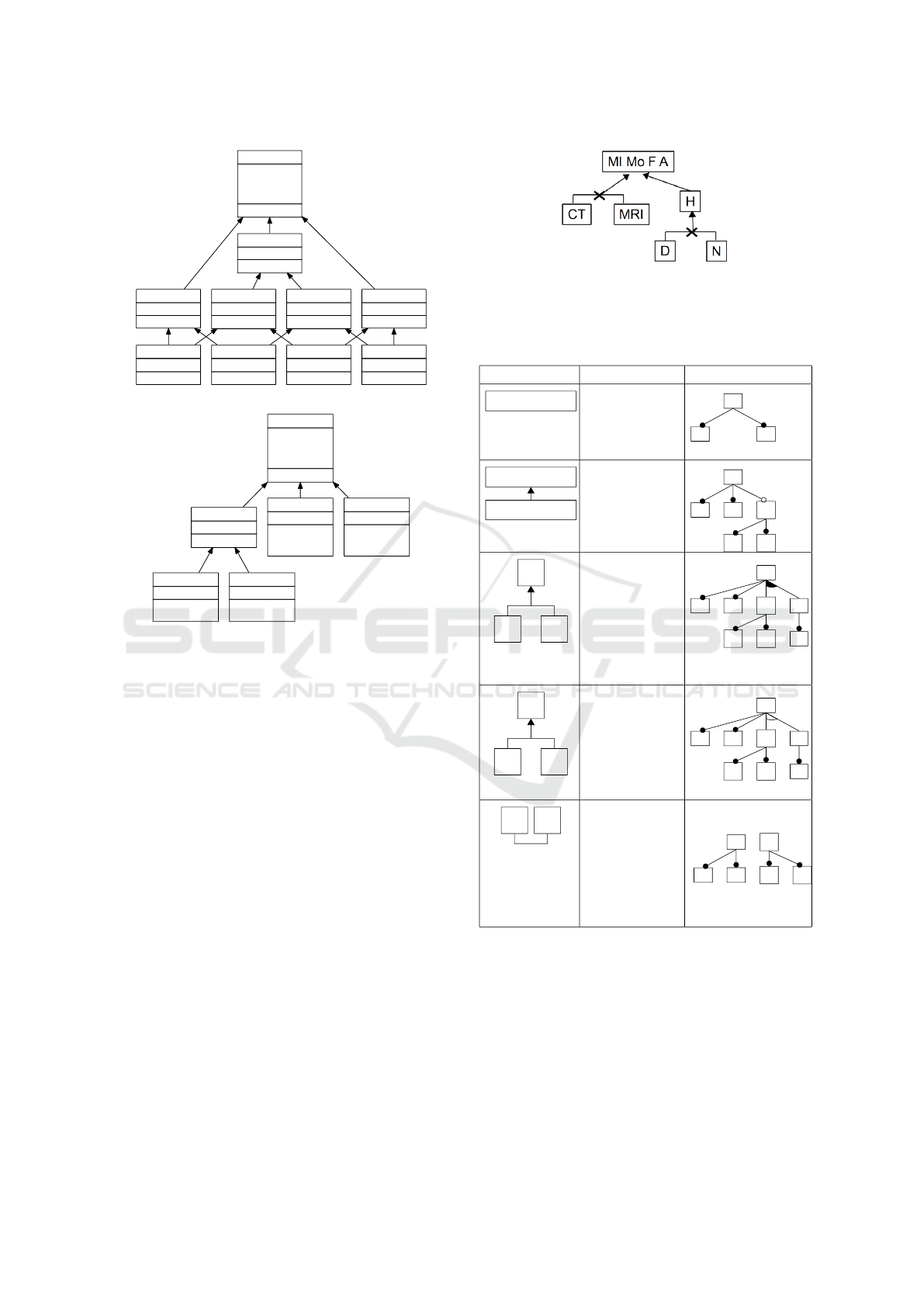
(a) AOC-poset
(b) AC-poset presented with leaves labeled by
the configurations
Figure 3: AOC-poset and AC-poset associated with formal
context of Table 1.
tures represent, in a unique way, this configuration
set: there is a unique concept lattice, a unique AOC-
poset, a unique AC-poset representing the FM. There-
fore, any FM with the same configuration set has
the same associated conceptual structures. Thus if
we consider the AOC-poset (which is a good com-
promise in size and in information presentation (no
redundancy)) corresponding to FM1, FM1v and any
other feature model with the same configuration set,
all these FMs conform to it. This means that each de-
pendency expressed in these feature models matches
a dependency expressed in the corresponding AOC-
poset. For instance, if there is a child-parent ( f
c
, f
p
)
in a FM, it belongs to the AOC-poset in this way: let
C
c
the concept introducing f
c
and C
p
the concept in-
troducing f
p
, C
c
C
C
p
.
2.3 Equivalence Class Feature Diagram
However, the posets are hardly readable and far from
feature models. That is why we introduce another
equivalent structure (the equivalence class feature dia-
Figure 4: Equivalence class feature diagram (ECFD), alter-
native representation of the posets of Figure 3.
Table 2: Equivalence class feature diagram (ECFD): con-
structs and semantics. The third column gives an example
of conform feature model with n
A
= n
B
= 3 and n
C
= 2.
construct semantics ex. of conform FM
A = {a
1
, ··· , a
n
A
}
features a
i
are al-
ways present to-
gether (or absent)
a
1
a
3
a
2
A = {a
1
, ··· , a
n
A
}
B = {b
1
, ··· , b
n
B
}
When b
i
features
are present, all
a
i
features are
present as well
a
1
a
3
a
2
b
1
b
3
b
2
A
B
C
or-group: when
a
i
features are
present, either the
b
i
are present, or
the c
i
are present,
or the b
i
and the
c
i
are present
a
1
b
1
a
3
a
2
c
1
c
2
b
3
b
2
A
X
B
C
xor-group: when
a
i
features are
present, either the
b
i
are present, or
the c
i
are present
(not both)
a
1
b
1
a
3
a
2
c
1
c
2
b
3
b
2
A
B
X
mutex: features
a
i
and features b
i
are nether present
together
a
1
a
3
a
2
b
1
b
2
b
3
a
1
→ ¬b
1
b
1
→ ¬a
1
gram —ECFD), which is graphically closer to the fea-
ture models. An example of ECFD is shown in Figure
4, and the constructs and the semantics of the ECFD
are given in Table 2. Firstly, part of the information
of the ECFD comes from the concepts that introduce
the features. In our example, MI, Mo, F and A are
always together in configurations, thus a FM can con-
tain any relation set between these without changing
the semantics. MRI, CT and H can be connected to
any feature among MI, Mo, F or A (edges going to
ENASE 2017 - 12th International Conference on Evaluation of Novel Approaches to Software Engineering
30

the entire box). D (resp. N) can be a child of H. Sec-
ondly, other information comes from the concepts that
introduce the configurations and their subconcepts, as
highlighted in (Ryssel et al., 2011). As the introducers
of MRI and CT (resp. D and N) have no lower bound
in the AOC-poset (or their lower bound is the bottom
in the lattice), we deduce the mutual exclusion be-
tween them. We also observe in valid configurations
(concepts introducing at least one configuration) the
fact that one of both has to be present. Thus (MRI,
CT) and (D, N) are xor groups in the ECFD.
Both FM1 and FM1v are conform to the ECFD
of Figure 4 in the sense that their dependencies match
the information extracted from it. Note that for FM1v,
three constraints have to be added to the graphical rep-
resentation in order to express the xor information.
The ECFD describes the equivalence class of FMs
that have the same set of configurations, provides a
graphical view and is pretty interesting to guide an
expert from a configuration set to a satisfying FM. To
assist the expert, a process should be developped so
as to ease the derivation of a feature model, such a
process is not described in this paper.
3 CONCEPTUAL STRUCTURES
AND MERGE OPERATIONS
In this section, we detail how FCA can be used to
assist merge (composition) operations on FMs.
3.1 Overview of Merge Operations
Several design situations may require FM composi-
tion, for example when several experts work on de-
signing variability and independently develop their
FMs with different concerns, or when several prod-
ucts have to be merged. Another reason comes from
the need for product line decomposition. Indeed, for
large product lines, it is hardly possible to describe
the variability in a single, complex, feature model.
To manage the complexity, the usually-adopted so-
lution is apply the separation-of-concerns principle,
decomposing the feature model at design time, each
sub-feature model focusing on a given concern. Then
the sub-feature models are to be composed back into
a global feature model. For that, merge operations
are needed. To focus the study, we consider the two
merge operations that are defined in (Acher et al.,
2010): merge-intersection and merge-union. In this
work, the semantics of the merge operations is given
using the configuration semantics.
Definition 4 (Merge Operations(Acher et al.,
2010)).
• The merge intersection operation, denoted by ∩,
builds a feature model FM
3
from two feature mod-
els FM
1
and FM
2
such that [[FM
3
]]=[[FM
1
]]∩
[[FM
2
]].
• The merge union operation, denoted by ∪, builds
a feature model FM
3
from two feature mod-
els FM
1
and FM
2
such that [[FM
3
]]=[[FM
1
]]∪
[[FM
2
]].
Figure 5 illustrates these two merge operations
on the medical imaging services presented in (Acher
et al., 2010). We consider again the service whose
variability is described by FM1v (Figure 1). The vari-
ability of another service of medical imaging is de-
scribed by FM2 (on the right-hand-side of Figure 5).
The set of configurations of FM2 is given in Table 3.
Table 3: FM2 configuration set (and formal context).
MI2
A
CT
D
F
H
MI
MRI
Mo
PET
MI2c0 × × × × × × ×
MI2c1 × × × × × ×
MI2c2 × × × ×
MI2c3 × × × × × × ×
MI2c4 × × × × × × ×
MI2c5 × × × × ×
MI2c6 × × × × × ×
MI2c7 × × × ×
MI2c8 × × × × ×
MI2c9 × × × × ×
MI2c10 × × × ×
MI2c11 × × × × × ×
Such operations are complex to perform based on the
structure of FM since two feature models representing
two close sets of configurations can be very different,
as shown in Figure 5.
3.2 Definition of Merge Operations
based on Conceptual Structures
Based on the definitions, our approach for building
the intersection (resp. the union) of two feature mod-
els can be decomposed in three steps: 1) building the
table representing the configurations that appear in the
two initial feature models (resp. in at least one), 2)
building the AC-poset associated with the obtained ta-
ble, which describes the equivalence class of possible
intersection (resp. union) feature models, and 3) ex-
tracting the ECFD from the AC-poset. The ECFD will
be presented to the expert to guide him/her in choos-
ing a FM representation. This approach absorbs,
Feature Model Composition Assisted by Formal Concept Analysis
31
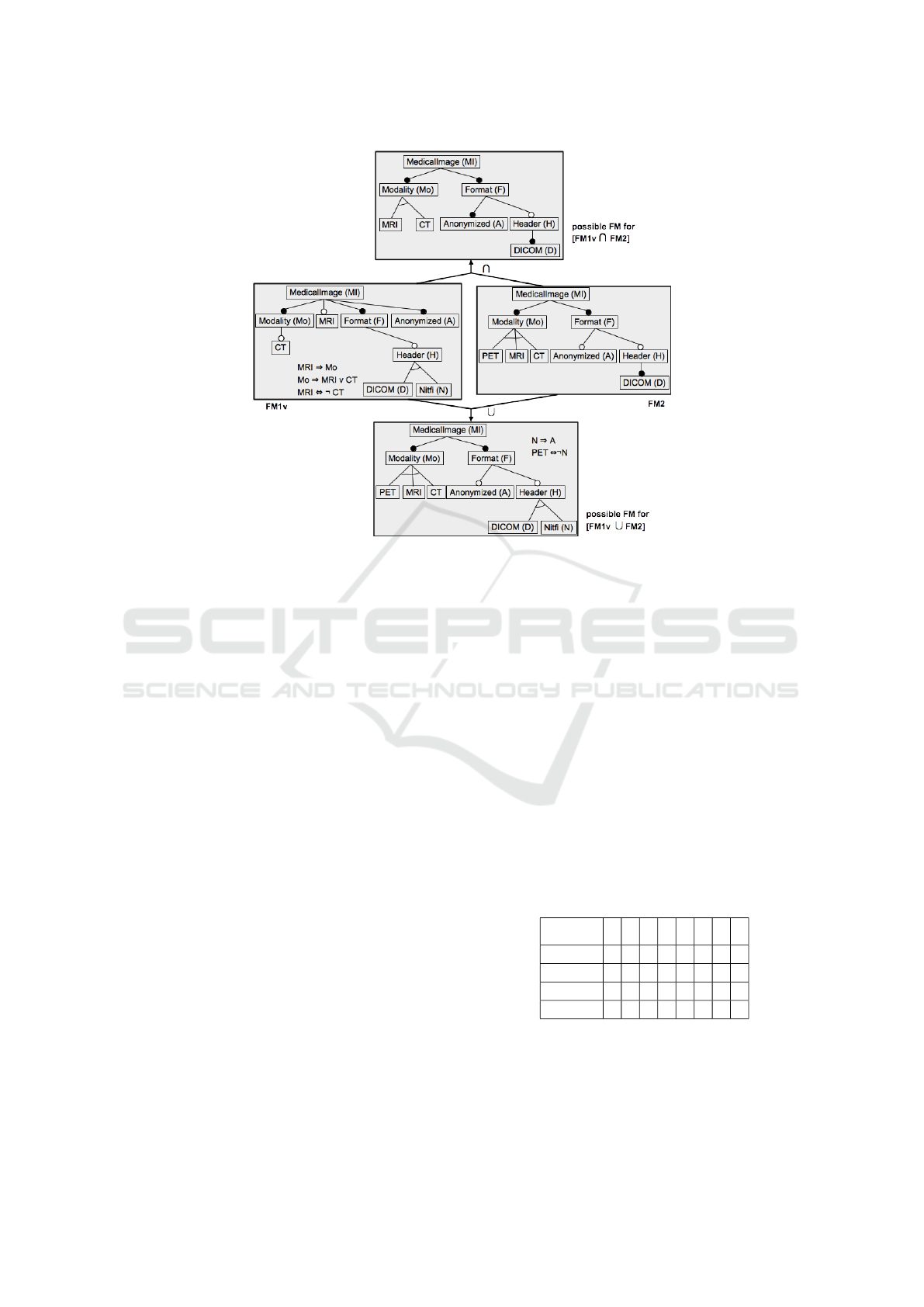
Figure 5: FM1v and FM2, with possible intersection and union Feature models. Figure adapted from (Acher et al., 2010).
during the merge operation, the differences in the
structure and the representation choices of the feature
models and their cross-tree constraints. We consider
in the definitions of the rest of this section two formal
contexts K
1
= (G
1
, M
1
, I
1
) and K
2
= (G
2
, M
2
, I
2
). K
1
and K
2
are supposed to be cleaned so that there do not
exist two identical configurations (rows) in them.
3.2.1 Intersection Formal Context
(Merge-intersection)
We first introduce the notion of equality of objects
(configurations), denoted ,, as objects having the
same set of attributes.
Definition 5 (Equality of objects, ,).
g
1
, g
2
⇔ g
1
∈ G
1
, g2 ∈ G
2
and I
1
(g
1
) = I
2
(g
2
)
In tables and figures, which are generated by tools,
MI1c0 , MI2c3 is denoted by ”MI1c0=MI2c3”.
We then define the formal context associated with
merge-intersection as the rows that are present in the
two initial formal contexts. A labeling of rows is
added to indicate their origin.
Definition 6 (Merge-intersection Formal
Context). The formal context of merge in-
tersection Inter(K
1
, K
2
) is K
Inter(K
1
,K
2
)
=
(G
Inter(K
1
,K
2
)
, M
Inter(K
1
,K
2
)
, I
Inter(K
1
,K
2
)
) such that:
• G
Inter(K
1
,K
2
)
= {g
g
1
,g
2
| ∃(g
1
, g
2
) ∈ G
1
× G
2
, g
1
, g
2
}
• M
Inter(K
1
,K
2
)
= M
1
∩ M
2
• I
Inter(K
1
,K
2
)
= {(g
g1,g2
, m) | m ∈ M
Inter(K
1
,K
2
)
, g
g1,g2
∈
G
Inter(K
1
,K
2
)
, (g1, m) ∈ I
1
(or equiv. (g2, m) ∈ I
2
)}
Table 4 shows the merge-intersection formal con-
text for the example. The corresponding AC-poset is
presented in Figure 6. The extracted ECFD is pre-
sented in the l.h.s of Figure 7. From this ECFD, an
expert can extract several FMs representing the in-
tersection. In fact, to guide the designer in his/her
choices, decorations can be added on the ECFD, like
ontological relation of the initial feature models, or
similar groups from the same parent or mandatory in-
formation. By choosing an ontological semantics to
the ECFD, one derives a feature model description
which conforms with this ECFD. Such a derivation is
shown in the r.h.s of Figure 7, and the corresponding
FM is represented in Figure 5 (top).
Table 4: Merge-intersection formal context.
Int12
A
CT
D
F
H
MI
MRI
Mo
MI1c0=MI2c3 × × × × × × ×
MI1c1=MI2c4 × × × × × × ×
MI1c2=MI2c8 × × × × ×
MI1c3=MI2c9 × × × × ×
3.2.2 Union Formal Context (Merge-union)
Let us now define the formal context associated with
merge-union.
ENASE 2017 - 12th International Conference on Evaluation of Novel Approaches to Software Engineering
32
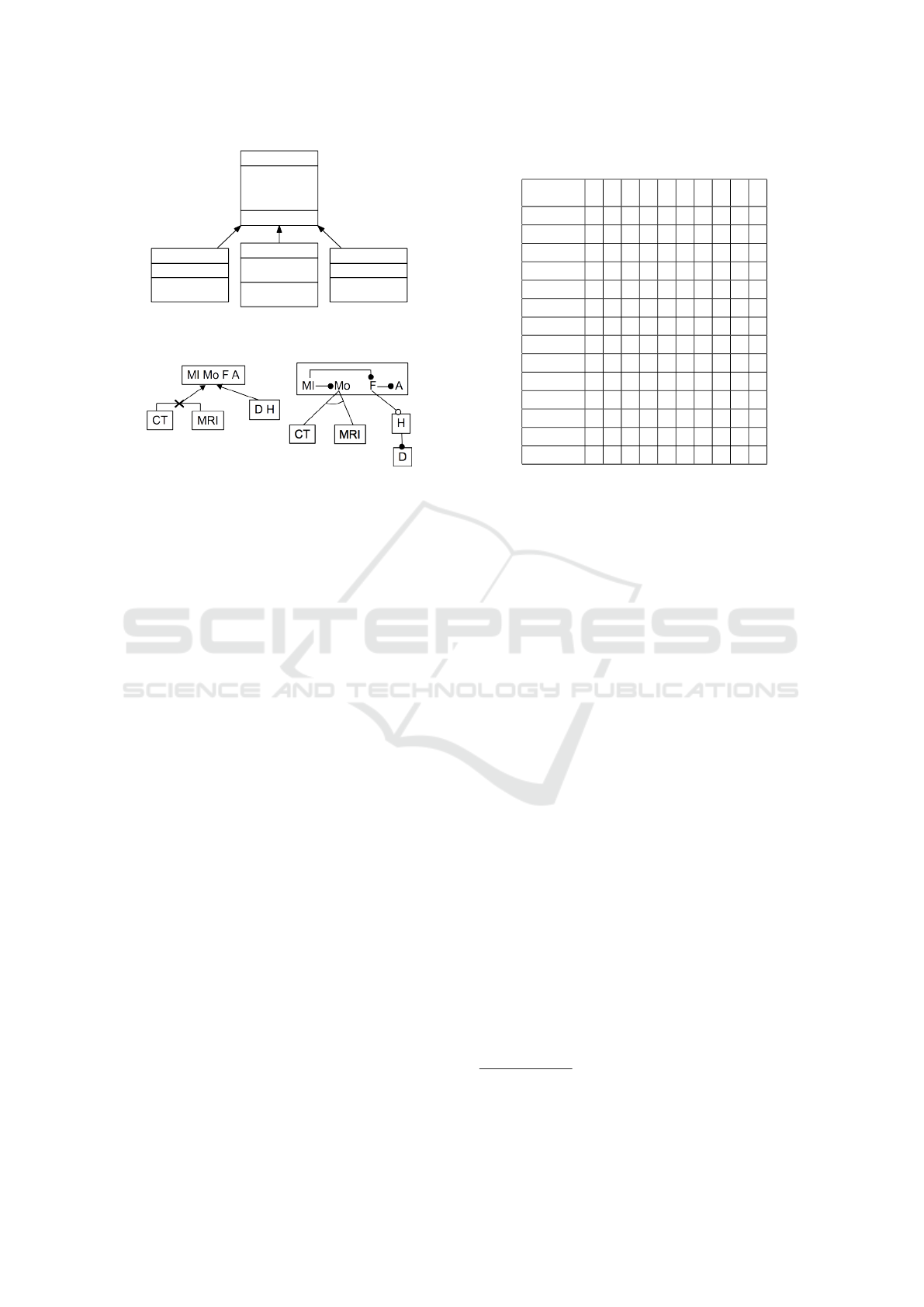
Figure 6: AC-poset associated with merge-intersection for-
mal context of Table 4.
Figure 7: ECFD of AC-poset from Figure 6, and derivation
of intersection FM from Figure 5 on ECFD.
Definition 7 (Merge-union Formal Context). Let us
consider:
• the set of common configurations (from Def. 6)
G
Inter(K
1
,K
2
)
and the corresponding relation I
Inter(K
1
,K
2
)
• the set of configurations specific to G
1
: SPE(G
1
) =
{g1 | g1 ∈ G
1
and @g2 ∈ G
2
, with g
g1,g2
∈
G
Inter(K
1
,K
2
)
}
• the set of configurations specific to G
2
: SPE(G
2
) =
{g2 | g2 ∈ G
2
and @g1 ∈ G
1
, with g
g1,g2
∈
G
Inter(K
1
,K
2
)
}
The formal context of merge-union Union(K
1
, K
2
) is:
K
Union(K
1
,K
2
)
= (G
Union(K
1
,K
2
)
, M
Union(K
1
,K
2
)
, I
Union(K
1
,K
2
)
)
such that:
• G
Union(K
1
,K
2
)
= G
Inter(K
1
,K
2
)
∪ SPE(G
1
) ∪ SPE(G
2
)
• M
Union(K
1
,K
2
)
= M
1
∪ M
2
• I
Union(K
1
,K
2
)
= I
Inter(K
1
,K
2
)
∪{(g, m) | g ∈ SPE(G
1
), m ∈ M
Union(K
1
,K
2
)
, (g, m) ∈ I
1
}
∪{(g, m) | g ∈ SPE(G
2
), m ∈ M
Union(K
1
,K
2
)
, (g, m) ∈ I
2
}
Table 5 shows the merge-union formal context for
the example. The corresponding AC-poset is pre-
sented in Figure 8. The ECFD associated with the
AC-poset is presented in the l.h.s of Figure 9. An ex-
pert can choose the union FM of Figure 5 (bottom)
that can be derived from the ECFD as shown in the
r.h.s of Figure 9.
4 IMPLEMENTATION AND
VALIDATION
The approach has been implemented and validated
with several feature models or variations of them,
Table 5: Merge-union formal context.
Union12
A
CT
D
F
H
MI
MRI
Mo
N
PET
MI1c0=MI2c3 × × × × × × ×
MI1c1=MI2c4 × × × × × × ×
MI1c2=MI2c8 × × × × ×
MI1c3=MI2c9 × × × × ×
MI1c4 × × × × × × ×
MI1c5 × × × × × × ×
MI2c0 × × × × × × ×
MI2c1 × × × × × ×
MI2c2 × × × ×
MI2c5 × × × × ×
MI2c6 × × × × × ×
MI2c7 × × × ×
MI2c10 × × × ×
MI2c11 × × × × × ×
taken from the SPLOT repository
1
, from the Fa-
miliar
2
website, or from the literature. The pro-
cess is presented in Figure 10 and uses Famil-
iar for building the configuration set of an FM
and rcaexplore
3
to build the AC-poset from which
the ECFD structure (nodes and edges) is extracted.
We also developed additional tools specific to this
project: a first tool (ConfigSet2FormalContext)
builds a formal context (within input format of rcaex-
plore) from a configuration set extracted from Famil-
iar, a second tool (ComputeInterAndUnion) builds
the intersection and union formal contexts, and a
third tool (ComputeGroupsAndMutex) computes the
groups Xor, Or and the mutex of the ECFD.
The goal of the experiments described in this sec-
tion is to assess that the built structure, namely the
ECFD, has humanely-tractable dimensions. Indeed,
raw structures stemming from Formal Concept Anal-
ysis can hardly be handled by experts, due to their
size. Here we measure the main characteristics of the
obtained ECFD on a small benchmark and show that
the numbers of groups of features and relations be-
tween the groups remain low, and thus that the ECFD
can be used by an expert.
Table 6 shows the feature models on which we
have tested our approach. For each feature model,
we give the number of features, configurations, Xor
groups, Or groups and constraints. We also compute
the ECFD and indicate the number of Xor groups,
Or groups, mutex and situations where a box in the
ECFD has several direct parents (multi-par.). The
number of groups, e.g. Xor groups, may vary be-
1
http://www.splot-research.org/
2
http://familiar.variability.io/
3
http://dolques.free.fr/rcaexplore/
Feature Model Composition Assisted by Formal Concept Analysis
33
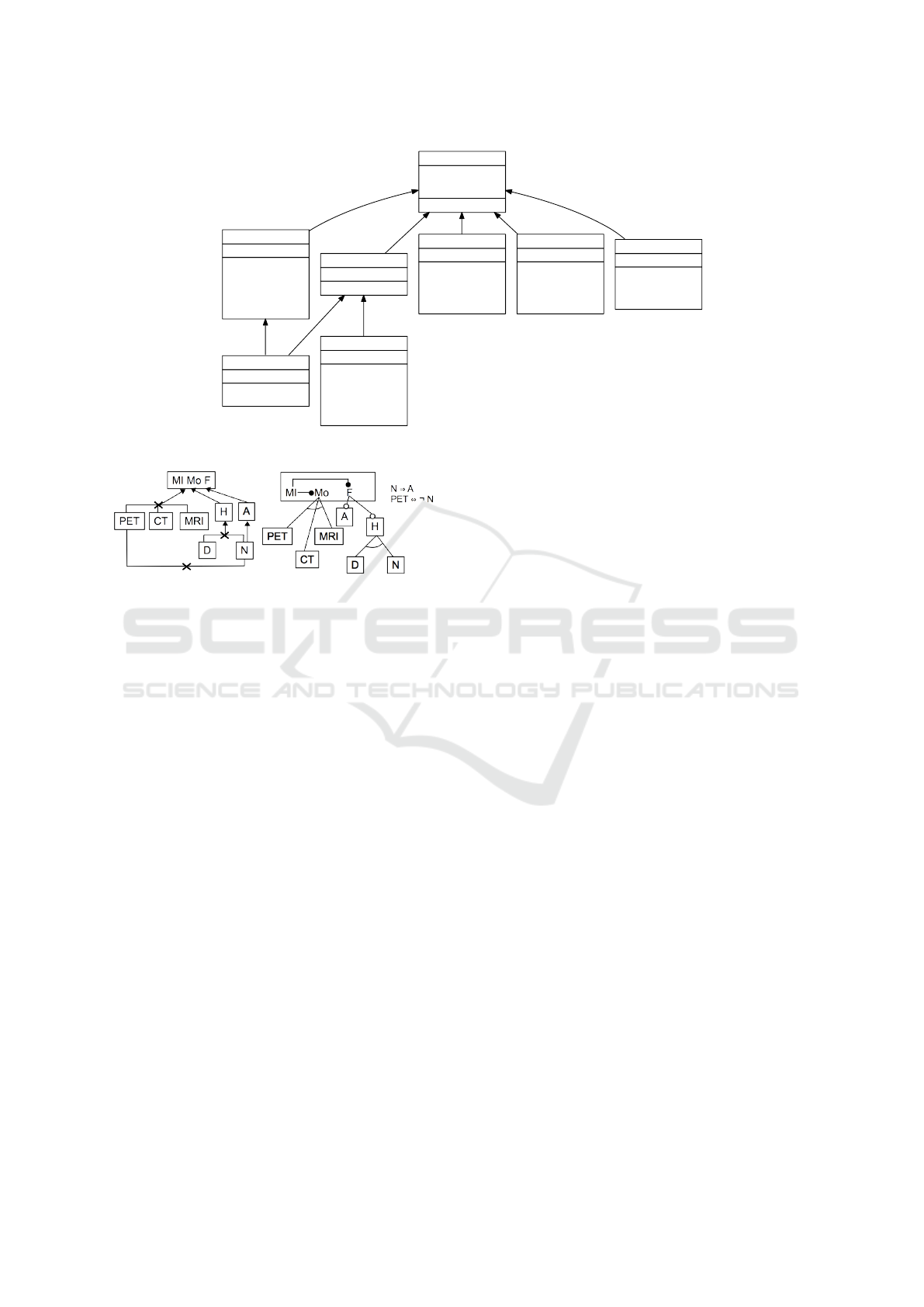
Figure 8: AC-poset associated with merge-union formal context of Table 5.
Figure 9: ECFD for AC-poset from Figure 8, and derivation
of union FM from Figure 5 on ECFD.
tween the FM and the ECFD. For example, one Xor
group of the ECFD may combine several Xor groups
of the FM when there are additional constraints, or
the ECFD may reveal more possible Xor groups than
initially indicated in the FM.
Table 7 shows the information about ECFDs of the
intersection (when it is not empty) and the union of
the initial FMs that we obtain with our approach. As
these ECFDs are intended to guide a designer towards
a FM, it is important to notice that their size remains
reasonable compared to the input FMs. The number
of groups is not very high, and the number of mutex,
except in three cases is also low. Multi-parent situ-
ations mainly offer two representation choices: im-
plication or child-parent edge in the FM and they are
very few.
Concept lattices, and thus, a fortiori, AOC-posets
and AC-posets can be built for large datasets, e.g.
in (Wray et al., 2016), the authors mention a large
dataset, the Rijksmuseum collection which contains
100,000 objects and 1,716 attributes, giving 994,967
concepts computed in 68ms in average with FCbO
update algorithm. The computation of the groups
can be a hard task, as pointed out in (Ryssel et al.,
2011). Many FMs have a very large configuration
set, as Video player FM from SPLOT, with 71 fea-
tures and more than 1 billion configurations. We do
not address these cases, as we more specifically ad-
dress the contexts where the FMs have a reasonable
number of configurations, which corresponds in par-
ticular to FMs coming from real-world product lines.
Concerning product lines inducing a number of con-
figurations not tractable by FCA, our approach could
benefit from product line decomposition: dividing a
feature model according to scopes, concerns or teams
into less complex interdependent feature models.
Product comparison matrices (PCMs) studied in
(B
´
ecan et al., 2014) give an overview of this type
of dataset where many datasets could be investigated
using our method: 75 PCMs, corresponding to 211
matrices that have 2 to 241 rows, and 3 to 51 possi-
bly valued columns, with about 43% of the cells have
boolean value (and the others should be translated into
boolean features via FCA scaling (Ganter and Wille,
1999)).
5 RELATED WORK
Previous research work has used FCA for Software
Product Line Engineering (SPLE), mainly in the con-
text of reengineering concrete product lines. Fea-
ture model analysis or synthesis have been done in
(Loesch and Ploedereder, 2007), (Ryssel et al., 2011),
(Al-Msie’deen et al., 2014), (Shatnawi et al., 2015).
In (Niu and Easterbrook, 2009), the authors present an
approach based on aspect-oriented SPLE where they
classify scenarios by functional requirements. Using
FCA for feature location has been studied by (Xue
et al., 2012), (Salman et al., 2013), and (Al-Msie’deen
et al., 2013). Traceability links between features and
code have been established by (Salman et al., 2013).
Another available tool in the framework of FCA is the
notion of implicative systems, already used in (Ryssel
ENASE 2017 - 12th International Conference on Evaluation of Novel Approaches to Software Engineering
34
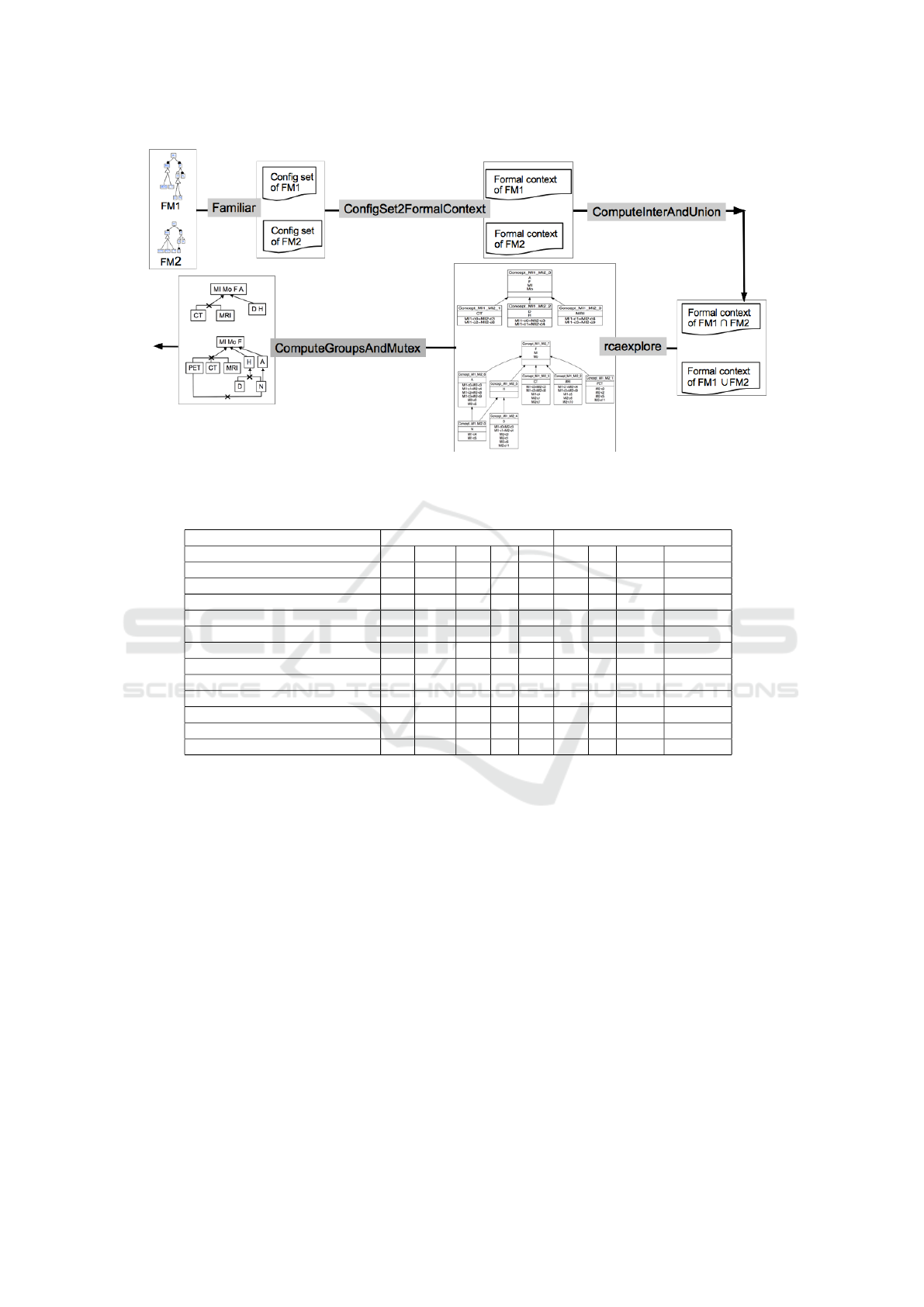
Figure 10: The implemented process.
Table 6: Features models (and the corresponding ECFD) used for testing the approach. var. stands for variant. Cst stands for
Constraint.
FM Feature Model ECFD
#feat #conf. #Xor #Or # Cst #Xor #Or #mutex #multi-par.
MI1 (Acher et al.) 9 6 2 0 0 2 0 0 0
MI2 (Acher et al.) 9 12 1 0 0 1 0 0 0
Martini Eshop (SPLOT) 11 8 1 1 1 1 2 1 1
Tang Eshop (SPLOT) 10 13 1 1 2 1 2 1 1
Toacy Eshop (SPLOT) 12 48 1 2 0 1 2 0 0
Wiki V1 (Familiar example) 14 10 4 0 4 3 2 5 2
Wiki V2 (Wiki V1 var.) 17 50 4 1 4 6 13 1 1
Wiki V3 (Wiki V1 var.) 18 120 3 2 6 2 2 1 0
Bicycle1 (Mendonca SPLOT var.) 19 64 2 0 2 1 0 0 0
Bicycle2 (Mendonca SPLOT var.) 22 192 5 0 1 6 1 6 0
Bicycle3 (Mendonca SPLOT var.) 25 576 4 0 2 5 1 8 0
Bicycle4 (Mendonca SPLOT var.) 26 864 5 0 2 6 1 8 0
et al., 2011). This is another logical encoding of the
formula underlying in (and equivalent to) a concept
lattice (or a feature model), which can be rather com-
pact. The paper (Carbonnel et al., 2016) gives a pro-
cedure to derive (in a polynomial time) an implicative
system directly from a feature model, thus without us-
ing the configuration set which may be an obstacle in
some cases as noticed by (Ryssel et al., 2011).
Acher et al. compare various approaches for FM
model merging in (Acher et al., 2010) and (Acher
et al., 2013). Some approaches, such as (Schobbens
et al., 2007) and (Heymans et al., 2008) maintain sep-
arately the input feature models and establish links
between them through constraints. The approach of
(Acher et al., 2009) establishes, in a first phase, the
matching between similar elements, then an algo-
rithm recursively merges the feature models. Cat-
alogs of local transformation rules are proposed in
(Segura et al., 2007), (Alves et al., 2006). Other ap-
proaches encode the FMs into propositional formula
(Batory, 2005), then compute the formula represent-
ing the intersection (resp. the union), then synthe-
size a FM from the boolean formula (Czarnecki and
Wasowski, 2007). Logical formulas are equivalent to
the conceptual structures we build, however, the in-
troduced structure, namely the ECFD, has a graphical
form closer to feature models, it is thus easier to de-
rive a feature model from an ECFD than from logical
formulas.
Our proposal can be analyzed with the criteria of
(Acher et al., 2010). Concerning quality of the re-
sult: The configuration-semantics is preserved. The
non-contradictory ontological child-parent edges are
preserved. We do not reduce the set of features, ex-
cept if some of them are not used, they will appear in
the bottom concept and they can be eliminated. The
result is not final in our case, an FM has to be chosen
based on the ECFD. About criterion Error handling:
Feature Model Composition Assisted by Formal Concept Analysis
35
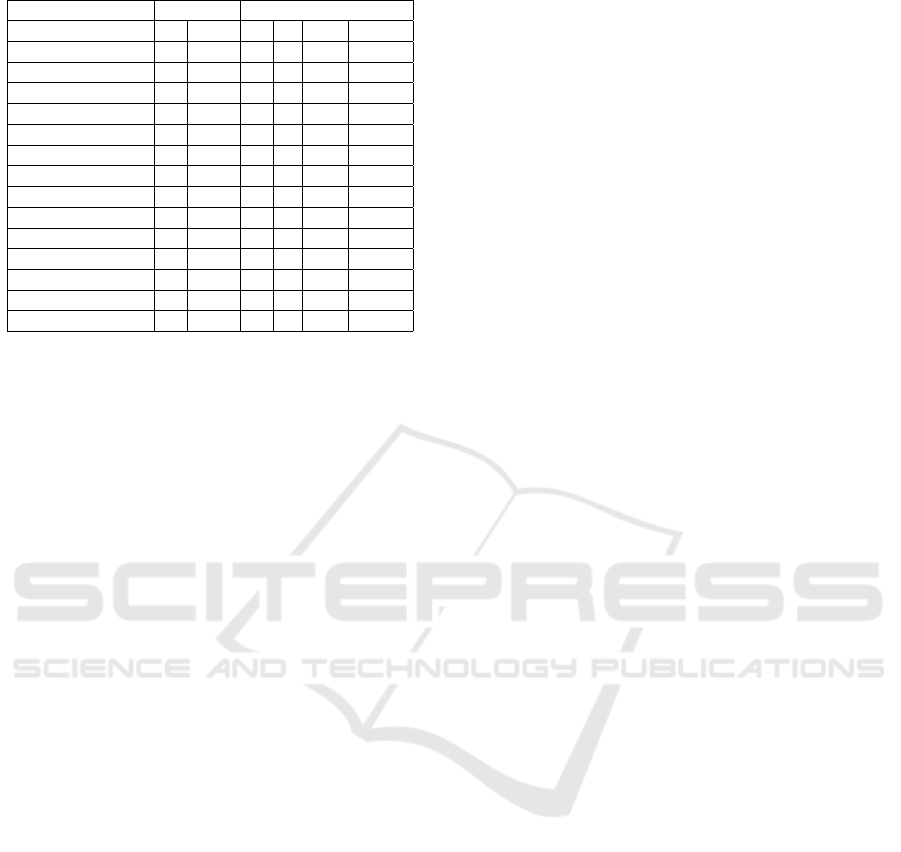
Table 7: Intersection and union ECFDs.
FM Formal context ECFD
#feat #conf. #Xor #Or #mutex #multi-par.
MI1∩MI2 8 4 1 0 0 0
MI1∪MI2 10 14 2 0 1 1
Martini∪Tang 12 21 1 2 3 1
Martini∪Toacy 14 56 1 1 4 0
Tang∩Toacy 8 5 1 2 0 0
Tang∪Toacy 13 56 1 1 4 1
WikiV1∪WikiV2 20 60 5 9 26 0
WikiV1∪WikiV3 23 130 3 4 42 0
WikiV2∩WikiV3 14 50 0 6 0 0
WikiV2∪WikiV3 21 120 0 16 8 1
Bicycle1∩Bicycle2 14 8 1 0 0 0
Bicycle1∪Bicycle2 26 248 6 1 32 2
Bicycle3∩Bicycle4 23 288 5 1 8 0
Bicycle3∪Bicycle4 27 1152 6 1 8 0
errors like empty intersection are detected. When in-
tersection is empty, the designer should conclude to
an error or an incompatibility that he/she may want to
fix. But in spite of empty intersection, feature mod-
els may have common parts in their structure, lead-
ing to incomplete configurations. The union, in this
case, can be read to highlight such common parts. We
do not make Assumption on input FMs: There is no
specific assumption in our method. Cross-tree con-
straints are taken into account in the conceptual struc-
tures (implicitly, thanks to the position of the features
or to the position of the configurations in subcon-
cepts). When there are hierarchy mismatches, the AC-
poset manages this information (see FM1 and its vari-
ant) but the vocabulary (feature names) has to be the
same (it can be aligned before the merge operations).
Then about Aspects of the implementation: The ap-
proach needs to know the list of configurations, thus
as such, the proposed solution is restricted to some
contexts: FMs that have limited number of configura-
tions; real-world product lines given with configura-
tion sets. There is no ”testing” effort since the logical
semantics is guaranteed by the FCA theory. The com-
putational complexity is polynomial for AC-posets, in
the size of the number of configurations and the num-
ber of features. As detailed by (Ryssel et al., 2011),
group and mutex computation might be exponential in
the number of configurations or features but remains
reasonable in typical situations, with an optimized im-
plementation.
6 CONCLUSION
In some design situations, combining various real-
word product lines, or various FMs, given through
their configuration set is a useful step in the design
of a variability model. In this paper, we propose an
approach, based on Formal Concept Analysis (FCA),
that aims to assist a designer during this task. We ex-
ploit the properties of the AC-poset to build a canoni-
cal structure, the ECFD, which represents all the FMs
with the same configuration semantics. The merge-
intersection and merge-union operators are encoded
in the framework of FCA, that allows us to compute
the ECFD for intersection and union. These ECFDs
may be used to guide the expert in deriving a repre-
sentative feature model conform to the ECFD.
As a current work, we are designing the pro-
cess for guiding the expert while building the feature
model, in choosing the child-parent edges, the groups
and the constraints among those that are included in
the ECFD. Besides, the approach is currently based
on a configuration set, but FCA offers other struc-
tures, such as the implicative systems. We are cur-
rently investigating the transformation of an FM into
such an implicative system (without computing the
configuration set), then the computation of the AC-
poset and the groups and mutex of the ECFD from the
implicative system. This will enlarge the scope of ap-
plicability of the approach to cases where the config-
uration set can hardly be computed. As a future work,
we also would like to apply our method to other FMs,
and to PCMs, which involves a substantial work to
translates the many-valued cells into FCA framework
and to synthesize associated FMs.
REFERENCES
Acher, M., Collet, P., Lahire, P., and France, R. B. (2009).
Composing feature models. In van den Brand, M.,
Gasevic, D., and Gray, J., editors, Software Language
Engineering, Second International Conference, SLE
2009, Denver, CO, USA, October 5-6, 2009, Revised
Selected Papers, volume 5969 of Lecture Notes in
Computer Science, pages 62–81. Springer.
Acher, M., Collet, P., Lahire, P., and France, R. B. (2010).
Comparing approaches to implement feature model
composition. In Modelling Foundations and Applica-
tions, 6th European Conference, ECMFA 2010, Paris,
France, June 15-18, 2010. Proceedings, pages 3–19.
Acher, M., Combemale, B., Collet, P., Barais, O., Lahire,
P., and France, R. (2013). Composing your Compo-
sitions of Variability Models. In ACM/IEEE 16th In-
ternational Conference on Model Driven Engineering
Languages and Systems (MODELS’13), volume Lec-
ture Notes in Computer Science, page 17 p., Miami,
United States.
Al-Msie’deen, R., Huchard, M., Seriai, A., Urtado, C., and
Vauttier, S. (2014). Reverse engineering feature mod-
els from software configurations using formal concept
analysis. In 11th Int. Conf. on Concept Lattices and
Their Applications (ICFCA)., pages 95–106.
ENASE 2017 - 12th International Conference on Evaluation of Novel Approaches to Software Engineering
36

Al-Msie’deen, R., Seriai, A., Huchard, M., Urtado, C.,
Vauttier, S., and Salman, H. E. (2013). Mining Fea-
tures from the Object-Oriented Source Code of a Col-
lection of Software Variants Using Formal Concept
Analysis and Latent Semantic Indexing. In 25th Conf.
on Soft. Eng. and Know. Eng. (SEKE), pages 244–249.
Alves, V., Gheyi, R., Massoni, T., Kulesza, U., Borba, P.,
and de Lucena, C. J. P. (2006). Refactoring prod-
uct lines. In Jarzabek, S., Schmidt, D. C., and Veld-
huizen, T. L., editors, Generative Programming and
Component Engineering, 5th International Confer-
ence, GPCE 2006, Portland, Oregon, USA, October
22-26, 2006, Proceedings, pages 201–210. ACM.
Batory, D. S. (2005). Feature Models, Grammars, and
Propositional Formulas. In 9th Int. Conf. on Soft.
Product Lines (SPLC), pages 7–20.
B
´
ecan, G., Sannier, N., Acher, M., Barais, O., Blouin, A.,
and Baudry, B. (2014). Automating the formaliza-
tion of product comparison matrices. In Crnkovic, I.,
Chechik, M., and Gr
¨
unbacher, P., editors, ACM/IEEE
International Conference on Automated Software En-
gineering, ASE ’14, Vasteras, Sweden - September 15
- 19, 2014, pages 433–444. ACM.
Carbonnel, J., Bertet, K., Huchard, M., and Nebut, C.
(2016). FCA for software product lines representa-
tion: Mixing product and characteristic relationships
in a unique canonical representation. In Proceedings
of the Thirteenth International Conference on Con-
cept Lattices and Their Applications, Moscow, Russia,
July 18-22, 2016., pages 109–122.
Czarnecki, K. and Wasowski, A. (2007). Feature Diagrams
and Logics: There and Back Again. In 11th Int. Conf.
on Soft. Product Lines (SPLC), pages 23–34.
Ganter, B. and Wille, R. (1999). Formal concept analysis -
mathematical foundations. Springer.
Heymans, P., Schobbens, P., Trigaux, J., Bontemps, Y., Mat-
ulevicius, R., and Classen, A. (2008). Evaluating for-
mal properties of feature diagram languages. IET Soft-
ware, 2(3):281–302.
Kang, K. C., Cohen, S. G., Hess, J. A., Novak, W. E.,
and Peterson, A. S. (1990). Feature-Oriented Domain
Analysis (FODA): Feasibility Study. Technical Report
CMU/SEI-90-TR-21 - ESD-90-TR-222.
Krueger, C. W. (2002). Practical strategies and techniques
for adopting software product lines. In Proceedings of
the 7th International Conference on Software Reuse:
Methods, Techniques, and Tools (ICSR-7), pages 349–
350.
Loesch, F. and Ploedereder, E. (2007). Restructuring Vari-
ability in Software Product Lines using Concept Anal-
ysis of Product Configurations. In 11th Eur. Conf. on
Soft. Maintenance and Reengineering (CSMR), pages
159–170.
Niu, N. and Easterbrook, S. M. (2009). Concept analysis for
product line requirements. In 8th Int. Conf. on Aspect-
Oriented Software Development (AOSD), pages 137–
148.
Pohl, K., B
¨
ockle, G., and van der Linden, F. J. (2005). Soft-
ware Product Line Engineering: Foundations, Prin-
ciples, and Techniques. Springer Science & Business
Media.
Ryssel, U., Ploennigs, J., and Kabitzsch, K. (2011). Ex-
traction of feature models from formal contexts. In
15th Int. Conf. on Soft. Product Lines (SPLC) Work-
shop Proceedings (Vol. 2), page 4.
Salman, H. E., Seriai, A., and Dony, C. (2013). Feature-to-
code traceability in a collection of software variants:
Combining formal concept analysis and information
retrieval. In 14th Conf. on Inf. Reuse and Integration
(IRI), pages 209–216.
Schobbens, P., Heymans, P., Trigaux, J., and Bontemps, Y.
(2007). Generic semantics of feature diagrams. Com-
puter Networks, 51(2):456–479.
Segura, S., Benavides, D., Cort
´
es, A. R., and Trinidad, P.
(2007). Automated merging of feature models using
graph transformations. In L
¨
ammel, R., Visser, J., and
Saraiva, J., editors, Generative and Transformational
Techniques in Software Engineering II, International
Summer School, GTTSE 2007, Braga, Portugal, July
2-7, 2007. Revised Papers, volume 5235 of Lecture
Notes in Computer Science, pages 489–505. Springer.
Shatnawi, A., Seriai, A.-D., and Sahraoui, H. (2015). Re-
covering architectural variability of a family of prod-
uct variants. In 14th Int. Conf. on Soft. Reuse (ICSR),
pages 17–33.
She, S., Lotufo, R., Berger, T., Wasowski, A., and Czar-
necki, K. (2011). Reverse engineering feature models.
In 33rd Int. Conf. on Software Engineering, (ICSE),
pages 461–470.
Wray, T., Outrata, J., and Eklund, P. W. (2016). Scal-
able performance of fcbo algorithm on museum data.
In Proceedings of the Thirteenth International Con-
ference on Concept Lattices and Their Applications,
Moscow, Russia, July 18-22, 2016., pages 363–376.
Xue, Y., Xing, Z., and Jarzabek, S. (2012). Feature location
in a collection of product variants. In 19th Working
Conf. on Reverse Engineering (WCRE), pages 145–
154.
Feature Model Composition Assisted by Formal Concept Analysis
37
