
Distributed Transmit Power Control for Beacons in VANET
Forough Goudarzi and Hamed S. Al-Raweshidy
Department of Electrical Engineering, Brunel University, London, U.K.
Keywords: Beacon Power Control, Congestion Control, Game Theory, VANET.
Abstract: In vehicle to vehicle communication, every vehicle broadcasts its status information periodically in its
beacons to create awareness for surrounding vehicles. However, when the wireless channel is congested due
to beaconing activity, many beacons are lost due to packet collision. This paper presents a distributed
congestion control algorithm to adapt beacons transmit power. The algorithm is based on game theory, for
which the existence of the Nash Equilibrium (NE) is proven and the uniqueness of the NE and stability of the
algorithm is verified using simulation. The proposed algorithm is then compared with other congestion control
mechanisms using simulation. The results of the simulations indicate that the proposed algorithm performs
better than the others in terms of fairness, bandwidth usage, and the ability to meet the application
requirements.
1 INTRODUCTION
In Vehicular Ad hoc NETworks (VANETs), vehicles
periodically broadcast Basic Safety Messages
(BSMs), also known as beacons, to inform other
vehicles of their status such as position, speed, and
acceleration. The performance of safety applications
is dependent on how precisely a vehicle knows the
status of its neighbouring vehicles thus, it is very
important that enough beacons from each vehicle
reaches its neighbours. In dense vehicular traffic,
many beacons become lost due to packet collision.
Thus, considerable efforts have been made to limit the
channel usage to around 0.65 (ideally with a range
between 0.4 and 0.8), so that the number of
successfully delivered messages are maximised
(Fallah, Huang et al. 2011). The proposed approaches
are generally based on reducing the rate (Bansal,
Kenney et al. 2013, Kim, Kang et al. 2014, Egea-
Lopez, Pavon-Marino 2016) or range (Egea-Lopez,
Alcaraz et al. 2013, Torrent-Moreno, Mittag et al.
2009) or both rate and range (Huang, Fallah et al.
2010) of BSMs. This paper specifically focuses on
transmission range or power control.
The problem of beacon’s power control is
presented as a non-cooperative game. It is proven the
Nash Equilibrium (NE) exists for the game and that
the NE regarding appropriate range of the parameters
is unique and stable. An algorithm is presented to find
the equilibrium point in a distributed manner. The
current approach differs from previous works in this
area for two main reasons: First, the fairness is
obtained whiteout exchanging information between
nodes, which results in bandwidth saving. The
fairness in this protocol is obtained based on the
fairness concept of the NE. Second, weighted fairness
in power allocation is achieved which is useful to
meet application requirements (Sepulcre, Gozalvez et
al. 2010). Some safety applications require that the
status of vehicles be disseminated longer distances
thus, assigning the same power to vehicles with
different requirements cannot meet this goal.
Like other beacon power control approaches for
VANET (Egea-Lopez, Alcaraz et al. 2013, Torrent-
Moreno, Mittag et al. 2009), it is assumed that there
is no power restriction and every node transmits its
beacons with the maximum allowed power level.
When there is congestion in the network, vehicles
reduce their power level to prevent BSM loss due to
collision.
The remaining of this paper is organized as
follows. Section 2 introduces the non-cooperative
power control game. Section 3 discusses the NE’s
existence and its uniqueness and stability and presents
a distributed algorithm for power control. Selection
of the parameters of the algorithm is presented in
Section 4. The simulation results and performance
evaluation and comparison with other approaches are
presented in Section 5. Section 6 concludes the paper.
Goudarzi, F. and Al-Raweshidy, H.
Distributed Transmit Power Control for Beacons in VANET.
DOI: 10.5220/0006289401810187
In Proceedings of the 3rd International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS 2017), pages 181-187
ISBN: 978-989-758-242-4
Copyright © 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
181

2 NON-COOPERATIVE POWER
CONTROL GAME
Let =
,
∈
,
ℱ
∈
denotes the Non-
cooperative Power Control (NPC) game, where =
1,…,N
is the set of players (vehicles), and
is the
set of possible beaconing powers for player .
is
called the strategy set of player i and the power
∈
is called the strategy of player i. Each player
selects its strategy independently. The vector =
(p
,p
,…,p
)∈ shows the selected power of all
the players, where =
∏
. ℱ
is the payoff
function of player i and is indicated as ℱ
(
)
=
ℱ
(p
,
), where
denotes the vector consisting
of the beacon powers of all the players except the ith
player.
Every vehicle transmits its beacons with a power
between 1 and 100 mW (Kenney 2011). Thus, the
strategy set of vehicle i is
=
1,100
. A higher
power is desired because the beacon is disseminated
over larger distance thus, it creates higher awareness
under normal conditions. But high power has a
negative effect on awareness in congested situations.
Therefore, the desirable payoff function would yield
lower payoff with the same power in situations with
high levels of congestion. To fulfil this goal, the pay-
off function is modeled as the difference between a
utility function (U
(
p
)
) and a price function
(J
(
p
,
)
). Accordingly, the payoff for player i is as
follows:
ℱ
(
p
,
)
=U
(
p
)
−J
(
p
,
)
=u
ln
(
p
)
−c
p
CBR
(
)
(1)
where u
and c
are positive parameters, ln
(
.
)
is
natural logarithm, and CBR
(
)
is the channel busy
ratio that player i senses, and it is a function of all the
players’ power level.
The first term in the payoff function is called
utility, it is an increasing function of BSM power
level. A logarithmic function has been selected as
utility because it is increasing and has nice concavity
properties. The second term (c
p
CBR
(
)
), is the
price function. Which indicates that a user should pay
more price at higher congestions. This term is a
function of CBR because CBR is a good indicator of
successful information dissemination in VANET
(Fallah, Huang et al. 2011); high CBR results in poor
inter-vehicle awareness. The price function becomes
larger in scenarios with higher levels of congestion,
yielding a lower payoff.
∇
ℱ
(
)
=
ℱ
(
)
is the marginal payoff of player
i. The vector of marginal payoffs of all the players is
given as
∇ℱ
(
)
=∇
ℱ
(
)
,∇
ℱ
(
)
,…,∇
ℱ
(
)
(2)
and its Jacobian as G
(
)
.
For CBR
(
)
, the mathematical model developed
in (Chen, Jiang et al. 2011), given below, is used.
CBR
(
)
=
∑
h
r (3)
where
h
=T
×
,
(
)
(4)
Ω
=
(
)
(5)
Γ(.) is gamma function,Γ(.,.) is upper incomplete
gamma function, C
is the threshold power level of
carrier sense, p
is beacon transmit power of player i,
d
is the distance between jth and ith players, r is the
beaconing frequency, m is Nakagami fading
parameter, λ is the wavelength, γ is the path loss
exponent, and T
is the time required to send a
BSM packet.
3 THE NASH EQUILIBRIUM OF
THE GAME
According to theorem 1 in (Rosen 1965), if the
strategy spaces of the players are convex, closed and
bounded, and each player’s payoff function is
concave in its own strategy, an equilibrium point
exists. The payoff functions (1) are twice
differentiable, and their first and second derivatives
are:
ℱ
=
−c
CBR
(
)
(6)
ℱ
=−
<0 (7)
The second derivative of ℱ
is always negative,
which means that the payoff functions are concave
and at least one Nash Equilibrium exists. It is worth
VEHITS 2017 - 3rd International Conference on Vehicle Technology and Intelligent Transport Systems
182

noting that CBR
(
)
is independent of p
because
considering (4), d
=0 thus,
(,
)
()
=1.
In NPC, −G
(
)
is an N×N matrix with diagonal
elements:
g
=−
ℱ
=
(8)
and off-diagonal elements:
g
=−
∂
ℱ
∂p
∂p
=
c
rT
Γ
(
m
)
∂Γm,
mC
Ω
∂p
=
(
)
×
e
i≠j(9)
where
k
=
()
(10)
Localizing the eigenvalues of −G
(
)
using
analytical methods, if not impossible, is very difficult.
In such conditions, numerical-based or simulation-
based techniques are used (Alpcan, Basar et al. 2005),
to ensure the uniqueness and stability of the system.
In the next sections, simulation in high density
scenarios is used, to show the stability of the system
under the gradient method. However first in the next
paragraph it is justified that it is very likely that
−G
(
)
has positive eigenvalues.
To derive the condition for the uniqueness of the
equilibrium easier, we assume that all the players
have the same
and apply the Gershegorin theorem
for the positivity of eigenvalues over columnjth.
Thus, we have:
>
(
)
∑
e
(11)
We can rewrite (11) as:
>
(
)
∑
e
(12)
The minimum of Γ
(
m
)
is about 0.8 and happens for
≈1.4 . For any less than 1 or greater than 2,
Γ
(
m
)
is greater than 1. Regarding the exponential
term with negative power, the term
(
)
always
has small value. With the nominal beaconing rate of
10Hz and the average beacon size of 500 byte and
data rate of 6 Mbit/s, rT
=
×
×
=6.6×10
.
Thus, the right-hand side of (12) should be a small
number even for a large number of vehicles (N); then
by selection of appropriate values for parameters
and (
larger than the right-hand side of (12)), we
can be sure that the condition for the uniqueness and
stability of the Nash equilibrium is met. Besides, the
derived condition (12) is a sufficient condition for the
uniqueness of the NE, which means even if this
condition is violated still the algorithm might be
stable.
The gradient method has been used, finding the
NE in a distributed manner; thus, in NPC, every
vehicle updates its beacon power, according to the
gradient method, as follows.
=
ℱ
=
−c
CBR
(
)
(13)
Algorithm 1 shows the NPC mechanism.
Algorithm 1. Beacon’s power updates based on
gradient method
.
1. Every node measures CBR
2. Update the beacon power as
=
+
−
(
)
and
are 100 mW and 1 mW, respectively
(Kenney 2011). As Algorithm 1 shows, every vehicle
updates its BSM power, according to the locally
measured CBR in each iteration of the algorithm, and
vehicles do not communicate their information.
4 SELECTION OF THE
PARAMETERS
As discussed before, the purpose of the NPC is to
control the CBR around 0.65 (according to (Fallah,
Huang et al. 2011) between 0.4 and 0.8); thus,
simulations are run, in order to find the appropriate
values for
and . For this purpose, OMNeT++ as
network simulator and SUMO as mobility generator
have been used. The simulation parameters are
summarized in Table 1.
Distributed Transmit Power Control for Beacons in VANET
183

Table 1: Simulation Parameters.
Parameter Value
Thermal Noise -100 dBm
Carrier Sense Threshold -90 dBm
MAC Protocol IEEE 802.11p
Carrier Frequency 5.89 GHz
Bit Rate 6 Mbps
Beacon Size 500 Byte
Beacon Rate 10 Hz
Sampling Time 500 msec
Propagation Model Nakagami m = 2.0
N
max
(SBCC-N) 98.3
C
max
(SBCC-C) 0.65
Simulations were run for a scenario of a track with
three lines and a total number of vehicles N= 396
vehicles, with a homogeneous distribution. Figure 1
shows that by increasing c, the CBR is controlled at a
lower level and vehicles tend to use less power. The
increase of u has the reverse effect. The Figure also
shows that for c=20 and u=300, the CBR is controlled
around the desirable level 0.65. Thus, these values are
used to compare our algorithm with SBCC-N and
SBCC-C (Egea-Lopez, Alcaraz et al. 2013); however,
later it is shown that vehicles can change their u
parameter individually, in order to meet their
application requirements, while they do not need to
communicate their parameter with other vehicles and
the algorithm works properly and is stable.
5 PERFORMANCE EVALUATION
The same scenario in the previous section; the track
with length 1000 m and N= 396 vehicles; with c=20
and u=300 is used to compare NPC algorithm with
SBCC-N and SBCC-C (Egea-Lopez, Alcaraz et al.
2013). Figure 2 shows power and CBR for the
vehicles in the scenario; as it is evident, NPC is fairer
in power allocation. The Jain Index (Jain, Chiu et al.
1984) for allocated power for SBCC-N and
SBCC-C
and NPC are 0.57, 0.83 and, 0.98, respectively, which
indicates NPC is fairer than the others. This Figure
also shows that the CBR over the track has more
fluctuations with SBCC-N than the other algorithms
do. In addition, the functionality of SBCC algorithms
relies on the exchange of excess information in
beacons; every vehicle should include its transmit
power in its beacons. Thus, NPC is better, in terms of
bandwidth usage too.
Figure 1: Beacon power and CBR for a 1000 m track with
three lines and homogenous distribution of 396 vehicles,
for different values of u and c parameters.
To show the stability of the algorithm and the
uniqueness of the NE in a scenario with a higher
number of vehicles, the next scenario is selected so
that there are 850 vehicles randomly distributed, over
a track with a length of 1400 m and with six lines. The
scenario has been repeated with different initial
values of power for vehicles: when all the vehicles
have an initial power 1 mW, 100 mW and when every
vehicle has a random initial power between 1 and
100 mW. For all the conditions, NPC converges to the
same level of power and CBR, which indicates the
uniqueness and stability of the algorithm.
Figure 3 shows the power and CBR for this
scenario, for the three algorithms. It is clear that NPC
is much fairer in terms of power allocation than
SBCC algorithms and that CBR is smoother along the
track. NPC achieves fairness because NE is unique
and at the NE point, players with the same payoff
function will have the same power. If there is no
fairness at the equilibrium point, some vehicles can
change their strategy unilaterally to obtain higher
payoff, and this is in contradiction with the NE point
concept.
VEHITS 2017 - 3rd International Conference on Vehicle Technology and Intelligent Transport Systems
184

Figure 2: Beacon power and CBR for the algorithms.
Figure 3: Beacon power and CBR for a 1400 m track with
six lines and random distribution of 850 vehicles.
In SBCC algorithms, vehicles require to compute
average power used by neighboring nodes. They also
estimate channel parameters such as path loss
component and shape parameter in Nakagami fading
model. In SBCC-N the number of neighboring
vehicles should be estimated too. Because different
vehicles might estimate different values for above
mentioned parameters, unfairness happens in beacon
power.
Figure 4 shows the changes in power against
iteration of the algorithms, for a vehicle at a position
almost middle of the track (almost x=700) for NPC
with the three different initial conditions and also for
SBCC-N and SBCC-C. It is observed that NPC
converges in less than ten iterations of the algorithm.
Figure 4: Beacon power changes versus the iteration of the
algorithms for a 1400 m track, with six lines and a random
distribution of 850 vehicles.
In the next experiment, it is indicated how NPC
can assign different power levels to vehicles with
different application requirements. In the proposed
power control algorithm, every vehicle can adjust its
u parameter to meet its application requirement. For
example, when there is a traffic jam in one side of a
highway and there is free flow on the other side, it is
desired that vehicles with higher speed will have
higher power. Such a scenario has been simulated in
the next experiment. In the scenario, there is a traffic
jam on one side of a highway, so vehicles are static.
On the other side of the highway, vehicles move with
speeds of 10, 15 or 20 m/s. Every vehicle adjusts its u
parameter proportional to its speed, as follows.
u
=50∗
v
(14)
where
is the speed of the vehicle. Thus, for
example, the utility factor for static vehicles would be
50×4=200 and, for vehicles with 10 m/s speed it
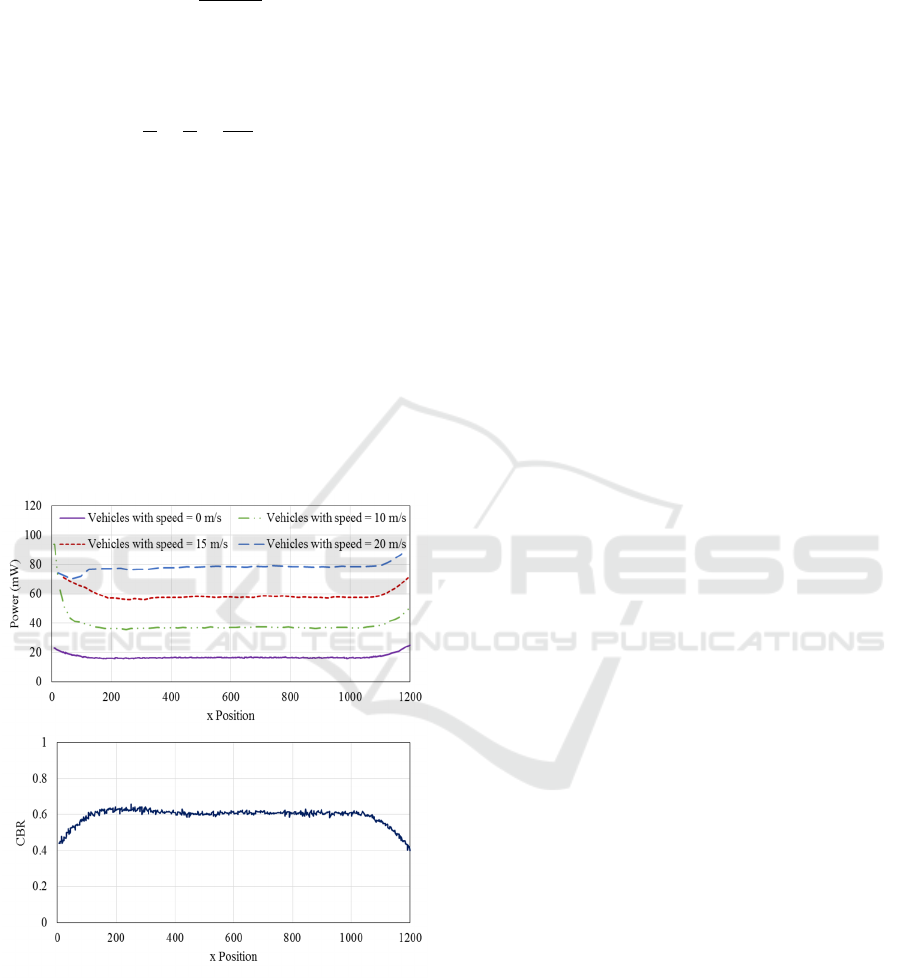
would be 50×10=500. Figure 5 shows that for
vehicles far enough from the edges of the scenario,
the vehicles with higher speeds use higher power for
beaconing and the CBR is controlled. This could be
explained in this way that, at equilibrium point:
ℱ
=
−c
CBR
(
)
=0 (15)
Distributed Transmit Power Control for Beacons in VANET
185
thus,
p
=
(
)
(16)
The vehicles i and j at the same x position sense the
same CBR; so:
=
=
(17)
Thus the allocated power is proportional to the speed
of vehicles. In other words, the NPC algorithm has
per vehicle parameter u
i
that every vehicle can
change it without communicating it with other
vehicles to meet its application requirement.
Besides, it is seen that there is fairness in power
amongst the vehicles that have the same application
requirement (in this example the same speed). The
parameter u
i
could be a function of acceleration,
deceleration….. so that the vehicles which are in a
status that needs to have a longer beaconing range,
can obtain this by adjusting their u
i
parameter, while
the CBR is controlled at the desired level.
Figure 5: Beacon power and CBR for a 1200 m track, with
vehicles which have different speeds of 0, 10, 15 and 20
m/s.
6 CONCLUSION
A distributed algorithm for congestion control, by
adapting BSM power for VANET, was proposed. The
algorithm is based on non-cooperative game theory
and it was indicated that it has unique NE for a large
number of vehicles. The algorithm was compared
with other power control algorithms and it was
indicated that it performs much better in terms of
fairness and band width usage. In addition, NPC can
meet the application requirements; it has per vehicle
parameter so that every vehicle can obtain appropriate
power for its requirement by adapting them, while
congestion is controlled.
In very dense traffic situations, vehicles might be
required to reduce both their beacon power and rate.
ETSI DCC proposes a joint beacon rate and power
control mechanism. However, several researches
have revealed that ETSI DCC suffers unfairness and
oscillation (Kuk, Kim 2014, Autolitano, Campolo et
al. 2013, Marzouk, Zagrouba et al. 2015). A joint
beacon rate and power control mechanism that does
not suffer such problems is the subject of the future
work.
REFERENCES
Alpcan, T., Basar, T. and Tempo, R., 2005. Randomized
algorithms for stability and robustness analysis of high-
speed communication networks. IEEE Transactions on
Neural Networks, 16(5), pp. 1229-1241.
Autolitano, A., Campolo, C., Molinaro, A., Scopigno, R.M.
and VESCO, A., 2013. An insight into Decentralized
Congestion Control techniques for VANETs from ETSI
TS 102 687 V1. 1.1, Wireless Days (WD), 2013 IFIP
2013, IEEE, pp. 1-6.
Bansal, G., Kenney, J.B. and Rohrs, C.E., 2013. LIMERIC:
A Linear Adaptive Message Rate Algorithm for DSRC
Congestion Control. IEEE Transactions on Vehicular
Technology, 62(9), pp. 4182-4197.
Chen, Q., Jiang, D., Tielert, T. and Delgrossi, L., 2011.
Mathematical modeling of channel load in vehicle
safety communications, Vehicular Technology
Conference (VTC Fall), 2011 IEEE 2011, IEEE, pp. 1-
5.
Egea-Lopez, E., Alcaraz, J.J., Vales-Alonso, J., Festag, A.
and Garcia-Haro, J., 2013. Statistical beaconing
congestion control for vehicular networks. IEEE
Transactions on Vehicular Technology, 62(9), pp.
4162-4181.
Egea-Lopez, E. and Pavon-Marino, P., 2016. Distributed
and Fair Beaconing Rate Adaptation for Congestion
Control in Vehicular Networks. IEEE Transactions on
Mobile Computing, (1), pp. 1-14.
VEHITS 2017 - 3rd International Conference on Vehicle Technology and Intelligent Transport Systems
186

Fallah, Y.P., Huang, C., Sengupta, R. and Krishnan, H.,
2011. Analysis of Information Dissemination in
Vehicular Ad-Hoc Networks With Application to
Cooperative Vehicle Safety Systems. IEEE
Transactions on Vehicular Technology, 60(1), pp. 233-
247.
Huang, C., Fallah, Y.P., Sengupta, R. and Krishnan, H.,
2010. Adaptive intervehicle communication control for
cooperative safety systems. IEEE Network, 24(1), pp.
6-13.
Jain, R., Chiu, D. and Hawe, W.R., 1984. A quantitative
measure of fairness and discrimination for resource
allocation in shared computer system. Eastern Research
Laboratory, Digital Equipment Corporation Hudson,
MA.
Kenney, J.B., 2011. Dedicated short-range communications
(DSRC) standards in the United States. Proceedings of
the IEEE, 99(7), pp. 1162-1182.
Kim, B., Kang, I. and Kim, H., 2014. Resolving the
Unfairness of Distributed Rate Control in the IEEE
WAVE Safety Messaging. IEEE Transactions on
Vehicular Technology, 63(5), pp. 2284-2297.
Kuk, S. and Kim, H., 2014. Preventing Unfairness in the
ETSI Distributed Congestion Control. IEEE
Communications Letters, 18(7), pp. 1222-1225.
Marzouk, F., Zagrouba, R., Laouiti, A. and
MUHLETHALER, P., 2015. An empirical study of
Unfairness and Oscillation in ETSI DCC. arXiv
preprint arXiv:1510.01125, .
Rosen, J.B., 1965. Existence and uniqueness of equilibrium
points for concave n-person games. Econometrica:
Journal of the Econometric Society, , pp. 520-534.
Sepulcre, M., Gozalvez, J., HäRri, J. and Hartenstein, H.,
2010. Application-Based Congestion Control Policy for
the Communication Channel in VANETs. IEEE
Communications Letters, 14(10), pp. 951-953.
Torrent-Moreno, M., Mittag, J., Santi, P. and Hartenstein,
H., 2009. Vehicle-to-vehicle communication: fair
transmit power control for safety-critical information.
IEEE Transactions on Vehicular Technology, 58(7), pp.
3684-3703.
Distributed Transmit Power Control for Beacons in VANET
187
