
Using Linear Logic to Verify Requirement Scenarios in SOA Models
based on Interorganizational WorkFlow Nets Relaxed Sound
K
ˆ
enia Santos de Oliveira, Vin
´
ıcius Ferreira de Oliveira and St
´
ephane Julia
Computing Faculty, Federal University of Uberl
ˆ
andia, Uberl
ˆ
andia, Brazil
Keywords:
Interorganizational WorkFlow Net, Petri Nets, Linear Logic, Service-oriented Architecture.
Abstract:
This paper presents a method for requirement verification in Service-Oriented Architecture (SOA) models
based on Interorganizational WorkFlow nets which are not necessarily deadlock-freeness. In this method,
a requirement model corresponds to a public model that only specify tasks which are of interest of all par-
ties involved. An architectural model is considered as a set of private processes that interact through asyn-
chronous communication mechanisms in order to produce the services specified in the corresponding require-
ment model. Services can be seen as scenarios of WorkFlow nets. For each scenario that exists in the re-
quirement model a proof tree of Linear Logic can be produced, and for each scenario correctly finalized, a
precedence graph that specifies the task sequence can be derived. For each scenario of the architectural model,
similar precedence graphs can be produced. The precedence graphs of the requirement and architectural model
are then compared in order to verify if all existing scenarios of the requirement model also exist at the architec-
tural model level. The comparison of behavior between distinct discrete events models is based on the notion
of branching bisimilarity that prove behavioral equivalence between distinct finite automata. The example
used to illustrate the proposed approach, shows that the method can be effective to identify if a SOA-based
system satisfy the business needs specified by a model of public requirements.
1 INTRODUCTION
To represent the collaboration processes that involve
multiple organizations, consideration has been given
to interorganizational workflow processes. An in-
terorganizational workflow processes allows organi-
zations with complementary skills to perform jobs
that are not within the range of a single organization.
Interorganizational workflows can be easily repre-
sented by Interorganizational WorkFlow nets (van der
Aalst, 2000).
To verify the correctness of an interorganizational
workflow process, the soundness property is often
used. However, a wide variety of interorganiza-
tional workflow processes are not completely sound
and may lead the interorganizational business process
to deadlock situations, for example (Fahland et al.,
2011). Therefore, in (Passos and Julia, 2014), an ap-
proach is presented for deadlock-freeness scenarios
detection in interorganizational workflow processes
modeled by Interorganizational WorkFlow nets.
An important issue in Software Engineering is to
ensure that a software architecture proposal repro-
duces the behavior of the requirement analysis model.
The verification that the behavior of the requirement
model exists within the corresponding architectural
model minimizes risks of failure in projects, increas-
ing the guarantee of software quality and avoiding re-
work costs (Goknil et al., 2014). Only a few work-
studies address this problem (Zernadji et al., 2015)
in the specific context of Software-Oriented Architec-
ture (SOA). It is then of great interest to propose an
approach that verifies if the requirements defined in
analysis models (in terms of dynamic behavior) are
also present in SOA models. In a more specific sense
in those models considered as not sound, it is of great
interest to consider deadlock-freeness scenarios as the
main features of the requirement analysis.
This article presents an approach based on a kind
of comparative analysis between requirement and ar-
chitectural models in context of SOA. Through this
comparative analysis, it is possible to verify if the
main business relationship between the organizations
involved can be provided without leading the sys-
tem to a deadlock situations. Such an analysis can
be based on Linear Logic proofs produced from in-
terorganizational workflow processes modeled by In-
terorganizational WorkFlow nets. As a matter of fact,
some studies have already shown the relationship be-
tween the Petri net theory and Linear Logic, such as
254
Oliveira, K., Oliveira, V. and Julia, S.
Using Linear Logic to Verify Requirement Scenarios in SOA Models based on Interorganizational WorkFlow Nets Relaxed Sound.
DOI: 10.5220/0006290202540262
In Proceedings of the 19th International Conference on Enterprise Information Systems (ICEIS 2017) - Volume 2, pages 254-262
ISBN: 978-989-758-248-6
Copyright © 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

(Girault et al., 1997) and (Riviere et al., 2001), since
there is an almost direct translation of the structure of
a Petri net into formulas of Linear Logic. To show
the equivalence of two distinct models (requirement
and architectural models), a new definition of seman-
tic equivalence for distinct models can be produced,
as already performed, for example, in the context of
process algebras with the notion of bisimulation (Bas-
ten, 1998). A new definition of semantic equivalence
in the context of Linear Logic compatible with the
notion of bisimulation was then be introduced in this
work. This in order to verify if requirements speci-
fied in a kind of public model also exist in the corre-
sponding SOA model. The architectural model is be
based on Interorganizational WorkFlow net not nec-
essarily sound. The proposed approach accept in par-
ticular relaxed sound processes (when all the activi-
ties of the system appeared in at least one process that
ended correctly).
The remainder of the article is organized as fol-
lows. In section 2, the definition of Interorganiza-
tional WorkFlow nets nets are presented as well as an
overview of Linear Logic and the notion of Branching
Bisimilarity. The approach to formally detect require-
ments present in SOA models is proposed in section
3. Finally, section 4 concludes this work.
2 THEORETICAL BACKGROUND
2.1 Interorganizational WorkFlow Net
Collaboration processes that involve multiple orga-
nizations can be represented as interorganizational
workflow processes. Essentially, an interorganiza-
tional workflow process is a set of loosely coupled ‘lo-
cal’ workflow processes involved in a same ‘global’
workflow process (van der Aalst, 2000). In order to
model an interorganizational workflow process, an In-
terorganizational WorkFlow net (IOWF-net) can be
used. Each of the local workflow processes is de-
scribed by a Petri net called WorkFlow net (WF-net).
According to (van der Aalst, 1998), the formal defini-
tion of a IOWF-net is based on a tuple IOWF − net =
{PN
1
, PN
2
, ..., PN
n
, P
AC
, AC}, where:
1. n ∈ N is the number of Local WorkFlow nets
(LWF-nets);
2. For each k ∈ {1, ..., n} : PN
k
is a WF-net with
source place i
k
and sink place o
k
;
3. P
AC
is the set of asynchronous communication el-
ements (communication places).
4. AC corresponds to the asynchronous communi-
cation relation. It specifies a set of input transi-
tions and a set of output transitions for each asyn-
chronous communication element.
To clarify the concepts defined above, consider the
synthetic example presented in Figure 1. This IOWF-
net has two LWF-nets: A and B. Each one has only
one source place (iA for LWF-A and iB for LWF-B)
and one sink place (oA for LWF-A and oB for LWF-
B). The places PC1, PC2 and PC3 are the communi-
cation places.
Figure 1: An IOWF-net example.
In (van der Aalst, 1998), Unfolded Interorganiza-
tional WorkFlow nets U(IOWF-net) are defined. The
unfolding of an IOWF-net corresponds to the trans-
formation of an IOWF-net into a simple WF-net. In
the U(IOWF-net), all the LWF-nets are included into a
single workflow process considering a start transition
and a termination transition. A global source place ‘i’
and a global sink place ‘o’ have then to be added in or-
der to respect the basic structure of a simple WF-net,
and the asynchronous communication elements exist-
ing between the different LWF-nets are mapped into
ordinary places. In section 3 an example of U(IOWF-
net) can be observed (Figure 4).
The correctness of a workflow process is asso-
ciated to the verification of the soundness property
(van der Aalst, 1996). This property ensure that all
the process instances of a WF-net will be correctly
treated and finalized and will not have tasks not exe-
cuted in the process verified. Many studies have al-
ready considered the analysis of the soundness prop-
erty in the interorganizational workflow process case
as in (van der Aalst, 1998) and (Passos and Julia,
2013). It is interesting for the organizations, in cases
where the classical soundness correction criterion is
not satisfied for a given IOWF-net, to identify sce-
narios that satisfy the business requirements. In this
context, variants of the soundness criterion were pro-
posed. In (Passos, 2016), it is defined an approach
to identify if a IOWF-net is sound, relaxed sound or
weak sound. An IOWF-net is relaxed sound if each
process task is considered in at least one of the runs
that finishes correctly. An IOWF-net is weak sound
if there is no deadlock in the model and the correct
completion of the process is guaranteed, even in cases
where the analyzed process presents dead tasks.
Using Linear Logic to Verify Requirement Scenarios in SOA Models based on Interorganizational WorkFlow Nets Relaxed Sound
255

2.2 Linear Logic
Instead of emphasizing truth, as in classical logic, or
proof, as in intuitionistic logic, Linear Logic (Girard,
1987) emphasizes the role of formulas as resources.
In the Linear Logic there are several connectives,
but, in this paper only tow are used. The times
connective (denoted by ‘⊗’) represents simultaneous
availability of resources; for instance, ‘A ⊗ B’ rep-
resents the simultaneous availability of resources ‘A’
and ‘B’. The linear implies connective (denoted by
‘(’) represents a state change; for instance, ‘A ( B’
denotes that consuming ‘A’, ‘B’ is produced; after the
production of ‘B’, ‘A’ will not be available anymore.
The following definition presented in (Riviere
et al., 2001) shows how to translate a Petri net model
into Linear Logic formulas:
• A marking M is a monomial in ⊗ and is repre-
sented by M = A
1
⊗ A
2
⊗ ... ⊗ A
k
where A
i
are
place names.
• A sequent M, t
i
` M
0
represents a scenario where
M and M’ are respectively the initial and final
markings, and t
i
is a list of non-ordered transi-
tions. For instance, in the LWF-A shown in Figure
1, the sequent iA, TA1, TA2 ` oA represents one
possible scenario of this WorkFlow net.
A sequent can be proven by applying the rules
of the sequent calculus. In this paper, the following
rules are used: (
L
rule - expresses a transition firing
and generates two sequents (the right sequent repre-
sents the subsequent remaining to be proved and the
left sequent represents the consumed tokens by this
firing); ⊗
L
rule - is used to transform a marking in
an atoms list; ⊗
R
rule - transforms a sequent such as
A, B ` A ⊗B into two identity ones A ` A and B ` B.
Linear Logic proof tree is read from the bottom-
up. The proof stops when the identity sequent o ` o
( ‘o’ correspond to a sink place) is produced, when
there is not any rule that can be applied or when all
the leaves of the proof tree are identity sequents.
The Linear Logic proof trees can be transformed
into precedence graphs, as shown in (Diaz, 2009) by
labeling the corresponding proof trees. To label a
proof tree, each time the (
L
rule is applied, the corre-
sponding transition t
i
label the application of the rule,
as well as the atoms produced and consumed. Fur-
thermore, the initial event must be labeled by i
i
and
the final event must be labeled by f
i
. The labels are
shown in the proof tree above the atoms and below
the rules (
L
. In a precedence graph, the vertices are
events and the arcs are identity sequent, i.e relation
between the event that produced the atom and one that
consumed the atom (Diaz, 2009). The subsection 3.2
shows how proof trees and the corresponding label-
ings are built.
In (Passos and Julia, 2013), the Linear Logic proof
trees was used to analyze the soundness criterion in an
IOWF-nets. For this, it is necessary to verify sound-
ness for each LWF-net that composes the IOWF-net
and for the unfolded net, U(IOWF-net). A WorkFlow
net is sound if it respects the restriction 1 and 2 shown
below.
1. For each scenario of the analysed WorkFlow net,
at the end of the proof tree: (a) there is not any
available atom for consumption (all places of the
WorkFlow net are empty); (b) there is not any
available transition formula that was not fired; (c)
just one identity sequent o ` o was produced (just
one token appears in the sink place).
2. Considering all scenarios for the WorkFlow net
analyzed, each transition t
i
has to appear in, at
least, one scenario (the activities of the WorkFlow
net will appears in at least one process).
A similar approach can be used to verify variants
of the soundness criterion (relaxed and weak sound)
presented in subsection 2.1. According to (Passos,
2016), an IOWF-net is relaxed sound if the proof trees
of the U(IOWF-net) scenarios respect the restriction 1
(a and c), and for each scenario that satisfy this restric-
tion, the restriction 2 is also respected. An IOWF-net
is weak sound if all the proof trees of the U(IOWF-
net) scenarios respect the restriction 1 (a and c).
2.3 Branching Bisimilarity
The idea of bisimilarity was first introduced in (Park,
1981) and can be interpreted in the following man-
ner: two processes are equivalent if and only if they
can always copy or simulate the actions of each other.
Bisimilarity does not make the distinction between
external (observable) actions and internal (silent) ac-
tions; therefore it is not a suitable equivalence concept
for processes with internal behavior.
Branching bisimilarity was first introduced in (van
Glabbeek and Weijland, 1996) and is a variant of
bisimilarity; however, branching bisimilarity distin-
guishes external behavior from internal behavior. The
distinction between external and internal behavior
captures the idea that an environment observing two
processes might not be able to see any differences in
their behavior while internally the two processes per-
form different computations (Basten, 1998). There-
fore, to be able to make a distinction between external
and internal behavior (hidden events), silent actions
can be introduced. Silent actions are actions that can-
not be observed. Usually, silent actions are denoted
ICEIS 2017 - 19th International Conference on Enterprise Information Systems
256
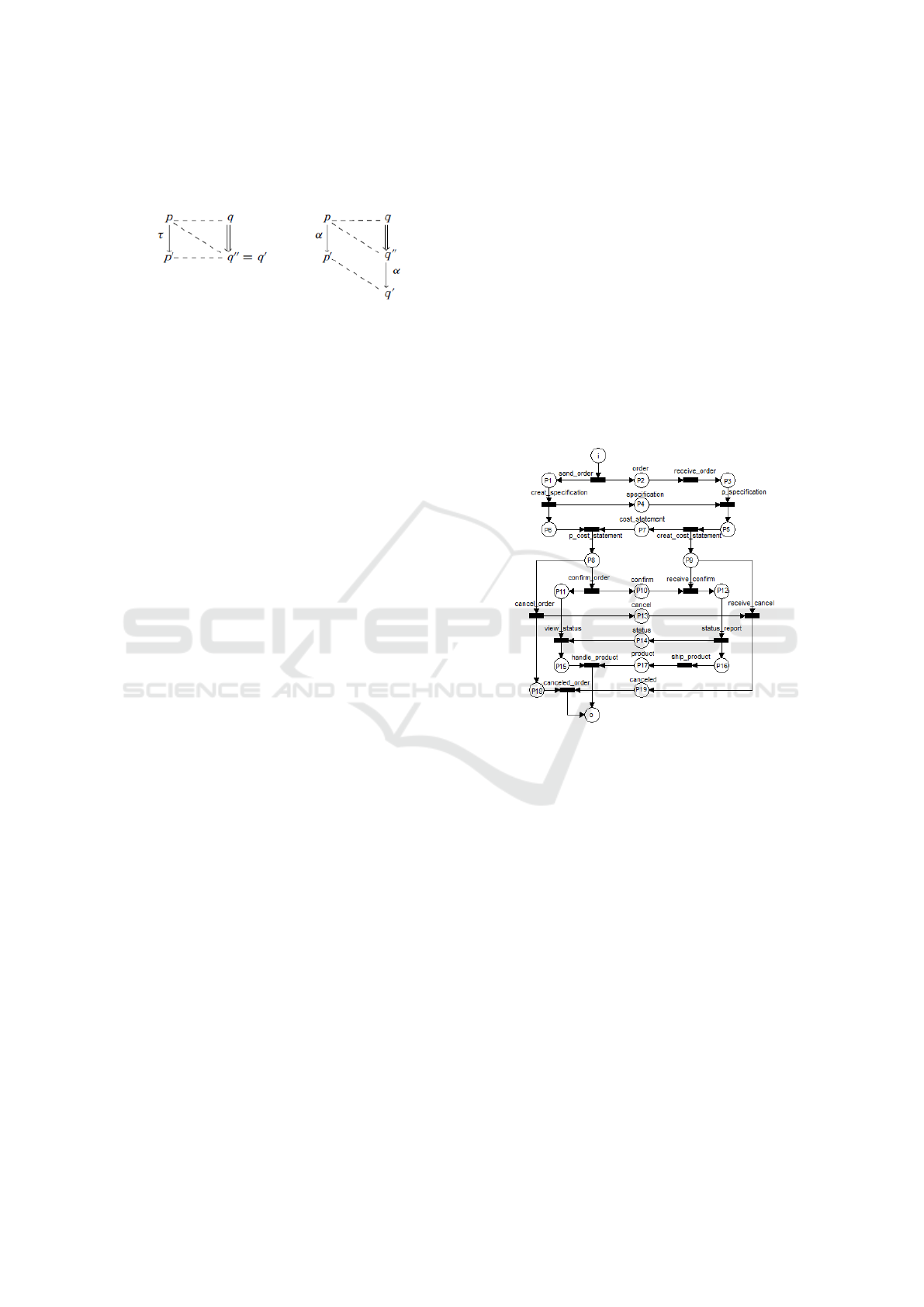
with the action label τ. The Figure 2 presented in
(Basten, 1998) shows the essence of branching bisim-
ulation.
Figure 2: The essence of branching bisimulation.
In Figure 2, τ represents a silent action, α repre-
sents an observable action, and p, q, p
0
, q
0
, q
00
repre-
sent processes. On the left side of Figure 2, the pro-
cess p can evolve into another process p
0
by executing
a silent action (τ) and the process q can evolve into
another process q
00
by executing a sequence of zero
or more τ actions (such a fact represented by relation
‘=⇒’). Then, it is possible to observe on the left side
of the figure that the process p has an equivalence re-
lation with the processes q and q
00
and the process p
0
has an equivalence relation with the process q
00
. These
facts clearly state that two equivalent processes will
continue equivalent after the introduction of some ad-
ditional silent actions in one of the processes or even
in both.
On the right side of Figure 2, the process p can
evolve into another process p
0
by executing an observ-
able action (α), the process q can evolve into another
process q
00
by executing a sequence of zero or more τ
actions (relation ‘=⇒’) and the process q
00
can evolve
into another process q
0
by executing an observable ac-
tion (α). Then, it is possible to observe on the right
side of the figure that the process p has an equivalence
relation with the processes q and q
00
, and the pro-
cess p
0
has an equivalence relation with the process
q
0
. These facts clearly state that two equivalent pro-
cesses will continue equivalent after the introduction
of some additional observable actions in one of the
processes only if the same observable actions also ex-
ist in the other process and respect the same sequence
constraints in both processes.
3 VERIFICATION OF
DEADLOCK-FREENESS
REQUIREMENT SCENARIOS
IN SOA MODELS
In (van der Aalst, 2003), Aalst defined the P2P-
WorkFlow nets. The approach is used to represent
interorganizational workflow processes and was pro-
posed to ensure that the local implementation of a
workflow does not create all kinds of anomalies over
organizational borders. In such an approach, two
views of the system are considered: the public one
and the private one. A public WF-net specifies the ex-
pected system requirements the parties involved will
have to perform. A private WF-net typically con-
tains several tasks which are only of local interest and
which do not appear in the public WF-net model.
The Figure 3 represents a public WF-net exam-
ple and Figure 4 represents the corresponding private
models (LWF - contractor and LWF - subcontractor)
modeled by an IOWF-net. In Figure 4, a global source
place i and a global sink place o were added in order
to respect the basic structure of a simple WF-net as
explained in subsection 2.1. Therefore, this model is
a U(IOWF-net).
Figure 3: Public Model (requirement).
The P2P approach presented by Aalst (van der
Aalst, 2003), ensures that a IOWF-net obtained from
a private WF-nets respecting the construction rules
presented by Aalst should be deadlock-freeness (i.e.
sound). In particular, such rules restrain the design
patterns allowed for the construction of private mod-
els and are based on the concept of branching bissim-
ilarity presented in subsection 2.3. But, in practice,
organizations build theirs workflow processes with-
out worrying too much about rules (Fahland et al.,
2011). Considering this fact, Passos and Julia (Passos
and Julia, 2014) presented an approach that verifies
if the main business relationships between involved
organizations can be provided safely. The approach
identifies deadlock-freeness scenarios in interorgani-
zational workflow processes modeled by IOWF-nets
through the use of Linear Logic proof trees. In par-
ticular, the approach can be applied to models that re-
spect relaxed versions of the soundness criterion as
explained in subsection 2.2.
Using Linear Logic to Verify Requirement Scenarios in SOA Models based on Interorganizational WorkFlow Nets Relaxed Sound
257

Figure 4: Private Models (architecture) composed in an
U(IOWF-net).
Therefore, our approach is based on the ideas pre-
sented in (van der Aalst, 2003) and (Passos and Ju-
lia, 2014) whose main purpose is to verify, in the
context of SOA, if the behavior defined in a require-
ment model (public model) is also present in the
corresponding architectural proposal (private models)
without depending on rigid construction rules that en-
sure the soundness of the process.
3.1 Proposed Method
The approach presented in this work considers that
the requirement model corresponds to a public WF-
net and the architectural model (type SOA) is the set
of private WF-nets that interact through asynchronous
communication mechanisms in order to produce the
services specified by the requirement model. There-
fore, the architectural model corresponds to an IOWF-
net. The services of the SOA model are then the sce-
narios of the IOWF-net. A scenario in the context
of a workflow process corresponds to a well defined
route mapped into the corresponding WF-net and, if
the WF-net has more than one route (places with two
or more output arcs), more than one scenario has to be
considered then. Because the qualitative analysis of
the approach is based on relaxed soundness correction
criteria, it is necessary then to identify all deadlock-
freeness scenarios in the architectural model proposal
that satisfy the scenarios specified in the requirement
model.
To introduce the proposed approach, the examples
presented in Figures 3 and 4 are used. It is important
to note that the U(IOWF-net) of Figure 4 is not sound
(the possibility to reach a deadlock situation within
the existing scenarios of the model exists); as a con-
sequence, such architectural proposal was not built
based on the construction rules proposed by Aalst in
(van der Aalst, 2003).
In this work, iterative routes of WF-net models are
replaced by simple global tasks, as it is generally the
case of hierarchical approaches based on the notion of
well formed blocks (Valette, 1979). Figure 5 shows
an example of iterative route constraint that exist in
the WF-net of Figure 4 (LWF-contractor) and their
transformation into single tasks.
Figure 5: Transformation of iterative route constraints into
single tasks.
The proposed method in this work respects the fol-
lowing sequence of steps: (1) build the Linear Logic
proof trees for each scenario of the public WF-net cor-
rectly executed (requirement model) and transformed
the obtained proof trees into the corresponding prece-
dence graphs; (2) build the Linear Logic proof trees
for each scenario of the private WF-net composed
in an U(IOWF-net) correctly executed (architecture
model) and transformed the obtained proof trees into
the corresponding precedence graphs; (3) verify the
equivalence between the precedence graphs of the
public model and the precedence graphs of the private
model.
Because the precedence graphs show in a formal
way the sequencing constraints of a set of activities
performed by a WF-net, they can be seen as a king
of operational semantic associated to a workflow pro-
cess. The equivalence between two WF-nets (the pub-
lic and the private one) can consequently be verified
using the branching bisimilarity concept presented in
subsection 2.3 whose purpose is to compare opera-
tional semantics of distinct formal behavioral models.
In our approach, the activities of the private model
that do not appear in the public model are then con-
sidered as silent actions. When removing the silent
actions of the precedence graphs of the private mod-
els, the obtained reduced graphs should be the same
of the public WF-net when the behavior of the archi-
tectural model reproduces the behavior of the require-
ment model.
3.2 Method Application
To illustrate the approach, we use the examples pre-
sented in Figures 3 and 4. The transitions of the mod-
ICEIS 2017 - 19th International Conference on Enterprise Information Systems
258

els are named according to the initial letters of the ac-
tivities associated to them. For example, send order
and receive order are represented by t
so
and t
ro
, re-
spectively. The transitions (activities) of the require-
ment model (WF-net of Figure 3) are represented by
the following formulas of Linear Logic:
t
so
= i ( P
1
⊗ P
2
, t
ro
= P
2
( P
3
,
t
cs
= P
1
( P
4
⊗ P
6
, t
ps
= P
3
⊗ P
4
( P
5
,
t
pcs
= P
6
⊗ P
7
( P
8
, t
ccs
= P
5
( P
7
⊗ P
9
,
t
c f o
= P
8
( P
10
⊗ P
11
, t
rc f
= P
9
⊗ P
10
( P
12
,
t
sr
= P
12
( P
14
⊗ P
16
, t
vs
= P
11
⊗ P
14
( P
15
,
t
co
= P
8
( P
13
⊗ P
18
, t
rc
= P
9
⊗ P
13
( P
19
,
t
sp
= P
16
( P
17
, t
cdo
= P
18
⊗ P
19
( o,
t
hp
= P
15
⊗ P
17
( o.
The requirement model contains two scenarios
called respectively Sr1 and Sr2. Before the construc-
tion of the precedence graph, it is necessary to prove
the sequent corresponding to each scenario of the
public WorkFlow net are syntactically correct in ac-
cordance with Linear Logic theory.
Considering the scenario Sr1 of the public Work-
Flow net of Figure 3, the following sequent needs to
be proven:
i, t
so
, t
ro
, t
cs
, t
ps
, t
ccs
, t
pcs
, t
co
, t
rc
, t
cdo
` o.
The corresponding proof tree for scenario Sr1 is
the following:
P
18
`P
18
P
19
`P
19
P
18
,P
19
`P
18
⊗P
19
⊗
R
o`o
(
L
P
9
`P
9
P
13
`P
13
P
9
,P
13
`P
9
⊗P
13
⊗
R
P
18
,P
19
,P
18
⊗P
19
(o`o
(
L
P
9
,P
13
,P
18
,P
9
⊗P
13
(P
19
,t
cdo
`o
⊗
L
P
8
`P
8
P
9
,P
13
⊗P
18
,P
9
⊗P
13
(P
19
,t
cdo
`o
(
L
P
6
`P
6
P
7
`P
7
P
6
,P
7
`P
6
⊗P
7
⊗
R
P
9
,P
8
,P
8
(P
13
⊗P
18
,t
rcl
,t
cdo
`o
(
L
P
6
,P
7
,P
9
,P
6
⊗P
7
(P
8
,t
co
,t
rc
,t
cdo
`o
⊗
L
P
5
`P
5
P
6
,P
7
⊗P
9
,P
6
⊗P
7
(P
8
,t
co
,t
rc
,t
cdo
`o
(
L
P
3
`P
3
P
4
`P
4
P
3
,P
4
`P
3
⊗P
4
⊗
R
P
6
,P
5
,P
5
(P
7
⊗P
9
,t
pcs
,t
co
,t
rc
,t
cdo
`o
(
L
P
3
,P
4
,P
6
,P
3
⊗P
4
(P
5
,t
ccs
,t
pcs
,t
co
,t
rcl
,t
cdo
`o
⊗
L
P
1
`P
1
P
3
,P
4
⊗P
6
,P
3
⊗P
4
(P
5
,t
ccs
,t
pcs
,t
co
,t
rc
,t
cdo
`o
(
L
P
2
`P
2
P
1
,P
3
,P
1
(P
4
⊗P
6
,t
ps
,t
ccs
,t
pcs
,t
co
,t
rc
,t
cdo
`o
(
L
P
1
,P
2
,P
2
(P
3
,t
cs
,t
ps
,t
ccs
,t
pcs
,t
co
,t
rc
,t
cdo
`o
⊗
L
i`i P
1
⊗P
2
,P
2
(P
3
,t
cs
,t
ps
,t
ccs
,t
pcs
,t
co
,t
rc
,t
cdo
`o
(
L
i,i(P
1
⊗P
2
,t
ro
,t
cs
,t
ps
,t
ccs
,t
pcs
,t
co
,t
rc
,t
cdo
`o
To generate the precedence graph, the proof tree
must be labeled as explained in subsection 2.2. For
reasons of space, only part of the proof trees presented
in this work are labeled. For example, for the proof
tree of scenario Sr1, part of the labeling is the follow-
ing one:
t
co
P
18
`
t
cdo
P
18
t
rc
P
19
`
t
cdo
P
19
t
co
P
18
,
t
rc
P
19
`
t
cdo
P
18
⊗
t
cdo
P
19
⊗
R
t
cdo
o `
f
i
o
(
L
t
cdo
.
.
.
i
i
i `
t
so
i
t
so
P
1
⊗
t
so
P
2
,P
2
(P
3
,t
cs
,t
ps
,t
ccs
,t
pcs
,t
co
,t
rc
,t
cdo
`o
(
L
t
so
i
i
i ,i(P
1
⊗P
2
,t
ro
,t
cs
,t
ps
,t
ccs
,t
pcs
,t
co
,t
rc
,t
cdo
`o
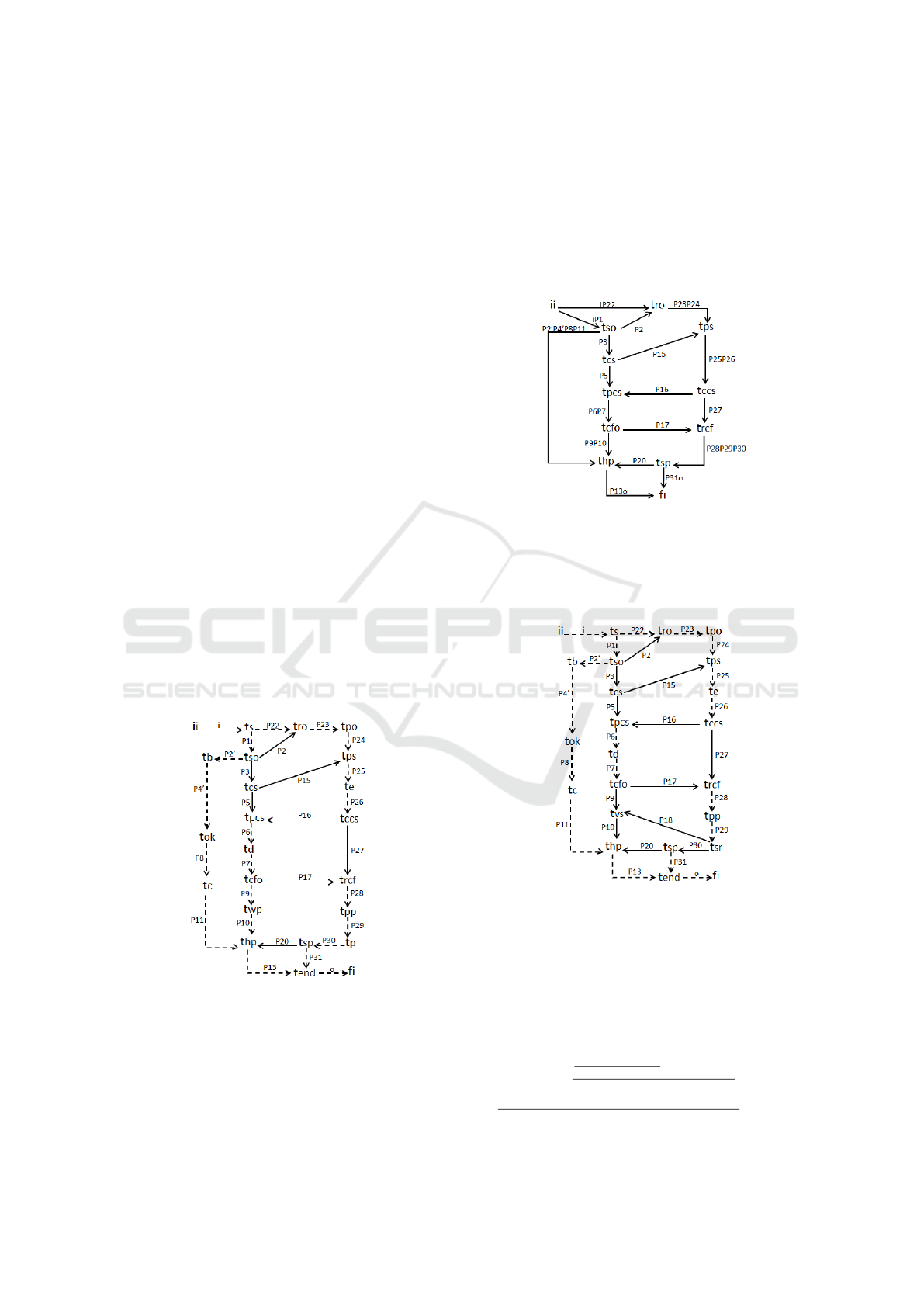
The complete precedence graph of scenario Sr1
for the requirement model is presented in Figure 6.
In this graph, the vertices represented the activities,
and the arcs the conditions that activate the activities.
This is noted, in particular, as the formal specifica-
tion of the requirement (in terms of the behavior) ex-
pected from the SOA where such a service will be
implemented. It represents too a possible view of the
operational semantic associated to the corresponding
workflow process.
Figure 6: Precedence graph for scenario Sr1.
Considering the scenario Sr2 of the public Work-
Flow net of Figure 3, the following sequent needs to
be proven:
i, t
so
, t
ro
, t
cs
, t
ps
, t
ccs
, t
pcs
, t
c f o
, t
rc f
, t
sr
, t
vs
, t
sp
, t
hp
` o
For reasons of space, we do not show the proof
trees for scenario Sr2. The precedence graph for sce-
nario Sr2 of the requirement model is presented in
Figure 7.
Figure 7: Precedence graph for scenario Sr2.
The U(IOWF-net) of Figure 4 (architectural
model) contain four scenarios called respectively Sa1,
Sa2, Sa3 and Sa4. The transitions of the architecture
Using Linear Logic to Verify Requirement Scenarios in SOA Models based on Interorganizational WorkFlow Nets Relaxed Sound
259
model are represented by the following formulas of
Linear Logic:
t
s
= i ( P
1
⊗ P
22
, t
so
= P
1
( P
2
⊗ P
3
⊗ P
14
,
t
ro
= P
22
⊗ P
14
( P
23
, t
po
= P
23
( P
24
,
t
b
= P
0
2
( P
0
4
, t
ok
= P
0
4
( P
8
, t
c
= P
8
( P
11
,
t
cs
= P
3
( P
5
⊗ P
15
, t
ps
= P
15
⊗ P
24
( P
25
,
t
e
= P
25
( P
28
, t
pcs
= P
5
⊗ P
16
( P
6
,
t
ccs
= P
26
( P
16
⊗ P
27
, t
d
= P
6
( P
7
,
t
co
= P
7
( P
12
⊗ P
19
, t
rc
= P
27
⊗ P
19
( P
21
⊗ P
31
,
t
cdo
= P
11
⊗ P
12
⊗ P
21
( P
13
, t
p
= P
29
( P
30
,
t
c f o
= P
7
( P
9
⊗ P
17
t
rc f
= P
17
⊗ P
27
( P
28
t
vs
= P
9
⊗ P
18
( P
10
, t
sr
= P
29
( P
18
⊗ P
30
,
t
wp
= P
9
( P
10
, t
hp
= P
11
⊗ P
10
⊗ P
20
( P
13
,
t
sp
= P
30
( P
20
⊗ P
31
, t
end
= P
13
⊗ P
31
( o.
Considering each scenario of U(IOWF-net) of
Figure 4, the following sequents needs to be proven:
• (scenario Sa1) i, t
s
, t
so
, t
ro
, t
b
, t
cs
, t
ok
, t
c
, t
po
, t
ps
, t
e
,
t
ccs
, t
pcs
, t
d
, t
c f o
, t
rc f
, t
wp
, t
pp
, t
t p
, t
sp
, t
hp
, t
end
` o
• (scenario Sa2) i, t
s
, t
so
, t
ro
, t
b
, t
cs
, t
ok
, t
c
, t
po
, t
ps
, t
e
,
t
ccs
, t
pcs
, t
d
, t
c f o
, t
rc f
, t
vs
, t
pp
, t
sr
, t
sp
, t
hp
, t
end
` o
• (scenario Sa3) i, t
s
, t
so
, t
ro
, t
b
, t
cs
, t
ok
, t
c
, t
po
, t
ps
, t
e
,
t
ccs
, t
pcs
, t
d
, t
co
, t
rc
, t
cdo
, t
end
` o
• (scenario Sa4) i, t
s
, t
so
, t
ro
, t
b
, t
cs
, t
ok
, t
c
, t
po
, t
ps
, t
e
,
t
ccs
, t
pcs
, t
d
, t
c f o
, t
rc f
, t
wp
, t
pp
, t
sr
, t
sp
, t
hp
, t
end
` o
For reasons of space, we do not show the proof
trees for scenarios Sa1, Sa2 and Sa3. The precedence
graph for scenario Sa1 is presented in Figure 8. In
this graph, all sequences of activities performed in the
U(IOWF-net) are clearly specified.
Figure 8: Precedence graph for scenario Sa1.
In the precedence graph for the private model,
dashed lines are used when an arc is a link to a silent
activity (one of its vertices corresponds to a silent ac-
tivity). As a matter of fact, these activities are of in-
terest only to their respective private WF-net. By re-
moving a silent action from the precedence graph for
scenario Sa1, it is necessary to connect the precedent
activity that is connected to the silent activity to the
successor activity of the silent activity. For example,
by removing the activity t
d
in Figure 8, a new directed
arc is created between the activities t
pcs
and t
c f o
. By
removing all the silent activities from the precedence
graph in Figure 8, the precedence graph of Figure 9 is
obtained.
Figure 9: Reduced precedence graph for scenario Sa1.
The precedence graph for scenario Sa2 is pre-
sented in Figure 10. By removing all the silent ac-
tivities from the precedence graph in Figure 10, the
precedence graph of Figure 11 is obtained.
Figure 10: Precedence graph for scenario Sa2.
The precedence graph for scenario Sa3 is pre-
sented in Figure 12. By removing all the silent ac-
tivities from the precedence graph in Figure 12, the
precedence graph of Figure 13 is obtained.
The proof tree corresponding to scenario Sa4 is
the following one (because of space limitation, only
the beginning and the end of the proof are presented):
P
31
`P
31
P
13
`P
13
P
31
,P
31
`P
31
⊗P
13
⊗
R
P
18
,o`o
(
L
.
.
.
i,i(P
1
⊗P
22
,t
so
,t
ro
,t
b
,t
cs
,t
po
,t
ps
,...,t
sr
,t
sp
,t
hp
,t
end
`o
ICEIS 2017 - 19th International Conference on Enterprise Information Systems
260
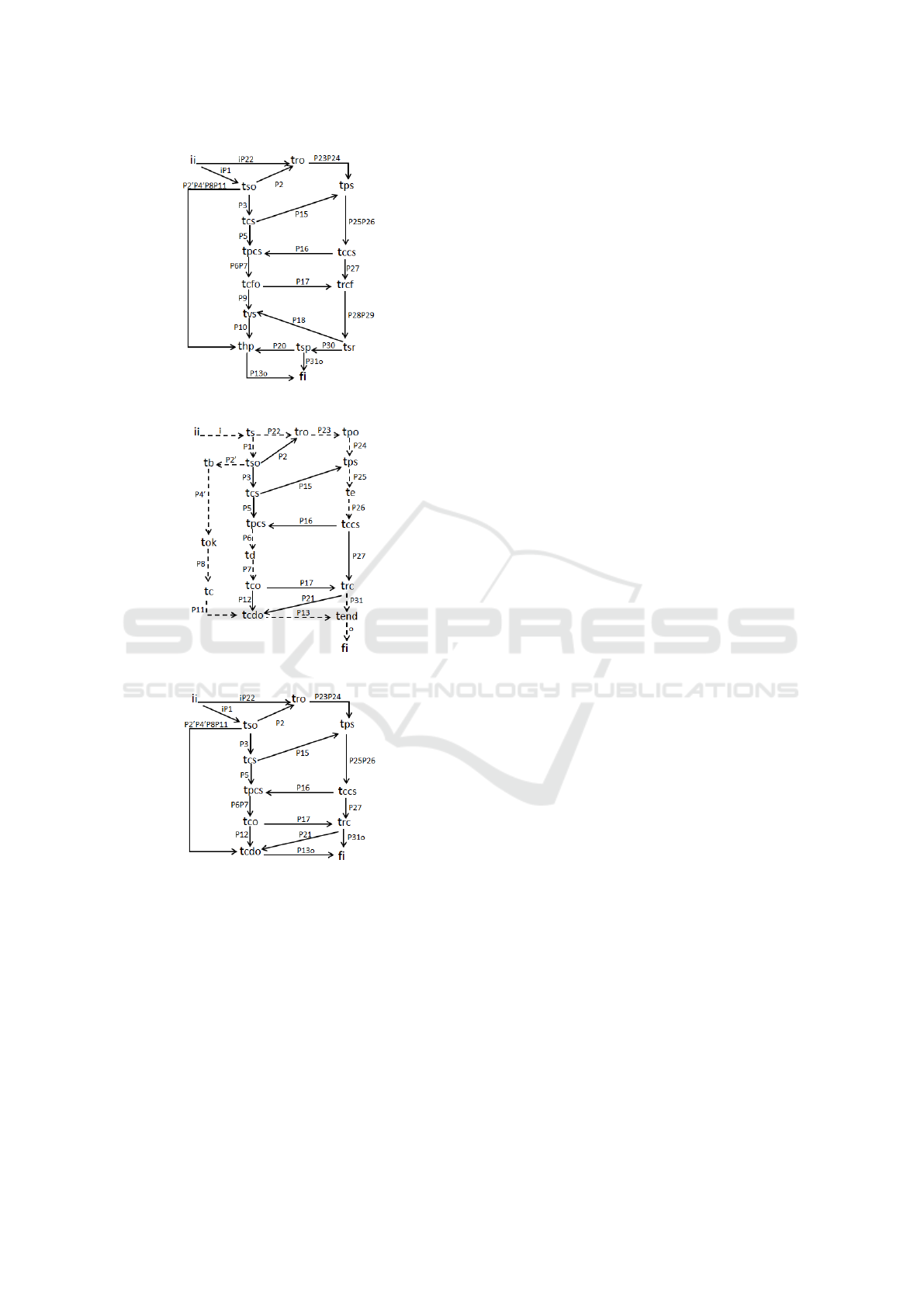
Figure 11: Reduced precedence graph for scenario Sa2.
Figure 12: Precedence graph for scenario Sa3.
Figure 13: Reduced precedence graph for scenario Sa3.
The last line of the proof tree clearly shows that
even with the last place ‘o’ of the U(IOWF-net)
marked, another token is present in the process in P
18
.
This means that scenario Sa4, in case it is executed,
will produce a kind of information duplication; such
a scenario does not correspond then to a sound be-
havior and will not be considered as part of the sce-
narios necessary to cover the business requirement of
the public model. As a direct consequence, the prece-
dence graph for scenario Sa4 is not produced.
The last step of the approach is to compare the
precedence graphs of the public model with the prece-
dence graphs of the private one to verify if the re-
quirements specified in term of behavior in the pub-
lic WorkFlow net are also present in the architectural
proposal specified in the private WorkFlow nets com-
posed in a U(IOWF). The precedence graphs obtained
from scenarios Sr1 and Sr2 have then to be compared
with precedence graphs obtained from scenarios Sa1,
Sa2 and Sa3.
The precedence graph for scenario Sr1 (Figure 6)
and the reduced precedence graph for scenario Sa3
(Figure 13) execute the same activities respecting the
same sequential constraints. The additional arcs iP
22
,
P
0
2
P
0
4
P
8
P
11
and P
31
o that exist in the graph of Figure
13, and that do not exist in the graph of Figure 6
are simply redundant constraints that can be removed
without modifying the requirement specification. For
example, the arc P
0
2
P
0
4
P
8
P
11
of Figure 13 simply states
that the activity t
so
has to happen before activity t
cdo
.
However, this statement already exists through the se-
quence of arcs P
3
, P
5
, P
6
P
7
, P
12
for example. By re-
moving the redundant arcs from the graph of Figure
13, the precedence graphs of Figure 6 and 13 are ex-
actly the same.
The precedence graph for scenario Sr2 (Figure 7)
and the reduced precedence graph for scenario Sa2
(Figure 11) execute the same activities respecting the
same sequential constraints. By removing the redun-
dant arcs from the graph in Figure 11, the precedence
graphs of Figure 7 and 11 are exactly the same.
The scenario Sa1 produces a behavior that was not
specified in the public model. This fact is predictable
since the architecture model is a set of private WF-
net that contains several tasks which are only of local
interest and which do not appear in the public WF-net
model.
Although the architectural model (Figure 4) does
not hold deadlock-freeness, the existing scenarios
(Sa1, Sa2 and Sa3) are correctly executed and verify
the requirements specified in the public model. Ac-
cording to the definition presented in subsection 2.2,
we can verify that the model is relaxed sound, i.e each
transaction (activity) appears in, at least, one scenario
that finishes correctly. Therefore, even though an ar-
chitectural model (type SOA) does not hold deadlock-
freeness, it is possible to verify if, at least, it possesses
the scenarios that correctly satisfy the business needs
defined in the analysis model. For the example shown
in this work, one concludes that the requirements de-
fined in the analysis model are well defined in the ar-
chitectural model. The requirements present in sce-
narios Sr1 and Sr2 of the analysis model are present
respectively in the scenario Sa3 and Sa2 of the archi-
tectural model.
Using Linear Logic to Verify Requirement Scenarios in SOA Models based on Interorganizational WorkFlow Nets Relaxed Sound
261

4 CONCLUSION
This paper presented an approach for requirement
verification in SOA models based on Interorgani-
zational WorkFlow nets relaxed sound and Linear
Logic. Our purpose was to show that, in context of
SOA, all scenarios present in a requirement model
(public model) are also present in the corresponding
architectural model (private models). This approach
was based in particular on the construction of Linear
Logic proof trees and of precedence graphs that show
the operational semantic of distinct models. With
the precedence graph it was possible to compare and
check the behavioral equivalence between the public
and private models, in particular if the models sim-
ulate each other’s behavior, respecting the notion of
branching bisimilarity. In this approach, precedence
graphs are only built for the sequents of Linear Logic
syntactically correct, i.e deadlock-freeness scenarios
that ended correctly the modeled business process.
One of the main advantage of this approach is to
define, through the use of Linear Logic and prece-
dence graphs, a new kind of operational semantic as-
sociated to business processes that allows to verify in
a formal way business requirements within the SOA
context. The presented approach considers architec-
tural models (type SOA) not necessarily sound. The
organizations do not have then to be constrained by
external actors to build their private workflow pro-
cesses, as is the case in practical when considering
existing enterprise systems. Therefore, the organi-
zations involved in interorganizational workflow pro-
cesses can simply verify if the set of requirement sce-
narios of an analysis model are present in an available
SOA model candidate for the implementation of the
required service. In this sense, the impacts and de-
viations generated by collaboration between different
organizations can be minimized.
In this article, only a kind of functional require-
ment was verified in the models. As a future work
proposal, we will associate explicit time constraints to
the models to evaluate the performance of the models
and apply a kind of quantitative analysis in the context
of SOA.
REFERENCES
Basten, T. (1998). In Terms of Nets System Design With
Petri Nets and Process Algebra. PhD thesis, Eind-
hoven University of Technology, Eindhoven, Nether-
lands.
Diaz, M. (2009). Petri Nets: Fundamental Models, Verifi-
cation and Applications. Wiley-ISTE, Reading, Mas-
sachusetts.
Fahland, D., Favre, C., Koehler, J., Lohmann, N., Volzer,
H., and Wolf, K. (2011). Analysis on demand: In-
stantaneous soundness checking of industrial business
process models. Data Knowledg Engineering, pages
448–466.
Girard, J.-Y. (1987). Linear logic. Theoretical Computer
Science, pages 1–102.
Girault, F., Pradin-Chezalviel, B., and Valette, R. (1997).
A logic for petri nets. Journal europ
´
een des syst
`
emes
automatis
´
es.
Goknil, A., Kurtev, I., and Berg, K. V. D. (2014). Genera-
tion and validation of traces between requirements and
architecture based on formal trace semantics. Journal
of Systems and Software, pages 112 – 137.
Park, D. (1981). Concurrency and automata on infinite
sequences. In 5th GI-Conference on Theoretical
Computer Science, pages 167–183. Springer Verlag,
Berlin, Germany.
Passos, L. M. S. (2016). A Metodology based on Lin-
ear Logic for Interorganizational Workflow Processes
Analysis. PhD thesis, Federal Univerty of Uberlandia.
Passos, L. M. S. and Julia, S. (2013). Qualitative analysis of
interorganizational workflow nets using linear logic:
Soundness verification. In IEEE 25th International
Conference on Tools with Artificial Intelligence, pages
667–673.
Passos, L. M. S. and Julia, S. (2014). Linear logic as a tool
for deadlock-freeness scenarios detection in interorga-
nizational workflow processes. In IEEE 26th Interna-
tional Conference on Tools with Artificial Intelligence,
pages 316–320.
Riviere, N., Pradin-Chezalviel, B., and Valette, R. (2001).
Reachability and temporal conflicts in t-time petri
nets. In 9th international Workshop on Petri Nets and
Performance Models.
Valette, R. (1979). Analysis of petri nets by stepwise re-
finements. Journal of Computer and System Sciences,
pages 35–46.
van der Aalst, W. M. P. (1996). Structural characteriza-
tions of sound workflow nets. Computing science re-
ports/23, Eindhoven University of Technology.
van der Aalst, W. M. P. (1998). Modeling and analyzing in-
terorganizational workflows. In International Confer-
ence on Application of Concurrency to System Design,
pages 262–272. IEEE Computer Society Press.
van der Aalst, W. M. P. (2000). Loosely coupled interorga-
nizational workflows: modeling and analyzing work-
flows crossing organizational boundaries. Information
and Management, pages 67–75.
van der Aalst, W. M. P. (2003). Inheritance of interorgani-
zational workflows: How to agree to disagree without
loosing control? Information Technology and Man-
agement, pages 345–389.
van Glabbeek, R. J. and Weijland, W. P. (1996). Branching
time and abstraction in bisimulation semantics. Jour-
nal of the ACM, pages 555–600.
Zernadji, T., Tibermacine, C., Cherif, F., and Zouioueche,
A. (2015). Integrating quality requirements in engi-
neering web service orchestrations. Journal of Sys-
tems and Software, pages 463 – 483.
ICEIS 2017 - 19th International Conference on Enterprise Information Systems
262
