Enhancing Models Correctness through Formal Veriﬁcation: A Case

Study from the Railway Domain

Davide Basile, Felicita Di Giandomenico and Stefania Gnesi

Istituto di Scienza e Tecnologia dell’Informazione “A. Faedo”, Consiglio Nazionale delle Ricerche, ISTI-CNR, Pisa, Italy

Keywords:

Veriﬁcation, Cyber-Physical System, Communication-centric Applications.

Abstract:

Model-based approaches are widely used for analysing systems belonging to a variety of domains, including

the transportation sector. A critical issue with models is their validation, in order to justiﬁably put reliance

on the analysis results they provide (including non functional indicators such as reliability, performance and

energy consumption). Typically, cross-validation is performed, e.g. through exercising modelling by different

formalisms/tools or through forms of experimental analysis. In this paper, we address validation of a case

study from the railway domain via formal techniques, speciﬁcally with automata-based models. Validation of

interaction aspects of Stochastic Activity Networks models of rail road switch heaters, developed for the pur-

pose of evaluating energy consumption and reliability indicators, is performed through a tool based on contract

automata, a recently introduced formalism for verifying properties of communication-based applications.

1 INTRODUCTION

Stochastic model-based analysis is a widely adopted

methodology for evaluating measures of interest re-

lated to dependability and efﬁciency aspects, such

as performance, energy consumed and probability of

failures. This analysis approach is useful for express-

ing the stochastic nature of physical phenomena in-

volved in Cyber-Physical Systems (CPS) (Lee, 2008),

where digital control units interact with continuous

phenomena describing the surrounding environment.

Formalisms as (extensions of) Petri Nets (Balbo,

2007; Sanders and Meyer, 2000; David and Alla,

2001) and (Non) Markov based models (Sanders and

Meyer, 2000; Bause and Kritzinger, 1996) are used

for modelling and evaluating CPS, where reward

structures (Reibman et al., 1989) are deﬁned in or-

der to evaluate measures of interest (e.g. reliability,

performance, energy consumption) at the variation

of relevant parameters, either analytically or through

simulation. However, in general these measures are

assessed without performing any validation of the

model through which they are obtained, especially

when error prone communication-based applications

are involved. These errors may compromise the trust-

worthiness of the results obtained through analysis,

which means a loss of time and moneys for industries.

Hence, models validation is paramount for safety crit-

ical applications.

In this paper, we propose a case study from the

railway domain. In particular, we verify the sound-

ness of interaction aspects of a rail road switch heat-

ing system, originally modelled through Stochastic

Activity Networks (Sanders and Meyer, 2000) (SAN)

for evaluating the energy consumption and the proba-

bility of failure of these devices (Basile et al., 2016a;

Basile et al., 2016e). Rail road switch heaters are es-

sential components for the correct functioning of rail-

way stations, in absence of which possible disasters

can take place (i.e. derailments, trains collision). In

particularly cold regions, ice and snow can prevent

the switches from working properly, hence heaters

are used for guaranteeing the correct functioning of

the rail road switch system. In the analysed system

a central control unit is in charge of managing poli-

cies of energy consumption while satisfying reliabil-

ity constraints, by communicating with the network

of switches to manage the energy supply.

Representation of the interactions between the

system of heaters and the central control unit con-

stitutes a critical part of the developed SAN mod-

els. It is therefore beneﬁcial to provide evidences of

the correct modelling, which is the goal of this pa-

per. We will adopt the contract automata (CA) for-

malism (Basile et al., 2016b; Basile et al., 2016d),

that has been originally introduced for composing

and verifying services. The interactions of the anal-

ysed system will be modelled with CA for guarantee-

Basile, D., Giandomenico, F. and Gnesi, S.

Enhancing Models Correctness through Formal Veriﬁcation: A Case Study from the Railway Domain.

DOI: 10.5220/0006291106790686

In Proceedings of the 5th International Conference on Model-Driven Engineering and Software Development (MODELSWARD 2017), pages 679-686

ISBN: 978-989-758-210-3

679

ing their soundness. Contract automata are endowed

with a speciﬁc tool, called Contract Automata Tool

(CAT) (Basile et al., 2016c), that implements the the-

oretical results of CA, using techniques of control the-

ory and linear programming. We automatically verify

the correctness of the interactions through CAT. It is

possible then to combine the quantitative assessment

of stochastic measures of interest with the qualitative

veriﬁcation of interactions correctness, so improving

the correctness of the obtained results.

Structure of the paper. A brief review of related work

is discussed in Section 2; while Section 3 introduces

the formalisms used in the paper, which are SAN and

CA. The proposed methodology is described in Sec-

tion 4, and in Section 5 we recall the formalization of

the proposed case study as SAN models and we ver-

ify the correctness of the interactions through CAT.

Finally, conclusions and future directions are in Sec-

tion 6.

2 RELATED WORK

In the literature, several approaches for the veri-

ﬁcation and validation of stochastic models have

been proposed, as for example testing, fault injec-

tion, model checking. In particular, model check-

ing (Clarke et al., 1999) is a widely-used and pow-

erful approach for the veriﬁcation of ﬁnite state sys-

tems, based on an exhaustive exploration of the state-

space. Generating the whole state space is in gen-

eral inefﬁcient, since the number of states grows ex-

ponentially in the number of components of a sys-

tem. Several techniques have been developed to over-

come this issue, among them we mention modular

model checking (Kupferman and Vardi, 1998), par-

tial order reduction (Clarke et al., ), symbolic model

checking (McMillan, 1993). Tools like SPIN (Holz-

mann, 2003) are widely-adopted for modelling and

verifying ﬁnite state systems, which implement the

above techniques. However, the continuous dynam-

ics nature of CPS is not always captured by ﬁnite

state systems, and models as Timed automata (Alur

and Dill, 1994), Hybrid Petri Nets (David and Alla,

2001), Stochastic Activity Networks (Sanders and

Meyer, 2000) have been proposed for modelling CPS,

where the evolution of the continuous variables can

be uniform or described by ordinary differential equa-

tions. Several tools have been proposed for their mod-

elling, evaluation and veriﬁcation, as for example UP-

PAAL (Larsen et al., 1997), Kronos (Yovine, 1997),

obius (Clark et al., 2001). When the continuous

time behaviours of CPS are subject to complex and

stochastic dynamics, the model checking problem is

undecidable (Henzinger and Ho, 1995), and gener-

ally an approximation to more tractable models, as for

example Timed automata, is performed. Statistical

Model Checking (SMC) (Legay et al., 2010) uses re-

sults from statistics on top of simulations of a system

to decide whether a given property is satisﬁed with

some degree of conﬁdence. UPPAAL-SMC (David

et al., 2015) has been proposed as a tool that imple-

ments the above techniques.

We will provide a validation of interaction aspects

of the analysed case study by formalising the interac-

tions into a ﬁnite state formal model, which allows to

apply formal veriﬁcation techniques.

3 BACKGROUND

In this section, we brieﬂy introduce the Stochastic Ac-

tivity Networks and contract automata formalisms.

3.1 Stochastic Activity Networks

The Stochastic Activity Networks (Sanders and

Meyer, 2000) formalism is widely used for perfor-

mance, dependability and performability evaluation

of complex systems, given its high expressiveness

and the powerful tools for modelling and evaluating

them (Clark et al., 2001). The SAN formalism is a

variant of Stochastic Petri Nets (Bause and Kritzinger,

1996), and has similarities with Generalised Stochas-

tic Petri Nets (Balbo, 2007). A SAN is composed

of the following primitives: places, activities, input

gates and output gates. Places and activities have

the same interpretation as places and transitions of

Petri Nets. Input gates control the enabling condi-

tions of an activity and deﬁne the change of mark-

ing when an activity completes. Output gates deﬁne

the change of marking upon completion of the activ-

ity. Each enabled activity may complete. Activities

are of two types: instantaneous and timed. Instan-

taneous activities complete once the enabling condi-

tions are satisﬁed. Timed activities take an amount

of time to complete following a temporal stochastic

distribution function. An enabled activity is aborted,

i.e. it cannot complete, when the SAN moves into a

new marking in which the enabling conditions of the

activity no longer hold. Cases are associated to ac-

tivities, and are used to represent probabilistic uncer-

tainty about the action taken upon completion of the

activity. When an activity completes, the following

steps are executed: (i) one of the cases of the activity

is chosen according to its marking-depending proba-

bility; (ii) the function of each input gate of the activ-

ity is executed; (iii) the function of each output gate

AMARETTO 2017 - International Special Session on domAin speciﬁc Model-based AppRoaches to vEriﬁcaTion and validaTiOn

680

linked to the case selected at ﬁrst step is executed.

The primitives of the SAN models are deﬁned using

C++ code. SAN models are deﬁned and solved by

using the multi-formalism multi-solvers tool M

obius

(Clark et al., 2001). M

obius is a tool that supports var-

ious formalisms such as SAN, PEPA, Fault Tree, and

different analytical and simulative solvers. M

obius

can be used for studying the reliability, availability,

and performability of systems. It follows a modular

modelling approach, where atomic models are build-

ing blocks that can be composed with proper opera-

tors Rep and Join to generate a composed model.

3.2 Contract Automata

Contract automata have been introduced in (Basile

et al., 2016d; Basile et al., 2016b) for modelling and

verifying contract-based services applications. A con-

tract automaton (see Deﬁnition 1 below) represents

the behaviour of a set of principals capable of per-

forming some actions. More precisely, the tuples of

actions are restricted to be offers/requests (a principal

performs an offer/request and the other principals stay

idle), or matches (two principals handshake their re-

quest/offer while the others stay idle). Consequently,

transitions of CA will be labelled with tuples of ele-

ments in the set L

def

= R ∪ O ∪ {} where: requests of

principals will be built out of R while their offers will

be built out of O, R ∩O =

0, and  6∈ R ∪O is a distin-

guished label to represent components that stay idle.

We let a, b,c, .. . range over L and ﬁx an involution

· : L → L such that R ⊆ O,O ⊆ R, ∀a ∈ R ∪O : a = a

and  = . As usual, offer actions will be topped

by bar (i.e. a). Service composition is naturally de-

scribed in terms of product automata. The matching

between offers and requests has to guarantee agree-

ment properties that amount to safe communications.

Intuitively, an automaton admits strong agreement if

it has at least one trace made only by match transi-

tions; and it is strongly safe if all the traces are in

strong agreement. Basically, strong agreement guar-

antees that the composition of services has a sound

execution, while strong safety guarantees that all ex-

ecutions of the composition are sound.

We borrow the following deﬁnition from (Basile

et al., 2016b), where the rank is the number of princi-

pals inside the contract automaton, and ~q stands for a

vector where ~q

(i)

is the i-th element.

Deﬁnition 1 (Contract automata). Assume as given a

ﬁnite set of states Q = {q

,. ..}. Then a contract

automaton A of rank n is a tuple hQ, ~q

,T,Fi,

where

• Q = Q

× ... × Q

⊆ Q

• ~q

∈ Q is the initial state

• A

⊆ R, A

⊆ O are ﬁnite sets (of requests and of-

fers, respectively)

• F ⊆ Q is the set of ﬁnal states

• T ⊆ Q × A × Q is the set of transitions, where

A ⊆ (A

∪ A

∪ {})

and if

(~q,~a,

) ∈ T then both the following conditions

hold:

– ~a is either a request or an offer or a match

– if ~a

(i)

=  then it must be ~q

(i)

A principal is a contract automaton of rank 1 such

that A

∩ co(A

) =

A principal is not allowed to make a request on

actions that it offers. Contract automata are endowed

with two (associative/non associative) operators of

composition that interleave or match the transitions of

their operands. Synchronisations are forced to happen

when two contract automata are ready on their respec-

tive request/offer action.

A tool called Contract Automata Tool

(CAT) (Basile et al., 2016c) has been imple-

mented for supporting the modelling and veriﬁcation

of contract automata. It provides functionalities

for generating and composing different models, for

synthesising the central orchestrator, and for check-

ing if the composition of automata is correct under

different properties, which amount to synchronous

or asynchronous interactions, for a closed or an

open-ended system. Moreover, in case one of such

properties is not satisﬁed, it is possible to point out

which principals in the composition are responsible

of violating the analysed property.

4 METHODOLOGY

In this section we brieﬂy describe the proposed ap-

proach to model and validate CPS. In the following

sections this approach will be concretely applied to a

representative case study.

Generally, in energy-saving CPS (Lee, 2008) the

supervision of the cyber-control is in charge of strate-

gies to supply energy to components of the physi-

cal system, necessary to keep them effective and re-

liable in the service they accomplish. Our interest

is in assessing measures that are representative of

the energy consumption, to be combined with other

dependability-related properties dictated by the crit-

ical domain the CPS is employed in. In the case

of critical systems, it is paramount to further guar-

antee the soundness of interactions among compo-

nents and the trusthworthiness of the related mea-

sures. Indeed, in case of misbehaving interactions,

Enhancing Models Correctness through Formal Veriﬁcation: A Case Study from the Railway Domain

681

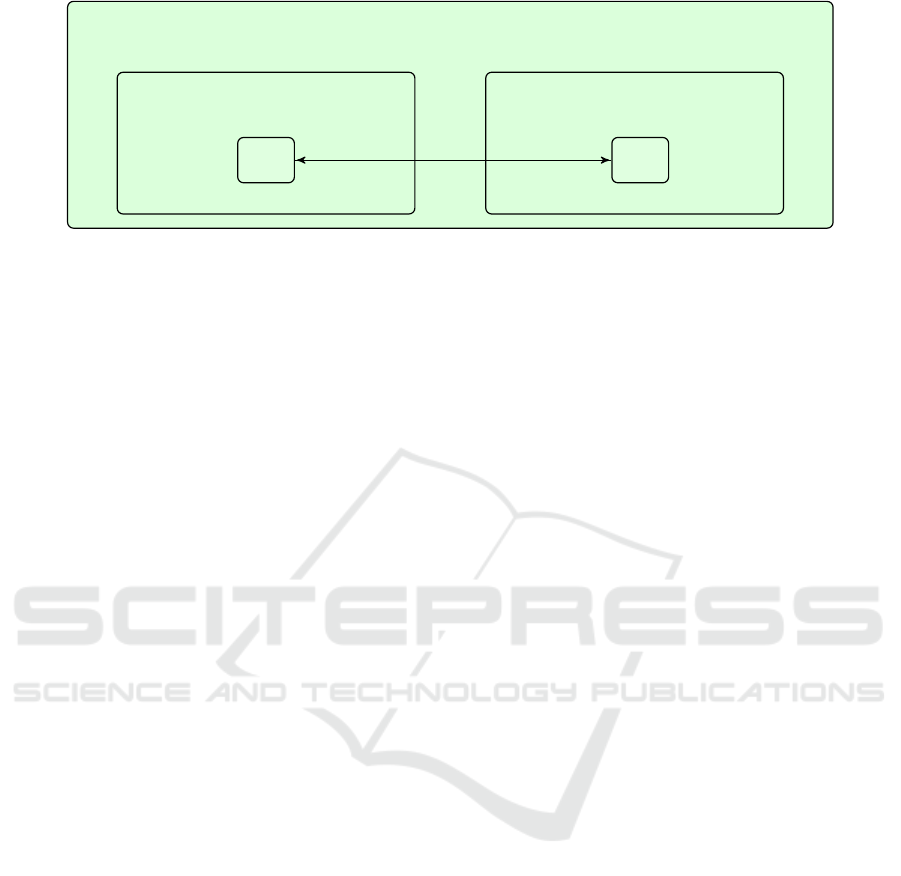
Cyber-Physical system

Veriﬁed Discrete aspects Continuous, Stochastic aspects

SAN

cross-modelling, mapping

–

Figure 1: The proposed approach for modelling CPS based on CA and SAN models.

wrong measures could be assessed. Unexpected eval-

uation results could be due to a non-optimal policy of

energy consumption but also to a wrong implemen-

tation of the adopted policy. Generally, identifying

these issues is not an easy task, and an optimal policy

could be discarded due to a wrong implementation of

it. In order to avoid this unpleasant situation, we aim

at formally proving the soundness of the interactions.

As mentioned in Section 2, the formal veriﬁcation of

stochastic hybrid systems is in general undecidable.

To overcome this difﬁculty, we propose to separately

model through different formalisms the cyber and the

physical modules of the analyzed system.

The diagram depicted in Figure 1 illustrates our

methodology. In particular, the discrete aspects con-

cerning the interactions among components will be

modelled and veriﬁed through CA, while SAN mod-

els will be also adopted for modelling the stochastic

hybrid behaviours of the analysed system and for as-

sessing the measures of interest. In the future, we plan

to formally relate these two formalisations. In the fol-

lowing case study, the CA models of interactions will

be extracted from the underlying SAN models that

were previously designed (Basile et al., 2016a; Basile

et al., 2016e) for evaluating energy consumption and

reliability measures of the analysed system.

5 CASE STUDY: RAIL ROAD

SWITCH HEATING SYSTEM

The considered case study is a rail road switch heating

system. A rail road switch is a mechanism enabling

trains to be guided from one track to another. It works

with a pair of linked tapering rails, known as points.

These points can be moved laterally into different po-

sitions, in order to direct a train into the straight path

or the diverging path. Such switches are therefore

critical components in the railway domain, and an er-

ror in the communications protocol of the system may

have potentially catastrophic consequences. During

winter, snow and ice can prevent the switches to work

properly, hence heaters are used so that the tempera-

ture of the rail road switches can be kept above freez-

ing. Different policies may be adopted to power the

heaters (by electricity), as for example to heat a selec-

tion of switches for a given amount of time or to heat

all the switches together.

5.1 Stochastic Model

We brieﬂy recall the SAN models of the system of

(remotely controlled) rail road switch heaters, which

have been used for evaluating energy and reliability

indicators in (Basile et al., 2016a). An on-off pol-

icy is considered for heating the switches, with para-

metric thresholds representing the temperatures trig-

gering the activation/deactivation of the heating. The

management of the heaters is automatic, and is re-

motely controlled by a central computational unit.

Generally, in a railway station there are tracks which

are less important than others, for example the side

tracks. In case of extremely cold conditions, the total

amount of energy available could not be sufﬁcient to

heat the overall system, hence it is important to assign

priorities to the heaters for identifying those that must

be primarily heated and those that may be later on.

We identify two main logical components describ-

ing the system: the heater and the central coordina-

tor. The network of heaters is realised by replicating

the heater component, and the activation/deactivation

of each heater is controlled by the central coordinator.

The policy employed to activate/deactivate the heat-

ing is based on two threshold temperatures: the warn-

ing threshold (T

) represents the lower temperature

that the track should not trespass. If the temperature

is lower than T

, then the risk of ice or snow can

lead to a failure of the rail road switch and therefore

the heating system needs to be activated; the work-

ing threshold (T

) is the working temperature of the

heating system. Once this temperature is reached, the

heating system can be safely turned off in order to

avoid an excessive waste of energy.

AMARETTO 2017 - International Special Session on domAin speciﬁc Model-based AppRoaches to vEriﬁcaTion and validaTiOn

682

Figure 2: The composed model.

The coordinator collects the requests of activation

from the pending heaters, and it manages the energy

supply according to a prioritized order. Indeed, the

ﬁrst heater which asks to be turned on will be the ﬁrst

to be activated. We assign priorities to switches based

on their criticality on the track; the purpose of con-

sidering priorities is to guarantee higher reliability to

those switches that are vital for the correct function-

ing of the overall station. If there is no energy avail-

able, each request will be enqueued in the queue of

pending heaters.

The overall model is obtained by the composition

of the atomic models, using the Join and Rep opera-

tors of the M

obius tool, as shown in Figure 2. Ba-

sically, with the Join operator different models are

linked by sharing some places, called shared places,

through which they interact. The Rep operator gener-

ates several instances of the same model, which can

be uniquely identiﬁed using a tailored SAN model

(SwitchIDSelector in our case).

The atomic model Coordinator is the central

coordinator. The submodel HeatherModuleM

is used for modelling an instance of a single

heater module, obtained by the composition,

using the join operator, of the four atomic

SAN models Pro f ileSelector, LocalitySelector,

SwitchIDSelector and RailRoadSwitchHeater,

which shares different parameters concerning a

single rail road switch heater. The submodel

HeatersNetM, obtained by replicating numRep times

the model HeatherModuleM, represents the network

of heaters, where the parameter numRep identiﬁes the

number of devices composing the network. Finally,

the model SwitchHeatingSysM, obtained using the

join operator, represents the overall system. Indeed

all the submodels share the same coordinator.

In Figure 3a the SAN model representing the rail

road switch heater is depicted. We identify three log-

ical components inside this SAN model: the init sub-

net, the clock sub-net and the heater sub-net. The

heater sub-net implements the protocol of communi-

cation between a single heater and the central coordi-

nator, while the remaining modules are used for ini-

tialising and evaluating other parameters concerning

the energy consumption and the probability of failure

of the modelled heater. The heater sub-net represents

the status of the rail road switch heater. The heater

can be activated (one token in the place on), wait-

ing for being activated (one token in the place ready),

turned off (one token in the place o f f ), or failed (one

token in the place f ailure). The heater sub-net inter-

acts with the Coordinator SAN model through places

shared among all the replicas of the heater model and

the Coordinator model implementing the logic de-

scribed below. For example, if a heater H is on state

ready, in order to be turned on, the input gate i1

ready2on

checks if the marking of the shared place noti f yIn is

equal to the marking of the place SwitchID of H(i.e.

its unique identiﬁer). This means that the coordinator

has notiﬁed H to be turned on.

We emphasise the cyber-physical nature of the

case study by brieﬂy describing its physical aspects.

The increment and decrement of the temperature of

the rail road track, respectively when the heater is

turned on or off, is modelled by a differential equa-

tion representing the balance of energy (Basile et al.,

2016a), where assuming that the values of the tem-

perature of the surrounding area T

and the previous

internal temperature T are known, the updated inter-

nal temperature T after time t is:

∂T

∂t

= −uA(T − T

) +

where u is the coefﬁcient of convective exchange;

c, the heat capacity of iron; A, the surface area ex-

posed to the external temperature; m, the mass of the

iron bar;

Q, the power used when the heater is turned

on, if the heater is turned off this value will be zero.

5.2 Formal Veriﬁcation of Interactions

Correctness

We now formally verify the interactions between the

network of heating switches and the central coordina-

tor, to improve the trusthworthiness of the results ob-

tained through the proposed SAN models in (Basile

et al., 2016a). For this purpose, we model the interac-

tions of the SAN models with contract automata. We

remark that we are not providing a generic mapping

from SAN models to CA models, which is matter of

future investigations. Indeed, here we focus on ver-

ifying the interactions of speciﬁc SAN models that

have been previously implemented. An over approx-

imation of all the possible behaviours of the system

will be veriﬁed against the property of strong agree-

ment of the product automaton, which only allows

Enhancing Models Correctness through Formal Veriﬁcation: A Case Study from the Railway Domain

683

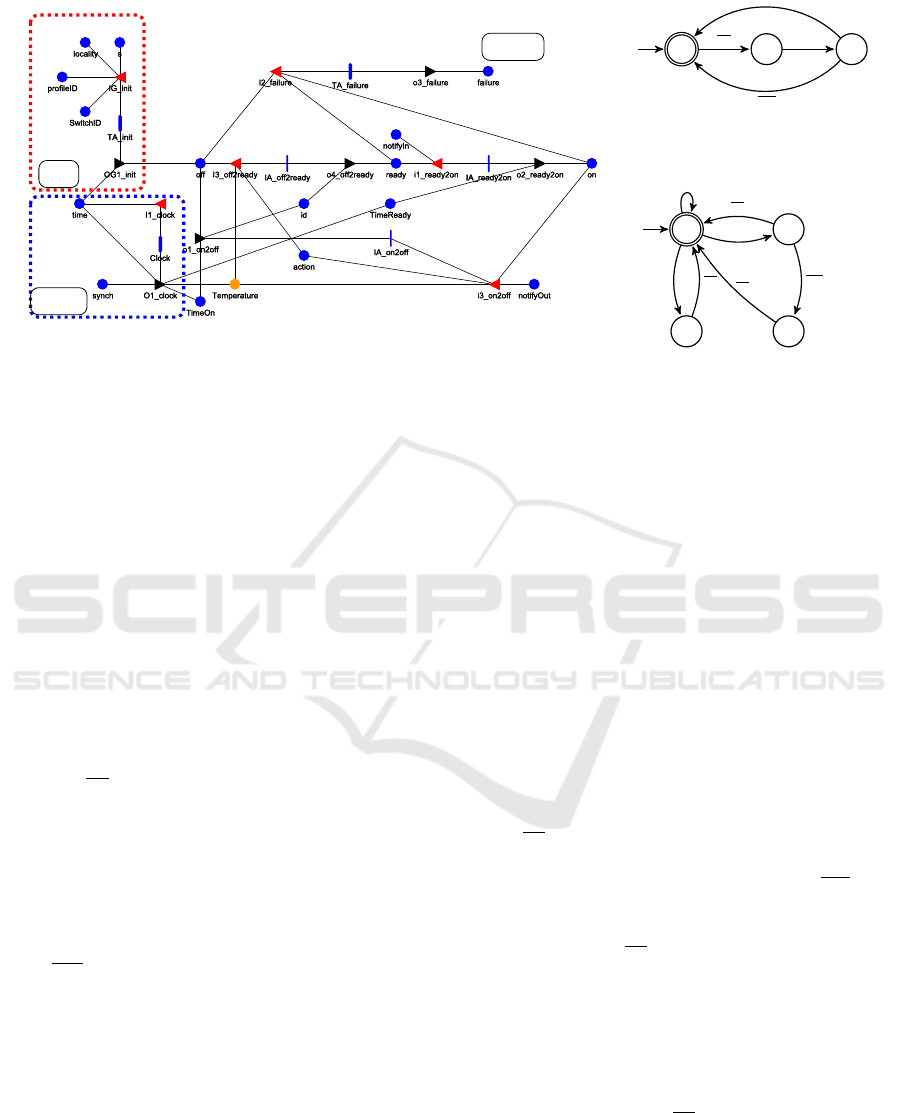
init

clock

heater

(a) The SAN model RailRoadSwitchHeater, log-

ically divided into three sub-nets: the init, clock

and heater sub-nets.

ins

rem

(b) the CA model of

the rail road switch

heater H

ins

ins/rem

rem

the coordinator Q

Figure 3: The SAN model and the contract automata models.

for synchronous interactions (i.e. traces only made

by match actions), as those are the behaviour showed

by the modelled system. In Figure 3b the contract

automaton representing a rail road switch heater H is

displayed, while the contract automaton of the coor-

dinator Q is in Figure 3c. We now describe all the

possible interactions between the central control unit

and the network of switches implemented in the SAN

models and modelled with CA:

• H: in the initial state q

the heater is switched off

and the internal temperature is above the warn-

ing threshold. Once the internal temperature goes

below the warning threshold, the heater issues a

request to be activated to the coordinator with the

action ins.

In state q

the internal temperature is below the

warning threshold and the heater is waiting a noti-

ﬁcation from the central coordinator to be turned

on. When the message NI (i.e. notify in) is re-

ceived, the heater is turned on, represented by the

state q

. From q

two transitions are allowed:

– rem (i.e. remove), the heater reaches an inter-

nal temperature above T

, and communicates

to the central coordinator the termination of the

heating phase and switches to state q

;

– NO (i.e. notify out) a second heater H

with

higher priority asks to be turned on. The energy

delivered to H is turned off and H is switched to

state q

, even though it has not yet reached

an internal temperature above T

(however the

temperature could be above T

: if it is not the

case there will be an instantaneous transition

from q

to q

as previously described).

The target state of both transitions is q

, which is

also the ﬁnal state of the heater.

• Q: in the initial (and ﬁnal) state q

the coordi-

nator is waiting for a message from one of the

heaters. Two messages can be received:

– ins: a heater asks to be activated. This request

can be rejected in case there is no available en-

ergy and the priority is not higher than those ac-

tivated heaters, which is modelled by the inner

loop (q

,ins, q

). In this case a notiﬁcation

of activation will be issued as soon as there is

energy available (see below).

Otherwise, the request is accepted and the tar-

get state is q

. In state q

two transitions are

allowed. In case there is enough available en-

ergy, the heater is activated with the message

NI. Otherwise, if there is no available energy

but H has a priority higher than one of the ac-

tivated heaters H

, ﬁrstly a message NO is is-

sued to H

, which will be consequently turned

off, and then the activation is notiﬁed to H with

the message NI;

– rem: a heater H notiﬁes the deactivation. If

there are no heaters H

activated or waiting for

being activated then no action is performed,

modelled with the inner loop (q

,rem,q

Otherwise, after receiving the message rem,

one of the pending heater H

is activated by is-

suing the message NI to H

The places o f f ,ready, on of the SAN model in

Figure 3a are modelled as states q

of the

corresponding automaton in Figure 3b. The mod-

elling of states of the SAN model Coordinator (not

AMARETTO 2017 - International Special Session on domAin speciﬁc Model-based AppRoaches to vEriﬁcaTion and validaTiOn

684

displayed here) with the contract automaton Q in

Figure 3c is similar. The interactions of H and Q

are modelled in the SAN models through the places

noti f yIn,noti f yOut, action and id that are shared

among the different replicas of the SAN models

for the heater and the unique SAN model of the

coordinator. More precisely, through the places

noti f yIn,noti f yOut the coordinator sends messages

to one of the heaters in the network, which is uniquely

identiﬁed by the number of tokens into these places.

These interactions are modelled as transitions of the

contract automata labeled by the actions NI and NO.

Similarly, the places action and id are used by the

heaters to communicate to the coordinator the action

ins or rem of the contract automata (respectively one

or two tokens in the place action) and the identity of

the sender (place id).

The contract automata models over approximate

the real behaviour of the system. For example, from

states q

of Q different transitions can be chosen non-

deterministically. Moreover, since here we want to

verify the progress of interactions, we do not consider

possible failures of heaters. By making the product

automaton of numRep instances of the heater model

H with the coordinator Q, it is possible to analyse the

behaviour of the overall system. For displaying pur-

poses, here we only discuss the veriﬁcation of a net-

work with two heaters and the coordinator, which is

composed of 29 transitions and 16 states.

We remark that this approach scales to more com-

plex systems. We have successfully analysed https://

github.com/davidebasile/CAT/tree/master/JaMata/

HeatersNet. The corresponding liable transitions (see

below) have been checked in few seconds.Note that

generally it is not decidable to verify the correctness

of a network with an arbitrary number of replicas

of a SAN model (through Rep operator), because

the different replicas can be uniquely identiﬁed.

Indeed, a reduction to the halting problem for Turing

machines is provided in (Apt and Kozen, 1986).

We check that no interactions between the cen-

tral coordinator and the heaters lead to a dead-

lock. For this purpose, CAT checks the pres-

ence of strongly liable transitions in the composed

automaton, which represent the bad behaviour of

the system (i.e. interactions responsible of leading

the composition to a deadlock). CAT detects dif-

ferent strongly liable transitions, displayed in Fig-

ure 4. In the ﬁrst row, we have the transition

((q

),(ins, ,ins), (q

)), where

interacts with Q by synchronising on the ac-

tion ins, and Q non deterministically decides to take

its inner loop, while H

stays idle. In the target

state, both heaters are on the state q

. In this

((q

),(ins, ,ins), (q

))

((q

),(, ins,ins), (q

))

((q

),(rem,, rem),(q

))

((q

),(, rem,rem),(q

))

((q

),(rem,, rem),(q

))

((q

),(, rem,rem),(q

))

Figure 4: The strongly liable transitions of H

⊗ H

⊗ Q.

conﬁguration Q cannot send the message NI any

more and the system gets stuck with both heaters

waiting their turn for being activated. Note that

in the source state of the transition (q

the component H

is in state q

, hence there are

no heaters activated. Indeed, this transition repre-

sents a false positive that is a behaviour that will

never be possible in the real system; because if

there are no activated heaters, a request of activa-

tion will never be refused. The second transition,

i.e. ((q

),(, ins,ins), (q

)), is

the symmetric case for the heater H

. All the other

liable transitions represent all the possible combina-

tions of interactions where none of the two heaters is

waiting for being activated on state q

, one heater

terminates the heating phase by sending the message

rem and the coordinator Q moves non deterministi-

cally to state q

, however no heater is waiting for

being activated and the message NI cannot be deliv-

ered. Once again, all these transitions are false posi-

tive. Indeed if no heater is in state q

, Q will never

send a NI message, because there are no heaters wait-

ing for being activated, and the inner loop of Q will

always be taken.

These false positives are automatically removed

by CAT, by computing the so-called most permis-

sive controller. In particular, the “bad” states ~q that

are removed are those satisfying the conditions: ∀i ∈

0. .. numRep − 1.~q

(i)

= q

∧ ~q

(numRep+1)

= q

∀i ∈ 0 ...numRep − 1.~q

(i)

6= q

∧~q

(numRep+1)

= q

No strongly liable transitions are found in the reﬁned

automaton, and we conclude that the interactions of

the system are sound: no deadlock will ever occur.

6 CONCLUSIONS

We have veriﬁed the correctness of the interactions of

a stochastic model of a cyber-physical system. The

selected case study is a system of rail road switch

heaters that have been modelled in (Basile et al.,

2016a) through SAN models in order to evaluate in-

dicators of the reliability and the energy consump-

Enhancing Models Correctness through Formal Veriﬁcation: A Case Study from the Railway Domain

685

tion. Starting from the SAN models, the interac-

tion patterns have been modelled with contract au-

tomata, so allowing the automatic veriﬁcation of the

progress of interactions through the Contract Au-

tomata Tool (Basile et al., 2016c).

Based on the obtained results, we are planning to

generalise the adopted technique to formally relate

SAN models and CA models and proving the cor-

rectness of the mapping. Moreover, we would like

to extend the comparisons with: (i) stochastic hybrid

automata that have been used in (Basile et al., 2017a)

to analyse rail road switch heating systems, and (ii)

an extension of contract autamata formalism to ex-

press necessary and mandatory requirements (Basile

et al., 2017b), useful for modelling critical requests

that must be fulﬁlled.

REFERENCES

Alur, R. and Dill, D. L. (1994). A theory of timed automata.

Theoretical Computer Science, 126(2):183 – 235.

Apt, K. R. and Kozen, D. (1986). Limits for automatic ver-

iﬁcation of ﬁnite-state concurrent systems. Inf. Pro-

cess. Lett., 22(6).

Balbo, G. (2007). Introduction to generalized stochastic

petri nets. In Bernardo, M. and Hillston, J., editors,

Formal Methods for Performance Evaluation, volume

4486 of LNCS. Springer.

Basile, D., Chiaradonna, S., Giandomenico, F. D., and

Gnesi, S. (2016a). A stochastic model-based approach

to analyse reliable energy-saving rail road switch heat-

ing systems. Journal of Rail Transport Planning &

Management, 6(2):163 – 181.

Basile, D., Degano, P., and Ferrari, G. L. (2016b). Au-

tomata for specifying and orchestrating service con-

tracts. CoRR, abs/1607.08363.

Basile, D., Degano, P., Ferrari, G.-L., and Tuosto, E.

(2016c). Playing with Our CAT and Communication-

Centric Applications, pages 62–73. Springer Interna-

tional Publishing, Cham.

Basile, D., Degano, P., Ferrari, G. L., and Tuosto, E.

(2016d). Relating two automata-based models of or-

chestration and choreography. Journal of Logical and

Algebraic Methods in Programming, 85(3).

Basile, D., Di Giandomenico, F., and Gnesi, S. (2016e).

Tuning energy consumption strategies in the railway

domain: a model-based approach. In 7TH Inter-

national Symposium on Leveraging Applications of

Formal Methods, Veriﬁcation and Validation, ISOLA

2016.

Basile, D., Di Giandomenico, F., and Gnesi, S. (2017a).

Statistical model checking of an energy-saving cyber-

physical system in the railway domain. In The 32nd

ACM Symposium on Applied Computing, SAC 2017.

(to appear).

Basile, D., Di Giandomenico, F., Gnesi, S., Degano, P., and

Ferrari, G.-L. (2017b). Specifying variability in ser-

vice contracts. In Proceedings of the 11th Interna-

tional Workshop on Variability Modelling of Software-

intensive Systems (Vamos), February 1 - 3. (to appear).

Bause, F. and Kritzinger, P. S. (1996). Stochastic petri nets:

An introduction to the theory. SIGMETRICS Perform.

Eval. Rev., 26(2).

Clark, G., Courtney, T., Daly, D., Deavours, D., Derisavi,

S., Doyle, J. M., Sanders, W. H., and Webster, P.

(2001). The m

obius modeling tool. In Proceedings

of the 9th International Workshop on Petri Nets and

Performance Models, pages 241–250.

Clarke, E., Grumberg, O., Minea, M., and Peled, D. State

space reduction using partial order techniques. In-

ternational Journal on Software Tools for Technology

Transfer, 2(3).

Clarke, Jr., E. M., Grumberg, O., and Peled, D. A. (1999).

Model Checking. MIT Press, Cambridge, MA, USA.

David, A., Larsen, K. G., Legay, A., Miku

aionis, M., and

Poulsen, D. B. (2015). Uppaal smc tutorial. Int. J.

Softw. Tools Technol. Transf., 17.

David, R. and Alla, H. (2001). On hybrid petri nets. Dis-

crete Event Dynamic Systems, 11(1-2):9–40.

Henzinger, T. A. and Ho, P. (1995). Algorithmic analysis of

nonlinear hybrid systems. In Computer Aided Veriﬁ-

cation, 7th International Conference, Proceedings.

Holzmann, G. (2003). Spin Model Checker, the: Primer

and Reference Manual. Addison-Wesley Professional,

ﬁrst edition.

Kupferman, O. and Vardi, M. Y. (1998). COMPOS’97,

chapter Modular Model Checking.

Larsen, K. G., Pettersson, P., and Yi, W. (1997). Uppaal in

a nutshell. Int. Journal on Software Tools for Technol-

ogy Transfer, 1.

Lee, E. A. (2008). Cyber physical systems: Design chal-

lenges. In Proceedings of the 2008 11th IEEE Sympo-

sium on Object Oriented Real-Time Distributed Com-

puting, ISORC ’08. IEEE Computer Society.

Legay, A., Delahaye, B., and Bensalem, S. (2010). RV 2010.

Proceedings, chapter Statistical Model Checking: An

Overview. Springer.

McMillan, K. L. (1993). Symbolic Model Checking. Kluwer

Academic Publishers, Norwell, MA, USA.

Reibman, A., Smith, R., and Trivedi, K. (1989). Markov

and markov reward model transient analysis: An

overview of numerical approaches. European Journal

of Operational Research, 40(2).

Sanders, W. H. and Meyer, J. F. (2000). Stochastic activity

networks: Formal deﬁnitions and concepts. In Lec-

tures on Formal Methods and Performance Analysis.

Yovine, S. (1997). Kronos: A veriﬁcation tool for real-

time systems. (kronos user’s manual release 2.2). In-

ternational Journal on Software Tools for Technology

Transfer, 1:123–133.

AMARETTO 2017 - International Special Session on domAin speciﬁc Model-based AppRoaches to vEriﬁcaTion and validaTiOn

686