An Analysis of the Impact of Diversity on Stacking Supervised Classifiers
Mariele Lanes
1
, Paula F. Schiavo
1
, Sidnei F. Pereira Jr.
1
, Eduardo N. Borges
1
and Renata Galante
2
1
Centro de Ci
ˆ
encias Computacionais, Universidade Federal do Rio Grande – FURG, Rio Grande, Brazil
2
Instituto de Inform
´
atica, Universidade Federal do Rio Grande do Sul – UFRGS, Porto Alegre, Brazil
Keywords:
Diversity, Stacking, Ensemble, Classification.
Abstract:
Due to the growth of research in pattern recognition area, the limits of the techniques used for the classification
task are increasingly tested. Thus, it is clear that specialized and properly configured classifiers are quite effec-
tive. However, it is not a trivial task to choose the most appropriate classifier for deal with a particular problem
and set it up properly. In addition, there is no optimal algorithm to solve all prediction problems. Thus, in
order to improve the result of the classification process, some techniques combine the knowledge acquired by
individual learning algorithms aiming to discover new patterns not yet identified. Among these techniques,
there is the stacking strategy. This strategy consists in the combination of outputs of base classifiers, induced
by several learning algorithms using the same dataset, by means of another classifier called meta-classifier.
This paper aims to verify the relation between the classifiers diversity and the quality of stacking. We have
performed a lot of experiments which results show the impact of multiple diversity measures on the gain of
stacking.
1 INTRODUCTION
The scientific community has made much effort on
pattern recognition area in order to develop ever better
techniques used for data analysis. In this context, ma-
chine learning has been highlighted, mainly because it
can perform pattern recognition by supervised learn-
ing. These learning methods can build from patterns
available in a training dataset models or functions ca-
pable of classify new patterns.
However, the quality of the classification results
will substantially depend on the quality and volume
of data samples used into the training phase as well as
the selection of features and the set up of parameters
(Kuncheva and Whitaker, 2003).
Although some classifiers individually provide so-
lutions which are considered effective, the experimen-
tal evaluation performed by (Dietterich, 2000) shows
a drop in the quality when there are large sets of pat-
terns and/or a significant number of incomplete data
samples or irrelevant features. That is, such classi-
fiers may not effectively and/or efficiently recognize
patterns in complex problems.
In order to improve the classification results, tech-
niques for combining classifiers have been used,
aiming to take advantage of several classification
schemes, where the outputs of each classifier can be
combined in a final decision that improves the ability
to generalization. Among these techniques, we high-
light stacking as a way to combine classifiers that con-
sists of using a second-level learning algorithm to op-
timally combine a collection of predictions made by
different models (Wolpert, 1992).
In the stacking method the choice of base al-
gorithms is very important. According to (Opitz
and Maclin, 1999), the performance of the stacking
strongly depends on the accuracy and diversity of
classifiers results. To verify this diversity, there are
several measures based on the (dis)agreement of the
classifiers (Kuncheva and Whitaker, 2003).
Therefore, the use of base algorithms with dif-
ferent particulars is ideal, since the patterns learned
tend not to be the same. Thus, even low accuracy
classifiers combined can generate a strong classifier,
providing gain for stacking. Otherwise, when sev-
eral classifiers agree on the vast majority of responses
(no diversity), the combination will possibly have the
same result, with no improvement in the stacking
quality.
The purpose of this paper is to evaluate the impact
of classifier diversity on the quality of stacking. The
experiments we have performed show the relationship
between multiple diversity measures and the gain of
stacking, considering 54 datasets extracted from UCI
Lanes, M., Schiavo, P., Jr., S., Borges, E. and Galante, R.
An Analysis of the Impact of Diversity on Stacking Supervised Classifiers.
DOI: 10.5220/0006291202330240
In Proceedings of the 19th International Conference on Enterprise Information Systems (ICEIS 2017) - Volume 1, pages 233-240
ISBN: 978-989-758-247-9
Copyright © 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
233

machine learning repository. The proposed idea is
based on the hypothesis that the greater the diversity
of patterns learned by base classifiers, the higher the
quality of stacking.
2 BACKGROUND
Classification is the most usual task among data min-
ing tasks. According to (Tan et al., 2005), clas-
sification can be defined as the process of finding,
through supervised learning, a model or function that
describes different classes of data. The purpose of
classification is to automatically label new instances
of the database with a given class by applying the
model or function previously learned. This model is
based on the fields of the training instances.
Classification algorithms can be organized into
different types according to the technical features they
use in learning. Each type is best suited for a particu-
lar dataset.
2.1 Combining Classifiers with Stacking
Classifiers that implement different algorithms poten-
tially provide additional information on the patterns
to be classified. The combination of the outputs of a
set of different classifiers aims to get a more precise
classification, i.e. to reach a greater accuracy. In this
context, stacking (Ting and Witten, 1999) is a widely
used method for combining multiple classifiers gen-
erated from different learning algorithms applied on
the same dataset. It is also known in the literature
as stacked generalization (Dzeroski and Zenko, 2004;
Wolpert, 1992).
Stacking method combines multiple base classi-
fiers trained by using different learning algorithms L
on a single dataset S, by means of a meta-classifier
(Merz, 1999; Kotsiantis and Pintelas, 2004). Each
training sample s
j
= (X
j
,y
j
) is a pair composed by an
array of features X
j
and the class label y
j
.
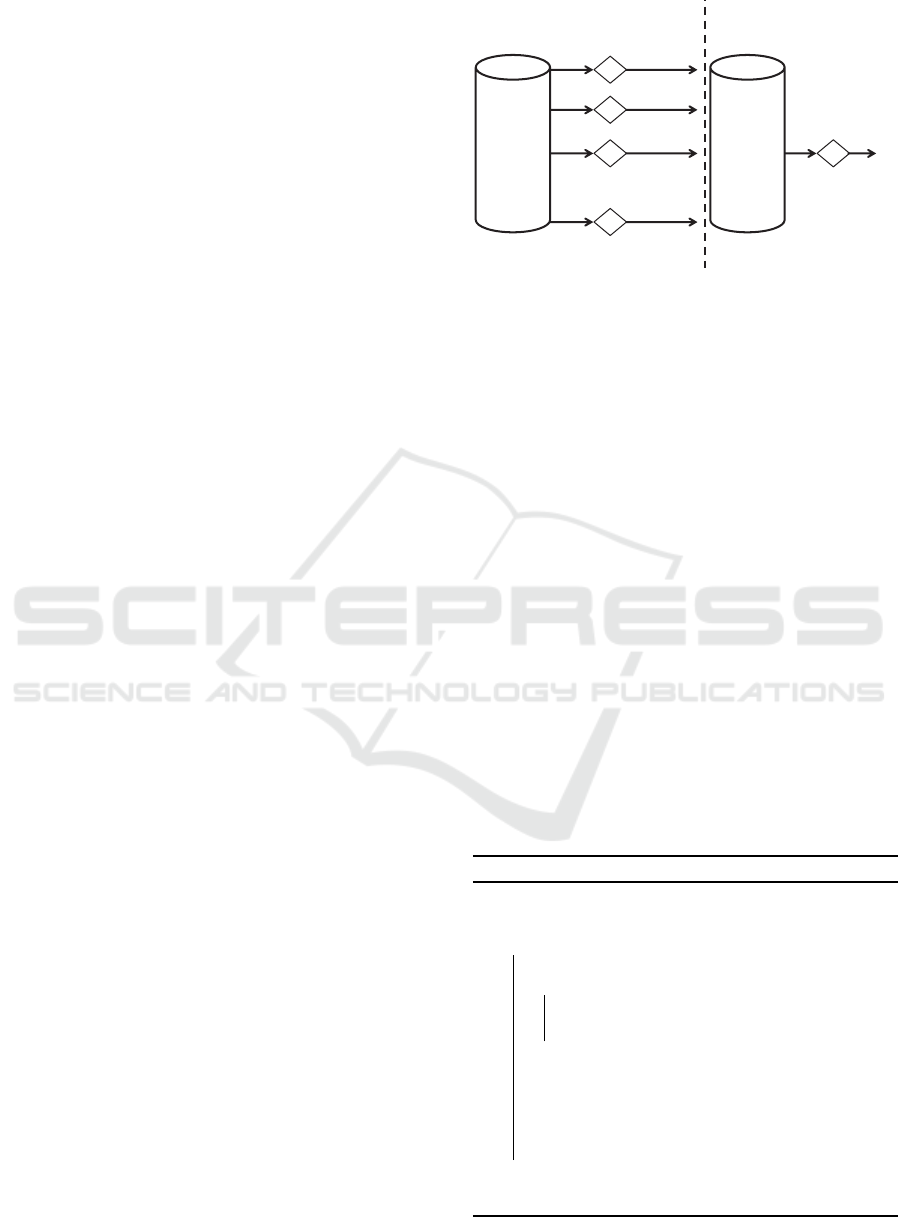
The process can be described in two distinct lev-
els as shown in Figure 1. The first level-0 defines a
set of N base classifiers, where C
i
= L
i
(S)|1 ≤ i ≤ N.
Level-0 classifiers are trained and tested using the
cross-validation or leave-one-out procedure. The out-
put dataset D used for training the meta-classier is
composed by examples ((y
1
j
,...,y
i
j
),y
j
), i.e. a vector
of predictions for each base classifier y
i
j
= C
i
(X
j
) and
the same original class label y
j
(Dzeroski and Zenko,
2004). In the second level-1, the meta-classifier com-
bines base classifiers outputs from D into a final pre-
diction y
f
j
. The stacking pseudocode can be seen in
Algorithm 1.
C
. . .
C
C
C
predictions
C
final
prediction
level-1
base classifiers
meta-classifier
1
2
3
N
input
dataset
output
dataset
level-0
Figure 1: Representation of the stacking algorithm, based
on (Opitz and Maclin, 1999).
According (Breiman, 1996), stacking can be used
successfully to form linear combinations of different
predictors for better accuracy. The authors have used
regression trees of different sizes as base classifiers
and a linear regression model in level-1. (Ting and
Witten, 1999) use a linear regression adaptation called
Multi-response Linear Regression (MLR) (Johnson
and Wichern, 2002) as meta-classifier. (Dzeroski and
Zenko, 2004) propose an extension of MLR stacking
method that uses a Multi-response Model Tree in the
meta-classifier. The training set used at level-1 has
the following fields: (i) the probability distribution
for each class, (ii) the probability distribution of each
class multiplied by the maximum probability consid-
ering all classes, and (iii) the entropy of the probabil-
ity distribution for each classifier. According to the
authors, experimental results show that this approach
is a good choice for learning in the meta-classifier, re-
gardless of the classifiers chosen at level-0.
Several approaches have proposed the use of
stacking to increase the classification quality in recent
years. (Ebrahimpour et al., 2010) present a suitable
Algorithm 1: Combining classifiers with stacking.
Input: training samples s
j
∈ S
Output: final predictions y
f
j
1 begin
2 Select N learning algorithms (L
1
,L
2
,. .., L
N
);
3 for i = 1,2, ... ,N do
4 Train C
i
= L
i
(S) using cross-validation;
5 y
i
j
= C
i
(X
j
);
6 end
7 Make up a new dataset D combining all
predictions y
i
j
;
8 Train M = L(D) using cross-validation;
9 y
f
j
= M(D);
10 end
11 return y
f
j
ICEIS 2017 - 19th International Conference on Enterprise Information Systems
234

solution using stacking to recognize low resolution
face images. (Ness et al., 2009) describe how stack-
ing can be used to improve the performance of an
automatic system for tagging audio tracks. (Lar-
ios et al., 2011) propose a method for automatic
identification of insects in species for biomonitor-
ing purposes using space histograms and RF clas-
sifiers. (Garc
´
ıa-Guti
´
errez et al., 2012) propose a
method called EVOR-STACK to improve the accu-
racy of thematic maps. (Ali and Majid, 2015) propose
a new system to predict amino acid sequences associ-
ated with breast cancer.
2.2 Diversity Measures
The diversity of predictions is a key issue in the
combination of classifiers. (Kuncheva and Whitaker,
2003) define several measures of diversity and relate
them to the quality of classification system. These
measures are based on the agreement or disagreement
of the classifiers used in the ensemble.
Let n be the number of instances evaluated by a
pair of classifiers C
a
and C
b
and R be a relationship
matrix between them, containing the number of in-
stances in which each classifier hits (1) and/or misses
(0) the prediction of the class label (Table 1). For
example, n
01
is the number of instances misclassified
by C
a
and correctly identified by C
b
. The main diag-
onal shows the number of instances equally labeled
by both classifiers. The secondary diagonal shows the
number of records in which the classifiers disagree.
The sum of all cells is the total number of instances
evaluated by the analyzed classifiers.
Table 1: The relationship matrix R between a pair of classi-
fiers C
a
and C
b
.
C
b
hits C
b
misses
C
a
hits n
11
n
10
C
a
misses n
01
n
00
n = n
11
+ n
10
+ n
01
+ n
00
The following subsections present several mea-
sures of diversity in classifier ensembles (Kuncheva
and Whitaker, 2003) used in the experimental evalua-
tion of this paper.
2.2.1 Double-fault d f
The double-fault measure d f is defined by Equation
1 as the proportion of instances simultaneously mis-
classified by a pair of classifiers (Giacinto and Roli,
2001). d f returns values in the closed range [0, 1] and
it is inversely proportional to the diversity between
classifiers.
d f =
n
00
n
00
+ n
01
+ n
10
+ n
11
(1)
2.2.2 Disagreement Dis
The disagreement measure Dis is defined by Equa-
tion 2 as the ratio between the amount of instances in
which the classifiers disagree and the total number of
instances (Ho, 1998). Dis varies in the closed range
[0,1] and it is directly proportional to the diversity be-
tween classifiers.
Dis =
n
01
+ n
10
n
00
+ n
01
+ n
10
+ n
11
(2)
2.2.3 Q Statistic
The Q statistic is pairwise measure of diversity de-
fined by Equation 3 (Afifi and Azen, 2014). This mea-
sure return values in the closed range [−1,1], being
inversely proportional to the diversity between classi-
fiers.
Q =
n
11
n
00
− n
01
n
10
n
11
n
00
+ n
01
n
10
(3)
2.2.4 Correlation Coefficient ρ
The correlation coefficient between two classifiers is
defined by the Equation 4 (Sneath and Sokal, 1973).
As the Q statistic, it returns values in the range [−1,1].
ρ it is also inversely proportional to the diversity.
ρ =
n
11
n
00
− n
01
n
10
p
(n
11
+ n
10
)(n
01
+ n
00
)(n
11
+ n
01
)(n
10
+ n
00
)
(4)
2.2.5 Kohavi-Wolpert Variance KW
The Kohavi-Wolpert variance measures the diversity
among a set of N classifiers (Kohavi et al., 1996). It
returns values in the range [0,1/2] and it is directly
proportional to the diversity. KW diverges from the
average of several pairwise disagreement measures
Dis
avg
by a coefficient, according to the Equation 5.
KW =
N − 1
2N
Dis
avg
(5)
2.2.6 Interrater Agreement k
The interrater agreement k is defined by Equation 6,
where ¯p denotes the average individual classification
accuracy (Dietterich, 2000). This measures performs
on the predictions of a set of N classifiers and returns
An Analysis of the Impact of Diversity on Stacking Supervised Classifiers
235

a value in the the closed range [−1,1]. It is inversely
proportional to the diversity among the classifiers.
k = 1 −
N
(N − 1) ¯p(1 − ¯p)
KW (6)
2.2.7 Entropy E
Entropy performs on the output of a set of N clas-
sifiers and is defined by Equation 7, where n is the
number of instances and l(s
j
) is the number of classi-
fiers that properly label the instance s
j
(Cunningham
and Carney, 2000). E varies in the range [0,1] and it
is directly proportional to the diversity among classi-
fiers.
E =
1
n
n
∑
j=1
min[l(s
j
),N − l(s
j
)]
N − [N/2]
(7)
3 PROPOSED METHOD
This section describes the proposed method for ana-
lyzing the impact of diversity on stacking supervised
classifiers, which are graphically represented in Fig-
ure 2.
For each analyzed dataset, different learning al-
gorithms are used to train multiple base classifiers.
The predictions returned by these classifiers are eval-
uated and used to perform several measures of di-
versity. These measures check whether and how the
classifiers agree or disagree on the predicted class la-
bel. At level-1, classifiers predictions for each origi-
nal instance are used to compose a new dataset that is
submitted to another algorithm for training the meta-
classifier. Final prediction is determined from the
combination of knowledge learned by the base clas-
sifiers.
C
. . .
C
C
C
predictions
C
final
prediction
level-1
base classifiers
meta-classifier
1
2
3
N
input
dataset
output
dataset
level-0
diversity
n
dddG ]ED  
21
Figure 2: The proposed method for analyzing the impact of
diversity on stacking supervised classifiers.
The gain of stacking G is computed as shown
by Equation 8, where E
MC
is the evaluation metric
achieved by the meta-classifier and E
C
best
by the best
base classifier.
G =

E
MC
E
C
best

− 1 (8)
Finally, the relationship between the diversity
measures and the gain of stacking computed previ-
ously for multiple datasets is induced by means of a
regression model.
3.1 Classifiers
The feature vectors for each training set are made up
of all data fields and the class label. The following
algorithms are used at level-0 of the stacking method.
This choice was motivated mainly because the algo-
rithms are quite heterogeneous, since they are based
on distinct particulars:
• MLP (Haykin, 2007) - artificial neural network,
based on function;
• SMO (Platt, 1999) - variation of SVM (Boser
et al., 1992), based on function;
• NB (John and Langley, 1995) - based on Bayes’s
theorem;
• RIPPER (Cohen, 1995) - based on rules;
• C4.5 (Quinlan, 1993) - based on decision trees;
• RF (Breiman, 2001) - based on a set of decision
trees.
The test method to generate the predictions is cross-
validation.
The meta-classifier is trained using any classifica-
tion algorithm combining the knowledge learned by
the base classifiers, and it is finally used to get a final
prediction. Training set fields for learning the meta-
classifier vary according to the base classifier algo-
rithms. For NB, the prediction is the posterior prob-
ability of a record belonging to the same class. For
RIPPER, C4.5 and RF algorithms, the prediction is
the precision of the rule or node that classified each
sample. In function-based algorithms, it is directly
mapped to the class label. Regardless of the base clas-
sifiers, the last field is the same original class label.
3.2 Analyzing the Impact of Diversity
The impact of diversity on stacking can be analyzed
by observing the relationship between diversity mea-
sures values and the gain of stacking for multiple
datasets. It is expected that the most diverse sets of
classifiers will contribute to the quality of stacking.
ICEIS 2017 - 19th International Conference on Enterprise Information Systems
236

This relationship is deduced using linear regres-
sion or regression model trees with the gain of stack-
ing G as the target field. The vector of features is
composed by the diversity measures d
1
,d
2
,...,d
n
pre-
viously computed. The regression models show how
much each measure pitches in with the gain of stack-
ing.
4 EXPERIMENTAL EVALUATION
This section describes the experiments conducted to
evaluate the proposed method for analyzing the im-
pact of diversity on stacking supervised classifiers.
Each algorithm cited in Section 3 was also used to
train the meta-classifier. Base classifiers and the
stacking were evaluated based on the accuracy (Tan
et al., 2005), which estimates the quality of classifica-
tion, i.e. the prediction capacity of the model.
The experiments were performed on a personal
computer using the data mining tool Weka
1
(Witten
and Frank, 2011). The algorithms were parameterized
with the default values of this tool, using 10 partitions
in the cross validation.
4.1 Datasets
We have used 54 classification datasets extracted
from UCI machine learning repository
2
: Abalone,
Annealing, Audiology (Std.), Balance Scale, Ban-
knote Authent., Blood Transf. Serv. Center, Breast
Cancer Wisconsin, Car Evaluation, Chess (K-R vs.
K-P), Chronic Kidney Disease, Congressional Vot-
ing Rec., Connect. Bench (S,M vs. R), Con-
nect. Bench (VR-DD), Contrac. Method Choice,
Credit Approval, Dermatology, Diabetic Retinopat.
Debrec., Dresses Attribute Sales, Ecoli, Forest type
mapping, Glass Identification, Hill-Valley, ILPD -
Indian Liver Patient, Ionosphere, Leaf, Low Reso-
lution Spectrometer, Mammographic Mass, Molec-
ular Bio. (S-junction), Multiple Features, Nurs-
ery, Opt. Recog. Handwrit. Dig., Page Blocks
Classification, Pen-based Recog. Handwrit., Phish-
ing Websites, Primary Tumor, QSAR biodegradation,
Qualitative Bankruptcy, Seismic-Bumps, Solar Flare,
Soybean (Large), Spambase, SPECT Heart, Stat-
log (Vehicle Silh.), Thoracic Surgery, Thyroid Dis-
ease (Hypothyr.), Thyroid Disease (Sick), Tic-Tac-
Toe Endgame, Turkiye Student Eval., Vertebral Col-
umn, Waveform Database Gen. (V2), Wholesale cus-
tomers, Wilt, Wine Quality, and Yeast.
1
http://www.cs.waikato.ac.nz/ml/weka
2
http://archive.ics.uci.edu/ml
The chosen datasets cover several areas of knowl-
edge: business, computer, financial, game, life, physi-
cal and social. Many of them were widely cited in the
scientific literature and they have sundry objectives.
The field data types can be integer, real or categorical.
The amount of instances ranges from 187 to 12,960.
The number of fields and class labels varies from 5
to 217 and from 2 to 48 respectively. These datasets
were deposited in the UCI repository from the year
1987 to 2015.
A set of preprocessing operations was applied in
order to standardize the content make the datasets
able to execute the algorithms in Weka. The main
operations were removal of double spaces between
instances, naming data fields, changing field delim-
iter and data types from numeric to nominal. After
preprocessing they were used to train heterogeneous
classification models, i.e. using different algorithms
described in the previous section. Base classifiers pre-
dictions are stacked composing the level-1 training set
on which the final classification model is learned.
4.2 Results
The experimental results are summarized in Table 2
that shows for each dataset the following information:
the computed diversity measures double fault (d f ),
disagreement (Dis), statistic (Q), correlation coeffi-
cient (ρ), interrater agreement (k), Kohavi-Wolpert
variance (KW ) and entropy (E); the algorithm used to
learn the best base classifier (L
0
) and its accuracy in
percentage (A
L
0
); the algorithm used to learn the best
meta-classifier (L
1
) and its accuracy (A
L
1
); and the
gain of stacking (G), used to sort the results, also in
percentage. Values of d f , Dis, Q and ρ are averages
of the computed values for each pair of base classi-
fiers. Moreover, this table presents Q
0
, ρ
0
, k
0
and KW
0
that are the original diversity measures standardized
in a distribution of values in the closed range [0,1], as
well as d f , Dis and E.
We showed the results about datasets that reached
the worst and best G values, i.e. we have omitted the
results when the gain of stacking is not significant
and ranges between -1 and 1%. Observing Table 2,
we notice that stacking worked well only for 8 out of
54 datasets, where the gain ranged from 1.2 to 5.1%
(lines 1-8). The best gain of stacking was reached by
Balance Scale dataset, in an already very accurate re-
sult (90.7%) which is very difficult to improve. The
most frequent algorithm that reaches the best accu-
racy for level-0 was MLP ranging 26.6 ≤ A
L
0
≤ 90.7,
followed by RF with 84.8 ≤ A
L
0
≤ 92.9. In the level-
1, the best meta-classifiers were trained with SMO
(26.9 ≤ A
L
1
≤ 94.9) and RF (83.7 ≤ A
L
1
≤ 95.4).
An Analysis of the Impact of Diversity on Stacking Supervised Classifiers
237

Table 2: Diversity measures and the stacking results.
Dataset d f ↓ Dis ↑ Q ↓ Q
0
↓ ρ ↓ ρ
0
↓ k ↓ k
0
↓ KW ↑ KW
0
↑ E ↑ L
0
A
L
0
L
1
A
L
1
G
1 Balance Scale 0.78 0.13 0.87 0.93 0.50 0.75 0.48 0.74 0.06 0.11 0.17 MLP 90.7 RF 95.4 5.1 2 Connect. Bench (S,M vs. R) 0.62 0.27 0.58 0.79 0.28 0.64 0.26 0.63 0.11 0.23 0.35 MLP 82.2 Jrip 85.6 4.1 3 Statlog (Vehicle Silh.) 0.55 0.30 0.64 0.82 0.32 0.66 0.28 0.64 0.13 0.25 0.37 MLP 81.7 RF 83.7 2.5 4 Diabetic Retinopat. Debrec. 0.49 0.32 0.56 0.78 0.29 0.65 0.29 0.64 0.13 0.27 0.41 MLP 72.0 SMO 73.8 2.4 5 Ionosphere 0.83 0.12 0.83 0.92 0.41 0.70 0.38 0.69 0.05 0.10 0.13 RF 92.9 SMO 94.9 2.2 6 Contrac. Method Choice 0.38 0.29 0.71 0.85 0.42 0.71 0.42 0.71 0.12 0.24 0.36 MLP 54.2 SMO 55.3 2.0 7 Vertebral Column 0.72 0.19 0.74 0.87 0.39 0.69 0.38 0.69 0.08 0.16 0.23 RF 84.8 RF 86.1 1.5 8 Abalone 0.09 0.28 0.47 0.74 0.21 0.60 0.21 0.60 0.12 0.24 0.36 MLP 26.6 SMO 26.9 1.2 9 Leaf 0.52 0.30 0.70 0.85 0.37 0.68 0.33 0.67 0.12 0.25 0.37 MLP 79.7 SMO* 78.8 -1.1
10 Glass Identification 0.49 0.32 0.61 0.80 0.33 0.66 0.30 0.65 0.13 0.27 0.40 RF 79.9 RF 79.0 -1.2 11 Credit Approval 0.77 0.14 0.85 0.93 0.50 0.75 0.48 0.74 0.06 0.12 0.17 RF 86.7 NB 85.7 -1.2 12 Ecoli 0.79 0.11 0.92 0.96 0.57 0.79 0.57 0.78 0.05 0.09 0.14 RF 87.2 RF 86.0 -1.4 13 Solar Flare 0.62 0.15 0.91 0.96 0.64 0.82 0.64 0.82 0.06 0.13 0.18 J48 72.1 SMO 70.9 -1.7 14 Dresses Attribute Sales 0.46 0.26 0.77 0.88 0.47 0.73 0.47 0.73 0.11 0.22 0.32 JRip 63.0 NB 60.2 -4.4 15 Audiology (Std.) 0.72 0.13 0.94 0.97 0.64 0.82 0.63 0.81 0.05 0.10 0.16 MLP 83.2 SMO 79.2 -4.8 16 Low Resolution Spectrometer 0.18 0.36 0.47 0.73 0.25 0.62 0.23 0.61 0.15 0.30 0.46 RF 54.0 SMO 51.0 -5.6 17 Primary Tumor 0.33 0.19 0.89 0.95 0.61 0.80 0.60 0.80 0.08 0.16 0.25 NB 50.1 RF 45.4 -9.4
Average (all 54 datasets) 0.74 0.15 0.76 0.88 0.41 0.71 0.39 0.69 0.06 0.13 0.19
* MLP reaches equal results
ICEIS 2017 - 19th International Conference on Enterprise Information Systems
238

However, stacking decreased the classification
quality for some datasets (lines 9-17) reaching in the
worst case G = −9.4%. The most frequent algorithms
with best accuracy were RF (L
0
) and SMO (L
1
). For
some datasets, more than one classifier used at level-1
returned the same result. For instance, SMO and MLP
reaches equal values (A
L
1
= 78.8%) for Leaf dataset
(line 9).
We have considered good values of diversity those
that were sufficiently larger or smaller than the aver-
age for all 54 datasets. These values are highlighted.
A general analysis of them indicates that there is more
diversity in the experiments in which there was gain
of stacking (lines 1-8) than in those in which there
was loss of quality (lines 9-17).
Abalone dataset (line 8) had the best value of dou-
ble fault d f due to the low accuracy presented by
the base classifiers (A
L
0
= 26.6%). Many of them
fail together because these is a multi-classification
problem involving 28 distinct class labels. We no-
tice that for this dataset, all the measures of diversity
return good values, collaborating with the hypothe-
sis that the greater the diversity, the greater the qual-
ity of stacking. However, the experiment involving
Low Resolution Spectrom eter dataset (line 16) re-
vealed the opposed behavior where the gain of stack-
ing was negative (G = −5.6%), i.e. the quality of
classification decreased considerably, even with high
values for all measures of diversity. These high val-
ues are returned because there are 531 instances dis-
tributed in 48 classes, making even hard the agree-
ment of many classifiers. Balance Scale dataset (line
1) is another counterexample in which there was no
diversity among classifiers, however the stacking has
reached the best G among all the performed experi-
ments.
The impact of diversity on the gain of stacking
was performed using a linear regression function and
a regression model tree induced by the algorithm M5
(Quinlan, 1992). We have trained these models with
only the 17 datasets present in Table 2 and consid-
ering all 54 datasets. Table 3 shows the best re-
sults comparing the evaluation of linear regression
and model trees, using correlation coefficient and root
relative squared error (RRSE).
Table 3: Evaluation of the regression models.
Datasets Model Correlation RRSE
54 linear 0.4081 91.58%
17 M5 0.5243 79.67%
Equation 9 shows the linear model. We notice that
only d f and KW had impact on the gain of stacking.
Other diversity measures were irrelevant in estimating
the gain.
G = 0.0971 d f + 0.3757 KW − 0.0957 (9)
The minimum number of instances to allow at a
leaf node in M5 ranged from 2 to 4, however the result
was the same tree with only one node containing the
model described by Equation 10. For this model, d f
remains having a positive impact on the gain but the
influence of ρ was negative. KW and other measures
were not used.
G = 0.1278 d f − 0.2189 ρ + 0.0168 (10)
5 CONCLUSION
This paper presented an analysis of the impact of di-
versity on stacking multiple classifiers. The experi-
ments we have performed show some link between
the studied diversity measures and the gain of stack-
ing considering 54 real datasets.
The regression models revealed connections be-
tween some measures and the quality of stacking. d f ,
KW and ρ are related to the final classification accu-
racy, but low values of the correlation coefficients and
high values of RRSE imply a weak relationship. So,
as suggested by the literature for bagging and major-
ity voting ensembles, predicting the improvement on
the best individual accuracy using diversity measures
is possible inappropriate.
As future work, we intend to conduct experiments
with additional diversity measures and with synthetic
datasets, aiming to better understand the relations be-
tween data distribution, classifiers diversity and the
quality of stacking.
REFERENCES
Afifi, A. A. and Azen, S. P. (2014). Statistical analysis: a
computer oriented approach. Academic press, New
York.
Ali, S. and Majid, A. (2015). Can-evo-ens. Journal of
Biomedical Informatics, 54(C):256–269.
Boser, B. E., Guyon, I. M., and Vapnik, V. N. (1992). A
training algorithm for optimal margin classifiers. In
Proceedings of the Annual Workshop on Computa-
tional Learning Theory, pages 144–152. ACM.
Breiman, L. (1996). Stacked regressions. Machine Learn-
ing, 24(1):49–64.
Breiman, L. (2001). Random forests. Machine learning,
45(1):5–32.
Cohen, W. W. (1995). Fast effective rule induction. In Pro-
ceedings of the International Conference on Machine
Learning, pages 115–123.
An Analysis of the Impact of Diversity on Stacking Supervised Classifiers
239

Cunningham, P. and Carney, J. (2000). Diversity ver-
sus quality in classification ensembles based on fea-
ture selection. In European Conference on Ma-
chine Learning, pages 109–116, Berlin, Heidelberg.
Springer Berlin Heidelberg.
Dietterich, T. G. (2000). An experimental comparison of
three methods for constructing ensembles of decision
trees: Bagging, boosting, and randomization. Ma-
chine Learning, 40(2):139–157.
Dzeroski, S. and Zenko, B. (2004). Is combining classi-
fiers with stacking better than selecting the best one?
Machine Learning, 54(3):255–273.
Ebrahimpour, R., Sadeghnejad, N., Amiri, A., and Mosh-
tagh, A. (2010). Low resolution face recognition using
combination of diverse classifiers. In Proceedings of
the International Conference of Soft Computing and
Pattern Recognition, pages 265–268. IEEE.
Garc
´
ıa-Guti
´
errez, J., Mateos-Garc
´
ıa, D., and Riquelme-
Santos, J. (2012). Evor-stack: A label-dependent evo-
lutive stacking on remote sensing data fusion. Neuro-
computing, 75(1):115–122.
Giacinto, G. and Roli, F. (2001). Design of effective neural
network ensembles for image classification purposes.
Image and Vision Computing, 19(910):699–707.
Haykin, S. (2007). Neural Networks: A Comprehensive
Foundation. Prentice-Hall, Inc., Upper Saddle River,
USA.
Ho, T. K. (1998). The random subspace method for con-
structing decision forests. IEEE Transactions on Pat-
tern Analysis and Machine Intelligence, 20(8):832–
844.
John, G. H. and Langley, P. (1995). Estimating continuous
distributions in bayesian classifiers. In Proceedings
of the Conference on Uncertainty in Artificial Intelli-
gence, pages 338–345. Morgan Kaufmann Publishers
Inc.
Johnson, R. A. and Wichern, D. W. (2002). Applied mul-
tivariate statistical analysis. Prentice hall Englewood
Cliffs.
Kohavi, R., Wolpert, D. H., et al. (1996). Bias plus variance
decomposition for zero-one loss functions. In Interna-
tional Conference on Machine Learning, pages 275–
83.
Kotsiantis, S. B. and Pintelas, P. E. (2004). A hybrid de-
cision support tool-using ensemble of classifiers. In
Proceedings of the International Conference On En-
terprise Information Systems, pages 448–453.
Kuncheva, L. I. and Whitaker, C. J. (2003). Measures
of diversity in classifier ensembles and their relation-
ship with the ensemble accuracy. Machine learning,
51(2):181–207.
Larios, N., Lin, J., Zhang, M., Lytle, D., Moldenke, A.,
Shapiro, L., and Dietterich, T. (2011). Stacked spatial-
pyramid kernel: An object-class recognition method
to combine scores from random trees. In Proceedings
of the IEEE Workshop on Applications of Computer
Vision, pages 329–335. IEEE.
Merz, C. J. (1999). Using correspondence analysis to com-
bine classifiers. Machine Learning, 36(1-2):33–58.
Ness, S. R., Theocharis, A., Tzanetakis, G., and Martins,
L. G. (2009). Improving automatic music tag annota-
tion using stacked generalization of probabilistic svm
outputs. In Proceedings of the ACM International
Conference on Multimedia, pages 705–708. ACM.
Opitz, D. and Maclin, R. (1999). Popular ensemble meth-
ods: An empirical study. Journal of Artificial Intelli-
gence Research, 11:169–198.
Platt, J. C. (1999). Probabilistic outputs for support vector
machines and comparisons to regularized likelihood
methods. In Proceedings of the Advances in Large
Margin Classifiers. MIT Press.
Quinlan, J. R. (1992). Learning with continuous classes. In
Proceedings of the Australian Joint Conference on Ar-
tificial Intelligence, volume 92, pages 343–348, Sin-
gapore. World Scientific.
Quinlan, J. R. (1993). C4.5: programs for machine learn-
ing. Morgan Kaufmann Publishers Inc., San Fran-
cisco, USA.
Sneath, P. H. A. and Sokal, R. R. (1973). Numerical taxon-
omy. The principles and practice of numerical classi-
fication. W.H. Freeman and Company, San Francisco,
USA.
Tan, P.-N., Steinbach, M., and Kumar, V. (2005). Introduc-
tion to Data Mining. Addison-Wesley.
Ting, K. M. and Witten, I. H. (1999). Issues in stacked
generalization. Journal of Artificial Intelligence Re-
search, 10:271–289.
Witten, I. H. and Frank, E. (2011). Data Mining: Practi-
cal machine learning tools and techniques. Morgan
Kaufmann.
Wolpert, D. H. (1992). Stacked generalization. Neural net-
works, 5(2):241–259.
ICEIS 2017 - 19th International Conference on Enterprise Information Systems
240