A Methodology to Reduce the Complexity of Validation Model Creation

from Medical Speciﬁcation Document

Francesco Gargiulo, Stefano Silvestri, Mariarosaria Fontanella and Mario Ciampi

Institute for High Performance Computing and Networking, ICAR-CNR, Via Pietro Castellino 111 - 80131, Naples, Italy

Keywords:

Clustering, Medical Speciﬁcation Document, Validation, Natural Language Processing (NLP), Schematron.

Abstract:

In this paper we propose a novel approach to reduce the complexity of the deﬁnition and implementation of a

medical document validation model. Usually the conformance requirements for speciﬁcations are contained

in documents written in natural language format and it is necessary to manually translate them in a software

model for validation purposes. It should be very useful to extract and group the conformance rules that have

a similar pattern to reduce the manual effort needed to accomplish this task. We will show an innovative

cluster approach that automatically evaluates the optimal number of groups using an iterative method based on

internal cluster measures evaluation. We will show the application of this method on two case studies: i) Patient

Summary (Proﬁlo Sanitario Sintetico) and ii) Hospital Discharge Letter (Lettera di Dimissione Ospedaliera)

for the Italian speciﬁcation of the conformance rules.

1 INTRODUCTION

The availability of medical information processing

systems and the digitalization of almost all informa-

tion in hospital and clinical processes provide an im-

portant support for the tasks of healthcare profession-

als. Dealing with digital documents and using custom

processing systems can improve their work, offering a

lot of innovative tools and instruments, ranging from

improved information retrieval systems to intelligent

image and text processing.

Focusing especially on text documents, we know

that an important part of the work of healthcare pro-

fessionals is the editing of many different clinical doc-

uments such as Patient Summaries, Laboratory Tests

Reports and Medical Prescriptions. All of them are

structured or semi-structured text documents and, fur-

thermore, they even require the presence of certain in-

formation, like, for example, a doctor name, a date or

a disease code. In addition, their structure and content

must respect ofﬁcial guidelines, often established by

law. These speciﬁcations propose to standardize the

structure of these digital documents, ensuring the cor-

rectness and the completeness of the content and of

the text format.

A standard like the ones promoted by HL7 not

only can ensure the semantic and formal correctness

of the digital version of these documents, but it sup-

ports an effective and reliable automatic processing

and the interoperability between different systems too

(Ciampi et al., 2016). In other words, it is crucial that

the exchanging of these documents between different

hospitals or physicians is error-free, without loss of

information.

Due to the importance of these tasks, the deﬁnition

of the conformance rules is a long and critical process,

that involves many specialists from medical, clinical,

legal and computer science ﬁelds and, of course, the

governments and health-care agencies. The results of

their work are usually documents written in natural

language, containing a set of conformance require-

ments rules for speciﬁcations that deﬁne the format

and the content each of them.

The need of conformance rule documents arises

from requirements of standards. Ofﬁcial medical nat-

ural language text documents must not only be auto-

matically processed easily, but even respect a format

and contain speciﬁc information. In Italy, Agencies

and government representatives, at this aim, have pro-

duced the conformance speciﬁcations documents for

the digital version of the Patient Summary, the Labo-

ratory Medicine Report, the Hospital Discharge Letter

and the Medical Prescription, that are actually part of

HL7 International standards in the Italian context.

As explained before, the speciﬁcations are docu-

ments written in natural language format, describing

the whole conformance rules for speciﬁcations and

the details of the implementation guide for each of

Gargiulo F., Silvestri S., Fontanella M. and Ciampi M.

A Methodology to Reduce the Complexity of Validation Model Creation from Medical Speciﬁcation Document.

DOI: 10.5220/0006291404970507

digital medical certiﬁcates listed above.

Among all the possible uses of conformance rules,

one of them could be the development of a validation

model, that ensures and tests the complete confor-

mance of the digital certiﬁcate to the standard state-

ments.

To implement this kind of functions, computer sci-

entists and engineers must perform a long and tedious

task, analysing the natural language text in the con-

formance speciﬁcations document to realize a com-

plete and reliable validation schema for each rule

listed in the standard (Gargiulo et al., 2016). This

task can be performed only by an hand-made trans-

lation of each natural language rule in a software

model for validation purposes, using, for example,

Schematron (ISO/IEC 19757-3:2016) (Jelliffe, 2001),

or other rule-based validation languages. Nowadays,

it is a critical task to extract automatically a valida-

tion schema from a set of rules described in natural

language.

A great boost in the realization of the validation

schema can be obtained simply reducing the complex-

ity of the problem, decreasing the number of asser-

tions that has to be manually built. This task can be

accomplished grouping the rules following the same

pattern: in this way, the same assertion function could

be applied to more rules, speeding up the develop-

ment of the validation model.

In this paper we propose an innovative method-

ology based on unsupervised machine learning tech-

niques, namely clustering, that extracts automatically

the text of the rules from the speciﬁcation documents

and groups them together. Each group contains all

the rules that belong to the same assertion schema.

The experiments have been performed on Italian lan-

guage speciﬁcation rule documents of medical topic,

but the proposed techniques are language independent

and they can be applied on documents in different lan-

guages, or to any kind of speciﬁcation document.

The paper is structured as follow: in Section 2

it will be given a critical review of the state of the

art related to automatically validation and clustering

optimization ﬁelds; in Section 3 it will be shown the

methodology and in Section 4 it will be detailed the

designed architecture; in Section 5 the methodology

correctness will be demonstrated for two use cases:

i) Patient Summary and ii) Hospital Discharge Let-

ter. Finally, in Section 6 it will be given the conclu-

sion and it will be draw up some key issues for future

works.

2 RELATED WORKS

Nowadays there is a big interest of scientists about

creation and automatic validation of conformance

rules in natual language, especially for medical do-

main. In (Bosc

a et al., 2015) the authors proposed and

described the archetypes to generate a rules in Natural

Language text and Schematron rules for the validation

of data instances. The goal was creating a formal doc-

ument with a formal value of archetype, but at same

time understandable by non-technical users.

In (Boufahja et al., 2015) the authors demon-

strated the conformance of their samples with HL7

CDA requirements and evaluated the capability of the

tools to check those requirements. They looked at the

conformance of the provided samples with the basic

HL7 CDA requirements as speciﬁed within the Clin-

ical Document Architecture, R2 Normative Edition,

and analysed the capability of the tools provided to

check the requirements. At the ﬁrst time, the authors

revisited the CDA speciﬁcations and extract the re-

quirements not covered by the CDA Schema, then

they checked the coverage of the requirements with

another validation tools.

In (Hamilton et al., 2015) the authors described

a method in which users realize the beneﬁts of a

standards-based method for capturing and evaluating

veriﬁcation and validation (V&V) rules within and

across metadata instance documents. The rule-based

validation and veriﬁcation approach presented has the

primary beneﬁt that it uses a natural language based

syntax for rule set, in order to abstract the computer

science-heavy rule languages to a domain-speciﬁc

syntax. As a result, the domain expert can easily spec-

ify, validate and manage the speciﬁcation and valida-

tion of the rules themselves.

In (Jafarpour et al., 2016) is evaluated the tech-

nical performance and medical correctness of their

execution engines using a range of Clinical Practice

Guidelines (CPG). They demonstrated the efﬁciency

of CPG execution engines in terms of CPU time and

validity of the generated recommendation in compar-

ison to existing CPG execution engines.

Clustering is an unsupervised machine learning

technique, that can well group together objects that

show similarity between each others. One of the main

problem in clustering, being unsupervised, is the clus-

ter validation, that, in fact, has long been recognized

as one of the crucial issues in clustering applications.

Validation is a technique to ﬁnd a set of clusters that

best ﬁts natural partitions without any class informa-

tion, ﬁnding the optimal number of clusters (Halkidi

and Vazirgiannis, 2001).

The measures used for cluster validation purposes

can be categorized into two classes: external and in-

ternal. The ﬁrst case can be used when a gold case is

available, verifying the correctness of results through

measures like F-measure, Entropy, Purity, Complete-

ness, Homogeneity, Jaccard coefﬁcient, Fowlkes and

Mallows index, Minkowski Score and others (Rend

et al., 2011), (Wu et al., 2009), (Handl et al., 2005),

(Rosenberg and Hirschberg, 2007). These papers

analysed and compared all the aspects of each mea-

sure to understand how well it ﬁts speciﬁc cluster al-

gorithm, application or topic, revealing the goodness

of the clustering. A common ground of external mea-

sures is that they can often be computed by the con-

tingency matrix (Wu et al., 2009).

When a gold case is not available, the second class

of cluster validation measures, namely the internal

ones, must be used. In this case, the goodness of

clustering results is based only on spatial character-

istics of cluster members, like their compactness or

separation. One of the ﬁrst internal cluster measure

proposed in literature is the silhouette (Rousseeuw,

1987). The silhouette is a numeric parameter that

takes in account the tightness and separation of each

cluster, showing which objects lie well within their

cluster and which ones are merely somewhere in be-

tween clusters. Many other internal measures have

been deﬁned in literature, like Dunns indices, SD and

bw validity indexes and others (Liu et al., 2010),

taking into account different aspects of the cluster-

ing results in addition to the separation and compact-

ness, like monotonicity, noise, density, sub-clusters

and skewed distributions, that can better show differ-

ent aspects of the results.

Internal cluster measures have been often used to

set the correct cluster number, not only optimizing

their global value (Kaufman and Rousseeuw, 2009),

but even obtaining some speciﬁc new measures from

the classical ones, to identify cluster characteristics of

a speciﬁc domain, as, for example, they did in (Pol-

lard and Van Der Laan, 2002). In (Dhillon et al.,

2002) an iterative clustering method is proposed to

improve spherical K-means algorithm results, that,

when applied to small cluster sizes, can tend to get

stuck at a local maximum far away from the opti-

mal solution. They presented an iterative local search

procedure, which reﬁnes a given clustering by incre-

mentally moving data points between clusters, thus

achieving a higher objective function value.

3 METHODOLOGY

In this Section we explain the details of the method-

ology applied in our experiments. We developed an

iterative cluster strategy, that aims to obtain the best

clustering solution. This is achieved through an in-

ternal measure cluster selection, described in 3.1 and

in 3.2. Then, to assess the whole methodology, we

manually built a gold case, validated using a custom

cluster external validation measure described in 3.3.

Gold case construction and validation assessment are

described in Section 5

3.1 Clustering Algorithm and Internal

Measures

Following the literature (Alicante et al., 2016a), we

decided to use the spherical K-means cluster algo-

rithm, a slight variation of the K-means algorithm,

and the cosine similarity. It has been shown that the

optimal distance for K-means based cluster applica-

tions for Italian natural language text of medical topic

is the cosine distance (Alicante et al., 2016b), that is

equals to inverse cosine similarity (eq. 1).

1 −

∑

i=1

· y

| x

|| y

(1)

The cosine similarity measure allows to use the

spherical K-means (Zhong, 2005) algorithm, that uses

a slight variation of the K-means algorithm exploiting

the cosine similarity measure: the classical K-means

minimizes the mean squared error from the cluster

centroid (eq. 2)

∑

kx − µ

k(x)

k (2)

where N is the total number of feature vectors and

k(x)

is the most similar centroid; instead, in spherical

K-means the objective function is deﬁned as (eq. 3)

∑

x · µ

k(x)

(3)

that is strictly related to the cosine similarity. Our

experiments conﬁrm the goodness of these choices

(see Section 5).

The determination of optimal partition is per-

formed through an iterative loop, based on cluster in-

ternal measure, described in details in Section 3.2.

As assessment of clustering results we can only

use internal measures, having no labelled data. For

validation purposes we have chosen the silhou-

ette (Rousseeuw, 1987), a classic cluster internal val-

idation measure, that takes into account two impor-

tant aspects of a clustering solution: i) the similarity

among elements of the same cluster and ii) the dissim-

ilarity among elements belong to different clusters.

Let call i a generic point of the data set and a(i) the

average dissimilarity of the point with the elements

of the same cluster. Dissimilarity is calculated with

inverse cosine similarity. A small a(i) means that the

point is quite close to all the other points in the cluster.

We deﬁne b(i) as the smallest average dissimilarity

between i and the elements of any cluster different

from the one i belongs, estimating how far the current

point is from the closest point not in the same cluster.

Then the silhouette s(i) of each point of a cluster

is deﬁned as:

s(i) =

b(i) − a(i)

max(a(i), b(i))

(4)

where the opposite of a(i) is considered so that

its effect is in favour of compactness. The silhouette

value is in the range [−1, 1], and a larger silhouette in-

dicates a better assignment of that point to its cluster.

The silhouette is negative whenever the other points

in the cluster are, on average, farther from the point i

than the closest point outside of the cluster. Silhouette

can then be averaged on all points of a cluster to as-

sess the compactness of that cluster with respect to the

others. In this case, a negative number of silhouette

means that the diameter of the cluster is larger than

the distance from the closest point out of the cluster.

The average silhouette over all elements i could

be used to compare clustering results and to select

the optimal number of clusters k by maximizing it

over a range of possible values for k (Kaufman and

Rousseeuw, 2009). The method of maximizing av-

erage silhouette can be used with any clustering al-

gorithm and any distance metric, but it has the dis-

advantage that measures only the global structure of

the solution. To take in account ﬁner behaviour we

have proposed an alternative parameter. Let con-

sider the average silhouette of the j

cluster as S

We then call MAS the median of average silhouettes

S = {S

, S

, . . . , S

}, a value equals to:

MAS = median(S) (5)

The MAS can give a synthetic clue about the good-

ness of the entire cluster solution, but, differently

from the simple average of all silhouettes s(i), it can

take into account each cluster validity.

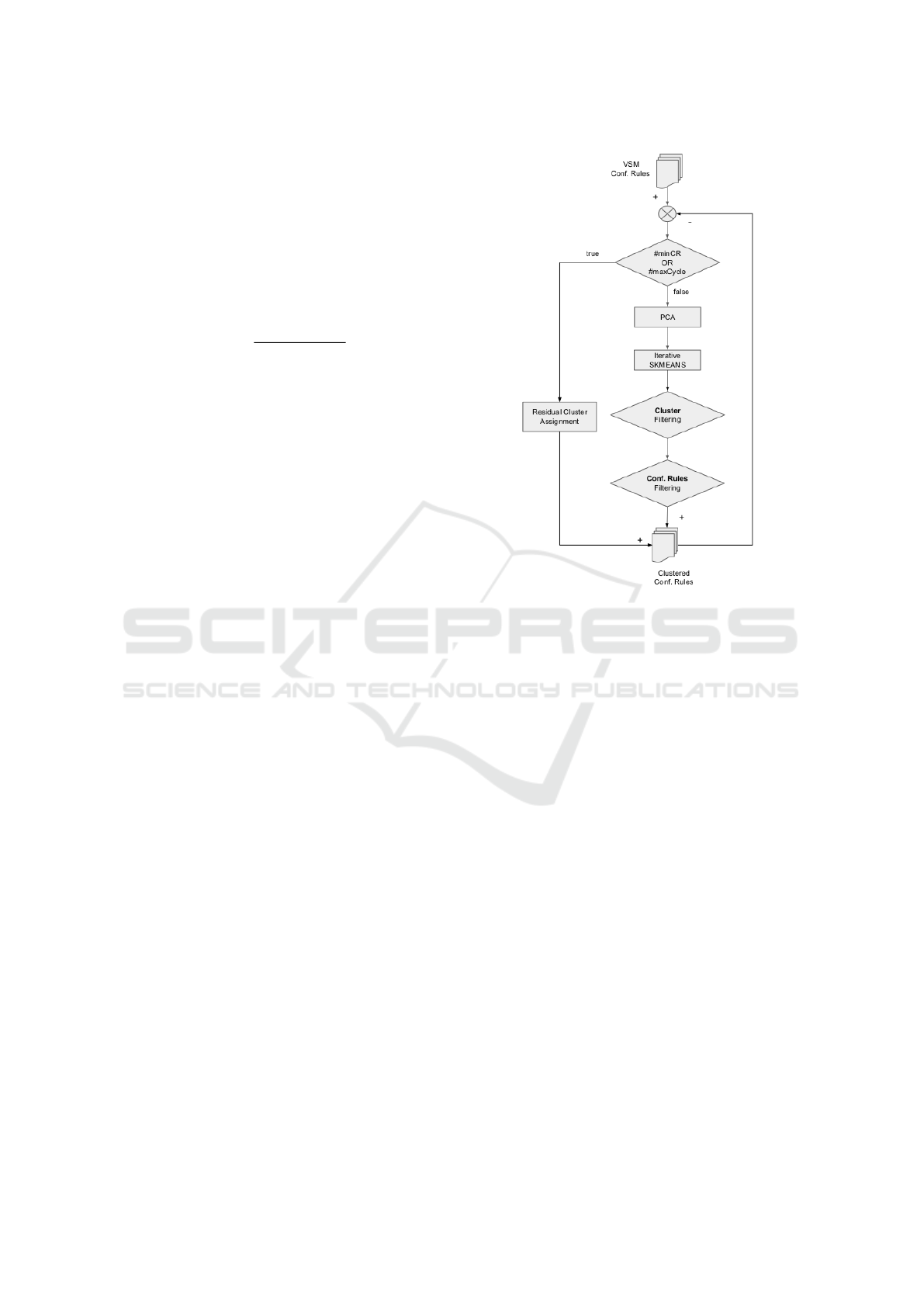
3.2 Iterative Cluster Optimization

To obtain a more precise clustering we proposed an

iterative clustering optimization algorithm, based on

MAS optimization. In Figure 1 is depicted ﬂow chart

diagram, representing the proposed methodology.

After constructing a Vector Space Model (VSM)

of the Conformance Rules, we have deﬁned an it-

erative cycle. The ﬁrst task is a de-noising of the

input data, using a Principal Component Analysis

Figure 1: Flow chart of the methodology used to cluster the

conformance rules.

(PCA) methodology for feature reduction (Cao et al.,

2003). We set the selection of information content of

PCA at 96%: this value has been obtained observing

the higher mean silhouette value of clustering exper-

iments. The feature reduction is performed at each

step of the iterative cluster algorithm, reducing each

iteration the number of extracted features.

Then, an Iterative Spherical K-means algorithm,

depicted in Figure 2, is applied to evaluate the opti-

mal cluster solution. We perform Spherical K-means

with cluster number ranging from 2 to total Confor-

mance Rules number. The optimal cluster solution

is the one with highest MAS value in the range of

all solutions obtained during the iteration. From the

whole solution with highest MAS we select only clus-

ters whose mean silhouette is bigger than MAS (in-

ter cluster selection); then, in these selected clusters,

we ﬁlter out the elements whose silhouette is smaller

MAS (intra cluster selection). The clusters obtained

with this ﬁltering operations are selected as part of

the ﬁnal solution and the remaining elements are iter-

atively re-processed in the same way, until the num-

ber of remaining documents is smaller than a given

threshold #minCR or the number of iterations is big-

ger than a threshold #maxCycle (see Figure 1).

When the termination condition is reached, the

Figure 2: Flow chart of the implemented Iterative Spherical

K-Means.

residual conformance rules are assigned to their own

cluster (one element cluster), considering that each

rules have a low silhouette value.

3.3 Cluster Validation Measure

The evaluation of the clustering goodness consider-

ing an handmade gold case is obtained using external

measures, that are often computed by the contingency

matrix (Wu et al., 2009).

The contingency matrix (see Tab.1) is deﬁned as

follow: given a data set D with n objects, assume that

we have a partition C = {C

, . . . , C

} of D, where

i=1

= D and C

0 for 1 ≤ i 6= j ≤ K

, and

is the number of clusters. If we have a Gold Case,

we can have another partition on D : P = {P

, . . . , P

where

i=1

= D, P

0 and K is the number of

classes. Each element n

i j

of the matrix denotes the

number of objects in cluster C

from class P

Table 1: The Contingency Matrix.

. . . C

∑

. . . n

1·

. . . n

2·

· · · . . . · ·

. . . n

K·

∑

·1

·2

. . . n

·K

From the contingency matrix it is possible to de-

ﬁne for each obtained cluster C

and for each gold

case cluster P

the following two measures (Rosen-

berg and Hirschberg, 2007):

• Homogeneity Hom(C

): a clustering must assign

only those data-points that are members of a sin-

gle class to a single cluster. It can be calculated

as:

Hom(C

) =

· j

max

i j

) (6)

• Completeness Com(P

): a clustering must assign

all of those data-points that are members of a sin-

gle class to a single cluster. Completeness is sym-

metrical to Homogeneity.

Com(P

) =

i·

max

i j

) (7)

These two measures are both needed to character-

ize the goodness of the clustering partition, taking into

account two complementary aspects. Using them, we

deﬁned a new measure for the whole dataset parti-

tion named as Clustering Goodness (CG) deﬁned as

the weighted mean of the Hom and Com (see eq. 8).

The weighting is necessary because the goodness of

cluster solution is related even to the correct choice

of cluster number and not only to Hom and Com.

In other words, if clusters number is close to docu-

ments number, the mean(Hom) value tends towards

one; on the other hand, if the clustering solution is

made by only one cluster, the mean(Com) tends to-

wards one. This extreme cases demonstrate that an

arithmetic mean of these measures does not capture

clustering goodness in every case.

CG(C) =

K + K

∑

i=1

∑

j=1

α ·Com(P

) + (1 − α) · Hom(C

)

(8)

The α value must balance the negative effects

previously described, taking into account the cluster

number in function of the gold-case cluster number.

So we deﬁned α as:

α =

(

2·K

, if K ≤ K

2·(n−K

)

, otherwise

(9)

In this way, the value of equation 8 varies in range

(0, 1] and a perfect clustering solution has a CG value

equal to 1, meaning that the clustering is identical to

gold case partition, but the α value as deﬁned in 9 can

weight the importance of Hom and Com in function

of optimal cluster number too. We used the CG in

the experimental assessment in Section 5, showing the

effectiveness of the proposed methodology.

4 SYSTEM ARCHITECTURE

The system architecture is divided into six different

blocks, as shown in Figure 3.

Figure 3: Main System Architecture. In purple, the input

data; in grey, the blocks that are evaluated in this paper

and in light-blue the blocks that will be considered as fu-

ture works.

The ﬁrst block consists in a pre-processing stage

where the input speciﬁcation document is converted

into a more structured ﬁle, extracting and normaliz-

ing the conformance rules from the text. In the sec-

ond block, a vector space model is created, extract-

ing the features from the text of conformance rules

and the iterative clustering technique, previously de-

scribed, is applied, to obtain the group of rules that re-

spect the same pattern. In the third block, a clustering

evaluation is made considering hand-made gold cases.

In the fourth block, an implementation of an abstract

rule for each cluster is deﬁned. In the ﬁfth block we

plan to create a module that implements each confor-

mance rule according with its own abstract rule and,

ﬁnally, in the last block is planned to evaluate the cor-

rectness of the ﬁnal model obtained using hand-made

gold cases.

The whole pipeline has been implemented in Kn-

ime environment (Berthold et al., 2007), an open

platform for machine learning that natively supports

external scripts in the most common language (C,

Python, Java, R, Matlab, Weka and other). Using

Knime is possible to integrate many tools in a sin-

gle environment and design an optimized pipeline. In

Figure 4 is shown the workﬂow implemented for the

experiments.

The following subsections 4.1, 4.3, 4.4 describe

the details of each block and the tools used to realize

the system.

Figure 4: Example of Knime workﬂow. The grey blocks

represent a metanode that is a group of nodes which perform

complex operations.

4.1 Conformance Rule Extraction and

Normalization

The ﬁrst task of the system is the extraction of rules

text and its normalization, obtained after an analysis

of documents and conformance text structure. A spec-

iﬁcation document is often in pdf ﬁle format and the

ﬁrst operation needed to perform any kind of process-

ing is the conversion in a plain-text UTF-8 ﬁle.

We converted the conformance rule documents

used in our experiment using pdftotxt

, an open

source command-line utility, included by default

within many Linux distributions. The text ﬁle out-

putted from pdftotxt preserves most of the indentation

and the structure of the original pdf ﬁle and this is re-

ally important for the subsequent task of the system.

In fact, we need to extract only the natural language

text where each rule is deﬁned and stated. This task

has been accomplished writing some Python scripts

that, using the regular patterns of the text, extract the

index of the document, the paragraph names and the

rule texts. In our case, for example, all the confor-

mance rules have a well-deﬁned pattern: their deﬁni-

tions start with a tag (CONF-xx-yy) and end with an-

other rule tag (CONF-xx-zz) or a dot sign. The next

Figure 5 shows an example of the regular pattern from

the original conformance rules ﬁle.

Different conformance documents can be pro-

cessed only analysing their speciﬁc patterns. Python

scripts have in input the start and end rule delim-

iter, but they can be easily modiﬁed to be applied

to different and more complex patterns. The scripts

perform a normalization phase too, deleting punctu-

ation, the not-standard characters, symbols and stop

words (a list of Italian language stop words is pro-

vided by Lucene

). Then, using regular expressions,

http://www.foolabs.com/xpdf/home.html

https://lucene.apache.org/core/4 4 0/analyzers-

common/org/apache/lucene/analysis/it/ItalianAnalyzer.html

"#$!%&'()'!

"#$%&'()'*%+*,-./012324&5627)8)9'#':*;<=<*>=758!

!"#$%"&'()*("+,-."

/(0"-."

?&2(285@!AB2CD"ED!;'(A2CD@')(&5FGGAB24H75@')9=85@DI?G&2(285@I!JKL!

?&2(285@!AB2CD"ED!;'(A2CD&2(FM/NJLO$PKM</DI?G&2(285@I!

>)!4)@'97'!'!Q&&RFGGSSS=3'TB=54UG438BG438NKOO=Q&@(!R24!A(&24)54)!72&&'U()=!

/¶LQGLUL]]RGL3(&qWUDWWDWRFRPHXQDFRPXQHHPDLO!

>)!4)@'97'!'!1)3!<M!R24!A(&24)54)!72&&'U()=!!

!LMM!

/¶HQWLWj !"#$!%&'!(")*+'),"-).$/"*+'),"-)! V! A9! 2(2@29&5! !""#$%&'!($!! 8Q2! 859&)292! )!

7'&)!'9'U4'3)8)!72(!B5UU2&&5!72(('!R42B&'W)592=!!

)!*+,-./0%(!758A@29&5!1232!859&29242!O¶2(2@29&5!!"#$!%&'!(")*+'),"-).$/"*+'),"-)=!

!LML!

-XYX! 2BB242! R42B29&2! A9! 2(2@29&5! +'),"-)*-'0"1 85 9&2929&2! 95@2! 2! 85U95@2! 72(!

R'W)29&2!Z;27)! [!/=N!*!E24B592!27! \4U'9)WW'W)59)]=!^59!RA_! 2BB242!A&)()WW'&5 ! )(!9 A((`(';54!

SHULQGLFDUHO¶LQGLVSRQLELOLWjGHOGDWR!

)!*+,-4/0/¶HOHPHQWR +'),"-).$/"*+'),"-)! 1232! FRQWHQHUH O¶HOHPHQWRL<M!

+'),"-)*'%0,-,2)!'),3"4"-%"!5$%"!ZB2BB5]=!

)!*+,-5/0/¶HOHPHQWR +'),"-).$/"*+'),"-)! 678! FRQWHQHUH O¶HOHPHQWR  +'),"-)*6,!)7&,0"!

Z7'&'!7)!9'B8)&']=!

!L<L!

)!*+,-9/0/¶HOHPHQWR +'),"-).$/"*+'),"-)! 678! FRQWHQHUH O¶HOHPHQWR

+'),"-)*6,!)78/'#"*+/'#"*'%%!*#"-292&!'#)! 8Q2! 4)R54&'! )(! 857)82! %>a.a! 72(! (A5U5! 7)!

QDVFLWDGHOO¶DVVLVWLWR!

E24! )! 72&&'U()! 42('&);)! 'U()! 2(2@29&)! +'),"-)*-'0"! +'),"-)*'%0,-,2)!'),3"4"-%"!5$%"! 2!L/M!

+'),"-)*6,!)7&,0"!B)!4)@'97'!'!1)3!<M=!

1HO FDVR GL SD]LHQWH PLQRUH O¶HQWLWj !"#$!%&'!(")*+'),"-).$/"*+'),"-)! 678! 859&29242!

DQFKH O¶HOHPHQWR (9'!%,'-! 8Q2! 723)9)B82! 85(A)! 8Q2! 4'RR42B29&'! )(! B5UU2&&5! 72(('!

R42B&'W)592!Z2B=!)(!&A&542GU29)&542!8Q2!4'RR42B29&'!)(!@)9542]=!!L/L!

>)!4)@'97'!'!1)3!<M!R24!)!72&&'U()!42('&);)!DOO¶HOHPHQWR(9'!%,'-=!

!"#"!"$"#%&'()&*+,&-'./0,.1'2.3)4'/0&)51*'&6&-,217,.1)2%

/¶HOHPHQWR +!$3,%"!:!('-,;'),$-! R24@2&&2! 7)! &4'88)'42! U()! )729&)3)8'&);)! 72((2! 29&)&b! 85@2!

$]LHQGD 6DQLWDULD 'LSDUWLPHQWR 8QLWj 2SHUDWLYD FKH IDQQRJLRFDUH LO ³UXROR´ GL SD]LHQWHLNM!

'(('!R24B59'c!'882&&'975!('!4)8Q)2B&'!7)!2B28AW)592!7)!R42B&'W)59)=!

/¶HOHPHQWR!,%!;)292!AB'&5!4)R2&A&'@29&2!R24!8'4'&&24)WW'42!)9!@575!85@R(2&5!U()!2 9&)!85@2!

.W)297'! >'9)&'4)'c! -)R'4&)@29&5c! d9)&b! \R24'&);']! 8Q2! Q'! '882&&'&5! ('! R42B&'W)592!

DOO¶RULJLQHGHO42324&5=!LNL!

E24! 4)R54&'42! U()! )729&)3)8'&);)! 7 2((2! .W)2972! >'9)&'4)2c! V! R5BB):)(2! A&)()WW'42! ('! 857)3)8'!

@)9)B&24)'(2! `#><< H LQ WDO FDVR O¶DWWULEXWR <!$$)! 1232! HVVHUH YDORUL]]DWR FRQ O¶2,'

³´=!

Figure 5: An example of input document used for experi-

ment assessment. It is possible to observe the regular pat-

tern of conformance rules to be extracted. In addition, each

rules lies on a grey background.

we replace Logical Observation Identiﬁers Names

and Codes (LOINC

), TemplateId codes, Paragraphs

and Key Names with a generic identiﬁer (i.e. LOINC

33882 − 2 is substituted with the word *LOINC*).

We did this further normalization to reduce the noise

induced by different terminology associated to the

same concept, obtaining a better clustering results.

The output of this module is an xml ﬁle, whose

structure is depicted in Figure 6. As shown, the body

of CONF tags contains only the normalized text of

each conformance rule. The used tags are the follow-

ing:

• documento: the xml root, its body contains the

document title and all the paragraphs will be its

children;

• paragrafo: it contains the paragraph name in its

body and the paragraph number as id attribute. All

the CONF associated to it are its own children;

• CONF: it contains in its body the normalized text

of the original conformance rule. Its attributes are:

i) num in which is indicated the rule number and

ii) par that indicates the paragraph number.

Figure 6: Part of the output xml ﬁle obtained from text ex-

traction and normalization module.

http://loinc.org/

4.2 Feature Selection

The input to machine learning applications is repre-

sented through a Vector Space Model (VSM). In VSM

a vector is associated to each sample (in this case the

Conformance Rule) in which the elements of the vec-

tor correspond to the feature values.

Vectors of size M correspond to points in an M-

dimensional space; the main hypothesis underlying

the VSM is that similar objects are represented by

points which are closed in the M-dimensional space.

Achieving optimal results with a machine learning

technique based on VSM is strictly related to the cor-

rect choice of feature space (Amato et al., 2013).

In our case, the entity to be clustered are the con-

formance rules in natural language text, identiﬁed by

their name. The rules in a VSM are mapped as n-

grams of words. The correct selection of the n-gram

size, namely the length of n, is both language and

topic dependant (Cavnar and Trenkle, 1994) and so

there is not an absolute rule (Eder, 2011). In our case

we selected all n-grams with n ranging from 2 to 6,

observing the highest MAS (see equation 5) obtained

in different clustering experiments, varying both n

and the number of n-grams together. The high value

of n obtained (often only uni-grams, bi-grams and tri-

grams are used in literature) can be explained by the

repetitive structure of the patterns in the description of

a rule. We extract the features using internal KNIME

modules.

The VSM obtained can be represented by a high

dimensional sparse matrix. To reduce the noise

caused by not discriminant features and consequently

the space dimension, improving clustering perfor-

mance and providing a faster computation, we ap-

plied Principal Component Analysis (PCA) as feature

reduction method. The PCA has been implemented

through the Cran R built in function prcomp, a really

fast and accurate PCA algorithm. We set the selec-

tion of information content of PCA at 96%: this value

has been obtained observing the higher mean silhou-

ette value within all clustering experiments. The fea-

ture reduction is performed at each step of the itera-

tive cluster module, described in the next Section 4.3,

reducing each time the number of extracted features.

The use of n-grams directly extracted from the

dataset makes the whole process totally language in-

dependent; the same methodology can be applied on

conformance rules in any language and even to mixed

languages, or medical slang documents. Changing the

input dataset affects only the scripts for the normaliza-

tion and rule extraction, that must be slightly modiﬁed

as described in previous Section 4.1, but none of the

other modules, included the feature extraction one.

4.3 Iterative Clustering

As described in Section 3, to group the confor-

mance rules we applied iteratively a spherical K-

means algorithm, selecting at each step the best so-

lution according to MAS (equation 5), a cluster in-

ternal measure based on silhouette. After applying

PCA feature reduction, we used the Cran R skmeans

package (Hornik et al., 2012) with CLUTO algo-

rithm (Karypis, 2002) to iteratively calculate spher-

ical K-means with a cluster number range between 2

and the total number of rules, as described in Sec-

tion 3.2. To speed up the iterative clustering process

we used the doParallel Cran R package (Weston and

Analytics, 2014), running more cluster processes in

parallel.

4.4 Abstract Model Deﬁnition

The last implemented module performs the abstract

model deﬁnition. At this aim we use a functionality

of the standard Schematron that allows to deﬁne ab-

stract patterns. In this way, it is possible to implement

for each obtained cluster only one abstract model, ob-

taining a reduction of the complexity evaluable as:

∆(Complexity) =



1 −

Cluster Number

Conf. Rules Number



· 100

(10)

The Figure 7 represents the conceptual schema for

the creation of a Final Implemented Rule starting from

a Clustered Conformance Rule and an Abstract Pat-

tern Template.

An abstract pattern template is a way to general-

ize a class of possible instances of conformance rules

and, like the concept of Abstract Class in the Object

Oriented paradigm, it is possible to instantiate a spe-

ciﬁc Final Implemented Rule starting from it. The

Figure 7: Main Schema of the Conformance Rule Imple-

mentation starting from an Abstract Pattern Template and a

Clustered Conformance Rule.

Figure 8: Main Schema of the Conformance Rule Imple-

mentation starting from an Abstract Cluster Template.

Figure 8 shows a generic example written accord-

ing to the standard Schematron where, considering a

cluster partition identiﬁed by Cluster ID, it is created

an abstract pattern with all the parameters deﬁned as

generic variables (ex. $Context, $par1, $par2, etc.).

In the example we also deﬁned a generic function

assertion(·) to obtain complex tests using the deﬁned

variables.

In Figure 9, the abstract pattern is used to instan-

tiate a speciﬁc conformance rule that belongs to that

cluster. In this case the instantiation consists to de-

clare the abstract pattern to use and to specify each

parameter involved.

Figure 9: Main Schema of the Conformance Rule Imple-

mentation starting from an Abstract Cluster Template.

At the moment the abstract pattern template im-

plementation is manual and involves a human pro-

cessing. As future work, we are planning to autom-

atize this task, using NLP tools. In details, the use

of a Part of Speech (PoS) tagger and of a depen-

dency parser will automatically identify the subject,

the main verb and its objects of each cluster member.

In addition, a dedicated entity extraction can help to

classify the object types. Then, a rule based system

can build a pattern for each cluster.

5 EXPERIMENTAL RESULTS

To verify the effectiveness of described approach we

will show the application of the proposed method-

ology on two case studies, namely the Italian local-

ization of speciﬁcation of the conformance rules of:

i) Patient Summary

(in Italian Proﬁlo Sanitario Sin-

tetico, PSS) and ii) Hospital Discharge Letter

(in Ital-

ian Lettera di Dimissione Ospedaliera, LDO). The

conformance requirements and speciﬁcations are part

Patient Summary: http://www.hl7italia.it/sites/default/

ﬁles/Hl7/docs/public/HL7Italia-IG CDA2 PSS-v1.2-S.pdf

Hospital Discharge Letter: http://www.hl7italia.it/

webfm send/1709

Table 2: Gold case cluster number of each dataset.

Speciﬁcation Rules number Gold case Cluster number

LDO 104 42

PSS 259 129

PSS+LDO 363 159

of HL7-Italia (see Section 1 for more details). PSS

and LDO are both conformance requirements and

speciﬁcation documents written in semi-structured

natural language text. PSS contains 259 conformance

rules, while LDO a total number of 104. To ex-

tend the experimental assessment, we have applied

our methodology even to the sum of the rules from

both documents, clustering a new data set with a total

of 363 rules, named PSS+LDO. It could be useful in

real application group together similar conformance

rules documents, identifying the rules with the same

patterns from different documents.

The assessment is based on gold cases, formed by

the ideal grouping of the conformance rules of each

dataset belonging to the same pattern. The goodness

of the cluster results have been measured through the

CG (equation 8) applied on those gold cases. Each

gold case has been manually built by the software de-

velopers who previously implemented the whole con-

formance rule validation schema: they well know the

rules text and their patterns and so they produced a

reliable gold cases for each dataset used. The num-

ber of conformance rules grouped in each gold case is

shown in next Table 2.

We have compared the results obtained with our

approach, namely Iterative Spherical K-Means (IT-

SKM), with the ones obtained using a One Iteration

Spherical K-Means (1-SKM) method. In this case,

only one step of iteration process is performed, choos-

ing the cluster number of the partition with the MAS

function (equation 5), without selecting the elements

to be clustered in the following steps.

In Table 3 is shown the effectiveness of using IT-

SKM for evaluating the optimal number of clusters

through the synthetic external measure CG (eq. 8),

previously deﬁned in Section 3.3. We compared the

IT-SKM results with the 1-SKM results through the

CG measure for PSS, LDO and PSS+LDO cases. In

all experiments the best results have been obtained

with iterative approach IT-SKM. It is even worth not-

ing that cluster number obtained with IT-SKM is re-

ally close to the gold case.

To better understand and explain the results of our

experiments, we show in Figure 10 the Hom (in red)

and Com (in blue) percentage value distribution for

1-SKM and IT-SKM for all data sets. In details, the

ﬁgures depict the cluster distribution whose Hom and

Com have a certain value. All 1-SKM experiments

have an high number of clusters whose Hom is high,

due to the fact that the number of clusters obtained is

close to the total conformance rules number and many

clusters have only one element. So the high value of

Hom is caused simply by cluster formed by only one

element, not by a good cluster solution. On the other

side, the number of clusters with an high Com value is

only a little fraction of the whole partition, suggesting

a bad clustering.

Instead, IT-SKM experiments show in all cases a

very high fraction of clusters with both Hom and Com

equal to 100%. A perfect solution (identical to gold

case) has Hom and Com equal to 100% for each clus-

ter. The results in Figure 10 for IT-SKM show that

this condition is veriﬁed for an high number of clus-

ters, demonstrating the effectiveness of the proposed

methodology. In addition, the ﬁgure conﬁrms that CG

measure follows the correct behaviour and it is an use-

ful external measure.

6 CONCLUSION AND FUTURE

WORK

In this paper we proposed a novel approach to reduce

the complexity of the deﬁnition and implementation

of a medical document validation model.

We deﬁned an architecture to automatically pro-

duce a software speciﬁcation starting from a set of

conformance rules in semi-structured natural lan-

guage format. At this aim, we presented an innova-

tive cluster approach that automatically evaluates the

optimal number of groups using an iterative method

based on internal cluster measures evaluation.

The effectiveness of the proposed approach is

evaluated on two case studies: i) Patient Summary

(Proﬁlo Sanitario Sintetico) and ii) Hospital Dis-

charge Letter (Lettera di Dimissione Ospedaliera) for

the Italian localization speciﬁcation of the confor-

mance rules.

As future works we are planning to realize the re-

maining blocks of the architecture depicted in the Fig-

ure 3 and, in particular, the Final Model Creation and

Model Validation (the blocks have light-blue back-

ground in the Figure). Furthermore, we are consider-

ing to automatize the creation of the abstract pattern

template starting from a cluster, with the support of

natural language tools. At least, we are also investi-

gating more deeply on other unsupervised methods to

automatically grouping the conformance rule and in

particular on deep-learning approaches.

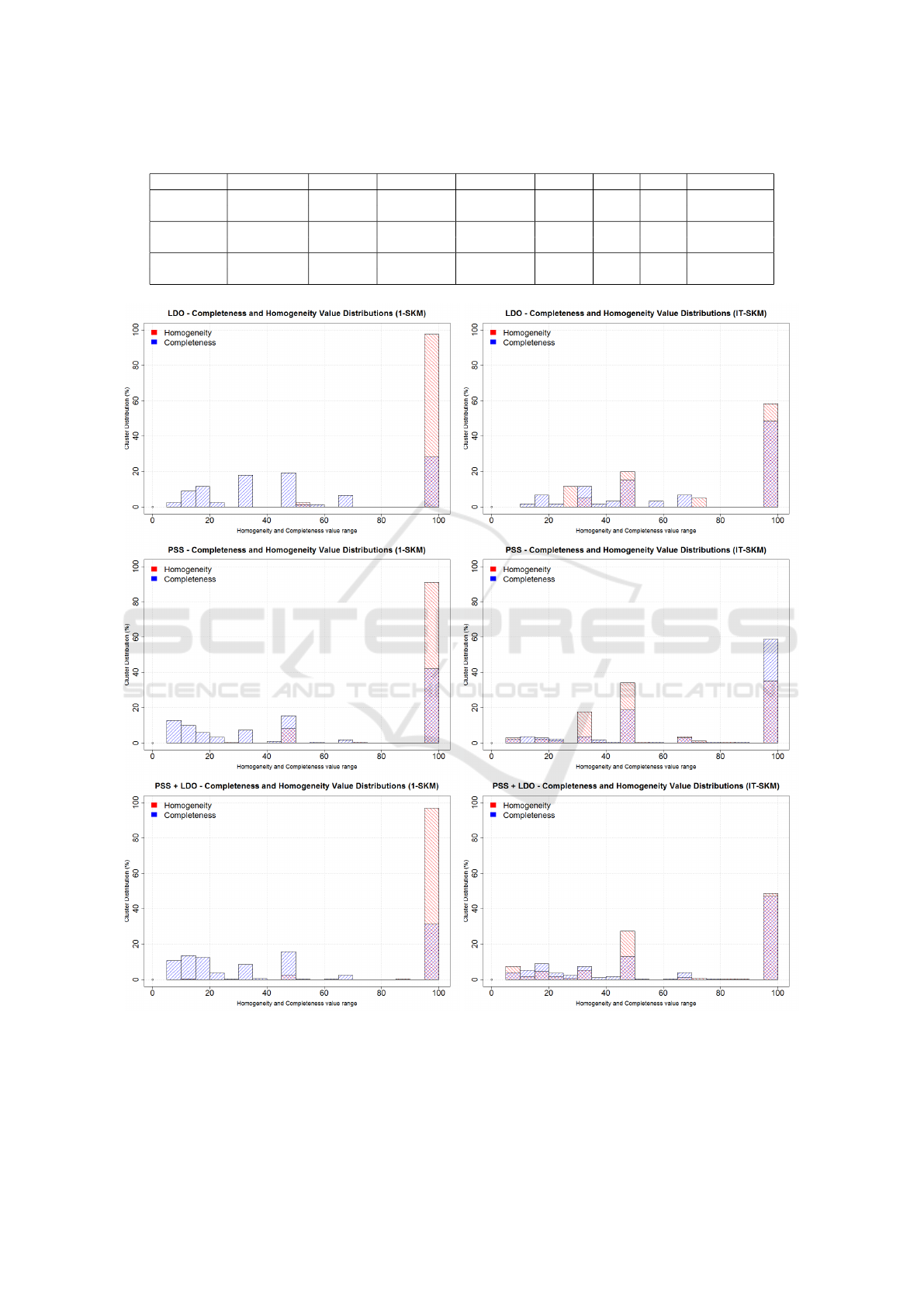
Table 3: Results. The best results are highlighted in bold.

Speciﬁcation Method Mean(CG) Mean(COM) Mean(HOM) #Cluster #Gold #Conf ∆(Complexity)

LDO

Iterative 74.21% 70.00% 76.77% 46

42 104

55.77%

One Iteration 70.85% 53.85% 98.72% 77 25.96%

PSS

Iterative 67.17% 75.88% 63.53% 108

129 259

58.30%

One Iteration 65.36% 58.37% 95.48% 211 18.53%

PSS+LDO

Iterative 66.88% 64.90% 68.16% 167

159 363

53.99%

One Iteration 60.34% 50.00% 98.43% 313 13.77%

Figure 10: Hom and Com value distributions for all experimental assessment.

ACKNOWLEDGEMENTS

This work has been partially supported by the Ital-

ian project Realization of services of the national in-

frastructure for interoperability for Electronic Health

Records, a Convention between the Agency for Digi-

tal Italy and the Italian National Research Council.

REFERENCES

Alicante, A., Corazza, A., Isgr

o, F., and Silvestri, S.

(2016a). Semantic cluster labeling for medical rela-

tions. Innovation in Medicine and Healthcare 2016,

60:183–193.

Alicante, A., Corazza, A., Isgr

o, F., and Silvestri, S.

(2016b). Unsupervised entity and relation extraction

from clinical records in Italian. Computers in Biology

and Medicine, 72:263–275.

Amato, F., Gargiulo, F., Mazzeo, A., Romano, S., and San-

sone, C. (2013). Combining syntactic and semantic

vector space models in the health domain by using a

clustering ensemble. In HEALTHINF 2013 - Proceed-

ings of the International Conference on Health Infor-

matics, pages 382–385.

Berthold, M. R., Cebron, N., Dill, F., Gabriel, T. R.,

otter, T., Meinl, T., Ohl, P., Sieb, C., Thiel, K.,

and Wiswedel, B. (2007). KNIME: The Konstanz In-

formation Miner. In Studies in Classiﬁcation, Data

Analysis, and Knowledge Organization (GfKL 2007).

Springer.

Bosc

a, D., Maldonado, J. A., Moner, D., and Robles, M.

(2015). Automatic generation of computable imple-

mentation guides from clinical information models.

Journal of Biomedical Informatics, 55:143–152.

Boufahja, A., Poiseau, E., Thomazon, G., and Berg

e, A.-G.

(2015). Model-based analysis of hl7 cda r2 confor-

mance and requirements coverage. EJBI, 11(2).

Cao, L., Chua, K. S., Chong, W., Lee, H., and Gu, Q.

(2003). A comparison of pca, kpca and ica for dimen-

sionality reduction in support vector machine. Neuro-

computing, 55(1):321–336.

Cavnar, W. B. and Trenkle, J. M. (1994). N-gram-based text

categorization. Ann Arbor MI, 48113(2):161–175.

Ciampi, M., Esposito, A., Guarasci, R., and Pietro, G. D.

(2016). Towards interoperability of ehr systems: The

case of italy. In Proceedings of the International

Conference on Information and Communication Tech-

nologies for Ageing Well and e-Health - Volume 1:

ICT4AWE,, pages 133–138.

Dhillon, I. S., Guan, Y., and Kogan, J. (2002). Iterative

clustering of high dimensional text data augmented

by local search. In Data Mining, 2002. ICDM 2003.

Proceedings. 2002 IEEE International Conference on,

pages 131–138. IEEE.

Eder, M. (2011). Style-markers in authorship attribution

a cross-language study of the authorial ﬁngerprint.

Studies in Polish Linguistics, 6(1):99–114.

Gargiulo, F., Fontanella, M., and Ciampi, M. (2016). Vali-

dazione di documenti sanitari strutturati in hl7 cda rel.

2.0 con schemi schematron. Technical report, Istituto

di Calcolo e Reti ad Alte Prestazioni (ICAR) del Con-

siglio Nazionale delle Ricerche (CNR).

Halkidi, M. and Vazirgiannis, M. (2001). Clustering valid-

ity assessment: Finding the optimal partitioning of a

data set. In Data Mining, 2001. ICDM 2001, Proceed-

ings IEEE International Conference on, pages 187–

194. IEEE.

Hamilton, J., Darr, T., Fernandes, R., Jones, D., and Mor-

gan, J. (2015). Rule-based constraints for metadata

validation and veriﬁcation in a multi-vendor environ-

ment. In International Telemetering Conference Pro-

ceedings. International Foundation for Telemetering.

Handl, J., Knowles, J., and Kell, D. B. (2005). Computa-

tional cluster validation in post-genomic data analysis.

Bioinformatics, 21(15):3201–3212.

Hornik, K., Feinerer, I., Kober, M., and Buchta, C. (2012).

Spherical k-means clustering. Journal of Statistical

Software, 50(10):1–22.

Jafarpour, B., Abidi, S. R., and Abidi, S. S. R. (2016). Ex-

ploiting semantic web technologies to develop owl-

based clinical practice guideline execution engines.

IEEE Journal of Biomedical and Health Informatics,

20(1):388–398.

Jelliffe, R. (2001). The schematron assertion language 1.5.

Academia Sinica Computing Center.

Karypis, G. (2002). Cluto-a clustering toolkit. Technical

report, DTIC Document.

Kaufman, L. and Rousseeuw, P. J. (2009). Finding groups

in data: an introduction to cluster analysis, volume

344. John Wiley & Sons.

Liu, Y., Li, Z., Xiong, H., Gao, X., and Wu, J. (2010). Un-

derstanding of internal clustering validation measures.

In 2010 IEEE International Conference on Data Min-

ing, pages 911–916. IEEE.

Pollard, K. S. and Van Der Laan, M. J. (2002). A method

to identify signiﬁcant clusters in gene expression data.

In Proceedings of SCI World Multiconference on Sys-

temics, Cybernetics and Informatics, pages 318–325.

Rend

on, E., Abundez, I., Arizmendi, A., and Quiroz, E.

(2011). Internal versus external cluster validation in-

dexes. International Journal of computers and com-

munications, 5(1):27–34.

Rosenberg, A. and Hirschberg, J. (2007). V-measure: A

conditional entropy-based external cluster evaluation

measure. In EMNLP-CoNLL, volume 7, pages 410–

420.

Rousseeuw, P. J. (1987). Silhouettes: a graphical aid to

the interpretation and validation of cluster analysis.

Journal of computational and applied mathematics,

20:53–65.

Weston, S. and Analytics, R. (2014). doParallel: Foreach

parallel adaptor for the parallel package. R package

version 1.0.8.

Wu, J., Xiong, H., and Chen, J. (2009). Adapting the right

measures for k-means clustering. In Proceedings of

the 15th ACM SIGKDD international conference on

Knowledge discovery and data mining, pages 877–

886. ACM.

Zhong, S. (2005). Efﬁcient online spherical K-means clus-

tering. In Proceedings of the IEEE International Joint

Conference on Neural Networks, volume 5, pages

3180–3185.