A CMOS Tracking System Approach for Cell Motility Assays

Cristina Martínez-Gómez

1,2

, Alberto Olmo

1,2

, Gloria Huertas

1,3

, Pablo Pérez

1,2

Andres Maldonado-Jacobi

1,3

and Alberto Yúfera

1,2

Instituto de Microelectrónica de Sevilla, CSIC- Universidad de Sevilla, Av. Americo Vespucio sn, 41092, Sevilla, Spain

Departmento de Tecnología Electrónica, ETSII, Universidad de Sevilla, Av. Reina Mercedes sn, 41010, Sevilla, Spain

Departamento de Electrónica y Electromagnetismo, F. Física, Universidad de Sevilla, Av. Reina Mercedes sn,

41010, Sevilla, Spain

Keywords: ECIS, Bioimpedance, Cell Culture, Cell Location, Cell Motility, Brownian Movement, CMOS.

Abstract: This work proposes a method for studying and monitoring in real-time a single cell on a 2D electrode

matrix, of great interest in cell motility assays and in the characterization of cancer cell metastasis. A CMOS

system proposal for cell location based on occupation maps data generated from Electrical Cell-substrate

Impedance Spectroscopy (ECIS) has been developed. From this cell model, obtained from experimental

assays data, an algorithm based on analysis of the 8 nearest neighbors has been implemented, allowing the

evaluation of the cell center of mass. The path followed by a cell, proposing a Brownian route, has been

simulated with the proposed algorithm. The presented results show the success of the approach, with

accuracy over 95% in the determination of any coordinate (x, y) from the expected center of mass.

1 INTRODUCTION

Cell motility plays an important role in many

biological processes, such as embryogenesis, wound

cicatrisation, immune response, and cancer evolution

(Ananthakrishnan, 2007). Tumour cell motility is

directly related with the processes of cancer

propagation, generating metastasis processes, which

is one of the main raison of death related with this

injury. The assays in-vitro of cell motility represents

a useful tool on the research on mechanism

regulation of the cancer cells migration, also to test

the efficiency of alternative drugs to combat cancer

at cellular level.

The most common methods for studying cell

motility are optics, based on microscopy, and with

fluorescence techniques. However, since these

methods are well established and referenced, they

require fluorescence markers, which can interfere on

correct function of some proteins, modifying the

normal cell evolution (Zhu, 2015). In addition, light

application at high intensity levels required for

exciting fluorescence compounds, can deliver or

generate some toxics elements at cells.

ECIS (Giaever and Keese, 1986) technique

allows cell culture research based on impedance

measurements done based on cell attachment

performance, to obtain cell properties, cell index,

etc. (Grimnes, 2008, Yeh, 2015). ECIS techniques

represent a non-invasive method for real time

monitoring of cells and definition of cell properties:

cell adhesion, motility, drug assays test, cell

growing, etc. (Sinclair 2012, Mondal, 2013).

Experimentally, ECIS technique requires of an

excitation signal, current (or voltage), applied to

obtain a voltage (or current) as response. The bio-

impedance information due to cell attachment to the

electrode is extracted from the signal response (real

and imaginary components, or magnitude and phase

(Mansor, 2015). The main problems to be solved for

extract this information are two. Firstly, bio-

impedance changes due to cell culture measurements

must be performed with accuracy using adequate

techniques and circuits with high performance

(Grimnes, 2008) (frequency programmable

voltage/current generators, amplifiers, demodulators,

etc). Secondly, data obtained for bio-impedance of

electrode-cell system should be decoded to rebuild

and find the information sought, in general, number

of cells in a culture.

The proposed system shown in Figure 1 can be

implemented in CMOS technology. It is composed

of a 2D matrix of electrodes, which act as “small

sensors” of bioimpedance (Yúfera, 2009), integrated

MartÃ nez-GÃ¸smez C., Olmo A., Huertas G., PÃl’rez P., Maldonado-Jacobi A. and YÃžfera A.

A CMOS Tracking System Approach for Cell Motility Assays.

DOI: 10.5220/0006291502290236

In Proceedings of the 10th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2017), pages 229-236

ISBN: 978-989-758-216-5

229

on the same or similar silicon substrate that

employed by the CMOS circuits for measuring and

acquisition (Huertas, 2015). The circuits allow

row/file selection to drive the actual “pixel” under

test, and optimal frequency selection to optimize

sensor sensitivity and voltage applied to electrodes

Figure 1: 2D electrode matrix and circuits for excitation

and acquisition electrical signals for biompedance test of a

cell culture.

The bio-impedance data obtained from cell

cultures can be employed to model the 2D system

proposed in Figure 1. In particular, it can be defined

the fill-factor parameter (ff) as the proportional area

filled by cell to the total area of one electrode. This

parameter oscillated from ff=0, when the electrode is

totally empty of cells (on top), to ff=1, if the

electrode is totally covered of cells. This system

gives us a dimensional matrix of numbers, one for

each pixel, in the range of 0 to 1, representative of a

cell culture status, as illustrated in Figure 2, for a

MCF7 cell line image, with an 8x8 electrode array.

In this way, black and white images can be created

from bio impedance measurements.

Figure 2: Fill-Factor map associated to each electrode, for

a MCF7 cell line image example.

The study proposed in this work focused on

spatial-temporal location of a single cell inside an

electrode matrix, using for that the information

obtained from sensors (pixels), in the form of ff map.

For that, it has been developed a Location Algorithm

implemented in Matlab. The proposed algorithm has

been applied to solve the problem to define the track

followed by a single cell in a culture, determining

the time evolution of its mass centre in a defined

period.

This document is organized as follows. Section 2

describes the proposed system structure and the

modelling of the cell under study. In section 3 it is

detailed how works the algorithm for locating a cell,

while section 4 describes its program

implementation, the simulations performed and the

validation process. Applications for a single cell

location and cell tracking will be shown. Finally,

section 5 will show the results obtained, and some

conclusions of the work, demonstrating the

correctness of the proposed algorithm to be applied

to study the metastasis problem.

2 SYSTEM MODELING

In this section, the proposed system structure to

develop the location algorithm is described. The first

step is addressed to model the cell which will be

used in the case study. There exists a wide variety of

cells with very different shapes and structures. For

the sake of simplicity, a circular cell is chosen in

such a way that it is defined by both the location of

the center of the circle (x, y) as well as the radio (r).

It should be taken into account that the circular cell

modelling is an ideal model and that elliptic

morphologies with variable radio could best

conform to the reality.

Once the shape and the size of the cell have been

specified, the second step is to define the

bidimensional array of electrodes. An array M of

NxN dimension, where each element M(i,j) includes

an electrode of fixed area, being i the position of the

row and j the position of the column. The array M

stores in each element its corresponding ff, generated

by the electrodes. These electrodes of the array are

considered squared and the side l.

To make easier the search algorithm and to

avoid, in advance, complex cases to be analysed,

when the cell is being located, the size of every

element of the array has taken equal or minor to the

cell diameter. The dimension of every element or

pixel (electrode) of the bidimensional array is equal

to the cellular diameter.

A series of concepts required during the

development of the system are defined below:

- Center of mass (cm): The center of mass of a

discrete masses system is a weighted average,

according to the individual mass, of the positions

of all the particles that compose it. It can be

calculated as:

BIODEVICES 2017 - 10th International Conference on Biomedical Electronics and Devices

230







∑









∑

















(1)

M, the total mass of the particle system

m, the mass of the i-th particle





, position vector of the i-th mass with respect to

the assumed reference system.

- Relative error (): Is the quotient obtained by

dividing the absolute error and the exact value,

being the absolute error the difference between

the exact value and the measured value.















100

(2)

3 LOCATION ALGORITHM

The goal of the proposed algorithm is to obtain the

center of mass (cm) of the cell, for a given and fixed

occupation map, based on the ff or occupancy levels

of the different electrode array elements. With this

objective, an iterative algorithm has been developed

which assigns weights to each element of array

according to whether the 8 adjacent elements contain

occupancy values. In the algorithm, several elements

are defined:

 The occupation array M above defined,

which includes the fill factor values. It

represents the data entry and is obtained

previously as a result of measurements made

on the system.

 An empty subdivision array M

of 2Nx2N

dimensions, is also defined. It represents the

subdivision of the occupation array, where

each element M (i, j) is split into four. This

subdivision allows a more precise calculation

of which areas of each element are occupied

by the cell. In each iteration of the algorithm,

the M

array is subdivided into 4 sub-

elements and so on until an optimal result is

reached. The greater the number of divisions,

the more accurate the calculated center of

mass, but also the longer the required

runtime. This array stores the weights that

indicate which elements of it are parts of the

area of the cell under study (see Figure 3).

Figure 3: Array M of 3x3 dimension (blue), array M

6x6 dimension (green) and the subdivision of M

12x12

(red). The occupation map will have non-null values in the

two first elements of the two first rows. The subdivision

allows to calculate both which elements are part of the cell

and which are not and as a consequence obtaining its area

more precisely.

 Taking the modeling references, the cell can

occupy a maximum of four elements of the

array M, i.e. there will be at most four non-

zero fill factors in the array. In this way, an

index vector I is defined that contains the

positions (i.j) of these four possible values of

 Array  which stores the central points of

the greater weight elements of M

adjudicated

by the algorithm described later.

The algorithm can be divided into three

execution steps:

Step 1: Initialization: The occupation map

elements of M have input values given by the filling

factors resulting from the experiments. Firstly, an

initialization process is performed, according to

which the occupation map elements M are

subdivided into 4 sub-elements and the weights are

assigned, initializing the matrix Ms. These initial

values are selected according to the algorithm

proposed.

Step 2: Iteration: Secondly, the iterative process is

developed where the subdivision array, which

contains the weights, is subdivided into 4 sub-

elements and so on, at each iteration. At each level

of the iteration process, the current area resulting

from the algorithm is calculated. The process ends

when the areas obtained from the selected sub-

elements, for a determined level of iteration, are the

closest to the occupancy values obtained by the

sensors (ff).

A CMOS Tracking System Approach for Cell Motility Assays

231

Step 3: Calculation of the Mass Center: The

center of mass is calculated according to the results

obtained. From the resulting center of mass, the ff

corresponding to this point, called in the algorithm

, are calculated and compared with the real ff

the given occupation map. With this step, the system

is feedback in such a way that the mass center is

recalculated according to the difference obtained

between the calculated and actual ff, causing a

translation of the center of mass. This recalculation

process reduces the error in most of the cases.

The actions involved in each of the algorithm

steps are described below in a more detailed way:

Step 1.- Initialization

This step begins by traversing the M array,

which initially contains the values of the filling

factors resulting from biomedical experimentation.

The goal is to assign values to the subdivision array

Starting from each element M(i,j) with a non-

zero value and smaller than 0.75, weights are

assigned to the four sub-elements of the array M

which correspond to this element M(i,j). The

assigned weights are determinate by the values of

the 8 adjacent elements of M(i,j). In particular, the

weights will depend on:

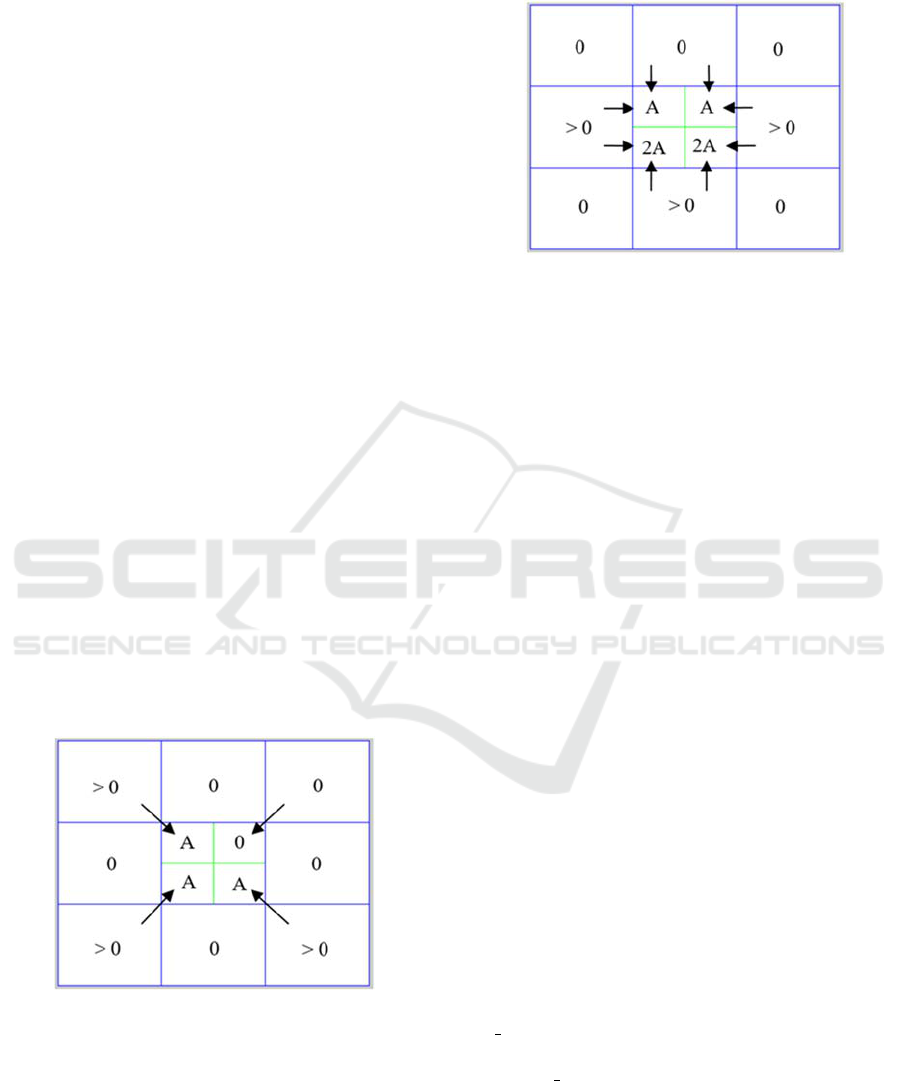
 If the neighbor of the diagonal contains a

non-zero value, then a constant A will be

added to the element M

adjacent to the

diagonal (see Figure 4).

Figure 4: It despicts the diagonal adjacency of the central

element. For each adjacent neighbor of the diagonal of M

(blue), a weight A is assigned to the corresponding

element of the array M

(green).

 If the remaining neighbors, which do not

conform the diagonal, contain a non-zero

value, then a constant A will be added to the

two elements of M

adjacent to the sides (see

Figure 5).

Figure 5: For each 4-adjacent neighbor of the array M

(blue), a constant value A is assigned to the two

corresponding elements of the array M

(green).

With this in mind, an element of M

will have at

most a weight of 3A.

On the other hand, if the value is higher than

0.75, the maximum weight, 3A, is straightaway

assigned to the 4 sub-elements (M

(2i-1,2j-1), M

(2i-

1,2j), M

(2i,2j-1), M

(2i,2j.

The array M is again examined and the following

conditions are established:

 If 0



,

)

0.25, only the two larger

weight sub-elements of the four possible sub-

elements that would form M(i,j) are stored in

the array M

 If 0.25  



,

)

0.50, the three larger

weight sub-elements are stored in.

 If 



,

)

0.50, the four sub-elements of

are stored.

Step 2.- Iterative process

In this step the iterative process starts in order to

increase the resolution to obtain the area that most

closely matches the real area of the cell under study.

In each iteration the 



array increases its dimension

as 2

numIter+1

N, being numIter, the iteration number in

which the process is and N the dimension of the M

array.

As in step 1, the M

array is examined and

weights are assigned to the new subdivision array,

s_iter

, according to the values of the adjacent

elements of M

. Calculating the weights of the new

array M

s_iter

elements, those that contain the

maximum weight with the same criteria established

in step 1 are selected. With these elements the

approached occupation area is calculated. As in each

iteration the subdivision increases, the area that

represents each element decreases and thus, the

BIODEVICES 2017 - 10th International Conference on Biomedical Electronics and Devices

232

percentage of occupation area of each element will

be given by:



(3)

At this point, the proposed by the algorithm

occupation area is evaluated, and compared to the

initial area, to which it must converge. If the

estimated by the algorithm area is equal to the

corresponding ff or approaches to a set range within

error margins, the iterative process is terminated.

Otherwise, step 2 is repeated to a maximum of 8

iterations. Once the iterative process is completed,

the geometric centers of the higher-weight elements

of the M

s_iter

array are stored in the array P. And in

turn, the mass center is calculated for each element

of index I, this calculation is based on the points P

contained within such elements. As discussed, there

will be a maximum of four ff values and therefore

four mass centers, calculated as follows:

















,)

,,







,)

,,

(4)

where k defines the k-th value of the I vector and M

defines the total mass of the system, in our case, is

the sum of the ff whose value is always unitary.

Step 3.- Mass center of the cell calculation

The iterative process results in the four mass

centers related to each ff. With these points and

following the above equation, it is calculated the

mass center of the whole set corresponding to the

mass center of the cell.



















(5)

To verify that the result is correct, our system is

feedback. The percentage of area occupied by the

obtained cell (ff

) is calculated, and it is compared

with the original ff

. The fill factor and the mass

center of the cell are recalculated:





_





















)









(6)

4 SOFTWARE

IMPLEMENTATION

The algorithm has been implemented in the

mathematical software tool Matlab. We divide this

section in two sections where different simulation

studies are carried out. First, in sub-section 4.1, an

example of the cellular localization based on the

localization algorithm is performed. Secondly, the

study and simulation of the cell trajectory described

in subsection 4.2 is implemented in Matlab.

4.1 Cellular Localization

In this section, an example of the operation and

results obtained with an array of 6x6 electrodes and

a 10μm diameter cell is shown. To properly simulate

the operation of cell cultures, the generation of the

position that the cell occupies on the surface of the

array is done in a random way. Once the mass center

is defined, the occupation map to be used by the

algorithm is calculated. Figure 6 shows an example

of the map obtained from a cell with center cm

real

(13µm, 48µm).

Figure 6: Occupation map of a cell with center in the

coordinates (x,y) = (13µm,48µm).

After five cycles of iteration, a set of points is

obtained, from which the center of the cell will be

calculated (Figure 7). Specifically two possible

centers are obtained, corresponding to the execution

of the algorithm without feedback (cm

cell

(12.63μm,

47.99μm)) and with feedback (cm

cell_fb

(12.87μm,

47.96μm)). The original cell is compared with the

two generated results and the relative error is

calculated with equation (7).















100

(7)

For the Y axis case both results are

approximated with an error lower than 0.05%.

However, for the X axis the error is reduced using

feedback (from 2.8% to a 1.0%). In Figure 8 it is

shown how calculated cells match real ones.

4.2 Cell Trajectory: Brownian Motion

The ECIS technique opens the possibility of

monitoring a cell culture in real time. In addition to

the estimation of the cellular location from a map of

A CMOS Tracking System Approach for Cell Motility Assays

233

Figure 7: Resulting set of points for the elements with the

higher weight, corresponding to the elements of the

occupation map. In the selected part it is shown the real

centre cm

real

(13µm,48µm) (blue circle), the center

obtained with the algorithm cm

cell

(12.63µm,47.99µm)

(green line) and the center obtained with feedback cm

cell_fb

(12.87µm,47.96µm) (red line).

Figure 8: Comparison of the original cell (blue line) with

the calculated cell without feedback (green line) and the

calculated cell with feedback (red line).

occupation obtained with this technique, it is

interesting to have tools to analyze the temporal

evolution of the cell. In this way, the trajectories

described by them could be analyzed.

The mathematical modeling of cell movement is

of great relevance in the fields of biology and

medicine. Movement models can take many different

forms, but the most commonly used are based on the

extensions of simple random motion processes.

Assuming that motion is allowed in any direction,

this process is essentially known as Brownian motion

(Wu 2014, Qu, 2010). The physical phenomenon of

Brownian motion is based on the random motion of

particles suspended in a fluid as a result of their

collision with rapidly moving atoms or molecules.

To generate a two dimensional random motion,

two independent random paths are used, one for each

coordinate in time using different random seeds.

Instead of using random steps from a Gaussian

distribution, an approximation to Brownian motion

can be constructed by taking random measurements

of simple probability functions, such as a delta

function or a constant probability density function

(Codling 2018).

A Brownian motion model is implemented in

Matlab, indicating the starting point from which the

cell will start and the number of time samples desired

to obtain the points of the trajectory. Random angles

are generated for each moment and each mass center

is produced following a stochastic process:









)







1

)

cos)









)







1

)

sin)

(8)

In addition, the generation of the trajectory is

limited according to the size of the culture matrix.

Figure 9 and 10 show a possible trajectory

generated by the cell under study. After obtaining the

occupation map for each time instant, it is simulated

the trajectory followed using the localization

algorithm, previously implemented. To be specific, it

is considered a cell with an average velocity of 0.1

μm/min. The example simulates the calculation of

sixteen occupation maps for three hours.

As we checked in the previous point, most of the

points obtained with feedback are closer to the real

points. Table 1 shows for each point the errors

committed without feedback and with feedback, the

number of iterations made and the time used by the

system. The measurements have been obtained using

an Intel® Core ™ i7-4501U processor at 2.60GHz

and 11.9GB of RAM.

BIODEVICES 2017 - 10th International Conference on Biomedical Electronics and Devices

234

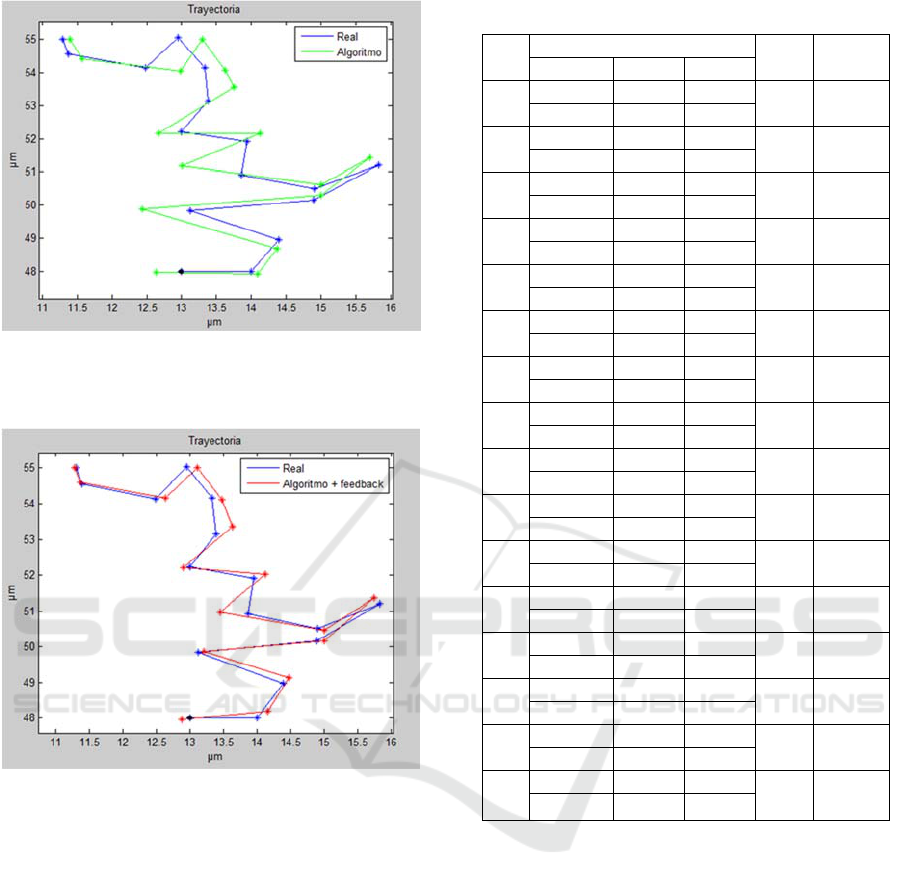
Figure 9: Real trajectory of a cell with radius 10µm (blue)

and trajectory calculated with the localization algorithm

(green).

Figure 10: Real trajectory of a cell with radius 10µm

(blue) and trajectory calculated with the localization

algorithm with feedback (red).

With these results we can verify that in most

cases the error decreases applying the feedback

process, being position 2 and 3 the only points where

the error is not improved. Even in these cases, errors

less than 3% are obtained. The majority of iterations

required to obtain the position is two cycles, reducing

the overall execution time of the trajectory. For

iterations less than 8 cycles the time spent is less than

60 seconds.

To confirm that the system developed in this

work is capable of robustly and accurately estimating

the position of the cell from the occupation maps, an

empirical study with more samples has been carried

out. These tests consist of the random generation a

cell track, with fifty points, each one with their

corresponding maps of occupation. The position

estimation of each of the cells generated applying the

Table 1: Error percentage for the 16 positions.

Pos

Relative error (

)

N_ite

CPU(s)

Axis x Axis y

Alg 2.85% 0.02%

56.70

Alg + fb 1.00% 0.08%

Alg 0.67% 0.14%

55.02

Alg + fb 1.12% 0.39%

Alg 0.12% 0,57%

70.50

Alg + fb 0.53% 0.33%

Alg 5.21% 0.06%

54.6

Alg + fb 0.64% 0.01%

Alg 0.74% 0.28%

54.01

Alg + fb 0.74% 0.01%

Alg 0.81% 0.46%

47.69

Alg + fb 0.49% 0.32%

Alg 0.67% 0.22%

47.90

Alg + fb 0.67% 0.06%

Alg 6.15% 0.51%

49.03

Alg + fb 2.95% 0.11%

Alg 1.34% 0.49%

48.21

Alg + fb 1.30% 0.24%

Alg 2.51% 0.14%

57.25

Alg + fb 0.70% 0.02%

Alg 2.76% 0.79%

48.14

Alg + fb 1.90% 0.41%

Alg 2.19% 0.16%

48.01

Alg + fb 1.07% 0.06%

Alg 2.68% 0.05%

51.4

Alg + fb 1.15% 0.05%

Alg 4.04% 0.15%

49.27

Alg + fb 1.18% 0.05%

Alg 1.72% 0.29%

47.90

Alg + fb 0.16% 0.07%

Alg 0.90% 0%

47.68

Alg + fb 0.24% 0%

algorithm and finally, the definition of the position of

each point generated applying the algorithm and its

feedback.

The highest errors obtained were located when

the occupation map collects most of the area in a

single element, but with connected elements with a

very low value. In contrast, when the cell is more

evenly divided into several elements, the error is very

small. And in the event that the cell is entirely in one

element or divided exactly in two or four elements,

the error obtained is null. Table 2 shows the

maximum and minimum error percentages obtained,

and an estimation of the mean error value.

A CMOS Tracking System Approach for Cell Motility Assays

235

Table 2: Experimental error percentages.

Relative error () Max. Min. Mean

Algorithm Eje x 8.35% 0% 2.19%

Eje y 2.69% 0 % 0.49%

Algorithm +

Feedback

Eje x 4.98% 0 % 0.95%

Eje y 1.05% 0 % 0.19 %

With this experimental study, it is concluded that the

maximum error that the system can have is below

5% for the X axis and below 1% for the Y axis.

5 CONCLUSIONS AND FUTURE

WORK

A cellular localization system has been developed

based on the occupation maps generated by electrical

impedance spectroscopy. The localization system has

been able to generate the approximated cell position

in a culture, with a maximum relative error of 4.98%,

and a typical error of 1%, when it is provided

feedback to the algorithm. Although sometimes the

feedback does not reduce the error, in most cases

improves it, decreasing the error by half. The

proposed tracking algorithm enables CMOS

technologies for Lab-on-a-Chip systems for cell

motility assays, particularly useful in cancer research.

In order to expand the study, possible cellular

trajectories have been randomly generated following

the modeling of the Brownian system. Starting from

the trajectory it will be possible to perform studies on

the cellular behavior in different situations of interest,

as can be the effects of drugs in the cellular activity.

From the results obtained in this study, new lines

of research are opened that can be of great scientific

interest. Firstly, the cellular morphology is very

uneven and irregular, so the modeling of the cell in a

circular form does not resemble the reality, and

supposes an excessively simple model. A possible

improvement of the system would be to use modeling

of cells with more common form, for example, as an

ellipse. Tests with real cases can also be carried out,

using electrode arrays and a cell line of interest, to

characterize its trajectory and study its behavior.

Furthermore, variable side electrodes that do not

occupy the entire pixel could be used, and study, this

way, how to solve dead zones where no information

is collected and can be occupied by the cells.

ACKNOWLEDGEMENTS

This work was supported in part by the Spanish

founded Project: TEC2013-46242-C3-1-P: Integrated

Microsystem for Cell Culture Assays, co-financed

with FEDER.

REFERENCES

Ananthakrishnan, R., Ehrlicher, A., 2007. The Forces

Behind Cell Movement. Int J Biol Sci, vol. 3, n

. 5, pp.

303–317.

Zhu, Z., Frey O., et al., 2015. Time-lapse electrical

impedance spectroscopy for monitoring the cell cycle

of single immobilized S. pombe cells. Scientific

Reports, vol. 5, p. 17180.

Giaever, I. and Keese, C. R., 1991. Micromotion of

mammalian cells measured electrically, Proc. Nail.

Acad. Sci. USA. Cell Biology, vol. 88, pp: 7896-7900.

Grimnes, S., Martinsen, O., 2008. Bio-impedance and

Bioelectricity Basics, Academic Press, Elsevier, 2

edition.

Yeh. C. F. et al., 2015. Towards an Endpoint Cell Motility

Assay by a Microfluidic Platform. IEEE Transactions

on NanoBioscience, vol. 14, n

. 8, pp. 835–840.

Sinclair, A. J. et. al, 2012. Bioimpedance analysis for the

characterization of breast cancer cells in suspension.

IEEE Trans Biomed Eng, vol. 59, n

. 8, pp. 2321–

2329.

Mondal, D., RoyChaudhuri, C., 2013. Extended electrical

model for impedance characterization of cultured

HeLa cells in non-confluent state using ECIS

electrodes. IEEE Trans Nanobioscience, vol. 12, n

. 3,

pp. 239–246.

Mansor, A. F. M., et al., 2015. Cytotoxicity studies of lung

cancer cells using impedance biosensor. In 2015

International Conference on Smart Sensors and

Application (ICSSA), pp. 1–6.

Huertas, G., Maldonado, A., Yúfera A., et al., 2015. The

Bio-Oscillator: A Circuit for Cell-Culture Assays.

IEEE Transactions on Circuits and Systems II, vol. 62,

. 2, pp. 164–168.

Yúfera, A., Rueda, A, 2009. A CMOS bio-impedance

measurement system. In 12

International Symposium

on Design and Diagnostics of Electronic Circuits

Systems, pp. 252–257.

Yúfera, A., Rueda, A., 2010. Design of a CMOS closed-

loop system with applications to bioimpedance

measurements. Microelectronics J. vol. 41, pp.231-

239.

Wu, P. H., et al, 2014. Three-dimensional cell

migrationdoes not follow a random walk. Proc

NatlAcad Sci U S A, vol. 111, n

. 11, pp. 3949–3954.

Codling E. A. et al., 2008. Random walk models in

biology. J R Soc Interface, vol. 5, n

. 25, pp. 813–834.

Qu B., Addison P. S., 2010. Modelling Flow Trajectories

Using Fractional Brownian Motion. In 2010

International Workshop on Chaos-Fractals Theories

and Applications (IWCFTA), pp. 420–424.

BIODEVICES 2017 - 10th International Conference on Biomedical Electronics and Devices

236