Derivation of Real Driving Emission Cycles based on Real-world

Driving Data

Using Markov Models and Threshold Accepting

Roman Liessner, Robert Fechert and Bernard Bäker

Dresden Institute of Automobile Engineering, TU Dresden, George-Bähr-Straße 1c, 01069 Dresden, Germany

Keywords:

Driving Cycle, Real Driving Emissions, RDE, Markov Model, Threshold Accepting.

Abstract:

The European Union has decided to bring the Real Driving Emissions (RDE) law into force in 2016. From this

point onward, the air pollutants a vehicle emits under real driving conditions will be measured by means of a

so-called Portable Emissions Measurement System (PEMS) and then used as the basis for licensing. Compared

to the emission values presently determined in the New European Driving Cycle (NEDC), a signiﬁcant rise can

be expected. This change is on the one hand caused by a substantially more dynamic driving style prescribed

by RDE regulations, and on the other hand by considerably larger variations of ambient conditions. A trend

of development resulting from this conversion is the creation of test cycles conforming to RDE regulations,

which enable vehicle development to adhere to the new licensing regulations. The validity of a RDE drive is

gradually veriﬁed based on multiple criteria before respective emission values are determined at the end of

the process. The contribution at hand presents a new approach for generating RDE substitute cycles. At ﬁrst,

the criterion of driving dynamics will be focussed upon. To realize this, combinatorics of a large set of real

driving data will be used to generate substitute cycles, which will exhibit driving dynamics as high as possible.

This speciﬁcation achieves universal, vehicle independent limitation cycles featuring high emission levels. By

using the described limitation cycles, a ﬁrst vehicle examination concerning the fulﬁlment of RDE regulations

is made possible.

1 INTRODUCTION

Because of the ongoing emission discrepancies be-

tween homologation measurement and real driving

measurement, the European Union has decided to

bring Real Driving Emission (RDE) tests for type test-

ing into force in January of 2016. The mentioned dif-

ference in measured emission values occurs because

the New European Driving Cycle (NEDC), which is

used for certiﬁcation in the EU, is barely representa-

tive for loading requirements when considering real

vehicle drives. In addition to this, it is possible to cre-

ate a speciﬁc calibration for a prescribed cycle’s al-

ready known velocity curve also known as cycle beat-

ing. Since the regulations specify a more dynamic

driving style and allow for signiﬁcantly more vari-

able ambient conditions compared to the NEDC, an

increase in emission is to be expected (Gerstenberg

et al., 2016). The requirements for a valid RDE drive

are extensive as time, velocity and distance standards

are an issue (see Table 1). Furthermore, driving dy-

namics and cumulative difference in height are ver-

iﬁed. In the event that these standards have been

met, a RDE measuring drive can initially be con-

sidered as formally valid, after which the emissions

calculation can be performed based on the currently

speciﬁed evaluation methods using the tools Emroad

or Clear. The applied evaluation methods normalise

the RDE measurement results during the post process

and make them comparable to results from World-

wide Harmonized Light-Duty Vehicles Test Cycle

(WLTC), which is intended to replace the NEDC as

a homologation cycle according to RDE regulations

(Maschmeyer et al., 2016).

The speciﬁed changes present a great challenge

for the development of vehicles. There will be no

more known and reproducible static cycle elements

and transients. A vehicle can no longer be applied to

single velocity proﬁles, as it was possible when work-

ing with a strictly prescribed cycle. Instead, RDE

conforming substitute cycles must be found. To en-

sure the adherence to RDE limits of respective pol-

lutants from a manufacturer perspective, drive cycles

will have to be generated and analysed during the de-

188

Liessner, R., Fechert, R. and Bäker, B.

Derivation of Real Driving Emission Cycles based on Real-world Driving Data - Using Markov Models and Threshold Accepting.

DOI: 10.5220/0006291701880195

In Proceedings of the 3rd International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS 2017), pages 188-195

ISBN: 978-989-758-242-4

velopment process.

In case of gasoline engines it can be assumed

that the pursued worst case cycles force the engine

into non-stoichiometric combustion conditions (scav-

enging, enriching), since especially these operating

points cause increased emission (Fraidl et al., 2016).

But in accordance with the gear transmission ratio, the

mentioned range is of no importance regarding cycles

such as the NEDC. In this light, one could question

which RDE challenges can be depicted in one single

substitute cycle, since multiple combinations of oper-

ating states, which would potentially increase emis-

sions, are imaginable.

During the development phase, it has to be en-

sured that the vehicle passes the real driving test under

any circumstances. For that reason worst case cycles

are necessary, because ensuing changes after Start of

Production (SOP) can lead to immense costs for the

manufacturer.

There already exist some approaches to meet

the mentioned challenges. Most of them like

Maschmeyer or Gerstenberg presented different ap-

proaches to concatenate the RDE requirements with

measurements on test benches and describe the cor-

responding tasks (Maschmeyer et al., 2016), (Ger-

stenberg et al., 2016). Steinbach illustrated a way

using model-based calibrations for which emission

models were utilised to adapt the calibration of con-

trol unit functions to RDE standards (Steinbach et al.,

2016). He validated the used simulation tool chain

with virtual calibration steps and showed the opportu-

nity to do different calibration changes in short time

and without having the physical hardware.

Most of the approaches didn’t describe precise

power demands for their tests. But to guarantee to

meet the RDE requirements driving cycles for the

mentioned test scenarios are necessary. This contri-

bution to the topic at hand examines an approach in-

tended to generate RDE worst case cycles for the test

measurement. For this purpose, cycles maximizing

the criteria of driving dynamics va

pos

from (European

Commission, 2016) will be developed. For the real-

ization of this project, real driving data has been used.

The data will be reassembled by means of combina-

torics to create cycles featuring the maximum driving

dynamics (va

pos

limitation value), and yet also depict-

ing realistic velocity proﬁles.

2 METHOD

As has been illustrated before, one of the central prob-

lems regarding RDE is ﬁnding a worst-case cycle,

which will give the manufacturer the guarantee that

the respective vehicle will meet RDE standards un-

der any circumstance. However, a cycle such as this

can only be generated by using a complex algorithm

because of different criteria.

Real measured drives of an arbitrary number of

drivers using the type of vehicle which has to be cali-

brated serve as the basis for the generation of replace-

ment cycles. The data volume should be chosen as

large as possible.

2.1 Splitting into Subproblems

The authors’ idea is based on breaking the cycle gen-

eration down into separate problems. The ﬂow chart

in Figure 1 illustrates the different steps. At ﬁrst,

only cycles conforming to general boundary condi-

tions (see Table 1) will be created, which will feature

the maximisation of vehicle dynamics in compliance

with the va

pos

_95 criterion. The focus in the paper

at hand will be the combinatorics approach employed

for this method of cycle generation.

speed curve

altitude profile

RDE

worst case

vehicle data

drive train

calibration

A B

D E

Figure 1: Subproblems for generating RDE replacement cy-

cles.

During the subsequent generation phase, an ele-

vation proﬁle will be added to the already generated

driving cycles. Afterwards, the cycles will be adapted

to the vehicle’s performance capability. It can be

assumed that the vehicle construction and the used

power train inﬂuence the searched worst-case cycle

immensely. During the last step, the cycles will be

modiﬁed according to critical emission scenarios re-

garding the respective engine.

In the following, the single steps for generating

real drive emission cycles will be introduced. The

ﬂow chart in Figure 2 illustrates the different steps.

2.2 Stochastic Modelling

During the method’s ﬁrst phase, the data basis is mod-

elled. In this context, Markov models, which are

stochastic process models describing the states and

transitions of unknown systems, have proved to be es-

pecially suitable. The Markov model is based on sim-

Derivation of Real Driving Emission Cycles based on Real-world Driving Data - Using Markov Models and Threshold Accepting

189

Generation of the complex data set

Data basis

Stochastic modelling

Separation in microtrips

Combinatorics

RDE speed curve

Figure 2: Schedule for generating replacement cycles.

pliﬁcation by means of a so-called Markov assump-

tion (memorylessness). Due to this, a system’s sub-

sequent state is only dependent on the current state,

which causes preceding states to have no effect at all

on the modiﬁcation of states. This correlation is ex-

pressed in equation 1. x

represents the current state

and x

n+1

represents the subsequent one. Preceding

states as well as their impact (in equation x

) are

neglected (Ließner et al., 2017). For further infor-

mation on the functionality of Markov models, see

(Stroock, 2013).

P(X

n+1

= x

n+1

= x

,..., X

= x

) =

P(X

n+1

= x

n+1

= x

)

(1)

Where,

P() = probability function,

= Markov variable,

= current state,

n+1

= Markov variable,

n+1

= following state

A state x

in this proposed application contains a

discrete value of velocity and acceleration as seen in

equation 2.

(

(2)

Where,

= state,

= velocity value,

= acceleration value

In order to transfer the data basis to the Markov

model, it is sufﬁcient to perform an elementary iter-

ative transfer of the respective state transitions from

one point of time to the next. Further processing is

based on the assumption that the saved state transi-

tions in the Markov model hold all relevant informa-

tion concerning this relation. This is because, after all,

the Markovmodel contains all recorded drive data in a

condensed and anonymized form. However, choosing

and combining appropriate elements of the complex

data set in such a way as to allow the derivationof rep-

resentative replacement cycles with similar properties

regarding the consumption is the actual challenge.

2.3 Generation Complex Data Set

The following strategy is suitable for deriving re-

cently mixed velocity progressions from the Markov

model. Based on a velocity and acceleration combi-

nation which has been set initially, a generation can

be performed by means of a query concerning the

saved state transition according to the Markov model.

Using a weighted draw in proportion to probabilities,

the subsequent velocity and acceleration combination

is chosen. The described procedure is repeated un-

til the desired scope of the complex data set has been

attained. In this manner, an arbitrarily large data set

is generated which contains recently mixed stochas-

tically weighted progressions. But afterwards, iden-

tifying the elements in the complex data set which

ultimately best represent RDE worst case scenarios

during the substitute cycle is very challenging. To

put this into practice, it is expedient to separate the

complex data set into smaller units, which can then

be processed separately.

2.4 Separation Into Microtrips

For disassembling the complex date set, a fragmenta-

tion into so-called ’microtrips’ has proven to be use-

ful. A microtrip is deﬁned as a drive starting at one

vehicle stop and ﬁnishing at the next (Fotouhi and

Montazeri-Gh, 2013). Figure 3 depicts a microtrip

segmentation into eight sections by using the WLTC

as an example. When such a segmentation is applied

to the complex data set, a very high number of mi-

crotrips is created. Finally, the major difﬁculty can

be seen in choosing and combining appropriate parts.

Approaches such as Lee pursue the aim of creating

vehicle-speciﬁc substitute cycles by analyzing the en-

ergy level at the periphery of the wheels and then

producing a selection of statistical key ﬁgures (Lee

and Filipi, 2010). In contrast to this, this contribu-

tion aims for a vehicle-independent combinatorics at

ﬁrst. This combinatorics would contain properties oc-

curring during the substitute cycle which are relevant

for driving dynamics: distribution (velocity, accelera-

tion, velocity multiplied by acceleration and stop) and

VEHITS 2017 - 3rd International Conference on Vehicle Technology and Intelligent Transport Systems

190

0 200 400 600 800 1000 1200 1400 1600

time in s

100

150

velocity in km/h

1 2 3 4 5 6 7 8

Figure 3: Separation of a drive in microtrips at the example of the WLTC.

the relative positive acceleration (RPA) index. Single

microtrips have to be combined into one single sub-

stitute cycle in order to have high dynamic RDE con-

formable cycle as closely as possible. To achieve this,

the following procedure can be employed.

2.5 Combinatorics

The main challenge in generating RDE substitute cy-

cles is combining the previously created microtrips in

such a manner as to form a substitute cycle, which

will then conform to the relevant RDE criteria.

Theoretically, it would be possible to try out all

variants (brute force method). Yet it becomes clear

that in a complex data set with K microtrips and for

the replacement cycle E necessary ones, K

combi-

nations emerge. For example, K = 1000 available

and ordinary E = 20 for the RDE replacement cy-

cle necessary microtrips as well as the assumption

that an evaluation takes 0.1 seconds, a duration of

2.7· 10

hours for the generation of the replacement

cycle would be set. Thus a brute force approach for

combination is not suitable (Ließner et al., 2017).

The RDE combinatorics outlined here is based on

the combinatorics for generating average substitute

cycles, as presented in (Ließner et al., 2017). In the

mentioned paper, a method is presented which en-

ables the combination of microtrips to form a sub-

stitute cycle by employing a so-called Threshold Ac-

cepting combinatorics algorithm. This procedure en-

sures that vehicle dynamic will be maximized.

Using an average substitute cycle as a basis for

RDE combinatorics has multiple advantages. RDE

certiﬁcation has the fundamental aim of deﬁning

boundary conditionswhich conform as closely as pos-

sible to real driving situations. Thus, it is made pos-

sible that an average cycle, which must feature the

respective duration and driving mode share, nearly or

completely meets RDE standards from the beginning

on. The following methodology uses the average sub-

stitute cycle and modiﬁes included shares until all cri-

teria are met. The modiﬁcation is performed in ac-

cordance with the Threshold Accepting Method ﬁrst

introduced in (Ließner et al., 2017). This is an algo-

rithm presented by Prof. Dueck to solve combinato-

rial problems (Dueck and Scheuer, 1990).

Besides meeting RDE standards, one additional

aim is to maximize vehicle dynamics. According

to RDE guidelines, the vehicle dynamics limit is as-

sessed by determining va

pos

_95 values for the respec-

tive area (urban, rural, motorway). These values rep-

resent, in dependence of average velocities, threshold

values ¯v

which must not be exceeded. The following

equation illustrates the exemplary conditions for the

urban area.

(v· a

pos

)

urban,ref

_95 ≤ (0.136· ¯v

urban

+ 14.44) (3)

Where,

(v· a

pos

)

urban,ref

_95 = 95th percentile va

pos

value,

¯v

urban

= average urban speed

The respective intermediate steps and the algo-

rithm for calculating va

pos

_95 can be found in (Eu-

ropean Commission, 2016). Hence, minimizing the

difference between the actual va

pos

_95 values and re-

spective set values can be seen as a possible approach

for the maximization of vehicle dynamics. The fol-

lowing function is a measure of quality for optimising

pos

_95 values:

J =

∑

·((v·a

pos

)

k,ref

_95−(v·a

pos

)

k,cur

_95)) (4)

Where,

k = {urban, rural, motorway},

(v· a

pos

)

k,ref

_95 = set value of 95th percentile,

(v· a

pos

)

k,cur

_95 = actual value of 95th percentile,

= number of elements with a

> 0.1m/s

Derivation of Real Driving Emission Cycles based on Real-world Driving Data - Using Markov Models and Threshold Accepting

191

The sampling of all courses, which have been used

in the context of RDE, is generally 1 Hz. Since the

route that is to be completed has the same length

of at least 16 km in all speed ranges, it can be de-

rived that the urban area exhibits the largest number

of measured values and hence, also the largest num-

ber of va

pos

_95 values. This consideration helps to

determine the weighting (equation 4). In this man-

ner, it can be ensured that the optimization preferably

covers the urban speed range. The weighting corre-

sponds logically to emission layers as well, since fre-

quently occurring partial loads, engine operation in

the scavenging range and unfavourable regeneration

conditions cause increased emissions in urban areas.

The va

pos

_95 value is only one scalar that characterise

the vehicle dynamicof the whole RDE cycle. It can be

used to check the validity of a RDE cycle. If it is the

aim to get the maximum possible vehicle dynamic in

a cycle all the sampling points around va

pos

_95 need

a high dynamic too. In the RDE context it means

that all sampling points under the va

pos

_95 bound-

ary, which is equivalent to 95 % of the elements with

> 0.1 in the respective area, should attain va

pos

val-

ues as close as possible to the va

pos

_95 value. The

other sampling points (5 %) should achieve the maxi-

mum possible dynamic of the respective vehicle.

Algorithm 1: RDE replacement cycle generation.

1: Load average cycle

2: Choose initial THRESHOLD T > 0

3: As long as improvement occurs

4: Modify driving cycle slightly (change one microtrip)

5: Calc. ∆E := quality(old conf.)-quality(new conf.)

6: If ∆E > T & RDE-criteria are satisﬁed

7: THEN old conf. := new conf.

8: If for too many iterations no improvement

9: THEN lower THRESHOLD T

10: If no further improvements are made

11: THEN stop

12: End

calc. = calculate, conﬁg. = conﬁguration

As can be understood through pseudocode above,

the combination process begins with an average sub-

stitute cycle featuring a length of 6300 seconds ±14

% (line 1) which met the RDE trip duration between

90 and 120 minutes. Additionally, an initial thresh-

old value T > 0 controlling the optimization process

has been set for the optimization (line 2). In (Dueck

and Scheuer, 1990), Prof. Dueck indicates that the

threshold parameter does not react very sensitively

to the solution quality and hence, does not have to

be elaborately optimized. Consequently, the iterative

modiﬁcation of the initially assembled substitute cy-

cle commences (line 3-12). During each respective

loop run, the substitute cycle is slightly modiﬁed (line

4). This modiﬁcation is achieved by randomly chang-

ing one of the E microtrips. Instead, a microtrip in

the complex data set is randomly chosen and then put

in. A subsequent evaluation of the quality assesses

this modiﬁcation. The modiﬁed substitute cycle is

only adapted as a new reference, if the quality has

improved for more than the given threshold value T,

if the resulting cycle meets all RDE standards and

the resulting cycle length corresponds to the prede-

ﬁned interval (line 5-7). By means of two further in-

ner loops, an adaptation of the optimization process

is achieved. On the one hand, the threshold value T

is reduced after a certain number of inexpedient mod-

iﬁcations (line 8-9), which incrementally reduces the

subsequent cycle’s demanded improvement as well.

These consequences lead to the fact that only solu-

tions performing substantially better can be adapted

as a new reference solution. The demanded improve-

ment is mitigated by the reduction of threshold val-

ues during the optimization process. But on the other

hand, the optimization process will be terminated if

after a large number of modiﬁcations, no further im-

provement has been achieved (line 10-11). This prac-

tice ensures that the optimization is only performed

in correspondence to the achievement of improve-

ments. Taking sample solutions during the optimiza-

tion process is made possible by the iterative approach

(Ließner et al., 2017).

3 RESULTS

This chapter illustrates various results of the gener-

ation of RDE replacement cycles which will be dis-

cussed in the following subsections. For the presen-

tation of individual aspects two examples based on

different data sets were prepared. The velocity curves

are shown in Figure 4 and 5. Figure 4 represents real

driving data. The cycle in Figure 5 was generated

with NEDC velocity curves. With the help of the re-

placement cycle based on the NEDC data it can be

demonstrated very well that the presented algorithm

provide the desired results. The evaluation of the cy-

cles from Figure 4 and 5 concerning to the RDE cri-

teria is shown in Table 1. It compares the different

characteristic values of the replacement cycles with

the given values of the RDE legislation.

3.1 Fulﬁllment of the RDE

Requirements

As is demonstrated in Table 1, all RDE standards con-

cerning vehicle dynamics can be met. This is not only

VEHITS 2017 - 3rd International Conference on Vehicle Technology and Intelligent Transport Systems

192

0 1000 2000 3000 4000 5000 6000 7000

time in s

100

150

velocity in km/h

Figure 4: RDE replacement cycle based on real driving data.

0 1000 2000 3000 4000 5000 6000 7000

time in s

100

150

velocity in km/h

Figure 5: RDE replacement cycle based on NEDC data.

the case when applying the described cycle, but by us-

ing the outlined combinatorics, any desired number of

RDE conforming cycles can be generated. The vari-

ability of usage cases is a great advantage because it

presents a broad basis for the optimization and vali-

dation of RDE cycles.

3.2 Impact of the Data Basis

The requirement for a successful generation is a rele-

vant database. Within the database, all areas (urban,

rural, motorway) have to be included to a sufﬁcient

extent. When attempting to create a RDE cycle by us-

ing data sets which omits velocities above 90 km/h,

this demand becomes much more transparent. In the

case stated above, the missing velocity shares render

a successful combinatorics impossible.

The respective route areas (urban, rural, motor-

way) are automatically determined by the employed

combinatorics. The speciﬁc distribution is not af-

fected in any way. The fundamental area distribu-

tion is shaped by the database’s quality. In this con-

text, the adherence to the permitted maximum veloc-

ity is not problematic. By screening microtrips with

higher maximum velocities than 160 km/h out of the

database beforehand, an expedient violation of this

criterion can occur.

3.3 Distribution of Stoppages

Stoppages (v = 0) within the original data have a sig-

niﬁcant role for an expedient combinatorics. The cy-

cle parameters ’average v

urban

’, ’stop ratio urban’, as

well as ’stops above 10 s’ and ’stops above 180 s’ un-

derline this. These parameters will not be represented

correctly in the substitute cycle if the stoppages do not

have the relevant quality.

In contrast to selecting suitable shares with a ve-

locity higher than zero, the generation of stoppages

(v = 0) is much more simple. Since these stoppages

only incorporate sequences of velocities of the value

zero, additional editing is possible. If, for example,

the criterion ’stop share urban’ > 10% has not been

met, the criterion can be fulﬁlled by manipulating the

already existing stoppages during the post processing.

However, the longest permitted driving duration must

not be violated.

The calculation of the va

pos

_95 and RPA values

only consists of measurements with a acceleration of

a > 0.1m/s

. Nonetheless, the assessment for validat-

ing vehicle dynamics is based on the average veloci-

ties of each area. Regarding the urban area, stoppages

are incorporated into the calculation as well.

3.4 Analysis of Replacement Cycles

The RDE substitute cycle, which is based on the

NEDC data set (see Figure 5), evidently contains a

great number of linear acceleration courses, such as

can also be found in the NEDC. The maximum ac-

celeration values are comparable to those found in the

NEDC. This attribute is also very prominent in the

NEDC and leads to the use of only a few engine op-

eration points while driving the cycle. The cycle in

Derivation of Real Driving Emission Cycles based on Real-world Driving Data - Using Markov Models and Threshold Accepting

193

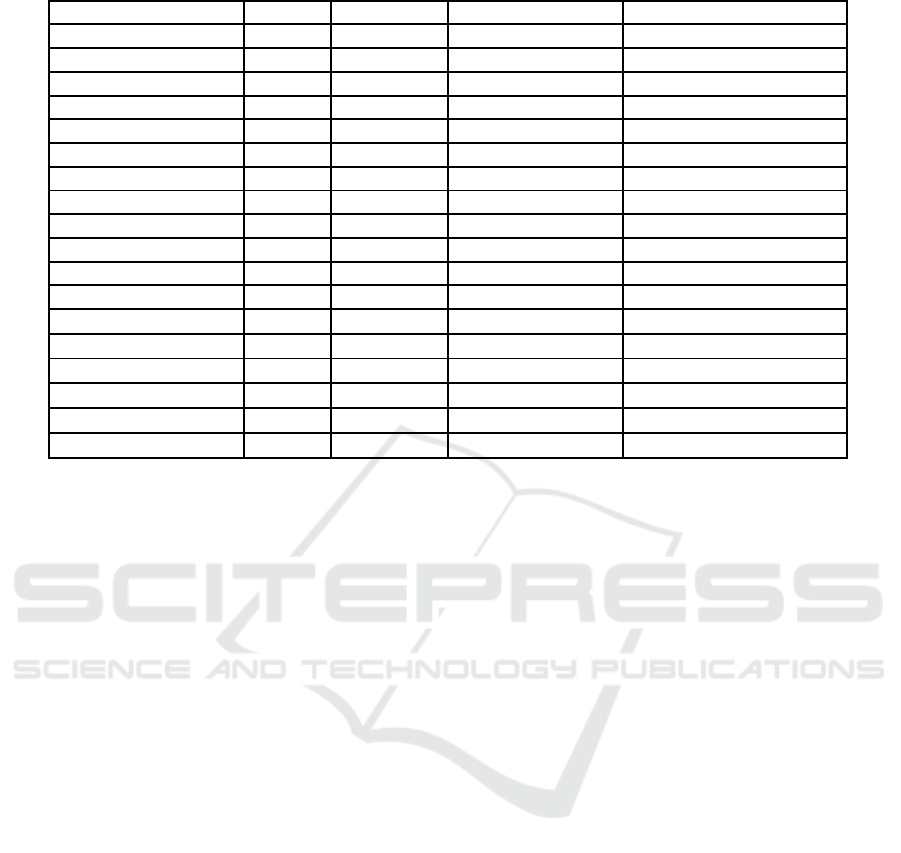
Table 1: Fullﬁllment of RDE requirements of the generated cycles.

Requirement Unit Set Value RDE Cycle NEDC RDE Cycle Real Driving

Trip duration [min] 90-120 113.63 105.40

Urban operation [%] 29-44 43.92 32.16

Rural operation [%] 23-43 26.43 30.82

Motorway operation [%] 23-43 29.65 37.01

Urban distance [km] ≥ 16 32.00 26.20

Rural distance [km] ≥ 16 19.25 25.11

Motorway distance [km] ≥ 16 21.60 30.15

Maximum speed [km/h] 145 120 134

Time v > 100 km/h [min] ≥ 5 6.65 10.82

Average Speed urban [km/h] 15-40 km/h 22.44 23.03

Stop ratio urban [%] ≥ 10 28.44 13.06

Stop t > 10 s [#] ≥ 2 51 16

pos

_95 urban [m

] < 17.57 7.72 16.05

pos

_95 rural [m

] < 24.51 10.03 24.23

pos

_95 motorway [m

] < 26.87 9.10 26.39

RPA urban [m/s

] > 0.14 0.14 0.28

RPA rural [m/s

] > 0.06 0.11 0.15

RPA motorway [m/s

] > 0.025 0.12 0.10

ﬁgure 5 ranks near the lower limit of the RPA value

for urban and ranks thereby also near the lower limit

of permitted vehicle dynamics. This effect highlights

how much more dynamic the drives used for the RDE

assessment will be compared to the ones that have

been used so far.

In contrast to this, the driving cycle based on real

drives (see Figure 4) represents a cycle ranked near

the higher limit for driving dynamics. A speciﬁc max-

imum value for the va

pos

_95 values cannot be derived

more easily, because the relevant reference value is

calculated by using the average velocity. The dis-

cussed phenomena concerning the NEDC substitute

cycle do not occur in this cycle, which is much more

similar to a real drive when looking at the character-

istics.

3.5 Worst Case Scenario

The worst-case cycle in connection to RDE driving

cycles has already been a subject of discussion in the

beginning of this paper. What is meant in this case

is a set of driving cycles, which operate the assessed

vehicle near the RDE validity limit. The objective has

to be that passing the RDE assessment by using these

cycles must ensure that all possible drives conform-

ing to RDE will pass the assessment. It has already

been discussed in section 2.1 that the paper at hand

only gives a ﬁrst, partial solution. Nevertheless, the

emissions have to be maximized already during this

partial step. One approach would be to increase the

driving cycle’s dynamics, which would also increase

the emissions regarding vehicles with a combustion

engine.

Another determining factor for the increase of

emissions during a driving cycle is the distribution of

stoppages (v = 0). Especially the conditions in the

exhaust gas aftertreatment system play an important

role here. To give an example, it is well-known that a

certain temperature in catalytic converters is a prereq-

uisite for best executing the required reaction of re-

ducing emissions. Should this not be the case, signif-

icantly higher values will occur during the cold start

phase. Even extensive idle times during a drive can

lead to similar effects. Such pauses should be imple-

mented into the worst-case case in a manner which

enables cooling processes to repeatedly cause compa-

rable situations.

A worst case cycle should also contain high dy-

namic maneuvers in the cold start phase. The end of

that cold start phase is deﬁned by a temperature of the

coolant over70

◦

C or after ﬁveminutes in the wording

of the law. So most of the combustion engines espe-

cially in cold environments don’t reach their normal

operating temperature during this time.

4 SUMMARY AND OUTLOOK

In the contribution at hand, the possibility of generat-

ing RDE cycles from real driving data has been il-

lustrated. By applying the outlined approach, spe-

ciﬁc substitute cycles for different types of vehicles

VEHITS 2017 - 3rd International Conference on Vehicle Technology and Intelligent Transport Systems

194

or markets, which can differentiate greatly in char-

acteristics or velocity distribution, can be developed.

The possibility of generating a large quantity of dif-

ferent cycles and using them during the development

process makes the avoidance of phenomena such as

cycle beating possible.

The main focus was not only on the generation of

RDE cycles, but these cycles were also supposed to

cause a larger quantity of emissions in the assessed

vehicles. To meet the requirements in a ﬁrst step,

the maximum permitted dynamics in the contest of

RDE ambient conditions were demanded. Addition-

ally, considerations were presented which increase

emissions due to the chosen sequence of operational

conditions, regardless of strictly set requirements.

In the future, RDE cycles will play an important

role in both the vehicle development and the assess-

ment of vehicle emission values. At present, RDE

drives are commonly selected on the basis of impre-

cise compilations of driving road criteria (see Table 1)

and then traced on real roads. This procedure is on the

one hand very time-consuming, and on the other hand

does not guarantee that RDE requirements will be

met, especially when unpredictable disruptions such

as trafﬁc jams occur. At some point, the recording

of RDE measurement drives will predominantly take

place on chassis dynamometers, since these can be

adapted to be nearly identical to the chosen ambient

conditions and can also follow the set velocity course

precisely.

During vehicle development, the usage of simula-

tions and procedures such as the model-based calibra-

tion will gain more importance due to RDE require-

ments. Even now, engineers face the challenge of

constantly reducing development periods and steadily

increasing numbers of vehicle variants while still us-

ing conventional development methods. Thus, the

majority of calibration will be executed at the com-

puter and at test benches of different complexity. A

signiﬁcant part of this practice will be various driv-

ing cycles, because they constitute the most realistic

testing scenarios in vehicle development.

Further contributions can continue the gradual

generation of RDE worst-case cycles (see Section

2.1). Correspondingly, an elevation proﬁle will be

overlaid in a next step, after which vehicle-speciﬁc

cycles can be derived. Based on this procedure, one

obtains a set of cycles representing the worst-case

case concerning emissions for the respective vehicle.

REFERENCES

Dueck, G. and Scheuer, T. (1990). Threshold accepting:

A general purpose optimization algorithm appearing

auperior to simulated annealing. Journal of Computa-

tional Physics, 90(1):161–175.

European Commission (2016). Comission Regulation (EU)

2016/646. Ofﬁcial Journal of the European Union.

Fotouhi, A. and Montazeri-Gh, M. (2013). Tehran driv-

ing cycle development using the -means clustering

method. Scientia Iranica, 20(2):286–293.

Fraidl, G., Kapus, P., and Vidmar, K. (2016). The gaso-

line engine and RDE challenges and prospects. In 16.

Internationales Stuttgarter Symposium, Wiesbaden.

Springer Fachmedien.

Gerstenberg, J., Hartlief, H., and Tafel, S. (2016). Introduc-

ing a method to evaluate RDE demands at the engine

test bench. In 16. Internationales Stuttgarter Sympo-

sium, Wiesbaden. Springer Fachmedien.

Lee, T.-K. and Filipi, Z. S. (2010). Synthesis and validation

of representative real-world driving cycles for plug-

in hybrid vehicles. In 2010 IEEE Vehicle Power and

Propulsion Conference (VPPC), pages 1–6.

Ließner, R., Dietermann, A., Lüpkes, K., and Bäker, B.

(2017). Generation of replacement vehicle speed cy-

cles based on extensive customer data by means of

markov models and threshold accepting. SIAT - Sym-

posium on International Automotive Technology 2017.

Maschmeyer, H., Beidl, C., Düser, T., and Schick, B.

(2016). Real Driving Emissions - Ein Paradigmen-

wechsel in der Entwicklung. MTZ - Motortechnische

Zeitschrift, 76:36–41.

Steinbach, M., Neumann, T., Kutzner, A., Lehmann, V.,

Kassem, V., and Dreiser, M. (2016). Model sup-

ported calibration process for future RDE require-

ments. In 16. Internationales Stuttgarter Symposium,

Wiesbaden. Springer Fachmedien.

Stroock, D. W. (2013). An introduction to Markov pro-

cesses. Graduate texts in mathematics. Springer,

Berlin, 2nd edition.

Derivation of Real Driving Emission Cycles based on Real-world Driving Data - Using Markov Models and Threshold Accepting

195