Characterizing Social Interactions in Online Social Networks:

The Case of University Students

M. E. Sousa-Vieira, J. C. L´opez-Ardao and M. Fern´andez-Veiga

Department of Telematics Engineering, University of Vigo, Spain

Keywords:

Online Social Networks, Collaborative Learning, Social Networks Analysis.

Abstract:

The widespread use of computing and communications technologies has enabled the popularity of social net-

works oriented to learn. In a previous work, we studied the nature and strength of associations between

undergraduate students of an introductory course on computer networks, using an online social network em-

bedded in a learning management system. With datasets from two offerings of the same course, we mined the

sequences of questions and answers posted by the students to identify structural properties of the social graph,

patterns of collaboration among students and factors inﬂuencing the ﬁnal achievements, concluding that the

structural properties most correlated to the ﬁnal academic results are robust measures of centrality (degree and

eigenvector), which are already detectable since the ﬁrst weeks of the course. In this work, we apply SNA to

graduate engineering students enrolled in a master level course in computer networks. The results obtained

show that quality participation in the social activities appears to be correlated with the ﬁnal outcome of the

course, and that good students tend to show denser egonetworks. Our analysis contributes to the understanding

of the role of social learning among highly educated students.

1 INTRODUCTION

Information technology is changing the ways we

learn. The widespread use of computing and com-

munications technologies has enabled the formation

of personalcommunications or online social networks

(OSNs), and it is behind the popularity of social net-

works oriented to learn. Social learning (Vassileva,

2008; Hart, 2011) emphasizes the role of knowl-

edge gained through social relationships (real or vir-

tual), that is, private conversations, public debates,

exchange of ideas, sharing knowledge, collaboration,

cooperation, etc., regardless these taking place be-

tween peers or with experts.

A properly designed software platform which in-

tegrates contents, users and educational experiences

is key for the effectiveness of any social learning en-

vironment (SLE). The popular learning management

systems (LMSs), e.g., Moodle, Claroline, Black-

board, cannot offer full functionality for embedding

OSN features like direct interaction among the stu-

dents, a reputation system, or the creation of infor-

mal learning activities. Consequently, some genuine

SLEs have been recently developed (Rodrigues et al.,

2011; Thoms, 2011; Sousa et al., 2016), with a focus

on collaborative work. Since these kind of learning

platforms collect a detailed record of each student’s

activity, a growing body of research aims to under-

stand to what extent the social interactions among the

students reinforce their learning process or improve

the quality of the learning outcomes.

This type of data has been used to analyze the in-

dividual behavior of users, potentially for identifying

the behavior patterns that lead to success in learn-

ing (Lykourentzou et al., 2009; Macfadyen and Daw-

son, 2010). In other studies, the datasets are mined to

quantify how the information ﬂow shapes the learn-

ing results, e.g., to discover the most inﬂuential stu-

dents or to ﬁnd out how collaboration among groups

of students arise, and the impact of relationships on

performance of learners. In other words, whether the

structure of the community to which a student belongs

while he/she is engaged in the SLE has any substan-

tial correlation on his/her performance. Thus, math-

ematical techniques from the ﬁeld of social network

analysis (SNA) are being increasingly applied to dis-

entangle the relationships taking place among social

actors in a SLE, and for understanding the distinctive

patterns arising from these interactions. The study

proposed in (Dawson, 2008) addresses learning com-

munities from a social network perspective, includ-

ing what relations are evident in these communities,

188

Sousa-Vieira, M., López-Ardao, J. and Fernández-Veiga, M.

Characterizing Social Interactions in Online Social Networks: The Case of University Students.

DOI: 10.5220/0006292701880199

In Proceedings of the 9th International Conference on Computer Suppor ted Education (CSEDU 2017) - Volume 2, pages 188-199

ISBN: 978-989-758-240-0

how media affect online relationships formation and

what beneﬁts can result from successfully maintain

learning networks. The work described in (Cadima

et al., 2012) analyses two distributed social learning

networks in order to understand how characteristics

of the social structure can enhance students’ success.

In (Hommes et al., 2012), authors study the inﬂuence

of social networks, motivation, social integration and

prior performance on learning, proposing degree cen-

trality as a key predictor for students learning. A

theoretical model is developed in (Chung and Pare-

des, 2015) to investigate the association between so-

cial network properties, content richness in academic

learning discourse and performance, concluding that

these factors cannot be discounted in the learning pro-

cess and must be accounted for in the learning design.

In (Gaggioli et al., 2015) authors investigate the rela-

tionship between social network indices, creative per-

formance and ﬂow in blended teams. The results in-

dicate that social network indices, in particular those

measuring centralization and neighbors interactions,

can offer useful insight into the creative collaboration

process. Related to the role of course facilitators, the

study proposed in (Skrypnyk et al., 2015) shows that

the teaching function becomes distributed among in-

ﬂuential actors in the network, both human and tech-

nological, but the ofﬁcial course teachers preserve a

high level of inﬂuence over the ﬂow of information

in the investigated course. Finally, the aim of the

study proposed in (Eid and Al-Jabri, 2016) is to em-

pirically examine various categories of social network

sites use, showing that there are signiﬁcant positive

relationships between them and students learning.

In a previous work (Sousa et al., 2015), we ap-

plied SNA techniques and tools to mine the data col-

lected through our software platform, SocialWire, in

two consecutive editions of an undergraduate course

on computer networks, for discovering what factors

or variables have measurable correlation with the per-

formance of the students: his/her level of participa-

tion in the system, his/her position (importance) in-

side the network graph or his/her neighborhood. We

concluded that the structural properties most corre-

lated to the ﬁnal academic results are robust measures

of centrality (degree and eigenvector), which are al-

ready detectable since the ﬁrst weeks of the course.

In this paper we report on a similar trial with students

engaged in a master’s degree in engineering.

The rest of the paper is organized as follows. In

Section 2 we give an overview of the core social

engine, and describe the general principles of our

learning-enhanced social platform. The methodol-

ogy employed in the master level course is reported

in Section 3. Section 4 contains the main results of

the data mining applied to the datasets. Finally, some

concluding remarks and guidelines for further work

are included in Section 5.

2 THE LEARNING PLATFORM

SocialWire (Sousa et al., 2016) is a SLE purposely

designed to provide a complete networked learning

paradigm, including features not available in other

SLEs. For instance, SocialWire uses games and social

meritocracy as conducting threads. The software plat-

form is based on ELGG, a popular engine for develop-

ing OSNs, and allows the creation, assessment and

reporting of a range of collaborative activities based

on social interactions among the students, offering a

reward mechanism by means of ranking and reputa-

tion.

The platform was developed upon four building

blocks:

• The online social network. SocialWire leverages

on the core of ELGG for reusing the fundamental

elements of a generic OSN. Every group (class-

room group) deﬁned in the system has its own

wall to maintain open communication among all

its members. The group can also use common

tools in the social web for its virtual classroom

activities: classroom blog, collaborative publish-

ing and document editing, creation of web pages,

social tagging, ﬁles repositories with hierarchi-

cal structure (including a viewer for images, au-

dio, video and the usual document formats), and

event calendars. All the activity unfolded in the

classroom gets eventually reﬂected on the pub-

lic wall, so it can be commented, highlighted or

voted. Sharing videos, uploading a ﬁle, save and

send a link are extremely simple actions which the

user can invoke through an user interface deliber-

ately similar to an OSN user interface. The user-

friendliness is higher, as a bonus, and the learning

curve of the platform itself is greatly softened.

• The formal learning processes. To furnish So-

cialWire with the usual features of a LMS, we

have developed custom software modules that ex-

tend the bare OSN based on ELGG. Speciﬁcally,

there exist modules for proposing and submitting

tasks (either online or ofﬂine), for the creation

and assessment of quizzes and questionnaires, for

the creation and processing of forms or polls, for

building an e-portfolio, for designing rubrics for

evaluation, and more. Another software module

gives the teachers the possibility of structuring

the learning units in their courses, for instance

Characterizing Social Interactions in Online Social Networks: The Case of University Students

189

weekly, monthly, by topic,... and adding to each

unit as many resources as they like.

• The informal learning processes. SocialWire

opens the possibility of carrying out other sort of

activities requiring a higher degree of social inter-

action. This is done by means of the questions and

contests modules. Besides the usual grading pro-

cedure used in formal courses (on a numeric scale

or by discrete levels), in SocialWire the students

can receive “points” or “marks” for their works.

The points accumulated along the course deter-

mine their position in the students’ ranking. This

ranking serves primarily to send signals to the stu-

dents about their relative performance, in a way

that directly stimulates comparisons and that au-

tomatically conveys the meaning of social reputa-

tion.

• The collaborative work processes. Most of the

popular software platforms for collaborative work

fail to give real, effective support for working col-

laboratively. First, the users are not given a virtual

workspace where direct communication and shar-

ing between colleagues can happen, so they must

resort to external programs to solve this (or in ex-

treme cases, physical meetings). Secondly, teach-

ers are not provided with the opportunity to man-

age, coordinate, assess, evaluate, share or com-

municate with the workgroups. SocialWire does

permit subgroups, i.e., smaller groups within an

existing group. The instructors are in charge of

deciding how many groups will be created, their

sizes and their membership policies, if any is due.

Every activity supported by SocialWire can be as-

signed to a group or to an individual, and in the

former case any group member is entitled to par-

ticipate in the role of group’s representative. Ad-

ditionally, every subgroup is internally a group

and has a private space so that their members and

the instructors can communicate.

3 APPLICATION

As explained in the previous Section, SocialWire pro-

vides a social networking platform for interaction be-

tween teachers and learners. The platform has been

conceived as a complementary tool to a traditional

course offering, so it provides two of the different

learning modes typically found in standard MOOCs:

video lectures/talks, assessments (in form of quizzes,

homework and exams), and social networking. So-

cialWire supports the last two modes, while the lec-

tures are still held in real classrooms.

The SocialWire platform has been used to teach

one master level course over two consecutive aca-

demic years, 2014/15 and 2015/16. This is an ad-

vanced course within the scope of the underlying

technologies in computer networks, continuing and

intensifying the introductory concepts studied in the

subjects of the degree. In both editions 16 students

followed the course. All had studied at least a sub-

ject in the degree following a methodology similar to

the one described in this paper. As to the students’

background, 9 in the ﬁrst edition and 7 in the second

held an undergraduate degree related to computer net-

works.

The course has a weekly schedule that lasts 14

weeks. The activities are organized as follows:

• Lectures/recitations, that mix the exposition of

the ideas, concepts, techniques and algorithms be-

longing to the lessons of the course with the reso-

lution of problems and theoretical questions in the

classroom.

• Laboratory sessions, in small study groups. These

are complementary sessions where the students

design and analyze different network scenarios

and with different protocols, using the GNS3 em-

ulator.

• Online activities (questions, tasks, tests, etc.), in

the virtual classroom.

Students and teachers belong to a single group in So-

cialWire, wherein general communication about the

topics covered takes place.

To encourage networked learning activities and

collaborative work, the teachers planned different ac-

tivities in SocialWire whereby the students may gain

points (the resulting ranking is made public to the

group):

• Collaborative answering of questions. This ac-

tivity consist in posing and solving any question,

doubt or problem about the subject. The students

send their questions, and so do the instructors oc-

casionally. From the questions posed by the stu-

dents, each question aligned to the course objec-

tives and not repeated receives some points. The

answers to any question (not absolutely correct,

since the effort to participate and try to answer is

also valuable) get also some points, depending on

their quality and completeness and the difﬁculty

of the underlying question. Correct answers are

clearly marked, so that there is no misunderstand-

ing.

• Tasks previous to the laboratory sessions. By

means of this activity the teachers successfully en-

courage the students to prepare the material cov-

ered in the laboratory sessions in advance.

CSEDU 2017 - 9th International Conference on Computer Supported Education

190

• Tests previous to the midterm exams.

Face-to-face interaction (in the classroom and in

the laboratory session) is still the bulk of the course,

for a total of 40 hours. But the social networking ac-

tivities occupy a signiﬁcant fraction of the indepen-

dent study time (an average of 10 hours). More im-

portantly, there is actually a connection between the

more formal face-to-face learning activities and the

online tasks, in that many discussions and homework

problems start in the classroom but take place further

through the online platform, and are ﬁnished there.

Though this subject may be passed with a single

ﬁnal examination covering all the material, students

are encouraged to follow the continuous assessment

path.

In the two academic years, the weight of the con-

tinuous assessment was 50%, and the remaining 50%

is awarded as the result of a ﬁnal exam held on two

different dates (January and July, non-exclusive). The

50% in the continuous assessment is split into a 30%

from two midterm exams and a 10% of the ﬁnal grade

comes out from the game points gathered by engag-

ing in the social activities commented above, to in-

crease the level of participation. While it is true that

one point in the ﬁnal grade might seem a too scarce

pay off for the best student, we believe it is impor-

tant that the full score is easily achievable by a sig-

niﬁcant fraction of the class. Thus, in order to con-

vert the point marks into a grade, if P

and P

med

are the average and median number of game points

per student and P

max

is the maximum, we compute

M = min{P

med

max

/2}. In the conversion scale,

M represents 0.5 grade points, and every student hav-

ing at least 2M game points gets the full 1 grade

possible with this part. In doing so, we try to pre-

serve the incentive-driveneffect whereby the average-

performing student is still engaged and the best stu-

dents attain fair pay offs.

3.1 Activity in the Questions and

Answers Game

In the ﬁrst edition of the course along the term the stu-

dents submitted 43 questions and 40 answers to the

platform. The quality of the answers was remarkable,

all got some game points and 18 were highlighted

by the teachers. Moreover, the teachers submitted 1

question, answered successfully by 8 students. In the

second edition of the course the students submitted

35 questions and 36 answers worthy of game points,

from which 6 were highlighted by the teachers. In

this case, the teachers submitted 3 questions along

the term, answered successfully by 8, 12 and 14 stu-

dents, respectively. As we can see in Figures 1 and 2

the activity is more concentrated around the second

midterm date (at the end of November) and one week

before the ﬁnal exam (January 20 and December 17,

respectively).

In our datasets we recorded all the events tak-

ing place within the game: users who post questions,

users who answer each question and the valuations

they received. With these data points, we build social

graphs where two nodes (i.e., students) are connected

by an edge if one has given an answer to a question

posted by the other (notice that these graphs are di-

rected, since it is important to know who made the

question and who is answering it).

In Figures 3 and 4 every node is a student identi-

ﬁed by his/her position in the ranking of game points

(the node with label 0 represents the teachers). The

light green points correspond to students that accom-

plished the subject in January, the dark green is for

students who passed in July, and the grey points are

for students who dropped off the course or failed the

subject in the end. The color in the answers (edges)

serves to classify them on the basis of the points re-

ceived (black means 0 points, blue 1 point, red 2

points, pink 3 points, orange 4 points and yellow 5

points).

In the graph of the ﬁrst edition of the course we

can see that 14 of the 16 students followed the contin-

uous assessment path and took part in this activity. All

of them ﬁnally passed the course, 11 in January and

3 in July (only one of them, node 6, with prior ex-

posure to computer networks). Moreover, of the two

students not engaged in continuous assessment (nei-

ther of them with a computer networks background)

only one ﬁnally succeeded in the course.

In this edition, among the most active students in

this game are those who reach the highest positions

in the ranking, a fact suggesting that they were com-

petent in solving the rest of the online activities pro-

posed along the academic year. In the graphs, nodes

6 and 8 correspond to students with medium or high

performance in the online activities, having average

grades in the midterms but who had to improve their

grade in the ﬁnals in order to pass.

In the second edition of the course, all the students

participated in this activity, and all but one were able

to pass, 12 in the ﬁrst call and 3 in the second one

(again only one of them, node 13, with a computer

networks background). Node 16 is a student without

previous specialization in computer networking who,

despite outstanding at this game, did not complete the

remaining online activities, so ended up relegated to

the last position in the ranking.

Finally, in Figures 5 and 6 we can see that in the

ﬁrst edition of the course the students in the lowest

Characterizing Social Interactions in Online Social Networks: The Case of University Students

191

10 november

17 november

24 november

1 december

8 december

15 december

22 december

29 december

5 january

12 january

teachers question

students questions and answers (1 point)

students questions and answers (2 points)

students answers (0 points) students questions and answers (3 points)

students questions and answers (4 points)

students questions and answers (5 points)

Figure 1: Activity in the questions and answers game in the ﬁrst edition of the course.

28 september

5 october

12 october

19 october

26 october

2 november

9 november

16 november

23 november

30 november

7 december

14 december

teachers question

students questions and answers (1 point)

students questions and answers (2 points)

students answers (0 points) students questions and answers (3 points)

students questions and answers (4 points)

students questions and answers (5 points)

Figure 2: Activity in the questions and answers game in the second edition of the course.

positions of the ranking concentrate the activity in two

weeks (two days in some cases). This fact suggests a

non-steady study of the subject along the term. The

same pattern is observed in students 5, 11 and 13 in

the second edition. All of them passed the subject in

July.

4 SOCIAL NETWORK ANALYSIS

In this Section we apply SNA techniques and tools to

mine the data collected. As we explained in the previ-

ous Section, we model the social relationships taking

place in the questions and answers game as directed

simple graphs, and aim to explain the basic structural

properties of such graphs as consequences of the so-

cial interactions among its agents. Formally, a graph

(N, g) consists of a set of nodes N = {1, 2,.. . ,n} and

a square matrix g, the adjacency matrix, where g

represents the relation between nodes i and j. The

neighborhood of a node i is the set of nodes that i is

linked to, N

(g) = { j : g

= 1 and/org

= 1}. The de-

gree of a node d

(g) is the number of links that involve

that node. For undirected graphs, d

(g) = #N

(g). In

directed graphs, the in-degree d

= #{ j : g

= 1} and

the out-degree d

out

= #{ j : g

= 1} count how many

edges ﬁnish (respectively, start) at that node.

4.1 Graph-level Measures

In social network analysis, the static or dynamic struc-

tural characteristics of the graph reveal key aspects of

the collective and individual behavior of the agents.

Let us brieﬂy report some of the typical descriptive

measures of a graph (Newman, 2010), and their val-

ues in our dataset.

CSEDU 2017 - 9th International Conference on Computer Supported Education

192

Figure 3: Interactions in the questions and answers game in

the ﬁrst edition of the course.

Figure 4: Interactions in the questions and answers game in

the second edition of the course.

4.1.1 Density

The density of a graph keeps track of the relative frac-

tion of edges that exist (compared to the maximum





of a complete simple graph with n nodes). It is

simply the ratio between the number of edges and

the total number of possible edges, with values rang-

ing from 0 (sparsest) to 1 (densest). Our dataset is

dynamic, i.e., the social graph starts empty and the

links are established as a result of the information ex-

changes between pairs of agents. In Table 1 we show

the graph density values of the two editions of the

course are moderate (and smaller in the second edi-

0 1 2 3 4 5 6 7 8 9

Figure 5: Activity per student in the questions and answers

game in the ﬁrst edition of the course.

0 2 4 6 8 10 12

Figure 6: Activity per student in the questions and answers

game in the second edition of the course.

tion that in the ﬁrst). This is due to the nature of the

links: only a part of the students provide answers to

each question.

4.1.2 Global Centrality

Global centrality is a graph-level measure that gives

an idea about the dependency of the graph on the ac-

tivity of a small group of nodes. Its normalized values

range from 0 (even distribution of activity) to 1 (the

most centralized graph). It is based on the underlying

node-level centrality measures.

Many different measures of centrality have been

developed, that capture different features of nodes’s

position in a graph, the following ones being some of

the most commonly used:

• Degree centrality: measures how connected a

node is, computing the (normalized) count of

neighbors to a node.

• Betweenness centrality: tries to capture the im-

portance of a node in terms of its role in con-

necting other nodes, computing the ratio between

the number of shortest paths that a node lies on

Characterizing Social Interactions in Online Social Networks: The Case of University Students

193

Table 1: Density.

Academic year 2014/15 Academic year 2015/16

Answers 0.2197 0.1916

Questions and Answers 0.4561 0.3375

Table 2: Global centrality.

Academic year 2014/15 Academic year 2015/16

Degree

In-degree 0.3431 0.1511

Out-degree

Answers 0.3431 0.3644

Questions and Answers 0.3901 0.3291

Eigenvector

Directed

Answers 0.6614 0.5602

Questions and Answers 0.8493 0.7847

Undirected

Answers 0.6079 0.4758

Questions and Answers 0.7895 0.4862

Table 3: Reciprocity.

Academic year 2014/15 Academic year 2015/16

0.2585 0.1304

Table 4: Transitivity.

Academic year 2014/15 Academic year 2015/16

Global 0.3278 0.3156

Average 0.3131 0.3415

Table 5: Number of cliques of different sizes.

# Academic year 2014/15 Academic year 2015/16

2 29 38

3 12 19

4 1 2

Table 6: Assortativity.

Academic year 2014/15 Academic year 2015/16

Degree 0.1121 −0.4153

Nominal (computer networks background) −0.1594 −0.1135

and the total number of possible shortest paths be-

tween two nodes.

• Closeness centrality: measures how easily a node

can reach other nodes, computing the inverse of

the average length of the shortest paths to all the

other nodes in the graph.

• Eigenvector centrality: a measure based on the

premise that a node’s importance is determined by

how importantor inﬂuential its neighbors are. The

scores arise from a reciprocal process in which the

centrality of each node is proportional to the sum

of the centralities of the nodes it is connected.

In our context, degree and eigenvector centralities

seem good indicators of the students’ activity. Nev-

ertheless, closeness and betweenness centralities are

inconsequential for our purposes, since in the under-

lying graph the exchange of information is always di-

rect, without relays or intermediate nodes, between

the source agent and the destination agent.

For the case of degree centrality, we consider sep-

arately the in-degree centrality (the number of an-

swers a student receives), and two measures of the

out-degree centrality: the number of answers given by

a student and the number of questions proposed and

answers given by a student. The results in Table 2

show that the out-degree centrality values are moder-

ate and similar in both datasets, but the in-degree cen-

trality is smaller in the last dataset, indicating a more

homogeneous distribution of the questions submitted

and the answers received by the participants.

For the eigenvector centrality, we have tested dif-

ferent conﬁgurations of the graph built up from the

datasets. In the ﬁrst, we remove the edges correspond-

CSEDU 2017 - 9th International Conference on Computer Supported Education

194

ing to questions posted by the student, and revert the

direction of the edges which model the answers. So,

in this case, an edge from node a to node b means that

student b has answered a question raised by a. We

apply this edge reversal operation to measure the cen-

trality of the students who answer some question, not

those who make the questions, because the eigenvec-

tor centrality measure is sensitive to the in-degrees of

nodes. Further, to understand the effect of mutual in-

teraction, we also consider an undirected version of

the latter graph. In the second conﬁguration, we in-

clude explicitly the questions posed by each student in

the graph, by adding a self-edge in such cases. Again,

both the directed and the undirected versions of this

graph have been used to analyze the datasets.

The results in Table 2 show larger values of the

eigenvector centrality (for the directed as well as for

the undirected graphs) when the self-edges are con-

sidered, which is reasonable. The normalized central-

ity values are noticeable and higher in the ﬁrst edition,

a hint of stronger centralization in the network, mean-

ing that not all nodes act as sources of information in

the same way.

4.2 Collaboration Among Groups of

Students

The social networking component of SocialWire

opens the door to collaboration among groups of stu-

dents. Therefore, we focus now on the discovery

of structural properties in the graph that reveal some

form of collaboration. Speciﬁcally, we analyze the

coefﬁcients of reciprocity, transitivity and assortativ-

ity (or homophyly).

4.2.1 Reciprocity

Reciprocity accounts for the number of mutual ex-

changes of information in the graph, happening in the

form of request-response pattern. In mutual collabo-

ration either part poses a question and receives at least

one answer from the other part. In other words, this

entails the existence of the edges (a,b) and (b,a) si-

multaneously.

In our setting, reciprocity can be used to assess

the degree of mutual collaboration or trust between

two given students who have discovered each other

either randomly or by a previous request-response ex-

change. Table 3 lists the average reciprocity in the

networks. The small values obtained suggest that in

the social environment mutual collaboration is rare.

This is not surprising, after all, since this is a not iter-

ative activity more effective in the formation of com-

munities (three or more students) than in encouraging

strong mutual relationships.

4.2.2 Transitivity

A broader form of collaboration is transitivity (the

fraction of closed loops with three nodes in the graph,

sometimes also called the clustering coefﬁcient). We

were also interested in detecting whether transitivity

is signiﬁcant in the student network. Thus, the stan-

dard transitivity coefﬁcient has been computed for the

two datasets, both the global transitivity coefﬁcient

and the average value of the local (individual) transi-

tivity coefﬁcients of the nodes. The results obtained

are shown in Table 4, and conﬁrm that transitivity is

noticeable. However, this is not entirely unexpected,

since the social network fosters direct relationships

between the participants. There is no beneﬁt in ac-

quiring or propagating information through a third

party, and the data are consistent with this observa-

tion. Consequently, both average and global transitiv-

ity are quite high.

4.2.3 Cliques

A clique is a maximal completely connected subgraph

of a given graph. So, a clique represents a strongly

tied subcommunitywhere each member interacts with

any other member. 3-cliques are the transitivity rela-

tions discussed in the last paragraph. Given the na-

ture of our datasets, though 3-cliques are likely, larger

cliques seem less probable. Table 5 lists the number

of cliques in the graphs by their size.

4.2.4 Assortativity

The assortativity coefﬁcient measures the level of ho-

mophyly of the graph, based on some labeling as-

signed to the nodes. It is positive if similar nodes tend

to connect to each other, and negative otherwise.

As we can see in Table 6 we have measured the

degree assortativity and the case of nominal assor-

tativity where each student is labeled according the

computer networks background. For the nominal as-

sortativity we have obtained low values, many of them

negative, suggesting randomness in the relationships.

For the degree assortativity, the high negative value of

the second edition of the course suggests relationships

between the less and the most active students, as it is

desirable.

Characterizing Social Interactions in Online Social Networks: The Case of University Students

195

35 40 45 50

points

neighbors average points

5.0 5.5 6.0 6.5 7.0 7.5 8.0

5.2 5.4 5.6 5.8 6.0

final grade

neighbors average final grade

Figure 7: Neighborhood composition vs. students’ performance in the ﬁrst edition of the course (points -top- and ﬁnal grades

-bottom-).

45 50 55

points

neighbors average points

4 5 6 7

3.5 4.0 4.5 5.0 5.5 6.0

final grade

neighbors average final grade

Figure 8: Neighborhood composition vs. students’ performance in the second edition of the course (points -top- and ﬁnal

grades -bottom-).

4.3 Relationships between

Neighborhoods’ Composition and

Students’ Performance

Finally, we are interested in measuring to what ex-

tent the social peers (i.e., his/her neighborhood in the

social graph) inﬂuence the student’s performance at

the end of the course. A reasonable conjecture would

suggest that information exchange with other good

students improves the insights and the learning pace

gained by the followers, but this should be conﬁrmed

by the data, especially after having checked that the

assortativity in the graph is low.

To that end, because the small sample sizes are not

suitable to obtain accurate enough correlation mea-

sures, we have represented the students’ performance

vs. the average performance of their neighborhood.

As we can see in Figures 7 and 8, there is no clear

evidence that a student’s performance has a signiﬁ-

cant inﬂuence on that of their neighbors. This is partly

because the dataset is small, but the main reason is the

design of the assessment: the main part of the ﬁnal

grade still comes from traditional evaluation activi-

ties, not from the online participation.

Finally, Figures 9 and 10 show the egonetworks

of some of the students of each edition that are rep-

resentative of different patterns of activity. We see

that in the ﬁrst edition good students tend to show

denser egonetworks. Nevertheless, in the second edi-

tion, the egonetworks are always quite dense for the

reason that the relationships between the less and the

more active students are more likely.

In Figure 9, node 1 is the most active students in

the online activities and node 5 correspondsto the stu-

dent with higher ﬁnal grade in the subject. Nodes

6 and 7 are in the middle of the ranking (both with

the same number of points): the ﬁrst one is a student

with a computer networks background that passed in

July, whereas the second one is a student without

previous specialization in computer networking that

passed in January due to the fact that he obtained bet-

ter results in the middle and ﬁnal exams. Node 11 is

CSEDU 2017 - 9th International Conference on Computer Supported Education

196

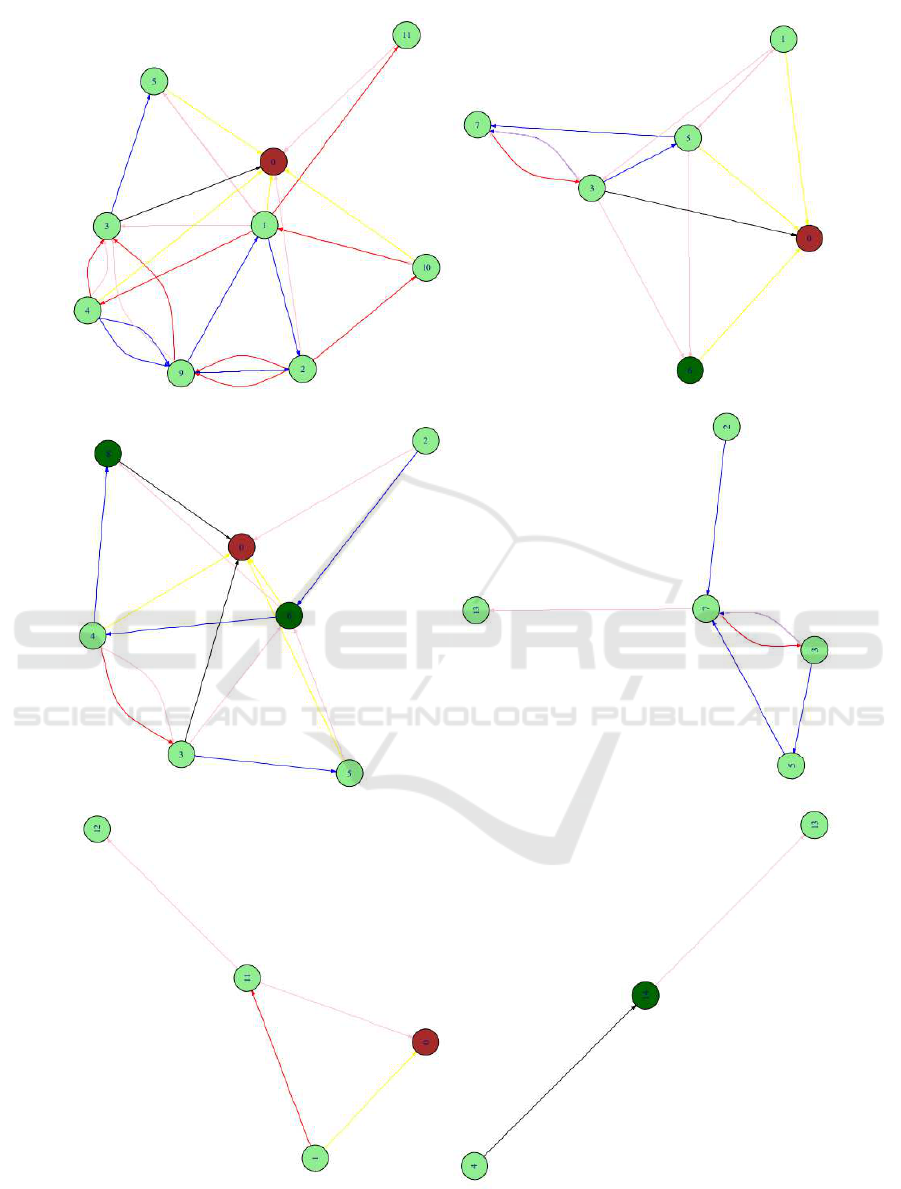
Figure 9: Egonetworks in the ﬁrst edition of the course (nodes 1, 5, 6, 7, 11 and 14).

Characterizing Social Interactions in Online Social Networks: The Case of University Students

197

Figure 10: Egonetworks in the second edition of the course (nodes 1, 6, 5, 13, 15 and 16).

CSEDU 2017 - 9th International Conference on Computer Supported Education

198

a good student with computer networks background

and medium performance in the online activities. Fi-

nally, node 14 represents the less active student in the

online activities of those that followed the continuous

assessment in this edition.

In Figure 10, node 1 is the student with more

points and higher ﬁnal grade in the subject, and node

6 is the second high performing student. Nodes 5 and

13 are two of the student that concentrate the activity

in few days: the ﬁrst one is a student without previous

specialization in computer networks, whereas the sec-

ond one is a student with a computer networks back-

ground. Both passed the subject in July. Node 15 is

a good student with computer networks background

and medium performance in the online activities. Fi-

nally, node 16 is the student who, despite outstanding

at this game, did not complete the remaining online

activities, so ended up relegated to the last position in

the ranking.

5 CONCLUSIONS

In this work, we studied the nature and strength of

associations between students using an online social

network embedded in a learning management system.

With datasets from two offerings of the same course,

we mined the sequences of questions and answers

posted by the students to identify 1) structural prop-

erties of the social graph; 2) patterns of collaboration

among groups of students; 3) factors inﬂuencing (or

not) the ﬁnal achievements of students. Though the

dataset is small, we found that quality participation

in the online activities appears to be correlated with

the ﬁnal outcome of the course, and that good stu-

dents tend to show denser egonetworks. These ﬁnd-

ings can help instructors to early detect and classify

the students’ ability, contributing to a better under-

standing of the learning experience and possibly to an

enhanced design of the academic activities.

REFERENCES

Cadima, R., Ojeda, J., and Monguet, J. (2012). So-

cial networks and performance in distributed learn-

ing communities. Educational Technology & Society,

15(4):296–304.

Chung, K. and Paredes, W. (2015). Towards a social net-

works model for online learning & performance. Ed-

ucational Technology & Society, 18(3):240–253.

Dawson, S. (2008). A study of the relationship between

student social networks and sense of community. Ed-

ucational Technology & Society, 11(3):224–238.

Eid, M. and Al-Jabri, I. (2016). Social networking, knowl-

edge sharing and student learning: The case of univer-

sity students. Computers & Education, 99:14–27.

Gaggioli, A., Mazzoni, E., Milani, L., and Riva, G. (2015).

The creative link: Investigating the relationship be-

tween social network indices, creative performance

and ﬂow in blended teams. Computers in Human Be-

havior, 42(1):157–166.

Hart, J. (2011). Social learning handbook. Centre for

Learning and Performance Technologies.

Hommes, J., Rienties, B., Grave, W., Bos, G., Schuwirth,

L., and Scherpbier, A. (2012). Visualising the invisi-

ble: A network approach to reveal the informal social

side of student learning. Advances in Health Sciences

Education, 17(5):743–757.

Lykourentzou, I., Giannoukos, I., Nikolopoulos, V., Mpar-

dis, G., and Loumos, V. (2009). Dropout prediction

in e-learning courses through the combination of ma-

chine learning techniques. Computers & Education,

53(3):950–965.

Macfadyen, L. and Dawson, S. (2010). Mining LMS

data to develop an ”early warning system” for edu-

cators: A proof of concept. Computers & Education,

54(2):588–599.

Newman, M. (2010). Networks: An introduction. Oxford

University Press.

Rodrigues, J., Sabino, F., and Zhou, L. (2011). Enhancing e-

learning experience with online social networks. IET

Communications, 5(8):1147–1154.

Skrypnyk, O., Joksimovic, S., Kovanovic, V., Gasevic, D.,

and Dawson, S. (2015). Roles of course facilitators,

learners and technology in the ﬂow of information of a

cMOOC. International Review of Research in Online

and Distance Learning, 16(3):743–757.

Sousa, E., L´opez, J., Fern´andez, M., Rodr´ıguez, M., and

Herrer´ıa, S. (2016). An open-source platform for us-

ing gamiﬁcation and social learning methodologies in

engineering education: Design and experience. Com-

puter Applications in Engineering Education.

Sousa, E., L´opez, J., Fern´andez, M., Rodr´ıguez, M., and

L´opez, C. (2015). Mining relations in learning-

oriented social networks. In DSAA’15, 2nd. IEEE

International Conference on Data Science and Ad-

vanced Analytics.

Thoms, B. (2011). A dynamic social feedback system to

support learning and social interaction in higher edu-

cation. IEEE Transactions on Learning Technologies,

4(4):340–352.

Vassileva, J. (2008). Toward social learning environ-

ments. IEEE Transactions on Learning Technology,

1(4):199–214.

Characterizing Social Interactions in Online Social Networks: The Case of University Students

199