Improvement of the Detection of the QRS Complex, T and P Waves in an

Electrocardiogram Signal using 12 Leads versus 2 Leads

Maxime Yochum

, Charlotte Renaud

and Sabir Jacquir

LTSI UMR 1099 Inserm, Universit

e de Rennes 1, 35042 Rennes, France

Centre Hospitalier Universitaire, 21000 Dijon, France

Le2i FRE 2005, CNRS, Arts et Mtiers, Univ. Bourgogne Franche-Comt, 9 avenue Alain Savary, 21078 Dijon, France

Keywords:

ECG, P, QRS, T Waves, Delineation, Wavelet Transform.

Abstract:

The electrical ﬁeld potential of the heart recorded from the thoracic part of the human body is depicted by the

electrocardiogram signal. This last one is complex and depends on many factors: Position of heart, thickness

of the body skin, surface electrode conductivity, acquisition noise and many others. In clinical use, the ECG

signal is analysed using twelve leads but in many works in the literature, the analysis methods of the ECG

is based on two leads. We present a new method to delineate QRS complexes and T and P waves from

electrocardiogram signal. It is based on the continuous wavelet transform. The method is applied on several

leads, recorded simultaneously, to improve the localization of the detection. Indeed, if a delineation method is

applied on only one lead with some disturbances in it, the result of the delineation could be affected. As the

method proposed here merges the result of several leads, the delineation is less affected by disturbances on

few leads. The results from this method and from a doctor in medicine are compared. That shows the good

ability to separate waves and the enhancement of delineation accuracy when several leads are used.

1 INTRODUCTION

The QRS, P and T waves detection in the electro-

cardiogram (ECG) represents a great interest to di-

agnose pathological conditions (Navoret et al., 2013;

Mahamat et al., 2016a; Mahamat et al., 2016b). How-

ever, their extraction from ECG is not an easy task.

Some methods exist, including mathematical mod-

els (Madeiro et al., 2013), peak detection (Zhu and

Dong, 2013), nonlinear transforms (Sun and Sup-

pappola, 1994), ﬁltering (Bashir et al., 2014). The

shapes of QRS, P and T waves are well known, es-

pecially their time and frequency components which

depend on the physiological characteristics of peo-

ple. It may be difﬁcult to extract ECG complexes be-

cause their frequency compositions are close to some

noises. The algorithm presented here uses the contin-

uous wavelet transform (CWT) which keeps a good

frequency resolution. Wavelet transforms (Addison,

2005; Li et al., 1995; Zidelmal et al., 2012) have al-

ready been applied to ECG signals to enhance QRS

detection, to delineate the ECG feature, and to re-

duce computation time. However, the major part of

ECG delineation methods deals with Discret Wavelet

Transform, which loses frequency resolution due to

re-sampling at each decomposition. That is not the

case in CWT. The method was tested with The Com-

puters in Cardiology Challenge 2011 database be-

cause it contains 12 leads for each ECG. From this

collection, a set of ﬁfty 12 leads ECGs, chosen in

the ”acceptable records” list given by Physionet, was

used for our tests. In addition, this database provides

ECG from patients with different pathologies leading

to some irregularities in ECGs. Therefore, our algo-

rithm (Yochum et al., 2016) was tested on several par-

ticular ECGs such as arrhythmias and extrasystoles.

Our method uses the 12 leads together to extract QRS,

P and T waves from each ECG, which improve the lo-

calization. The method performs a serial detection of

the components of the ECG signal as these compo-

nents usually follow a decrease in their energy (QRS

complexes contain more energy than T wave, and T

waves contain more energy than P waves). Results

show the use of 12 leads simultaneously reinforces

the detection and also avoids misdetections if distur-

bances exist on few leads.

Yochum, M., Renaud, C. and Jacquir, S.

Improvement of the Detection of the QRS Complex, T and P Waves in an Electrocardiogram Signal using 12 Leads versus 2 Leads.

DOI: 10.5220/0006293300730078

In Proceedings of the 2nd International Conference on Complexity, Future Information Systems and Risk (COMPLEXIS 2017), pages 73-78

ISBN: 978-989-758-244-8

0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5

100

200

ECG

0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5

−500

500

Time (s)

100 150 200 250 300 350 400 450 500 550 600

Value of C

Number of

Point

0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5

100

200

Time (s)

QRS

Figure 1: a. Example of V

ECG

signal from Physionet collec-

tion. b. CWT transformation of V

ECG

signal with a

= 38

corresponding to the maximum of C

a,b

coefﬁcient. We can

also see the representation of the difference between max-

ima of C

coefﬁcients during QRS complexes (cross) and

maxima C

coefﬁcients during T complexes (plus) which

allows the localization of QRS complexes. Both dashed

lines are the h threshold representation of positive and neg-

ative parts computed with the equation 2. c. Histogram

of local maxima values. We distinguish a bimodal distribu-

tion. d. V

QRS

result example with m

QRS

mask applied on the

ECG

signal in a. A good localization of QRS complexes are

observed.

2 METHOD

The algorithm is remained in this part, but all the de-

tails can be found in (Yochum et al., 2016). It pro-

ceeds in four steps. The ﬁrst step determines the

best scale factor which exists between the ECG sig-

nal (V

ECG

) and a mother wavelet (ψ the Daubechie

wavelet) according to a set of scale factors. A CWT

is applied between V

ECG

and ψ on a discrete grid of

scale factors a and a position b on the time axis. Such

as:

a,b

ECG

(t), ψ(t)) =

∞

−∞

ECG

(t)

√



t −b



dt,

(1)

Scale factors go from 1 to 100 by step of 1. This

range allows the analysis of various sizes of ECG

complex. To ﬁnd the best scale factor a

, we esti-

mate the scale factor which corresponds to the maxi-

mal value of the CWT coefﬁcients, named C

a,b

. The

second step builds a temporal mask in the wavelet do-

main by using the C

coefﬁcient which is a vector.

This mask allows the extraction of QRS complexes

from the ECG signal. Figure 1b shows an example

of a CWT applied on a V

ECG

(see panel a in Figure

1). Notice that C

values corresponding to QRS

complexes are higher than C

values correspond-

ing to T or P waves, which is not always the case

in V

ECG

. Using this fact, QRS complexes is distin-

guished from V

ECG

with a thresholding method. A

0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5

−50

ECG

without

QRS complexes

0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5

−200

200

0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5

−20

0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5

−30

−20

−10

Time (s)

Figure 2: a) V

ECG

signal without QRS complexes corre-

sponding to the examples in Figures 1. b) C

coefﬁcients

from CWT with a

scale factor. Both dashed lines are the

h threshold representation for positive and negative parts

computed from the equation 2. c.V

result example. d.V

example. A good localization of T and P waves is observed.

threshold is created automatically using a local max-

ima method. Those maxima are represented in Figure

1b, by crosses (during QRS) and plus (during T). In

Figure 1c, the histogram of those maxima is plotted.

It shows a bimodal distribution. To ﬁnd automatically

the threshold, the centroid of these points in the his-

togram is computed:

h =

∑

i=1

∑

i=1

, (2)

where h is the threshold, x

are the local maxima C

values, y

are the distribution value of C

coefﬁ-

cients and n represents the histogram range. Then,

once the threshold is computed, a mask is created us-

ing



absolute coefﬁcient values and the thresh-

old h. A preliminary mask (m

) is equal to 1 if



are above the threshold, which corresponds to the

QRS complexes. The mask is equal to 0 if



are below the threshold, corresponding to the T or P

wave parts. To avoid some glitches in the mask, an

erosion algorithm (a mathematical morphology oper-

ation (Serra, 1982)) is applied to the m

and gives

the ﬁnal mask named m

QRS

. The third step localizes

QRS complexes by multiplying the mask m

QRS

with

the V

ECG

signal.

QRS

(t) = V

ECG

(t) ·m

QRS

(t), (3)

An example of V

QRS

is shown in Figure 1d which cor-

responds to V

ECG

signal in Figure 1a. As we can

see, QRS complexes are well localized in V

ECG

sig-

nal. The last step of the method is to repeat the three

ﬁrst steps on the V

ECG

signal without QRS complexes.

An example is shown in Figure 2a. In Figure 2b, we

see C

coefﬁcients corresponding to the CWT of the

COMPLEXIS 2017 - 2nd International Conference on Complexity, Future Information Systems and Risk

ECG

signal without QRS complexes. The local max-

ima are represented by crosses (during T waves) and

plus (during P waves). Thanks to those local max-

ima, the threshold was computed. It is plotted with

the dashed line. Then, the mask m

is created to ﬁnd

T waves signal V

with:

(t) = V

ECG

(t) ·m

(t) (4)

An example of V

is shown in Figure 2c which corre-

sponds to the V

ECG

signal in Figure 1a. As we can see,

T waves are well localized from V

ECG

signal. The P

waves are detected as the rest of the V

ECG

signal with-

out QRS complexes and T waves. In addition, the

smallest remaining segments are removed. An exam-

ple is displayed in Figure 2d.

0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5

QRS

0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5

Time (s)

Figure 3: Examples of results of reliability indexes in a) for

the QRS complexes, in b) for the T complexes and in c) for

the P complexes. The threshold is plotted with dashed lines

for each complex as the mean of the reliability index.

To improve the localization of each complex QRS,

T and P in an ECG, the results of several leads were

combined. In cardiac diagnostic test, it is common

to have several leads in ECG signal. In this case,

even if few leads are unusable, merging results of each

lead could increase the localization of each complex

or wave. Masks m

QRS

, m

and m

created for each

lead (where k = [1,12], k ∈ N according to the lead)

are then used to compute a reliability index. If the lo-

calization result is common to the twelve leads, then

there is a strong probability that the QRS complexes

or P and T waves are well detected. On the other hand,

if there are only few localizations among the twelve

leads, then there is a low probability that the local-

ization result is true. A reliability index of each QRS

complex or P and T wave is then computed as the sum

of twelve lead masks:

(t) =

∑

k=1

(t) (5)

where w is QRS, T or P. Therefore, the reliability in-

dexes are respectively I

QRS

for QRS complexes, I

for

T waves and I

for P waves. A good localization is

more likely if the index is close to 12. In the oppo-

site case, a good localization is unlikely if the index is

Time (s)

0 5 10

ECG

(mV)

-100

100

lead N° 3

OndeQRS

OndeT

Onde P

Figure 4: Application of the algorithm on 1 lead very noisy

ECG signal. Note that the detection is not correct.

Time (s)

0 5 10

ECG

(mV)

-100

100

lead N° 3

Time (s)

0 5 10

-2000

2000

lead N° 10

OndeQRS

OndeT

Onde P

Figure 5: Application of the algorithm on 2 leads, a very

noisy one and a disturbed one. Note that the detection is not

correct. The colors correspond to the legend in Figure 4.

close to 0. In Figure 3, a result of reliability indexes

is shown (in a for the QRS, in b for the T and in c for

the P). An automatic threshold is computed for each

wave as the mean of reliability index. In Figure 3,

these three thresholds are plotted with dashed lines.

The localization of a complex is considered true if the

value of the reliability index is above the threshold

otherwise it is considered false.

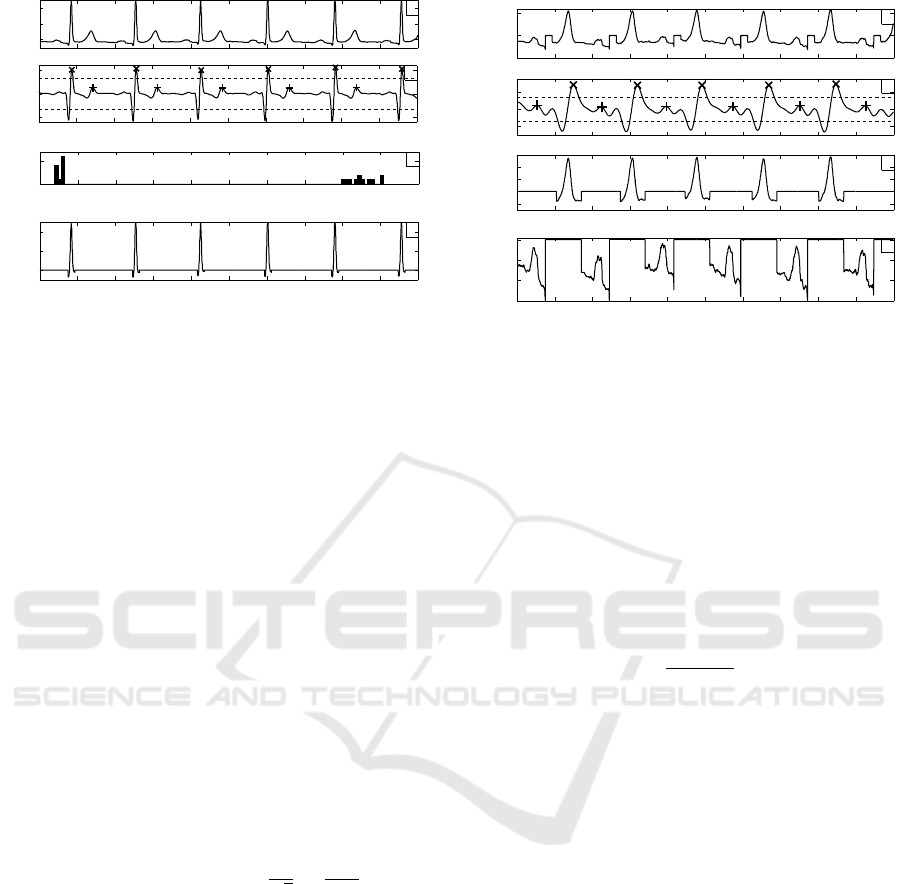
To illustrate the advantage of using more than one

lead, Figures 4 to 7 present the result of the method

with 1, 2, 4 and 12 leads. In Figure 4 just one noisy

lead is used. Note that the detection is incorrect. In

Figure 5 only two leads are used, a noisy one and a

disturbed one. Note, once again, that the detection is

incorrect. In Figure 6 only four leads are used with a

noisy one and a disturbed one. Note that, this time,

the detection is visually correct, even if two leads are

perturbed. Because the algorithm used multi-lead in-

stead of just one, the algorithm is able to compensate

disturbances on several leads. The same fact is shown

in Figure 7.

3 RESULTS

In Figure 8, four different examples are given show-

ing some particular cases where the determination of

QRS complex, T and P waves might be difﬁcult. In

panel a, the SNR ratio of the ECG is really low. Nev-

ertheless, the different waves are well detected by the

algorithm without any post acquisition process (de-

noising, amplitude enhancement,...). In panel b, T

waves are higher than QRS waves. That could lead

to mix up of those two if a thresholding technique

Improvement of the Detection of the QRS Complex, T and P Waves in an Electrocardiogram Signal using 12 Leads versus 2 Leads

0 5 10

ECG

(mV)

100

200

lead N° 1

0 5 10

100

200

lead N° 2

Time (s)

0 5 10

ECG

(mV)

-100

100

lead N° 3

Time (s)

0 5 10

-2000

2000

lead N° 10

OndeQRS

OndeT

Onde P

Figure 6: Application of the algorithm on 4 leads with a

very noisy one and a disturbed one. Note that the detection

is visually correct even if two leads are very perturbed. The

colors correspond to the legend in Figure 4.

0 5 10

ECG

(mV)

100

200

lead N° 1

0 5 10

100

200

lead N° 2

0 5 10

-100

100

lead N° 3

0 5 10

ECG

(mV)

-200

-100

lead N° 4

0 5 10

-50

100

150

lead N° 5

0 5 10

-50

100

150

lead N° 6

0 5 10

ECG

(mV)

-200

-100

lead N° 7

0 5 10

-200

-100

100

lead N° 8

0 5 10

-200

200

lead N° 9

Time (s)

0 5 10

ECG

(mV)

-2000

2000

lead N° 10

Time (s)

0 5 10

100

200

lead N° 11

Time (s)

0 5 10

100

200

lead N° 12

Figure 7: Application of the algorithm on 12 leads with a

very noisy one and a disturbed one. Note that the detec-

tion is visually correct even if two leads are very perturbed.

Colors correspond to the legend in Figure 4.

was used directly on the ECG signal. However, as

the thresholding is done in the wavelet domain, the

result shows a correct complexe detection. It is possi-

ble that the baseline of an ECG is not stable. This

is the case in panel c. Despite that, the algorithm

shares correctly each wave without low frequency ﬁl-

tering. In panel d, we can see that all waves are in

the same range of amplitude which could lead to mix

them. However, the robustness of our algorithm pre-

vents this and the results are therefore not affected.

In this case, standard thresholding algorithms are un-

able to discriminate correctly QRS complexes and T

waves, they could be mixed.

4 APPLICABILITY

The results of our algorithm applied to the Physionet

collection is compared with delineation determined

by a doctor in medicine. The interest is to know the

beginning and the end for each ECG complexes from

an expert as a true result. The physician chooses one

1 2 3 4 5

ECG

-40

-20

Time (s)

2 4 6 8 10

ECG

-50

100

150

200

Time (s)

0 1 2 3 4 5

-40

-20

QRS

0 1 2 3 4 5

-40

-20

Figure 8: Example of results with some cases where the

ECG complexes are usually difﬁcult to distinguish. a) the

ECG has got a law SNR ratio. We see that the algorithm

is able to discriminate each wave without ﬁltering. b) the

T waves are higher than the QRS waves. These two waves

could be mix up if we use a thresholding technique directly

on the ECG signal. However, in our case the thresholding is

done in the wavelet domain. c) The baseline of the ECG is

not stable. Despite that, the algorithm share correctly each

wave. d) All waves are in the same range of amplitude and

the results are not affected. QRS (black lines), T (dark gray

lines) and P (pale gray lines).

lead from the twelve leads and determines for each

QRS complex, P and T wave of this lead the begin-

ning and the end times. These data are then used as

correct result of ECG delineation. From the algorithm

and the physician, two results by ECG are obtained:

the real moments of QRS, T and P in the ECG tagged

by the doctor, and the results given by the algorithm.

Thanks to our algorithm and the physician, two re-

sults for 12 ECG leads are obtained: the real mo-

ments D

(n) of QRS, T and P in the ECG tagged by

the physician and the results A

(n) given by our algo-

rithm. A

(n) and D

(n) are equal to 1 if the QRS, T

or P wave is detected and 0 (noted

(n) and D

(n))

if is not, they are therefore logical vectors. For each

(n) and D

(n) pair, the coverage rate Se

is com-

puted (w denotes QRS, T and P waves.). This cov-

erage is determined as a logical AND between A

(n)

and D

(n) divided by D

(n) as shown in the eq.(10).

The coverage gives the common result between the

algorithm and the physician determination. This cov-

erage is well known as the sensitivity which is com-

puted thanks to TP (True Positive), TN (True Neg-

ative), FP (False Positive) and FN (False Negative)

where

T P

∑

n=0

(n) ·D

(n), (6)

T N

∑

n=0

(n) ·D

(n), (7)

∑

n=0

(n) ·D

(n), (8)

COMPLEXIS 2017 - 2nd International Conference on Complexity, Future Information Systems and Risk

∑

n=0

(n) ·D

(n). (9)

Those values are then scalars. Therefore, the sensitiv-

ity Se

is computed as:

T P

+ FN

. (10)

shows the ability of our algorithm to give the

same results as the physician. For each ECG, the

speciﬁcity has been determined.

T N

+ FP

. (11)

From the equations (6) to (11), the Youden Y

and the

accuracy Acc

indexes can be deﬁned:

= Se

+ Sp

−1, (12)

Acc

T P

+ T N

T P

+ T N

+ FP

+ FN

. (13)

The reliability indexes introduced above, have been

calculated on the results of the ﬁfty ECG samples and

their mean values are given in Table 1. These in-

Table 1: Mean values of sensitivity, speciﬁcity, Youden in-

dex and accuracy from the ﬁfty ECG samples.

Waves Se(%) Sp(%) Y (%) Acc(%)

QRS 99.87 98.42 98.29 98.64

T 99.17 93.21 91.38 94.83

P 99.06 91.21 90.27 92.44

dexes show a good ability of the algorithm to local-

ize ECG complexes since indexes are close to one.

The speciﬁcity for T and P complexes are a little bit

lower because our algorithm detects a larger area than

the doctor which induces higher TN values. Our al-

gorithm is able to well determine the duration of the

QRS complexes in the ECGs. However, the durations

for the T and P waves are longer than for the doc-

tor delineation. Nevertheless, the coverage shows that

our algorithm contains the entire parts determined by

the doctor. Therefore, some other treatments could be

done to improve the localization of T and P complexes

or to ﬁnd other characteristics such as amplitudes and

interspike durations for instance.

In addition, to better quantify the quality of the re-

sults, Table 2 presents the sensitivity index for the use

of different number of leads. As we can see, the algo-

rithm gives better results if a high number of leads is

used. It is particularly the case for the P wave.

Table 2: Improvement of wave detection with the increase

of leads.

Leads/Wave QRS T P

1 0.9134 0.3420 0.1643

2 0.9059 0.5103 0.5371

3 0.9752 0.7082 0.6396

4 0.9851 0.9939 0.9611

5 0.9802 0.9963 0.9717

6 0.9752 0.9988 0.9806

7 0.9802 1 0.9788

8 0.9823 1 0.9851

9 0.9876 1 0.9851

10 0.9912 1 0.9851

11 0.9929 1 0.9851

12 0.9951 1 0.9912

5 CONCLUSIONS

The algorithm proposed here to delineate QRS, T

and P waves in ECG signal uses a wavelet domain

transform with CWT. It can simultaneously detect

the QRS, T and P patterns on each ECG lead. A

thresholding method separates the complexes in the

wavelet domain instead of in the temporal domain.

Indeed, the amplitudes among waves are more differ-

ent in wavelet domain than in the temporal domain,

which helps the detection. To improve QRS, T and P

wave localizations in ECG signal, results from several

leads are combined with a fusion method. A compar-

ison with doctor tags thanks to sensitivity, speciﬁcity,

Youden and accuracy indexes shows the efﬁciency of

this method. In addition, the utility of using several

leads instead of only one has been proven, in par-

ticular when some leads are disturbed. We plan to

improve this method by detecting also ﬁducial mark-

ers which are useful for pathologic diagnosis. This

method could be implemented in a hardware setup

in order to help physicians and to facilitate the ECG

analysis.

REFERENCES

Addison, P. (2005). Wavelet transforms and the ecg: A re-

view. Physiol. Meas., 26:R155–R199.

Bashir, S., Bakhshi, A. D., and Maud, M. A. (2014). A tem-

plate matched-ﬁlter based scheme for detection and

estimation of t-wave alternans. Biomedical Signal

Processing and Control, 13:247–261.

Li, C., Zheng, C., and Tai, C. (1995). Detection of ecg

characteristic points using wavelet transforms. IEEE

Trans. Biomed. Eng., 42(1):21–28.

Madeiro, J. P., Nicolson, W. B., Cortez, P. C., Marques,

Improvement of the Detection of the QRS Complex, T and P Waves in an Electrocardiogram Signal using 12 Leads versus 2 Leads

J. A., V

azquez-Seisdedos, C. R., Elangovan, N., Ng,

G. A., and Schlindwein, F. S. (2013). New approach

for t-wave peak detection and t-wave end location in

12-lead paced ecg signals based on a mathematical

model. Medical engineering & physics, 35(8):1105–

1115.

Mahamat, H., Jacquir, S., Khalil, C., Laurent, G., and

Binczak, S. (2016a). Automatic detection of the wolff-

parkinson-white (wpw) syndrome from electrocardio-

grams (ecgs). In 43rd Annual International Con-

ference of the IEEE Computers in Cardiology, vol-

ume 43, pages 417–420. IEEE.

Mahamat, H., Jacquir, S., Khalil, C., Laurent, G., and

Binczak, S. (2016b). Wolff-parkinson-white (wpw)

syndrome : The detection of delta wave in an electro-

cardiogram (ecg). In 38th Annual International Con-

ference of the IEEE Engineering in Medicine and Bi-

ology Society, volume 38, pages 3809–3812. IEEE.

Navoret, N., Jacquir, S., Laurent, G., and Binczak, S.

(2013). Detection of complex fractionated atrial elec-

trograms (cfae) using recurrence quantiﬁcation analy-

sis. IEEE Trans. Biomed. Eng., 60(7):1975–1982.

Serra, J. (1982). Image analysis and mathematical mor-

phology, v. 1. Academic press.

Sun, Y. and Suppappola, S. (1994). Nonlinear transforms

of ecg signals for digital qrs detection: a quantitative

analysis. Biomed. Eng., 41(4):397–400.

Yochum, M., Renaud, C., and Jacquir, S. (2016). Automatic

detection of p, qrs and t patterns in 12 leads ecg sig-

nal based on cwt. Biomedical Signal Processing and

Control, 25:46–52.

Zhu, H. and Dong, J. (2013). An r-peak detection method

based on peaks of shannon energy envelope. Biomed-

ical Signal Processing and Control, 8(5):466–474.

Zidelmal, Z., Amirou, A., Adnane, M., and Belouchrani, A.

(2012). Qrs detection based on wavelet coefﬁcients.

Comp. Met. and Prog. in Biomed., 107(3):490–496.

COMPLEXIS 2017 - 2nd International Conference on Complexity, Future Information Systems and Risk