Optimal Combination Rebate Warranty Policy with Second-hand

Products

Sriram Bhakthavachalam

, Claver Diallo

, Uday Venkatadri

and Abdelhakim Khatab

Department of Industrial Engineering, Dalhousie University, 5269 Morris Street, Halifax, Canada

Laboratory of Industrial Engineering, Production and Maintenance (LGIPM), Lorraine University,

National School of Engineering, Metz, France

Keywords:

Second-hand Products, Warranty Policy, Consumer Perspective, Remaining Useful Life.

Abstract:

With the increased awareness for sustainability, many engineered products are being recovered and recondi-

tioned for secondary useful lives. These second-hand products can serve as replacement products to honour

warranty pledges. This paper presents two mathematical models to determine the optimal combination rebate

warranty policy when refurbished products are used for replacements from both the manufacturer and consu-

mer point of views. Several numerical experiments are conducted to derive useful managerial knowledge.

1 INTRODUCTION

A warranty is a contractual agreement offered by the

manufacturer at the point of sale of a product (Blis-

chke, 1995), (Blischke, 1993). The use of warran-

ties is universal and serves numerous purposes. It

helps the buyers to rectify all the failures occurring

within the warranty period at lower or no cost. Whe-

reas, for manufacturers, it acts as a promotional tool

to increase sales and revenue (Blischke, 1995). Ame-

rican manufacturers spend over 25 billion dollars to

service warranty claims which is about 2% of their an-

nual revenue from sales (Chukova and Shaﬁee, 2013;

Shaﬁee and Chukova, 2013). In the 2009 General

Motors annual report, the company had a total re-

venue of $104.2 billion and the future warranty cost

on sold cars estimated to be $2.7 billion, about 2.6%

of the revenue (Shaﬁee and Chukova, 2013). When

buying a product, the consumer usually faces the dif-

ﬁcult task of deciding between buying the warranty

or not. And when the decision is made to get the war-

ranty, choosing between different characteristics and

warranty policies is another daunting task. When the

warranty period is optional, the consumer has to de-

cide if the warranty is worth the additional cost based

a very limited knowledge of the product. This is beco-

ming more and more important, since there is a gro-

wing trend among the manufacturers to offer exten-

ded term warranties. These involve additional costs,

and the terms can vary considerably (Blischke, 1995;

Blischke, 1993; Yun et al., 2008). Blischke & Murthy

gave the example of a warranty or extended warranty

that might cover both labor and parts initially and only

cover parts later in the warranty period. The con-

sumer has to decide, often at the time of purchase

and based on very limited information, whether to opt

for an extended warranty or not and to determine the

best extended terms for his situation when there are

multiple options (Blischke, 1995), (Blischke, 1993).

The everyday consumer is not capable of conducting

a mathematical analysis before making a choice be-

cause the consumer neither has the expertise for such

an analysis nor the bargaining power to obtain rele-

vant data from the manufacturer. However, consumer

bureaus and regulatory agencies can carry out such

analyses and inform the consuming public. Any mo-

del developed from the consumer’s point of view in

this chapter is then assumed to have been done for a

consumer agency on behalf of all consumers and with

data obtained by the agency from the manufacturers

or from established and recognized independent re-

viewing bodies such as the Consumer Reports maga-

zine.

There are many different types of warranty poli-

cies designed to cover the needs of manufacturers,

dealers and consumers. A policy which is based

on one factor (usually age) alone is said to be one-

dimensional, on the other hand a two dimensional

warranty is limited by two factors, usually age and

a measure of usage of the product. One-dimensional

policies are selected for products which are known to

last for a ﬁxed time period. This is common in the

Bhakthavatchalam S., Diallo C., Venkatadri U. and Khatab A.

Optimal Combination RebateWarranty Policy with Second-hand Products.

DOI: 10.5220/0006293504910498

In Proceedings of the 6th International Conference on Operations Research and Enterprise Systems (ICORES 2017), pages 491-498

ISBN: 978-989-758-218-9

491

marketplace for products such as cell-phones, com-

puters, and projectors. Two-dimensional warranties

apply to products that display wear and tear, degra-

dation with usage. Automobiles, aircraft and heavy-

duty machinery are examples of products with 2-D

warranty policies. It is common to see car advertise-

ments stating coverage of 60 months, 120 000 kilo-

metres which ever occurs ﬁrst.

Some basic warranty types are the Free replace-

ment (FRW), Pro-rata (PRW), and Rebate warranty.

1. Free replacement warranty (FRW): The manu-

facturer agrees to repair/replace a failed item du-

ring the warranty period at no charge to the custo-

mer. Example: small household appliances, elec-

tronics.

2. Pro-rata warranty (PRW): The customer covers

a proportion of the repair cost prorated to the age

of the item at failure. Example: Tires.

3. Rebate warranty: The seller agrees to refund

some proportion of the sale price to the buyer,

if the product fails during the warranty period.

The refund amount may be a linear or non-linear

function of the failure time. Example: Money

back Guarantee for electronic components such as

hard drives, computer screens, and storage devi-

ces.

A basic taxonomy of warranty policies is presen-

ted by (Blischke, 1993; Blischke, 1995). An in-

tegrated warranty-maintenance taxonomy based on

three categories ,i.e. product type, warranty policy,

and maintenance strategy, is proposed in (Shaﬁee and

Chukova, 2013).

Hybrid (combination) warranties are designed

to utilize the desirable characteristics of the pure

warranties and downplay some of their drawbacks

(Blischke, 1993; Blischke, 1995). The combination

warranty gives the buyer full protection against

full liability for later failures, where the buyer has

received nearly the full amount of service that was

guaranteed under the warranty. It has a signiﬁcant

promotional value to the seller while at the same time

providing adequate control over costs for both buyer

and seller. An example for hybrid warranty is seen

in the FRW/PRW policy offered on Firestone tires.

During the ﬁrst 2 years of service, the tire is replaced

free of charge. Beyond year 2, the replacement

price is pro-rated based on years of service from

the original purchase date. Some advantages of

combination warranties are improved protection

towards the product, customer satisfaction, higher

ownership lifetime for the buyers and higher sales

volume to increase proﬁt to manufacturers.

Combination warranty is a good type of war-

ranty for second-hand products (SHPs) as its offers a

good protection to both manufacturers and consumers

(Chari, 2015). Two main problems faced by the con-

sumers acquiring SHPs are their uncertainty and du-

rability (Shaﬁee and Chukova, 2013) due to the lack

of past usage and maintenance history. In order to re-

duce the risk and impact of product malfunctioning,

dealers offer generous warranty policies. A review of

warranty models currently available in the literature

for SHPs show that there are very few of them and all

deal with the manufacturers perspective (Shaﬁee and

Chukova, 2013; Chari et al., 2016b; Su and Wang,

2016; Diallo et al., 2016). The goal of this article is to

address this shortcoming by proposing a warranty po-

licy and develop mathematical models from both the

manufacturer and consumer perspectives.

2 OPTIMAL COMBINATION

WARRANTY MODELS USING

SHPS

For most warranty policies, failed products are re-

paired or replaced with new components or products.

In the context of remanufacturing, second-hand pro-

ducts may be available and can therefore be re-used as

replacements when consumers return failed products

(Yeh et al., 2005; Yeh et al., 2011; Chari et al., 2016a).

In doing so, the manufacturers can lower their costs

and consumers can extend their ownership of the pro-

ducts. However, due to the lower reliability of SHP,

it is crucial to determine the optimal parameters of

the warranty policy to be offered to avoid higher costs

to the manufacturer and less than anticipated perfor-

mance/ownership time for the consumer. In this ar-

ticle, we will develop two mathematical models for

a combination rebate warranty policy using SHPs as

replacement products.

2.1 Proposed Warranty Policy

Under the proposed warranty policy, a brand new pro-

duct is sold with a total warranty coverage period of

length w. Under this policy, the seller will replace a

defective product with:

• A new product if the failure occurs before w

(Phase 0);

• A refurbished product of high quality if the failure

occurs between w

and w

(Phase 1);

• A refurbished product of normal quality if the fai-

lure occurs between w

and w

(Phase 2).

ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems

492

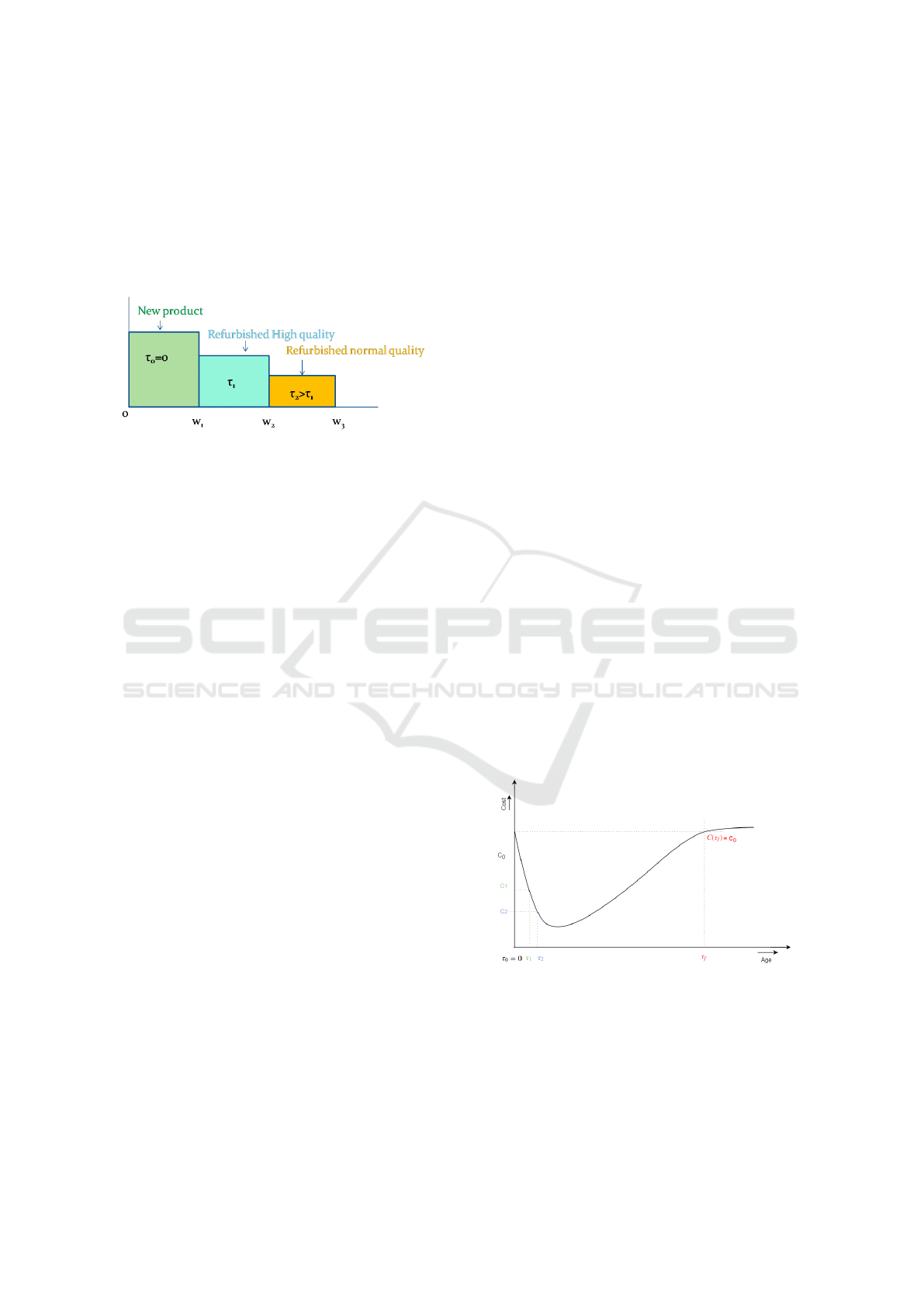
It should be noted that w = w

. The pro-

posed warranty policy is depicted in Figure 1. New

products have age τ

= 0. Refurbished or second-

hand products of high quality have age τ

that is grea-

ter than 0. Refurbished or second-hand products of

normal quality have age τ

that is greater than τ

Therefore, we have: 0 < τ

< τ

Figure 1: Proposed Warranty Policy.

The policy offered here is Non Renewing Free Re-

placement Warranty policy (NRFRW). The following

notation is used.

2.1.1 Parameters

: Cost of replacement product in phase i

: Unit cost for a new product

: Warranty cost

a: Price coefﬁcient

: Warranty coefﬁcient

: Market demand amplitude factor

ε,η: Age coefﬁcients for the acquisition

cost of reconditioned components

β: Slope parameter of the Weibull distribution

θ: Scale parameter of Weibull distribution

λ: Inverse of the Scale parameter (λ = 1/θ)

m: Number of warranty periods

2.1.2 Functions

f (t): lifetime prob. density function (pdf)

F(t): Cumulative distribution (cdf)

π: Expected unit proﬁt

P (p, w

,τ

): Total expected proﬁt for the Seller

D(p,w

): Total demand

EOT : Expected ownership time

MT T F

: Expected lifetime of the original new

product

MT T F

: Expected lifetime for high quality SHPs

MT T F

: Expected lifetime for low quality SHPs

EOCR

: EOT per cost ratio of the product when

warranty is purchased

EOCR

: EOT per cost ratio of the product

without warranty

2.1.3 Decision Variables

p: Unit sale price of the new product

: Warranty periods

: Age of the SHP products offered as

replacements in phase i

In the following section, two mathematical mo-

dels will be developed for the maximization of the

manufacturer’s expected proﬁt and the maximization

of the consumer’s ownership time.

2.2 Model 1: Maximization of

Manufacturer’s Expected Proﬁt

If the product fails within w

, a full refund of C

given to the customer to buy a new product. When

it fails between w

and w

a refund of C

is returned

to the customer that is sufﬁcient to buy a high reliabi-

lity SHP. When the product fails between w

and w

a lump sum C

is given back to the consumer which

is sufﬁcient to buy a normal quality SHP. Warranty is

not extended when the system fails.

C(τ

), the unit cost of a replacement product with

age τ

, is given by Equation (1) where C

is the base

price and ε,η are positive parameters (Chari, 2015).

Parameter ε represents the discount rate offered on

used products, and parameter η models the increase

in cost due to aging.

C(τ

) = C

× (1 + τ

)

(−ε)

+ τ

(1)

A new product will therefore cost

C(τ

= 0) = C(0) = C

(2)

Figure 2: Cost as a function of age.

The proﬁle of C(τ

) is depicted in Figure 2.

The cost of replacement products initially decrease

with age (refurbished cost less) but reaches a mini-

mum then increases with age to account for techni-

cal and practical difﬁculties encountered when trying

to disassemble and recondition very old products

Optimal Combination RebateWarranty Policy with Second-hand Products

493

(availability of parts, obsolescence, corrosion, etc.).

Beyond this point C(τ

) = C

, customers should buy

a new product rather than a second-hand product be-

cause the cost of a new product is less than SHP.

C(τ

) = C

= C

× (1 + τ

)

(−ε)

+ τ

(3)

C(τ

) = C

= C

× (1 + τ

)

(−ε)

+ τ

(4)

The probability that a product will fail between

i−1

and w

for i = 1, ...,m is given by:

[F(w

) − F(w

i−1

)] (5)

where w

= 0.

The total expected warranty cost (C

) is given by

the weighted average of the replacement costs in each

phase i given in Equation (7) shown below.

∑

i=1

C(τ

) × [Prob. failure in phase i] (6)

= C

∑

i=1



(1 + τ

i−1

)

−ε

i−1



[F(w

) − F(w

i−1

)]

(7)

Failure Distribution:

The Weibull distribution is used as the product fai-

lure distribution. The lifetime cumulative distribution

function of the product is then given by

F(x) = 1 − exp

−(

)

, 0 ≤ x (8)

Demand Function:

The market demand function D(p,w

) for the pro-

duct is modelled to take into account consumers’ pre-

ferences for lower prices and longer warranty co-

verage. D(p,w

) is modelled as a displaced log-linear

function of w

and p as in (Glickman and Berger,

1976; Chari et al., 2016b).

D(p,w

) = d

−a

i−1

+ w

)

(9)

Parameter a is the rate of decrease of the sales vo-

lume with the increasing price of the product. Para-

meters b

are the rate of increase of the sales volume

with the increasing of the warranty lengths w

. The

factor d

is the demand amplitude and d

is the war-

ranty displacement constant.

Total Expected Proﬁt:

The total expected proﬁt (TEP) P is the product of the

expected unit proﬁt with the demand as in Equation

(10). The expected unit proﬁt is obtained in Equation

(11) by subtracting the cost of the original product C

and the expected warranty cost C

from the sale price

p of each unit sold.

P = π · D(p, w

) (10)

P = (p −C

−C

) · D(p,w

) (11)

2.2.1 Numerical Results

For illustration purposes and without loss of genera-

lity, an example with only two decision variables is

considered by setting τ

as a proportion of τ

using:

= k · τ

. For the arbitrarily chosen parameter va-

lues given below, we solve for the solution (p,τ

)

which maximizes the manufacturers’ total expected

proﬁt: w

= 0.5;w

= 1;w

= 2 : m = 3, θ = 1.5,β =

1.5;C

= 15; d

= 100,000; a = 2.6;b

= 1.9,b

1.5,b

= 1.1; ε = 3.3; η = 0.7; λ = 1/θ; k = 1.5. Fi-

gure 3 shows a 3D-plot of the total expected proﬁt P

as a function of purchase price p and age τ

. There

is a clear optimal solution at p

∗

= $30.68, τ

∗

= 1.43

and P

∗

= $3,287.

Several numerical experiments have been con-

ducted to analyze the behavior of the model when key

parameters change. The ﬁrst experiment consisted in

varying the values of k, a parameter that dictates how

old the replacement products are in phase 2 in com-

parison with the replacement products used in phase

1 according to the formula: τ

= k · τ

. The results

obtained are plotted in Figures 4 to 6.

In Figure 4, P increases until the value of k rea-

ches 1 and after that point, P decreases. For k = 1,

the replacement products in phase 1 and 2 are the

same. This represents the best case scenario as pro-

ﬁt is maximum and price is the lowest. For k < 1,

phase 2 replacement products are younger than phase

1 products, which is bad because components failing

in phase 1 are replaced with older parts and the larger

proportion of failures occurring in phase 2 are covered

with newer products which are more expensive. This

explains why the slope when k < 1 is steeper than the

slope when k > 1. Figure 5 shows that price p beha-

ves in an exact opposition to the behavior of P . For

values near and around k = 1, it is the cheapest to ho-

nour the warranty, so the manufacturer can afford to

reduce the price of the product and therefore increase

demand, which in return boosts proﬁt.

Figure 6 depicts the relationship between the op-

timal value τ

∗

and τ

∗

. For smaller values of τ

∗

the

model uses larger values of τ

∗

to keep warranty costs

under control. When the values of τ

∗

start to incre-

ase (1 < τ

∗

< 3), the model restricts the values of τ

∗

between values of 3 and 1.5 to keep warranty costs

low by decreasing the probability of failure in phase

2. For values of τ

∗

> 3 the values of τ

∗

tend to stabi-

lize around 1 and 1.5 for the same reasons as before.

ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems

494

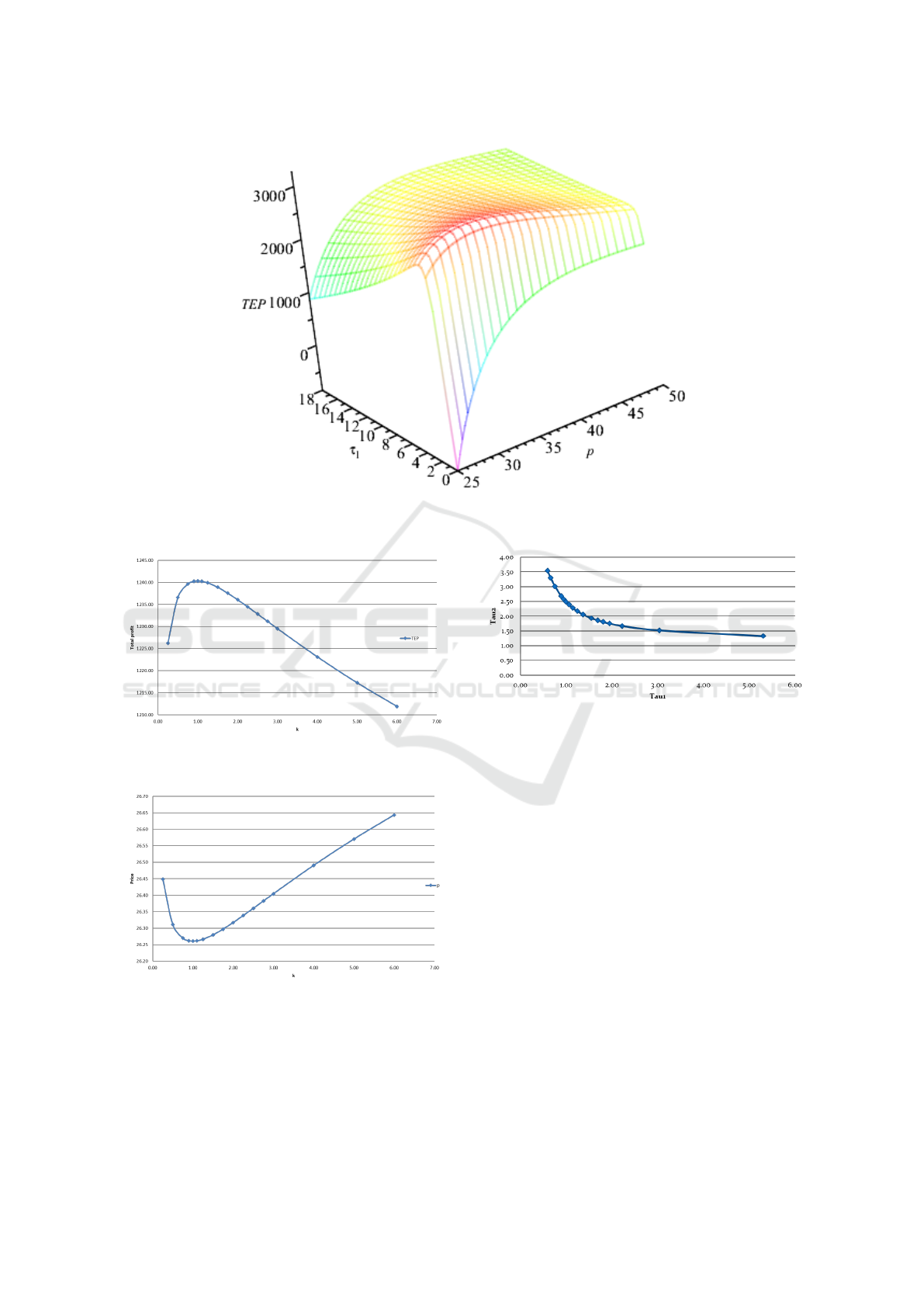
Figure 3: Total expected proﬁt as a function of purchase price p and age τ

Figure 4: Seller expected proﬁt as a function of k.

Figure 5: Optimal price as a function of k.

Another set of numerical experiments was con-

ducted by varying β, the shape parameter of the Wei-

bull distribution. The results are plotted on Figure 7.

In general, the ﬁgure shows an increasing trend and a

plateau after β = 4. Increasing the shape parameter β

Figure 6: τ

vs τ

for varying values of k.

newpage

increases reliability of the product so that the warranty

cost reduces. There is very little return on investment

to improve reliability of the products beyond β = 4.

Figure 8 shows that with improving reliability (incre-

asing β), the warranty costs reduce and therefore the

model can afford to reduce the unit price which in-

creases proﬁts. For the same reliability reasons, when

β increases, the model can afford to use newer parts

which causes τ

∗

to decrease as depicted in Figure 9.

2.3 Model 2: Maximization of

Customers’ Expected Ownership

Time

In the previous model, the focus was on the manufac-

turers’ interests. In this subsection, a model develo-

ped from the consumer’s perspective will be presen-

ted. The warranty policy introduced in sub-section

Optimal Combination RebateWarranty Policy with Second-hand Products

495

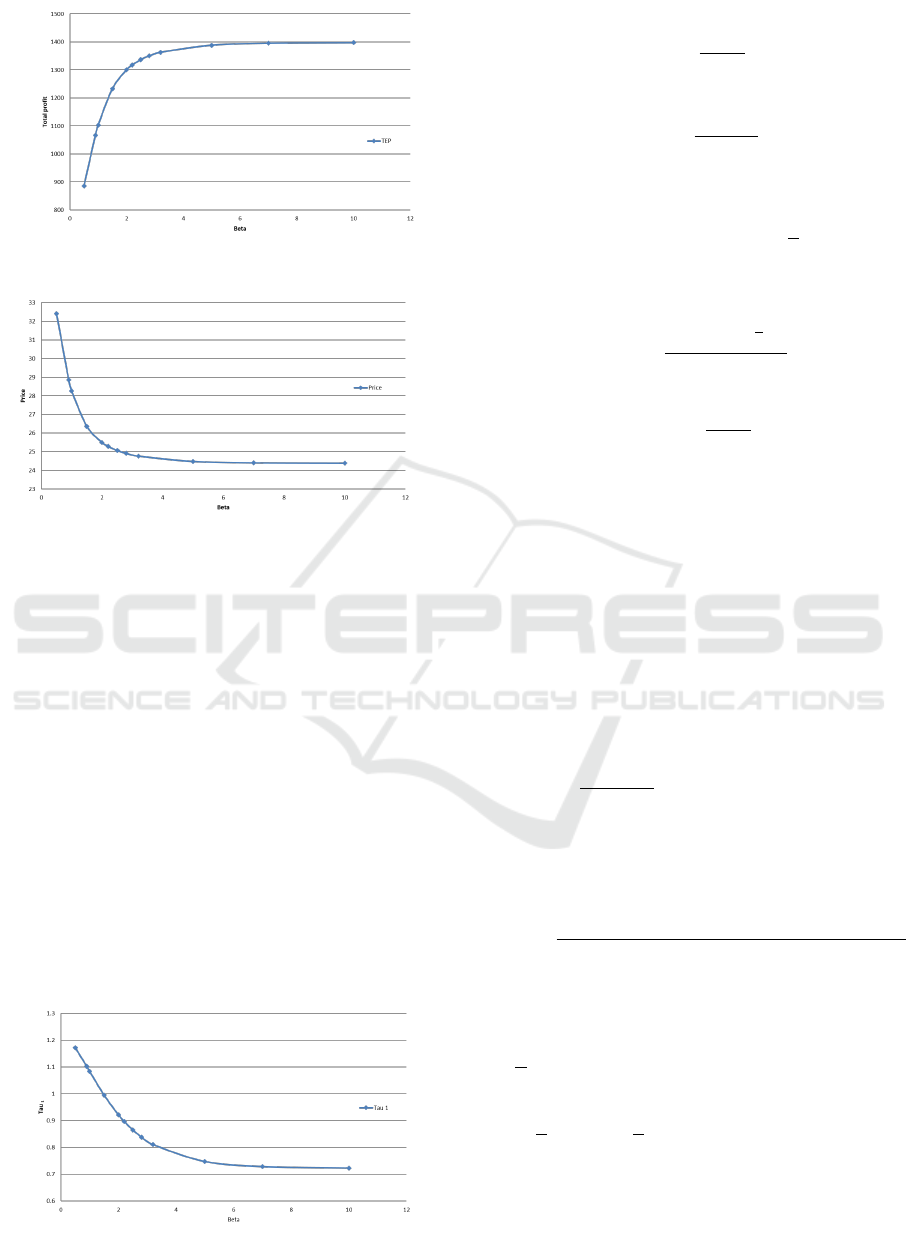
Figure 7: Seller’s expected proﬁt as β varies.

Figure 8: Selling price for varying β.

2.2 is still under consideration here.

At time of purchase, the consumer has two choices:

• Option 1: Buy the original product without war-

ranty at a fraction ρ (0 ≤ ρ ≤ 1) of the price p set

by the manufacturer and determined using model

1 presented above; or

• Option 2: Buy the original product with warranty

at price p.

The goal of model 2 is to formulate the Expected

Ownership Time per Cost Ratio (EOCR

) for both op-

tions (i = 1,2) and compare their behaviour through

the analysis of their difference ∆:

∆ = EOCR

− EOCR

. (12)

Figure 9: Proﬁle of the optimal τ

as β varies.

Option 1: without warranty

EOCR

EOT

ρ · p

EOCR

MT T F

ρ · p

where MT T F

is the expected lifetime of the ori-

ginal product

EOT

= MT T F

= θ · Γ



1 +





Γ(.) is the gamma function. Therefore,

EOCR

θ · Γ

1 +



i

ρ · p

. (13)

Option 2: with warranty

EOCR

EOT

(14)

A consumer enjoys his original new product from

purchase time up to the instant of the ﬁrst failure

which has expected duration MT T F

. At failure, the

consumer gets a replacement product that will have an

expected remaining lifetime of length RMT T F

if the

failure occurred in phase i. The original product fails

in phase i with probability [F(w

) − F(w

i−1

)]. There-

fore, the expected ownership time for option 2 is given

EOT

= MT T F

∑

i=1

RMT T F

i−1

[F(w

) − F(w

i−1

)]

(15)

where

RMT T F

1 − F(τ

)

∞

[1 − F(x)].dx ∀i ∈ 1, 2.

(16)

By deﬁnition, RMT T F

= MT T F

. Combining Equa-

tions (14) and (15), gives the expression for EOCR

EOCR

MT T F

∑

i=1

RMT T F

i−1

[F(w

) − F(w

i−1

)]

(17)

Finally, Equations (12) becomes:

∆ =

MT T F

∑

i=1

RMT T F

i−1

[F(w

) − F(w

i−1

)]

−

· Γ



1 +





(18)

The obtained mathematical model is solved for va-

rious scenarios in order to derive decision making po-

licies for the consumer organizations.

ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems

496

2.3.1 Numerical Results

Experiment #1: Change in w

and varying β

The ﬁrst set of experiments is designed to analyze the

recommendations made by the model for 4 warranty

policies when β changes. The 4 warranty policies dif-

fer in their value of w

. The values of w

and w

are

the same for all policies. Table 1 presents the results

obtained.

Table 1: Values of ∆ for various w

and varying β.

= .5 w

= .75 w

= 1 w

= 2

β w

= 2 w

= 2

= 3 w

= 3

0.5 0.06 0.05 0.04 0.03

0.9 0.02 0.02 0.02 0.02

1.0 0.02 0.02 0.02 0.02

1.5 0.01 0.01 0.01 0.02

2.0 0.01 0.01 0.01 0.01

3.0 0.00 0.01 0.01 0.02

4.0 0.00 0.00 0.01 0.02

5.0 0.00 0.00 0.01 0.02

6.0 -0.01 0.00 0.01 0.02

The results are also plotted on Figure 10 from

where two clear zones can be deﬁned. The zone deli-

mited by the red dotted outline depicts the area where

products can be bought without warranty. Products

falling in the zone above the red zone need to be pur-

chased along with one of the 4 warranty policies offe-

red. The following other observations can be made:

• The general proﬁle of each plot of ∆ as a function

of β shows a fast decrease for low values of β and

a stabilization for higher values. ∆ is higher for

β << 1 because early failures make the purchase

of warranty more valuable. ∆ stabilizes when in-

creasing β because of the resulting increase in re-

liability which decreases the likelihood of failure

and therefore the purchase of warranty does not

add signiﬁcant value to the consumer.

• Different warranty policies have different slopes

of the same proﬁle.

• A clear crossover point can be noticed on Figure

10. Policies with shorter Phase 0 (shorter w

) that

are preferred before the crossover point perform

poorly after the crossover point when the products

have higher reliability. Conversely, policies with

longer Phase 0 (longer w

) perform better after the

crossover point. In other words, a policy that is

good for newly designed products do worse with

seasoned or proven products with good reliability.

• Warranty policies with longer w

coverage are

less sensitive to increase in β values. It can be seen

on Figure 10 that the 4th policy has the smallest

amplitude over the complete range of β.

Experiment #2: Change in ρ and varying β

Here, numerical results are generated for two values

of ρ (0.95 and 0.85) to analyze the impact of the sel-

ling price over the decision to purchase the warranty

or not. The results obtained are in Table 2.

Table 2: Values of ∆ for varying β.

= .75 w

= 2 w

= 3

β ρ=0.95 ρ=0.85

0.5 0.06 0.05

0.9 0.03 0.02

1.0 0.02 0.02

1.5 0.02 0.01

3.0 0.01 0.01

4.0 0.01 0.00

6.0 0.00 0.00

As in the previous experiment, ∆ shows a decre-

asing trend with increasing β. The higher the price

without warranty (or the lower the warranty cost over

premium ratio) the higher the return or incentive to

buy the warranty.

3 CONCLUSIONS

This paper presented two mathematical models to de-

termine the optimal combination rebate warranty po-

licy when refurbished products are used for repla-

cements from both the manufacturer and consumer

point of views. One model was developed from the

manufacturers’ point of view to maximize the total

expected proﬁt and the second model dealt with the

maximization of the consumer’s expected ownership

time. Numerical experiments showed that appropri-

ate optimal decisions can be reached in the reuse of

second-hand products in honouring warranty. Both

the manufacturer and consumer groups can use these

models to improve proﬁtability levels and increase

ownership durations.

The authors are currently investigating a joint analysis

that considers both the seller and buyers’ perspectives

by formulating a multi-objective model to integrate

key factors such as brand loyalty and incentives. Case

studies from an appliance remanufacturer will be con-

ducted to validate the theoretical results obtained. A

Optimal Combination RebateWarranty Policy with Second-hand Products

497

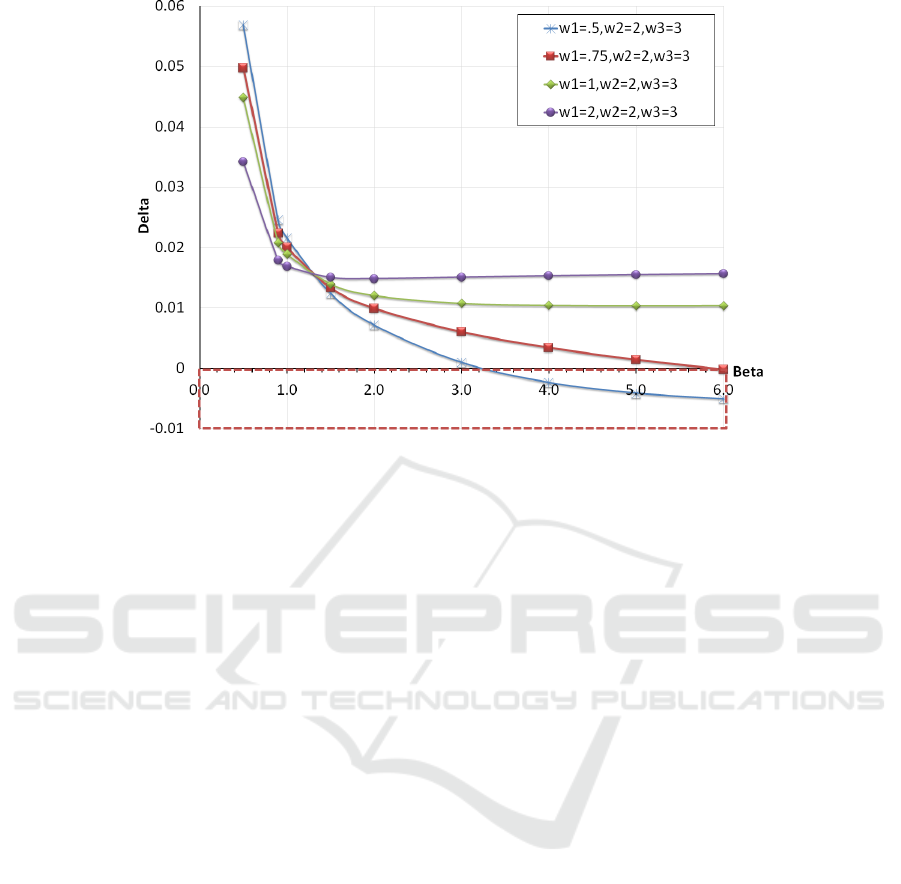
Figure 10: Proﬁle of ∆ for varying β.

variability analysis on a reduced set of selected so-

lutions (with high expected values) will also be per-

formed to test the robustness of the solutions. Future

extensions of this study can also cover new warranty

models suited for remanufactured products such as

pro-rata and hybrid pro-rata policies, and integration

of reconditioned products of different quality levels.

REFERENCES

Blischke, W. (1993). Warranty cost analysis. CRC Press.

Blischke, W. (1995). Product warranty handbook. CRC

Press.

Chari, N. (2015). Thematic Development of Recovery, Re-

manufacturing, and Support Models for Sustainable

Supply Chains. PhD thesis, Dalhousie University, Ha-

lifax.

Chari, N., Diallo, C., Venkatadri, U., and A

ıt-Kadi, D.

(2016a). Production planning in the presence of re-

manufactured spare components: an application in the

airline industry. The International Journal of Advan-

ced Manufacturing Technology, pages 1–12.

Chari, N., Diallo, C., Venkatadri, U., and Khatab, A.

(2016b). Modeling and analysis of a warranty policy

using new and reconditioned parts. Applied Stochastic

Models in Business and Industry, 32:539–553.

Chukova, S. and Shaﬁee, M. (2013). One-dimensional war-

ranty cost analysis for second-hand items: an over-

view. International Journal of Quality & Reliability

Management, 30(3):239–255.

Diallo, C., Venkatadri, U., Khatab, A., and Bhakthavatcha-

lam, S. (2016). State of the art review of quality, re-

liability and maintenance issues in closed-loop supply

chains with remanufacturing. In Press, International

Journal of Production Research, 0(0):1–20.

Glickman, T. S. and Berger, P. D. (1976). Optimal price

and protection period decisions for a product under

warranty. Management Science, 22(12):1381–1390.

Shaﬁee, M. and Chukova, S. (2013). Maintenance models

in warranty: A literature review. European Journal of

Operations Research, 229(3):561–572.

Su, C. and Wang, X. (2016). Optimal upgrade policy for

used products sold with two-dimensional warranty.

Quality and Reliability Engineering International.

Yeh, R. H., Chen, G.-C., and Chen, M.-Y. (2005). Optimal

age-replacement policy for nonrepairable products un-

der renewing free-replacement warranty. IEEE Tran-

sactions on Reliability, 54(1):92–97.

Yeh, R. H., Lo, H.-C., and Yu, R.-Y. (2011). A study of

maintenance policies for second-hand products. Com-

puters & Industrial Engineering, 60(3):438–444.

Yun, W. Y., Murthy, D. N. P., and Jack, N. (2008). Warranty

servicing with imperfect repair. International Journal

of Production Economics, 111(1):159–169.

ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems

498