Long Range Optical Truck Tracking

Christian Winkens and Dietrich Paulus

University of Koblenz-Landau, Institute for Computational Visualistics, Universit¨atsstr. 1, 56070 Koblenz, Germany

Keywords:

Off-road Platooning, Optical Tracking, Kalman ﬁlter, Autonomous Vehicles.

Abstract:

Platooning applications require precise knowledge about position and orientation (pose) of the leading vehicle

especially in rough terrain. We present an optical solution for a robust pose estimation using artiﬁcial mark-

ers and a camera as the only sensor. Temporal coherence of image sequences is used in a Kalman ﬁlter to

obtain precise estimates. Furthermore based on the marker detections we utilize an adaptive model building

algorithm which learns a keypoint based representation of the leading vehicle at runtime. The model is contin-

uously updated and allows a markerless tracking of the vehicle for up to 70 meters even when driving at high

velocities. The system is designed for and tested in off-road scenarios. A pose evaluation is performed in a

simulation testbed.

1 INTRODUCTION AND

MOTIVATION

A basic requirement for an intelligent vehicle is the

ability to detect and track other vehicles on its path

in order to perform platooning, namely, the automatic

following of a preceding vehicle. Therefore the so

called visual object tracking is an important platoon-

ing and computer vision problem which needs to full-

ﬁll realtime requirements. One of the main challenges

of such a tracking system is the handling of appear-

ance changes of the vehicle during platooning. Ap-

pearance changes can be caused varying illumination,

out-of-plane rotation and vehicle motion. Put simply,

the goal is to localize the target vehicle in a video se-

quence, given a bounding box that deﬁnes the object

in an initial frame. Long-term tracking algorithms

generally consist of three different modules: a tracker,

that estimates object motion, a detector, that local-

izes the object in the current frame and a learner that

updates the object/background model. A variety of

approaches have been proposed however they mostly

differ in the choice of the object representation, that

can include: object silhouette, geometric primitives,

points and more. Many proposed algorithms use key-

points for object representation where the main idea

is to break down the object into individual parts that

are easier to match to a descriptor database than a

complete representation of the object. The tracker is

initialized by taking the initial bounding box as the

source for positive samples and the surrounding as the

tracked vehicle

image plane

Figure 1: Imaging process P and measurements used for

pose estimation.

source for negative samples. One drawback of using

keypoints is that due to similar descriptors of object

and background elements matching is error-prone and

methods like RANSAC are needed to ﬁlter outliers.

The goal of our approach is to allow convoys to

move off-roads on rough terrain at relatively high ve-

locities, enabling precise position and orientation esti-

mation even with large distances between leading and

following vehicle. In order to solve these problem,

we use a mono-camera setup with a high image res-

olution and artiﬁcial markers on the leading vehicle

that allows an accurate pose reconstruction and makes

use of temporal coherence in order to track the lead-

ing vehicle with high precision in a short distance up

to 25 meters without any plane-world assumption as

proposed in (Winkens et al., 2015). Furthermore we

extend this approach and utilize a model learning al-

gorithm which uses the information from the marker

330

Winkens C. and Paulus D.

Long Range Optical Truck Tracking.

DOI: 10.5220/0006296003300339

In Proceedings of the 9th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2017), pages 330-339

ISBN: 978-989-758-220-2

reconstruction to initialize a keypoint based model

which is continuously updated and allows a marker-

less tracking of the vehicle for up to 70 meters even

when driving at high velocities or in rough terrain.

Our algorithm does not need any prior training or spe-

cial hardware for processing and relies only on artiﬁ-

cial markers for initialization.

This work is structured as follows: Section 2 gives

an overview of related work and the pre-requisites for

the work presented. Our approach is then introduced

(Section 3)). An evaluation is presented in Section 4

and discussed in Section 5.

2 RELATED WORK

Several research topics have to be taken into account

when developing an extended pose estimation system

that utilizes marker-based and marker-less tracking

mechanisms. In the following paragraphs, the rele-

vant state-of-the-art techniques are brieﬂy discussed.

2.1 Platooning

Platooning has already been discussed in many publi-

cations. Bergenheimet al. (Bergenhem et al., 2012)

provide a good overview to the topic. Vehicle-To-

Infrastructure Communication (V2I) or Vehicle-To-

Vehicle Communication (V2V) is utilized by a lot of

already published approaches such as (Gehring and

Fritz, 1997; Tank and Linnartz, 1997).

Benhimaneet al. (Benhimane et al., 2005) use a

camera and compute homographies to estimate the

pose of a leading vehicle. And Manzet al. (Manz

et al., 2011) utilize a particle ﬁlter, whereas

Frankeet al. (Franke et al., 1995) use triangulation.

2.2 Artiﬁcial Markers

Artiﬁcial markers are of common use, especially in

augmented reality (AR) and tracking applications.

Various different libraries have been developed and

are available free for use (Kato and Billinghurst,

1999; Schmalstieg et al., 2002; Fiala, 2005; Olson,

2011). We decided to use AprilTags (Olson, 2011) in

our system, to track a leading vehicle and to learn fea-

tures of it in an initialization phase. AprilTags allow

the full 6D localization of features from a single cam-

era image, which allows us a pose reconstruction of

an leading vehicle.

2.3 Tracking

The Kalman ﬁlter (Kalman, 1960) is of common use

in tracking applications. For example, Barth and

Franke (Barth and Franke, 2009; Barth and Franke,

2008) proposed a method for image-based tracking

of oncoming vehicles from a moving platform using

stereo-data and an extended Kalman ﬁlter. They used

images with a resolution of 640px by 480px.

Several surveys (Smeulders et al., 2014; Wu et al.,

2015) recently compared tracking performance of

several markerless trackers. According to the Vi-

sual Object Tracking challenge (VOT) (Kristan et al.,

2015; Kristan et al., 2016) challenge the top perform-

ing trackers applied learned features by convolutional

neural nets (CNN), which are quite new to the track-

ing community. The differences are found in differ-

ent localisation strategies. Due to the introduction of

neural networks huge progress have been made in re-

cent years. The MDNet tracker (Nam et al., 2014)

proposed by Nametal. is trained using a convolu-

tional neural network (CNN) and a set of videos with

ground-truth annotations to compute a generic repre-

sentation of the desired object. The winner of VOT

2016 (Nam et al., 2016) uses multiple collaborating

CNNs to track objects in visual sequences. Although

trackers based on neural networks deliver very good

results, they are mostly too slow, as the results of

(Kristan et al., 2015) indicate, to use them in realistic

tracking scenarios with real-time requirements right

now. Furthermore often special and costly GPUs are

needed for the algorithms to work. Usually it’s not

possible to train an object model a priori, the algo-

rithm must adapt to an object at runtime, which poses

a major drawback for CNN based methods which of-

ten rely on an a priori training.

Zhu et al. (Zhu et al., 2015) proposed an algo-

rithm which searches in the entire image for infor-

mative contours to adapt a generic edge-based object-

ness measure. Another method using kernel correla-

tion ﬁlters using the Fast Fourier Transform (FFT) is

presented by Henriquesetal. (Henriques et al., 2015),

which achieves good performance but cannot han-

dle the occlusion problem well. An real-time capa-

ble algorithm is presented by Henriqueset al. (Hare

et al., 2011), which extends an online structured out-

put SVM learning method, which is learned online,

to suit the tracking problem. Unfortunately Struck

does not handle scale variation, which is a major prob-

lem in our scenario where large scale variations ap-

pear. Another approach is to build models on the

distinction of the target against background by using

point features like BRISK (Leutenegger et al., 2011),

FREAK (Ortiz, 2012) or ORB (Rublee et al., 2011).

Long Range Optical Truck Tracking

331

Examples are proposed by Maresca et al. (Maresca

and Petrosino, 2013) and Nebehayetal. (Nebehay and

Pﬂugfelder, 2015). Nebehay uses BRISK features and

a static model in a combined matching and tracking

framework and a consensus-based clustering for out-

lier detection. Maresca however uses multiple key

point-based features together in combination with a

learning module which updates the object model, uti-

lizing a growing and pruning approach. Here the use

of multiple features sacriﬁces speed for improved ro-

bustness. As (Wu et al., 2015) stated, the use of a mo-

tion or a dynamic model is crucial for robust object

tracking, but the most evaluated trackers do not incor-

porate such components. Altough it could speed up

and improve robustness and efﬁciency. An active ap-

pearance model is used by Matthewset al. (Matthews

et al., 2004) to update models in an visual tracking

scenario.

3 OPTICAL TRACKING

APPROACH

In our setup we use a high resolution camera, which

is mounted on a vehicle that pursues a leading vehi-

cle. Two static artiﬁcial markers are mounted at the

back of the leading vehicle. This marker setup is ob-

served by the camera mounted on the following ve-

hicle. Obeserving the marker setup, our systems is

ablew to reconstruct the pose of the leading vehicle

at ranges up to 25 m and at the same time we learn a

model of the vehicle, so that a tracking of the vehi-

cle is possible when the markers can no longer recon-

structed because of a great distance from the preced-

ing vehicle. Furthermore, the learned model is used

to increase the stability of pose reconstruction done

by the Kalman ﬁlter in the close range.

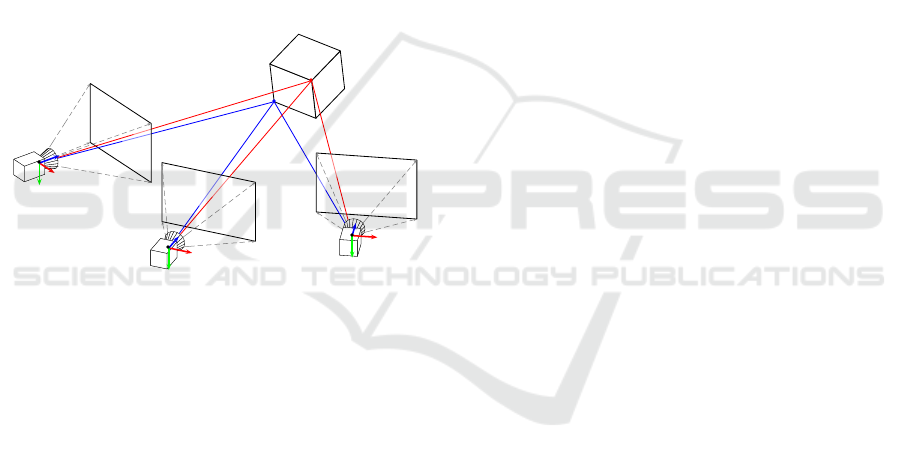
Figure 2 and Figure 3 illustrate the geometric

setup of the camera and the markers and deﬁne the

coordinate systems used in our system:

Symbol Coordinate System

C Camera

T Following Vehicle

Marker M

V Leading Vehicle

A pose is deﬁned as the position and orientation

of an object in 3-D space. It is deﬁned as a tuple

p = hs, qi with s ∈ IR

the position of the object rela-

tive to the origin of the coordinate system and q ∈ IR

the vector representation of a unit quaternion for the

rotation relative to the coordinate system’s orthonor-

mal bases.

x-direction

y-direction

z-direction

Figure 2: Deﬁned coordinate systems and orientation of the

orthonormal bases.

Figure 3: Artiﬁcial marker mounted on leading vehicle.

Our system can deal with various marker setups

and conﬁgurations, but at least one marker is required

for our method to work. The precision of the pose

estimation will increase with higher numbers of (vis-

ible) markers.

In our setup, two artiﬁcial markers are mounted

on the back of the leading vehicle. They are slightly

rotated in order to be viewable from the side as well

(see Figure 3).

3.1 Kalman Filter

As the estimation of the pose of the leading vehicle

is prone to uncertainties, a Kalman ﬁlter (Kalman,

1960) is utilized to improve the pose estimate. The

dynamic Kalman state of the vehicle pose is repre-

sented by a vector:

x =



, q

, v

, ω



∈ IR

Where s = (s

, s

)

the position and q ∈

, q = (q

, q

)

, the vector representation of

a unit quaternion, deﬁne the position and orientation

ICAART 2017 - 9th International Conference on Agents and Artiﬁcial Intelligence

332

of the leading vehicle relative to the following vehi-

cle. The vectors v ∈ IR

and ω ∈ IR

describe the sys-

tem’s linear and angular velocity. For more details on

our kalman tracking system please refer to (Winkens

et al., 2015).

3.2 (Re-)Initialization

At ﬁrst our system searches for our marker-system in

the given camera image. If visible the mounted mark-

ers are detected by our tracking system and a Kalman

ﬁlter is initialized. The pose of the leading vehicle

is tracked using the Kalman ﬁlter using a linear mo-

tion model. A good initial value of the pose p in the

dynamic state x is vital for proper estimation. When

launching the pose estimation process, pose p is ini-

tialized by solving the point correspondence problem

using the raw marker corner detections. If the algo-

rithm is not able to detect markers over a certain time,

it will fall back to the initialization mode.

3.3 Markerless Tracking

The maximum possible tracking range is directly lim-

ited by marker size and camera resolution. In order to

increase the range of the existing tracking system, it

is necessary not only to detect the markers and track

them, but to use the size of the vehicle and track the

vehicle itself. This requires to learn an abstracted

model of the vehicle, which is then used to track the

vehicle in each new frame of the data stream. As with

other trackers, the problem is then reduced to deter-

mine a bounding box enclosing the object, in each

frame. Our markerless tracking system is initialized

with the reconstructed pose and an initial bounding

box b

provided by the Kalman ﬁlter. The algorithm

then calculates keypointsκ

, ..., κ

on the initial frame

and splits them in object points K

= {κ

, ..., κ

}

and background points B

= {κ

, ..., κ

} by using the

supported bounding box as illustrated in Figure 4.

Based on this bounding box we calculate ORB fea-

tures and store them in two separate models for each

element of the two sets of points. In addition, the cen-

ter of the bounding box and the pairwise distances be-

tween the feature locations is calculated and stored.

Furthermore, the object points are normalized by the

relative position of the feature points to the bound-

ing box center. After receiving the next frame F

the marker-based (Kalman ﬁlter) tracking ﬁrst tries

to reconstruct a pose using the detected marker cor-

ners. In a second step the markerless tracking tries

to locate the desired object in the picture. A naive

approach would be to calculate the features through-

out the frame F

and search for correspondences with

Figure 4: Initialization of markerless tracker with K

nodel points (green) and B

as background points (red).

the object model. However, since the feature cal-

culation on a full resolution image would be very

time consuming the search space must be restricted

to meet real-time requirements. The initial object

model points are used to calculate the optical ﬂow

(yves Bouguet, 2000) between the two frames:

(x, y, t) = κ

(x+ dx, y + dy, 0 + dt) (1)

By utilizing optical ﬂow a potential region of interest

can be estimated, which is expanded by a certain fac-

tor to account for uncertainties. This bounding box

deﬁnes a subregion F

of the frame, which is taken to

compute the features. The features {κ

, ..., κ

} ∈ F

are now matched against a model consisting of object

and background features. To prevent from false corre-

spondences between the model and candidates all fea-

tures that correlate with background features are di-

rectly discarded from the matching process. The rest

is matched utilizing the distance ratio method (Lowe,

2004) to ﬁlter false positives. The correspondences

thus found now give the set of ϒ

. After that the

matched correspondences using optical ﬂow estima-

tion and global matching are fused, wherein the opti-

cal ﬂow matches overrule the global matching. Using

the matched features we estimate scale s and rotation

α as proposed by (Kalal et al., 2010) and (Nebehay

and Pﬂugfelder, 2014).

s = med

(

||κ

− κ

||κ

− κ

, i 6= j

(2)

α = med({atan(κ

−κ

)− atan(κ

−κ

), i 6= j}) (3)

A static appearance model is used, which is based

on the initial appearance of the object, composed of

Long Range Optical Truck Tracking

333

the initial descriptors K

. The model can not adapt to

appearance changes of the object or the background.

This is in the present scenario particularly relevant as

very large changes occur in the scaling of the object,

also the background can underly massive changes. To

account for this, the background model is adapted pe-

riodically to account for changes in the environment.

Features from the background database are picked

randomly and replaced by features from the current

frame, which do not intersect with the detected ob-

ject. Furthermore a homography is estimated based

on the matched features using the RANSAC method

(Fischler and Bolles, 1981). Correspondences which

do not correspond to the calculated homography are

sorted out as outliers. Thus, a correct data associa-

tion, which is essential for the reconstruction of the

points, can be achieved.

3.4 Feature Pose Reconstruction

Figure 5: Shematic description of our feature pose recon-

struction approach.

To support the marker based pose estimation, we

use features from the previouslylearned object model,

as described previously in 3.3. We try to estimate the

3-D position of these points, relative to the origin of

the preceding vehicle by accounting different obser-

vations of the feature in different frames during track-

ing, as illustrated by Figure 5. Knowing the 3-D po-

sition of the these feature points we could use their

observations in new frames to update the Kalman ﬁl-

ter and support marker-based tracking.

The observation of a feature d

which is seen from

camera pose c

can be expressed as an measurement

in the form:

h(m

, c

) = P (T (c

)

−1

· m

) (4)

Where P denotes the intrinsic camera model and

T (c

)

−1

describes the transformation of the feature

points in the coordinate system of the camera. Using

this prediction function the total back projection error

over alle features can now denoted as:

argmin

∗

∑

||h(m

, c

) − d

(5)

Which deﬁnes the sum of all differences between the

predicted h(., .) and the actually observed positions

of feature d

. The minimum represents the opti-

mum utilization of all 3D feature positions and cam-

era poses. The optimization of this non-linear least-

squares problem is solved using the library Ceres

(Agarwal et al., ). The basic prerequisite for the bun-

dle adjustment described above is the robust tracking

of feature points from different camera views. Since

feature tracking is never perfect, the system must be

able to deal with outliers, or mistracked points. For

this reason, we use a robust loss function which lim-

its the inﬂuence of coarse outliers and effectively pre-

vents individualwrong tracked features from mislead-

ing the reconstruction.

Equation 5 is non-linear and non-convex. As a re-

sult, the convergence of the optimization process to

the correct solution strongly depends on initialization

parameters. We take the initialization of the camera

poses from the marker-based tracking and initialize

the feature locations in the origin of the preceding ve-

hicle. Simultaneously, a prior is set on the feature lo-

cations, which expresses a low certainty that the fea-

ture lies in the vicinity of the origin of the preceding

vehicle. This is useful to limit the uncertainty in z-

direction especially in the case of only a few observa-

tions with low baseline.

The used artiﬁcial markers are visible in nearly all

camera frames, which are used to reconstruct the fea-

tures and the corners of these markers can be seen as

normal feature points. But their position in the coor-

dinate system is ﬁxed and known to our system, so we

use them to enhance the reconstruction because Ceres

allows selective ﬁxing of parameters during optimiza-

tion. Therefore we add the corner points to the opti-

mization problem and declared them as ﬁxed. The

ﬁxed corner points also deﬁne the scale of the op-

timized points that could not be determined without

such a metric reference.

Solving this system of equations is computation-

ally intensive and requires much time. Each new

frame provides, according to the correspondences

found, new terms to the optimization problem, which

will bloat the system of equations in a short period of

time. Furthermore provide frames which are tempo-

rally close to each other little new information, since

the spatial distance between them is very low. Also

note that great distances between camera and vehicle

lead to worse results in feature matching and tracking.

Because the risk of false correspondencesheavily cor-

relates with increasing distance.

Therefore we ensure that only information from

camera poses with a euclidean distance of 0.2m and

more to the others is added to the system. In addition,

ICAART 2017 - 9th International Conference on Agents and Artiﬁcial Intelligence

334

only camera poses are added, which are below a dis-

tance of 20m to the vehicle driving ahead to minimize

risk of false correspondences.

Due to the automatic initialization of the mark-

erless tracking it is possible that features are used,

which do not belong to the vehicle or are very weak.

This may distract the tracking system in the long run

because it raises the chance of false correspondences.

Therefore, a model management has been integrated,

which periodically checks the quality of the model

and exchanges weak features. We calculate the re-

projection error of all reconstructed feature positions

with respect to all reconstructed poses and take the

mean. In a second step all features with an reprojec-

tion error greater than the mean are removed from the

model and new features are added instead.

3.5 Pose estimation

The learned and 3-D reconstructed model points are

additionally used by the Kalman ﬁlter at runtime to

improve the pose estimation. For this purpose, the

observations z

of the reconstructed keypoints m

are used as measurements for additional kalman up-

date steps. Observations are predicted similar to the

marker corner points using the measurement model:

= P (T

T→C

· T

V→T

, q

) · m

) + g

(6)

The two-dimensional random variable g

∼ N (0, R

)

models the measuring noise, which is assumed here

as 1px in the u- or v-direction.

The measurement model transforms the model

point m

using the p

, q

from the dynamic system

state x

of the Kalman ﬁlter into the coordinate sys-

tem of the following vehicle. Using the known po-

sition of the camera in the rear-running vehicle, the

point is transformed into the camera coordinate sys-

tem C. The function P performs a projection onto

the image plane as well as the radial distortion of the

point, just as before applying the known intrinsic cal-

ibration of the camera. The described Kalman update

step is executed exactly once for the model points ob-

served in the current frame. The remaining procedure

of the Kalman ﬁlter remains unchanged.

4 EVALUATION

The system is designed to work at high velocities

and in off-road scenarios. Therefore capturing ground

truth data for evaluation is a difﬁcult issue, as a high

precision in the pose of both the following and the

leading vehicle is mandatory. External position track-

ing systems do not suit the demands as the required

off-road track is too long and it is therefore too cost-

and time-intense to equip with appropriate hardware.

Standaerd radio based position systems such as GPS

or Galileo do not offer an adequate pose quality.

Equipping one of the vehicles with hardware like 3-

D LIDAR sensors does not present a solution as well,

because the sensors themselves have uncertainties. To

make things worse, we consider an off-road scenario

where a full 6-D pose is required as a ground truth.

4.1 Evaluation using Synthetic Camera

Images

Our approach for evaluation of the marker-based

tracking is based on a virtual testbed. A simula-

tion environment is utilized for the generation of

synthetic camera images: The simulation environ-

ment used is derived from published approaches for

pose estimate evaluations (Fuchs et al., 2014b; Fuchs

et al., 2014a) using synthetic images. Its adaptive

architecture allows an easy integration. The camera

in the simulation environment can be conﬁgured to

match various resolutions and opening angles to test

the impact on the pose quality. The intrinsic cam-

era parameters needed for the pose tracking can eas-

ily be derived from the simulation conﬁguration fol-

lowing the method described by Fuchsetal. (Fuchs

et al., 2014b). The evaluation results of our marker-

based tracking system were proposed previously in

(Winkens et al., 2015). A distance measurement de-

ﬁned by Park (Park, 1995) was used and discussed by

Huynh (Huynh, 2009):

Γ(q, q

′

) = klog(Φ(q), Φ(q

′

)

Where Φ : IR

→ IR

3×3

converts a quaternion to a ro-

tation matrix. In a ﬁrst evaluation, the rendered image

sequences have directly been processed the Kalman

tracking as proposed above. In a second pass, Gaus-

sian noise N (0, I

2×2

) was added to the raw marker

detections extracted from the image. This way, we

were able to quantify the robustness of our method

using noisy data. The synthetic tests, as published

in (Winkens et al., 2015) show that the tracking sys-

tem has a translation error of 7, 3 cm at a distance of

8m.The average error in the orientation (avg|Γ|) is

0.06Rad ≈ 3.4Deg proving the robustness and preci-

sion of the system proposed.

4.2 Off-road Testing Scenario

Evaluation of the marker-free tracking extension for

long range outdoor tracking is difﬁcult, as these syn-

thetic tests are not applicable. A good evaluation

Long Range Optical Truck Tracking

335

(a) Markerless tracking in the rain. The tracked vehicle is

marked with red bounding box.

(b) Magniﬁed version, with tracked vehicle in red bounding-

box and matched features (colored circles).

Figure 6: Visualization of our long range markerless track-

ing during rain.

would require two Real Time Kinematic (RTK) sys-

tems mounted on both vehicles. Unfortunately, we

do not own such a system, but we plan to equip

our vehicles with it in the near future. Therefore

pose estimation system as proposed in this publication

has been tested and evaluated using datasets specif-

(a) Long range markerless tracking. The tracked vehicle is

marked with a red bounding box.

(b) Magniﬁed version of the above image with matched fea-

tures from object model (colored circles).

Figure 7: Visualization of our long range markerless track-

ing.

ically recorded for this purpose with velocities up

to 60km/h. A truck with a artiﬁcial marker system

mounted on its back was followed by another vehicle

equipped with a high resolution camera. The recorded

data is used as the input for our system and is pro-

cessed in realtime. The vehicle tracked by our track-

ing system is highlighted with a red bounding-box in

the camera images, facilitating a visual examination

of our results in Figure 6 and Figure 7. Addition-

ICAART 2017 - 9th International Conference on Agents and Artiﬁcial Intelligence

336

ally we provide a video which can be viewed here

The examination showed that the system provided a

robust tracking up to a range of 70 m while process-

ing at 10 to 15Hz on standard mobile-computer hard-

ware. However, a quantitative analysis of the system

cannot be done in this scenario, because no reliable

ground truth pose information is available. Together

with this work we provide a video, which allows the

visual evaluation of the quality of the tracker.

5 CONCLUSION

We proposed an extended optical tracking mechanism

that only uses one camera and artiﬁcial markers to

track a vehicle driving at high velocities and great dis-

tances. A Kalman ﬁlter is utilized to include the ad-

vantages of temporal coherence. Our system is able

of estimating the relative pose between two vehicles

in real-time up to 26 m and tracking the vehicle itself

within a range up to 70 m. At an average distance of

8m, the average absolute of the Kalman ﬁlter error in

the translation, including artiﬁcial noise, (avg|∆|) is

about 7.3cm with an average error in the orientation

of(avg|Γ|) 0.06Rad ≈ 3.4Deg.

With the pose estimation and markerless track-

ing proposed, we introduced an algorithm capable of

tracking leading vehicles in off-road platooning sce-

narios, without the need for communication and/or in-

frastructure. The leading vehicle could therefore be a

regular truck equipped with a marker pattern. This

saves time and reduces costs signiﬁcantly, as no com-

plex setup is necessary. The system works indepen-

dently from any external services and infrastructure.

The proposed system learns a model by detecting fea-

tures on the leading vehicle at runtime, so that the

pose of the vehicle can still be estimated even when

the leading vehicle gets too far away to detect the arti-

ﬁcial markers. In closer range scenarios, dynamic fea-

tures improve the accuracy of the estimated pose. We

will further investigate the use of a second camera to

enhance tracking and pose estimation precision. Fur-

thermore we will equip our vehicles with some RTK

systems to provide a ground truth and allow a proper

evaluation in the near future.

ACKNOWLEDGEMENTS

This work was partially funded by Wehrtechnische

Dienststelle 41 (WTD), Koblenz, Germany.

https://www.dropbox.com/s/ly15h24085uyggp/

longrangetracking.mp4

REFERENCES

Agarwal, S., Mierle, K., and Others. Ceres solver.

Barth, A. and Franke, U. (2008). Where will the oncom-

ing vehicle be the next second? In IEEE Intelligent

Vehicles Symposium, pages 1068–1073.

Barth, A. and Franke, U. (2009). Estimating the driving

state of oncoming vehicles from a moving platform

using stereo vision. IEEE Transactions on Intelligent

Transportation Systems, 10(4):560–571.

Benhimane, S., Malis, E., Rives, P., and Azinheira, J.

(2005). Vision-based control for car platooning using

homography decomposition. In IEEE International

Conference on Robotics and Automation, pages 2161–

2166.

Bergenhem, C., Shladover, S., Coelingh, E., Englund, C.,

and Tsugawa, S. (2012). Overview of platooning sys-

tems. In Proceedings of the 19th ITS World Congress,

Vienna.

Fiala, M. (2005). Artag, a ﬁducial marker system using

digital techniques. In IEEE Computer Society Con-

ference on Computer Vision and Pattern Recognition,

volume 2, pages 590–596. IEEE.

Fischler, M. A. and Bolles, R. C. (1981). Random sample

consensus: a paradigm for model ﬁtting with appli-

cations to image analysis and automated cartography.

Communications of the ACM, 24(6):381–395.

Franke, U., Bottiger, F., Zomotor, Z., and Seeberger, D.

(1995). Truck platooning in mixed trafﬁc. In IEEE

Intelligent Vehicles Symposium, pages 1–6.

Fuchs, C., Eggert, S., Knopp, B., and Z¨obel, D. (2014a).

Pose detection in truck and trailer combinations for

advanced driver assistance systems. In IEEE Intelli-

gent Vehicles Symposium Proceedings, pages 1175–

1180. IEEE.

Fuchs, C., Z¨obel, D., and Paulus, D. (2014b). 3-d pose de-

tection for articulated vehicles. In 13th International

Conference on Intelligent Autonomous Systems (IAS).

Gehring, O.and Fritz,H. (1997). Practical results of a longi-

tudinal control concept for truck platooning with vehi-

cle to vehicle communication. In IEEE Conference on

Intelligent Transportation System (ITSC), pages 117–

122.

Hare, S., Saffari, A., and Torr, P. H. (2011). Struck: Struc-

tured output tracking with kernels. In Computer Vi-

sion (ICCV), 2011 IEEE International Conference on,

pages 263–270. IEEE.

Henriques, J. F., Caseiro, R., Martins, P., and Batista, J.

(2015). High-speed tracking with kernelized corre-

lation ﬁlters. Pattern Analysis and Machine Intelli-

gence, IEEE Transactions on, 37(3):583–596.

Huynh, D. (2009). Metrics for 3d rotations: Comparison

and analysis. Journal of Mathematical Imaging and

Vision, 35(2):155–164.

Kalal, Z., Mikolajczyk, K., and Matas, J. (2010). Forward-

backward error: Automatic detection of tracking fail-

ures. In In Proceedings of the 2010 20th International

Conference on Pattern Recognition, ICPR 10, pages

2756–2759. IEEE Computer Society.

Long Range Optical Truck Tracking

337

Kalman, R. E. (1960). A new approach to linear ﬁltering

and prediction problems. Journal of Fluids Engineer-

ing, 82(1):35–45.

Kato, H. and Billinghurst, M. (1999). Marker tracking and

hmd calibration for a video-based augmented reality

conferencing system. In 2nd IEEE and ACM Inter-

national Workshop on Augmented Reality. (IWAR’99)

Proceedings., pages 85–94. IEEE.

Kristan, M., Leonardis, A., Matas, J., Felsberg, M.,

Pﬂugfelder, R.,

Cehovin, L., Voj´ır, T., H¨ager, G.,

Lukeˇziˇc, A., Fern´andez, G., Gupta, A., Petrosino, A.,

Memarmoghadam, A., Garcia-Martin, A., Sol´ıs Mon-

tero, A., Vedaldi, A., Robinson, A., Ma, A. J., Var-

folomieiev, A., Alatan, A., Erdem, A., Ghanem, B.,

Liu, B., Han, B., Martinez, B., Chang, C.-M., Xu,

C., Sun, C., Kim, D., Chen, D., Du, D., Mishra, D.,

Yeung, D.-Y., Gundogdu, E., Erdem, E., Khan, F.,

Porikli, F., Zhao, F., Bunyak, F., Battistone, F., Zhu,

G., Roffo, G., Subrahmanyam, G. R. K. S., Bastos,

G., Seetharaman, G., Medeiros, H., Li, H., Qi, H.,

Bischof, H., Possegger, H., Lu, H., Lee, H., Nam, H.,

Chang, H. J., Drummond, I., Valmadre, J., Jeong, J.-c.,

Cho, J.-i., Lee, J.-Y., Zhu, J., Feng, J., Gao, J., Choi,

J. Y., Xiao, J., Kim, J.-W., Jeong, J., Henriques, J. F.,

Lang, J., Choi, J., Martinez, J. M., Xing, J., Gao, J.,

Palaniappan, K., Lebeda, K., Gao, K., Mikolajczyk,

K., Qin, L., Wang, L., Wen, L., Bertinetto, L., Ra-

puru, M. K., Poostchi, M., Maresca, M., Danelljan,

M., Mueller, M., Zhang, M., Arens, M., Valstar, M.,

Tang, M., Baek, M., Khan, M. H., Wang, N., Fan,

N., Al-Shakarji, N., Miksik, O., Akin, O., Moallem,

P., Senna, P., Torr, P. H. S., Yuen, P. C., Huang, Q.,

Martin-Nieto, R., Pelapur, R., Bowden, R., Lagani`ere,

R., Stolkin, R., Walsh, R., Krah, S. B., Li, S., Zhang,

S., Yao, S., Hadﬁeld, S., Melzi, S., Lyu, S., Li, S.,

Becker, S., Golodetz, S., Kakanuru, S., Choi, S., Hu,

T., Mauthner, T., Zhang, T., Pridmore, T., Santopietro,

V., Hu, W., Li, W., H¨ubner, W., Lan, X., Wang, X.,

Li, X., Li, Y., Demiris, Y., Wang, Y., Qi, Y., Yuan,

Z., Cai, Z., Xu, Z., He, Z., and Chi, Z. (2016). The

Visual Object Tracking VOT2016 Challenge Results,

pages 777–823. Springer International Publishing.

Kristan, M., Matas, J., Leonardis, A., Felsberg, M.,

Cehovin, L., Fernandez, G., Vojir, T., H¨ager, G.,

Nebehay, G., Pﬂugfelder, R., Gupta, A., Bibi, A.,

Lukeˇziˇc, A., Garcia-Martin, A., Saffari, A., Petrosino,

A., Montero, A. S., Varfolomieiev, A., Baskurt, A.,

Zhao, B., Ghanem, B., Martinez, B., Lee, B., Han,

B., Wang, C., Garcia, C., Zhang, C., Schmid, C., Tao,

D., Kim, D., Huang, D., Prokhorov, D., Du, D., Ye-

ung, D.-Y., Ribeiro, E., Khan, F. S., Porikli, F., Bun-

yak, F., Zhu, G., Seetharaman, G., Kieritz, H., Yau,

H. T., Li, H., Qi, H., Bischof, H., Possegger, H., Lee,

H., Nam, H., Bogun, I., chan Jeong, J., il Cho, J.,

Lee, J.-Y., Zhu, J., Shi, J., Li, J., Jia, J., Feng, J.,

Gao, J., Choi, J. Y., Kim, J.-W., Lang, J., Martinez,

J. M., Choi, J., Xing, J., Xue, K., Palaniappan, K.,

Lebeda, K., Alahari, K., Gao, K., Yun, K., Wong,

K. H., Luo, L., Ma, L., Ke, L., Wen, L., Bertinetto, L.,

Pootschi, M., Maresca, M., Danelljan, M., Wen, M.,

Zhang, M., Arens, M., Valstar, M., Tang, M., Chang,

M.-C., Khan, M. H., Fan, N., Wang, N., Miksik, O.,

Torr, P. H. S., Wang, Q., Martin-Nieto, R., Pelapur,

R., Bowden, R., Laganiere, R., Moujtahid, S., Hare,

S., Hadﬁeld, S., Lyu, S., Li, S., Zhu, S.-C., Becker, S.,

Duffner, S., Hicks, S. L., Golodetz, S., Choi, S., Wu,

T., Mauthner, T., Pridmore, T., Hu, W., H¨ubner, W.,

Wang, X., Li, X., Shi, X., Zhao, X., Mei, X., Shizeng,

Y., Hua, Y., Li, Y., Lu, Y., Li, Y., Chen, Z., Huang, Z.,

Chen, Z., Zhang, Z., and He, Z. (2015). The visual

object tracking vot2015 challenge results.

Leutenegger, S., Chli, M., and Siegwart, R. Y. (2011).

Brisk: Binary robust invariant scalable keypoints. In

Proceedings of the 2011 International Conference on

Computer Vision, ICCV ’11, pages 2548–2555, Wash-

ington, DC, USA. IEEE Computer Society.

Lowe, D. G. (2004). Distinctive image features from scale-

invariant keypoints. International Journal of Com-

puter Vision, 60:91–110.

Manz, M., Luettel, T., von Hundelshausen, F., and Wuen-

sche, H.-J. (2011). Monocular model-based 3d vehi-

cle tracking for autonomous vehicles in unstructured

environment. In IEEE International Conference on

Robotics and Automation (ICRA), pages 2465–2471.

Maresca, M. E. and Petrosino, A. (2013). Image Analy-

sis and Processing – ICIAP 2013: 17th International

Conference, Naples, Italy, September 9-13, 2013, Pro-

ceedings, Part II, chapter MATRIOSKA: A Multi-

level Approach to Fast Tracking by Learning, pages

419–428. Springer Berlin Heidelberg, Berlin, Heidel-

berg.

Matthews, I., Ishikawa, T., and Baker, S. (2004). The tem-

plate update problem. IEEE Transactions on Pattern

Analysis & Machine Intelligence, (6):810–815.

Nam, H., Baek, M., and Han, B. (2016). Modeling and

propagating cnns in a tree structure for visual tracking.

arXiv preprint arXiv:1608.07242.

Nam, H., Hong, S., and Han, B. (2014). Online graph-based

tracking. In Computer Vision–ECCV 2014, pages

112–126. Springer.

Nebehay, G. and Pﬂugfelder, R. (2014). Consensus-based

matching and tracking of keypoints for object track-

ing. In Applications of Computer Vision (WACV),

2014 IEEE Winter Conference on, pages 862–869.

IEEE.

Nebehay, G. and Pﬂugfelder, R. (2015). Clustering of

Static-Adaptive correspondences for deformable ob-

ject tracking. In Computer Vision and Pattern Recog-

nition. IEEE.

Olson, E. (2011). AprilTag: A robust and ﬂexible visual

ﬁducial system. In 2011 IEEE International Con-

ference on Robotics and Automation (ICRA), pages

3400–3407. IEEE.

Ortiz, R. (2012). Freak: Fast retina keypoint. In Proceed-

ings of the 2012 IEEE Conference on Computer Vision

and Pattern Recognition (CVPR), CVPR ’12, pages

510–517, Washington, DC, USA. IEEE Computer So-

ciety.

Park, F. C. (1995). Distance metrics on the rigid-body mo-

tions with applications to mechanism design. Journal

of Mechanical Design, 117(1):48–54.

Rublee, E., Rabaud, V., Konolige, K., and Bradski, G.

(2011). Orb: An efﬁcient alternative to sift or surf. In

Proceedings of the 2011 International Conference on

ICAART 2017 - 9th International Conference on Agents and Artiﬁcial Intelligence

338

Computer Vision, ICCV ’11, pages 2564–2571, Wash-

ington, DC, USA. IEEE Computer Society.

Schmalstieg, D., Fuhrmann, A., Hesina, G., Szalav´ari, Z.,

Encarnac¸ao, L. M., Gervautz, M., and Purgathofer, W.

(2002). The Studierstube augmented reality project.

Presence: Teleoperators and Virtual Environments,

11(1):33–54.

Smeulders, A. W., Chu, D. M., Cucchiara, R., Calder-

ara, S., Dehghan, A., and Shah, M. (2014). Visual

tracking: An experimental survey. Pattern Analy-

sis and Machine Intelligence, IEEE Transactions on,

36(7):1442–1468.

Tank, T. and Linnartz, J.-P. (1997). Vehicle-to-vehicle com-

munications for avcs platooning. IEEE Transactions

on Vehicular Technology, 46(2):528–536.

Winkens, C., Fuchs, C., Neuhaus, F., and Paulus, D. (2015).

Optical truck tracking for autonomous platooning.

In Azzopardi, G. and Petkov, N., editors, Computer

Analysis of Images and Patterns: 16th International

Conference, CAIP 2015, Valletta, Malta, volume 9257

of LNCS, pages 38–48, Cham. Springer.

Wu, Y., Lim, J., and Yang, M.-H. (2015). Object track-

ing benchmark. Pattern Analysis and Machine Intelli-

gence, IEEE Transactions on, 37(9):1834–1848.

yves Bouguet, J. (2000). Pyramidal implementation of the

lucas kanade feature tracker. Intel Corporation, Mi-

croprocessor Research Labs.

Zhu, G., Porikli, F., and Li, H. (2015). Tracking randomly

moving objects on edge box proposals. arXiv preprint

arXiv:1507.08085.

Long Range Optical Truck Tracking

339