A Global Path Planning Strategy for a UGV from Aerial Elevation

Maps for Disaster Response

D. C. Guastella, L. Cantelli, C. D. Melita and G. Muscato

Dipartimento di Ingegneria Elettrica Elettronica e Informatica, Università degli Studi di Catania, Catania, Italy

Keywords: Outdoor Environments, Rough Terrain, Unmanned Aerial Vehicle, Tracked Vehicle, Traversability, Path

Planning.

Abstract: An approach for global path planning of an Unmanned Ground Vehicle (UGV) is proposed, including basic

traversability analysis of the rough terrain to get through. The navigation capabilities of the UGV, in

performing such analysis, are considered. The here proposed solution is organized into two following

phases: first an aerial scan of the environment is executed by a UAV (Unmanned Aerial Vehicle) and the

elevation map of the area is built; after that, a set of processing algorithms is applied to such surface model

to derive a 2D costmap (whose costs are based on the prior traversability analysis) which is given as input of

a D* path planner. The resulting path can be eventually delivered as a sequence of waypoints for a

navigation controller on the field mobile platform.

1 INTRODUCTION

The need to have an autonomous robot moving

across outdoor unstructured environments is not

fully fulfilled by current state of the art in robotics,

although it does represent a crucial point especially

for disaster-response robots. Cooperative systems,

namely unmanned aerial and ground vehicles wor-

king together, appear to show good performances for

the above mentioned applications, thus justifying the

increased interest on such approach in robotics

research. A recent result is reported by Siegwart et

al., (2015), where mechanical and structural aspects

of a legged robot and a fixed-wing unmanned aerial

vehicle are enhanced in order to improve their

autonomy and stability in those harsh environments

resulting from natural disasters. In some cases, the

development of cooperative multi-robot systems has

been encouraged by international robotics

competitions, like EuRathlon (Schneider,

Wildermuth and Wolf, 2015) or RoboCup Rescue

(Kitano and Tadokoro, 2001), as in the case

represented by ICARUS team, described by

Marques et al. (2016), which was able to create

cooperating robotic platforms in ground, air, and

even maritime domains. It is apparent that there is

the need to combine the contributions of

heterogeneous platforms, especially when facing

search and rescue scenarios. In addition, the

difficulty of dealing with such risky environments is

the severely limited possibility to perform non-

destructive trials in the area of interest with the

robotic platforms, in particular for UAVs. To

address this issue some solutions have been

proposed (Astuti et al., 2008).

The aim of the present work is to set up a

procedure for the global path planning of an

unmanned ground vehicle within an outdoor

unstructured environment, taking into account the

specific motion capabilities of the considered

vehicle. The planning procedure is described as

follows: starting from a Digital Elevation Model

(DEM), which is built from the aerial photographic

scan of the environment done by a multi-rotor, a

traversability analysis on such terrain surface is

performed, and finally an optimal path is computed,

in terms of reducing the traversing cost. The path is

planned with the D* algorithm (Stentz, 1994). The

latter was preferred over other planning methods

since it gives the possibility to include costs into the

map and, moreover, it is optimized in replanning

whenever such map of costs, i.e. the costmap,

changes. The robotic platform considered in this

work is the U-Go Robot, a tracked vehicle designed

for rough terrain navigation (Bonaccorso et al.,

2012), shown in Figure 1.

Guastella D., Cantelli L., Melita C. and Muscato G.

A Global Path Planning Strategy for a UGV from Aerial Elevation Maps for Disaster Response.

DOI: 10.5220/0006298303350342

In Proceedings of the 9th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2017), pages 335-342

ISBN: 978-989-758-219-6

335

The details about the digital elevation model

reconstruction are given in Section 2, while Section

3 describes the first basic processing on such model,

focusing on our case study. Then Section 4 reports

the generation of the costmap, taking into account

the traversability of the terrain with respect to our

robotic platform. This point is the core and

innovative part of the work. In Section 5 the results

provided by the D* planner are shown, confirming

the avoidance of those areas particularly hostile to

be traversed. The final section includes a summary

and an outlook for the current project.

Figure 1: The U-Go Robot.

2 DEM RECONSTRUCTION

The starting data of the whole procedure is the DEM

of the outdoor environment under inspection. This

kind of model is typically referred to as 2.5D

representation of the real world. The terrain surface

to be represented is divided into cells and for each

cell the highest altitude is stored, thus obtaining a

matrix of altitudes. The result is a top view of the

environment; therefore, the main drawback of the

elevation maps consists of the impossibility to

include overhanging structures or multiple height

levels for one cell. However, they are still a good

trade-off between computing power and

representation accuracy in modeling outdoor areas.

Each value inside the elevation matrix is pointed out

with a couple of integers indicating its row and

column. However, these heights have a relative

distance in the real world, given by the resolution of

the DEM, i.e. the size of the cells the terrain was

divided into.

An innovative aspect lies in the DEM

reconstruction. In particular, a scanning mission is

previously performed by a quad-copter, during

which the UAV autonomously covers the whole area

to be reconstructed and takes regularly spaced

pictures by means of a stabilized on-board camera.

Then a commercial mapping software, Pix4Dmapper

Pro, processes all the acquired pictures to recreate

the 3D structure of the scanned terrain. Among

different kind of processing outputs, the mapping

software delivers the digital elevation model, along

with its georeferencing information.

The environment considered in this case study is

the external area of D.I.E.E.I. laboratories of the

University of Catania. The resulting DEM is given

in UTM coordinates (Universal Transverse of

Mercator) with ellipsoidal heights (WGS84).

Furthermore, we focused our attention on a

specific area within the outdoor environment, which

resembles a landslide scenario, including areas with

different slopes and level of navigation difficulties.

The 3D textured mesh of this area is reported in

Figure 2.

With an average flight altitude of 30 m and an

on-board camera of 12.4 megapixels, the

reconstructed digital elevation model has a

resolution lower than 1 cm/cell (0.986 cm/cell)

along both the North and East directions.

Figure 2: The 3D textured mesh of the landslide-like area

recreated by the mapping software.

3 DEM PRE-PROCESSING

The overall processing of the elevation map is

carried out in Matlab. Firstly the DEM, saved in

geotiff format, is loaded in Matlab including its

georeferencing information. At the same time the

DEM is downsampled, thus obtaining a final spatial

resolution of 9.86 cm/cell for the elevation map.

This downsampling is performed to reduce the

computing burden in the following processing steps

and also for geometric considerations related to the

robotic platform. In fact, the U-Go is a 75 cm long

and 88 cm large tracked vehicle, with 18 cm wide

rubber tracks. Therefore, working with height values

ICAART 2017 - 9th International Conference on Agents and Artiﬁcial Intelligence

336

spaced roughly every 10 cm is a sufficient

approximation of the terrain surface over which the

robot is supposed to move. Finally, from the whole

DEM the region of interest is cropped, i.e. the

landslide-like area. The final digital elevation model

under study is a 451×337 matrix, representing an

area of 44.47×33.23 m.

Since the idea was to generate a costmap

including both maximum non-traversable slopes and

height steps, a virtual wall was included into the

digital elevation model by adding a fixed value to a

rectangular shaped contour. Therefore, the final

matrix considered for the global path planning is a

slightly modified version of the original one, and in

Figure 3 the resulting surface is depicted.

Figure 3: The reconstructed surface of the region of

interest, after virtual wall insertion.

4 MAP GENERATION

Once defined the digital elevation model of the area

under investigation, the following steps consist of

processing such model in order to derive the

costmap required by the path-planning algorithm.

4.1 U-Go Traversability Capabilities

A proper path planning cannot be conceived without

taking into account the real motion actuation

performed by the specific robotic platform,

especially when the UGV is asked to autonomously

cover hostile terrains and so a terrain traversability

analysis must be included as well.

This task has been accomplished in literature in

different manners. A remarkable example in this

sense is shown by Santamaria-Navarro et al. (2015),

which consists of application of learning models for

traversable and non-traversable area classification.

In that work the ground truth was made up of terrain

appearance and geometry acquired by the vehicle

while being teleoperated in the environment. A very

similar method was also pursued by Silver, Bagnell,

and Stentz (2010), where a skid-steering platform

was firstly maneuvered by an expert, while learning

a mapping between sensor data and path planning

costs. Therefore, the vehicle usually learns in two

senses: inferring its motion dexterity and/or

determining the features of traversable and non-

traversable terrain patches.

In our work, the U-Go was initially teleoperated

over some testing areas, bringing its navigation

performances to the limit. During these first experi-

mental sessions a huge amount of proprioceptive

data have been acquired; among them, the robot

pose (roll, pitch and yaw angles of the vehicle) and

the GPS coordinates.

As a first approach, two simple measures, in

defining the U-Go motion capabilities, have been

considered. From the inspection of pitch excursion,

the minimum and maximum values recorded for this

angle were respectively -29° and 32°; however

nearly all the remaining values were within the [-

25°, 25°] interval, whose limits are around the 80%

of the two extreme values detected. Therefore, the

maximum traversable slope for preventing the

vehicle overturning is established at 25°, thus

including a safety margin angle. Finally, the

maximum height step that the U-Go is capable to

climb was observed to be 15 cm.

4.2 Binary Occupancy Grids

Generation

The georeferenced digital elevation model, descry-

bed in Section 3, is thus delivered to a Matlab

processing function, which requires only maximum

traversable slope and maximum climbable height, as

inputs, and provides two binary occupancy grids, as

outputs. The algorithm consists of the following

main steps:

 Surface normals estimation in each point of

the map;

 Height steps detection for each point of the

map;

 Binary occupancy grids generation based on

maximum slope and maximum climbable

height.

Normals are used for the terrain slope

assessment. The choice of using normals is justified

by the possibility of quantitatively determining the

slope exhibited by the terrain patch surrounding a

given point. Using normals we essentially look at the

z-component of these vectors. In fact, this compo-

A Global Path Planning Strategy for a UGV from Aerial Elevation Maps for Disaster Response

337

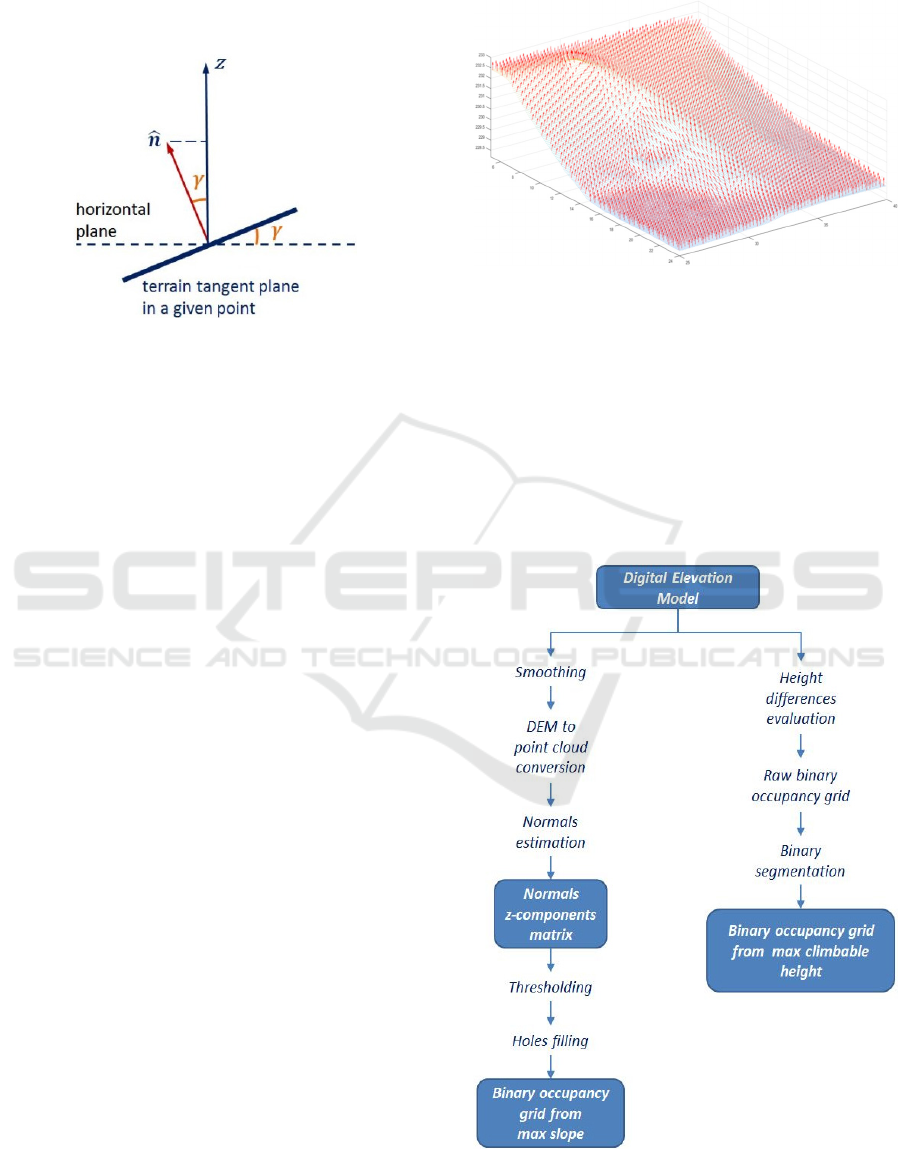
nent depends only on the cosine of the slope of the

plane tangent to the surface in the considered point,

with respect to the horizontal plane, as shown in

Figure 4.

Figure 4: Normal z-component and tangent plane slope.

Normals estimation is performed using the imple-

mentation employed by Taylor, Nieto and Johnson

(2015), which, however, is conceived to handle

point clouds, i.e. xyz coordinates in the space.

Therefore, in order to carry out this processing step,

the DEM has to be previously converted into a point

cloud.

The normals estimation algorithm computes a

covariance matrix of a user-defined number of

nearest neighbors of each query point and then

performs a principal component analysis (PCA). The

eigenvector associated to the minimum eigenvalue

gives the best normal direction estimate of the

tangent plane in the query point (Rusu, 2009).

Furthermore, this PCA-based technique requires the

indication of a point of view, to determine the

normal vectors orientations, consistently with the

surface. In our case a point of view in the center of

the surface, with a high altitude value, was chosen,

in order to have nearly all normals pointing in the

positive direction of the z-axis, thus allowing us to

deal with positive z-components.

Normals estimation has been carried out on a

smoothed version of the DEM, which has been

obtained by applying a Gaussian convolutional filter

over the matrix. The standard deviation of the

Gaussian filter establishes the kernel size of the

convolutional filter. In our case a standard deviation

equal to 2 is chosen, leading to a kernel size equal to

2∙



2



1=9. This particular value has been

chosen since it has shown to improve the quality of

the normal estimation results, generating a less noisy

output, without compromising too much the final

resolution, thinking of the robotic platform size.

Then the smoothed matrix has been converted into a

point cloud and normals for each point have been

computed. In Figure 5 a sample graphical result is

shown.

Figure 5: Detail of normals estimated over the terrain.

The z-components of these normals are

rearranged as a matrix, in order to have a one-to-one

matching with the original DEM. This matrix of z-

components is finally compared with a threshold,

which is the cosine of the slope above which the

terrain is non-traversable, i.e. 25° (see Figure 4). In

this manner the first binary occupancy grid is

generated. To exclude areas all surrounded by non-

traversable points (and then unreachable), holes in

the binary image are immediately filled.

Figure 6: Scheme of the processing phases of the two

occupancy grids generation.

ICAART 2017 - 9th International Conference on Agents and Artiﬁcial Intelligence

338

Then the Matlab processing function builds the

second binary occupancy grid, which looks for

discontinuities in the height values exceeding a

maximum threshold (namely steps or walls). The

method to realize this binary occupancy grid is

straightforward: for each element of the DEM we

compute all the absolute differences between the

element value and the values of its eight adjacent

surrounding elements; if at least one of these

differences is above the threshold, the cell is marked

as an obstacle. It is apparent that such solution does

not hold for the DEM boundaries; therefore, they are

discarded in the following steps. Finally, a binary

segmentation is performed on the occupancy grid:

this allows to exclude unreachable isolated areas (all

surrounded by non-traversable cells) and, more

importantly, to make the shapes of these real

obstacles stand out, rather than simply filling holes

as in the previous case. In Figure 6 a sketch of the

processing steps carried out within the Matlab

function is reported.

4.3 Costmap

The last map to create is the global costmap for the

D* path planner (Stentz, 1994), depending on which

the algorithm identifies the optimal path, i.e. the

route with lower cumulative cost. The costs within

this map are generically values greater than zero; in

the implementation that we use, included in the

robotics toolbox v. 9.10 (Corke, 2011), the algorithm

works in particular with costs greater than one. In

any case obstacles are mapped with infinite values.

A second Matlab function is in charge of

generating this costmap. Firstly a global binary

occupancy grid is built by simply merging the two

occupancy grids described in the previous section

(i.e. taking the union of their non-traversable cells).

Note that in this binary map obstacles and free cells

are respectively represented with one and zero, but

in the final costmap they will be respectively

remapped with infinity and one. Furthermore, the

costs of non-obstacle cells are derived as explained

below.

To prevent the path planner from choosing cells

too close to those marked as obstacles, the costs of

all these cells are increased by dilating obstacle

areas, applying a large-sized Gaussian kernel to the

binary occupancy grid and multiplying the resulting

matrix by a magnifying factor. In this way only costs

of the desired cells are increased, since the ones

farther from obstacles still have a zero value after

the dilation, which obviously is not affected by the

multiplication. A second contribution included in

non-obstacle cells costs is the slope. In fact,

although all cells with slope higher than 25° are

already marked as obstacles, it is still preferable to

avoid to have the robot traversing terrain patches

with high slope and, in general, to move along a path

with as lower steepness as possible, both for safety

and energy efficiency reasons. Therefore, starting

from the matrix of normals z-components (described

in the previous subsection), we associate higher

costs to those cells with inclination close to 25° (i.e.

whose values in the matrix is close to cos(25°)), and

costs close to 1 (i.e. traversable cells in the D*

costmap) to those cells with slope close to 0° (i.e.

whose value in the matrix is close to 1).

A further feature, which was considered in the

first instance of the costmap derivation, was the

terrain unevenness. In fact, PCA analysis performed

on the point cloud allows to acquire information on

both the terrain irregularity and the terrain normals

at the same time, since they are respectively related

to the smallest eigenvalue and the corresponding

eigenvector of the covariance matrix. However, this

kind of information was not included in the final

costmap since, in our case study, it appeared to

introduce only noise in the planned path, without

any remarkable quality increase, since highly

irregular areas have been already marked as

obstacles.

Figure 7: Scheme of the overall procedure, starting from

the digital elevation model up to waypoints generation.

A Global Path Planning Strategy for a UGV from Aerial Elevation Maps for Disaster Response

339

Eventually, to obtain the global costmap for the

D* algorithm, all matrices are merged together: the

global occupancy grid, including cells with infinite

costs (i.e. obstacles), with the two matrices of costs

for obstacle-closeness and costs for cells slopes.

Once provided the costmap, the path planner can

compute the optimal route, which is converted into a

sequence of waypoints. In Figure 7 a summarizing

scheme of the overall workflow is shown.

5 RESULTS AND SIMULATIONS

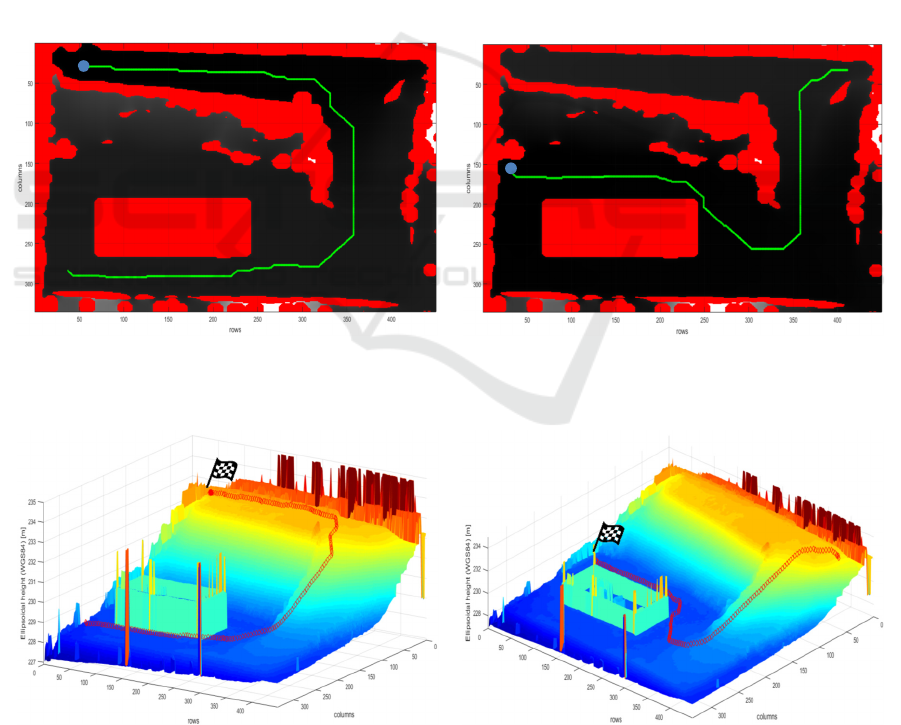
Two sample paths have been computed, from two

different couples of starting and final points,

delivering them to the D* planner. In Figure 8 these

paths are shown: both the starting points, and the

final points (indicated with blue dots) are chosen to

make the vehicle reaching the upper part of the area

starting from the lower part and vice-versa. The

lighter grey shades are those cells of the costmap

with higher cost, while red areas are absolutely non-

traversable zones (i.e. those marked as obstacles in

the global binary occupancy grid described in the

previous subsection).

Then these trajectories are converted into UTM

and longitude/latitude coordinates, in order to be

provided as references to the waypoint navigation

controller on board of the tracked vehicle. A Matlab

script running on a laptop, acting as a control base

station, is employed to interact with the vehicle by

means of the ROS (Robot Operating System)

communication middleware, thanks to the Robotics

System Toolbox, which provides an interface

between Matlab and the ROS network.

In Figure 9 the red tracks represent the 3D

reconstructions of the paths over the terrain surface.

a) b)

Figure 8: Examples of computed paths: a) path #1 (path length: 75.62 m); b) path #2 (path length: 56.20 m).

a) b)

Figure 9: Track of the vehicle over the terrain: a) path #1; b) path #2.

ICAART 2017 - 9th International Conference on Agents and Artiﬁcial Intelligence

340

6 CONCLUSIONS AND FUTURE

DEVELOPMENTS

The work presented in this paper is an end-to-end

procedure to perform a global path planning for a

UGV, starting from a digital elevation model built

from an aerial photographic acquisition, carried out

by a UAV, of the field over which the ground

vehicle has to move. This approach is particularly

relevant for search and rescue scenarios, where the

environment to cope with is strongly unstructured,

heterogeneous and not known a priori.

Thanks to the simple kind of analysis performed

on the surface model, the procedure allows to obtain

a traversable path in a very brief time interval,

avoiding dangerous steep slopes and steps. In this

manner, the vehicle is capable to start operating over

the area to be rescued, while more task-specific

missions can be planned in a longer time. Moreover,

the solution here presented can constitute a good

background to be integrated with a local obstacle

avoidance controller, supported by the optimized

replanning method of the D* algorithm.

A future development could be to move to a full

3D representation of the outdoor environment, for

instance by using octomaps (Hornung et al., 2013),

or dense point clouds. In this manner overhanging

structures, which are quite often present in disaster

areas, and terrain roughness analysis could be

included, thus allowing to find more traversable

paths. Moreover, some solutions to obtain the

environment reconstruction in real-time could be

introduced such as the one reported in Pizzoli,

Forster and Scaramuzza (2014).

However, the work here reported, even if much

simpler, could be smartly integrated into a more

complex solution to reduce computing burden, for

instance, focusing only on those traversable terrain

areas identified by the costmap generation process.

Another point to be enhanced is the overall

system robustness. The communication system

should not only rely on the ROS framework, which

is more suitable for reliable communication network.

The capability of moving also in GPS-denied

environments should be included, by resorting to

SLAM or Visual Odometry, as done by Siegwart et

al. (2015) and Weiss, Scaramuzza and Siegwart

(2011), thus avoiding to trust only on GPS

information, not always available in disaster areas.

Matlab and ROS have been used in this prototyping

phase to study the first results of the procedure;

however, everything should be embedded in a

companion PC on-board to the vehicle, thus making

the whole planning strategy much less “manual”,

once platform-dependent parameters have been

properly tuned.

Finally, while computing the path, the orientation

of the platform with respect to the terrain was not

considered. This would result in too much of a

conservative representation of the area, in terms of

traversability, because for each terrain cell only

maximum slope is considered. Therefore a first

integration will be to use a modified version of the

D* planner and to consider also the physical size of

the platform and not just schematize it as a point

mass.

ACKNOWLEDGEMENTS

This work was carried-out in the framework of the

CLARA PON project. The Project CLARA (CLoud

plAtform and smart underground imaging for natural

Risk Assessment) is funded by MIUR under the

program PON R&C SCN_00451.

REFERENCES

Siegwart, R., Hutter, M., Oettershagen, P., Burri, M.,

Gilitschenski, I., Galceran, E., Nieto, J., 2015. Legged

and flying robots for disaster response. In World

Engineering Conference and Convention 2015

(WECC2015).

Schneider, F.E., Wildermuth, D., Wolf, H. L., 2015.

ELROB and EURATHLON: improving search &

rescue robotics through real-world robot competitions.

In IEEE 10th International Workshop on Robot

Motion and Control (RoMoCo).

Kitano, H., Tadokoro, S., 2001. Robocup rescue: a grand

challenge for multiagent and intelligent systems. In AI

magazine, vol. 22(1).

Marques, M. M., Parreira, R., Lobo, V. et al., 2016. Use of

multi-domain robots in search and rescue operations -

contributions of the ICARUS team to the euRathlon

2015 challenge. In Oceans 2016.

Astuti, G., Longo, D., Melita, C. D., Muscato, G., Orlando

A., 2008. HIL tuning of UAV for exploration of risky

environments. In International Journal on Advanced

Robotic Systems, Vol. 5(4).

Stentz, A., 1994. The D* algorithm for real-time planning

of optimal traverses. Tech. Rep. CMU-RI-TR-94-37,

The Robotics Institute, Carnegie-Mellon University.

Bonaccorso, F., Longo, D., Muscato, G., 2012. The U-Go

Robot, a multifunction rough terrain outdoor tracked

vehicle. In Proceedings of the 2012 World Automation

Congress WAC2012.

Santamaria-Navarro, A., Teniente, E. H., Morta, M.,

Andrade-Cetto, J., 2015. Terrain classification in

complex three-dimensional outdoor environments. In

Journal of Field Robotics, vol. 32(1), pp. 42-60.

A Global Path Planning Strategy for a UGV from Aerial Elevation Maps for Disaster Response

341

Silver, D., Bagnell, J. A., Stentz, A., 2010. Learning from

demonstration for autonomous navigation in complex

unstructured terrain. In The International Journal of

Robotics Research vol. 29(12), pp.1565-1592.

Taylor, Z., Nieto, J., Johnson, D., 2015. Multimodal

sensor calibration using a gradient orientation

measure. In Journal of Field Robotics, vol. 32(5), pp.

675-695.

Rusu, R. B., 2009. Semantic 3D object maps for everyday

manipulation in human living environments. PhD

thesis, Computer Science department, Technische

Universität Müchen, Germany.

Corke, P. I., 2011. Robotics, Vision & Control, Springer.

Hornung, A., Wurm, K. M., Bennewitz, M., Stachniss, C.,

Burgard, W., 2013. OctoMap: an efficient probabilistic

3D mapping framework based on octrees. In

Autonomous Robots, vol. 34(3), pp. 189-206.

Pizzoli, M., Forster, C., Scaramuzza, D., 2014. REMODE:

probabilistic, monocular dense reconstruction in real

time. In IEEE International Conference on Robotics

and Automation (ICRA), pp. 2609-2616.

Weiss, S., Scaramuzza, D., Siegwart, R., 2011.

Monocular-slambased navigation for autonomous

micro helicopters in gps-denied environments. In

Journal of Field Robotics, vol. 28(6), pp. 854-874.

ICAART 2017 - 9th International Conference on Agents and Artiﬁcial Intelligence

342