Can Matrix Factorization Improve the Accuracy of Recommendations

Provided to Grey Sheep Users?

Benjamin Gras, Armelle Brun and Anne Boyer

KIWI, Universit

e de Lorraine - LORIA, Campus scientiﬁque BP 239, 54506, Vandœuvre-l

es-Nancy, France

Keywords:

Recommender Systems, Grey Sheep Users, Matrix Factorization.

Abstract:

Matrix Factorization (MF)-based recommender systems provide on average accurate recommendations, they

do consistently fail on some users. The literature has shown that this can be explained by the characteristics

of the preferences of these users, who only partially agree with others. These users are referred to as Grey

Sheep Users (GSU). This paper studies if it is possible to design a MF-based recommender that improves

the accuracy of the recommendations provided to GSU. We introduce three MF-based models that have the

characteristic to focus on original ways to exploit the ratings of GSU during the training phase (by selecting,

weighting, etc.). The experiments conducted on a state-of-the-art dataset show that it is actually possible to

design a MF-based model that signiﬁcantly improves the accuracy of the recommendations, for most of GSU.

1 INTRODUCTION

Being different is a property shared by each person

since everyone is unique. Current information sys-

tems exploit what data share, as well as their close-

ness, as a bond between them. They do not man-

age their differences. Although unique, most peo-

ple share or are close on several characteristics. But

what if a person does not share enough characteris-

tics with others? What if a person is too different? In

the frame of recommender systems (Goldberg et al.,

1992) that manage users’ preferences, it results in the

Grey Sheep Users (GSU) problem (Claypool et al.,

1999; Ghazanfar and Prugel-Bennett, 2011).

RS suggest users of a system some resources,

within a huge set of resources, with the aim to in-

crease their satisfaction. The popularity of RS is con-

tinuously increasing and they are becoming an every-

day part of our lives. They are used in many applica-

tion domains, including e-commerce (Huang, 2011),

e-learning (Verbert et al., 2012), tourism (Zanker

et al., 2008), etc. RS have been extensively studied

these last twenty years, the most prevalent approach

is collaborative ﬁltering (CF). CF relies on the infor-

mation collected about users, most of the time pref-

erences, and assumes that users’ preferences are con-

sistent among users. So, to infer the preferences of

a user, the active user, CF relies on the preferences

of a community of users (Resnick et al., 1994); the

resources with the highest estimated preferences are

suggested to the active user.

CF-based recommender systems now provide on

average highly accurate recommendations (Castagnos

et al., 2013). Providing users with accurate recom-

mendations is essential, as it is one of the key to suc-

cess of the service on which the recommender system

runs. In e-commerce, accurate recommendations in-

crease customer retention; in e-learning they improve

learners’ learning process; etc. However, some users

still get inaccurate recommendations.

The literature has recently emphasized that the

singular preferences of some users, in comparison

to those of the others, may explain why they get

inaccurate recommendations (Ghazanfar and Prugel-

Bennett, 2011). These users, who only partially agree

(or disagree) with any community of users, are re-

ferred to as Grey Sheep Users (GSU) and are often

opposed to “normal” users (Claypool et al., 1999).

The Matrix Factorization (MF) recommendation tech-

nique has proven to be highly accurate and is now the

most commonly used CF technique. MF techniques

use an optimization process to form a model that ﬁts

the training data. More speciﬁcally this process re-

lies on the overall accuracy of the recommendations.

Within the entire set of users, GSU not only have

singular preferences, but are also outnumbered. As

a consequence, GSU might be overlooked within the

sheer amount of normal users, so standard MF tech-

niques do not accurately model GSU and do not pro-

vide them with high quality recommendations (Gras

Gras, B., Brun, A. and Boyer, A.

Can Matrix Factorization Improve the Accuracy of Recommendations Provided to Grey Sheep Users?.

DOI: 10.5220/0006302700880096

In Proceedings of the 13th International Conference on Web Information Systems and Technologies (WEBIST 2017), pages 88-96

ISBN: 978-989-758-246-2

et al., 2016).

We believe that providing GSU with accurate rec-

ommendations is one way to improve the global accu-

racy of the system. The question addressed in this pa-

per is thus: ”Can we improve the accuracy of the rec-

ommendations provided to grey sheep users through

matrix factorization?”.

(Grifﬁth et al., 2012) has shown that it may be pos-

sible to improve the accuracy of the recommendations

provided to each user by learning a speciﬁc model.

Thus, we ask if GSU can beneﬁt from a model dedi-

cated to them.

Few works in the literature have been interested in

providing accurate recommendations to GSU. These

works either simply split the set of users into normal

and abnormal users (Del Prete and Capra, 2010), and

then learn a model dedicated to each set, or rely on

clustering (Ghazanfar and A., 2014), or design new

similarity measures between users (Bobadilla et al.,

2012).

As GSU have singular preferences, we assume

that a unique model cannot accurately model both

normal users and GSU. So, we consider a recom-

mender system that relies on two models: a standard

MF-based model from the state-of-the-art, used to

provide recommendations to normal users and a MF

model dedicated to GSU. The design of this second

model is the focus of this paper.

Section 2 presents an overview of Collaborative

Filtering and GSU modeling techniques. Section 3

introduces the MF models we design to ﬁt GSU pref-

erences. Section 4 focuses on the experiments con-

ducted to evaluate each model and highlights the ben-

eﬁts of each of them. Finally, we discuss and con-

clude our work.

2 RELATED WORKS

2.1 Collaborative Filtering and Matrix

Factorization

Collaborative Filtering (CF) relies on the preferences

of some users on resources (items) to provide the ac-

tive user u with some personalized recommendations.

Let U be the set of n users and I be the set of m re-

sources. The set of preferences, generally ratings, is

represented in the form of a matrix R, where r

u,i

de-

notes the preference of u on the item i.

Two main approaches are used in CF: memory-

based and model-based. Memory-based ap-

proaches (Resnick et al., 1994) exploit users’ pref-

erences, without pre-processing. A commonly used

technique is the user-based KNN (K Nearest Neigh-

bors) that computes the similarity of preferences be-

tween each pair of users, and estimates the miss-

ing preferences of u by exploiting the preferences

of his/her K nearest neighbor users (the item-based

KNN technique that exploits the K nearest neighbor

items is also commonly used). This technique is accu-

rate, easy to implement and it automatically takes into

account each new preference in the recommendation

process. However, it hardly scales due to the compu-

tation cost of the similarities (Rashid et al., 2008) and

it suffers from the extreme sparsity of the preference

dataset (the similarity between two users or resources

may not be computable, or two similarity values may

not be comparable) (Grcar et al., 2005b; Grcar et al.,

2005a).

Model-based approaches learn a model of prefer-

ences. Among the various techniques we can ﬁnd Ma-

trix Factorization (MF), that has recently proved to

be highly accurate (Koren et al., 2009; Takacs et al.,

2009). It is now the most commonly used technique,

especially due to its high scalability. The general idea

of MF is modeling user-resource interactions (ratings)

through factors that represent latent characteristics of

the users and of the resources, such as preference

classes of users or category classes of resources. In

practice, MF computes two sub-matrices with k la-

tent features: the matrix P (dimension n ∗ k) repre-

sents user-factors, and the matrix Q (dimension m ∗k)

represents resource-factors. The factorization aims at

accurately approximating R through the product of P

and Q: PQ

≈ R. The accuracy of this approximation

relies on the error on each rating r

u,i

in R, following

equation (1):

u,i

= r

u,i

− P

, (1)

where P

is the k-dimensional representation of user

u and Q

is the k-dimensional representation of item i.

P and Q are obtained through an optimization pro-

cess, by exploiting a loss function L. In recommender

systems, loss functions are often based on the nonzero

squared loss:

argmin

P,Q

L(R, P, Q) = argmin

P,Q

∑

u,i

∈R

u,i

(2)

Alternating least squares (ALS) and stochastic gra-

dient descent (SGD) are two popular approaches to

solve this optimization problem. ALS solves the

problem iteratively. At each iteration, one of the ma-

trices (P or Q) is ﬁxed, while the other matrix is modi-

ﬁed (using equation (2)). At each iteration, the matrix

ﬁxed changes. SGD learns the matrices by iteratively

evaluating the error e

u,i

for each rating r

u,i

in R. Both

matrices P and Q are updated by taking a step in the

Can Matrix Factorization Improve the Accuracy of Recommendations Provided to Grey Sheep Users?

opposite direction to the gradient of the loss function

(equation (2)), following equations (3) and (4).

= p

+ α(e

u,i

), (3)

= q

+ α(e

u,i

), (4)

where α is the learning rate. In both approaches, these

steps are repeated until the loss function does not sig-

niﬁcantly decrease or until a predeﬁned number of it-

erations is reached.

To avoid overﬁtting, a regularization constraint is

commonly incorporated, through the use of a regular-

ization term in the loss function (equation (5)).

argmin

P,Q

L(R, P,Q) = argmin

P,Q

∑

u,i

∈R

u,i

+ λ reg(P, Q)

(5)

The two most commonly used terms for regu-

larization are L

and L

norms. The L

regulariza-

tion (Zheng et al., 2004) manages the absolute val-

ues in matrices P and Q, whereas L

manages the

squares of the values (Nigam, 1999) (see equation

(6)). In practice, L

regularization shows better results

on datasets with many instances and few features (Yu

et al., 2014), which corresponds to RS datasets.

regL

(P, Q) = ||P

+ ||Q

(6)

2.2 Grey Sheep Users

Grey sheep users (GSU) is a term commonly used

in recommender systems. GSU are also referred to

as deviant users, abnormal users, atypical users, un-

usual users, etc. (Del Prete and Capra, 2010; Ghaz-

anfar and Prugel-Bennett, 2011). They refer to these

users whose opinions do only partially agree or dis-

agree with any community of users (Claypool et al.,

1999). Inconsistent users (Bellog

ın et al., 2014) may

also be related to GSU. Inconsistency is deﬁned as

users’ inherent noise when interacting (rating) with a

recommender system. Notice that inconsistency ex-

ploits only information about a user, not in compari-

son to other users.

Several techniques have been proposed to perform

the identiﬁcation of GSU in RS. Most of them exploit

the properties of the ratings of the resources: Abnor-

mality (Del Prete and Capra, 2010) evaluates to what

extent the ratings of a user is distant from the aver-

age rating of the resources he/she rated, Abnormality-

CRU (Gras et al., 2015) includes the variance of the

ratings for each resource, whereas DILikelihood (Gras

et al., 2016) relies on the distribution of the ratings,

etc.

Once GSU are identiﬁed, the question related to

their management has to be addressed. (Grifﬁth et al.,

2012) mentionned that it may be possible to learn

a speciﬁc model for each user, whereas (Penn and

Zalesne, 2007) emphasizes that preferences of grey

sheep users are difﬁcult to understand and to guess.

So, the management of their preferences, as well as

the conception of a recommendation model that ﬁts

their proﬁle, seems to be a challenge.

The literature highlights the fact that GSU get

inaccurate recommendations as the correlation of

their ratings with other users could be low. Al-

though neighbor-based recommendation approaches

rely heavily on ﬁnding close neighbors (Manouselis

et al., 2014), all the works have focused on these ap-

proaches. (Del Prete and Capra, 2010) divide users

into two distinct subsets: mass like-minded users

(normal users) and individual users (GSU); two rec-

ommendation models are formed: each one is learnt

on and dedicated to one subset of users. Authors pro-

pose an adapted similarity measure between individ-

ual users. It relies on the fact that it does not rep-

resent to which extent two users rate resources sim-

ilarly, but to which extent they similarly differ from

the entire community. The accuracy of the recom-

mendations provided to individual users is slightly

improved. (Bellog

ın et al., 2014) have studied the

accuracy of the recommendations that inconsistent

users receive. The entire set of users is also split

into easy users (normal users) and difﬁcult (incon-

sistent) users. The accuracy of the recommendations

provided to difﬁcult users is not improved when only

difﬁcult users are used in the training set. This conclu-

sion is contradictory to the one presented in (Del Prete

and Capra, 2010). (Bobadilla et al., 2012) have pro-

posed to take into account the singularity of prefer-

ences of users in the evaluation of the similarity be-

tween two users. Rating values are categorized and a

rating is singular if it does not correspond to the pre-

dominant category on this resource. When computing

the similarity between two users, the more a rating is

singular, the greater its importance. Using this new

similarity measure slightly improves the accuracy of

recommendations provided to grey sheep users. Al-

though this work is not directly dedicated to the man-

agement of GSU, it is a way to take into account the

speciﬁc preferences of users in the way to compute

recommendations.

To manage the preferences of GSU, (Ghazanfar

and A., 2014) propose to rely on a pure content-based

approach. The experiments conducted show that such

an approach is more adequate to model GSU, the re-

sulting model is more accurate than with a CF ap-

proach. Nevertheless, as most of the current datasets

do not include resources metadata, this approach may

not always be applicable.

WEBIST 2017 - 13th International Conference on Web Information Systems and Technologies

Managing cold-start users may be considered as

closely related to managing GSU. Cold-start users are

users who have not provided enough information to

the system, to accurately model them. The problem

of managing GSU is different. The GSU are not new

users, they are users with preferences that do not align

with those of other users.

3 DESIGNING MODELS OF GSU

Similarly to the works presented in the previous sec-

tion, the recommendation system we focus on relies

on two sub-models: one model is dedicated to nor-

mal users (a standard MF model), the other model is

dedicated to GSU. The work here is dedicated to the

design of the latter model.

The identiﬁcation of GSU is made upstream train-

ing the model, and upstream any recommendation

process. To compute recommendations to a user,

his/her category is identiﬁed (normal user or GSU),

then the adequate recommendation model is used. As

the detection of GSU is not the focus of this paper, we

propose to use a recent state-of-the-art detection tech-

nique, that relies on the DILikelihood measure (Gras

et al., 2016).

Recall that the literature has mostly focused on the

neighbor-based approaches to model GSU (see sec-

tion 2.2). As MF has proved to be the most accurate

CF technique in the general case (Koren et al., 2009),

we propose to design a MF-based recommendation

model dedicated to GSU. To the best of our knowl-

edge, it is the ﬁrst attempt to study MF with this goal.

We are convinced that the reason why GSU do

not get accurate recommendations with MF models

not only lies in their singular preferences, but also in

their number. Indeed, by deﬁnition, GSU are rare in-

stances, so there are considerably more normal users

than GSU. As the criterion optimized by MF is the

global recommendation accuracy (on the entire set of

users), the accuracy on GSU does not, or slightly, im-

pact the global accuracy; so the resulting model tends

to accurately model normal users, whatever is the ac-

curacy of this model on GSU.

SGD and ALS are nowadays two popular methods

to factorize matrices (Yu et al., 2014). The MF models

we propose can be used on the frame of both methods.

For the sake of concision, we present these models

with one of these methods. We choose SGD.

We propose three MF models dedicated to GSU.

Algorithm 1: Standard SGD Algorithm.

Input:

R = {r

u,i

} - set of ratings of users u on items i,

k - number of features of the model,

α - learning rate of the factorization,

λ - regularization parameter

Output:

Latent factor matrices P and Q

procedure SGD(R, k, α, λ)

initialize random factor matrices P and Q

while no Stop do

for each r

u,i

∈ R do

u,i

= (r

u,i

− p

) // Error estimation

← q

+ α ∗ (e

u,i

− λ.q

)

← p

+ α ∗ (e

u,i

− λ.p

)

return P and Q

no Stop is a boolean that represents if the stop crite-

rion is reached (number of iterations or convergence

of the loss function).

3.1 The GSUOnly Model

The ﬁrst model we introduce aims at evaluating to

what extent a GSU can beneﬁt from other GSU only.

The model is trained on the ratings of the set of GSU,

the ratings of normal users being dismissed. This

model is referred to as the GSU Only model.

For this model, no amendments of the standard

SGD algorithm (Algorithm 1) will be made. The only

difference lies in the set of ratings used in the train-

ing phase, which is reduced to the ratings of GSU.

The running time required to learn this model is re-

duced compared to standard models as the dimen-

sion of the matrices (R, P and Q) is highly reduced

(|GSU | << n).

Note that this model cannot be used to provide rec-

ommendations to users who do not belong to the set of

GSU (normal users), as the resulting matrices P and

Q do not contain any value for these users.

3.2 The WeightedGSU Model

The second model we introduce, called

WeightedGSU, weights GSU during the learn-

ing process. In standard algorithms both GSU and

normal users have the same weight.

We will consider W

GSU

as the weight of GSU and

normal

as the weight of normal users. Equation (7)

presents the relation between both weights.

GSU

normal

= 1.0 (7)

We are convinced that the weight of GSU has to be

more important than the one of normal users. In this

Can Matrix Factorization Improve the Accuracy of Recommendations Provided to Grey Sheep Users?

way, the rating speciﬁcities of GSU will be better ad-

dressed, while still using ratings of normal users. The

ratings of normal users represent additional informa-

tion in the learning process and are a way to cope with

the lack of data from the small set of GSU. We aim at

ﬁnding the W

GSU

value that optimizes the accuracy of

the recommendations GSU get.

WeightedGSU also relies on Algorithm 1, in

which we introduce modiﬁcations to manage the var-

ious weights. More speciﬁcally, the error estimation

step is modiﬁed, to ﬁt equation (8):

u,i

= W

∗ (r

u,i

− p

), (8)

where W

is the weight of user u, with W

= W

GSU

if u is a GSU and W

= W

normal

if u is a normal user.

3.3 The SingleGSU Model

The last model forms one model for each GSU. It is

designed to evaluate to what extent a model dedicated

to a speciﬁc GSU improves the accuracy of the recom-

mendations provided to this user. This model, named

SingleGSU , is learnt on the ratings of one GSU (the

user the model is dedicated to) as well as on the rat-

ings of additional users. We choose to select the ad-

ditional users within the set of normal users to thor-

oughly study the inﬂuence of normal users on the ac-

curacy of the recommendations provided to GSU, and

exclude the possible negative impact that the ratings

of some GSU may have on other GSU. The number

and the way these additional normal users are chosen

has to be studied.

Notice that this model is more a proof of concept

than a model that can be used on real datasets. Indeed,

it is not acceptable to compute a model for each GSU,

in the context where data is overwhelming. Neverthe-

less, it is a way to study in depth the ability of MF to

accurately model GSU.

4 EXPERIMENTS

This section presents the experiments we conduct to

study to what extent the Matrix Factorization models

we propose can improve the accuracy of the recom-

mendations provided to GSU.

4.1 Dataset

The experiments are conducted on the

MovieLens 20M dataset

, made up of 20 mil-

lion ratings from 138,493 users on 27,278 movies

http://grouplens.org/datasets/movielens/

(resources). The rating scale ranges from 0.5 to 5.0

stars, with half-star increments. This dataset was

published in April 2015 and is the current standard

dataset for the evaluation of CF recommenders.

To not bias the evaluation, we choose to dis-

card users who may be associated with the cold-

start problem: those with less than 20 ratings in the

dataset (Schickel-Zuber and Faltings, 2006). The set

of users is then reduced to 123,053 users (88.8% of

the original set of users) and is made up of 19.6 mil-

lion ratings (98% of the original set of ratings). In the

resulting dataset, users have provided up to 8,400 rat-

ings, with an average number of 159 ratings per user.

The sparsity of this dataset is higher than 99%, which

is extremely sparse.

4.2 Evaluation Setup

The models studied are evaluated in terms of rec-

ommendation accuracy. More precisely, we use the

RMSE (Root Mean Squared Error) measure. RMSE

evaluates the discrepancy between the rating a user

assigned to a resource and the rating estimated by the

recommender, computed by equation (9).

RMSE =

∑

u,i∈R

u,i

− n

∗

u,i

)

||R||

, (9)

where n

∗

u,i

is the estimated rating of user u on item i

and R = {r

u,i

} is the set of user-item ratings.

The set of ratings of the dataset is split into two

sets: Train that contains 80% of the ratings randomly

chosen and that will be used to train the different mod-

els, and Test that contains the 20% remaining ratings

and that will be used to evaluate the accuracy of the

models. Each of these sets is in turn split into two

subsets: the subset made up of the ratings of GSU

(Train

GSU

and Test

GSU

) and the subset made up of the

ratings of normal users (Train

normal

and Test

normal

The accuracy of the models proposed is compared

to that of standard MF models. ALS and SGD factor-

ization techniques are studied. As the optimization of

the parameters of these techniques is not the focus of

this work, we ﬁx them to the state-of-the-art values,

used on a comparable dataset (Yu et al., 2014). 20

features are used, with a learning rate of 0.001 and a

regularization parameter set to 0.02. Matrices P and

Q are initialized randomly. A dozen runs are executed

to avoid the bias introduced by the random initial-

ization. The stop criterion used in the algorithms is

the convergence of the RMSE on GSU. These models

will further be considered as baselines.

The ﬁrst two lines of Table 1 present the RMSE

of the two standard MF models (trained on Train and

WEBIST 2017 - 13th International Conference on Web Information Systems and Technologies

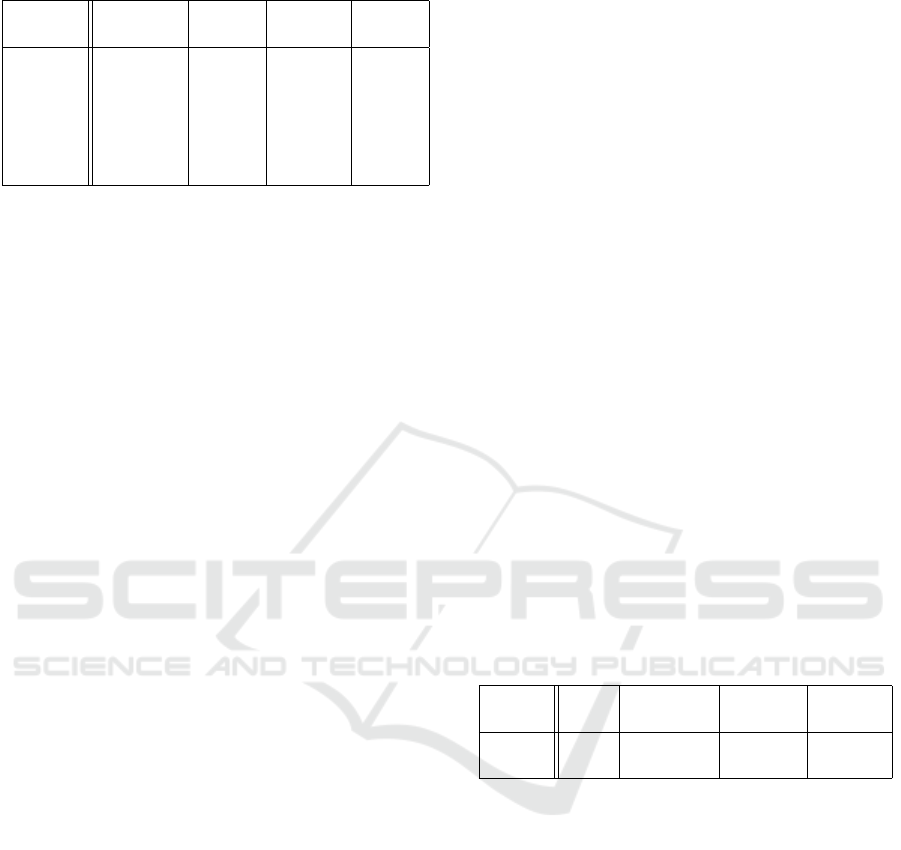
Table 1: RMSE of standard models.

Model Test RMSE RMSE RMSE

set Q1 Median Q3

SGD Test 0.66 0.80 0.97

ALS Test 0.66 0.82 1.00

SGD Test

GSU

1.01 1.18 1.35

ALS Test

GSU

1.12 1.28 1.45

SGD Test

normal

0.65 0.78 0.95

SGD-L1 Test

GSU

1.04 1.21 1.39

evaluated on Test ) with ALS and SGD factorization

techniques and the L

regularization. SGD slightly

outperforms ALS (by 2.5% for the median), which is

consistent with what is usually reported in the litera-

ture (Yu et al., 2014).

The identiﬁcation of GSU is performed with the

DILikelihood measure, introduced in (Gras et al.,

2016). We experimentally deﬁned the set of GSU as

the 6% of users with the highest DILikelihood values.

This set of GSU has an average number of ratings of

103 per user, which conﬁrms they are not cold-start

users. The third and ﬁfth lines of Table 1 present

the RMSE of normal users (Test

normal

) and of GSU

(Test

GSU

) respectively, using a standard SGD model

(the same as in the ﬁrst line). With a median RMSE

of 1.18 on GSU and a median RMSE of 0.78 on nor-

mal users, the RMSE on GSU is 51% higher than the

RMSE on normal users. We can conﬁrm that GSU do

actually get less accurate recommendations than nor-

mal users. In addition, the third quartile of the RMSE

of normal users is lower than the ﬁrst quartile of the

RMSE of GSU. Moreover, the median RMSE of the

entire set of users (Test) is 0.80, which conﬁrms that

the number of GSU is so small that they have a limited

impact on the RMSE of the entire set of users.

From the third and the fourth lines of Table 1, we

can see that as on the Test set, SGD provides more

accurate recommendations on the Test

GSU

than ALS.

Furthermore, the difference on Test

GSU

is larger than

on Test: SGD is 8% more accurate than ALS. SGD

seems to be more adapted to model GSU.

We ask now if the L

regularization (see last line

of Table 1) could be a better choice for the regular-

ization term to model GSU, referring to (Ng, 2004;

Yu et al., 2014). The median RMSE with L

is 1.21,

which is 3% higher than the one obtained with the L

regularization. We can conclude that modifying the

regularization term on a model learnt on Train is not

the adequate solution to better model GSU.

The following experiments will be conducted to

study if the models proposed in Section 3 are a way

to better model GSU than standard MF models.

4.3 The GSUOnly Model

This section is dedicated to the evaluation of the ac-

curacy of the GSUOnly model, that is trained on the

ratings of GSU: namely the Train

GSU

subset. Table 2

displays the resulting median RMSE.

Modeling GSU by relying only on the preferences

of the set of GSU leads to a model less accurate than a

model trained on the ratings of the entire set of users

(the RMSE is increased by 8%). These conclusions

are consistent with those reported in (Bellog

ın et al.,

2014), that showed that with a neighbor-based ap-

proach, exploiting only inconsistent users to compute

recommendations for inconsistent users does not lead

to accurate recommendations.

We can conclude that GSU beneﬁt from the pres-

ence of normal users in the learning process of the

factorization technique. This is also the conclusion re-

ported in (Bellog

ın et al., 2014): “less coherent users

need information from outside of their own cluster”.

Using the L

regularization, the RMSE is compa-

rable to the one obtained with L

regularization (L

outperforms L

by only 1%, which is not signiﬁcant).

Thus, L

seems to be more adapted to the GSUOnly

model than to a standard one. However, it does not

improve the L

regularization. So, we conﬁrm that L

remains the most accurate regularization. For the fol-

lowing experiments, we will use L

as regularization

term.

Table 2: RMSE of the GSUOnly model.

Model Reg. Train Test RMSE

Median

SGD L

Train

GSU

Test

GSU

1.27

SGD L

Train

GSU

Test

GSU

1.29

4.4 The WeightedGSU Model

The previous experiments showed that, when train-

ing the model on the ratings of GSU (Train

GSU

)

only, GSU do get recommendations less accurate than

when training the model on the ratings of the entire set

of users. However, even in this latter model, GSU do

not get accurate recommendations. We think that the

weight of GSU in such a model is too small to accu-

rately model them. So, in this section we further study

to what extent allowing a higher weight to GSU is a

way to better model them: the WeightedGSU model.

Figure 1 presents the evolution of the median

RMSE, according to the weight of GSU (W

GSU

ranges from 0.1 to 1.0, with respect to equa-

tion (7). Let us notice that the case where W

GSU

= 0.0

cannot be studied as it would come down to not con-

sider GSU during training, so the matrix P would

Can Matrix Factorization Improve the Accuracy of Recommendations Provided to Grey Sheep Users?

contain random values in the vectors that correspond

to GSU. A weight equals to 1.0 represents the case

where normal users are not taken into account at all

(the GSU Only model), the corresponding RMSE is

1.27. A weight equals to 0.5 is equivalent to a stan-

dard model (GSU and normal users have a similar

weight); the RMSE is 1.18.

Figure 1: RMSE of GSU according to the weight of GSU

during the factorization process.

Two main trends are observed in Figure 1. In the

case where W

GSU

< 0.5, the RMSE increases along

with the decrease of the weight of GSU (up to 1.3).

The smaller the impact of GSU on the factorization

process, the worse the accuracy of their recommenda-

tions, which was expected. In the case where W

GSU

0.5, the RMSE increases along with the weight of

GSU. It varies from 1.17 to 1.27. Thus, the higher the

impact of GSU in the factorization process, the worse

the accuracy of their recommendations. The lowest

RMSE value is reached when W

GSU

= 0.5, which is

equivalent to the standard MF model.

The evolution of the RMSE in the case where

GSU

> 0.5, is not intuitive, we expected that giving

a larger weight to GSU in the factorization would in-

crease the accuracy of the recommendations provided

to them. We wonder if the presence of the ratings of

the entire set of GSU interferes with GSU modeling.

4.5 The SingleGSU Model

In the next experiments we propose to study the

SingleGSU model that forms one model per GSU.

Each model is trained on the ratings of a single GSU

as well as those of a subset of normal users. We

choose to not exploit the ratings of other GSU to dis-

card their possible negative inﬂuence. The question

here is twofold: (i) how many normal users have to

be used to learn the model? and (ii) how to select the

normal users?

The ﬁrst experiment we conduct exploits normal

users that are the most similar to the single GSU, ac-

cording to the Pearson Correlation Coefﬁcient.

As we consider 6% of the complete set of users

as GSU (more than 7K GSU), the number of MF pro-

cesses to be run is too high. We propose to randomly

select 300 GSU and learn one SingleGSU model for

each of them. The DILikelihhood of these 300 GSU

is equally distributed within the set of GSU.

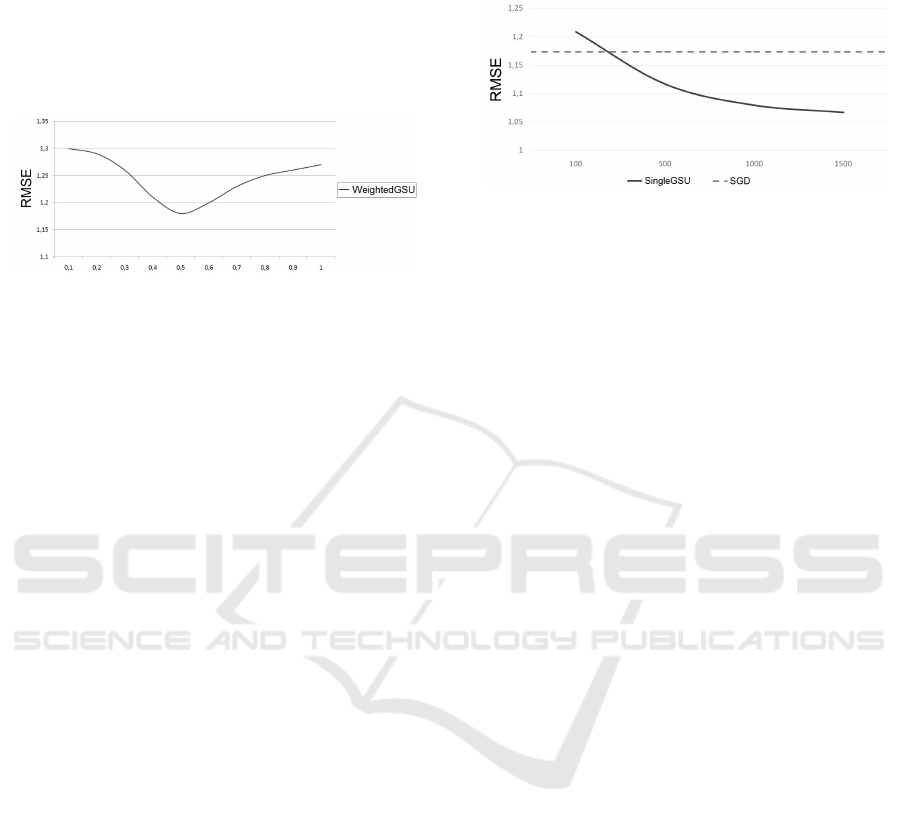
Figure 2: Median RMSE of GSU w.r.t. the number of simi-

lar users selected.

Figure 2 presents the median RMSE of GSU with

respect to the number of similar users selected. This

number varies from 100 to 1,500. Figure 2 also

presents the baseline RMSE (the one obtained with

a standard SGD model). When 100 similar nor-

mal users are selected, the average RMSE of the

SingleGSU model is 1.21, which is higher than the

RMSE of a standard model. The higher the number of

normal users, the lower the RMSE. When about 250

normal users are selected, the RMSE is similar to the

one of a standard model. The decrease of the RMSE

seems to stagnate from 700 normal users (the RMSE

equals to 1.09). When 1,500 normal users are selected

the RMSE is equal to 1.06, which corresponds to an

improvement of 9% of standard models (from 1.17 to

1.06). Obviously, the more normal users are used, the

longer the computation time to learn the model. The

best tradeoff between the running time and the accu-

racy of recommendations provided to GSU seems to

be 700 normal users (7% improvement).

Those ﬁrst results represent an average improve-

ment of the RMSE. It implies a disparity in the im-

provement of the RMSE, among GSU. To go further,

we study the individual distribution of those improve-

ments. First of all, the SingleGSU model improves

the RMSE of more than 72% of the 300 GSU selected.

If we focus on a more signiﬁcant improvement, 54%

of the GSU have an improvement of their RMSE of

more than 10%. So, the SingleGSU model, with nor-

mal users selected through their similarity with the

single GSU, signiﬁcantly improves the accuracy of

the recommendations of more than half of the GSU.

In addition, 32% of the GSU have an improvement of

their RMSE of more than 20%. Furthermore, 20% of

the selected GSU have a RMSE lower than the me-

dian RMSE of normal users (0.8), which is high.

What about the 46% of GSU who have either

an improvement of their RMSE lower than 10% or

have an increase in their RMSE? We propose to build

SingleGSU models for these users, with a random se-

lection of the normal users. For each user, several

WEBIST 2017 - 13th International Conference on Web Information Systems and Technologies

random selections are performed, until forming a set

of normal users that signiﬁcantly improves (by at least

10%) the accuracy of the recommendations of the sin-

gle GSU, in the limit of 500 trials. Such an improve-

ment is reached for 62% of these GSU. Several at-

tempts have been conducted to characterize the sets

of normal users that improve the recommendations

provided to those GSU. For now, no clear link has

emerged.

To summarize, the SingleGSU model is able to

signiﬁcantly improve (by more than 10%) the ac-

curacy of the recommendations provided by a stan-

dard MF model, for more than 82% of the selected

GSU. This indicates that it is possible to increase the

accuracy of the recommendations provided to GSU

through a MF technique. The experiments conducted

tend to show that one reason why GSU do not receive

accurate recommendations with standard MF models

may lie in the users used in the factorization process.

5 DISCUSSION AND

CONCLUSION

This work aimed at studying the possibility to de-

sign a MF-based model that improves the accuracy of

the recommendations that standard MF-based models

provide to grey sheep users (GSU).

To reach this goal, we relied on the idea that when

training a model, the ratings of GSU have to be con-

sidered differently than those of normal users. We

proposed three models that either exploit only the rat-

ings of GSU (the GSU Only model), or weight differ-

ently the ratings of GSU and those of normal users

(the WeightedGSU model) or model each GSU inde-

pendently (the SingleGSU model).

The SingleGSU model, that forms a model for

each GSU independently, improves the accuracy of

the recommendations provided to GSU. This model

exploits the ratings of one GSU (the user the model

is dedicated to) as well as those of a subset of normal

users (no rating about other GSU are included). When

normal users are selected according to their similarity

to the GSU, 72% of GSU actually get more accurate

recommendations, which is highly signiﬁcant. Fur-

thermore, 52% of GSU have an improvement larger

than 10%. This rate even reaches 82% if an additional

way to select normal users is used.

To summarize, we wondered if some MF-models

could improve the accuracy of the recommendations

provided to GSU. Actually, the MF-based SingleGSU

model signiﬁcantly improves this accuracy, even by

more than 10% for most of GSU.

These results need to be extended to study to what

extent this improvement can be even more improved.

This may rely on a modiﬁcation of the correlation

measure used to select the normal users to be used in

the SingleGSU model, or designing a completely new

MF technique. In addition, as noticed in section 3,

designing one model per GSU is not practicable, es-

pecially if the number of GSU reaches several thou-

sands of users. So, we would like to study if some

GSU could be grouped together to reduce the number

of models to be developed.

So far, the experiments conducted did not allow to

identify how to select the set of normal users to use,

given one GSU. Some GSU beneﬁt from the selection

of the most similar users, others do not. Being able to

identify which users beneﬁt from these similar users

will also be highly interesting.

REFERENCES

Bellog

ın, A., Said, A., and de Vries, A. (2014). The magic

barrier of recommender systems - no magic, just rat-

ings. In Proc. of the 22nd Conf. on User Modelling,

Adaptation and Personalization (UMAP).

Bobadilla, J., Ortega, F., and Hernando, A. (2012). A col-

laborative ﬁltering similarity measure based on singu-

larities. Inf. Process. Manage., 48:204–217.

Castagnos, S., Brun, A., and Boyer, A. (2013). When di-

versity is needed... but not expected! In IMMM 2013,

The Third Int. Conf. on Advances in Information Min-

ing and Management.

Claypool, M., Gokhale, A., and Miranda, T. (1999). Com-

bining content-based and collaborative ﬁlters in an on-

line newspaper. In Proceedings of the SIGIR Work-

shop on Recommender Systems: Algorithms and Eval-

uation.

Del Prete, L. and Capra, L. (2010). differs: A mobile rec-

ommender service. In Proc. of the 2010 Eleventh Int.

Conf. on Mobile Data Management, MDM ’10, pages

21–26, Washington, USA. IEEE Computer Society.

Ghazanfar, M. and Prugel-Bennett, A. (2011). Fulﬁlling the

needs of gray-sheep users in recommender systems, a

clustering solution. In 2011 Int. Conf. on Information

Systems and Computational Intelligence.

Ghazanfar, M. A. and A., P.-B. (2014). Leveraging cluster-

ing approaches to solve the gray-sheep users problem

in recommender systems. Expert Systems with Appli-

cations, 41:3261–3275.

Goldberg, D., Nichols, D., Oki, B., and Terry, D. (1992).

Using collaborative ﬁltering to weave an information

tapestry. Communications of the ACM, 35:61–70.

Gras, B., Brun, A., and Anne, B. (2016). Identifying Grey

Sheep Users in Collaborative Filtering: a Distribution-

Based Technique. In ACM UMAP, page 9, Halifax,

Canada.

Gras, B., Brun, A., and Boyer, A. (2015). Identifying users

with atypical preferences to anticipate inaccurate rec-

ommendations. In Proceedings of the 11th Interna-

Can Matrix Factorization Improve the Accuracy of Recommendations Provided to Grey Sheep Users?

tional Conference on Web Information Systems and

Technologies.

Grcar, M., Mladenic, D., Fortuna, B., and Grobelnik, M.

(2005a). Advances in Web Mining and Web Usage

Analysis, volume 4198, chapter Data Sparsity Issues

in the Collaborative Filtering Framework, pages 58–

76. Springer.

Grcar, M., Mladenic, D., and Grobelnik, M. (2005b). Data

quality issues in collaborative ﬁltering. In Proc. of

ESWC-2005 Workshop on End User Aspects of the Se-

mantic Web.

Grifﬁth, J., O’Riordan, C., and Sorensen, H. (2012). Inves-

tigations into user rating information and predictive

accuracy in a collaborative ﬁltering domain. In Proc.

of the 27th ACM Symposium on Applied Computing.

Huang, S. (2011). Designing utility-based recommender

systems for e-commerce: Evaluation of preference-

elicitation methods. Electronic Commerce Research

and Applications, 10(4).

Koren, Y., Bell, R., and Volinsky, C. (2009). Matrix factor-

ization techniques for recommender systems. Com-

puter, 42:30–37.

Manouselis, N., Kyrgiazos, G., and Stoitsis, G. (2014). Ex-

ploratory study of multi-criteria recommendation al-

gorithms over technology enhanced learning datasets.

Journal of e-Learning and Knowledge Society, 10(1).

Ng, A. Y. (2004). Feature selection, l1 vs. l2 regular-

ization, and rotational invariance. In Proceedings of

the Twenty-ﬁrst International Conference on Machine

Learning, ICML ’04, pages 78–, New York, NY, USA.

ACM.

Nigam, K. (1999). Using maximum entropy for text classi-

ﬁcation. In In IJCAI-99 Workshop on Machine Learn-

ing for Information Filtering, pages 61–67.

Penn, M. and Zalesne, K. (2007). Mircotrends: the small

forces behind tomorrow’s big changes. Twelve.

Rashid, A., Lam, S., LaPitz, A., Karypis, G., and Riedl, J.

(2008). Web Mining and Web Usage Analysis, chap-

ter Towards a Scalable kNN CF Algorithm: Exploring

Effective Applications of Clustering. Springer.

Resnick, P., Iacovou, N., Suchak, M., Bergstrom, P., and

Riedl, J. (1994). Grouplens: An open architecture

for collaborative ﬁltering of netnews. In Proc. of the

1994 ACM Conf. on Computer Supported Cooperative

Work, CSCW’94.

Schickel-Zuber, V. and Faltings, B. (2006). Overcoming in-

complete user models in recommendation systems via

an ontology. In Proc. of the 7th Int. Conf. on Knowl-

edge Discovery on the Web, WebKDD’05, pages 39–

57, Berlin. Springer.

Takacs, G., Pilaszy, I., Nemeth, B., and Tikk, D. (2009).

Scalable collaborative ﬁltering approaches for large

recommender systems. Journal of Machine Learning

Research, 10:623–656.

Verbert, K., Manouselis, N., Ochoa, X., and Wolpers,

M. (2012). Context-aware recommender systems for

learning: A survey and future challenges. IEEE Trans-

actions on Learning Technologies, 5.

Yu, H.-F., Hsieh, C.-J., Si, S., and Dhillon, I. S. (2014). Par-

allel matrix factorization for recommender systems.

Knowl. Inf. Syst., 41:793–819.

Zanker, M., Fuchs, M., H

opken, W., Tuta, M., and Muller,

N. (2008). Information and communication technolo-

gies in tourism, chapter Evaluating recommender sys-

tems in tourism a case study from austria. Springer.

Zheng, A. X., Jordan, M. I., Liblit, B., and Aiken, A.

(2004). Statistical debugging of sampled programs.

In Thrun, S., Saul, L. K., and Sch

olkopf, B., editors,

Advances in Neural Information Processing Systems

16, pages 603–610. MIT Press.

WEBIST 2017 - 13th International Conference on Web Information Systems and Technologies