Towards Integrated Infrastructures for Smart City Services: A Story of

Trafﬁc and Energy Aware Pricing Policy for Charging Infrastructures

Upama Nakarmi and Mahshid Rahnamay Naeini

Department of Computer Science, Texas Tech University, Lubbock, TX, U.S.A.

Keywords:

Critical Infrastructures, Smart City, Integrated Framework, Probabilistic Modeling, Electric Vehicles,

Charging Infrastructure, Power Grid, Pricing Mechanism, Load Distribution.

Abstract:

Developing smart-city solutions and services, which lead to optimal utilization of cities’ limited resources and

enhancement of their reliability and efﬁciency, requires collaboration of currently vertical and isolated city

infrastructures. The interdependency among critical infrastructures makes such collaborative solutions even

more essential. In this paper, two of such critical infrastructures, including the electric-vehicle (EV) charging

infrastructure and the electric infrastructure, are considered and an integrated framework for modeling their

interactions are developed. This model is a probabilistic model based on a networked Markov chain frame-

work, which enables capturing of stochastic aspects of these two systems and how they affect each other.

Using the developed model and a proposed algorithm, which works hand in hand with the model, charging

prices are assigned for the EV charging stations with the goal of increasing the likelihood of having balanced

charging and electric infrastructures. The role of the cyber infrastructure in such collaborative solutions are

discussed through the charging and power infrastructure pricing scheme. The presented results show the im-

portance of integrated modeling and the pricing solution, which considers the state of both systems. We hope

that this study and modeling approach can be extended to other smart city solutions and other interdependent

infrastructures.

1 INTRODUCTION

Cities are key elements in developing resilient and

sustainable societies and nations. The global urban

population is expected to grow by 72% by 2050 ac-

cording to recent studies (Heilig, 2012). Such urba-

nization trend suggests the need for smarter solutions

for managing future cities. We believe one of the key

enablers of smarter solutions for cities is collabora-

tion and cooperation among various smart-city infra-

structures in order to optimize city services and so-

lutions. The importance of this cooperation is due to

the increasing interdependency among critical infra-

structures and the fact that the operation state of one

infrastructure can affect the operation of other infra-

structures. In this paper, we will focus on energy and

transportation critical infrastructures and discuss how

their cooperation can lead to a more reliable opera-

tion of the energy system and improve certain aspects

of transportation systems through one source of their

interdependency: the electric vehicles (EVs) charging

infrastructure. On the other hand, the cyber infra-

structure will play a key role in enabling such collabo-

ration and cooperation among infrastructures, while

also explicitly beneﬁt from the reliable energy system

as the source of electricity.

The increase in the number of hybrid electric

transportation systems, including plugin hybrid EVs

and hybrid electric trains have introduced new inter-

dependencies between the energy and transportation

infrastructures (He et al., 2013), (Liu, 2012), (Rah-

man et al., 2014), (Hatton et al., 2009), (Lee et al.,

2015), (Recker and Kang, 2010), (Bass and Zim-

merman, 2013). For instance, vehicle-to-grid (V2G)

technology allow EVs to discharge their energy to

the power grid using bi-directional power electronic

dc/ac interfaces, which can help in stabilizing the po-

wer grid during disturbance and power shortage (Pil-

lai and Bak-Jensen, 2010), (Liu et al., 2011). Another

source of interdependency between energy and trans-

portation infrastructures comes from the EV charging

infrastructure. The EV charging infrastructures are

emerging in cities (Sioshansi, 2012) similar to the tra-

ditional gas stations. On one hand, in the charging

infrastructure, trafﬁc patterns and population distribu-

tion can affect the energy demand in the electric grid

at various times and locations. On the other hand,

the demand on the energy grid can affect the char-

208

Nakarmi, U. and Naeini, M.

Towards Integrated Infrastructures for Smart City Services: A Story of Trafﬁc and Energy Aware Pricing Policy for Charging Infrastructures.

DOI: 10.5220/0006303202080218

In Proceedings of the 6th International Conference on Smart Cities and Green ICT Systems (SMARTGREENS 2017), pages 208-218

ISBN: 978-989-758-241-7

ging price and consequently affect the trafﬁc pattern

in the transportation system. Such interdependencies

are important as, for instance, during the peak-energy-

consumption hours, inappropriate energy pricing sig-

nals at charging stations that motivate EV users to use

speciﬁc charging stations, along with other factors,

can lead to energy demand proﬁles that result in in-

stability of the electric grid and in worse cases power

outages (Wagner et al., 2013). As such, it is essential

to design and operate these charging infrastructures

while considering the interdependency between elec-

tric and transportation systems and the state of these

systems. In particular, designing pricing incentives

can provide a controlling mechanism for interdepen-

dency and reliable operation of these systems. The

incentives will be communicated to the users through

the cyber infrastructure.

Since various aspects of the energy and transporta-

tion systems are dynamic and stochastic, in this paper

we adopt an abstract probabilistic approach to mo-

del the demand and trafﬁc distribution in EV char-

ging infrastructures. The goal of the model is to iden-

tify incentives, when and where they are needed, to

design dynamic energy pricing signals based on the

state of both of the systems, such that the incentives

help in appropriate distribution of load in both sys-

tems and orchestrating their operation. The propo-

sed approach is based on the inﬂuence theory (Asa-

vathiratham, 2000), which is a mathematically trac-

table probabilistic framework based on a network of

Markov chains. This framework allows modeling of

interactions among components of both the charging

and the electric infrastructures based on a data-driven

dynamic probabilistic approach. Based on this pro-

babilistic model, we identify incentives in terms of

charging price using a topological sort on the active

inﬂuence graph of the charging infrastructure. The

identiﬁed incentives based on this model lead to hig-

her probabilities of stable and balanced systems.

2 BACKGROUND

In this paper, we review the related work in two main

categories. First, as the focus of this paper is on

charging infrastructures, we review efforts on diffe-

rent aspects of design, operation and optimization of

charging infrastructures. Second, we brieﬂy review

work on modeling, simulation, operation and design

of integrated and interdependent infrastructure frame-

works for smart cities.

2.1 Charging Infrastructures

In recent years, a large body of work is focused on op-

timal placement of EV charging stations (Hess et al.,

2012), (He et al., 2013), (Wagner et al., 2013), (Sweda

and Klabjan, 2014), (Chen and Hua, 2014), (Guo and

Zhao, 2015), (Li et al., 2015), (Vazifeh et al., 2015),

(Xiong et al., 2015). In particular, optimization for-

mulations with various criteria have been used for ad-

dressing this problem (Hess et al., 2012), (Wagner

et al., 2013), (Li et al., 2015), (Guo and Zhao, 2015).

Examples of such criteria include, minimizing the trip

time of EVs to access charging stations (Hess et al.,

2012), maximizing the coverage of charging stations

(Wagner et al., 2013), minimizing trip and queuing

time (Li et al., 2015), and maximizing sustainability

from the environment, economics and society per-

spective (Guo and Zhao, 2015). In the work presented

in (Chen and Hua, 2014), (Vazifeh et al., 2015), the

set cover algorithm is used to optimize the location of

charging stations from a set of possible locations. In

addition, agent-based (Sweda and Klabjan, 2014) and

game-theoretic approaches (He et al., 2013), (Xiong

et al., 2015) have also been adopted in characterizing

optimal deployment of charging infrastructures. Re-

ference (Islam et al., 2015) presents a more detailed

review of various approaches used for the optimal de-

ployment of EV charging stations.

Another research aspect of charging infrastructu-

res is their pricing mechanisms. Studies of traditio-

nal fueling infrastructures (Walsh et al., 2004), (Weis

et al., 2010) show that the price of fuel impact the

behavior of drivers, which suggests that the charging

price for EVs can also impact the users’ choice and

behavior. Speciﬁcally, authors in (Xiong et al., 2016),

discuss that the optimal placement of charging sta-

tions will be insufﬁcient to handle rapid changes in

trafﬁc patterns and urbanization, hence an efﬁcient

pricing model that also minimize the social cost of

trafﬁc congestion and congestion at EV charging sta-

tions is needed. As another example, the impact of

energy price and the interplay between the price and

other factors, such as cost and emissions, on the char-

ging decisions have been studied in (Sioshansi, 2012).

Besides the studies on the impact of price on charging

decisions and trafﬁc patterns, some efforts are focused

on designing and optimizing pricing and analyzing

their impact on the users’ behavior and the system

operation. Examples of such efforts include the work

presented in (Lee et al., 2015), which uses a game

theoretical approach to study the price competition

among EV charging stations with renewable power

generators and also discusses the beneﬁts of having

renewable resources at charging stations. Similarly,

game-theoretic approaches that model a game bet-

Towards Integrated Infrastructures for Smart City Services: A Story of Trafﬁc and Energy Aware Pricing Policy for Charging Infrastructures

209

ween the electric grid and their users, speciﬁcally for

EV charging, in order to design pricing schemes, have

been studied, for example in (Tushar et al., 2012). The

model in (Tushar et al., 2012) provides strategies to

EV chargers to choose the amount of energy to buy

based on a pricing scheme to operate the charging in-

frastructures at their optimal levels.

The work presented in this paper is closest to the

studies on pricing mechanism design and also the in-

terplay between the electric and EV charging infra-

structures. At the same time, it is different in the ap-

proach as it considers the stochastic dynamics of the

interdependent EV charging infrastructures and the

electric grid and their local interactions in designing

the charging prices at stations.

2.2 Integrated and Interdependent

Infrastructures for Smart Cities

The vision of smart cities has been described in diffe-

rent ways among practitioners and academia (Chou-

rabi et al., 2012). Hall (Bowerman et al., 2000) vi-

sions the smart city as a city that monitors and in-

tegrates conditions of all of its critical infrastructu-

res to optimize its resources and services to its ci-

tizens. Similar smart city visions has been descri-

bed in (Harrison et al., 2010), (Commission et al.,

2014). In the last decade a large body of work has

emerged in modeling and understanding interdepen-

dent infrastructures. The general concepts of interde-

pendencies among critical infrastructures, challenges

in modeling interdependent systems and their cont-

rol and recovery mechanisms have been intensively

discussed in (Amin, 2002), (Little, 2002), (Rinaldi,

2004), (Min et al., 2007). These works mainly dis-

cuss the intrinsic difﬁculties in modeling interdepen-

dent systems and suggest new methodologies for their

modeling and simulation as a single coupled system.

The majority of the integrated infrastructure modeling

has been focused on analyzing the reliability of cou-

pled systems and the negative aspects of the interde-

pendencies among critical infrastructures (Shao et al.,

2011), (Shin et al., 2014), (Das et al., 2014). The work

presented in the current paper is an effort to present an

abstract and uniﬁed framework to model interactions

among infrastructures, which can be used to design

various smart-city solutions based on the state of inte-

racting systems, for instance, the pricing mechanism

based on the state of the EV charging infrastructure

and the electric grid.

3 SYSTEM MODEL

In this section, we describe our system model for the

interdependent EV charging and energy infrastructu-

res; however, the model is adequately general to be

applied to any interdependent infrastructure with in-

teracting components. The schematics of the system

under study is depicted in Figure 1. As the ﬁgure

shows, our study considers three layers in the system:

(1) the power/electric grid layer, (2) the EV charging

infrastructure layer, and (3) the cyber layer, which

enables the collaborative solution for the pricing bet-

ween layer 1 and 2. Our modeling is mainly focused

on the electric and the EV charging infrastructures.

While the cyber layer is not a part of the theoreti-

cal model, we will discuss its key role in Section 3.1.

The interactions among the layers of this system can

be summarized as following. The EV charging in-

frastructure receives energy from the power grid and

thus the load on charging stations may affect the load

on power substations. The pricing scheme, which de-

pends on the state of both power and EV charging in-

frastructures, will be communicated through the cyber

layer to the users. Finally, the communicated price

will affect the load distribution over the charging in-

frastructure and subsequently the load on power sub-

stations.

First, let us present the system model for the

charging infrastructure. We denote the set of char-

ging stations in a region in the smart city by C =

,...,C

}. For simplicity, we assume that the

charging stations are distributed over a grid region

such that each cell in the grid holds one charging sta-

tion as shown in Figure1a). The charging stations are

connected over a directed graph G = (C ,E), where

E represents the set of directed links specifying the

possibility of travel between charging stations for the

users. For instance, e

i j

∈ E implies that users in the

cell containing the station C

can travel to station C

for charging. These links help specifying the con-

straints on the travel for charging, for instance, based

on the distance that the users are willing to travel and

the distance that a EV with the need for charging can

travel before it runs out of energy. We will explain

later that when the right incentives are applied then

there is a likelihood for each user to travel to other

stations with direct links. In this paper, we focus on

a graph, in which charging stations in adjacent cells

are connected. Other graphs with different topologies

can also be considered and will not change the model.

Next, we describe the power infrastructure layer.

In this paper and as the ﬁrst step toward this mo-

deling, we simplify the intra-system model for the po-

wer infrastructure by only considering the power grid

substations denoted by S = {S

,...,S

} and their

SMARTGREENS 2017 - 6th International Conference on Smart Cities and Green ICT Systems

210

Abstract

Substation

(b)

(a)

CYBER

POWER

TRANSPORT

Substation

Figure 1: Interconnected networks of electric/power, charging infrastructure and cyber infrastructure.

internal dynamics (as will be explained in Section

3.1). In other words, we do not focus on the com-

plete power grid model with generators and power li-

nes; instead we only focus on substations as abstract

and aggregated points of contact with the EV char-

ging infrastructure. In future, we will expand the mo-

del to capture more detailed internal interactions in

the power system. To model the inter-system inte-

ractions between the power and charging infrastruc-

tures we assume that multiple charging stations be-

long to the distribution network of one substation, as

such we consider a set of inter-system links denoted

by L, where L

i j

∈ L speciﬁes that charging station C

affect the load of substation S

. In this model, C

∈ C

should have a link to one speciﬁc S

∈ S while each S

can have multiple incoming links from different ge-

ographically co-located charging station. Also, note

that there will be no links from S

to any node in C .

Such interactions and the effects of power substations

on charging stations will be indirectly through the in-

centives communicated by the cyber layer. Based on

the above discussion, the total integrated system can

be denoted by a graph as G

= (C ∪S ,E ∪L). Howe-

ver, the model for the system is not simply a graph.

Next, we will explain how each component in this

graph stochastically and dynamically evolves and in-

teracts with other components. We will speciﬁcally

present a model to capture such dynamics. We have

chosen a probabilistic approach for the modeling as

various aspects of this system is stochastic. For in-

stance, the state of a charging station (e.g., being busy

or not) varies probabilistically at different times of the

day and week and due to EV users mobility pattern

and behavior. The state of the load in a substation

also varies due to stochastic nature of the demand.

The interactions among components are also stochas-

tic and as components inﬂuence each other depending

on their state. For instance, if charging stations, which

have a link to substation S

, become busy and overlo-

aded with lots of demand then this increased demand

will increase the likelihood of S

to become overlo-

aded and hinder the stability of the power grid. In

such cases, we would like to distribute the load in the

system using pricing incentives to increase the wil-

lingness of EV users to travel to other charging stati-

ons. These stochastic interactions and dynamics will

be modeled in an Inﬂuence Theoretic framework as

explained next.

3.1 Inﬂuence Model for Integrated

Infrastructures

Here, we brieﬂy review the Inﬂuence Model (IM) as

ﬁrst introduced in (Asavathiratham, 2000), (Asavathi-

ratham et al., 2001) and present an IM-based frame-

work for modeling the integrated charging and power

infrastructures.

The IM is a framework consisting of a weighted

and directed graph of interconnected nodes, in which,

the internal stochastic dynamics of each node is re-

presented by a Markov Chain (MC) and the states of

the nodes varies in time due to the internal transitions

of MCs as well as the external transitional inﬂuen-

ces from other nodes. The weights on the directed

links represent the strength of inﬂuences that nodes

receive from one another. In the following, we put

the IM model in perspective with respect to the inte-

grated charging and power infrastructures. In our mo-

del, graph G

with two types of links and nodes (as

introduced in Section 3) will serve as the underlying

graph for the IM. To represent the internal dynamics

of nodes, we consider that the state of the charging

Towards Integrated Infrastructures for Smart City Services: A Story of Trafﬁc and Energy Aware Pricing Policy for Charging Infrastructures

211

stations can be abstracted to three levels: (1) underlo-

aded, (2) normal, and (3) overloaded levels. As such,

we deﬁne a MC with state space of size three for each

∈ C . These states help describing the load (in terms

of energy demand) on a charging station at each time.

In general, the state of a C

may change due to de-

parture or arrival of EV users. On the other hand, we

model a substation S

with an internal MC, which has

two possible states: normal and stressed. These states

specify if a power substation is overloaded and stres-

sed or it is working under normal conditions. The

transition probability matrix of the internal MC for a

node, say node i ∈ C ∪ S , is denoted by A

, which is

an m × m row stochastic matrix, where m is the size

of the state space. We use a data driven approach to

characterize the transition probabilities of these inter-

nal MCs based on datasets of system dynamics and

simulations as will be explained later. The links in

graph G

specify the inﬂuence relation among the no-

des. In particular, there are two types of inﬂuences

in our model: (1) when a charging station inﬂuences

another charging station, then it means there is a like-

lihood that it will send users (using proper incentives)

to the inﬂuenced station, and (2) when a charging sta-

tion inﬂuences a power substation, then it means that

there is a likelihood that the charging station increases

the energy load on the power substation to a level that

could change the state of the power substations (e.g.,

from normal to stressed). The weights on the links

also specify the strength of the inﬂuence. Speciﬁcally,

the inﬂuences among the nodes of the network is cap-

tured by the inﬂuence matrix denoted by D, where

each element d

i j

is a number between 0 and 1 repre-

senting the amount of inﬂuence that node i receives

from node j. The larger the d

i j

is the more inﬂuence

the node i receives from node j; with the two extreme

cases being d

i j

= 0 meaning that node i does not re-

ceive any inﬂuence from node j and d

i j

= 1 meaning

that the next state of node i deterministically depends

on the state of node j. Note that receiving inﬂuence

from a node itself, i.e., d

, speciﬁes how much the

state evolution of a node depends on its internal MC.

The total inﬂuence that a node receives should add up

to unity i.e.,

∑

j=1

i j

= 1, and therefore, matrix D is a

row stochastic matrix too.

In IM, the status of a node, say node i, at time

t is denoted by s

[t], a vector of length m, where m

is the number of possible states for the node. At

each time, all the elements of s

[t] are 0 except for

the one which corresponds to the current state of the

node (with value 1). In our model, s

[t], s

[t], and

[t] correspond to overloaded, normal and underlo-

aded states, respectively, for charging stations. Simi-

larly, s

[t] and s

[t] correspond to normal and stres-

sed states for power substations, respectively. The sta-

tuses of all the nodes concatenated together as S[t] =

[t]s

[t]...s

[t]) described the state of the whole sy-

stem in time t, where n = |C ∪ S | and |.| denotes the

cardinality of the set.

The inﬂuence matrix D speciﬁes how much two

nodes inﬂuence each other. In order to specify how

the states of the nodes will change due to the inﬂuen-

ces, we also need state-transition matrices A

i j

, which

capture the probabilities of transiting to various states

due to the state of the inﬂuencing node. Matrix A

represents the special case of self-inﬂuence, which is

described by the internal MC of the node. Note that

the A

i j

matrices are row stochastic. In the general

IM (Asavathiratham, 2000), the collective inﬂuences

among the nodes in the network is summarized in the

total inﬂuence matrix H deﬁned as:

H = D

⊗ {A

i j

} =







··· d







, (1)

where D

is the transpose of the matrix D and ⊗ is

the generalized Kronecker multiplication of matrices

(Asavathiratham, 2000). Finally, based on the the to-

tal inﬂuence matrix H the evolution equation of the

model is deﬁned as

p[t + 1] = S[t]H, (2)

where vector p[t + 1] describes the probability of va-

rious states for all the nodes in the network in the next

time step. Steady state analysis of IM has some simi-

larities with that of MCs and has been discussed for

various scenarios in (Asavathiratham, 2000), (Asava-

thiratham et al., 2001). For a more detailed discus-

sion on the IM please refer to (Asavathiratham, 2000),

(Asavathiratham et al., 2001).

The work in (Siavashi, 2016) extends the original

IM to a constraint or rule-based inﬂuence framework

such that the inﬂuences among the nodes can dynami-

cally get activated and deactivated depending on the

state of the system. Also, as explained in (Siavashi,

2016), inﬂuencing can change the state of the inﬂu-

encer as well (transiting from overload to normal due

to sending load to another station). (Siavashi, 2016)

speciﬁcally deﬁned a constraint matrix C, where the

entry c

i j

for i, j ∈ C ∪ S is a binary variable speci-

fying whether node i gets inﬂuenced by node j or not.

In particular, c

i j

= 1 indicates that node i gets inﬂu-

enced by node j and c

i j

= 0 indicates otherwise. Mo-

reover, each node always inﬂuences itself based on

its internal MC (i.e., c

= 1 for all i ∈ C ∪ S ). As

explained in (Siavashi, 2016), one can deﬁne the va-

lue of c

i j

according to boolean logic to capture the

rules of interactions in the network. In other words,

SMARTGREENS 2017 - 6th International Conference on Smart Cities and Green ICT Systems

212

i j

s are functions of the state of the nodes. For in-

stance, when a charging station in the EV charging

infrastructure is in overloaded state and based on G

it has a link to another station, which is underloaded,

the inﬂuence over that link should get activated to

motivate the EV users to travel from the overloaded

state to underload state. These types of rules can be

speciﬁed using boolean functions such as the follo-

wing examples. Function c

i j

= s

+ s

, where

i, j ∈ C speciﬁes the rules that can be applied to the

transport layer of the model to show inﬂuences from

charging station j to charging station i. Speciﬁcally, a

transport node i will receive inﬂuence from transport

node j if node i is underloaded and node j is over-

loaded or if node i is normal and node j is overloa-

ded. Also, the power substations receive inﬂuences

from the charging stations because overloaded char-

ging stations can cause a power substation to go to

overloaded state. Example of boolean function des-

cribing this rule is c

k

= s

∏

j∈C

∏

j∈C

where k ∈ S and  ∈ C and C

⊆ C is the set of

charging stations connected to the power substation

k. Speciﬁcally, a power substation, say k will receive

inﬂuence from charging station  when all the char-

ging stations connected to the power substation are

overloaded. As a power station is generally built with

a capacity to accommodate large demand, the power

substation will go to a stressed state provided that all

the inﬂuence links connected to it are activated. This

is just one example of inﬂuence rule and other condi-

tions to specify the rules are also possible.

Note that as the goal of the integrated study of

these two systems is to increase the probability of ha-

ving power substations in normal conditions and char-

ging stations not overloaded, the interaction rules de-

ﬁned in C should support this goal. In order to achieve

this goal the inﬂuences among the charging stations

should be engineered such that it forces the whole

system toward desirable states. The second type of

inﬂuence, which is from the charging station to po-

wer substations cannot be engineered and we assume

that when the charging stations, which are receiving

energy from a substations, are overloaded they inﬂu-

ence (increase the likelihood) the substation to transit

to a stressed state.

In (Siavashi, 2016), the constraint matrix C

and the inﬂuence matrix D are used to deﬁne the

constraint-based inﬂuence matrix denoted by E, as

E = D ◦ C + I ◦ (D × (1 − C

)), (3)

where ◦ is the Hadamard product (aka entrywise pro-

duct), 1 is the matrix with all elements equal to 1 and

is the transpose of matrix C. Using E, the IM-

based state evolutions can be summarized as

H = E

⊗ {A

i j

}, (4)

and p[t + 1] = S[t]H.

As discussed in (Siavashi, 2016), this formulation

may or may not allow the asymptotic analysis of the

behavior of the system. However, no matter if the ana-

lytical solution of the model exists or not, this model

can be used for Monte-Carlo simulation of the beha-

vior of the system in order to study how inﬂuences

and interactions affect the state of the whole system.

Based on this formulation, as the state of the system

varies in time, various sets of inﬂuences get activated.

Note that in IM, when a node inﬂuences another node,

it may result in state change for the inﬂuenced node

based on the adjusted transition probabilities that are

captured through H and the formulation of p[t + 1].

As such, an activated inﬂuence in our model increa-

ses the probability of transitioning to a normal state

for an underloaded charging station due to receiving

load from the inﬂuencer (based on our deﬁnition of

inﬂuence). In real-world, proper incentives for the

users are needed to make that inﬂuence occur (trans-

fer of load from one charging station to another). As

such, to achieve the goal of the system which is incre-

asing the probability of normal states, we use the sta-

tus of the inﬂuence links (active or inactive) to guide

the charging price design. In the next section, we ex-

plain how this model will help in designing proper

prices and together with the rules of interactions can

lead to more balanced system for both EV charging

and power infrastructures.

4 MECHANISM FOR DESIGNING

CHARGING PRICE AT EV

CHARGING STATIONS

The model described in the previous section needs an

external factor in real-world scenarios to provoke an

EV user to travel from one charging station to another

for charging (i.e., activating the described inﬂuence

between charging stations in real-world). This exter-

nal factor can be in terms of incentives or hampers

that an EV user may get if they move from one cell

to another. A good incentive would be lower char-

ging prices (whenever the inﬂuence should be active)

in the station, which should receive some load. The

lower prices can motivate the EV users to move from

their currently occupied cell to the other station. Ho-

wever, not every EV user will respond to such incen-

tives in the same way and thus not every user will

travel from the ﬁrst cell. Particularly, the probabilistic

nature of the IM helps in capturing the random beha-

vior of the users. Intuitively, the higher the inﬂuence

strength the more we expect that the users travel to

Towards Integrated Infrastructures for Smart City Services: A Story of Trafﬁc and Energy Aware Pricing Policy for Charging Infrastructures

213

the other station, which can help in characterizing the

price reduction that is needed. A key point to notice is

that the cyber layer plays a key role in letting the de-

sired inﬂuences to occur to let the system identify its

next states based on IM. Speciﬁcally, the cyber layer

should communicate the lower charging price only to

the users in the cell that is inﬂuencing the station. Ot-

herwise, if the reduced price is communicated in the

system globally and all the EV users in the city know

about the reduced price in a station, this will activate

inﬂuences among neighbor stations (neighbors are de-

ﬁned as according to G

) that should not be activated

according to the IM model. Thus, in order to only

activate the inﬂuences that the IM model identiﬁes for

leading the system to a more balanced system in each

step, the cyber layer plays a key role in communica-

ting the prices to the right EV users based on their

location.

Algorithm 1: Algorithm for Price Assignment to Char-

ging Stations.

1: Input  Graph of active

inﬂuences, G

(C ,E

(t)). A maximum electricity

price limit A and a reduction factor in price, α.

2: Output  Charging price in each charging

station in C such that the price of the inﬂuencer

station is higher than the inﬂuenced station.

3: Calculate the topological sort T for G

4: for i=1 to |C | do

5: if |I(T(i))| = 0 then

6: Price(T(i)) = A

7: else

8: Price(T(i))=

∑

j∈I(T(i))

Price( j)/|I(T(i))|

9: end if

10: end for

11: Return Price.

In our model based on IM, whenever the set of

activated inﬂuence links varies, we need to identify

new set of prices for each station such that if station

say i has an active inﬂuence link to station j, then the

price at station i should be higher than that of station

j. To identify the set of prices that satisfy this con-

dition in the whole system, we propose the algorithm

presented in Algorithm 1. This algorithm is similar

to a constrained graph coloring problem. However,

the problem of price assignment to the stations based

on the above constraint is solvable with complexity

O(|C | + |E|), which is because the graph of active in-

ﬂuences denoted by G

(C ,E

(t)) and obtained from

simulation of IM at step t is a directed and acyclic

graph (note that E

(t) ⊆ E , also note that E

(t) does

not include self-inﬂuences as they do not affect the

pricing). This property is due to the rule set with the

goal of balancing the load in the system, which ne-

ver result in a cycle in the graph of active inﬂuences.

In other words, the rule set in the model is very im-

portant to ensure that the load is not circulating in the

system and purposely directed to the proper charging

stations. Algorithm 1 for price assignment uses a to-

pological sort of the graph and then assigns the prices

based on the identiﬁed order such that the prices ens-

ure that the stations appearing later in the topological

sort have lower prices (as they should receive inﬂuen-

ces or loads). In our algorithm, we consider a maxi-

mum price limit of A and each price reduction occurs

by a constant α. The values of A and α are conside-

red ﬁxed in this paper for simplicity, but can be varia-

ble and adjusted based on other factors in the system.

In this algorithm, function I(.) receives a node and

returns the set of nodes, which inﬂuences the input

node.

5 EVALUATION AND RESULTS

In order to demonstrate the process of assigning pri-

ces to the charging stations dynamically as the system

evolves in time while trying to lead both systems to

more balanced states, we use an example network as

shown in Figure 2 with 12 charging stations, which

receive their energy from two power substations. In

this example, we used a data driven approach to ex-

tract some of the parameters of the IM using available

data sets of trafﬁc information. Speciﬁcally, we used

the taxi data in (Piorkowski et al., 2009), which con-

tained GPS trajectories of 536 taxis in San Francisco,

California from May 17, 2009-July 10, 2009 speciﬁ-

cally to estimate A

s. An example of A

based on the

dataset is as following, where rows and columns are

ordered from overload to normal and then underload:





0.89473684 0.1052632 0.00000000

0.07262570 0.8770950 0.05027933

0.07142857 0.2142857 0.71428571





(5)

In addition to A

s, which characterize the internal dy-

namics of each station, we also need to consider A

i j

to specify how the inﬂuences between two stations re-

sult in state transitions. An example of A

i j

is shown

in (6) in which each column speciﬁes the probability

of transition to overload, normal, and underload, re-

spectively, depending on each row, which speciﬁes

the state of the inﬂuenced node. For simplicity and

due to lack of detailed information in the datasets to

characterize this matrix for all cells, we have simpli-

ﬁed this matrix to have equal transition probabilities

independent of the state of the inﬂuenced node (i.e.,

the same rows). Based on our model and the rules of

SMARTGREENS 2017 - 6th International Conference on Smart Cities and Green ICT Systems

214

inﬂuences, in order to lead the systems to balanced

states a station only tries to send load to another sta-

tion if the other station is not overloaded. As such the

last row of the matrix in (6) does not play a role in the

analysis.

i j





0.2 0.5 0.3





. (6)

Similarly, an example of A

for power substations

is as following where rows and columns are ordered

from normal to stressed:



0.8 0.2

0.5 0.5



. (7)

Since the detailed dynamics of the power grid is not

considered in this paper, we only focus on how their

state change when they are stressed by charging stati-

ons. But to consider the effects of internal dynamics

of the power grid, we consider a small probability that

a power substation changes state from normal to stres-

sed due to different parameters in the system other

than the charging stations (here this value is chosen to

be 0.2). When the system is stressed (i.e., the second

row on the matrix in (7)) then we assume there is an

equal chance to get into normal state or stay stressed

based on internal dynamics. However, as a part of

inﬂuences in our IM-based model whenever the char-

ging stations go back to normal or underloaded states

then they can externally help the power substation to

transit back to the normal state. Speciﬁcally, the set of

rules for this study can be described as: (1) node i gets

inﬂuenced by node j if and only if node i is underlo-

aded and node j is overloaded or node i is in normal

state and node j is overloaded for charging stations,

and (2) for the inﬂuences between the power substa-

tions and the charging stations, the power substation

gets inﬂuenced by a charging station if the power sta-

tion is normal and the charging stations receiving po-

wer service from the substation are overloaded or if

the power substation is stressed and the charging sta-

tions are normal or underloaded.

As mentioned earlier, based on the state of the

components in the system, the inﬂuences among no-

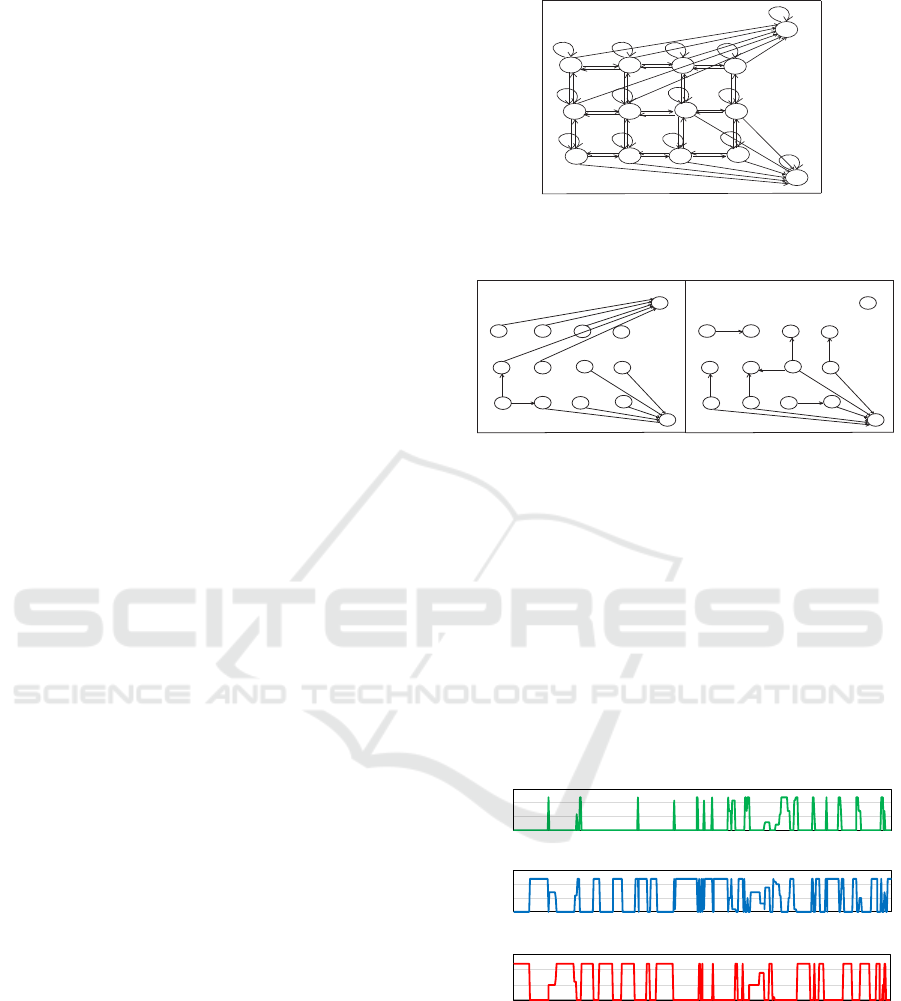
des may get activated and deactivated. In Figure 3, we

show two samples of active inﬂuence graphs for the

network shown in Figure 2. The activated links bet-

ween charging stations suggest that the load should be

transferred from one station to the station on the end

of the directed link.

The set of activated inﬂuences in each iteration

prompts a change of state in the charging stations and

power substations as shown in Figures 4 and 5. Spe-

ciﬁcally, Figures 4a, 4b and 4c show the distribution

5 6

Transport Nodes

Initial State

Substation

Figure 2: The integrated charging and power infrastructures

model with 12 charging stations and two substations (i.e.,

graph G

5 6

Transport Nodes

Iteration 34

Substation

5 6

Transport Nodes

Iteration 477

Substation

Figure 3: Two samples of active inﬂuence graph.

of the number of charging stations in underload, nor-

mal and overload states in each iteration respectively.

Although the distributions are ﬂuctuating but it can

be observed from Figures 6 and 7 that the aggregated

behavior of the system is independent of the initial

state of the system as the likelihood of normally loa-

ded charging stations and normal power substations is

higher than other states. The results in Figures 8 and

9 are obtained over 1000 steps of the IM simulation.

Figure 8 shows the state distribution of the charging

stations and power substations with various initial sta-

tes.

(a)

(b)

101

121

141

161

181

201

221

241

261

281

301

321

341

361

381

401

421

441

461

481

(c)

Figure 4: Number of charging stations in each iteration in:

(a) underloaded, (b) normal, and (c) overloaded, states.

An important aspect of the inﬂuence model is the

set of rules that specify how the nodes should interact

and inﬂuence each other. To show how the rules of the

interactions affect the behavior of the system, here,

we have considered other inﬂuence rules similar to

the rules of interactions deﬁned in (Siavashi, 2016) as

Towards Integrated Infrastructures for Smart City Services: A Story of Trafﬁc and Energy Aware Pricing Policy for Charging Infrastructures

215

(a)

1 21 41 61 81 101 121 141 161 181 201 221 241

(b)

Figure 5: Number of power substations in each iteration in

various states: (a) normal state, and (b) stressed state.

1000

2000

3000

4000

5000

6000

7000

121

161

201

241

281

321

361

401

441

481

521

561

601

641

681

721

761

801

841

881

921

961

Overload

Normal

Underload

Figure 6: Aggregated states distribution for overloaded,

normal and underloaded states for charging stations.

200

400

600

800

1000

1200

121

161

201

241

281

321

361

401

441

481

521

561

601

641

681

721

761

801

841

881

921

961

Normal

Stressed

Figure 7: Aggregated state distribution for normal and stres-

sed states for the power substations.

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Transport

Overload and

Power Normal

Transport

Overload and

Power

Stressed

Transport

Normal and

Power Normal

Transport

Normal and

Power

Stressed

Transport

Underload

and Power

Normal

Transport

Underload

and Power

Stressed

Transport Overload Transport Normal Transport Underload

Power Normal Power Stressed

Figure 8: State distribution of charging stations and power

substations with various initial states for the components.

follows:

• Rule 1: Node i gets inﬂuenced by node j if and

only if (iff) node i is underloaded and node j is

overloaded or node i is in normal state and node j

is overloaded.

• Rule 2: Node i gets inﬂuenced by (receives wor-

kload from) node j iff node i is underloaded and

node j is overloaded.

• Rule 3: Node i gets inﬂuenced by node j iff node

i is underloaded and node j is overloaded or node

i is underloaded and node j is in normal state.

• Rule 4: Node i gets inﬂuenced by node j iff either

node i is underloaded and node j is overloaded,

node i is underloaded and node j is in normal state

or node i is in normal state and node j is overloa-

ded.

• Rule 5: Node i gets inﬂuenced by node j iff either

node i is underloaded and node j is overloaded,

node i is underloaded and node j is in normal

state, node i is in normal state and node j is over-

loaded or node i is in normal state and node j is in

normal state too.

Note that these rules only focus on the interactions

among the charging stations and the inﬂuences among

charging stations and the power substations are assu-

med to be as before. Figure 9 shows the state distribu-

tion of nodes with all charging stations initially over-

loaded and all power substations initially normal for

different rules applied to the model. It can be seen that

rule 5 performs the worst among the all as the number

of overloaded charging stations are higher compared

to other cases.

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Rule 1

Rule 2

Rule 3

Rule 4

Rule 5

Transport Overload Transport Normal Transport Underload

Power Normal Power Stressed

Figure 9: State distribution of charging stations and power

substations with all charging stations initially overloaded

and all power substations initially in normal states for diffe-

rent rules of interactions.

To design the incentives that enable inﬂuences and

lead to the results shown in Figures 6, 7, 8 and 9, we

need to design the prices for each charging station. To

do so, we have used Algorithm 1 over the active in-

ﬂuence graph obtained at each step of the simulation

whenever there was a change in the active inﬂuence

graphs. Note that Algorithm 1 receives graphs simi-

lar to the ones shown in Figure 3 where the self-edges

are omitted. The price assignment based on this algo-

rithm at each station is shown in Table 1 for sample

steps of our simulation (with Rule 1). As it can be

observed from the table, initially all the twelve stati-

ons have the same price of A but the prices vary over

the network as the stochastic dynamics of the system

change the states of the nodes.

In this section, we showed our preliminary study

of collaborative pricing solution between the EV char-

ging and electric infrastructures based on our IM-

based model. Key takeaways from our results include:

SMARTGREENS 2017 - 6th International Conference on Smart Cities and Green ICT Systems

216

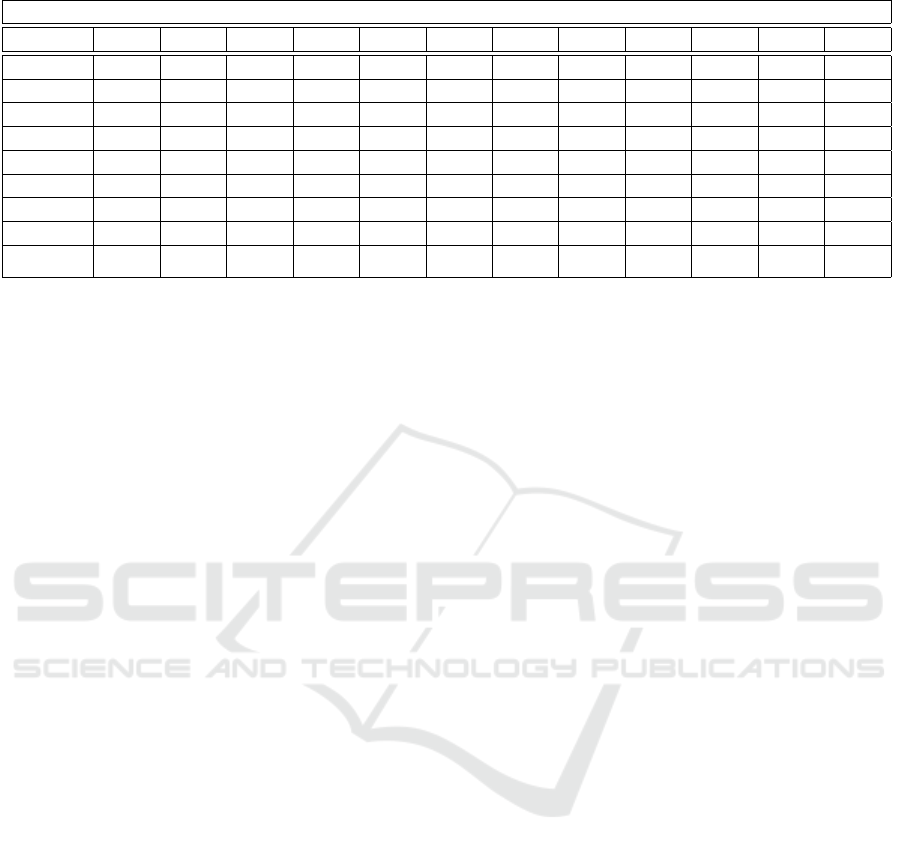
Table 1: Charging prices in each EV charging station over various iterations.

Charging Stations

Iteration 1 2 3 4 5 6 7 8 9 10 11 12

1 A A A A A A A A A A A A

18 A - α A A A A A A A A A A A

245 A A - α A A A - α A A A A A A A

246 A A A A A A A A A A A A

247 A A A - α A A A A - α A - α A - α A A A

261 A A A A - α A - α A - α A - α A A A - α A A - α

446 A - α A A A A A A A A A A A

650 A A A A - α A - α A - α A - α A A A - α A A - α

892 A A A A - α A - α A - α A A A A - α A - α A - α

(1) by designing proper rules of interactions among

the integrated systems, the load distribution can be

improved in both systems, and (2) the pricing assig-

nment based on the obtained active inﬂuence graph

enables the implementation of appropriate inﬂuences.

6 CONCLUSIONS

In this paper, we discussed the importance of collabo-

rative solutions among critical infrastructures of smart

cities. We speciﬁcally emphasized that the smart city

solutions should consider the state of various systems

interacting with each other rather than only an indi-

vidual infrastructure. To demonstrate this point, in

this paper, we focused on interdependent EV char-

ging and the electric infrastructures and developed an

integrated framework for modeling their interactions

based on inﬂuence model, which is a networked Mar-

kov chain framework. We also proposed an algorithm,

which assigns prices to charging stations based on the

set of active links that can lead to more balanced sys-

tems. We discussed the role of the cyber infrastructure

in enabling this pricing scheme, which considers the

state of both of the systems. The work presented in

this paper is an effort toward using integrated models

for infrastructures to develop collaborative solutions

for smart cities. In future, we will study, both analy-

tically and using simulations, the role of various pa-

rameters of the model in the behavior of the system.

We also hope that this study and modeling approach

can be extended to other smart city solutions and in-

terdependent infrastructures.

REFERENCES

Amin, M. (2002). Toward secure and resilient interdepen-

dent infrastructures. Journal of Infrastructure Sys-

tems, 8(3):67–75.

Asavathiratham, C. (2000). The inﬂuence model: A tracta-

ble representation for the dynamics of networked mar-

kov chains. PhD thesis, Citeseer.

Asavathiratham, C., Roy, S., Lesieutre, B., and Verghese, G.

(2001). The inﬂuence model. IEEE Control Systems,

21(6):52–64.

Bass, R. and Zimmerman, N. (2013). Impacts of electric

vehicle charging on electric power distribution sys-

tems.

Bowerman, B., Braverman, J., Taylor, J., Todosow, H., and

Von Wimmersperg, U. (2000). The vision of a smart

city. In 2nd International Life Extension Technology

Workshop, Paris, volume 28.

Chen, C. and Hua, G. (2014). A new model for optimal

deployment of electric vehicle charging and battery

swapping stations. International Journal of Control

& Automation, 8(5).

Chourabi, H., Nam, T., Walker, S., Gil-Garcia, J. R., Mel-

louli, S., Nahon, K., Pardo, T. A., and Scholl, H. J.

(2012). Understanding smart cities: An integrative

framework. In System Science (HICSS), 2012 45th

Hawaii International Conference on, pages 2289–

2297. IEEE.

Commission, I. E. et al. (2014). Orchestrating infrastruc-

ture for sustainable smartcities. Published in Geneva,

Switzerland.

Das, A., Banerjee, J., and Sen, A. (2014). Root

cause analysis of failures in interdependent power-

communication networks. In Military Communicati-

ons Conference (MILCOM), 2014 IEEE, pages 910–

915. IEEE.

Guo, S. and Zhao, H. (2015). Optimal site selection of

electric vehicle charging station by using fuzzy topsis

based on sustainability perspective. Applied Energy,

158:390–402.

Harrison, C., Eckman, B., Hamilton, R., Hartswick, P.,

Kalagnanam, J., Paraszczak, J., and Williams, P.

(2010). Foundations for smarter cities. IBM Journal

of Research and Development, 54(4):1–16.

Hatton, C., Beella, S., Brezet, J., and Wijnia, Y. (2009).

Charging stations for urban settings the design of a

product platform for electric vehicle infrastructure in

dutch cities. In Towards zero emission: EVS 24 In-

ternational Battery, Hybrid and Fuel Cell Electric

Vehicle Symposium & Exhibition, 13-16 May 2009,

Towards Integrated Infrastructures for Smart City Services: A Story of Trafﬁc and Energy Aware Pricing Policy for Charging Infrastructures

217

Stavanger, Norway. European Association of Electric

Road Vehicles.

He, F., Wu, D., Yin, Y., and Guan, Y. (2013). Optimal de-

ployment of public charging stations for plug-in hy-

brid electric vehicles. Transportation Research Part

B: Methodological, 47:87–101.

Heilig, G. (2012). World urbanization prospects: The 2011

revision. new york: United nations, department of

economic and social affairs (desa), population divi-

sion. Population Estimates and Projections Section.

Hess, A., Malandrino, F., Reinhardt, M. B., Casetti, C.,

Hummel, K. A., and Barcel

o-Ordinas, J. M. (2012).

Optimal deployment of charging stations for electric

vehicular networks. In Proceedings of the ﬁrst works-

hop on Urban networking, pages 1–6. ACM.

Islam, M. M., Shareef, H., and Mohamed, A. (2015). A re-

view of techniques for optimal placement and sizing

of electric vehicle charging stations. Przeglad Elek-

trotechniczny, 91(8):122–126.

Lee, W., Xiang, L., Schober, R., and Wong, V. W. (2015).

Electric vehicle charging stations with renewable po-

wer generators: A game theoretical analysis. IEEE

Transactions on Smart Grid, 6(2):608–617.

Li, Y., Luo, J., Chow, C.-Y., Chan, K.-L., Ding, Y., and

Zhang, F. (2015). Growing the charging station net-

work for electric vehicles with trajectory data analy-

tics. In 2015 IEEE 31st International Conference on

Data Engineering, pages 1376–1387. IEEE.

Little, R. G. (2002). Controlling cascading failure: Un-

derstanding the vulnerabilities of interconnected in-

frastructures. Journal of Urban Technology, 9(1):109–

123.

Liu, J. (2012). Electric vehicle charging infrastructure as-

signment and power grid impacts assessment in bei-

jing. Energy Policy, 51:544–557.

Liu, R., Dow, L., and Liu, E. (2011). A survey of pev im-

pacts on electric utilities. In Innovative Smart Grid

Technologies (ISGT), 2011 IEEE PES, pages 1–8.

IEEE.

Min, H.-S. J., Beyeler, W., Brown, T., Son, Y. J., and Jo-

nes, A. T. (2007). Toward modeling and simulation of

critical national infrastructure interdependencies. Iie

Transactions, 39(1):57–71.

Pillai, J. R. and Bak-Jensen, B. (2010). Impacts of electric

vehicle loads on power distribution systems. In 2010

IEEE Vehicle Power and Propulsion Conference, pa-

ges 1–6. IEEE.

Piorkowski, M., Saraﬁjanovic-Djukic, N., and Grossglau-

ser, M. (2009). Crawdad data set epﬂ/mobility (v.

2009-02-24).

Rahman, I., Vasant, P. M., Singh, B. S. M., and Abdullah-

Al-Wadud, M. (2014). Intelligent energy allocation

strategy for phev charging station using gravitational

search algorithm. In AIP Conference Proceedings, vo-

lume 1621, pages 52–59.

Recker, W. W. and Kang, J. E. (2010). An activity-based

assessment of the potential impacts of plug-in hybrid

electric vehicles on energy and emissions using one-

day travel data. University of California Transporta-

tion Center.

Rinaldi, S. M. (2004). Modeling and simulating critical in-

frastructures and their interdependencies. In System

sciences, 2004. Proceedings of the 37th annual Ha-

waii international conference on, pages 8–pp. IEEE.

Shao, J., Buldyrev, S. V., Havlin, S., and Stanley, H. E.

(2011). Cascade of failures in coupled network

systems with multiple support-dependence relations.

Physical Review E, 83(3):036116.

Shin, D.-H., Qian, D., and Zhang, J. (2014). Cascading

effects in interdependent networks. IEEE Network,

28(4):82–87.

Siavashi, E. (2016). Stochastic modeling of net-

work interactions: Conditional inﬂuence model.

Texas Tech Master Thesis (https://ttu-ir.tdl.org/ttu-

ir/handle/2346/67107).

Sioshansi, R. (2012). Or forum-modeling the impacts of

electricity tariffs on plug-in hybrid electric vehicle

charging, costs, and emissions. Operations Research,

60(3):506–516.

Sweda, T. M. and Klabjan, D. (2014). Agent-based infor-

mation system for electric vehicle charging infrastruc-

ture deployment. Journal of Infrastructure Systems,

21(2):04014043.

Tushar, W., Saad, W., Poor, H. V., and Smith, D. B. (2012).

Economics of electric vehicle charging: A game the-

oretic approach. IEEE Transactions on Smart Grid,

3(4):1767–1778.

Vazifeh, M. M., Zhang, H., Santi, P., and Ratti, C. (2015).

Optimizing the deployment of electric vehicle char-

ging stations using pervasive mobility data. arXiv pre-

print arXiv:1511.00615.

Wagner, S., G

otzinger, M., and Neumann, D. (2013). Op-

timal location of charging stations in smart cities: A

points of interest based approach.

Walsh, K., Enz, C. A., and Canina, L. (2004). The impact

of gasoline price ﬂuctuations on lodging demand for

us brand hotels. International Journal of Hospitality

Management, 23(5):505–521.

Weis, C., Axhausen, K., Schlich, R., and Zbinden, R.

(2010). Models of mode choice and mobility tool ow-

nership beyond 2008 fuel prices. Transportation Rese-

arch Record: Journal of the Transportation Research

Board, (2157):86–94.

Xiong, Y., Gan, J., An, B., Miao, C., and Bazzan, A. L.

(2015). Optimal electric vehicle charging station pla-

cement. In Proceedings of the 24th International Joint

Conference on Artiﬁcial Intelligence (IJCAI), pages

2662–2668.

Xiong, Y., Gan, J., An, B., Miao, C., and Soh, Y. C. (2016).

Optimal pricing for efﬁcient electric vehicle charging

station management. In Proceedings of the 2016 Inter-

national Conference on Autonomous Agents & Multi-

agent Systems, pages 749–757. International Founda-

tion for Autonomous Agents and Multiagent Systems.

SMARTGREENS 2017 - 6th International Conference on Smart Cities and Green ICT Systems

218