Highway Reservation Strategy: Analytical Modeling Approach

Peng Su

, B. Brian Park

and Sang H. Son

Center for Transportation Studies, University of Virginia, Charlottesville, VA, U.S.A.

Cyber Physical Systems Center, DGIST, Daegu, Republic of Korea

Keywords: Highway Reservation, Traffic Management Strategy, Analytical Modeling Approach.

Abstract: Inspired by the success of reservation systems in airlines industries, and the Connected Vehicle technology

supporting vehicular communications, this paper investigated a highway reservation and developed a

mathematical optimization formulation to solve the optimal trip scheduling plan for a traffic network. The

performance was quantified by total monetary cost of travel time and applicable early arrival time or late

arrival time. In the two numerical case studies with an assumption of 100% compliance of the users to the

reservation system’s scheduling, the system cost was 24.1% and 21.7% lower than those of the two

corresponding user equilibrium solutions. The reservation system effectively redistributed the peak hour

demand to the non-peak hours by limiting the reservation maximum flow rate of the reservation links.

1 INTRODUCTION

Metropolitan transportation road networks are

typically congested due to concentrated travel

activities and consequently faced with increased

travel times, air pollution, noise, and traffic crashes.

As shown by the annual person-hours of highway

traffic delay per auto commuter, between 1982 and

2014, provided by the 2015 National Transportation

Statistics (Bureau of Transportation Statistics, 2015),

congestion has increased substantially over the 30

years. The delay per commuter in 2014 was 42 hours.

In the very large urban areas (3 million and over

population), the average auto commuter delay is 63

hours. Adding more capacity by providing more road

lanes and more public transportation is the most

fundamental congestion solution in most growing

urban regions to satisfy the increasing travel demand.

However, transportation system capacity almost

always increases at a slower rate than the demand

growth. As shown by the Road Growth and Mobility

Level Exhibit (Schrank et al., 2012), 56 in 101 study

areas have travel demand growth 30% faster than

supply, and only 17 areas have a less than 10% gap

between demand and supply growth. Even if the

capacity growth perfectly matches with travel

demand, new problems would occur as reduction in

congestion induces departure time shifts into peak-

hour (Hendrickson and Plank, 1984). In addition,

crashes or work zones may create bottlenecks on the

highway and seriously downgrade the highway

capacity. While the Intelligent Transportation

Systems helped mitigating the congestion impact by

providing solutions to efficient use of highway

systems, transportation system can benefit from a

new innovative approach to address congestion

problem.

Chow found that the necessary condition for

transportation system optimum is having the inflow

equal to the bottleneck capacity for all routes and all

departure time intervals in use (Chow, 2009). This

requires dispersing the peak hour travel demand by

time, and can be realized by adopting a highway

reservation concept (Edara and Teodorovic, 2008; Su

et al., 2013). Travelers in such a reservation system

need to book in advance for the right of using the

highway segments during their desired time. If some

time slots have been fully booked, additional travelers

need to book an alternative time or route. A major

difference between reserving airline seats and

highway slots is that an airline seat is a well-defined

object that is clearly identifiable, but a highway slot

is difficult to define in practice. The travelers need to

be shown the “edges” of a slot in time and space, and

to be indicated of admittance into the system as well

as being notified of violations. While existing

transportation system is not likely to handle highway

reservation system due to lack of real-time

communications and computation power, the

252

Su, P., Park, B. and Son, S.

Highway Reservation Strategy: Analytical Modeling Approach.

DOI: 10.5220/0006305702520259

In Proceedings of the 3rd International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS 2017), pages 252-259

ISBN: 978-989-758-242-4

connected vehicle technology would make the

highway reservation idea feasible.

A proof-of-concept simulation study was

conducted to investigate the potential benefits of the

highway reservation system (Su et al., 2013). If a time

interval is fully booked, the booking center will

recommend other intervals in close proximity, and the

travelers choose which one to accept. This algorithm

was applied to a carefully designed microscopic

simulation testbed and the reservation scenario

outperformed the baseline in terms of total delay time

and emissions.

In this paper, we developed a highway reservation

system using an analytical modeling approach, and

solved the optimal trip plans using an analytical

scheduling algorithm. The remainder of the paper is

organized as follows: “2 Literature Review” section

briefly discusses previous studies and concepts on

highway reservation and departure time choice

problem. “3 Model” section describes a big picture,

the system objective, solution approach and two case

studies of the proposed analysis approach, followed

by “4 Conclusions and Future Research” section.

2 LITERATURE REVIEW

The concept of road reservation or trip-booking is

mentioned in the literature as early as 1990s, but

extensive modeling efforts have not been done till the

recent 5 years. Some researchers conducted surveys

to explore travelers’ acceptance of the reservation

system and its effectiveness (Akahane and Kuwahara,

1996; Kim and Kang, 2011). Akahane and Kuware

found, if the participation compliance rate is 90%, a

15-minute adjustment of the departure time could

eliminate congestion over single bottleneck (Akahane

and Kuwahara, 1996). Kim and Kang found that

73.4% of the respondents would participate in or

accept if an expressway reservation system is

implemented during South Korea’s national holiday

(Kim and Kang, 2011). Wong (Wong, 1997), Iftode

and Gerla et al. (Gerla and Iftode, Undated; Iftode,

Smaldone, Gerla, and Misener, Undated; Ravi,

Smaldone, Iftode, and Gerla, Undated) pioneered the

discussions of the basic functions, advantages and

difficulties of a highway booking system. Wong

suggested slicing the highway capacity into time

intervals on which trip bookings are based. Several

researchers (Gerla and Iftode, Undated; Iftode et al.,

Undated; Ravi et al., Undated) proposed the

coexistence of reserved lanes with general-purpose

lanes, so that opted-out or rejected users can always

use the general-purpose lanes. A merging/diverging

assistance system is needed because of the lane

separations.

Koolstra was the first that brought the scheduling

cost into the highway reservation system (Koolstra,

2000). They evaluated the queuing and scheduling

costs with single bottleneck and heterogeneous

travelers. They found all queuing costs can be

eliminated without increasing the average

rescheduling costs. Their study also supported that a

freeway reservation might be more effective in

practice than road pricing. And reservation system

with variable booking fees is an option to incorporate

the benefits of congestion pricing. Veeraraghavan et

al. showed, from the standpoint of queuing theory,

that a reservation system is necessary to avoid

waiting, when the average waiting time is large at the

optimal point of operation (Veeraraghavan et al.,

2009). De Feijter et al. stated that the objective of trip-

booking is improving reliability and predictability of

travel times, and his simulation experiments showed

exactly so (de Feijter et al., 2004). Edara and

Teodorovic took the lead in conducting extensive

modeling work of reservation system by proposing a

Highway Allocation System (HAS) and Highway

Reservation System (HRS) (Edara and Teodorovic,

2008). HAS selects trips from received booking

requests to maximize the total Passenger-Miles-

Traveled over a period. HRS works in an on-line

mode to decide whether a request should be accepted

or rejected. Edara et al. showed that HAS produced

35% to 45% more Passenger-Miles than the two

ramp-metering algorithms (Edara et al., 2011).

Different from the idea of sliced highway capacity

by time, Wong and Liu et al. proposed a token-based

reservation idea (Wong, 1997; Liu et al., 2013). Each

road segment has a set of tokens, and the number of

tokens is the product of the segment length and

critical density, or the total number of vehicles on the

link when the capacity condition occurs. A

reservation request is accepted only if at least one

token on the requested segment is available, and the

requested time slot does not overlap with any of the

existing reserved time slots on this token.

Greenshield’s linear speed-density model is used in

Liu’s study, thus the optimal density is a half of jam

density, and optimal speed is a half of free flow speed.

Liu’s work is a meaningful exploration of different

ways of modeling the reservation system.

The highway reservation system works by

rescheduling the travelers’ departure time as well as

route choice to avoid over-capacity traffic flows.

Thus, the departure time choice modeling methods

are useful for this study. The most commonly used

travel time model is Vickrey’s bottleneck link model

(Vickrey, 1969). This has been used in numerous

departure time studies (Arnott et al., 1990; Chow,

2009; Hendrickson and Kocur, 1984; Huang and

Highway Reservation Strategy: Analytical Modeling Approach

253

Lam, 2002). Hendrickson and Kocuranalyzed the

users’ departure time decisions in a single bottleneck

under three different settings (Hendrickson and

Kocur, 1984). Arnott et al. studied user equilibrium,

system optimum and various toll regimes for a

network with parallel routes between one OD pair

(Arnott et al., 1990). Huang and Lam solved a user

equilibrium with route and departure time choices

(Huang and Lam, 2002). Other than Vickrey’s model,

Mahmassani and Herman (Mahmassani and Herman,

1984) used Greenshield’s traffic flow relationship in

an ideal arterial to represent congestion effects. This

model works only for routes with single uninterrupted

link, as it is difficult to calculate the exact exit flow

rate.

Some other studies developed discrete choice

models based on survey data to see what factors can

affect travelers’ departure time choices (Hendrickson

and Plank, 1984; Robert and Small, 1995; Small,

1982). Small’s work (Small, 1982) is the very first

econometric study of the trip scheduling behaviors at

the individual level. The discrete logit model of the

commuters’ work trip scheduling provides useful

information of time values, the relative magnitude of

them is consistent with Hendrickson and Plank

(Hendrickson and Plank, 1984): late arrivals at work

have the highest value of time, early arrivals have the

lowest, and the value of wait time on the road is

between them. Noland and Small (Robert and Small,

1995) analyzed the effect of uncertain travel times on

the commuting departure time choice. They found

that travel time uncertainty can account for a large

proportion of the morning commute cost. A few

researchers analyzed theoretically the dynamic traffic

assignment problem with departure time choice (Wie

et al., 1995; Friesz and Mookherjee, 2006; Chow,

2009). Wie et al. (1995) formulated the user

equilibrium and system optimum conditions and

compared the two using a numerical example.

Under system optimum, travelers with different

departure time might have different total cost, and

they have incentive to adjust departure time and

arrive at user equilibrium. Some researchers

(Hendrickson and Kocur, 1984; Hendrickson and

Plank, 1984; Vickrey, 1969) suggest using time

dependent tolls to help balance the unequal total cost,

so that different departure time will generate the same

cost. With the optimization model’s results provided

in this paper, the exact time dependent toll pattern can

also be identified. This toll idea works under two

conditions: the exact travel demand pattern is known,

and all the travelers are homogeneous. However,

neither of the two is satisfied in practice.

3 MODEL

3.1 Big Picture

According to two economic studies of commuters’

traveling behavior (Hendrickson and Plank, 1984;

Small, 1982), late arrivals at work have the highest

value of time, early arrivals have the lowest, and the

value of wait time on the road is between them. That

means, if there is anticipated congestion, the

commuters have the incentive to depart earlier (also

arrive earlier) to avoid the congestion. Highway

reservation system provides a reliable mechanism for

them to do so. Another advantage of highway

reservation system is reducing the travel time

uncertainty, as “travel time uncertainty can account

for a large proportion of the morning commute cost”

(Robert and Small, 1995). These economic studies lay

the foundation for the highway reservation system.

To provide a proper “edge” of the reservation

token to the user, highway system is divided into

multiple links by on- and off-ramps, and time is

discretized into intervals with link capacity sliced

(Wong, 1997). A reservation slot is defined as the

combination of several consecutive links and time

intervals. For example, a user can reserve a 3 mile-

long segment (may have multiple links) between time

8:30 am and 8:33 am. Certain tolerance could be

defined by the local traffic conditions to

accommodate inaccurate travel time estimate. For

example, ±5 minutes tolerance could be used if the

local traffic is unpredictable. This segment’s

operational speed is set to be 60 mph. That’s why

travel time is 3 minutes. Such accurate arrival time

and speed control would be feasible by transmitting

speed and lane-change advisories messages from the

operation center with Connected Vehicle technology.

The proposed highway reservation system works

by redistributing the peak hour travel demand earlier

or later to non-peak hours. Its validity depends on

how the users respond. Some of them may have

flexible schedule and are willing to accept any

rescheduling, while some of them may not cooperate.

The users’ attitude depends on a lot of factors, such

as work schedule flexibility, experience with the

reservation system, etc. In this paper’s model, it is

assumed that the highway users will fully corporate

with the booking center, meaning they accept any

rescheduling, and will travel by the planned schedule.

Another assumption is that all the lanes on the

highway are reserved in this paper’s model.

Compared with HOV lane usage strategy,

reservation system produces higher utilization of the

highway capacity when the demand level is low, as

there might not be enough vehicles to occupy the

HOV lane. HOT strategy might be able to lower the

VEHITS 2017 - 3rd International Conference on Vehicle Technology and Intelligent Transport Systems

254

tolls to make better use of the capacity, but the

elasticity of the demand to the toll is difficult to be

estimated. Sometimes it could be too late to increase

the tolls to avoid congestion if the travel demand

bumps up. All these challenges do not exist in the

reservation system. In a sense, it makes the traffic

information transparent to both demand and supply

side beforehand.

3.2 System Objective

All the notations used in the models are listed in Table

1 of Appendix. The objective of the reservation

system is minimizing the total cost of its users, a

weighted sum of early arrival or late arrival cost and

travel time cost (Equation 1). While this appears to be

similar to departure time choice model, the main

difference is that the proposed research system

ensures reliable travel time along the roadways within

the reservation system by enforcing the capacity

constraints. The decision variable is V

ijkrl

. The C

ijkrl

calculated by the Successive-Update approach

mentioned in the next section of the paper, and there

is explicit expression for it. So the objective function

in Equation 1 is just for illustration purpose. In

implementation, we could remove indices of i, j, and

r, when all possible routes are identified and indexed.

That’s why the decision variable dimension becomes

R×K×DAT, instead of O×D×K×Rij×DAT. C

ijkrl

is the

total cost of the trips that belong to V

ijkrl

, including

early/late schedule cost and travel time cost. These

decision variables have to satisfy the OD demand

constraint and non-negative constraint. Also, the

inflow rate of each of the links in all the time intervals

has to be lower than or equal to the “reservation link

capacity.” It is noted that the reservation capacity

ensures vehicles on the reservation system travel at

reliable speed. The vehicles are propagated through

the traffic network by using a successive-update

method, as discussed in the following section.

(1)

ijkrl

= w

× max(DAT

– AAT

ijkrl

, 0) + w

max(AAT

ijkrl

– DAT

, 0) + w

× TravelTime

ijkrl

Subject to:

Inflow

,

<Capacity

,

forallkandlk

Where,

ijkrl

= The number of trips between OD (i, j) with

desired arrival time DAT

using route r that start the

trip from the k

time interval

ijkrl

=Total travel cost of a trip between OD (i, j)

with desired arrival time DAT

using route r that

start the trip from the k

time interval

Inflow

k,lk

= The inflow of link lk in the k

time

interval

Capacity

k,lk

= The capacity of link lk in the k

time

interval (currently it does not change by time)

DAT = Desired Arrival Time

AAT = Actual Arrival Time

We adopted Vickrey’s Model (Vickrey, 1969) for

the link behaviors. It is a deterministic queuing model

that considers each link to be free flowing with a

constant travel time, and a bottleneck at the beginning

or end of the link with fixed capacity. Delays will

occur when the traffic inflow continuously exceeds

the capacity for a substantial period. If there is no

queue, the outflow rate is equal to the inflow rate, and

the travelers have no delay. It assumes relatively

stable inflows, without considering stochastic

variations. Vickrey’s queue model is selected in this

study because 1) the maximum flow rate can be

considered explicitly and 2) it is easy to calculate the

exit flow time and rate, and propagate the exit flow

into the successor links. The queue length evolves as

shown in Huang and Lam (2002). When 



(



)

higher than 



, the capacity of link a, the queue length

increases from 



( − 1) to 



(), and if 



(



)

lower than 



, the queue length decreases.

∆ ∗ 



(



)

is the number of vehicle arrived at link

a in time interval k. The exit time of these vehicles

from link a and the associated exit flow rate depend

on the current queue length and the relative

magnitude of 



() and 



(2)



(k): Queue length on link a at the end of time

interval k

∆t: Length of the time interval



(k): Inflow rate of the k

time interval



: Capacity of the link segment a

: Travel time under “typical” speed

3.3 Successive-Update Approach

The link bottleneck model can calculate exit time and

rate from each link. The exited vehicles enter the

successor link, together with vehicles from other

routes that also use the successor link. The

successive-update approach uses an INFLOW vector

and OUTFLOW vector to keep the flow information

for each link, and updates them in each time step, until

11111

ODK DAT

ijkrl ijkrl

ijkrl

in V C

=====



for all , and

ijlkr ijl

VDemand ijl



0 and integer for all , , , and

ijlkr

Vijkrl>

() max[ ( 1) ( () ),0]

aa aa

qk qk t k

=−+Δ−

Highway Reservation Strategy: Analytical Modeling Approach

255

all the vehicles have reached their destination. The

capacity constraint is realized by including a penalty

term in the objective function when the inflow rates

exceed capacity. The routes between each OD pair are

predetermined either manually (e.g., identifying

commuters’ habitual routes by analyzing their routes

over adequate time period) or by a route-searching

algorithm (e.g., k-shortest path algorithm), and stored

in ROUTES, an R by m matrix, where R is the total

number of routes. m is the maximum number of links

in a route. All the routes are numbered by the row ID

in ROUTES, no matter which OD pair they connect.

The initial traffic assignment is stored in INPUT, an

R by K by DAT matrix. Note that it is assumed that

the users’ desired arrival time is not continuous but

belongs to a set of discrete time points, as they are

determined by morning commuters’ work start time,

which is not continuous most of the time.

INFLOW

and OUTFLOW

record the flow

propagation process for link a. They are 2K by R

matrices. 2K is used because the propagation process

runs for 2K time intervals, in case some trips cannot

finish at the end of K

interval. For the links that are

the beginning of any route, their INFLOW matrices

are initialized using INPUT. For example, if link b is

the first link of route r, INFLOW

(r, k) is initialized

by summing up INPUT(r, k, 1:DAT). During the

traffic propagation process, in each time step k,

sum(INFLOW

(1:R, k)) vehicles enter link a, and

OUTFLOW

is updated according to the calculated

exit flow time and rate based on Vickrey’s model. To

maintain flow conservation, at the end of each time

step, INFLOW

(r, 1:2K) of all the links are updated

by taking in vehicles from the predecessor links’

OUTFLOW. A QUEUE

vector records the queue

length of link a in all the time intervals. A DEPART

vector records the flow exit time of link a. The time

interval is set to be shorter than the shortest travel

time of all the links, so that the outflow of the links

will never affect the successor’s inflow in the same

time interval. When the propagation process is

finished, the DEPART vectors have the exit time of

the trips from each link. By tracking down the

DEPART vectors of the links on route r, we obtain the

arrival time at the final destination of the vehicles

using route r. With the final arrival time, the system

objective is calculated.

3.4 Solving the Optimization Problem

This study adopted the Interior Point Method (IPM)

(Nocedal and Wright, 2006). Since there is no close-

form formula, the algorithm used finite-difference

equation to find the search direction. Given an initial

solution, the algorithm began the iterative process to

search for the next solution. The initial solution

assumed that the demand is evenly distributed in all

the routes and all the time intervals.

3.5 Numerical Example

This paper uses a numerical example illustrated in

Huang’s study (Huang and Lam, 2002). Huang solved

the user equilibrium route and departure time choice

problem. Thus, using the same example makes it

consistent to compare the performance of the

highway reservation system with user equilibrium

solution.

The grid network, as shown in Figure 1, includes

nine nodes, 12 links and two OD pairs (from A to C

and from B to C). All the typical travel time and

capacity of the links are shown in the figure. The trip

demands from A to C and from B to C are 20,000 and

10,000 veh, respectively. All the other settings are the

same with the previous example. The network is

symmetric as well as the input data, so there are only

three unique routes: 1 (6 is the same with 1), 2 (3, 4

and 5 are the same with 2), and 7 (8 is the same with

7). The program treated all the routes independently,

and symmetric outputs are indeed found.

Figure 1: Grid Network (Huang and Lam, 2002).

Using IPM, the optimality condition was satisfied

after one hour run. The computation time is a topic of

future research when a real size network and travel

demand is dealt with. Figure 2 shows the inflow rate

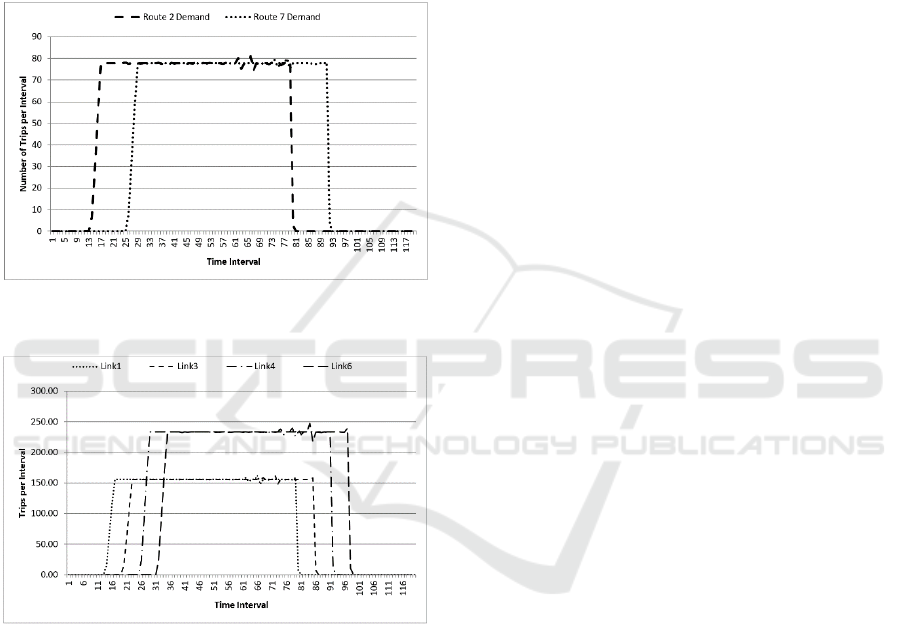
of the three unique routes. There are no trips on route

1 (6), because route 1 (6) have longer travel time than

route 2 (3, 4, 5), and all of them share bottleneck links

6 and 12. This model has the potential of identifying

critical links and under-utilized links. Figure 3 shows

the traffic flow rates of six unique links. It is noted

that links 2 (10) and 5 (9) have no traffic at all, and

link 6 (12) has reached capacity. This is easy to

understand since all trips ending in zone C need to use

either link 6 or link 12. All other links have some

traffic but not saturated. This is an evidence that links

6 and 12 are the bottlenecks in this grid network.

A total of 23,909 vehicles arrive earlier than 9 am,

and the average early arrival time is 0.855 hr. A total

of 6,091 vehicles arrive later than 9 am, and the

VEHITS 2017 - 3rd International Conference on Vehicle Technology and Intelligent Transport Systems

256

average late arrival time is 0.218 hr. The average cost

of all the vehicles between A and C is about 7.91

dollars, and 8.03 dollars between B and C. Huang’s

user equilibrium average cost is about 11 dollars

between A and C, and 7 dollars between B and C

(Huang and Lam, 2002). Although B-to-C distance is

shorter than A-to-C, the B-to-C traveler average cost

is higher than A-to-C travelers. This is clearly shown

in Figure 2 that some of the trips on route 7 (B-to-C)

arrive late, and the late arrival cost is much higher

than early arrival and travel time.

Figure 2: Optimized Traffic Flow of Three Unique Routes

[note: Route 1 has no traffic].

Figure 3: Optimized Traffic Flow of Six Unique Links

[note: Links 2 and 5 have no traffic].

3.6 Discussions

The proposed model sliced the highway capacity into

time intervals as proposed by Wong (Wong, 1997). It

is noted that the token-based approach (Liu et al.,

2013) is not adopted because 1) it is difficult to

determine the time each token is occupied, and 2) too

many overlapped tokens being reserved will lead to

short-term excessive demand not properly handled.

Even though coexistence of reserved lanes and

general-purpose lanes is not modeled explicitly in the

paper, the model can be modified to reflect this

coexistence, e.g. setting the reservation flow rate as

capacity of a single lane. In the co-existing lanes

scenario, controlling the speed differential is critical

to enable lane-changes occurring in a safe manner,

otherwise it would be difficult to enter and exit the

reserved lanes. While a previous study of Koolstra

(2000) that evaluated a single bottleneck, our model

is capable of simulating multiple connected links

being reserved and is scalable. Unlike Edara and

Teodorovic (2008), our model explicitly considers the

scheduling cost that incorporates the impacts of

departure time changes.

Given 100% compliance rate is used, the results

should be treated as an “up-ceiling” of the reservation

system’s benefits. To consider realistic compliance

rate, one could implement auction based reservation

system (Su and Park, 2015). To ensure efficient speed

operations in the reserved lane, one could consider a

cooperative adaptive cruise control (CACC)

technology (Park et al., 2011; Schakel et al., 2010).

4 CONCLUSIONS AND FUTURE

RESEARCH

This paper proposed an innovative highway

reservation system as a travel management strategy,

and formulated and solved it as an optimization

model. This model is capable of finding an optimal

scheduling plan that the reservation system could

make for optimal system performance, under a

constraint that all the links are operated below the

capacity level. In two case studies, by applying the

reservation concept over highway networks, the total

monetary costs reduced by 20% to 25%, comparing

with user-equilibrium traffic assignments. Given the

optimization model works under the assumption that

all the users are fully compliant with the scheduling

plan, it is recommended the future research should

consider an agent-based modeling approach to

consider diverse user behaviors.

A few critical issues related to implementation are

discussed. Another main challenge is how to handle

non-recurrent congestions due to crashes or incidents.

A few strategies that would help mitigate include (i)

activating reserved capacity (that is saved for

emergency vehicles), (ii) accepting no more on-the-

fly reservations, (iii) providing incentives to drivers

willing to give up their near future reservations, and

(iv) implementing route guidance system to diverge

the demand.

ACKNOWLEDGEMENTS

This research was in part supported by the Global

Research Laboratory Program through the NRF

Highway Reservation Strategy: Analytical Modeling Approach

257

funded by the Ministry of Science, ICT and Future

Planning of South Korea (2013K1A1A2A02078326).

REFERENCES

Akahane, H., and Kuwahara, M., 1996. A basic study on

trip reservation systems for recreational trips on

motorways. Paper presented at the 3rd World Congress

on Intelligent Transportation Systems, Orlando,

Florida.

Arnott, R., de Palma, A., and Lindsey, R., 1990. Departure

time and route choice for the morning commute.

Transportation Research Part B: Methodological, 24(3),

209-228. doi: http://dx.doi.org/10.1016/0191-

2615(90)90018-T.

Bureau of Transportation Statistics, 2015. National

Transportation Statistics.

Chow, A. H. F., 2009. Properties of system optimal traffic

assignment with departure time choice and its solution

method. Transportation Research Part B:

Methodological, 43(3), 325-344. doi:

http://dx.doi.org/10.1016/j.trb.2008.07.006.

de Feijter, R., Evers, J. J. M., and Lodewijks, G., 2004.

Improving travel-time reliability by the use of trip

booking. IEEE Transaction on Intelligent

Transportation Systems, 5(4), 288-292.

Edara, P., and Teodorovic, D., 2008. Model of an advance-

booking system for highway trips. Transportation

Research Part C, 16, 36-53.

Edara, P., Teodorovic, D., Triantis, K., and Natarajan, S.,

2011. A simulation-based methodology to compare the

performance of highway space inventory control and

ramp metering control. Transportation Planning and

Technology, 34(7), 705-715.

Friesz, T. L., and Mookherjee, R., 2006. Solving the

dynamic network user equilibrium problem with state-

dependent time shifts. Transportation Research Part B,

40(3), 207-229.

Gerla, M., and Iftode, L., Undated. Intelligent traffic

management in future highways (position paper).

Retrieved from varma.ece.cmu.edu/Auto-

CPS/Iftode_Rutgers.pdf.

Hendrickson, C., and Kocur, G., 1984. Schedule Delay and

Departure Time Decisions in a Deterministic Model.

Transportation Science, 15(1), 62-77.

Hendrickson, C., and Plank, E., 1984. The flexibility of

departure times for work trips. Transportation Research

Part A: General, 18(1), 25-36. doi:

http://dx.doi.org/10.1016/0191-2607(84)90091-8.

Huang, H.-J., and Lam, W. H. K., 2002. Modeling and

solving the dynamic user equilibrium route and

departure time choice problem in network with queues.

Transportation Research Part B: Methodological, 36(3),

253-273. doi: http://dx.doi.org/10.1016/S0191-

2615(00)00049-7.

Kim, Y., and Kang, S.-C., 2011. Innovative traffic demand

management strategy: expressway reservation system.

Transportation Research Record: Journal of the

Transportation Research Board, 2245, 27-35.

Koolstra, K., 2000. Potential benefits of a freeway slot-

reservation system: Queuing costs versus scheduling

costs. Paper presented at the 2nd KFB Research

Conference, Lund, Sweden.

Liu, K., Chan, E., Lee, V., Kapitanova, K., and Son, S.,

2013. Design and evaluation of token-based reservation

for a roadway system. Transportation Research Part C,

26, 184-202.

Mahmassani, H., and Herman, R., 1984. Dynamic user

equilibrium departure time and route choice on

idealized traffic arterials. Transportation Science,

18(4), 362-384.

Nocedal, J., and Wright, S., 2006. Numerical Optimization

(2nd ed.). New York: Springer.

Park, B., Malakorn, K., and Lee, J., 2011. Quantifying

benefits of cooperative adaptive cruise control toward

sustainable transportation system. Center Transp. Stud.,

Univ. Virginia, Charlottesville, VA, USA.

Ravi, N., Smaldone, S., Iftode, L., and Gerla, M., Undated.

Lane reservation for highways (position paper). Rutgers

University. Retrieved from

www.cs.rutgers.edu/~iftode/ILR-ITSC07.pdf.

Robert, N., and Small, K. A., 1995. Travel-time

uncertainty, departure time choice, and the cost of the

morning commute. Transportation Research

Record(1493), 150-158.

Schakel, W. J., Van Arem, B., and Netten, B. D., 2010.

Effects of Cooperative Adaptive Cruise Control on

traffic flow stability. Paper presented at the Intelligent

Transportation Systems (ITSC), 2010 13th

International IEEE Conference on.

Schrank, D., Eisele, B., and Lomax, T., 2012. TTI's 2012

Urban Mobility Report, Powered by INRIX Traffic

Data: Texas AandM Transportation Institute.

Small, K. A., 1982. The scheduling of consumer activities:

work trips. The American Economic Review, 72(3),

467-479. doi: 10.2307/1831545.

Su, P., Park, B., Lee, J., and Sun, Y., 2013. Proof-of-

concept study for a roadway reservation system: an

integrated traffic management approach.

Transportation Research Record: Journal of the

Transportation Research Board (2381), 1-8. doi:

http://dx.doi.org/10.3141/2381-01.

Su, P., and Park, B. B., 2015. Auction-based highway

reservation system an agent-based simulation study.

Transportation Research Part C: Emerging

Technologies, 60, 211-226. doi:

http://dx.doi.org/10.1016/j.trc.2015.07.018.

Veeraraghavan, M., McGinley, M., and Zhu, X., 2009.

Bandwidth-sharing mechanisms: reservation systems

versus queueing systems. Unpublished work.

University of Virginia. Retrieved from

http://www.ece.virginia.edu/mv/pdf-

files/reservations.pdf.

Vickrey, W. S., 1969. Congestion theory and transport

investment. The American Economic Review, 59(2),

251-260. doi: 10.2307/1823678.

VEHITS 2017 - 3rd International Conference on Vehicle Technology and Intelligent Transport Systems

258

Wie, B.-W., Tobin, R., Bernstein, D., and Friesz, T. L.,

1995. A comparison of system optimal and user

equilibrium dynamic traffic assignments with schedule

delays. Transportation Research Part C, 3(6), 389-411.

Wong, J.-T., 1997. Basic concepts for a system for advance

booking for highway use. Transport Policy, 4, 109-114.

APPENDIX

Table 1: Notations used in the Link Bottleneck Model and

Successive-Update Approach.

Notation Type Description

i Integer Index of origin, a member of

{1, 2, … O}

j Integer Index of destination, a member

of {1, 2, … D}

k Integer Index of time interval, a

member of {1, 2… K}

r Integer Index of a route in R

, a

member of {1, 2, … R

}

l Integer Index of a desired arrival time,

a member of {1, 2, … DAT}

a Integer Index of a link, a member of

{1, 2, … A}

m Integer The maximum number of links

of all the routes

n Integer Each link has a number of

routes that start from it. n is the

largest number.

O Integer Total number of origins

D Integer Total number of destinations

K Integer Total number of time intervals

Integer Total number of routes

between OD (i, j). R

is a

subset of R

R Integer Total number of routes

between all the ODs pairs

DAT Integer Total number of desired arrival

times

A Integer Total number of links in the

network

Double Value of time for the early

arrival

Double Value of time for the late

arrival

Double Value of time for travel time

ijkrl

Integer Number of vehicles between

OD (i, j) with desired arrival

time DAT

that travel on route

is one of the routes in R)

and start in the k

interval.

This is the decision variable

of the model.

ijkrl

Double Average cost of the vehicles

krl

AAT

ijkrl

Double Actual arrival time of the

vehicles V

krl

ROUTES R by m

matrix

Each row represents a route’s

links.

GP - General Purpose Lane

Table 1: Notations used in the Link Bottleneck Model an

Successive-Update Approach. (Cont.)

Demand

ijl

Integer The number of trips between

OD (i, j) with desired arrival

time DAT

INPUT R by K

DAT

matrix

Each cell (r, k, l) means the

number of trips on route r with

desired arrival time l and

depart in time interval k.

ARRIVALTIME R by K

by 2

matrix

Cell (r, k, 1) and (r, k, 2) mean

arrival time range of the trips in

INPUT (r, k), or the trips on

route r that depart in interval k.

TRAVELTIME R by K

matrix

Cell (r, k) means the average

travel time of the trips in

INPUT (r, k), or the trips on

route r that depart in interval k.

LINKSINITIAL-

ROUTES

A by n Each row a represents the

routes that start from link a.

The row has zeros if no routes

start from it.

QUQUE

1 by

vector

Queue length at the end of each

time interval on link a

INFLOW

R by

matrix

If a is the first link of some

routes, the corresponding rows

of INFLOW

are initialized by

that travel demand.

Other rows remain empty.

OUTFLOW

R by

matrix

Initialized as empty.

DEPART

2K by

matrix

Cell (k, 1) and (k, 2) means the

exit flow time range of the

vehicles that entered link a in

interval k.

LINKS A by 2

matrix

Cell (a, 1) is the typical travel

time on link a. Cell (a, 2) is the

bottleneck capacity of link a.

TotalTravelTime Double The total travel time of all the

vehicles.

TotalEarlyArrival Double The total early arrival time of

all the vehicles

TotalLateArrival Double The total late arrival time of all

the vehicles

Highway Reservation Strategy: Analytical Modeling Approach

259