On the Performance of a One-way Car Sharing System in Suburban

Areas: A Real-world Use Case

Haitam M. Laarabi

, Chiara Boldrini

, Raffaele Bruno

, Helen Porter

and Peter Davidson

IIT-CNR, Via G. Moruzzi 1, 56124, Pisa, Italy

PDC, Northbridge Road, HP4 1EH, Berkhamsted, U.K.

Keywords:

Car sharing, User-based Relocation, Multi-agent Transportation Simulation, Travel Surveys.

Abstract:

In recent years, one-way car sharing systems have gained momentum across the world with their promise

to encourage more sustainable urban mobility models. However, economic viability of car sharing is still

uncertain due to high investment cost for station and ﬂeet deployment, as well as high operation cost for ﬂeet

management and rebalancing. Furthermore, existing car sharing are typically conﬁned to city centres with

signiﬁcant business and residential concentrations. In this study, we evaluate the performance of a novel one-

way car sharing system that will be deployed in a suburban area of the city of Lyon using a detailed multi-agent

and multi-modal transport simulation model. Data from a recent large-scale household travel survey is used

to determine the travel demands on different transportation alternatives. We analyse the impact of different

coverage constraints on the system capacity in terms of number of trips and vehicle availability. We also

investigate the potential of user-based relocation strategies to increase the efﬁciency of the car sharing service.

The model shows that: (i) the car sharing system is most sensitive to the infrastructure and ﬂeet sizes, and (ii)

user-based relocation does not have a signiﬁcant impact on the total number of car sharing trips.

1 INTRODUCTION

Car sharing systems are innovative mobility services

that are increasingly becoming popular in urban and

sub-urban areas and have the potential to solve real-

world problems of urban transports (Hampshire and

Gaites, 2011). The principle of a car sharing sys-

tem is that customers can rent for limited period of

times a car from a ﬂeet of shared vehicle operated by a

company or a public organisation. Although car shar-

ing services have been proposed in the early 1970s,

they have emerged as a worldwide phenomenon only

in the last decade. This is due to the deployment of

one-way car sharing systems in which the customers

are allowed to leave the rented car at a drop-off lo-

cation different from the pickup location (Barth and

Shaheen, 2002). This provides an increased ﬂexibil-

ity for the users compared to two-way systems.

Typically, one-way car sharing systems suffer

from unbalance distribution of available vehicles in

the service area. Speciﬁcally, some locations can be

more popular than others at different times of the day

(e.g., residential areas at night-time as opposed to in-

dustrial and commercial areas at peak hours). This

imbalance of demand easily results into situations in

which vehicles accumulates in areas where there is a

lower number of rental requests, while at the same

time there is shortage of vehicles where they are more

needed (Barth et al., 2004). When this happens, the

operator can resort to rebalancing policies, i.e., re-

distributing vehicles from where they are not needed

(taking into account the expected demand in the near

future) with the objective of serving more effectively

the travel demands. Clearly, this has a cost for the op-

erator, thus redistribution should be performed only

when economically viable.

However, before the operator resorts to rebalanc-

ing, he needs to know the optimal solution for infras-

tructure planning, giving the high investments costs

and travel demand. In other words, he needs to deter-

mine the number, size and location of parking stations

to deploy in the area where the car sharing system is

supposed to operate in. In the literature, this prob-

lem is generally solved considering a spatial-temporal

formulation of a MILP (de Almeida Correia and An-

tunes, 2012; Boyacı et al., 2015). In our previous

work, we formulated a set-covering model coupled

with queuing theory to guarantee certain level of ser-

vice to customers (Boldrini et al., 2016).

Different approaches for vehicle relocation in car

102

Laarabi, H., Boldrini, C., Bruno, R., Porter, H. and Davidson, P.

On the Performance of a One-way Car Sharing System in Suburban Areas: A Real-world Use Case.

DOI: 10.5220/0006307901020110

In Proceedings of the 3rd International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS 2017), pages 102-110

ISBN: 978-989-758-242-4

sharing systems exist (Weikl and Bogenberger, 2013).

Operator-based solutions require the use of dedicated

staff for executing the redistribution tasks. On the

contrary, user-based solutions rely on users willing to

relocate vehicles to locations where they are needed,

usually on the basis of an economic incentive. How-

ever, both approaches can be costly. Furthermore, it

is still uncertain whether users are willing to accept

incentives for deviations from their destinations. Fi-

nally, the design of optimisation frameworks for the

decision of which vehicles to relocate to which loca-

tion can become intractable due to the extremely large

number of relocation variables (Boyacı et al., 2015).

To cope with the aforementioned issues, in this

paper we design a relocation algorithm that is in-

spired by physical arguments and leverages on an

analogy between relocation tasks and thermal con-

duction. Speciﬁcally, the redistribution of vehicles

from locations where they get accumulated to loca-

tions where there is a shortage of vehicles is modelled

as a temperature gradient. Another key feature of the

proposed relocation algorithm is that it is designed

to operate with a new class of lightweight vehicles,

called ESPRIT cars, which can be stacked, recharged

and driven in a road train (ESPRIT, 2015). This is

supposed caters for more efﬁcient relocations since

a single customer can relocated two vehicles at the

same time.

To validate the performance of the proposed re-

location strategy on a meaningful case we use the

city of Lyon as case study. Speciﬁcally, we use a

multi-agent simulation framework that we have pre-

viously designed (Laarabi and Bruno, 2016). It is

based on MATSim, a popular open-source and agent-

based trafﬁc simulation platform, which supports dy-

namic trafﬁc assignment, large scenarios and detailed

modelling of transportation networks (Balmer et al.,

2004). Then we set up a scenario using data from

the 2015 Lyon conurbation household travel survey,

which provides information about more than three

million trips, and public data on the Lyon’s public

transit systems. Then, we analyse the impact of the

infrastructure planning strategy (Boldrini et al., 2016)

as well as the user-based relocation on the car sharing

performance in terms of number of rental trips.

The remainder of this paper is organised as fol-

lows. Section 2 provides an overview of related lit-

erature on infrastructure planning, vehicle relocation

and car sharing performance evaluation. Section 3 in-

troduces the ESPRIT car sharing system and the user-

based relocation in such a system. Section 4 describes

the Lyon case scenario and travel demand. Section 5

discusses the simulation results. Finally, Section 6

draws ﬁnal remarks and outlines future work.

2 RELATED WORK

There is vast body of research work on the design of

optimal solutions for the planning and operation of

car sharing systems. In the following, we overview

previous works that are most related to this study.

2.1 Models for Infrastructure Planning

Infrastructure planning tries to determine the number,

size and location of parking stations in a car sharing

system in order to maximise some performance mea-

sure, such as demand coverage or proﬁt. From a gen-

eral point of view, this is an instance of the facility

location problem, which is an optimisation problem

extensively studied in the ﬁeld of logistics and trans-

portation planning (Farahani et al., 2012).

Existing planning frameworks typically rely on

time-space optimisation approaches, which are mod-

els that assume a deterministic knowledge of the de-

mand of vehicles at each time interval of the control

period. For instance, A MILP formulation is used

in (de Almeida Correia and Antunes, 2012) to max-

imise the proﬁts of car-sharing system, which simul-

taneously optimises the location of parking stations

and the ﬂeet size under several trip fare schemes. The

proposed model is then used to analyse a case study

in Lisbon. A recent work (Boyacı et al., 2015) ad-

dresses the planning of an electric car-sharing sys-

tem using a multi-objective MILP model that simul-

taneously determines the number, size and locations

of stations, as well as the ﬂeet size taking into ac-

count vehicle relocation and electric vehicle charg-

ing requirements. More recently, new modelling ap-

proaches (eg. queuing theory and ﬂuid models) have

been proposed to take into account that the demand

process of customers is stochastic and exhibits sea-

sonal effects. For instance, a closed queuing net-

work modelling of a vehicle rental system is proposed

in (George and Xia, 2011) to derive some basic prin-

ciples for the design of system balancing methods. In

our previous work (Boldrini et al., 2016), we formu-

lated a set-covering model that minimises the cost of

deployment (in terms of number of stations and their

capacity) and leveraged on queuing theory to also

guarantee a pre-deﬁned level of service to the cus-

tomers (in terms of probability of ﬁnding an available

car/parking space).

2.2 Relocation Strategies

Vehicle relocation strategies can be classiﬁed into

the following two broad categories: (i) user-based

schemes, which incentive customers to participate

On the Performance of a One-way Car Sharing System in Suburban Areas: A Real-world Use Case

103

in the relocation program, and (ii) operator-based

schemes, which leverage on dedicated staff for relo-

cation activities.

In (Kek et al., 2006) two operator-based strate-

gies are simulated. The shortest time strategy relo-

cates vehicles to minimise the travel times of staff

members. The inventory balancing strategy moves

vehicles from over-supplied stations to stations with

vehicle shortage. In (Kek et al., 2009) an inter-

programming model is developed to minimise the

costs associated to staff-based relocation. A similar

model is developed in (Jorge et al., 2014) to max-

imise the proﬁt of the car sharing operator. In (Nair

and Miller-Hooks, 2011) a stochastic MIP model is

formulated to optimise vehicle relocations, which has

the advantage of considering demand uncertainty. A

multi-objective MILP model for planning one-way

car-sharing systems is developed in (Boyacı et al.,

2015) taking into account vehicle relocation, sta-

tion deployment and electric vehicle charging require-

ments. The design of optimal rebalancing algorithms

with autonomous, self-driving vehicles has been re-

cently addressed in (Pavone et al., 2012) using a ﬂu-

idic model, and (Zhang and Pavone, 2016) using a

queueing-theoretical model. An alternative approach

for operator-based relocation scheme consists in se-

lecting trips so as to reduce vehicle imbalance, for in-

stance by rejecting trips to stations with parking short-

age (Uesugi et al., 2007; de Almeida Correia and An-

tunes, 2012).

User-based relocation policies are typically con-

sidered more convenient for the car sharing operator

as they do not require the use of a staff. However,

it is still uncertain whether users would be willing to

participate in a rebalancing program by accepting an

alternative destination or a more distant vehicle (Her-

rmann et al., 2014). For this reason, most of the stud-

ies in this ﬁeld focus on designing pricing incentive

policies for encouraging users to relocate the vehicles

themselves (Febbraro et al., 2012; Clemente et al.,

2013). Clearly, the effectiveness of these schemes

highly depends on users’ participation and their will-

ingness to accept changes of their travel behaviours.

2.3 Simulation of Car Sharing Systems

In general, evaluating the performance of a car shar-

ing system is a difﬁcult task due to the complex and

time-variant interplay between the demand and sup-

ply processes. Speciﬁcally, the availability of vehi-

cles in a car sharing system is intrinsically depen-

dent on trips that are demanded by the customers and

vice-versa. In addition, there are several operational

conditions that add uncertainties to the system about

the future location of vehicles, such as the impact of

pricing schemes impact on the decisions of individ-

ual users. Therefore, a simulation approach can be

very useful to cope with operation complexities and

to quickly evaluate the effectiveness of different plan-

ning and operation models.

Studies of micro-simulation for performance eval-

uation of carsharing system has been investigated as

early as 1982 (Bonsall, 1982). During that period,

there was not yet the large panel of trafﬁc simulation

tools that are existing nowadays. Thus, the critics held

by the author in (Bonsall, 1982) regarding the com-

putational complexity and availability of data should

be taken in moderation. In 1999, a queuing-based

transport simulation has been proposed by (Barth and

Todd, 1999) for the assessment of the performance

of a shared one-way vehicle system. Different mea-

sures of efﬁciency were determined, such availability

of vehicles, their distribution and energy consump-

tion, while some relocation strategies were tested.

However, the simulation model is exactly predictive

and does not capture the inherent uncertainty of real

world systems. A more detailed car sharing simula-

tion model and open source was introduced by (Ciari

et al., 2013), where it is based on multi-modal agent-

based trafﬁc simulator, such that each agent seeks to

fulﬁls its daily plan as a set of activities connected by

legs. In our previous work, we designed a similar but

more sophisticated car sharing simulator (Laarabi and

Bruno, 2016), in such a way to separate the carshar-

ing mobility simulation model from the operational

and demand model. The purpose is to allow users test

different operational models and strategies using the

same tool. We have, therefore, used this simulation

model to study the performance of a new car sharing

system deployed in a suburban area of Lyon.

3 ESPRIT: RELOCATION CASE

The underlying design principles of cars are rapidly

evolving and the design of innovative lightweight ve-

hicles is coming to the fore of current academic and

industrial research programs. The long-term vision is

to reinvent urban mobility systems by leveraging on

vehicles speciﬁcally designed for city use with sig-

niﬁcant smaller spatial use and carbon footprints, as

well as considerably less expensive to own and op-

erate (Mitchell et al., 2010). For instance, several

concept prototypes of stackable, and foldable two-

seat urban electric cars are currently under develop-

ment, such as the MIT BitCar (Vairani, 2009), or EO

Smart (Birnschein et al., 2012). A step forward is take

by the ESPRIT European Project that is designed and

VEHITS 2017 - 3rd International Conference on Vehicle Technology and Intelligent Transport Systems

104

prototyping a new vehicle that is stackable with me-

chanical and electrical coupling, and it can be driven

in road trains as shown in Figure 1.

Figure 1: The architecture of an ESPRIT-based car-sharing

system (ESPRIT, 2015).

ESPRIT vehicles have the potential to facilitate

the deployment of one-way car sharing by also sup-

porting more efﬁcient operational procedures. In par-

ticular, redistribution is made easier because the vehi-

cles can be driven in a road train. As a consequence,

a single staff can drive a road train of up to eight ve-

hicles, or users may drive a road train of two vehicles

with a conventional driving license. As discussed in

the previous section, one of the main hurdles for user-

based relocation strategies is to encourage the users to

change their destination to perform a relocation task.

With ESPRIT, we can afford a different way of

user-based relocation, where operator can take advan-

tage of actual trips and augmenting their relocation ef-

ﬁciency by delivering two vehicles instead of just one.

However, this strategy has been proven, in the follow-

ing paper, to have a low impact on the total number of

car sharing trips.

Typically, current relocation systems are based

on complex integer programming models that do not

scale to the size of real-world car sharing systems. In

this study we adopt an alternative approach that is in-

spired by the physical laws that describe heat conduc-

tion. Speciﬁcally, we assume that car sharing stations

behave as heat source in the ﬁeld, while relocated ve-

hicles behave as particles that conduct heat from the

stations to each other. Then, the difference in vehicle

availability at each station is assume to be equivalent

to temperature difference in a ﬁeld. More formally, let

us denote the temperature T

(t) of a station s

during

time interval [t, t +τ] as follows

(t) = T

(t) + λ

(t) − µ

(t) (1)

where T

(t) is deﬁned as the number of vehicles that

are parked at station s

at the beginning of the time

interval [t, t + τ]. According to formula 1, a station

is an hot spot if vehicles accumulate at the station,

while is a cold spot if vehicles disappear from the sta-

tion during the time interval [t,t + τ]. Then, vehicle

rebalance would require to move heat from hot spots

to cold spots.

However, a vehicle relocation task has a cost for

the operator because the customer must be incentive

to participate in the rebalancing program. Thus, it is

reasonable to assume that relocation opportunities are

limited. Thus, rebalancing activities should be pri-

oritized by given precedence to relocations between

stations with the maximum temperature difference

(i.e., the maximum unbalance of vehicle availability).

More formally, let R

(t) be a ranked list of the hot

spots, in which the stations are sorted in descending

order of temperature (i.e., the top ranked station is the

one with the highest vehicle surplus). Similarly, let

(t) the ranked list of the cold spots, in which the

stations are sorted in ascending order of temperature

(i.e., the top ranked station is the one with the high-

est vehicle shortage). Then, relocation trips are only

allowed between the m top-ranked stations in the two

lists. This policy ensures that relocation trips are per-

formed only to stations that have a potentially high

number of blocked customers, and that vehicles are

taken only from stations with a large vehicle surplus.

Note that necessary conditions for the feasibility of

a relocation trip between station s

and destination s

are: i) T

(t) ≥ 0 ≥ T

(t); and ii) p

i j

> 0. Clearly, the

closer m is to n, the larger is the number of feasible re-

location trips that are actually performed. The reloca-

tion model could be further complicated by assuming

that customer k interested in travelling from station s

to station s

is willing to accept to relocate a second

vehicle by receiving an economic incentive e

i j

with a

probability:

i j

) : R

≥0

−→ [0, 1]. (2)

It is reasonable to assume that a relocation be-

tween station s

and station s

is more effective if

the difference ∆T

i j

(t) = T

(t) − T

(t) is high. Thus,

the economic incentive could be determined in such a

way that the probability of accepting a relocation task

is proportional to ∆T

i j

(t). Finally, our rebalancing al-

gorithm can be brieﬂy summarised as follows:

1. At time t

∈ [t,t + τ] a customer k generates a re-

quest for a rental vehicle from location O to loca-

tion D;

2. The central controller of the car sharing system

determine the station s

that is the closest to loca-

tion O with an available vehicle, and the station s

that is the closest to location D with an available

parking space;

3. The central controller checks if ∆T

i j

(t) > 0 and

if both station s

and station s

are ranked in the

ﬁrst m top positions of ranking R

(t) and R

(t),

respectively. If yes, a relocation task is decided;

On the Performance of a One-way Car Sharing System in Suburban Areas: A Real-world Use Case

105

4. The central controller offers to customer k an eco-

nomic incentive to ensure that the customer accept

the relocation task with a probability that is pro-

portional to ∆T

i j

(t).

For the sake of simplicity, in the following evalu-

ation we assume that g

i j

) = 1, i.e. a customer is

always willing to participate to the relocation activi-

ties. The incorporation of the users choice models in

the rebalancing design is left as future work.

4 SCENARIO AND TRAVEL

DEMAND DATA

Our simulation model is applied to a case study in

the city of Lyon. The operating area of the simulated

car sharing system is shown in Figure 2, and corre-

sponds to three suburban district of the city of Lyon.

The road network is constructed from OpenStreetMap

data. Regarding the public transit systems, we use

data publicly available from Grand Lyon Data plat-

form

to deﬁne transit routes and modes (buses, tram,

underground), transit stops, as well as schedules and

vehicles capacities.

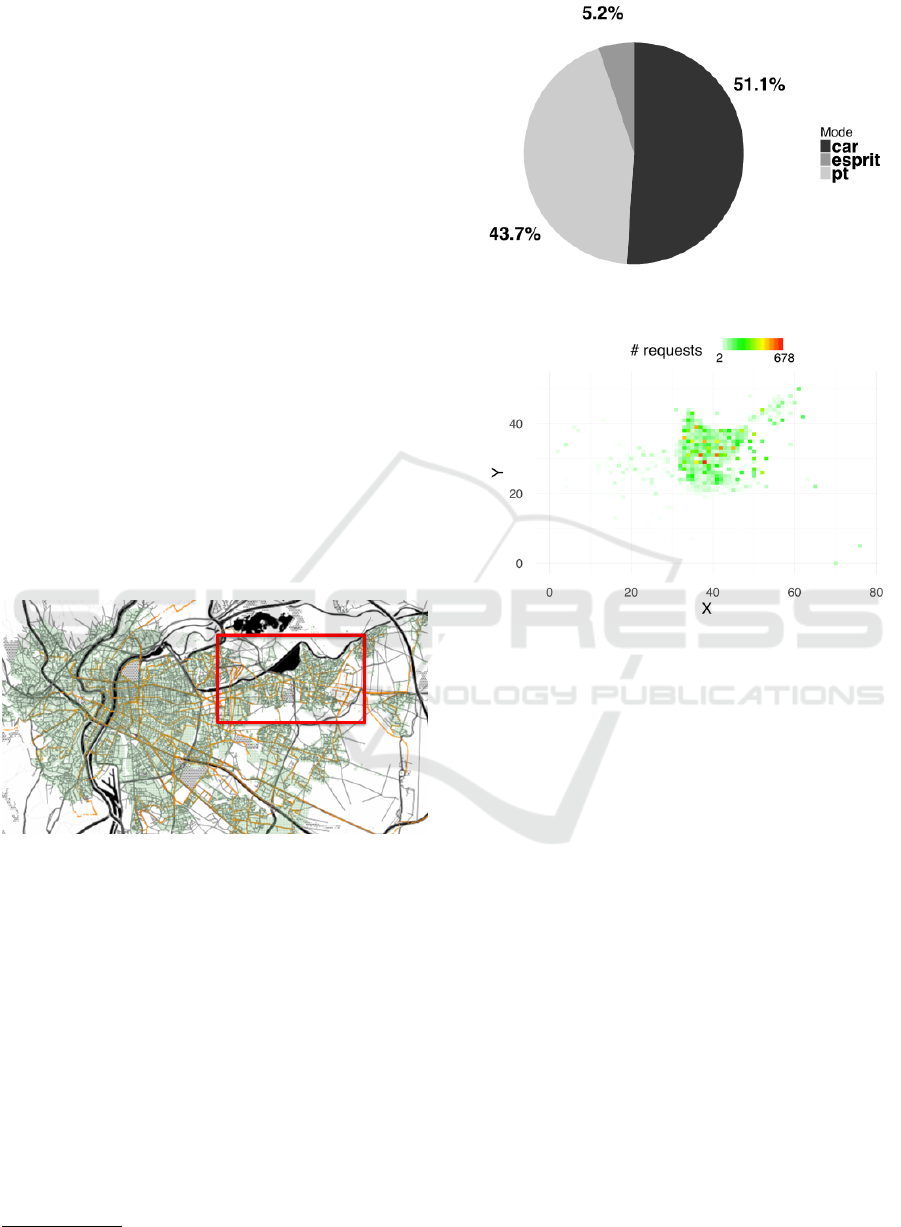
Figure 2: Lyon map on Via trafﬁc visualizer, showing the

road network (gray lines), the public transit network (orange

lines), the facilities (green dots), and the study area marked

with the rectangular frame.

One of the most important modelling task is to

construct the travel demand for different transporta-

tion modes. Traditionally, travel demand data is

organised as trip origin/destination (O/D) matrices,

which simply contain the number of trips that are

taken from an origin node to a destination node in a

speciﬁc period of time.

However, since we use a multi-agent modelling

approach, the travel demands are constructed as in-

dividual daily plan dairies, which contain sequence

of activities and the preferred transportation mode for

trips between activities. Then, we use data from the

http://data.grandlyon.com/.

(a) The modal share: private cars, ESPRIT car sharing,

and public transport

(b) Estimated spatial distribution of the demand by num-

ber of requests

Figure 3: The simulated demand of the Lyon Scenario.

2015 Lyon Travel Survey to synthesise the popula-

tion of travellers and their travel demands. More

precisely, the trafﬁc demand is provided in terms of

travel modes and travel purposes of 20,244 house-

holds distributed across the area. Census data is used

to expand the travelling population of the survey to

133,981 travellers. Four types of travel purposes are

considered: work, shopping, leisure, and school. Ac-

tivities are performed in related facilities, which are

randomly placed within the area based on travellers’

densities. Note that our travel demand includes only

trips that have an origin/destination in the case-study

area or that go through the study area (thus, contribut-

ing to trafﬁc congestion).

The constructed demand is depicted by both the

modal share in Figure 3(a) and the spatial distribution

in Figure 3(b). On one hand, 5.2% of the trips are car

sharing trips. To put it in numbers: the people who

would like to use ESPRIT in Lyon study area are 8345

out of 133981, while the car sharing trips represents

18952 out of 363502. On the other hand, there are

surrounding areas with very low number of potential

car sharing requests. This led us to wonder whether it

VEHITS 2017 - 3rd International Conference on Vehicle Technology and Intelligent Transport Systems

106

is worthwhile to provide a car sharing service in those

areas!

5 RESULTS AND DISCUSSION

Our car sharing model is implemented in MATSim,

a popular open-source and agent-based trafﬁc simula-

tion platform, which supports dynamic trafﬁc assign-

ment, large scenarios and detailed modelling of trans-

portation networks (Laarabi and Bruno, 2016; Balmer

et al., 2004). We evaluate the performance of the pro-

posed rebalancing algorithm from the perspective of

the car sharing provider. Speciﬁcally, the car shar-

ing operator is interested in maximizing its net proﬁt.

Clearly, a key contribution to the operators proﬁt is

due to revenues from the rental services provided to

the customers. Note that users are charged for the dis-

tance they travel, or the time they reserved the car, or

both. Thus, the ﬁrst metric of interest is the total num-

ber of rental trips. However, the potential increase

in the transportation demand or a rebalanced system

comes at cost of additional trips due to vehicle reloca-

tions. Thus, the next metrics of interest are the num-

ber of relocation trips and the average length of re-

location trips. The latter metric is important because

relocation trips consume energy and vehicle battery

have to be recharged before a rental trip.

Before assessing relocation performance, we set

up two scenarios such as each one of them corre-

spond to a different infrastructure planning, using the

our approach previously discussed in (Boldrini et al.,

2016). The objective is to compare the two scenarios

on the basis of the ﬁrst metric, that is the number of

trips. We refer to the ﬁrst deployment with Coverage

1, as in Figure 5(a), such that there are 135 stations

with 1023 parking space and 409 car sharing vehicles,

while each station is assumed to have a coverage ra-

dius of 380 meters. Figure 5(b) shows the second de-

ployment, called Coverage 2, which sets 72 stations

with 549 parking space and 220 car sharing vehicles

and a coverage radius of 635 meters. Note that the

ﬂeet size represents 40% of the total parking space, a

percentage considered as a rule of thumb, as it is the

case for Autolib in Paris.

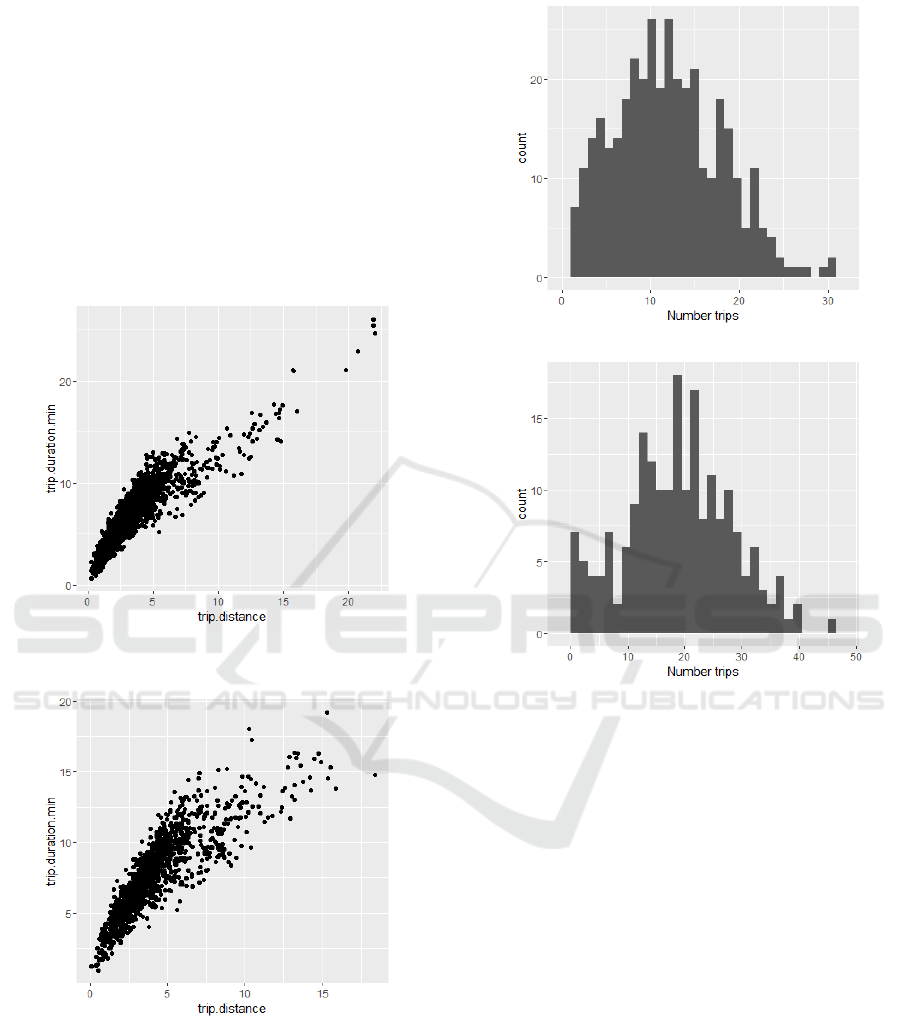
Results are depicted by Figure 5 that refers to the

availability of cars and parking spaces in stations in

the case of both coverages, and Figures 6-7, which

refers to the number of trips and distances covered by

each trip.

We observe then that our deployment strategy is,

on one hand, very effective in ensuring parking avail-

ability, while car availability is much more difﬁcult

to ensure. Since deploying large stations in a dense

(a) Coverage 1: 135 stations with a radius of 380m

(b) Coverage 2: 72 stations with a radius of 635m

Figure 4: Station deployment such that cost of station is

equivalent to cost of parking spaces.

(a) Coverage 1

(b) Coverage 2

Figure 5: Car & Park availability.

manner is not sufﬁcient, because ﬂeet size remains

an important factor. On the other hand, with less de-

On the Performance of a One-way Car Sharing System in Suburban Areas: A Real-world Use Case

107

ployed station parking availability becomes more crit-

ical, which requires improving the strategy to better

capture availabilities in sparse networks.

From the ﬁgures related to the ﬁrst and second

metric, we remark longer trips duration and less num-

ber of trips (rotations) per vehicle for Coverage 1.

While with Coverage 2 the results show shorter trips

and wider difference between trips distance and travel

time, as well as more rotations per vehicle. It is worth-

while to mention that the high number of rotations per

vehicle is due to the small size of the suburban area

where the car sharing system is deployed.

(a) Total number of trips is 10760 (56.7% of the

total demand), with R=380m, S=135, K=1023,

V=409

(b) Total number of trips is 6552 (34,5% of the to-

tal demand), with R=635m, S=72, K=549, V=220

Figure 6: The proportion trip distance per travel time.

When applying user-based relocation strategy to

both deployment, the improvement (new trips) was

only 0.04%. Figure 8 shows that there are many sta-

tions that seem to have a good potential for relocation,

such as red triangles refer to high temperature stations

i.e. many more drop-offs than pick-ups, while blue

(a) R=380m, S=135, K=1023, V=409

(b) R=635m, S=72, K=549, V=220

Figure 7: The proportion trip distance per travel time.

triangles refer to low temperature stations i.e. many

more pick-ups than drop-offs. However, due to the

fact that the model is constrained by real trips, which

happens to not be going from hot stations to cold sta-

tion, user-based relocation cannot take advantage of

the unbalance in the system unless we encourage cus-

tomers to change their destination, such as trips com-

ing from hot station would be directed to cold stations.

Besides, some stations with hot temperature might not

be that hot as there are many high pick-ups/drop-offs

events during a short period of time, and any deci-

sion of relocation from such stations might disturb the

original car sharing trafﬁc ﬂow.

Finally, the availability of vehicles is signiﬁcantly

high during the day as shown by Figure 9. This is

due to the fact that very few trips are connecting hot

stations with cold stations, as mentioned before hand,

and therefore inviting a customer to take a second ve-

hicle with him/her cannot solve the situation. There-

fore, an operator-based relocation would clearly ad-

dress this issue with more ﬂexibility, which leaves the

door open for a possible theoretical hybrid approach

VEHITS 2017 - 3rd International Conference on Vehicle Technology and Intelligent Transport Systems

108

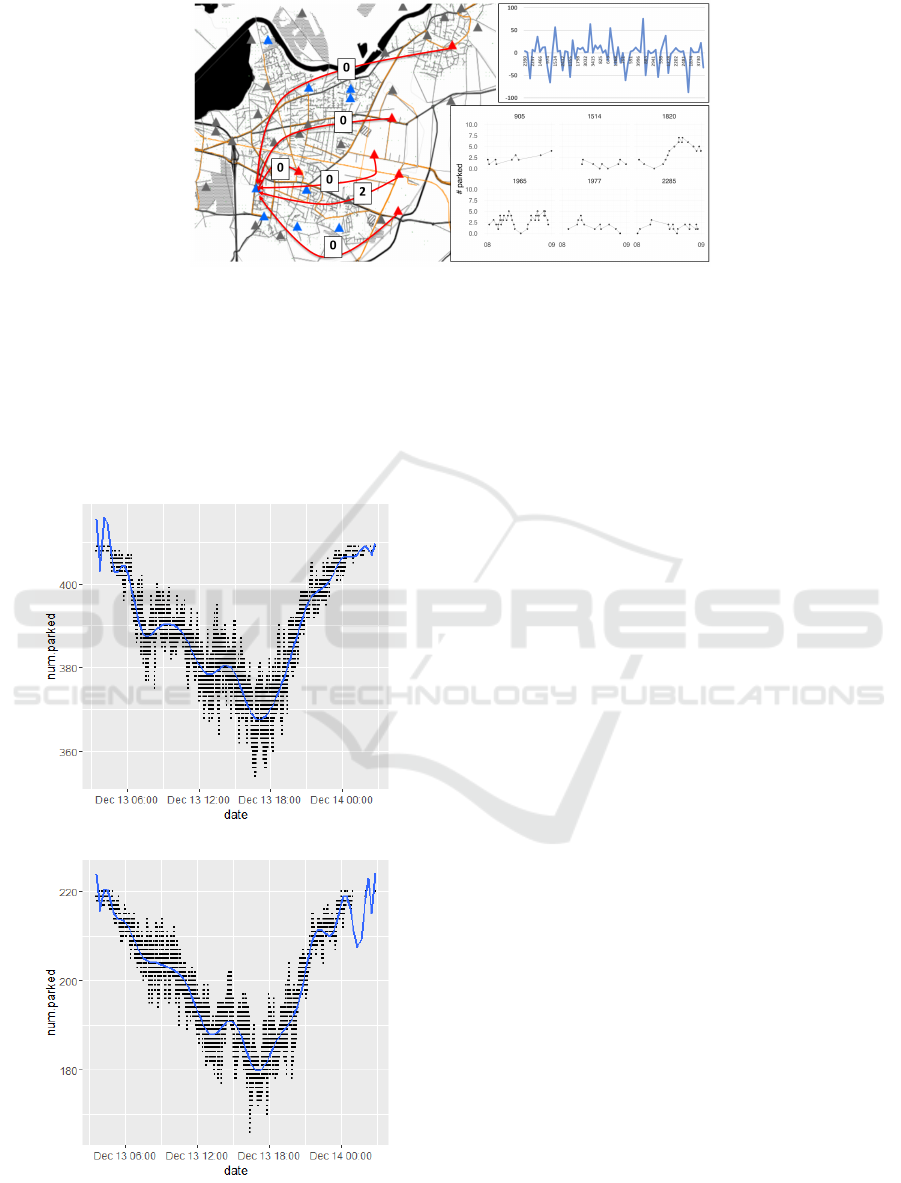
Figure 8: On the left: Study area map between 8:00AM and 8:30 AM on which blue triangle refers to very cold stations, while

red triangles refers to very hot stations. Numbers in boxes refer to number of trips going from hot stations to cold stations

during same period. On the top right, temperature graphs of stations between 8:00AM and 8:30 AM, while bottom right,

temperature of individual stations during same period.

where both operator and user relocation co-exists to

solve the unbalancing problem while minimizing the

operational costs.

(a) R=380m, S=135, K=1023, V=409

(b) R=635m, S=72, K=549, V=220

Figure 9: Vehicle availability during the whole simulated

day.

6 CONCLUSION

The objective of the paper is to evaluate the perfor-

mance of a one-way car sharing system in a suburban

area of Lyon, France. Two different deployments have

been generated then tested with the car sharing simu-

lation framework. While we have obtained clear dis-

tinction in the number rotations per vehicle and trips

distances between the two deployments, we have de-

duced also that user-based relocation does not have a

signiﬁcant impact on the total number of car sharing

trips. For this reason, as an ongoing work, we intend

to focus on the operator-based relocation as it offers

better guarantee for solving the unbalancing problem

and signiﬁcantly increase of the number of total trips.

REFERENCES

Balmer, M., Cetin, N., Nagel, K., and Raney, B. (2004).

Towards truly agent-based trafﬁc and mobility sim-

ulations. In Proc. of AAMS’04, pages 60–67. IEEE

Computer Society.

Barth, M. and Shaheen, S. (2002). Shared-use vehicle

systems: Framework for classifying carsharing, sta-

tion cars, and combined approaches. Transportation

Research Record: Journal of the Transportation Re-

search Board, (1791):105–112.

Barth, M. and Todd, M. (1999). Simulation model perfor-

mance analysis of a multiple station shared vehicle

system. Transportation Research Part C: Emerging

Technologies, 7(4):237–259.

Barth, M., Todd, M., and Xue, L. (2004). User-based vehi-

cle relocation techniques for multiple-station shared-

use vehicle systems.

Birnschein, T., Kirchner, F., Girault, B., Y

uksel, M., and

Machowinski, J. (2012). An innovative, comprehen-

sive concept for energy efﬁcient electric mobility-eo

On the Performance of a One-way Car Sharing System in Suburban Areas: A Real-world Use Case

109

smart connecting car. In Proc. of IEEE ENERGY-

CON’12, pages 1028–1033. IEEE.

Boldrini, C., Bruno, R., and Conti, M. (2016). Character-

ising demand and usage patterns in a large station-

based car sharing system. In The 2nd IEEE INFO-

COM Workshop on Smart Cities and Urban Comput-

ing.

Bonsall, P. (1982). Microsimulation: its application to car

sharing. Transportation Research Part A: General,

16(5):421–429.

Boyacı, B., Zografos, K. G., and Geroliminis, N. (2015). An

optimization framework for the development of efﬁ-

cient one-way car-sharing systems. European Journal

of Operational Research, 240(3):718–733.

Ciari, F., Schuessler, N., and Axhausen, K. W. (2013). Es-

timation of Carsharing Demand Using an Activity-

Based Microsimulation Approach: Model Discussion

and Some Results. International Journal of Sustain-

able Transportation, 7(1):70–84.

Clemente, M., Fanti, M. P., Mangini, A. M., and Ukovich,

W. (2013). The vehicle relocation problem in car

sharing systems: modeling and simulation in a petri

net framework. In International Conference on Ap-

plications and Theory of Petri Nets and Concurrency,

pages 250–269. Springer.

de Almeida Correia, G. H. and Antunes, A. P. (2012). Opti-

mization approach to depot location and trip selection

in one-way carsharing systems. Transportation Re-

search Part E: Logistics and Transportation Review,

48(1):233–247.

ESPRIT (2015). Esprit h2020 eu project - easily distributed

personal rapid transit. http://www.esprit-transport-

system.eu/. Accessed: 2016-12-12.

Farahani, R. Z., Asgari, N., Heidari, N., Hosseininia, M.,

and Goh, M. (2012). Covering problems in facility lo-

cation: A review. Computers & Industrial Engineer-

ing, pages 368–407.

Febbraro, A., Sacco, N., and Saeednia, M. (2012). One-way

carsharing: solving the relocation problem. Trans-

portation Research Record: Journal of the Trans-

portation Research Board, (2319):113–120.

George, D. K. and Xia, C. H. (2011). Fleet-sizing and ser-

vice availability for a vehicle rental system via closed

queueing networks. European Journal of Operational

Research, 211(1):198–207.

Hampshire, R. and Gaites, C. (2011). Peer-to-peer carshar-

ing: Market analysis and potential growth. Trans-

portation Research Record: Journal of the Trans-

portation Research Board, (2217):119–126.

Herrmann, S., Schulte, F., and Voß, S. (2014). Increas-

ing acceptance of free-ﬂoating car sharing systems us-

ing smart relocation strategies: a survey based study

of car2go hamburg. In International Conference on

Computational Logistics, pages 151–162. Springer.

Jorge, D., Correia, G. H., and Barnhart, C. (2014). Compar-

ing optimal relocation operations with simulated relo-

cation policies in one-way carsharing systems. IEEE

Transactions on Intelligent Transportation Systems,

15(4):1667–1675.

Kek, A., Cheu, R., and Chor, M. (2006). Relocation sim-

ulation model for multiple-station shared-use vehicle

systems. Transportation Research Record: Journal of

the Transportation Research Board, (1986):81–88.

Kek, A. G., Cheu, R. L., Meng, Q., and Fung, C. H. (2009).

A decision support system for vehicle relocation op-

erations in carsharing systems. Transportation Re-

search Part E: Logistics and Transportation Review,

45(1):149–158.

Laarabi, M. H. and Bruno, R. (2016). A generic software

framework for car sharing modelling based on a large-

scale multi-agent trafﬁc simulation platform. In Agent

Based Modelling of Urban Systems, volume 10051.

Springer.

Mitchell, W. J., Borroni-Bird, C. E., and Burns, L. D.

(2010). Reinventing the automobile: Personal urban

mobility for the 21st century. MIT press.

Nair, R. and Miller-Hooks, E. (2011). Fleet management for

vehicle sharing operations. Transportation Science,

45(4):524–540.

Pavone, M., Smith, S. L., Frazzoli, E., and Rus, D. (2012).

Robotic load balancing for mobility-on-demand sys-

tems. The International Journal of Robotics Research,

31(7):839–854.

Uesugi, K., Mukai, N., and Watanabe, T. (2007). Opti-

mization of vehicle assignment for car sharing sys-

tem. In International Conference on Knowledge-

Based and Intelligent Information and Engineering

Systems, pages 1105–1111. Springer.

Vairani, F. (2009). bitCar: design concept for a collapsible

stackable city car. PhD thesis, Massachusetts Institute

of Technology.

Weikl, S. and Bogenberger, K. (2013). Relocation Strate-

gies and Algorithms for Free-Floating Car Sharing

Systems. IEEE Intelligent Transportation Systems

MagazineI, 5(4):100–111.

Zhang, R. and Pavone, M. (2016). Control of robotic

mobility-on-demand systems: a queueing-theoretical

perspective. The International Journal of Robotics Re-

search, 35(1-3):186–203.

VEHITS 2017 - 3rd International Conference on Vehicle Technology and Intelligent Transport Systems

110