A Linear Logic based Synchronization Rule for Deadlock Prevention in

Web Service Composition

Vin

ıcius Ferreira de Oliveira

, St

ephane Julia

ıgia Maria Soares Passos

and K

enia Santos de Oliveira

Computing Faculty, Federal University of Uberl

andia, Uberl

andia, MG, Brazil

Computer Science Department, Federal Rural University of Rio de Janeiro, Nova Iguac¸u, RJ, Brazil

Keywords:

Petri Nets, Linear Logic, Deadlock Situation, Web Services, Composition, Synchronization Rule.

Abstract:

This paper presents a prevention method for deadlock situations in Web Services composition. This method

considers the Petri net theory and is based on the analysis of Linear Logic proof trees. Initially, it is necessary

to detect deadlock scenarios by analyzing the Linear Logic proof trees built for each different scenario of the

modules from which the composed system is built. Following on from this, a synchronization rule is proposed

in order to prevent deadlock situations in these deadlock scenarios. The basic principle of such a rule is to

force workﬂow modules to execute speciﬁc tasks respecting a local scheduling policy in order to remove the

situations responsible for the deadlocks. This paper therefore presents a synchronization strategy to prevent

deadlock situations in Web Services composition that are deadlock-free within the local workﬂow modules

but not necessarily deadlock-free when considering the entire composed system.

1 INTRODUCTION

There exists an increasing acceptance of Service-

Oriented Architecture (SOA) as a paradigm for the

integration of disparate software components within

and across organizational boundaries using Internet

protocols (Klai et al., 2013), (Xiong et al., 2010).

These components, called Web Services (WS), are

available in the distributed environment of the In-

ternet. As consequence, the organizations attempt

to provide their own services through complex tasks

which can be resolved using a combination (or com-

position) of several WS (Klai et al., 2013).

In many cases, multiple WS need to invoke each

other dynamically to accomplish service requestors

manifold requirements (Xiong et al., 2010). Orches-

tration and choreography are two different viewpoints

for WS interactions (Barros et al., 2005). The former

considers one particular service that directs the logical

order of all other services, while the latter considers

the case where individual services work together in a

loosely coupled network (Xiong et al., 2010), (Barros

et al., 2005).

When two services are composed through a kind

of Petri net modeling, the common elements are

merged becoming the new interface of the system

(Martens, 2005). Even if services have a syntactically

compatible interface, the resulting distributed process

may lead to a deadlock situation (Martens, 2005). Ac-

cording to (Klai et al., 2013), this is also due to the

fact that whilst the control ﬂow constructs of WS have

been designed in a way to ensure that no “individual”

service process execution can deadlock, some combi-

nations of structured activities with control links can

lead to situations where some activities are “unreach-

able”.

Many studies have already considered Petri nets

as an appropriate model for specifying and analysing

WS composition. In (Martens, 2005), a framework

for modeling and analyzing WS based business pro-

cesses by help of Petri nets is presented. In this ap-

proach, the services, named modules, are classiﬁed as

usable or not usable (modules that can not be used

in any composition). In (Klai et al., 2013), the au-

thors address the problem of abstracting and checking

correctness of WS composition, taking into consid-

eration four variants of Soundness property (van der

Aalst et al., 2011) (Soundness, Weak Soundness, Re-

laxed Soundness and Easy Soundness). For additional

information concerning these variations, see (van der

Aalst et al., 2011). This approach only considers the

analysis of the composed model. Since one criteria

is not satisﬁed, it is necessary to redesign the whole

model in order to satisfy the required property. In

316

Oliveira, V., Julia, S., Passos, L. and Oliveira, K.

A Linear Logic based Synchronization Rule for Deadlock Prevention in Web Service Composition.

DOI: 10.5220/0006308303160323

In Proceedings of the 19th International Conference on Enterprise Information Systems (ICEIS 2017) - Volume 2, pages 316-323

ISBN: 978-989-758-248-6

(Passos and Julia, 2015), an approach is presented

to ensure that the existing deadlock-free scenarios in

WS composition guarantee the business relationship,

avoiding in particular deadlock situation. In such an

approach, the scenarios that can lead the system to a

deadlock situation are not removed from the model.

In this paper, an approach based on Linear Logic

is proposed to deal with deadlock situations in the

WS composition modeled by Petri nets, where the

workﬂow modules are deadlock-free but not neces-

sarily the composed system. The method set in this

paper is to replace some of the asynchronous com-

munication places of the composed system (the ones

responsible for the deadlock situation) by a kind of

synchronous communication mechanism, forcing lo-

cal workﬂow modules to initiate speciﬁc tasks at the

same time. In particular, the detection of the com-

munication places of the composed system respon-

sible for the deadlock situations and the non respect

of the deadlock-freeness is based on the analysis of

the proof trees of Linear Logic sequents which corre-

spond to deadlock scenarios in the composed system.

The remainder of this paper is presented as fol-

lows. In section 2 the deﬁnitions of WorkFlow net,

module and composed system along with an overview

of Linear Logic are provided. The synchronization

rule based on Linear Logic for deadlock prevention in

composed systems is presented in section 3. Finally,

the last section concludes this work with a short sum-

mary, an assessment of the presented approach and an

outlook for future work.

2 THEORETICAL BACKGROUND

A Web Service (WS) consists, according to (Martens,

2005), of internal structures that realize local pro-

cesses and of an interface that allows for communi-

cation with other WS. Thus, a WS can be modeled

through the help of a WorkFlow net (WF-net) (van der

Aalst et al., 2011) supplemented by an interface; such

a model is called a workﬂow module (Martens, 2005).

As the deﬁnition of a workﬂow module is based on the

deﬁnition of WF-nets, these nets are also presented.

In the following, the formal deﬁnition of WF-nets

is presented.

Deﬁnition 1 (WorkFlow Net). A Petri net PN =

(P,T,F) is a WF-net if and only if (van der Aalst et al.,

2011):

1. PN has two special places: i and o. Place i is

a source place: •i = φ. Place o is a sink place:

o• = φ.

2. Every node x ∈ P ∪ T is on a path from i to o.

The formal deﬁnition of workﬂow module is the

following.

Deﬁnition 2 (Workﬂow Module). A ﬁnite Petri net

M = (P,T,F) is called a workﬂow module (module

for short), if and only if (Martens, 2005):

1. The set of places is divided into three disjoint

sets: internal places P

, input places P

and out-

put places P

2. The ﬂow relation is divided into internal ﬂow

⊆ (P

× T ) ∪ (T × P

) and communication

ﬂow F

⊆ (P

× T ) ∪ (T × P

3. The net N(M) = (P

,T, F

) is a WF-net.

4. No transition is connected both to an input place

and an output place.

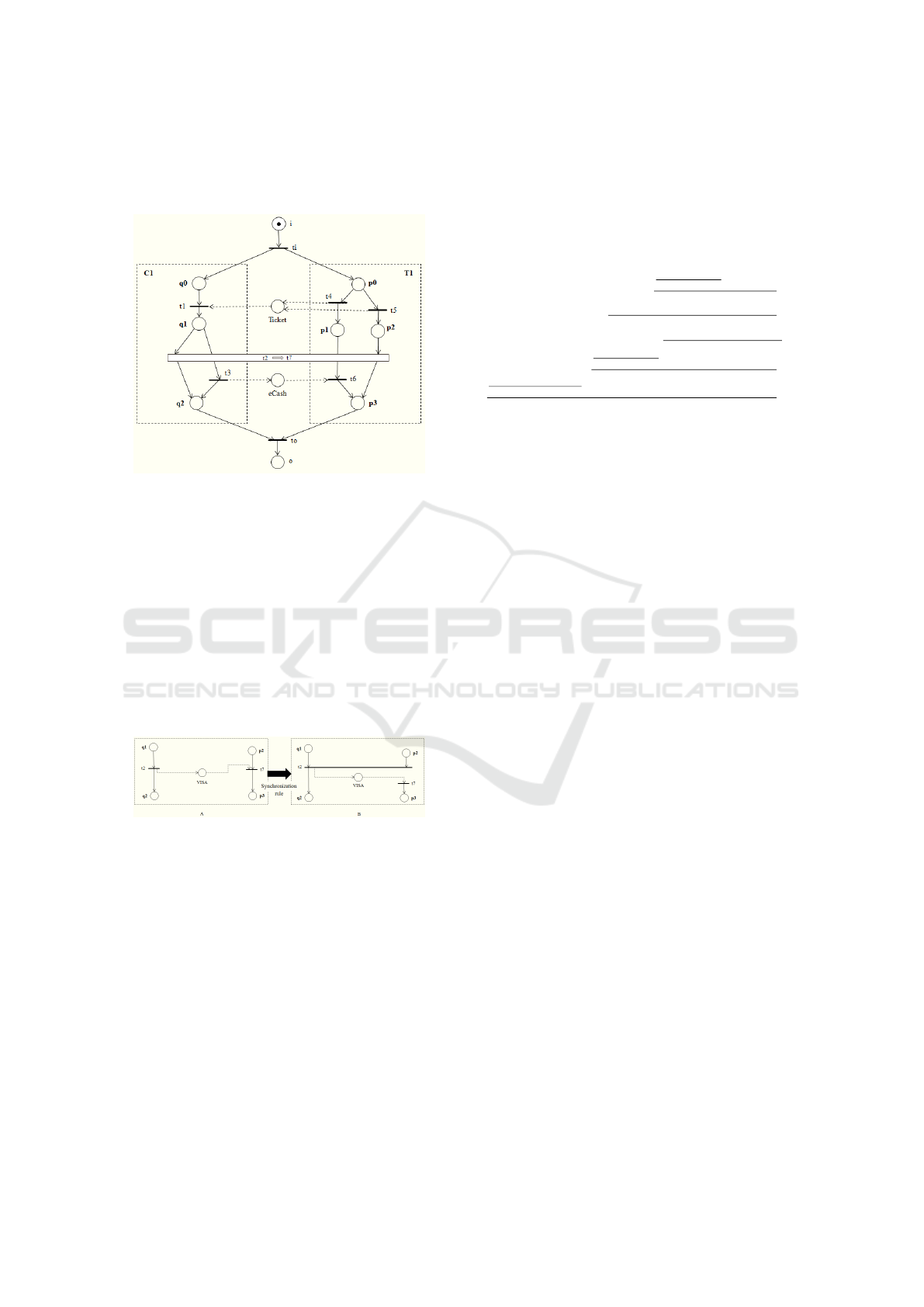
Figure 1: Modules Customer (C1) and Ticket (T1).

To clarify the concept deﬁned above, consider

the modules C1 and T1 of Figure 1, presented in

(Martens, 2005). The module C1 represents a cus-

tomer and the module T1 models a Ticket service.

The internal places of C1 are places q0, q1 and q2.

The input place of C1 is the place Ticket and the out-

put places of C1 are V ISA and eCash.

According to (Martens, 2005), two modules are

called syntactically compatible if both internal pro-

cesses are disjoint and each common place is an out-

put place of one module and an input place of the

other. By considering the modules C1 and T1 shown

in Figure 1, it is easily recognizable that these mod-

ules are syntactically compatible. In the approach

presented in (Martens, 2005), when two modules are

composed, their common places are merged and the

dangling input and output places become the new

interface. To achieve a syntactically correct work-

ﬂow module, it is necessary to add new components

for initialization and termination. In this context,

(Martens, 2005) deﬁned the composed system con-

cept presented in Deﬁnition 3.

Deﬁnition 3 (Composed System). Let A =

) and B = (P

) be two syntacti-

cally compatible modules. Let i,o /∈ (P

∪ P

)

be two new places and t

/∈ (T

∪ T

) two

new transitions. The composed system A ⊕ B

is given by (P

), such that P

= P

∪ P

∪

A Linear Logic based Synchronization Rule for Deadlock Prevention in Web Service Composition

317

{i,o}, T

= T

∪ T

∪ {t

} and F

= F

∪ F

∪

{(i,t

),(t

,α

),(t

,α

),(ω

),(t

,o)}.

Figure 2: The composed system C1 ⊕ T1.

As an example, Figure 2 shows the composed sys-

tem C1 ⊕ T1. Note that the Ticket service (T1) solves

an internal conﬂict and sends the Ticket to the cus-

tomer module C1. Thereafter, module T1 is either in

state p1 waiting for eCash only, or in state p2 waiting

for V ISA only. The customer (C1) receives the Ticket

and has the choice between either kind of payment,

V ISA or eCash. It is important to note that module C1

does not know the internal state of module T1, i.e. p1

or p2. According to (Martens, 2005), when an inter-

nal decision is made and is not communicated prop-

erly to an external WS, a problem, already well un-

derstood by literature happens - the non local choice

problem that can be responsible for the occurrence of

deadlock situations.

Linear Logic was proposed in 1987 by Girard (Gi-

rard, 1987). In Linear Logic, propositions are consid-

ered as resources which are consumed and produced

at each state change (Riviere et al., 2001). In this pa-

per just two connectives of Linear Logic will be used:

• The times connective, denoted by ⊗, represents

simultaneous availability of resources.

• The linear implies connective, denoted by (,

represents a state change.

The translation of a Petri net into formulas of Lin-

ear Logic (Riviere et al., 2001) is a relatively simple

process: a marking M is a monomial in ⊗ and is rep-

resented by M = A

⊗ A

⊗ ... ⊗ A

where A

are

place names; a sequent M,t

` M’ represents a sce-

nario where M and M’ are respectively the initial and

ﬁnal markings, and t

is a list of non-ordered transi-

tions; a sequent can be proven by applying the rules of

the sequent calculus. It was proven in (Girault et al.,

1997) that a proof of the sequent calculus is equiva-

lent to a reachability problem in a Petri net model.

In this paper, just some Linear Logic rules will be

considered. These rules will be used to build proof

trees. To achieve this, F, G, and H will be consid-

ered as formulas and Γ and ∆ as blocks of formulas.

The following rules will be those used in this paper

(Riviere et al., 2001):

• The (

rule,

Γ ` F ∆,G ` H

Γ,∆, F ( G ` H

(

, expresses a

transition ﬁring and generates two sequents, such

that the right sequent represents the subsequent,

which remains to be proven and the left sequent

represents the tokens consumed by this ﬁring.

• The ⊗

rule,

Γ,F,G ` H

Γ,F ⊗ G ` H

⊗

transforms a

marking in a list of atoms.

• The ⊗

rule,

Γ ` F ∆ ` G

∆,Γ ` F ⊗G

⊗

transforms a se-

quent such as A,B ` A ⊗ B into two identity se-

quents A ` A and B ` B.

In the approach presented in this paper, a Linear

Logic proof tree is read from the bottom-up. The

proof stops when the atom that represents the place

o is produced, i.e. the identity sequent o ` o appears

in the proof tree, when there is not any rule that can

be applied or when all the leaves of the proof tree are

identity sequents.

3 SYNCHRONIZATION RULE

The approach proposed in this paper considers the

WS composition modeled by workﬂow modules that

are deadlock-free. Such a statement does not neces-

sarily mean that the composed system is deadlock-

free. In such systems, the addition of the interface

(common places merged among modules) can lead

to situations where some activities are “unreachable”

(Klai et al., 2013), causing the deadlock situation. Ac-

cording to (van der Aalst, 1998), in the context of WF-

nets, a deadlock situation can be corrected by replac-

ing an asynchronous communication element (a com-

munication place) by a synchronous communication

element (a transition of synchronization).

The approach in this paper consists of replacing

some of the asynchronous communication places (in-

terface) of the composed system with new commu-

nication mechanisms partially synchronous in order

to prevent the occurrence of lost messages that, in

case of deadlock situations, are generally trapped in-

side one of the communication places, thus preventing

the composed system from respecting the deadlock-

freeness property. Such a substitution can be seen

therefore as a kind of synchronization rule.

ICEIS 2017 - 19th International Conference on Enterprise Information Systems

318

To apply such a synchronization rule, it is nec-

essary ﬁrst to identify scenarios responsible for

deadlock situations and more speciﬁcally the asyn-

chronous communication elements that can lead the

system to inconsistent states (terminal states with a

token trapped in one or more of the asynchronous

communication places). The detection of inconsistent

states in this work will be based on Linear Logic se-

quent proof trees that correspond to potential scenar-

ios in a composed system.

Initially, the elements of the composed system

have to be represented through the use of Linear Logic

formulas. For each potencial scenario of the com-

posed system, a Linear Logic sequent is then pro-

duced. The detailed method for the obtaining of all

Linear Logic sequent candidates for possible collab-

orations among two or more workﬂow processes was

presented in (Passos and Julia, 2013).

As shown in (Passos and Julia, 2013), a scenario in

the context of WF-nets corresponds to a well deﬁned

route mapped into the corresponding module, and if

the module has more than one route (places with two

or more output arcs), it is necessary then to build a

different Linear Logic sequent for each existing sce-

nario. After the deﬁnition of the Linear Logic se-

quents that represent all the possible scenarios of the

composed system, these Linear Logic sequents need

to be proven through the building of Linear Logic

proof trees.

If the last sequent of a Linear Logic proof tree

built for a speciﬁc scenario is different from the iden-

tity sequent o ` o, then there is no token in the sink

place of the composed system, i.e. a deadlock situa-

tion occurs before the termination of the process (Pas-

sos and Julia, 2013).

In the present method, it is necessary to identify

the last transition ﬁred before the occurrence of the

deadlock situation. This transition will be called t

To identify such a transition t

, it is necessary to ver-

ify in a Linear Logic proof tree leading to a deadlock

situation, the transition ﬁring that produces the atom

which remains in one of the communication places

(interface) until the conclusion of the Linear Logic

proof tree. For each transition of type t

, a corre-

sponding transition of type t

exists. Such a tran-

sition, when a deadlock situation occurs, is the out-

put transition of a marked communication place that

corresponds to an atom trapped in the interface of

the composed system. The deadlock situation corre-

sponds therefore to the death of transition t

(tran-

sition not enabled until the end of the Linear Logic

proof).

In order to prevent the death of transition t

, it is

necessary to introduce a kind of synchronization rule

that corresponds to the following scheduling strategy:

each time a transition of type t

is ﬁred, the corre-

sponding transition of type t

has to be ﬁred in se-

quence in order to empty the communication place

in which an atom was produced. In practice, such

a policy corresponds to the guarantee that for each

message (the activity associated to the transition t

)

sent by a local process WS, the corresponding answer

of the local workﬂow module (the activity associated

to the transition t

) will occur with certainty. After

the synchronization rule application, the cause of the

deadlock (a token trapped in a communication place)

is removed and the Linear Logic proof can be cor-

rectly ﬁnalized with, as the ﬁnal state, a single atom

produced in the place o (last place of the composed

system).

To illustrate the approach, the composed sys-

tem shown in Figure 2 is considered. As shown

in (Martens, 2005), the modules Customer (C1) and

Ticket (T1) shown in Figure 1 that make up the com-

posed system are deadlock-free but the composed sys-

tem of Figure 2 is not deadlock-free.

For the composed system shown in Figure 2, there

exist four different scenarios to be studied. The ﬁrst

scenario, Sc

, where transitions t

and t

will be ﬁred.

The second scenario, Sc

, where transitions t

and t

will be ﬁred. The third scenario, Sc

, where transi-

tions t

and t

will be ﬁred. Finally, the fourth sce-

nario, Sc

, where transitions t

and t

will be ﬁred.

Each one of these scenarios is then represented by

a speciﬁc Linear Logic sequent that considers the ini-

tial and ﬁnal markings of the composed system and

a non-ordered list of transitions involved in it (Passos

and Julia, 2015).

The transitions of the composed system shown in

Figure 2 are represented by the following formulas of

Linear Logic:

= i ( q0 ⊗ p0, t

= q0 ⊗ Ticket ( q1,

= q1 ( V ISA ⊗ q2, t

= q1 ( eCash ⊗ q2,

= p0 ( Ticket ⊗ p1, t

= p0 ( Ticket ⊗ p2,

= p1 ⊗ eCash ( p3, t

= p2 ⊗V ISA ( p3,

= q2 ⊗ p3 ( o.

The four different scenarios, and consequently

Linear Logic sequents, are thus the following:

= i, t

, t

` o,

= i, t

, t

` o,

= i, t

, t

` o,

= i, t

, t

` o.

Presented in the following are the Linear Logic

proof trees for each of these scenarios. For a better

analysis of the approach, the proof tree for scenario

was divided into two parts, remembering that a

Linear Logic proof tree is read from the bottom-up.

Part 1 of the proof tree for scenario Sc

is in black

A Linear Logic based Synchronization Rule for Deadlock Prevention in Web Service Composition

319

text, while Part 2 of the proof for scenario Sc

is in

blue text. The proof tree for scenario Sc

is as follows:

q2`q2 p3`p3

q2,p3`q2⊗p3

⊗

o`o

(

p1`p1 eCash`eCash

p1,eCash`p1⊗eCash

⊗

q2,p3,q2⊗p3(o`o

(

p1,eCash,q2,p1⊗eCash( p3,t

⊗

q1`q1 p1,eCash⊗q2,t

(

q0`q0 Ticket`Ticket

q0,Ticket`q0⊗Ticket

⊗

p1,q1,q1(eCash⊗q2,t

(

q0,Ticket,p1,q0⊗Ticket(q1,t

⊗

p0`p0 q0,Ticket⊗p1,t

(

q0,p0,t

,p0(Ticket⊗p1,t

⊗

i`i q0⊗p0,t

(

i,i(q0⊗p0,t

For a better analysis of the approach, the Linear

Logic proof tree for scenario Sc

was also divided into

two parts. Part 1 of the proof tree for scenario Sc

in black text, while Part 2 of the proof for scenario

is in blue text. The proof tree for scenario Sc

as follows:

q2`q2 p3`p3

q2,p3`q2⊗p3

⊗

o`o

(

p2`p2 VISA`VISA

p2,V ISA`p2⊗V ISA

⊗

q2,p3,q2⊗p3(o`o

(

p2,VISA,q2,p2⊗V ISA( p3,t

⊗

q1`q1 p2,VISA⊗q2,t

(

q0`q0 Ticket`Ticket

q0,Ticket`q0⊗Ticket

⊗

p2,q1,q1(VISA⊗q2,t

(

q0,Ticket,p2,q0⊗Ticket(q1,t

⊗

p0`p0 q0,Ticket⊗p2,t

(

q0,p0,t

,p0(Ticket⊗p2,t

⊗

i`i q0⊗p0,t

(

i,i(q0⊗p0,t

The proof tree for scenario Sc

is the following:

p1,VISA,q2,t

⊗

q1`q1 p1,VISA⊗q2,t

(

q0`q0 Ticket`Ticket

q0,Ticket`q0⊗Ticket

⊗

p1,q1,q1(VISA⊗q2,t

(

q0,Ticket,p1,q0⊗Ticket(q1,t

⊗

p0`p0 q0,Ticket⊗p1,t

(

q0,p0,t

,p0(Ticket⊗p1,t

⊗

i`i q0⊗p0,t

(

i,i(q0⊗p0,t

And ﬁnally the proof tree for scenario Sc

is as

follows:

p2,eCash,q2,t

⊗

q1`q1 p2,eCash⊗q2,t

(

q0`q0 Ticket`Ticket

q0,Ticket`q0⊗Ticket

⊗

p2,q1,q1(eCash⊗q2,t

(

q0,Ticket,p2,q0⊗Ticket(q1,t

⊗

p0`p0 q0,Ticket⊗p2,t

(

q0,p0,t

,p0(Ticket⊗p2,t

⊗

i`i q0⊗p0,t

(

i,i(q0⊗p0,t

The last sequent in the proof trees for scenarios

and Sc

is o ` o; then these are deadlock-free sce-

narios. The last sequent for scenario Sc

is p1, V ISA,

q2, t

, t

` o and the last sequent for scenario Sc

p2, eCash, q2, t

, t

` o; then scenarios Sc

and Sc

are the scenarios where the deadlock situations occur.

It is then necessary to apply the synchronization rule

in each of these scenarios to remove the deadlock.

Considering ﬁrst scenario Sc

, the last transition

that was ﬁred before the deadlock situation is transi-

tion t

marked in bold type in the proof tree. In partic-

ular, the last atoms q2 and V ISA of the last sequent of

the proof tree for scenario Sc

are produced when the

transition t

is ﬁred. However, due to the deadlock sit-

uation, these atoms are not consumed at the end of the

proof. Hence, transition t

will correspond to a transi-

tion of type t

of the approach, transition t

to a tran-

sition of type t

, and the atom V ISA to the marked

asynchronous communication place (interface).

The asynchronous communication place VISA,

present in the last sequent of the proof tree of scenario

, is an output place of transition t

(last transition

ﬁred in the proof tree). This communication place is

the input place of transition t

of module T1. There-

fore, transition t

corresponds, in scenario Sc

, to a

dead transition.

Figure 3 shows the synchronization rule applica-

tion in scenario Sc

of the composed system shown in

Figure 2. The synchronization rule, shown in Figure

3, is not a true transition; it is a transition rule that

synchronizes part of the communication structure be-

tween the modules C1 and T1. The transformation

of the pure asynchronous communication mechanism

into a partial synchronous mechanism after the appli-

cation of the synchronization rule is presented in Fig-

ure 4. In Figure 4A, the ﬁring of transition t

(transi-

tion of type t

) corresponds only to a necessary con-

dition for the ﬁring of transition t

(transition of type

). Such an asynchronous communication protocol

does not provide a guarantee for the receiving of a

ICEIS 2017 - 19th International Conference on Enterprise Information Systems

320

sent message; in particular, for scenario Sc

, after the

ﬁring of transition t

, a token will remain trapped in

the communication place V ISA.

Figure 3: Applying the synchronization rule in scenario Sc

of the composed system shown in Figure 2.

On the contrary, in Figure 4B, the fact of synchro-

nizing the execution of the ﬁrst activity associated to

transition t

(transition of type t

) on both modules

C1 and T1, corresponds to guaranteeing the execu-

tion of the called activity t

(transition of type t

). In

fact, the ﬁring of a transition of type t

, after the ap-

plication of the synchronization rule, corresponds to

a necessary and sufﬁcient condition for the ﬁring of

the transition of type t

, and at the end of the associ-

ated scenario, no token will remain in any intermedi-

ary communication place.

Figure 4: Before and after the application of the synchro-

nization rule to scenario Sc

After the synchronization rule application, the

deadlock situation is removed and scenario Sc

will

not be able to occur in the composed system. In prac-

tice, scenario Sc

is then removed from potential sce-

narios that exist when considering the composed sys-

tem shown in Figure 2.

According to Figure 4B, transitions t

and t

of the

composed system are modiﬁed after the synchroniza-

tion rule. They are now represented by the following

new formulas of Linear Logic:

= q1 ⊗ p2 ( V ISA ⊗ q2, t

= V ISA ( p3.

Transitions t

and t

do not appear in the Linear

Logic sequents of scenario Sc

and Sc

, and the alter-

ation of the model does not modify the proof trees of

the corresponding scenarios. On the other hand, both

transitions appear in scenario Sc

. Part 1 of the proof

tree for scenario Sc

continues unchanged after the

application of the synchronization rule. Part 2 of the

proof tree needs to be computed again and becomes

then:

q2`q2 p3`p3

q2,p3`q2⊗p3

⊗

o`o

(

V ISA`V ISA q2,p3,q2⊗p3(o`o

(

V ISA,q2,V ISA( p3,t

⊗

q1`q1 p2`p2

q1,p2`q1⊗p2

⊗

V ISA⊗q2,t

(

q0`q0 Ticket`Ticket

q0,Ticket`q0⊗Ticket

⊗

p2,q1,q1⊗p2(V ISA⊗q2,t

(

The last sequent in the proof tree for the new sce-

nario Sc

is o ` o; as a consequence, after the applica-

tion of the synchronization rule, scenario Sc

is still a

deadlock-free scenario.

Since the model has more than one deadlock sce-

nario, it is also necessary to apply the synchronization

rule to scenario Sc

. Considering now scenario Sc

the last transition that was ﬁred before the deadlock

situation is transition t

marked in bold type in the

proof tree. In particular, the last atoms q2 and eCash

of the last sequent of the proof tree for scenario Sc

are produced when the transition t

is ﬁred. How-

ever, due to the deadlock situation, these atoms are

not consumed at the end of the proof tree. Therefore,

transition t

will correspond to a transition of type t

transition t

to a transition of type t

, and atom eCash

to the marked asynchronous communication place.

The asynchronous communication place eCash

present in the last sequent of the proof tree of scenario

is an output place of transition t

(last transition

ﬁred in the proof tree). This communication place is

the input place of transition t

of module T1. Hence,

transition t

corresponds, in scenario Sc

, to the dead

transition.

Figure 5 shows the synchronization rule applica-

tion in scenario Sc

of the composed system as shown

in Figure 2. As mentioned in scenario Sc

, the syn-

chronization rule, shown in Figure 5, is not a true tran-

sition; it is a transition rule that synchronizes part of

the communication structure between the modules C1

and T1. The transformation of the pure asynchronous

communication mechanism into a partial synchronous

mechanism after the application of the synchroniza-

tion rule is presented in Figure 6. In Figure 6A, the

ﬁring of transition t

(transition of type t

) corre-

sponds only to a necessary condition for the ﬁring of

transition t

(transition of type t

). Such an asyn-

A Linear Logic based Synchronization Rule for Deadlock Prevention in Web Service Composition

321

chronous communication protocol is therefore, not a

guarantee for the receiving of a sent message. In par-

ticular, for scenario Sc

, after the ﬁring of transition

, a token will remain trapped in the communication

place eCash.

Figure 5: Applying the synchronization rule to scenario Sc

of the composed system as shown in Figure 2.

On the contrary, in Figure 6B, the fact of synchro-

nizing the execution of the ﬁrst activity associated to

transition t

(transition of type t

) on both modules

C1 and T1, corresponds to guaranteeing the execution

of the called activity t

(transition of type t

Figure 6: Before and after the application of the synchro-

nization rule in scenario Sc

After the synchronization rule application, the

deadlock situation is removed and scenario Sc

will

not be able to occur in the composed system. In prac-

tice, scenario Sc

is then removed from potential sce-

narios that exist when considering the composed sys-

tem as shown in Figure 2.

According to Figure 6B, transitions t

and t

of the

composed system are modiﬁed after the synchroniza-

tion rule. They are now represented by the following

new formulas of Linear Logic:

= q1 ⊗ p1 ( eCash ⊗q2, t

= eCash ( p3.

Transitions t

and t

do not appear in the Linear

Logic sequents of scenario Sc

and the alteration of

the model do not modify the proof tree of the corre-

sponding scenario. On the other hand, both transi-

tions appear in scenario Sc

. Part 1 of the proof tree

for scenario Sc

continue unchanged after the appli-

cation of the synchronization rule. Part 2 of the proof

tree needs to be computed again, and becomes then:

q2`q2 p3`p3

q2,p3`q2⊗p3

⊗

o`o

(

eCash`eCash q2,p3,q2⊗p3(o`o

(

eCash,q2,eCash( p3,t

⊗

q1`q1 p1`p1

q1,p1`q1⊗p1

⊗

eCash⊗q2,t

(

q0`q0 Ticket`Ticket

q0,Ticket`q0⊗Ticket

⊗

p1,q1,q1⊗p1(eCash⊗q2,t

(

The last sequent in the proof tree for the new sce-

nario Sc

is o ` o; then after the application of the

synchronization rule, scenario Sc

is still a deadlock-

freeness scenario.

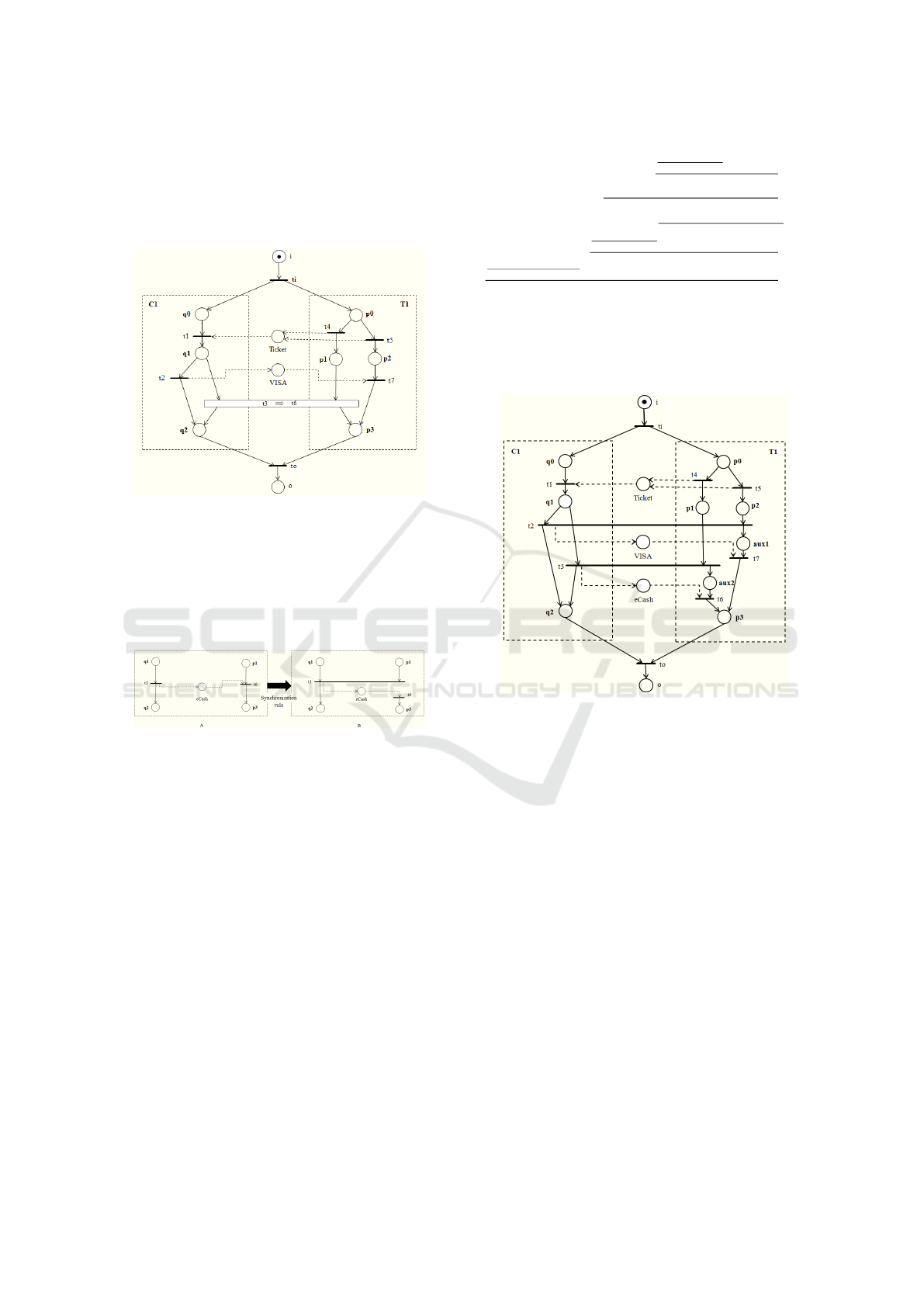
Figure 7: Final model after the application of the synchro-

nization rule.

Figure 7 shows the ﬁnal model after the synchro-

nization rule application in scenario Sc

and Sc

the composed system shown in Figure 2. Note that

additional places aux1 e aux2 were produces in the ﬁ-

nal model in order to respect the workﬂow module

deﬁnition (as a matter of fact, transitions t

and t

need at least one input transition in order to respect

the basic structure of a WF-net). Such places, con-

sidering the Petri net theory (Murata, 1989), are im-

plicit places and do not alter the good properties of

the corresponding model; then the results produced

by the study of Linear Logic proof trees (removal of

the scenarios leading to deadlock situations) will still

be valid. In particular, the deadlock scenarios Sc

and

are removed from the ﬁnal model, with only the

two deadlock-free scenarios remaining, Sc

and Sc

Remembering here that scenarios Sc

and Sc

were

slightly modiﬁed after the synchronization rule appli-

cation.

A great advantage of the Linear Logic based ap-

proach presented in this paper is that when a deadlock

ICEIS 2017 - 19th International Conference on Enterprise Information Systems

322

situation occurs, only the asynchronous part of the

net altered by the synchronous rule needs to be repro-

cessed; the rest of the Linear Logic proof tree will re-

main unaltered. Therefore, the analysis of the model

only happens on the modiﬁed part of the model.

4 CONCLUSIONS

This paper presented an approach to prevent dead-

lock situations in WS compositions modeled by Petri

nets. In WS Composition where the workﬂow mod-

ules are deadlock-free, deadlock problems can occur

at the level of a composed system (collaboration be-

tween at least two workﬂow modules). Generally, it

is the interface (communication places between the

workﬂow modules) that provokes the deadlock situa-

tion. The synchronization rule presented in this paper

implements a kind of local scheduling strategy that

guarantees that each time a message is sent, the corre-

sponding answer of the local workﬂow module will,

in fact, occur.

The advantages of such an approach are diverse.

The proposed method is based on the construction and

analysis of proof trees of Linear Logic that represent

scenarios of a composed system. As was shown in

(Passos and Julia, 2009), the time complexity to prove

a Linear Logic sequent that corresponds to a scenario

of a workﬂow process is linear. The fact of working

with Linear Logic permits the identiﬁcation of com-

munication places (interface) responsible for the oc-

currence of deadlock situations. Furthermore, work-

ing with Linear Logic, it is possible to reuse unaltered

fragments of a proof tree produced before the appli-

cation of the synchronization rule i.e. the analysis of

the model is only executed on the part of the model

responsible for the deadlock.

As a future work proposal, it will be interesting to

propose a kind of quantitative analysis based on sym-

bolic dates, considering in this manner the proof trees

of Linear Logic with dates, as presented in (Riviere

et al., 2001). Such an analysis will be able to evaluate

the effect of the synchronization rule on the perfor-

mance of the system.

ACKNOWLEDGEMENTS

The authors would like to thank FAPEMIG, FAPERJ,

CNPq and CAPES for ﬁnancial support.

REFERENCES

Barros, A., Dumas, M., and Oaks, P. (2005). Standards

for Web Service Choreography and Orchestration:

Status and Perspectives. In International Confer-

ence on Business Process Management, pages 61–74.

Springer.

Girard, J.-Y. (1987). Linear logic. Theoretical computer

science, 50(1):1–101.

Girault, F., Pradier-Chezalviel, B., and Valette, R. (1997).

A logic for Petri nets. Journal europ

een des syst

emes

automatis

es, 31(3):525–542.

Klai, K., Ochi, H., and Tata, S. (2013). Formal abstraction

and compatibility checking of Web services. In Web

Services (ICWS), 2013 IEEE 20th International Con-

ference on, pages 163–170. IEEE.

Martens, A. (2005). Analyzing Web Service Based Busi-

ness Processes. In International Conference on Fun-

damental Approaches to Software Engineering, pages

19–33. Springer.

Murata, T. (1989). Petri nets: Properties, Analysis and Ap-

plications. Proceedings of the IEEE, 77(4):541–580.

Passos, L. M. S. and Julia, S. (2009). Qualitative Analy-

sis of WorkFlow nets using Linear Logic: Soundness

Veriﬁcation. In Systems, Man and Cybernetics, 2009.

SMC 2009. IEEE International Conference on, pages

2843–2847. IEEE.

Passos, L. M. S. and Julia, S. (2013). Qualitative Analy-

sis of Interorganizational WorkFlow nets using Linear

Logic: Soundness Veriﬁcation. In 2013 IEEE 25th

International Conference on Tools with Artiﬁcial In-

telligence, pages 667–673. IEEE.

Passos, L. M. S. and Julia, S. (2015). Deadlock-Freeness

Scenarios Detection in Web Service Composition.

In Information Technology-New Generations (ITNG),

2015 12th International Conference on, pages 780–

783. IEEE.

Riviere, N., Pradin-Chezalviel, B., and Valette, R. (2001).

Reachability and temporal conﬂicts in t-time Petri

nets. In Petri Nets and Performance Models, 2001.

Proceedings. 9th International Workshop on, pages

229–238. IEEE.

van der Aalst, W. M. P. (1998). Modeling and Analyzing

Interorganizational Workﬂows. In International Con-

ference on Application of Concurrency to System De-

sign, pages 262–272.

van der Aalst, W. M. P., van Hee, K. M., ter Hofstede, A.

H. M., Sidorova, N., Verbeek, H. M. W., Voorhoeve,

M., and Wynn, M. T. (2011). Soundness of workﬂow

nets: classiﬁcation, decidability, and analysis. Formal

Aspects of Computing, 23(3):333–363.

Xiong, P., Fan, Y., and Zhou, M. (2010). A Petri Net

Approach to Analysis and Composition of Web Ser-

vices. IEEE Transactions on Systems, Man, and

Cybernetics-Part A: Systems and Humans, 40(2):376–

387.

A Linear Logic based Synchronization Rule for Deadlock Prevention in Web Service Composition

323