Optimizing Energy Consumption of Hot Water System in Buildings with
Solar Thermal Systems
Wen-Tai Li, Kannan Thirugnanam, Wayes Tushar, Chau Yuen and Kristin L. Wood
Singapore University of Technology and Design (SUTD), 8 Somapah Road, Singapore 487372, Singapore
Keywords:
Solar Thermal, Optimal Scheduling, Online Algorithm, Hot Water Storage, Optimization.
Abstract:
This paper investigates the operation of a solar thermal system in a building, and seeks to craft a solution
that would reduce the cost of electricity to the building manager, while concurrently ensuring that the water
demand and the temperature of water are conform to the requirement of the building occupants. In particular,
two energy management mechanisms are studies for controlling the multiple heat pumps that are connected
to the solar thermal system for providing the system with heat when there is not enough solar energy. In this
context, two control strategies are proposed, on-demanding control (ODC) and optimal day-ahead scheduling
(ODS) with different degrees of information such as the water demand, weather, and so on. Moreover, three
different types of scenarios are considered based on solar energy generation pattern and hot water demand of a
commercial facility, and optimal number and operation schedules of heat pumps are identified for each of the
scenario. It is shown that the ODS approach is more effective in saving energy and related costs in comparison
with the systems ODC approach if the information of the weather conditions and hot demands are available
for next 24 hours, and the performance improvement is corroborated numerically.
1 INTRODUCTION
Buildings account for around 40% of the worldwide
energy usage (Kolokotsa, 2016), and therefore, the
building sector has become the focus of many go-
vernmental and institutional energy reduction initia-
tives and research to achieve more sustainable and
energy efficient buildings (Azar and Menassa, 2012).
In this context and due to the fact that solar energy
is one of the most encouraging ecological solution
to combat catastrophic climate change. Solar energy
can be captured and transferred to electricity power
though photovoltaic (PV) panel, and therefore photo-
voltaic panels have been widely installed in buildings
such as commercial buildings and EV charging sta-
tions for energy management schemes (Tushar et al.,
2015; Tushar et al., 2016a; Tushar et al., 2016a; Tus-
har et al., 2016b). Alternative use of solar energy
sources such as solar thermal has also been very popu-
lar to use in both commercial and residential buildings
for the past few years (Buker and Riffat, 2015). The
studies on solar thermal technology and its related ap-
plication for building can be divided in two general
categories. The first category mainly studies the de-
sign and optimization of solar thermal collectors with
a view to increase their efficiency. For instance, in
(Chauhan et al., 2016), the authors present the effect
of flow and geometric parameters in the performance
of solar thermal collector provided with impinging
air jets. Based on multiple life cycle impact asses-
sment methodologies, a comprehensive evaluation of
the environmental profile of a building-integrated so-
lar thermal collector is conducted in (Lamnatou et al.,
2015). A comparative study on the suitability of diffe-
rent type of solar thermal collectors for use in a com-
bined heat and power system at the UK market is de-
monstrated in (Freeman et al., 2015). Other studies in
this category also include (Visa et al., 2015; Tanaka,
2015).
On the other hand, the second category of stu-
dies deal with different aspects of control strategies
of solar thermal assisted power generation units. For
instance, an energy scheduling problem for a house-
hold equipped with a solar assisted heating, ventila-
tion, and air conditioning, and water heating system is
studied in (Nguyen et al., 2015) to minimize the elec-
tricity cost while maintaining user’s thermal comfort
requirements. In (Li et al., 2015), the authors develop
a dynamic model to maximize the solar energy har-
ness ability of a variable speed dish stirling solar ther-
mal system. The dynamics of solar thermal plants-the
first model covering all processes between market de-
266
Li, W-T., Thirugnanam, K., Tushar, W., Yuen, C. and Wood, K.
Optimizing Energy Consumption of Hot Water System in Buildings with Solar Thermal Systems.
DOI: 10.5220/0006309402660273
In Proceedings of the 6th International Conference on Smart Cities and Green ICT Systems (SMARTGREENS 2017), pages 266-273
ISBN: 978-989-758-241-7
Copyright © 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

mand through power output at millisecond resolution-
for the purpose of control design is modelled in (Luo
et al., 2016), and the authors in (Cirocco et al., 2015)
demonstrate the use of linear programming and Pon-
tryagin’s principle to determine how storage should
be operated in a solar thermal power plant to maxi-
mise the revenue.
As such, most of these existing studies have put
moderate (or, very low) focus on the scheduling as-
pect of the solar thermal system. Although efficient
solar thermal collector can considerably improve the
generation of solar energy, the efficient use of these
energy within the building necessitates the practice
of effective energy scheduling process. Hence, such
scheduling is particularly requires for solar thermal
systems with heat pumps (for heating the water when
solar energy is not enough).
This is due to the fact that the heat pumps are ge-
nerally driven by the electricity from the main grid.
Hence, if the fossil fuel driven heat pumps are run
inefficiently to heat the water, the impact on the en-
vironment will be detrimental, and thus against the
main purpose of using solar thermal system. In this
context, there are needs for effective scheduling me-
chanism of heat pumps to heat the water within a solar
thermal system such that, on the one hand, the water
and heat demand of the building is fulfilled. On the
other hand, the use of electricity for running the heat
pumps is minimized. As such, this paper has made
the following contributions to address this issue.
• We consider a real solar thermal system, which is
currently being operated within a commercial fa-
cility in Singapore. Then based on the real data
of the specification of the system, heat water de-
mand of the facility, and weather, we model the
system, and show that significant energy savings
is possible by scheduling the heat pumps without
compromising the water and heat demand of the
occupants.
• To do so, we propose two scheduling strategies
based on on-demanding control (ODC) and opti-
mal day-ahead scheduling (ODS). We show that
although the system can effectively be controlled
based on ODC scheme, the ODS performs better
in terms of increasing energy efficiency and redu-
cing cost if the future information on the weat-
her condition and customers hot water demand is
available prior 24 hours.
To this end, now we describe the considered sy-
stem for this study and the related problem formula-
tion in the subsequent sections.
S
Heat&water&storage
Heat&water&consumer
Heat&pumps
Scheduler
Flat&plate&solar&
thermal&collector
Evacuated&tube&solar&
thermal&collector
Main&water
Supply
Figure 1: Demonstration of the solar thermal system consi-
dered in this work.
2 SYSTEM MODEL
Consider a solar thermal system of a building, as
shown in Figure 1, that consists of a hot water storage,
Z heat pumps, K circulator pumps, and both flat-plate
and evacuated tube solar thermal collector (STC) ar-
rays. The sets of heat pumps and circulator pumps
are Z and K respectively. The hot water storage is
connected to the main water supply of the public uti-
lity board (PUB), and is responsible for supplying hot
water to each unit n ∈ N of the building, where N is
the set of all units within the building. The hot water
storage mainly uses the heat extracted by circulating
water through the STCs via circulator pumps. Then
the extracted heat is transferred to the water inside the
hot water storage through heat exchangers. However,
if the heat from the STCs is not enough to heat the
water to the desired temperature, the deficient heat is
supplied by the connected heat pumps of the system.
In this context, let us assume that at any time slot
h ∈ {1,2,...,H} of a day, where H is the total number
of time slots, the heat water demand of each unit n ∈
N is W
n,h
with a required temperature T
n,h
. Hence,
the necessary thermal energy q
n,h
to heat the water
from PUB supply to the desired temperature is
q
n,h
= σW
n,h
(T
n,h
− T
pub,h
), (1)
where σ is the specific heat of water, and T
pub,h
is the
temperature of the water from PUB. Therefore, the
total amount of required heat energy to meet the de-
mand of all units within the building can be expressed
as
Q
d
h
=
N
∑
n=1
q
n,h
. (2)
Now, if the power of the solar irradiance is I
h
W/m
2
at h and the panel area of the flat-plate and evacuated
tube STC array are A
f
and A
e
respectively, the total
effective power generation from the two STCs is
Q
θ
h
= I
h
A
f
η
f
M
f
+ I
h
A
e
η
e
M
e
. (3)
Optimizing Energy Consumption of Hot Water System in Buildings with Solar Thermal Systems
267

In (3), η
f
and η
e
are the thermal efficiency
1
of the
flat-plate and evacuated tube STCs respectively, M
f
and M
e
are the respective number of flat-plat and eva-
cuated plat solar thermal panels. Now, depending on
the total heat Q
θ
h
produced by the solar thermal system
and the total heat demand of the building, the number
of circulator pumps K
on,h
≤ K that needs to be turned
on is determined.
For simplification, we assume that each circulator
pump k ∈ K , while circulates water at its maximum
capacity, can extract Q
cp
h
= Q
θ
h
/K heat from the STCs,
which it transfers to the water within the hot water
storage. Therefore, if the building manager want to
extract the amount of heat energy Q
w
h
, (Q
w
h
≤ Q
θ
h
, ∀h),
form STCs at each time slot h, the total number of
circulator pumps K
on,h
that needs to be in operation at
each time slot h can be calculated as
K
on,h
=

Q
w
h
Q
cp
h

, (4)
which can be translated to a total electricity consump-
tion of circulator pumps as
E
cp
total,h
= E
cp
k
× K
on,h
. (5)
Here, E
cp
k
is the power that each circulator pump k ∈
K consumes when it runs at its rated capacity, and d·e
refers to the next closest integer operation.
Indeed, if the total demand of heat water is hig-
her than the amount that can be produced with Q
θ
h
,
the excess amount of heat Q
d
h
− Q
θ
h
needs to be sup-
plemented by the heat pumps connected to the solar
thermal system. For this case, we assume that all the
heat pumps in Z have only on and off control and
equal heating capacity, and are run at their maximum
heating capacity Q
hp
z
while they are turned on. In this
regard, the number of heat pumps that needs to be tur-
ned on to produce the deficient heat energy at h can be
expressed as
Z
on,h
=
&
Q
d
h
− Q
θ
h
Q
hp
z
'
. (6)
Now, if the rated electricity consumption by each
pump z is E
hp
z
Watt-hour, the total electricity con-
sumption by the heat circulator pump at h is
E
hp
total,h
= E
hp
z
× Z
on,h
. (7)
Accordingly, the total cost J
Total
of total electricity
consumed by the heat pumps and the circulator pumps
for the whole day (i.e., H time slots) is
J
Total
=
H
∑
h=1

E
hp
total,h
+ E
cp
total,h

C
h
, (8)
1
That is how much heat energy is produced per unit of
incidence I
h
on the surface.
where C
h
is the price per unit of electricity from the
grid at h.
Based on (6), (7), and (8), the total amount of
electricity consumed by the heat pumps contingent
on three factors including 1) the generation of solar
heat by the STCs, 2) the amount of heat water de-
mand by each unit of the building, and 3) the num-
ber of pumps running in each time slot h to meet the
excess demand. In particular, we study the optimal
control strategies of the heat pumps that can be dri-
ven by suitably controlling the on-off time of the heat
and circulator pumps so that minimum number of heat
and circulator pumps are in operation at any time slot
h, and thus reduce the overall consumption of elec-
tricity. Such control strategy will explain in the next
section.
3 CONTROL STRATEGIES OF
HEAT PUMPS
The objective of this work is to devise strategies, in
which the building manager would be able to pur-
sue its own economic objective of reducing total cost
J
Total
of electricity usage, while maintaining all the
relevant system constraints to meet the hot water de-
mand of the consumers within the building. In this
context, we propose two different approaches to cont-
rol the operation of heat pumps within the considered
system:
1. On-demanding control (ODC) approach, which
does not require any future information of the we-
ather condition and water demand. Thus, this con-
trol approach is practical and implementable in
real time.
2. Optimal day-ahead scheduling (ODS) approach
with the assumption that the future 24-hours infor-
mation of weather and water demands are known.
The solution of this approach can be used as a lo-
wer bound for the cost of the considered system.
3.1 ODC Approach
ODC approach aims to estimate the optimal num-
ber of heat pumps and circulator pumps that needs to
be turned on with minimal electricity consumption at
each time slot h so as to reduce total electricity cost
J
Total
. The functional flowchart of ODC approach is
shown in Figure 2.
First, the ODC approach estimates the hot wa-
ter demand W
n,h
of each unit and the power of so-
lar irradiance I
h
at time slot h. Then it calculates the
heat energy Q
d
h
necessary to heat the water from PUB
SMARTGREENS 2017 - 6th International Conference on Smart Cities and Green ICT Systems
268

stop
M
f
;M
e
;´
f
;´
e
;A
f
;A
e
;¾;H
Intialize:
1. Calculate the required heat energy by Eq.(1)-(2)
2. Estimate the supplied heat energy from STCs by Eq.(3)
Yes
No
No
Yes
h = h +1
start
Calculate total cost by Eq.(5),(7),(8)
1. Control HPs and CPs to be turned on.
2. Record
Estimate and load the real time information:
W
n;h
;I
h
;T
n;h
;T
pub;h
;C
h
;Q
hp
z
1. Calculate the excess solar energy
2. Estimate the no. of CPs required to
be turned on by Eq.(4)
3. Let
1. Let
2. Estimate the no. of HPs required
to be turned on by Eq.(5)
Figure 2: Demonstration of the functional flowchart of
ODC approach.
(with the initial temperature T
pub,h
) to the desired tem-
perature T
n,h
and the heat energy Q
θ
h
it can extract
from the STCs. The ODC prefer to meet the requi-
red heat energy Q
d
h
by the solar energy Q
θ
h
as much
as possible because the electricity consumption of ci-
rculator pumps is generally smaller than that of heat
pumps. Therefore, if Q
d
h
≤ Q
θ
h
, no further heat energy
is required from the heat pump (i.e., Z
on,h
= 0). Ho-
wever, the excess solar power Q
θ
exc,h
, if there is any,
will be wasted because ODC purposes to minimize
the total electricity consumption at each time slot h .
On the other hand, the heat pumps will be turned
on if Q
d
h
> Q
θ
h
, and the number of the required heat
pumps Z
on,h
will be estimated via (6). Finally, the ra-
ted electricity consumption E
cp
total,h
and E
hp
total,h
at each
time slot h can be calculated as well as the cost J
total
.
This simple real-time algorithm provides a simple so-
lution, and serves as an upper bound on the worst case
performance of a system.
3.2 ODS Approach
Although ODC can rapidly respond via controlling
the heat pumps to meet the hot water demand in real
time, it cannot effectively exploit the property of hot
water storage such as a buffer thermal storage. Spe-
cifically, for ODC approach, the hot water storage is
just considered a medium that facilitates to transfer
heat from STCs and heat pumps to demand side. It
is due to that fact that ODC approach lacks the fu-
ture information such as the weather condition and
hot water demand. Indeed, if we can exactly forecast
future information of the weather condition and water
demand, we can efficiently schedule the operations of
heat pumps and circulator pumps of STCs. In that
case, for instance, the building manager can have the
flexibility to turn on more heat pumps to produce ex-
cess heat to store into hot water storage beforehand
in order to meet the coming peak demand. Also, the
building manager can turn on more circulator pumps
to store the excess solar energy considered by ODC
into hot water storage so as to supply toward hot wa-
ter demand.
In this context, we briefly explain some key con-
straints and assumptions that are needed to be satis-
fied with the characteristics of hot water storage as
follows:
• At any time slot h,
¯
T
tank,h
needs to be at least more
than a lower temperature threshold
¯
T
tank,h
≥ T
min
. (9)
This constraint is necessary to establish the fact
that the requirement of energy to heat the water to
a desired level would never be significantly high.
• Similarly, at any time slot h,
¯
T
tank,h
always needs
to be lower than a maximum temperature thres-
hold
¯
T
tank,h
≤ T
max
, (10)
based on the type of the design and material of the
hot water storage tank. Otherwise, it would com-
promise the lifetime and operational efficiency of
the storage.
• At any time slot h, the average temperature of the
storage tank is influenced by
– Coefficient of heat loss G of the storage.
– Volume capacity V of the hot water storage.
– Average temperature of the tank in previous
time slot h − 1, i.e.,
¯
T
tank,h−1
.
– The hot water demand W
n,h
of each unit n ∈
N ∀n at h.
– The temperature difference ∆T
n,h
between T
n,h
and T
pub,h
, i.e., ∆T
n,h
= T
n,h
− T
pub,h
.
– Heat energy Q
cp
h
extracted by each circulator
pump k ∈ K from STCs at h.
– Heat energy Q
hp
z,h
generated by each heat pump
z ∈ Z at h.
As such, the average temperature
¯
T
tank,h
of the hot
water storage is determined via following relati-
Optimizing Energy Consumption of Hot Water System in Buildings with Solar Thermal Systems
269

onship:
¯
T
tank,h
= (1 − G)
¯
T
tank,h−1
−
∑
n
W
n,h
∆T
n,h
V
+
s
V σ
∑
z
Q
hp
z
u
z,h
+
∑
k
Q
cp
h
v
k,h
!
,
h = 1,2,... , H. (11)
where u
z,h
,v
k,h
∈ {0, 1} are boolean variables that
refer to the on/off status of each heat pump z ∈ Z
and circulator pump k ∈ K respectively at h. In
addition, s is the duration of time slot.
Since the control of both type of pumps is only possi-
ble through on/off control, searching for the optimal
choice of tuples (u
z,h
,v
k,h
) from set {0, 1} ∀h is the
ultimate target of this study. In this context, the ob-
jective of optimal day-ahead scheduling (ODS) pro-
blem can be expressed as
min
u
z,h
,v
k,h
∑
h
C
h
∑
z
u
z,h
E
hp
z
+
∑
k
v
k,h
E
cp
k
!
, (12)
Note that (12) is a modified version of (8) with the
explicit mention of possible on/off switching opera-
tion of each pump at h. Nonetheless, while minimi-
zing J
Total
as explained in (12), the building manager
also needs to meet the system constraints (9)–(11) for
the effective operation of hot water storage. As such,
ODS (12) is formulated as an integer programming
problem, and we employ built-in tool of MATLAB to
solve this problem.
4 CASE STUDY
In this section, the simulation results of the proposed
approaches are presented. To do so, we consider a
commercial facility in Singapore, which has a real so-
lar thermal system. We captured the historical data
of hot water demand used in this facility, and some
specifications of the solar thermal system. The initial
specifications and parameters setting are detailed in
Table 1.
4.1 Considered Data for Simulation
To demonstrate the effectiveness of the proposed
approaches, we run simulations for three particular
days with different weather conditions including a
rainy day (RD - 26/07/2015), a sunny day (SD -
05/07/2015), and a day with no solar (NS - worst
case). The RD and SD have been chosen based on the
Singapore weather data in the month of July 2015.
Furthermore, we conduct simulations for one month
Table 1: Initial specifications and parameters setting.
Initial temperature of water from PUB T
pub,h
, ∀h 25
◦
C
The required temperature of hot water T
n,h
, ∀n,h 65
◦
C
The maximum temperature of hot water storage T
max
75
◦
C
The minimum temperature of hot water storage T
min
65
◦
C
The heat loss coefficient of the storage during G 0.1%/hr
The number of flat-plate panels M
f
27
The number of evacuated-tube panels M
e
70
The number of circulator pump K 4
The absorber area of flat-plate panels A
f
2.8m
2
The absorber area of evacuated-tube panels A
e
2.8m
2
The thermal efficiency of flat-plate panels η
f
0.5
The thermal efficiency of evacuated-tube panels η
e
0.7
The heating capacity of heat pump Q
hp
z
∀z 40 kW
The electricity consumption of heat pump E
hp
z
∀z 12.85 kWh
The electricity consumption of circulator pump E
cp
k
∀k 1.375 kWh
Electricity price (Singapore dollar (SGD) ) C
h
∀h 0.22 $/kWh
The duration of time slots s 15 mins
The total number of time slots H 96
with the real daily data of solar irradiance and hot wa-
ter demand, and show the energy consumption by the
heat pumps, the number of required heat pumps, the
energy consumption by the circulator pumps, and the
total cost of electricity consumption for whole month
of July 2015. In Figure 3 and Table 2, we show
0 2 4 6 8 10 12 14 16 18 20 22 24
0
200
400
600
800
1000
1200
1400
Time (hrs)
I
h
(W/m
2
) and W
n,h
(lit.)
I
h
at NS I
h
at RD I
h
at SD W
n,h
at NS W
n,h
at RD W
n,h
at SD
Evening peaks from
18:30hrs to 21:30hrs
due to demand in
kitchen
Morning peaks from
6:30hrs to 10:00hrs due
to demand in shower
and kitchen
Figure 3: Illustration of solar irradiance I
h
(W/m
2
) and hot
water demand
∑
n
W
n,h
(lit.) of the building at each time slot
h on a rainy day (RD), sunny day (SD) and on a day with
no solar (NS).
the solar irradiance I
h
and the total amount of hot
water demand (i.e.,
∑
n
W
n,h
) on RD, SD, and NS at
each time slot h (of days with three considered weat-
her conditions) respectively. In Figure 3, the peaks in
the morning from 6:30 hrs to 10:00 hrs are due to sho-
wer and kitchen demand, and the peaks in the evening
from 18:30 hrs to 21:30 hrs due to kitchen demand of
the considered building. As can be seen from the fi-
gure and Table 2, the maximum hot water demand for
NS is 1048 liters, RD is 1128 liters, and SD is 1030
liters. Similarly, the solar irradiance is 455.7 W/m
2
and 770.0 W/m
2
for RD and SD respectively.
In Figure 4, we show the total hot water demand
and solar generation per day for the month of July
2015. The summary of the total and average hot water
demand, and average solar irradiance per day for the
same month is, however, shown in Table 2.
SMARTGREENS 2017 - 6th International Conference on Smart Cities and Green ICT Systems
270

Table 2: Information of the selected days and July 2015.
Description No solar Rainy day Sunny day Description July 2015
Total hot water demand
∑
h,n
W
n,h
(liter) 33046 36364 32692 Total hot water demand (liter) 978,163.0
Maximum hot water demand max
h
∑
n
W
n,h
(liter) 1048 1128 1030 Average daily hot water demand (liter) 31,553.6
Average hot water demand
¯
W
h
(liter) 344.2 378.8 340.5 Average hot water demand at each time slot
¯
W
h
(liter) 328.7
Maximum solar irradiance I
h
(W/m
2
) 0 455.7 770.0 Average daily solar irradiance (kWh/m
2
) 3.39
Average solar irradiance
¯
I
h
(W/m
2
) 0 55.2 209.1 Average solar irradiance at each time slot
¯
I
h
(W/m
2
) 140
12345678910111213141516171819202122232425262728293031
Days
0
1
2
3
4
5
Hot water demand (Liter)
×10
4
0
2
4
6
8
10
Solar irradiance (kWh/m
2
)
Daily solar irradiance Daily hot water demand
Figure 4: Demonstration of hot water demand (liter) and
solar irradiance (kWh) in each day of July 2015.
0 2 4 6 8 10 12 14 16 18 20 22 24
0
1
2
3
4
5
6
7
8
Time (hrs)
Number of HPs required at h
HPs required on NS HPs required on RD HPs required on SD
the required HPs increased due
to demand in kitchen
NS and RD, the HPs are
turned off due to the
required hot water demand
is zero
on SD, all the HPs are
turned off due to solar
energy
the required HPs increased due
to demand in kitchen and
shower
Figure 5: Demonstration of the number of heat pumps (used
as HP in the figure) required on the selected days performed
upon ODC.
4.2 Results for ODC
In Figure 5, ODC is performed to meet the demand of
hot water of the building, it shows the number of heat
pumps to be turned on at each time slot on selected
RD, SD, and NS separately. It is observed that the
maximum two heat pumps are necessary to maintain
the required hot water demand after 21:00 and before
06:00 hours for all the considered weather conditions.
For the remaining hours, however, the number of
the required heat pumps to fulfil the demand of hot
water varies with respect to the solar irradiance and
hot water demand. For instance, on the selected SD,
the heat pumps are turned off for a number of time
slots during the period from 11:00 to 16:00 due to
the abundant solar energy. However, the number of
turned on heat pumps varies from 4:00 to 10:00 in
the morning and from 20:00 to 22:00 in the evening
due to higher demand by the consumers. Similar va-
riation in the number of required heat pumps is also
found for the cases of NS and RD. For example, ac-
cording to Figure 5, a maximum of 6 heat pumps are
necessary to heat the water in the morning peak pe-
riod on NS and RD, whereas the number of required
heat pump is much less for other time slots of the re-
spective days. In Figure 6, we demonstrate the re-
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
300
400
500
600
700
800
E
total,h hp
(kWh)
0
1
2
3
4
5
6
7
8
9
Days
Number of HPs required per day
E
total,h
hp
(kWh)
No. HPs required per day
Figure 6: The daily electricity consumed by HPs and the
maximum no. of HPs required per day in July 2015 upon
ODC.
sults on the total number of required heat pumps and
subsequent energy consumption per day of July 2015
based on the ODC approach. It is observed that the
maximum number of heat pumps that is required to
fulfil the demand of hot water varies from 3 to 8 ba-
sed on the different amount of hot water demand and
the variation of weather conditions.
4.3 Results for ODS
0 2 4 6 8 10 12 14 16 18 20 22 24
Time (hours)
0
1
2
3
4
5
N
umbe
r
o
f H
Ps
(t
u
r
ned on
)
65
70
75
T
empe
r
a
t
u
r
e o
f
ho
t w
a
t
e
r
s
t
o
r
age
(
°
C)
No. on-HPs on NS No. on-HPs on RD No. on-HPs on SD Temp. on NS Temp. on NS Temp. on SD
Evening peck periodMorning peck period
Pre-heating during
pre-peck
all the HPs are turned off and keep
longer time than ODC due to storing the
excess solar energy for toward demand
Figure 7: Number of heat pumps required on the selected
days performed upon ODS.
As mentioned in Section 3.2, we assume that the
weather and demand information are known for the
next 24 hours for the proposed ODS approach. As
such, the ODS is first performed for the selected days
with individual weather conditions and the results are
shown in Figure 7.
Observably, the most four heat pumps are opera-
tional on NS and RD, whereas three heat pumps are
enough to meet the hot water demand on SD. Note
that these required amounts are significantly lower
Optimizing Energy Consumption of Hot Water System in Buildings with Solar Thermal Systems
271

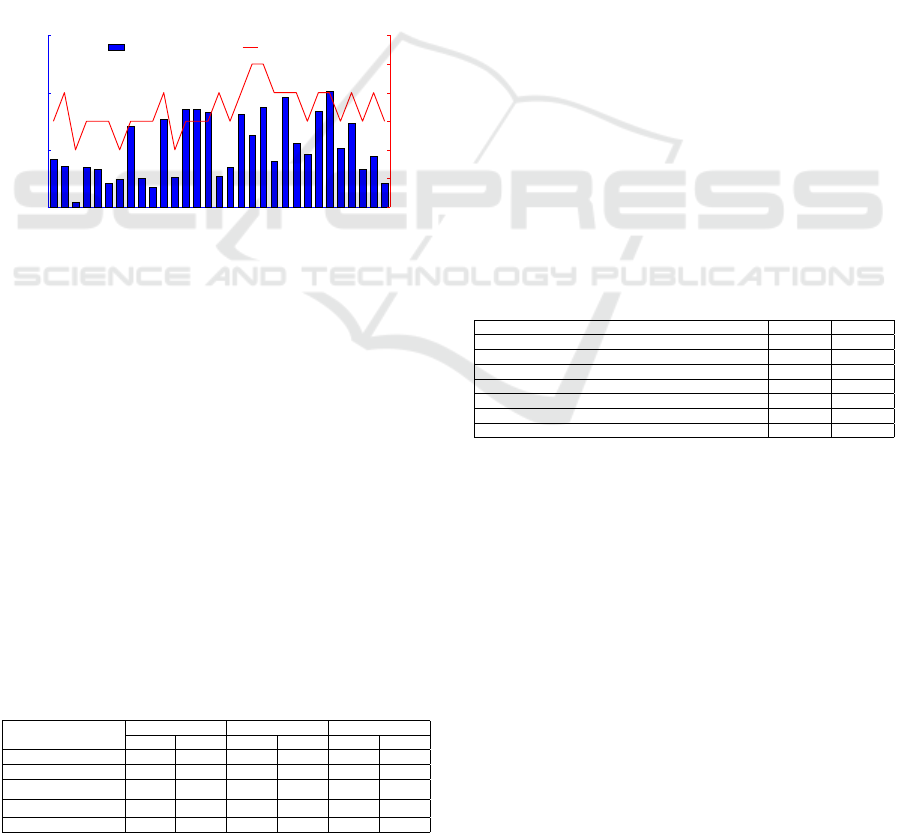
than that in ODC approach as a result of the know-
ledge of future information and the usage of buffer
thermal storage. It can be observed that more heat
pumps starts to be turn on at 5:00, and then the tem-
perature of hot water storage rises up significantly on
SD. This is owing to the awareness of the morning
peak that will be coming soon, and therefore, ODS
approach schedules 2 heat pumps that are early tur-
ned on to produce more heat energy and store in the
hot water storage.
Similar phenomenon is also observed before the
evening peak period. Furthermore, ODS approach
schedules more circulator pumps to be turned on so
as to store more solar energy into hot water storage
from 12:00 to 18:00 on SD. This is the reason why
the total turned off time of all heat pumps is longer
than that in ODC during the period of abundant solar
energy on SD. Also, we study the ODS approach for
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
Days
200
400
600
800
E
l
ec
tri
c
it
y consump
ti
on
(
k
W
h
)
0
1
2
3
4
5
6
N
umbe
r
o
f H
Ps
Daily electricity consumption of HPs Maximum no. of On-HPs
Figure 8: The daily electricity consumed by heat pumps
and the maximum number of heat pumps required per day
in July 2015 using ODS approach.
the whole month of July 2015 to determine the total
energy consumption by the heat and circulator pumps
as well as the overall cost as shown in Figure 8. It
can be observed that 2 to 4 heat pumps are usually
enough for most of the days whereas only two days
need 5 heat pumps to supply demand.
4.4 Summary of ODC and ODS
Now, based on the results of the selected days and
the whole month July 2015 with the both proposed
approaches, we provide an overview of the related
energy parameters for the considered selected days
and month of July 2015. First, we provide a sum-
Table 3: Summary of the proposed approaches on the se-
lected days.
No solar Rainy day Sunny day
ODC ODS ODC ODS ODC ODS
max
h
Z
on,h
6 4 5 4 6 3
Turned on time (hrs) 58.3 48.5 58.0 47.3 40.0 26.0
∑
h
E
hp
total,h
(kWh) 749.2 623.3 745.3 607.8 514.0 334.1
∑
h
E
cp
total,h
(kWh) 0.0 0.0 66.0 67.4 62.6 68.8
J
total
(SGD) 164.8 137.1 178.5 148.5 126.8 88.6
mary of comparison between the ODC and ODS ap-
proaches on different energy parameters for NS, RD,
and SD in Table 3. Table 3 shows the related energy
parameters including total turned on time of the heat
pumps, total energy consumption by the heat pumps,
total energy consumption by the circulator pumps,
and the total electricity cost of energy consumption.
According to this table, the electricity consumption
of heat pumps are 749.2 kWh, 745.3 kWh and 514.0
kWh on NS, RD, and SD respectively for ODC appro-
ach. These values for ODS approach are, however,
623.3 kWh, 607.8 kWh and 334.1 kWh, which are
16.8%, 18.4% and 35% less than the ODC approach
respectively on NS, RD, and SD. Furthermore, the to-
tal cost of the total electricity consumption on NS is
164.8 SGD, RD is 177.9 SGD, and SD is 128.2 SGD
for ODC case and 137.1 SGD, 148.5 SGD, and 88.6
SGD for the same respective day for ODS approach.
Clearly, the prior knowledge of weather condition and
demand makes the overall electricity cost of ODS lo-
wer than the ODC approach.
Noticeably, sunny days are most cost-effective for
the building manager. Interestingly, cost of energy
on the selected rainy day is greater than the day with
no solar. This is mainly due to the higher hot water
demand by the consumers for this particular day (see
Table 2). Nonetheless, for other days of the month, it
can have different values based on the demands of the
consumers.
Table 4: Summary of the proposed approaches for the
month of July 2015.
Parameters ODC ODS
Maximum number of the required heat pumps 8 5
Total turned on time of heat pumps (hrs) 1340.8 982.5
Total electricity consumption of heat pumps (kWh) 16491.2 12625.1
Total excess solar energy (kWh) 1452.46 305.0
Total turned on time of circulator pumps (hrs) 1449.3 1508.4
Total electricity consumption of circulator pumps (kWh) 1992.8 2074.1
Total electricity cost (SGD) 4066.5 3233.8
Then, we provide an overview of the related
energy parameters for the considered month of July
2015 in Table 4. According to Table 4, it is noted that
there is excess solar energy that can not be effectively
exploited by ODS as a results of the limited tempera-
ture of hot water storage. Indeed, we can set the hig-
her temperature bound to store more solar energy, but
that will reduce lift time of hot water storage. Howe-
ver, the amount of excess solar energy by ODS is still
much less than that by ODC. As for the energy con-
sumption of circulator pumps, it can be observed the
electricity consumption of circulator pumps for ODS
is slightly more than ODC because ODS keeps cir-
culator pumps running in order to store more solar
energy, which will be seen as excess by ODC, into
hot water storage. To sum up, the overall electricity
SMARTGREENS 2017 - 6th International Conference on Smart Cities and Green ICT Systems
272

cost of ODS is reduced by 20% of ODC’s in the one
month of July 2015. Furthermore, the number of heat
pumps required by ODS is less than that required by
ODC, which means that the cost of installation and
facilities will be significantly reduced if building ma-
nager adopts ODS approach.
5 CONCLUSION
In this paper, the operation of solar thermal system
within a building has been studied with a view to re-
duce the cost of electricity to the building manager.
Two control strategies including ODC and ODS ap-
proaches have been developed based on real data from
a facility in Singapore. In designing the strategies,
three different kinds of scenarios have been conside-
red, and the necessary number of heat pumps that is
needed to meet the demand of the building is identi-
fied. It has been shown that if the prior knowledge of
the weather condition and are available, ODS techni-
que is more effective compared to the ODC appro-
ach in terms of electricity cost reduction and increa-
sing energy efficiency. However, if such knowledge
is unavailable, ODC technique has been shown to be
still suitable for running the considered real system
and numerical solutions have been provided to sup-
port our claims.
In the future works, we will involve the prediction
methods in order to capture the prior knowledge of the
weather condition and demand, and consider various
possible scenarios such as dynamic pricing and peak
demand shifting.
ACKNOWLEDGEMENTS
This work is supported in part by the project fun-
ded by National Research Foundation (NRF) via the
Green Buildings Innovation Cluster (GBIC), adminis-
tered by Building and Construction Authority (BCA),
and in part by the SUTD-MIT International Design
Centre (IDC; idc.sutd.edu.sg).
REFERENCES
Azar, E. and Menassa, C. C. (2012). A comprehensive ana-
lysis of the impact of occupancy parameters in energy
simulation of office buildings. Energy and Buildings,
55:841–853.
Buker, M. S. and Riffat, S. B. (2015). Building integrated
solar thermal collectors - A review. Renewable and
Sustainable Energy Reviews, 51:327–346.
Chauhan, R., Singh, T., Thakur, N. S., and Patnaik, A.
(2016). Optimization of parameters in solar ther-
mal collector provided with impinging air jets based
upon preference selection index method. Renewable
Energy, 99:118–126.
Cirocco, L. R., Belusko, M., Bruno, F., Boland, J., and Pud-
ney, P. (2015). Controlling stored energy in a concen-
trating solar thermal power plant to maximise revenue.
IET Renewable Power Generation, 9(4):379–388.
Freeman, J., Hellgardt, K., and Markides, C. N. (2015).
An assessment of solar-thermal collector designs for
small-scale combined heating and power applications
in the United Kingdom. Heat Transfer Engineering,
36(14-15):45–58.
Kolokotsa, D. (2016). The role of smart grids in the building
sector. Energy and Buildings, 116:703–708.
Lamnatou, C., Notton, G., Chemisana, D., and Cristofari, C.
(2015). The environmental performance of a building-
integrated solar thermal collector, based on multiple
approaches and life-cycle impact assessment of met-
hodologies. Building and Environment, 87:45–58.
Li, Y., Choi, S. S., Yang, C., and Wei, F. (2015). Design
of variable-speed dish-stirling solar - Thermal power
plant for maximum energy harness. IEEE Transacti-
ons on Energy Conversion, 30(1):394–403.
Luo, Q., Ariyur, K. B., and Mathur, A. K. (2016).
Control-oriented concentrated solar power plant mo-
del. IEEE Transactions on Control Systems Techno-
logy, 24(2):623–635.
Nguyen, H. T., Nguyen, D. T., and Le, L. B. (2015).
Energy management for households with solar assis-
ted thermal load considering renewable energy and
price uncertainty. IEEE Transactions on Smart Grid,
6(1):301–314.
Tanaka, H. (2015). Theoretical analysis of solar thermal
collector and flat plate bottom reflector with a gap be-
tween them. Energy Reports, 1:80–88.
Tushar, W., Chai, B., Yuen, C., Smith, D. B., Wood,
K. L., Yang, Z., and Poor, H. V. (2015). Three-party
energy management with distributed energy resources
in smart grid. IEEE Transactions on Industrial Elec-
tronics, 62(4):2487–2498.
Tushar, W., Yuen, C., Huang, S., Smith, D. B., and Poor,
H. V. (2016a). Cost minimization of charging stations
with photovoltaics: An approach with EV classifica-
tion. IEEE Transactions on Intelligent Transportation
Systems, 17(1):156–169.
Tushar, W., Zhang, J. A., Yuen, C., Smith, D. B., and Has-
san, N. U. (2016b). Management of renewable energy
for a shared facility controller in smart grid. IEEE
Access, 4:4269–4281.
Visa, I., Duta, A., Comsit, M., Moldovan, M., Ciobanu, D.,
Saulescu, R., and Burduhos, B. (2015). Design and
experimental optimization of a novel flat plate solar
thermal collector with trapezoidal shape for facades
integration. Applied Thermal Engineering, 90:432–
443.
Optimizing Energy Consumption of Hot Water System in Buildings with Solar Thermal Systems
273