An Adaptive Data Driven Approach to Single Unit Residential

Air-conditioning Prediction and Forecasting using Regression Trees

Clement Lork

, Yuren Zhou

, Rajasekhar Batchu

, Chau Yuen

and Naran M. Pindoriya

Engineering Product Development, Singapore University of Technology and Design, 8 Somapah Road, Singapore

Department of Electrical Engineering, Indian Institute of Technology Gandhinagar, Gujarat, India

Keywords:

Residential AC Modelling, Data Driven, Forecasting, Regression Trees, Feature Selection, Machine Learning.

Abstract:

Residential Air Conditioning (AC) load has a huge role to play in Demand Response (DR) Programs as it is

one of the power intensive and interruptible load in a home. Due to the variety of ACs types and the different

sizes of residences, modelling the power consumption of AC load individually is non-trivial. Here, an adaptive

framework based on Regression Trees is proposed to model and forecast the power consumption of different

AC units in different environments by taking in just 6 basic variables. The framework consists of an automatic

feature selection process, a load prediction module, an indoor temperature forecasting module, and is capped

off by a load forecasting module. The effectiveness of the proposed approach is evaluated using data set from

an ongoing research project on air-conditioning system control for energy management in a residential test

bed in Singapore. Experiments on highly dynamic loads gave a maximum Mean Absolute Percentage Error

(MAPE) of 21.35% for 30min ahead forecasting and 27.96% for day ahead forecasting.

1 INTRODUCTION

1.1 Motivation

The electricity grid today faces a challenge in match-

ing supply and demand, as stochasticity within the

grid continues to climb. The nature of generation has

became much more unpredictable with the integra-

tion of highly variable renewables like solar and wind

power. On the demand side, the increase in human

population density and the adoption of electric vehi-

cles introduce much variances in electricity consump-

tion. Aside from using battery storage technology,

Demand Response (DR) programs could also help in

maintaining efﬁcient production and consumption of

electricity (Chan et al., 2012). These programs in-

volve changing the price of electricity, or requesting

for direct control in exchange for a fee, in order to

incentivize consumers to change their electricity con-

sumption habits. Within different energy consuming

sectors in the US, households take up to 37% of the

total electricity consumption (Yin et al., 2016). Vari-

ous household appliances have been targeted by DR

programs to balance the supply and demand in the

electricity market (Ding et al., 2014). Out of these

appliances, thermostatic loads like the Air Condition-

ing (AC) are most appropriate as they could be turned

off for short period of time without causing much dis-

comfort or inconvenience to the consumer. Besides

being ubiquitous in modern housing, AC constitutes

up to 45% of a customer’s electricity demand (Kalkan

et al., 2012). Due to its high demand response poten-

tial, any AC control mechanism that helps the cus-

tomer to save electricity beneﬁts both customers and

the utility. (Li et al., 2017) showed that just by carry-

ing out a model-free, pulse-width-modulation control

on a user’s AC power status, up to 33% of energy used

by the AC could be saved. However, in order to pro-

duce optimal AC control algorithms, the effects of a

control strategy will have to be quantiﬁed and tested

in advance via an effective model. Hence, accurate

modelling of AC units for load prediction and room

thermal states forecasting is critical for successful im-

plementation of DR in AC systems.

AC units can be roughly divided into two types:

hysteresis controlled (or on-off controlled) and in-

verter controlled. Inverter type AC units can vary their

compressor fan speed with regards to set point and in-

door temperature, as compared to the full power/no

power state of the hysteresis controlled ACs. This al-

lows inverter ACs to achieve more precise cooling of

the room as compared to hysteresis controlled ACs,

reducing energy consumption. Due to a much lower

Lork, C., Zhou, Y., Batchu, R., Yuen, C. and Pindoriya, N.

An Adaptive Data Driven Approach to Single Unit Residential Air-conditioning Prediction and Forecasting using Regression Trees.

DOI: 10.5220/0006309500670076

In Proceedings of the 6th International Conference on Smart Cities and Green ICT Systems (SMARTGREENS 2017), pages 67-76

ISBN: 978-989-758-241-7

energy consumption, inverter type AC units gradually

replaced the hysteresis controlled units and became

the dominant type in the market (Shao et al., 2004).

However, accurate modelling of an inverter type AC

unit is difﬁcult because of its complex working prin-

ciple and control mechanism. In current literature,

such an effective and efﬁcient method to model in-

verter type AC unit is still missing, and this paper is

aimed at ﬁlling this gap.

1.2 Related Works

Modelling of an AC unit often comes together with

modelling the room it is cooling, because one wants to

predict the power consumption and forecast the room

temperature for a long period. Thus the two are com-

bined as modelling an AC system in the following

context.

There are generally three distinctive approaches to

modelling AC systems: white-box modelling, grey-

box modelling and black-box modelling. Each of

them attempts to model AC load (power consump-

tion) and future room temperature as functions of sev-

eral variables, such as present room temperature, de-

sired room temperature, etc.

White-box modelling is based on physical prin-

ciples and derives the models based on the thermo-

dynamic properties of the AC unit and the room. A

number of studies simpliﬁed the complex thermody-

namic equations into an equivalent thermal parame-

ters model for simulation and forecasting of AC load

(Lu, 2012; Yin et al., 2016). However, the thermody-

namic properties of a room depend largely on human

occupancy, behaviour and furniture placement, which

are difﬁcult to observe in real life, resulting in inaccu-

racies.

Grey-box modelling adopts the physics equations

obtained from white-box modelling and applies data

driven approaches to estimate the equation param-

eters. An instance of a grey box model utilizes a

Resistive-Capacitance thermal model with model pa-

rameters found by genetic algorithm (Li et al., 2010).

Another instance learns the parameters affecting the

temperature change of a room using linear regres-

sion (Jain et al., 2016). Grey-box modelling generally

outperforms the white-box modelling because it uses

real data to tune the model parameters (Afram and

Janabi-Shariﬁ, 2015b). However, developing a grey-

box model requires lots of work and getting the data

types required by the physics functions is challenging

and expensive.

Black-box modelling uses purely statistical or ma-

chine learning methods to ﬁt a function of AC load or

room temperature of different features on historical

data. Contrary to grey-box modelling, model features

in black box modelling are not bounded by physics

equations, and could be chosen depending on the

available sensors in the environment. Examples in-

clude a stochastic tobit model (Horowitz et al., 2014)

and a machine learning Support Vector Regression

model for AC load (Xuan et al., 2015). (Afram and

Janabi-Shariﬁ, 2015a) compares the performance of

grey-box modelling and black-box modelling in mod-

elling different parts of a residential heating, ventila-

tion and air conditioning (HVAC) system. (Lork et al.,

2017) combines Artiﬁcial Neural Networks, Support

Vector Machines and Ensemble Trees for forecasting

of aggregated residential AC loads. The results show

that well designed black-box modelling yields better

accuracy than grey-box modelling. Although black-

box modelling is more promising in accuracy and

does not require physics equations, a good black-box

model requires careful selection of machine learning

models and features through multiple validation steps.

1.3 Contributions

To develop AC system models for Demand Response

purpose, it is important that the models can be scaled

up easily. Therefore a balance between the model

complexity and accuracy is critical. Hence, white-box

modelling is not suitable because of its lower accu-

racy compared with the other two and tedious work in

obtaining physics properties of different AC units and

rooms.

Among most of the works of grey-box modelling

and black-box modelling, many types of sensors are

used and some of them are usually not available in

normal households, making it difﬁcult to apply such

models in different houses (Tang et al., 2014; Afram

and Janabi-Shariﬁ, 2015a). (Qin et al., 2015; Jain

et al., 2016) make efforts to model AC systems while

using only a few common data types, such as indoor

temperature and outdoor temperature. Nevertheless,

the AC units they modelled are hysteresis controlled

units other than inverter type ones.

As a result, there is a need for data-driven mod-

elling methods for inverter type AC units, which

adopts only common sensors, reports a satisfactory

accuracy, and can be easily scaled up to a large group

of AC systems.

Here we set out to ﬁll this gap in literature by:

• Generating a list of features from collected data

types which represent the AC unit behaviour and

room thermal dynamics better;

• Designing an automatic feature selection algo-

rithm to select the best ones among the feature

SMARTGREENS 2017 - 6th International Conference on Smart Cities and Green ICT Systems

list for modelling AC unit power consumption and

room temperature respectively;

• Training two sets of regression trees to model AC

unit power consumption and room temperature re-

spectively;

• Combining the two trained models to forecast the

power consumption and room temperature.

Because our modelling approach only requires ba-

sic data types, namely indoor temperature, outdoor

weather data, and AC control inputs, it is applicable

in many different applications without the need of so-

phisticated or expensive infrastructure. It can be used

to guide users’ AC usage behaviour by forecasting the

potential power consumption given desired tempera-

ture and operation duration. In optimal control of in-

dividual AC units or Demand Response control of a

group of AC units, it can be used as the system model,

providing good forecasting ability to the control algo-

rithm, such as Model Predictive Control.

The remainder of the paper will be organized

in the following structure: Section 2 describes the

framework that was used, Section 3 recounts an ap-

plication on real world data. Finally, Section 4 wraps

up with conclusions and future scope.

2 FRAMEWORK

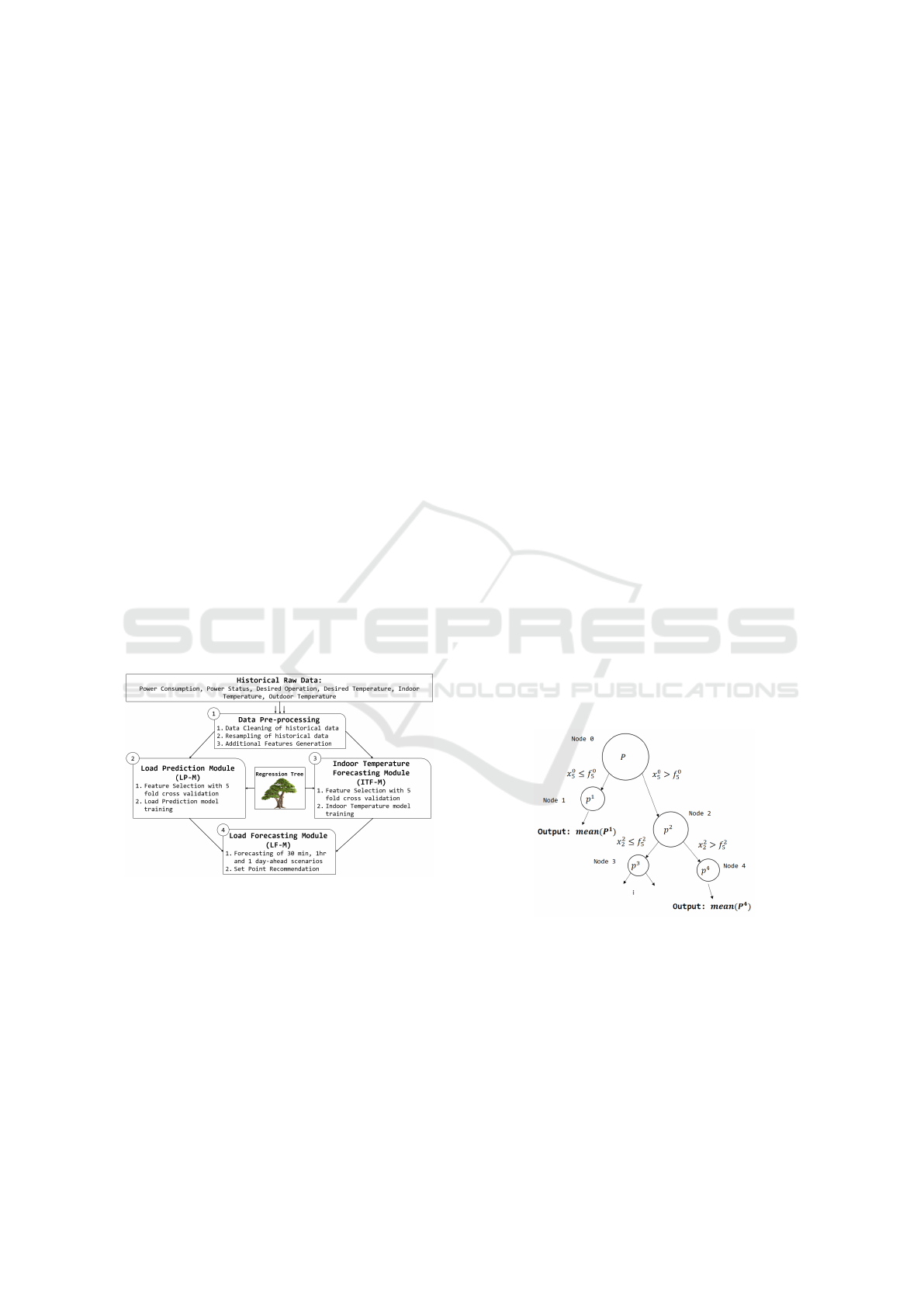
Figure 1: Framework for AC Load Modelling.

In this framework, we will have 4 separate modules

as seen in Fig. 1. This framework is self-adaptive

as it allows us to perform the same analysis on any

random AC unit in a different environment automat-

ically, to generate their own speciﬁc models. After

ofﬂine training with historical data based on regres-

sion trees, the load forecasting module could be used

for online forecasting and recommendation systems

or online optimal controllers.

2.1 Regression Tree

Regression tree modelling is a standard machine

learning technique that is growing increasingly pop-

ular in recent years. The surge in popularity could be

attributed to its speed, interpretability and robustness

towards outliers (Behl et al., 2016). If a regression

tree is used to ﬁt a set of power consumption values P

and variables X ⊃ (x

, ...x

), the regression tree will

recursively attempt to grow binary decision nodes in

order to segment P into smaller partitions such that

P ⊃ (p

, ... p

). At each node i when the algorithm

is deciding how to split P, various variables x

...x

and threshold f

will be recursively tried out until a

variable x

and a threshold f

is found to minimize

the mean squared error (MSE) of the regression tree

at the current stage of growth (Loh, 2011). Other-

wise, the node will become an end node that outputs

the mean of the P values sorted into the node, ﬁnding

the average of p

. Eventually the regression tree will

take on the structure as seen in Fig. 2. For predic-

tion, the regression tree will check the input feature

vector against the decision thresholds in the nodes,

and ﬁnally arrive at an end node with an output power

consumption value.

Not only can a regression tree be used for pre-

diction, the resulting model can also highlight each

feature’s importance. By summing up the change

in MSE of a variable when it is selected to split P

across all nodes, a qualitative measure of the impor-

tance of the variable can be found (Guyon and Elisse-

eff, 2003).

Figure 2: Model of a Regression Tree.

2.2 Data Preprocessing

The current operational framework accepts the 6 pri-

mary variables as inputs as shown in Fig. 1. Among

these primary inputs, there are cases of missing data

or erroneous data. These cases are identiﬁed and the

missing/erroneous data are linearly interpolated based

on the surrounding values. Different variables could

be sampled at different rates. For standardization,

An Adaptive Data Driven Approach to Single Unit Residential Air-conditioning Prediction and Forecasting using Regression Trees

all the variables were resampled to 10 mins interval,

which is in line with most smart meter data sampling

frequency (Kavousian et al., 2013).

Thereafter, additional features were derived from

the original 6 variables to better model the transient of

the system. The ﬁnal list of 38 features (variables) are

listed in Table. 1. The original features are embolden

in the table.

Table 1: Feature List.

Feature

Name

Feature Description

’power’ Power Consumption of AC

’power status’ Power Status of AC (0/1)

’do’ Operation Mode for AC, 1 for Dehumidiﬁer, 2 for Auto and 3 for Cooler

’dt’ Set Point Temperature of AC in deg C

’it’ Indoor Temperature of AC in deg C

’ot’ Outdoor Temperature in deg C

’dton’ Product of ’dt’ and ’power status’

’vardo’ Variance of ’do’ within current 10 min interval

’vardt’ Variance of ’dt’ within current 10 min interval

’varit’ Variance of ’it’ within current 10 min interval

’varot’ Variance of ’ot’ within current 10 min interval

’p1’ Power Consumption of AC 10 min before

’tonsin’ Rolling time step since the AC is switched on

’tsindt’ Rolling time step since ’dt’ remains the same as the previous value

’tlaston’ Time step since the AC is last switch on

’tlastoncounter’ Rolling time step since AC is switch off

’mavgot30min’ Moving Average of ’ot’ within previous 30 min interval

’mavgot1hr’ Moving Average of ’ot’ within prevous 1 hr interval

’mavgot2hr’ Moving Average of ’ot’ within prevous 2hr interval

’mvarot30min’ Variance of ’ot’ within previous 30 min interval

’mvarot1hr’ Variance of ’ot’ within previous 1hr min interval

’mvarot2hr’ Variance of ’ot’ within previous 2hr min interval

’mavgit30min’ Moving Average of ’it’ within previous 30 min interval

’mavgit1hr’ Moving Average of ’it’ within previous 1 hr interval

’mavgit2hr’ Moving Average of ’it’ within previous 2hr interval

’mvarit30min’ Variance of ’it’ within previous 30 min interval

’mvarit1hr’ Variance of ’it’ within previous 1hr min interval

’mvarit2hr’ Variance of ’it’ within previous 2hr min interval

’mavgdt30min’ Moving Average of ’dt’ within previous 30 min interval

’mavgdt1hr’ Moving Average of ’dt’ within previous 1 hr interval

’mavgdt2hr’ Moving Average of ’dt’ within previous 2hr interval

’mvardt30min’ Variance of ’dt’ within previous 30 min interval

’mvardt1hr’ Variance of ’dt’ within previous 1hr min interval

’mvardt2hr’ Variance of ’dt’ within previous 2hr min interval

’changeot30min’ Difference between ’mavgot30min’ and ’mavgot30min’ 1 time step before

’changeit30min’ Difference between ’mavgit30min’ and ’mavgit30min’ 1 time step before

’changedt30min’ Difference between ’mavgdt30min’ and ’mavgdt30min’ 1 time step before

’ditemp30min’ Difference between ’mavgdt30min’ and ’mavgit30min’

2.3 Load Prediction Module (LP-M)

and Indoor Temperature

Forecasting Module ITF-M)

The main focus of the LP-M is to predict AC power

consumption

power

based on the rest of the fea-

tures at the current time step. In order to achieve

load prediction on LP-M, we will need to know the

current control inputs, indoor conditions and outdoor

conditions. Outdoor conditions could be easily gath-

ered from online weather forecasts from websites

like weatherunderground.com, but the indoor condi-

tions will have to be extrapolated. Therefore, for

ITF-M, the focus is to forecast indoor temperature

based on information in the previous time step.

Using too many features to train a machine learn-

ing model might introduce noises and cause over-

ﬁtting problem. Since the impact of each feature

for prediction and forecasting is unknown, we de-

signed a careful feature selection process using re-

gression trees to obtain an optimal set of most relevant

features X

best

and the trained prediction/forecasting

model RTree(X

best

). For each module, the variable

list in Table. 1 is split into input set X and output

set Y . X and Y are then further divided into training

and testing data. The training data set is used for the

feature selection and model training, while the test-

ing data set is used for performance validation of the

model.

The criterion used in this paper to test the regres-

sion model validation is the Mean Absolute Percent-

age Error (MAPE), which is deﬁned by:

MAPE =

100

∑

t=1



− F



where A

is the actual value, F

is the forecast value,

and n is the length of the data set.

The feature selection process is encoded in Algo-

rithm. 1, and is aimed at selecting the top n most rel-

evant features from all available features in the input

set.

Algorithm 1: Logic for Feature Selection Process.

Initialize X

train

, Y

train

, X

test

, Y

test

1. Obtain k

regression tree models with X

train

, Y

train

segmented by k

fold cross validation

2. For each regression tree model from k

-fold cross

validation, obtain the normalized feature impor-

tance. The higher the value the more important

the feature.

3. Sum up the normalized feature importance and

sort the features in X according to their impor-

tance

4. for 1:n, with n being the number of features in X:

Train k

regression tree models with k

-fold cross

validation based on X

1:n

train

1:n

represents the matrix of X with the top n fea-

tures.

err

← Find and average the Mean Absolute Per-

centage Error (MAPE) of the k

models.

endfor

5. n

∗

← arg min

err

, X

best

← X

1:n

∗

train

Find the n

∗

that gives the minimum err

, and X

best

is the training set with the top n

∗

inputs

6. RTree(X

best

) is obtained by training another re-

gression tree model using X

best

. Validation is

done by using X

best

test

as the input to RTree(X

best

)

and ﬁnding the MAPE to Y

test

This algorithm is utilized by both LP-M and ITF-

M, but with different input sets X and output sets Y .

The model trained by LP-M with the process will be

SMARTGREENS 2017 - 6th International Conference on Smart Cities and Green ICT Systems

referred to as RTree

and the model trained by ITF-

M will be referred to as RTree

IT F

2.4 Load Forecasting Module

The load forecasting module takes in current sys-

tem states, control inputs, external weather variables

and attempts to forecast AC load by looping through

RTree

and RTree

IT F

trained in LP-M and ITF-

M respectively. The control inputs array [U] con-

sists of

vardt

vardo

and

power status

Weather variables array [W ] consist of only

and

can be taken from the internet. The forecasting model

is detailed in Algorithm. 2.

Algorithm 2: Logic for Load Forecasting.

Initialize starttime, duration, [U ], [W ],

[initialconditions], [ f orecastarray], [predictarray]

1. [initialconditions] ← all features at time ==

starttime

2. for i=1:duration

[ f orecastarray] ← [initialconditions]

best

IT F

new

← RTree

IT F

([ f orecastarray])

The features selected for forecasting at the current

time step are fed into the ITF model to forecasting

temperature for the next time step.

[

new

vardt

new

vardo

new

power status

new

] ← U(i)

new

← W (i)

[initialconditions] ← each feature in

[initialconditions] is recalculated from up-

dated features and is updated, except

power

which is to be updated in the following prediction

step

[predictarray] ← [initialconditions]

best

power

new

← RTree

([predictarray])

[initialconditions] ←

power

new

Newly updated features at a future time step is

used to predict power at that future time step.

The newly forecasted power is added to the

[initialconditions] array such that the process can

loop all over.

endfor

The time period for this AC load forecasting algo-

rithm could be selected to forecast an arbitrary num-

ber of steps ahead. In order to produce a temperature

set point recommendation system, the starttime point

could be set at the moment when the user switches on

the AC and the duration could also be speciﬁed by

the user. The Load Forecasting Module could try out

different control inputs [U ] corresponding to differ-

ent control strategy, together with [W ] that is taken

off the web, to generate a few different forecasted

power

curves. The

power

curves corresponding to

different control strategies could be shown to the user,

in hope that the user will choose the most energy-

efﬁcient strategy.

3 CASE STUDY

A case study was done on actual AC data collected

from a wireless sensor testbed from 1 May 2015 to 31

Dec 2015. This testbed is set up in the faculty housing

apartments at the Singapore University of Technology

and Design (SUTD), and consists of 20 homes be-

ing cooled by Panasonic inverter ACs (CU-S24PKZ).

Values of

power

power status

are

collected by a proprietary attachment to the Panasonic

AC system, with a data rate of 30 secs.

data are

taken from a weather station within SUTD and is up-

dated once every 30 minutes. Two rooms, Room1 and

Room2, were selected to test out the modelling tech-

nique proposed in this paper. Room1 has a smaller

ﬂoor area compared with Room2 but they both have

the exact same AC unit. Each of the two indoor AC

units is powered by a corresponding outdoor com-

pressor, of similar make. As per the data preprocess-

ing module mentioned in Section. 2.2, the data col-

lected undergo a data cleaning process to remove er-

roneous and missing data, before being resampled to a

frequency of 10 mins. Eventually additional features

were calculated to form a feature list denoted in Ta-

ble. 1. Five months worth of data from June 2015 to

November 2015 were selected to form the training set,

while two months worth of data from May 2015 and

December 2015 were selected to be the test set. Anal-

ysis of data is performed in MATLAB 2016a with

regression trees being built by the f itrtree() func-

tion. The trees are encouraged to grow as deep as

possible and keep making splits at nodes until the

MSE

a fter−node

is less than 0.0001*MSE

be f ore−node

3.1 Feature Selection by LP-M and

ITF-M

The two selected rooms undergo the same feature se-

lection process for load prediction and indoor tem-

perature forecasting. For load prediction, all the fea-

tures presented in the feature list in Table. 1 except

power

, were taken as inputs X.

power

, itself, was

taken as the output Y. For indoor temperature fore-

casting, the input features X taken are one time step

before that of the output features Y . All the features

except

vardo

vardt

varit

varot

and

were taken as inputs while

is taken as the output

An Adaptive Data Driven Approach to Single Unit Residential Air-conditioning Prediction and Forecasting using Regression Trees

(Y ). The importance of features for the prediction and

forecasting modules were investigated by training re-

gression trees for 5 times in a 5-fold cross validation

as described in step 1 of Algorithm. 1. The reason

for using cross validation in building the model is to

prevent overﬁtting in the training set, which results in

poor performance on the test set (Zhang, 1993). A

certain set of features might be representative of a set

of data, while not being so for another set.

The algorithm proposed in this paper automati-

cally sorts the features by their importance values and

identiﬁes the optimal feature set to adapt to differ-

ent scenarios. The importance value of each feature

for each model respectively is obtained during the

training of regression trees as introduced in Section.

2.1. At the end of step 3 of Algorithm. 2, we ob-

tained a importance-ranked list of features for both the

load prediction model and indoor temperature fore-

casting model respectively. The list of features and

their importance values is displayed in Table. 3. The

features used for

forecasting are sufﬁxed with a

to indicate that they are values from the previous

time step. The normalized importance value of each

feature ranges from 0 to 5, with 0 representing that

the feature has minimal impact on the regression tree

models. A feature with a value of 5 is at the other end

of the spectrum. From here, we are interested in the

minimum amount of top features that will allow our

models to have the best performance in cross valida-

tion as evaluated by the MAPE. Following step 4 of

Algorithm. 1, which loops across the number of fea-

tures available, we ﬁrst train another regression tree

model with the top feature that appears in the impor-

tance list and record down the cross validated MAPE

of the resulting model. Subsequent stages increase the

number of features that is fed into the model, from the

top two features, top three features to all the features.

In step 5, we compare across all the MAPE that is

gathered and ﬁnd the top n

∗

features that generated

the lowest MAPE for the models trained. The plots

of the MAPE values against the number of top most

important features used in each model for each sce-

nario are shown in Fig. 3 to 6. The ﬁgure within each

plot is the zoomed-in view of the plot. For each plot,

there is a point, n

∗

, indicated by a black dot, on which

the minimum MAPE is achieved. Beyond this point,

the error starts to increase due to noise from excessive

variables or potential overﬁtting.

Table 2: Final Model Validation MAPE.

RTree

Room1

RTree

Room1

ITF

RTree

Room2

RTree

Room2

IFT

Training 0.0624 0.0031 0.0353 0.0023

Testing 0.2068 0.0105 0.1079 0.0137

Figure 3: Error Plot of Cross Validated Regression Trees

with top 1:n Features with LP-M for Room1.

Figure 4: Error Plot of Cross Validated Regression Trees

with top 1:n Features with ITF-M for Room1.

Figure 5: Error Plot of Cross Validated Regression Trees

with top 1:n Features with LP-M for Room2.

Figure 6: Error Plot of Cross Validated Regression Trees

with top 1:n Features with ITF-M for Room2.

After getting the n

∗

for each model, the X

best

for

each model can then be obtained. Features belonging

to X

best

for the 4 models trained in this case study,

are embolden in Table. 3. As per step 6 in the algo-

rithm, we train the ﬁnal regression trees for each sce-

nario with their respective X

best

train

and validate against

the X

best

test

and Y

test

. The resulting MAPE values are

captured in Table. 2. Note that in the table the testing

errors are all slightly higher than the training errors,

SMARTGREENS 2017 - 6th International Conference on Smart Cities and Green ICT Systems

Table 3: Feature Selection Results.

n Features Room 1 LP-M Normalized Importance MAPE of 1:n Features Room 2 LP-M Normalized Importance MAPE of 1:n

1 ’p1’ 5 0.300511736 ’dt’ 5 0.425269107

2 ’tonsin’ 0.546464567 0.25613889 ’p1’ 2.229504903 0.1722657

3 ’ditemp30min’ 0.302132742 0.225410736 ’mavgit1hr’ 0.175892978 0.114627075

4 ’it’ 0.203769685 0.184159732 ’tonsin’ 0.169274939 0.106301354

5 ’dt’ 0.117708659 0.151078236 ’mavgit30min’ 0.153465653 0.103535235

6 ’varit’ 0.086242838 0.150839102 ’tlastoncounter’ 0.097634991 0.103640427

7 ’do’ 0.076026275 0.142621183 ’mavgdt30min’ 0.075141909 0.094776905

8 ’changeit30min’ 0.0601043 0.151721193 ’tsindt’ 0.052305914 0.090929191

9 ’ot’ 0.049193637 0.149417023 ’mvardt1hr’ 0.048716335 0.092222002

10 ’mvarit2hr’ 0.046315628 0.153185215 ’vardt’ 0.046750632 0.089856611

11 ’mavgot2hr’ 0.044044982 0.157504529 ’mvardt30min’ 0.038764716 0.088808819

12 ’mavgot1hr’ 0.03871963 0.154212055 ’ditemp30min’ 0.030874599 0.090148701

13 ’mavgot30min’ 0.035275138 0.153604236 ’changedt30min’ 0.029749423 0.091144285

14 ’mavgit30min’ 0.034512117 0.150444017 ’changeit30min’ 0.022911877 0.091096538

15 ’mvardt30min’ 0.020802706 0.151798587 ’mavgit2hr’ 0.020215566 0.091894589

16 ’mvarit1hr’ 0.019795968 0.153878896 ’mavgot2hr’ 0.016489804 0.091854609

17 ’tsindt’ 0.018422984 0.154598731 ’tlaston’ 0.014382804 0.091670433

18 ’mvarot2hr’ 0.018344337 0.154802141 ’it’ 0.012760316 0.091462106

19 ’mavgit1hr’ 0.018095013 0.150804239 ’mvarit30min’ 0.011440145 0.091275875

20 ’mvarot30min’ 0.017961545 0.151227054 ’varit’ 0.008412449 0.09130624

21 ’mavgit2hr’ 0.015143984 0.150956154 ’mavgot1hr’ 0.007887081 0.091710049

22 ’changeot30min’ 0.014847934 0.151405779 ’mavgdt2hr’ 0.006162069 0.091902927

23 ’vardt’ 0.013334774 0.154281321 ’mavgdt1hr’ 0.005895048 0.092193576

24 ’mavgdt30min’ 0.011798189 0.155449079 ’mavgot30min’ 0.005709894 0.092113118

25 ’mavgdt1hr’ 0.010710383 0.155781011 ’mvarit1hr’ 0.005468773 0.092516269

26 ’changedt30min’ 0.010654833 0.15446828 ’mvarit2hr’ 0.005200726 0.09289201

27 ’mvarit30min’ 0.009400498 0.154850841 ’ot’ 0.004586769 0.092535681

28 ’mvarot1hr’ 0.008841766 0.15466422 ’mvardt2hr’ 0.004529506 0.092903108

29 ’mavgdt2hr’ 0.003281657 0.154308461 ’mvarot1hr’ 0.002587819 0.092974254

30 ’mvardt2hr’ 0.002354067 0.15431396 ’mvarot2hr’ 0.002587263 0.093296134

31 ’vardo’ 0.001228529 0.15431396 ’changeot30min’ 0.001162669 0.093166362

32 ’mvardt1hr’ 0.001104164 0.155328966 ’mvarot30min’ 0.00076616 0.093169736

33 ’power status’ 0 0.155328966 ’power status’ 0 0.093169736

34 ’dton’ 0 0.155328966 ’do’ 0 0.093169736

35 ’varot’ 0 0.155328966 ’dton’ 0 0.093169736

36 ’tlaston’ 0 0.155328966 ’vardo’ 0 0.093169736

37 ’tlastoncounter’ 0 0.155328966 ’varot’ 0 0.093169736

n Features Room 1 ITF-M Normalized Importance MAPE of 1:n Features Room 2 ITF-M Normalized Importance MAPE of 1:n

1 ’mavgit30min1’ 5 0.009369312 ’mavgit30min1’ 5 0.010823976

2 ’tsindt1’ 0.204508081 0.009258808 ’power1’ 0.128241304 0.009067155

3 ’changeit30min1’ 0.184549408 0.008789746 ’mavgit1hr1’ 0.073826389 0.008635071

4 ’power1’ 0.096098917 0.008732118 ’ditemp30min1’ 0.061379441 0.008259862

5 ’mvarit30min1’ 0.079650603 0.008645971 ’dton1’ 0.030393942 0.00774464

6 ’mavgot2hr1’ 0.078441613 0.008712613 ’dt1’ 0.028070593 0.007648126

7 ’mvarit2hr1’ 0.05909354 0.008618668 ’changeit30min1’ 0.027032874 0.007311177

8 ’mavgit2hr1’ 0.057902336 0.008672379 ’tsindt1’ 0.018527454 0.007126983

9 ’mavgit1hr1’ 0.055958149 0.008671855 ’mavgit2hr1’ 0.01434755 0.007075553

10 ’ot1’ 0.052720068 0.008653909 ’tonsin1’ 0.013132361 0.007014234

11 ’tonsin1’ 0.047248711 0.008546118 ’mavgot2hr1’ 0.010929887 0.006902634

12 ’mvarot2hr1’ 0.047153313 0.008558489 ’mavgdt2hr1’ 0.009526018 0.006924036

13 ’mavgot1hr1’ 0.046200305 0.008627689 ’mvarit2hr1’ 0.009058123 0.006880701

14 ’mvarit1hr1’ 0.042701034 0.008580615 ’mvarit30min1’ 0.008611964 0.006912867

15 ’dton1’ 0.036195604 0.008546782 ’tlastoncounter1’ 0.0073374 0.006932536

16 ’ditemp30min1’ 0.033422691 0.008486991 ’mvarot2hr1’ 0.006958218 0.006946669

17 ’do1’ 0.018925811 0.008410064 ’mvarit1hr1’ 0.006946692 0.006921869

18 ’changeot30min1’ 0.018903914 0.008414293 ’changedt30min1’ 0.004799984 0.006926115

19 ’mavgot30min1’ 0.018594206 0.008432243 ’mvardt30min1’ 0.004441651 0.006927035

20 ’mavgdt2hr1’ 0.016388313 0.008428715 ’mavgdt1hr1’ 0.00429153 0.006883871

21 ’mvarot1hr1’ 0.016061363 0.008456917 ’mavgot1hr1’ 0.004158766 0.00690459

22 ’mvarot30min1’ 0.013617638 0.008482549 ’tlaston1’ 0.0041539 0.006881953

23 ’dt1’ 0.009487144 0.008501586 ’mvardt2hr1’ 0.004077719 0.006887224

24 ’mvardt2hr1’ 0.009240435 0.008495656 ’ot1’ 0.003873874 0.006874993

25 ’mvardt1hr1’ 0.007863585 0.008478085 ’mvarot1hr1’ 0.00344415 0.006896851

26 ’changedt30min1’ 0.007841566 0.008460171 ’changeot30min1’ 0.002966679 0.006876015

27 ’mvardt30min1’ 0.007499966 0.008468636 ’mvardt1hr1’ 0.002658473 0.006919493

28 ’mavgdt30min1’ 0.007199021 0.008469476 ’mavgot30min1’ 0.002607417 0.006907127

29 ’mavgdt1hr1’ 0.005834264 0.00847986 ’mavgdt30min1’ 0.002499976 0.006908189

30 ’power status1’ 0.00211583 0.008473187 ’mvarot30min1’ 0.001919621 0.006903403

31 ’tlaston1’ 0 0.008473187 ’power status1’ 0.001312232 0.006886679

32 ’tlastoncounter1’ 0 0.008473187 ’do1’ 0 0.006886679

which can be explained by inevitable but little model

overﬁtting to the training data set.

3.2 Load Forecasting by LF-M

After obtaining the regression tree models of the

two rooms, RTree

Room1

, RTree

Room1

IT F

, RTree

Room2

RTree

Room2

IFT

, respectively from LP-M and ITF-M, the

forecasting capabilities of LF-M is validated against

the test set. The goal is to see how well LP-M can

forecast the power output of the AC given a set of

control variables [U] and weather variables [W] from

the test set. The duration parameter controls how far

ahead the model is forecasting. Forecasting duration

of 30 min and one day ahead were investigated. The

difference between the two is that, in 30-min forecast-

ing, the system will receive updates on the state of the

room every 30 min. While for day-ahead forecasting,

LF-M will have to extrapolate the indoor temperature

of the room autonomously for one day. Hence, ex-

pected error of the day-ahead forecasting is more than

that of the 30-min forecasting. LF-M is looped over

the length of the entire test set and the output is com-

pared with the

power

variable in the test set.

An Adaptive Data Driven Approach to Single Unit Residential Air-conditioning Prediction and Forecasting using Regression Trees

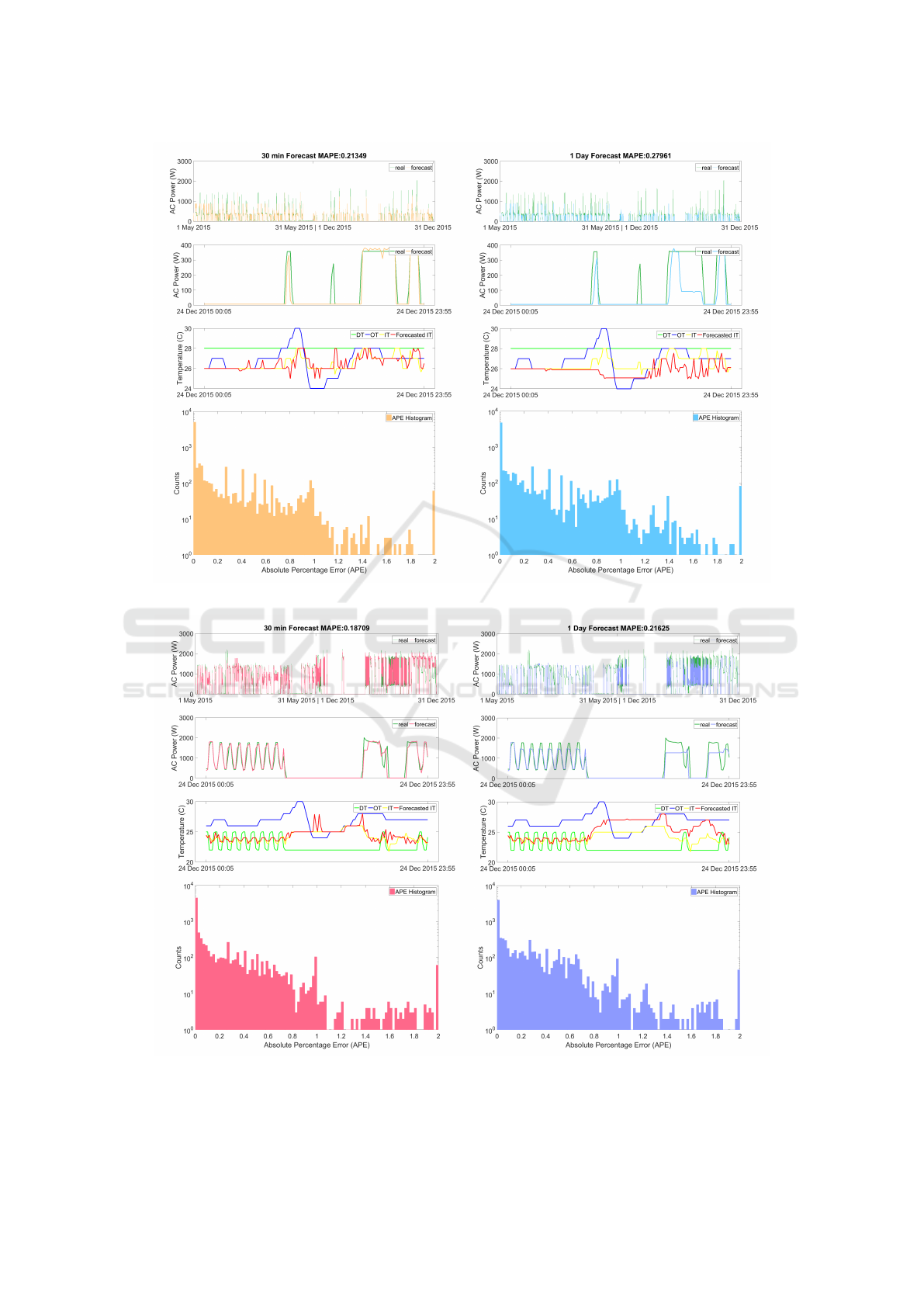
Figure 7: Results of LF-M on Room1.

Figure 8: Results of LF-M on Room2.

SMARTGREENS 2017 - 6th International Conference on Smart Cities and Green ICT Systems

The results of LF-M on Room1 is plotted in Fig.

7 and Room2 in Fig. 8. Within each ﬁgure, there

are four layers. The ﬁrst layer shows the plot of the

output of LF-M against the actual load proﬁle. The

second layer is a zoomed-in view of load forecast-

ing on a single day, 24 Dec 2015. The third layer

shows the change in

and the forecasted

from LF-M. The last layer is a histogram of the in-

dividual absolute percentage error (APE) between the

predicted power and the actual power. As expected,

the error for day-ahead forecasting for both rooms is

larger than that of the 30-min forecasting. Although

this error is just under 2% in the case of Room2, the

difference grows to around 6% in Room1. The error

histogram in Room1 is also visibly shifted to the right

when making day-ahead forecast: the number of data

points with a APE of 0.6 in the 30-min APE histogram

of Room1 is shifted to the region with APE of more

than 1. Comparing room1 and room2, the user behav-

ior in Room2 is much more dynamic. However, the

model is still able to capture the behavior of the sys-

tem and produce accurate forecasting results. In both

rooms, for day-ahead forecasting, inaccuracies arise

when the temperature forecast starts to drift from the

actually value. This is as for day-ahead forecasting,

the temperature forecasting loop will have to be run

144 times. If there is a slight error within each loop,

the error will accumulate and get carried to the ﬁnal

results. The current temperature sensor in the AC sys-

tem used for this experiment only reports integer val-

ues, which is a physical limitation. If the sensor could

be forced to output values with higher degrees of ac-

curacies, the modelling results could be improved.

3.3 Set Point Recommendation

The LF-M could also be used as set point Recommen-

dation system. Consider the day ahead forecasting

scenario on 24 Dec 2015 in Room2, LF-M is able to

show the power consumption with a change in [U].

Figure. 9 shows the power consumption of the AC

in Room2 if all the

for the day is shifted by +1

and by -1 deg Celsius. The total energy used for each

set of [U] is found by calculating the area under the

power curve. For input [U]-1, the total energy con-

sumed for the entire day of 24 Dec is 19.2 kWh. For

the original [U], the total energy is 16.4 kWh. When

[U]+1 is applied, the total energy consumption be-

comes 15.1 kWh.

The accuracy of this simulation will be deter-

mined by the duration simulated, considering that the

indoor temp forecasted by LP-M has a certain drift

with longer durations. Previously consumers have no

idea of how much electricity they will consume if they

Figure 9: Set Point Change.

set the AC at the certain temperature. With this sys-

tem, which could receive feedback on the impact of

their choice of AC set point, and could better plan

their electricity usage. Not only will this informa-

tion be useful for consumers, it will also be useful for

power distributors to estimate the amount of energy

they could save or store in a Demand Response pro-

gram, and optimize the actions for Demand Reponse.

4 CONCLUSIONS

In this paper, we presented a data driven approach

to modelling single unit residential AC unit using

a machine learning technique known as Regression

Trees. Based on the Regression Trees technique, we

designed an automatic feature selection algorithm to

select the best set of features to model individual

AC unit’s power consumption and room temperature.

These two models were then combined to forecast

power consumption and room temperature for a given

period. The technique is adaptive and can be applied

to rooms of different sizes, and possibly ACs of differ-

ent make, provided that the input data type is similar.

A test on two rooms of different sizes and with highly

dynamic loads gave a maximum MAPE of 21.35%

for 30-min ahead load forecasting and 27.96% for

An Adaptive Data Driven Approach to Single Unit Residential Air-conditioning Prediction and Forecasting using Regression Trees

day-ahead forecasting. The resulting system is use-

ful for set point recommendation and load estimation,

where it could forecast the electricity consumed by

ACs given a specﬁc control input and the weather

conditions during the period of consideration.

The current temperature sensor can only output

integer values. Future work will be to try out other

temperature sensors with higher accuracy and investi-

gate the impact on prediction results. Also, regres-

sion trees pruning techniques could be investigated

as a safeguard against model overﬁtting during the

training process. The next step is to integrate the sys-

tem into an automated demand response agent, min-

imizing the power consumption of households with

regards to price signals and human comfort.

ACKNOWLEDGEMENT

This work is supported in part by the project funded

by National Research Foundation (NRF) via the

Green Buildings Innovation Cluster (GBIC), adminis-

tered by Building and Construction Authority (BCA),

and in part by the SUTD-MIT International Design

Centre (idc; idc.sutd.edu.sg).

REFERENCES

Afram, A. and Janabi-Shariﬁ, F. (2015a). Black-box mod-

eling of residential hvac system and comparison of

gray-box and black-box modeling methods. Energy

and Buildings, pages 121–149.

Afram, A. and Janabi-Shariﬁ, F. (2015b). Gray-box model-

ing and validation of residential hvac system for con-

trol system design. Applied Energy, pages 134–150.

Behl, M., Smarra, F., and Mangharam, R. (2016). Dr-

advisor: A data-driven demand response recom-

mender system. Applied Energy, pages 30–46.

Chan, S.-C., Tsui, K. M., Wu, H., Hou, Y., Wu, Y.-C., and

Wu, F. F. (2012). Load/price forecasting and man-

aging demand response for smart grids: Methodolo-

gies and challenges. IEEE signal processing maga-

zine, pages 68–85.

Ding, Y. M., Hong, S. H., and Li, X. H. (2014). A de-

mand response energy management scheme for indus-

trial facilities in smart grid. IEEE Transactions on In-

dustrial Informatics, pages 2257–2269.

Guyon, I. and Elisseeff, A. (2003). An introduction to vari-

able and feature selection. Journal of machine learn-

ing research, pages 1157–1182.

Horowitz, S., Mauch, B., and Sowell, F. (2014). Forecast-

ing residential air conditioning loads. Applied Energy,

132:47–55.

Jain, M., Singh, A., and Chandan, V. (2016). Non-intrusive

estimation and prediction of residential ac energy con-

sumption. In 2016 IEEE International Conference

on Pervasive Computing and Communications (Per-

Com), pages 1–9. IEEE.

Kalkan, N., Young, E., and Celiktas, A. (2012). Solar ther-

mal air conditioning technology reducing the footprint

of solar thermal air conditioning. Renewable and Sus-

tainable Energy Reviews, pages 6352–6383.

Kavousian, A., Rajagopal, R., and Fischer, M. (2013). De-

terminants of residential electricity consumption: Us-

ing smart meter data to examine the effect of climate,

building characteristics, appliance stock, and occu-

pants’ behavior. Energy, pages 184–194.

Li, J., Poulton, G., Platt, G., Wall, J., and James, G. (2010).

Dynamic zone modelling for hvac system control. In-

ternational Journal of Modelling, Identiﬁcation and

Control, pages 5–14.

Li, W.-T., Gubba, S. R., Tushar, W., Yuen, C., Hassan,

N. U., Poor, H. V., Wood, K. L., and Wen, C.-K.

(2017). Data driven electricity management for resi-

dential air conditioning systems: An experimental ap-

proach. IEEE Transactions on Emerging Topics in

Computing.

Loh, W.-Y. (2011). Classiﬁcation and regression trees.

Wiley Interdisciplinary Reviews: Data Mining and

Knowledge Discovery, pages 14–23.

Lork, C., Batchu, R., Yuen, C., and Pindoriya, N. M. (2017).

How many watts: A data driven approach to aggre-

gated residential air-conditioning load forecasting. In

13th Workshop on Context and Activity Modeling and

Recognition (CoMoRea’17), pages 285–290. IEEE.

Lu, N. (2012). An evaluation of the hvac load potential for

providing load balancing service. IEEE Transactions

on Smart Grid, pages 1263–1270.

Qin, X., Lysecky, S., and Sprinkle, J. (2015). A data-driven

linear approximation of hvac utilization for predictive

control and optimization. IEEE Transactions on Con-

trol Systems Technology, pages 778–786.

Shao, S., Shi, W., Li, X., and Chen, H. (2004). Performance

representation of variable-speed compressor for in-

verter air conditioners based on experimental data. In-

ternational journal of refrigeration, pages 805–815.

Tang, F., Kusiak, A., and Wei, X. (2014). Modeling and

short-term prediction of hvac system with a clustering

algorithm. Energy and Buildings, pages 310–321.

Xuan, Z., Qing-dian, L., Guo-qiang, L., Jun-wei, Y., Jian-

cheng, Y., Lie-quan, L., and Wei, H. (2015). Multi-

variable time series forecasting for thermal load of air-

conditioning system on svr. In Control Conference

(CCC), 2015 34th Chinese, pages 8276–8280. IEEE.

Yin, R., Kara, E. C., Li, Y., DeForest, N., Wang, K., Yong,

T., and Stadler, M. (2016). Quantifying ﬂexibility of

commercial and residential loads for demand response

using setpoint changes. Applied Energy, pages 149–

164.

Zhang, P. (1993). Model selection via multifold cross vali-

dation. The Annals of Statistics, pages 299–313.

SMARTGREENS 2017 - 6th International Conference on Smart Cities and Green ICT Systems