Model Validation of an Open-source Framework for Post-processing

INS/GNSS Systems

Rodrigo Gonzalez

, Carlos A. Catania

, Paolo Dabove

, Juan Carlos Taffernaberry

and Marco Piras

GridTICs, National University of Technology, Mendoza, Argentina

ITIC, FCEyN, National University of Cuyo, Mendoza, Argentina

Department of Environmental, Land and Infrastructure Engineering (DIATI), Politecnico di Torino, Torino, Italy

Keywords:

GIS, Post-processing, INS, GNSS, Allan Variance, Model Validation, MATLAB, Navigation Systems.

Abstract:

The development of new approaches in the GIS research community may require the use of a computational

tool to post-process GNSS and inertial sensors data in order to get more accurate position, velocity, and orien-

tation angles (attitude) information. An open-source framework for simulating integrated navigation systems

(INS/GNSS) called NaveGo has been developed using MATLAB/GNU Octave and is freely available on-line.

Although preliminary tests have shown that NaveGo appears to work properly, a deep examination must be

carried out to conﬁrm that this framework is an adequate tool for post-processing INS/GNSS information.

The main goal of this work is to produce a validation methodology to show that NaveGo mathematical model

works within its speciﬁcations. Firstly, static measurements from inertial sensors are processed and analysed

by NaveGo applying the Allan variance for proﬁling typical errors. Some details of Allan variance procedure

are exhibited. Then, performances of NaveGo and Inertial Explorer, a closed-source commercial package

software for INS/GNSS integration, are compared for a real-world trajectory. It is statistically concluded that

NaveGo presents close accuracy to Inertial Explorer for attitude and position. Consequently, it is demonstrated

that NaveGo is an useful INS/GNSS post-processing framework that can be used in GIS applications.

1 INTRODUCTION

An integrated navigation system is an electronic de-

vice comprised of several types of sensors that takes

advantage of the strengths of each sensor so that to

get better estimates of position, velocity, and attitude

(PVA), where the latter is deﬁned as the orientation

of an object with respect to a particular frame of ref-

erence. Typically, an integrated navigation system

fusions the information provided by an inertial nav-

igation system (INS), which in turn is compounded

by an inertial measurement unit (IMU), and one or

more aiding sensors, commonly just a GNSS receiver

(GPS, GLONASS, etc.). This particular system is

known as an INS/GNSS system.

An INS provides PVA information with high rates

but with unbounded errors since its operation is based

on the integration of noisy inertial measurements. On

the other hand, a GNSS receiver gives position and

velocity with bounded errors but at a lower frequency

(Dabove et al., 2011). The fusion of observations in

the INS/GPS system is carried out by an extended

Kalman ﬁlter (EKF), which is a well-known algo-

rithm for moderate nonlinear systems that operates

recursively on both noisy input and output data to sta-

tistically produce optimal estimates of the EKF states

(Groves, 2008).

Prior to process IMU data in an INS/GNSS sys-

tem, it is mandatory to analyse and to measure the

inaccuracies that a particular IMU displays. Then,

the EKF can be conﬁgured with an accurate IMU

proﬁle to get a more precise PVA solution from the

INS/GNSS system. The Allan variance (Allan, 1966)

is a technique that has demonstrated to be useful

to identify and to quantify IMU noise processes, as

quantisation noise, angle random walk, and bias in-

stability, among others (IEEE-SA Standards Board,

1998; El-Sheimy et al., 2008). This procedure is one

of the most used for proﬁling IMU imprecisions.

Recently, INS/GNSS systems have gained re-

searchers’ attention from the GIS community for the

potential this technology has in certain GIS disci-

plines (Dabove et al., 2017). For example, land and

airborne mobile mapping are ﬁelds where INS/GNSS

systems offer more precise (sub-centimetre-level ac-

curacy) and reliable data than a GNSS-only solution

Gonzalez, R., Catania, C., Dabove, P., Taffernaberry, J. and Piras, M.

Model Validation of an Open-source Framework for Post-processing INS/GNSS Systems.

DOI: 10.5220/0006313902010208

In Proceedings of the 3rd International Conference on Geographical Information Systems Theory, Applications and Management (GISTAM 2017), pages 201-208

ISBN: 978-989-758-252-3

201

(Navidi and Landry, 2015). Besides, orientation of

the camera in the mobile mapping system is needed to

correctly superpose images and this information can-

not be provided by a GNSS receiver.

In the development of new research methodolo-

gies in GIS, it may be convenient to have at hand

a computational tool to post-process GNSS and INS

data from different sensors vendors. Some commer-

cial, closed-source software can be found in the mar-

ket for this purpose as TerraPos by TerraTec AS (Ter-

raTec AS, 2017), POINT by the University of Can-

terbury (Spatial Engineering Research Centre, Uni-

versity of Canterbury, 2017), Inertial Explorer by

NovAtel Inc. (NovAtel Inc., 2013), and Kinemat-

ica by Advanced Navigation (Advanced Navigation,

2016). According to the provided vendors’ informa-

tion, none of these software packages applies Allan

variance analysis. The license cost for these programs

ranges from USD 2,000 per year (Advanced Naviga-

tion, 2016) to USD 13,000 for a full, non-time limited

license (NovAtel Inc., 2013). This expense could be

prohibited for some research groups which are giving

their ﬁrst steps in Geomatics or GIS.

An open-source INS/GNSS simulation framework

could be a zero-cost alternative to commercial soft-

ware. In addition, an open-source software may let

some new ideas in the GIS community be rapidly

proved, but also enable other researchers to compare

their new approaches against already proposed GIS

solutions in a fairly and repeatability way, both cen-

tral aspects of the scientiﬁc method, by using the same

computational tool. Additionally, it could be inter-

esting that this open-source tool to offer a procedure

to apply the Allan variance to IMU measurements in

order to proﬁle the device intrinsic noises (Piras and

Dabove, 2016).

NaveGo is an open-source framework for simulat-

ing loosely-coupled INS/GNSS systems that is freely

available on-line (Gonzalez, 2016). It is developed

using MATLAB/GNU Octave due to this program-

ming language has become a de facto standard for

simulation and mathematical computing. Previous

publications have exposed its complete mathematical

model (Gonzalez et al., 2015a) and how inertial sen-

sors and GPS receiver can be simulated in a simpli-

ﬁed way (Gonzalez et al., 2015b). NaveGo has been

tested by processing real-world data from a real tra-

jectory (Toth et al., 2011). Results from that test have

been around expected values (Gonzalez et al., 2015a).

Although NaveGo has shown to work properly, a

more thoroughly examination must be carry out to

conﬁrm that this framework can be considered a se-

rious tool for post-processing INS/GNSS data. Thus,

the main goal of this paper is to successfully produce

an empirical model validation methodology that en-

sures that NaveGo conforms to its speciﬁcation. In

doing so, it is proposed to validate NaveGo model

by comparison to another reference model (Sargent,

2013), in particular to Inertial Explorer, a mature and

well-known commercial software for INS/GNSS in-

tegration. Model validation is done by comparison

of the results of both INS/GNSS solutions by pro-

cessing ﬁeld data sets. It is worth mentioning that

after an exhaustive search in the existing literature, it

has not been found previous works related to compare

INS/GNSS computational models.

In spite of the fact that some few another

INS/GNSS data processing software have been pro-

posed in the literature (Giroux et al., 2003; Niu et al.,

2015), these tools are neither open source nor freely

available. It is the authors’ believe that NaveGo

is the ﬁrst coordinated academic effort to develop

an open-source INS/GNSS processing framework for

both navigation and GIS communities.

The rest of this paper is organised as follows. In

Section 2, Allan variance procedure performed by

NaveGo is shown by processing static measurements

from the same IMU unit that will be used to validate

NaveGo mathematical model. Section 3 details the

kinematic data set that is used to validate NaveGo,

and presents the comparison method to analyse the

uncertainties from both NaveGo and a Inertial Ex-

plorer. Finally, Section 4 completes this paper com-

menting results and providing conclusions.

2 ALLAN VARIANCE

PROCEDURE

The Allan variance (AV) is a widely known tech-

nique to estimate particular inaccuracies in inertial

sensors. Though IMU manufacturers provide sensors

characterisation information, these are average val-

ues among several units from a particular production

batch. Often, a more precise inertial sensor proﬁle

may be needed to improve the PVA solution. Theo-

retical foundations about the AV can be found in the

literature (Allan, 1966; El-Sheimy et al., 2008; IEEE-

SA Standards Board, 1998) and are out of the scope

of this paper.

2.1 Static Data Set Description

AV analysis is performed by using data from an

Ekinox-D IMU which is a tactical-grade IMU from

SBG Systems (SBG Systems, 2016). This same IMU

will be used in Section 3 for processing a kinematic

solution with NaveGo.

GISTAM 2017 - 3rd International Conference on Geographical Information Systems Theory, Applications and Management

202

In applying the AV technique, it is mandatory

to only process static measurements (IEEE-SA Stan-

dards Board, 1998). Accordingly, a six-faces static

test is performed ﬁxing the Ekinox-D IMU on a non-

magnetic plate, and aligning the device by the y-axis

to exclude errors due to orientation. IMU data is ac-

quired about 6 hours at 200 Hz sampling rate in an

undisturbed environment. Complete procedure took

place at one of DIATI’s laboratories.

Statistical information obtained for each sensor

from static measurements are static bias, which is the

mean, and standard deviation. The latter is related to

the level of white noise presented in the sensor. Val-

ues of these two errors from the six Ekinox-D IMU

sensors in the three body axes XYZ are shown in Ta-

ble 1.

Table 1: Static biases and standard deviations from static

analysis of Ekinox-D inertial sensors.

Sensor Static bias Standard deviation

(rad/s) (m/s

) (rad/s) (m/s

)

Gyro X -0.2449E-3 1.0395E-2

Gyro Y 0.1287E-3 0.9951E-2

Gyro Z 0.1513E-3 0.9740E-2

Acc’r X -0.0117 2.7147E-3

Acc’r Y 0.0251 3.2494E-3

Acc’r Z 9.8051 2.5079E-3

2.2 Allan Variance Analysis under

NaveGo

The Allan variance estimator used in NaveGo is the

overlapping Allan variance (Howe et al., 1981). Eq.

1 shows the overlapping AV of a discrete time series,

(T ) =

(N −2n)

N−2n

∑

k=1

(θ

k+2n

−2θ

k+n

+ θ

)

(1)

where N is the number of consecutive data points

sampled at t

seconds, T is the ﬁxed length in time

of N, n is a group of consecutive data points forming

a cluster with n < N/2, and θ is the angle or velocity

measurements made at discrete times given by τ = kt

k = 1,2,3,...,N. Finally, the square-root of the Allan

variance σ(T ) is represented in a log-log plot versus

τ. This ﬁgure will show a curve with different slopes

that are associated to speciﬁc types of errors.

Something important to bear in mind is that ev-

ery error found in the AV plot has an intrinsic value

of dispersion due to the ﬁniteness of the number of

clusters, given by the following formula,

σ(δ) =

−1)

. (2)

Equation 2 shows that the computed error in a re-

gion of an AV plot is small if the number of data

points in a cluster n is low when compared to the total

number of data points N. Thus, it is important how

these regions are previously deﬁned and, as a conse-

quence, how the time vector τ(kt

) is built to get the

smallest σ(δ).

Since AV analysis is based on creating a log-log

plot, it makes sense that time vector τ(kt

) has a loga-

rithmic arrangement. Thus, τ(kt

) is built in NaveGo

according to Algorithm 1. Variable t0 is the period of

time vector, tM is the maximum value of time, and tm

is the minimum value of time. Pseudo code in Algo-

rithm 1 is similar to MATLAB code for convenience.

In the particular case of the static data set exposed

Algorithm 1: Procedure for creating time vector τ(kt

) for

AV analysis.

1: exp_min = log10(t0);

2: exp_max = log10(tM - tm)/2;

3: tau_v = 10ˆ(exp_min:exp_max);

4: for i from 1 to length(tau_v)-1 do

5: tau = [tau tau_v(i):tau_v(i):tau_v(i+1)];

6: end

in Sec. 2.1, time vector spans in a logarithmic fash-

ion from values greater than the minimum time be-

tween samples (0.005 s) to less than a half of total

time (11,044 s).

Figures 1 and 2 expose the square-root overlap-

ping Allan variances for Ekinox-D gyroscopes and

accelerometers, respectively.

Finally, Table 2 exhibits the values found by ap-

plying NaveGo AV method of dynamic biases (bias

instability) and angle random walks and velocity an-

gle random walks, respectively for gyroscopes and ac-

celerometers.

3 NAVEGO MODEL VALIDATION

In this section, NaveGo is validated by comparing its

performance for a real trajectory against a commer-

cial package software for INS/GNSS post-processing.

Testing and reference data sets are described. Then,

results from both frameworks are exposed. Finally, a

detailed statistical comparison of both performances

is carried out.

Model Validation of an Open-source Framework for Post-processing INS/GNSS Systems

203

Table 2: Dynamic biases and random walks from static analysis of Ekinox-D inertial sensors.

Sensor

Dynamic bias Error Random walk Error Correlation

(rad/s) σ(δ) (rad/s/

√

Hz) σ(δ) time (s)

(m/s

) (m/s

√

Hz)

Gyro X 1.5157E-4 ± 7.2115E-8 1.1450E-5 ± 5.5231E-9 300

Gyro Y 1.6544E-4 ± 7.8715E-8 1.1479E-5 ± 5.5119E-9 200

Gyro Z 1.7746E-4 ± 8.4438E-8 1.3313E-5 ± 6.3924E-9 200

Acc’r X 1.8686E-4 ± 8.8907E-8 9.6088E-5 ± 4.5758E-8 20

Acc’r Y 1.8301E-4 ± 8.7076E-8 7.3059E-5 ± 3.4918E-8 100

Acc’r Z 1.8593E-4 ± 8.8467E-8 7.4684E-5 ± 3.5597E-8 40

−2

−5

−4

−3

−2

τ (s)

σ (rad/s)

Gyro X

Gyro Y

Gyro Z

Figure 1: Square-root overlapping Allan variance for

Ekinox-D IMU gyroscopes.

−2

−4

−3

τ (s)

σ (m/s

)

Acc X

Acc Y

Acc Z

Figure 2: Square-root overlapping Allan variance for

Ekinox-D IMU accelerometers.

3.1 Kinematic Data Set Description

The kinematic data set was generated in the city of

Turin by the DIATI group. Several sensors were in-

stalled on a crosswise aluminium bar mounted on the

roof of a vehicle, as shown in Fig. 3. Two GNSS

geodetic antennas (yellow circles in Fig. 3) were in-

stalled at the opposite ends of the bar in the direction

of motion. Then, they were connected to the Ekinox-

D platform (blue circle in Fig. 3). The Ekinox-D unit

was inserted into an aluminium skeleton on which a

third geodetic antenna was placed using a plate, cen-

tred exactly on the source of the reference system of

the inertial sensor (XY centre).

Figure 3: Instruments located on the crosswise bar of a ve-

hicle.

The positions of both antennas and sensors are cal-

culated in planimetry and altimetry by a small net-

work of distances using StarNet 7.0 software (Mi-

croSurvey, 2016), following a least-squares approach,

and reaching a maximum root-mean square error of

about 2 mm. This enables the lever arm of the system

to be obtained with high accuracy.

This system was registered in a stretch of the Turin

road network. This trajectory is shown in Figure

4, being an urban section with minor obstruction in

terms of buildings. It presents full GPS-signal avail-

ability for the entire trajectory. This path covers about

2 kilometres and takes about 10 minutes. The Ekinox-

D IMU was conﬁgured with a sampling rate of 200

Hz, while internal Ekinox-D GNSS receiver was con-

ﬁgured to operate at 5 Hz.

Although various sensors are part of this data

set, in this work only measurements from Ekinox-D

device by SBG Systems (SBG Systems, 2016) are

GISTAM 2017 - 3rd International Conference on Geographical Information Systems Theory, Applications and Management

204

Figure 4: The kinematic trajectory in the city of Turin (cour-

tesy of Google Earth (Google Earth, 2016)).

taken into account. Ekinox-D equipment consists

of a tactical-grade IMU and an internal dual-antenna

GNSS receiver (GPS + GLONASS).

Before the logging of measurements, inertial in-

strumentation needs to be calibrated. This step allows

the Ekinox-D system to calculate the approximate

values of the types of biases that vary at each switch

(run-to-run biases). Calibration of IMU is mandatory

in order to get usable information in a post-processing

stage. The calibration phase consists of a path of at

least ten minutes during which it is performed accel-

erations and braking at an average speed of at least 30

km/h, while performing some curves in both clock-

wise and anticlockwise directions. This procedure is

inconvenient to take place in an ordinary street and

was run at an empty parking, as shown in Figure 5.

After the calibration phase, the entire trajectory

was logged without any stop, except of the common

stoppage due to trafﬁc. As seen in the top part of Fig-

ure 4, the kinematic trajectory also includes the ﬁnal

part of the calibration phase.

Figure 5: Calibration path at an empty parking.

3.2 Kinematic Reference Data Set

A reference data set is formed by processing

the Ekinox-D measurements using IE with tightly-

coupled integration with backward processing. GPS

data is corrected by using the TORI permanent sta-

tion (GNSS Positioning Service of Regione Piemonte

and Regione Lombardia, 2017) as a master GNSS sta-

tion, composed by a multi-constellation and multi-

frequency receiver. Its coordinates have millimetre

accuracy. This is the best possible PVA solution

that can be obtained by using effectively all available

hardware and software resources. The reference data

set comprises attitude and position variables. It has a

sampling frequency of 1 Hz. Table 3 shows the av-

erage standard deviations for each variable from the

kinematic trajectory of Figure 4.

Table 3: Average standard deviations from the reference

data set.

Average standard

deviation

Roll 1.429E-2 deg

Pitch 1.468E-2 deg

Yaw 5.765E-2 deg

Latitude 5.674 mm

Longitude 5.743 mm

Altitude 10.087 mm

3.3 Comparison between NaveGo

Model and Inertial Explorer

The performances of NaveGo and Inertial Explorer

(IE) are compared using the kinematic trajectory de-

scribed in Section 3.1.

Model Validation of an Open-source Framework for Post-processing INS/GNSS Systems

205

IE is a closed-source, commercial software devel-

oped by NovAtel Inc. (NovAtel Inc., 2013), a Cana-

dian ﬁrm better known for manufacturing GNSS and

GPS receivers. IE is targeted for integration of IMU

sensors data with GNSS information. IE implements

both loosely-coupled (LC) and tightly-coupled (TC)

integrations. In turn, each integration mode can be

combined with forward or backward (smoothing) pro-

cessing. It is worth mentioning that this tool does not

provide any routine to analyse IMU errors by apply-

ing the Allan variance.

Since NaveGo only supports forward, loosely-

coupled integration, the kinematic data set is also pro-

cessed in IE with this type of solution. For the sake of

a fair comparison, the same values are input to both

frameworks before INS/GPS processing. These in-

put data are IMU errors (speciﬁed in Tables 1 and

2), GPS errors, initial position, initial velocity, initial

IMU alignment, and lever arm.

After IMU and GPS data are processed, NaveGo,

IE and GPS estimates are linear-interpolated accord-

ing to the reference time vector (Sec. 3.2). Table

4 shows the root-mean-squared errors (RMSE) from

NaveGo and IE both compared against the reference

data set. RMSE from GPS-only solution are also pro-

vided for analysing INS/GPS improvements in posi-

tion.

Table 4: RMSE from NaveGo, IE, and GPS-only against

the reference data set.

NaveGo Inertial GPS-only

Explorer

Roll 1.34E-01 6.66E-02 − deg

Pitch 3.42E-01 8.54E-02 − deg

Yaw 9.10E-01 2.36E-01 − deg

Latitude 0.877 1.014 0.906 m

Longitude 1.071 0.531 0.782 m

Altitude 1.035 0.932 1.175 m

It can be seen from Table 4 that efﬁciencies from

both frameworks are close. Nevertheless, IE presents

better performance in attitude. IE also presents bet-

ter estimates in longitude and altitude, but NaveGo

shows better accuracy in latitude. Finally, as observed

in the third column of Table 4, none of the two pack-

ages provides a notably higher performance in posi-

tion when compared with the GPS-only solution.

Since RMSE is an average on the squared dif-

ferences between measurements of interest and ref-

erence values on an entire data set, it can be consid-

ered as a coarse, preliminary performance examina-

tion. Consequently, it is important to make a more

detailed analysis and to verify from a statistical point

of view the results obtained from just one data set.

For statistically evaluating the differences of the

generated navigation estimates from both software

packages, a set of 100 uniformly and randomly sam-

ples is created, with the same pattern for the three

data sets, i.e., interpolated IE, interpolated NaveGo,

and reference. Each sample consists of a ﬁxed-length

window encompassing the same stretch on the three

data sets. The size of each selected stretch is 55 for

this test, which is around the 10% of the size of each

data set. Then, RMSE is calculated for each window.

The sampling distribution of the RMSE for each nav-

igation output is shown in box plots from Figures 6 to

8 for attitude, and from Figures 9 to 11 for position.

IE NaveGo

RMSE (deg)

#10

-3

Figure 6: Roll RMSE distribution over 100 samples.

IE NaveGo

RMSE (deg)

#10

-3

Figure 7: Pitch RMSE distribution over 100 samples.

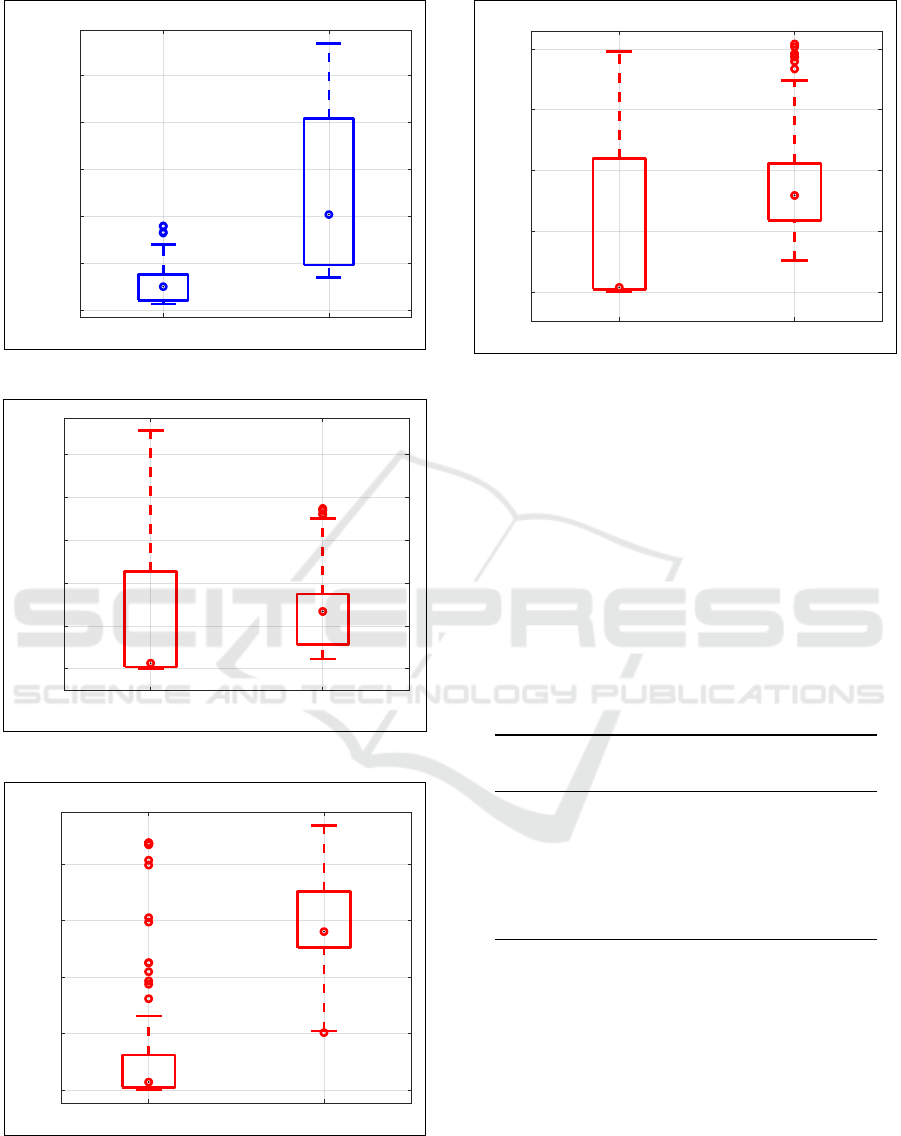
In general, IE framework shows one-magnitude

lower RMSE values when compared with NaveGo, a

situation that it is consequent with the results already

observed in Table 4. In particular, the IE RMSE distri-

bution is more concentrated around the median for at-

GISTAM 2017 - 3rd International Conference on Geographical Information Systems Theory, Applications and Management

206

IE NaveGo

0.005

0.01

0.015

0.02

0.025

RMSE (deg)

Figure 8: Yaw RMSE distribution over 100 samples.

IE NaveGo

0.5

1.5

2.5

RMSE (m)

Figure 9: Latitude RMSE distribution over 100 samples.

IE NaveGo

0.5

1.5

RMSE (m)

Figure 10: Longitude RMSE distribution over 100 samples.

titude (roll, pitch, and yaw). Such behaviour is not ob-

servable for the remaining three RMSE, latitude, lon-

gitude, and altitude, where IE shows more dispersion

IE NaveGo

0.5

1.5

RMSE (m)

Figure 11: Altitude RMSE distribution over 100 samples.

when compared to the position provided by NaveGo.

For statistically conﬁrming the differences shown

in Figures 6 to 11, a Student’s t-test is applied on the

sampled data. The Student’s t-test checks the null

hypothesis that both framework estimates have equal

means, i.e., no differences exist between them from

a statistical perspective. A p-value lower than 0.05

implies the rejection of the null hypothesis and gives

more conﬁdence on the results.

Table 5 shows the RMSE averages over 100 sam-

ples for both frameworks and the p-values for the six

navigation outputs.

Table 5: RMSE averages for 100 samples and p-values from

the Student’s t-test.

NaveGo Inertial P-value

Explorer

Roll 0.0016 0.0004 1.9E-13

Pitch 0.0054 0.0008 < 2.2E-16

Yaw 0.0132 0.0026 < 2.2E-16

Latitude 1.0E-07 9.3E-08 0.3471

Longitude 2.2E-07 6.4E-08 < 2.2E-16

Altitude 0.8741 0.5380 6.4E-05

With p-values considerably lower than 0.055, the

test concludes with a conﬁdence of 95% that a statis-

tical signiﬁcant difference between NaveGo and Iner-

tial Explorer is observable for all the navigation out-

puts except in the case of the latitude (highlighted in

bold font). In such case, a p-value of 0.3471 indi-

cates that it is not possible to conclude that a differ-

ence exists between both latitudes. To sum up, the

test results prove to be consistent with the differences

observables in Table 4 and the box plot ﬁgures.

Model Validation of an Open-source Framework for Post-processing INS/GNSS Systems

207

4 CONCLUSIONS

In this work, the performance of NaveGo mathemat-

ical model, an open-source MATLAB/GNU Octave

toolbox for Allan variance analysis and INS/GNSS

integration, is contrasted with Inertial Explorer, a

closed-source, commercial software package.

Firstly, Allan variance procedure by NaveGo is

exposed for characterising the errors of a tactical-

grade IMU. It is explained how the time vector for

Allan variance analysis is formed.

Then, performances of NaveGo and Inertial Ex-

plorer are compared for a real-world trajectory. It is

concluded that NaveGo presents similar accuracy to

Inertial Explorer, although the later has better preci-

sion in attitude. On the other hand, a detailed sta-

tistical analysis reveals that NaveGo presents a more

uniform distribution of RMSE in position.

Finally, the validation methodology unfolded in

this work points out that NaveGo algorithms for at-

titude estimation still have some room for improve-

ment, and some software development effort has to

be put into this direction for future work.

REFERENCES

Advanced Navigation (2016). Kinematica reference man-

ual, v1.2 edition.

Allan, D. W. (1966). Statistics of atomic frequency stan-

dards. Proceedings of the IEEE, 54(2):221–230.

Dabove, P., De Agostino, M., and Manzino, A. M. (2011).

Mass-market L1 GPS receivers for mobile mapping

applications: A novel approach. In Proceedings of

the 24th International Technical Meeting of The Satel-

lite Division of the Institute of Navigation (ION GNSS

2011), pages 1068–1074. ION.

Dabove, P., Gonzalez, R., Catania, C., and Piras, M.

(2017). NaveGo: an open-source software for inte-

grated GPS/IMU positioning (in Italian). In Confer-

ence on free open-source software and geographical

data (FOSS4G-IT), Genoa, Italy.

El-Sheimy, N., Hou, H., and Niu, X. (2008). Analysis

and modeling of inertial sensors using Allan variance.

IEEE Transactions on instrumentation and measure-

ment, 57(1):140–149.

Giroux, R., Landry, R. J., Leach, B., and Gourdeau, R.

(2003). Validation and performance evaluation of a

Simulink inertial navigation system simulator. Cana-

dian Aeronautics and Space Journal, 49(4):149–161.

GNSS Positioning Service of Regione Piemonte and

Regione Lombardia (2017). Network stations.

http://www.spingnss.it/spiderweb/frmIndex.aspx.

Gonzalez, R. (2016). NaveGo: an open-source MAT-

LAB/GNU Octave toolbox for simulating integrated

navigation systems and performing Allan variance

analysis. URL: www.github.com/rodralez/NaveGo/.

Gonzalez, R., Giribet, J. I., and Pati

no, H. D. (2015a). An

approach to benchmarking of loosely coupled low-

cost navigation systems. Mathematical and Computer

Modelling of Dynamical Systems, 21(3):272–287.

Gonzalez, R., Giribet, J. I., and Pati

no, H. D. (2015b).

Navego: a simulation framework for low-cost inte-

grated navigation systems. Journal of Control Engi-

neering and Applied Informatics, 17(2):110–120.

Google Earth (2016). Politecnico di Torino, Italy.

45.0625673187 N, 7.6574702408 W. Date of original

imagery: 8/6/2016. Date accessed: 12/18/2016.

Groves, P. D. (2008). Principles of GNSS, Inertial, and

Multisensor Integrated Navigation Systems. Artech

House, USA.

Howe, D. A., Allan, D., and Barnes, J. (1981). Proper-

ties of signal sources and measurement methods. In

Thirty Fifth Annual Frequency Control Symposium.

1981, pages 669–716. IEEE.

IEEE-SA Standards Board (1998). IEEE Standard Speciﬁ-

cation Format Guide and Test Procedure for Single-

Axis Interferometric Fiber Optic Gyros. IEEE Std

952TM-1997 (R2008). IEEE, 2008 edition.

MicroSurvey (2016). Startnet website. URL:

http://www.microsurvey.com/products/starnet/.

Navidi, N. and Landry, R. J. (2015). A new survey on

self-tuning integrated low-cost GPS/INS vehicle nav-

igation system in harsh environment. The Interna-

tional Archives of Photogrammetry, Remote Sensing

and Spatial Information Sciences, 40(1):75.

Niu, X.-j., Zhang, Q., Gong, L.-l., Liu, C., Zhang, H., Shi,

C., Wang, J., and Coleman, M. (2015). Development

and evaluation of GNSS/INS data processing software

for position and orientation systems. Survey Review,

47(341):87–98.

NovAtel Inc. (2013). Inertial Explorer

 User Guide ver-

sion 8.50, OM-20000106, Rev 9. Canada.

Piras, M. and Dabove, P. (2016). Comparison of two differ-

ent mass-market imu generations: bias analyses and

real time applications. In 2016 IEEE/ION Position,

Location and Navigation Symposium (PLANS), pages

34–41.

Sargent, R. G. (2013). Veriﬁcation and validation of simu-

lation models. Journal of Simulation, 7(1):12–24.

SBG Systems (2016). Ekinox-D: Dual GPS INS leaﬂet, v1.2

edition.

Spatial Engineering Research Centre, University of Canter-

bury (2017). POINT software leaﬂet.

TerraTec AS (2017). TerraPos website. URL:

www.terratec.se/terrapos/cms/125.

Toth, C., Brzezinska, D., Politi, N., and Kealy, A. (2011).

Reference data set for performance evaluation of

MEMS-based integrated navigation solutions. In FIG

Working Week 2011, Marrakech, Morocco.

GISTAM 2017 - 3rd International Conference on Geographical Information Systems Theory, Applications and Management

208