FzMEBN: Toward a General Formalism of Fuzzy Multi-Entity
Bayesian Networks for Representing and Reasoning
with Uncertain Knowledge
Riali Ishak, Fareh Messaouda and Bouarfa Hafida
LRDSI Laboratory, Faculty of Science, University Blida 1, Soumaa BP 270, Blida, Algeria
Keywords: MEBN, Fuzzy Logic, Uncertainty, Vagueness, Fuzzy Multi-Entity Bayesian Networks.
Abstract: Good representing and reasoning with uncertainty is a topic of growing interest within the community of
artificial intelligence (AI). In this context, the Multi-Entity Bayesian Networks (MEBNs) are proposed as a
candidate solution. It’s a powerful tool based on the first order logic expressiveness. Furthermore, in the last
decade they have shown its effectiveness in various complex and uncertainty-rich domains. However, in
most cases the random variables are vague or imprecise by nature, to deal with this problem; we have to
extend the standard Multi-Entity Bayesian Networks to improve their capabilities for good representing and
reasoning with uncertainty. This paper details a promising solution based on fuzzy logic; it permits to
overcome the weaknesses of classical Multi-Entity Bayesian networks. In addition, we have proposed a
general process for the inference task. This process contains four steps, (1) Generating a Fuzzy Situation
Specific Bayesian Networks, (2) Computing fuzzy evidence, (3) Adding virtual nodes, and (4) finally, the
fuzzy probabilistic inference step. Our process is based on the virtual evidence method in order to
incorporate the fuzzy evidence in probabilistic inference, moreover, approximate or exact algorithms can be
used, and this choice of inference type depends to the contribution of the domain expert and the complexity
of the problem. Illustrative examples taken from the literatures are considered to show potential
applicability of our extended MEBN.
1 INTRODUCTION
Bayesian networks (BNs) (Pearl, 1988; Delcroix et
al., 2013) have been applied successfully to model
and resonate with the problems where uncertainty is
prevalent. it’s a hybrid model in which it is a
combination between the graph theory and the
probability theory, they can represent a qualitative
knowledge such as (dependencies between random
variable) and a quantitative knowledge
(probabilities), currently they have been widely used
in lots of fields such as medical diagnosis, risk
analytic…etc. Furthermore, in the last few years
various researchers tried to improve the classical
BNs by proposing new extensions such as the Multi-
Entity Bayesian Networks (MEBNs) (Laskey, 2008),
Object oriented Bayesian networks (Koller, 1997;
Liu et al.,2016)…etc., these extensions have been
proposed to enhance and enrich the classical BNs to
be expressive enough in order to better represent the
real world’s problems and complex systems.
On one hand, Multi-Entity Bayesian Networks
are proposed as an extension of the classical
Bayesian networks by integrating the first order
logic (FOL) in this later, in order to face the
randomness. But they are unable to represent the
vague and imprecise knowledge.
On the other hand, fuzzy logic and fuzzy sets
theory (Zadeh, 1975) were introduced to deal with
vague and imprecise knowledge. But they are
unable to represent and deal with the randomness.
Nowadays, the real world problems are not only
complex in its large structure but also, in the
knowledge's nature which involved within, where
the uncertainty is indispensible in many cases.
Furthermore, the most of real world problems
involve several kinds of the uncertainty at the same
time such as randomness, vagueness and imprecise
knowledge. It seems very important to develop a
hybrid models for good representing and reasoning
with such complex systems and real world’s
problems, where lot of kinds of uncertainty appear
simultaneously, for this reason, we propose a new
extension of the MEBNs we named FuZzy MEBN
520
Ishak, R., Messaouda, F. and Hafida, B.
FzMEBN: Toward a General Formalism of Fuzzy Multi-Entity Bayesian Networks for Representing and Reasoning with Uncertain Knowledge.
DOI: 10.5220/0006317205200528
In Proceedings of the 19th International Conference on Enterprise Information Systems (ICEIS 2017) - Volume 1, pages 520-528
ISBN: 978-989-758-247-9
Copyright © 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

(FzMEBN) using fuzzy logic and fuzzy sets theory
to benefit of the advantages of two models.
Moreover, as key feature of our FuZzy MEBN, is
very powerful model due to its capability to express
and reasoning over several kinds of uncertainty at
the same time, which is inherently present in lots of
real world problems.
The rest of this paper is organized as follow:
Section 2 explores the theoretical background.
Section 3 presents the related work. Then section 4
introduces a detailed presentation of the proposed
FuZzy-MEBN, including its detailed structure, and
the inference mechanism in this later. Finally, we
aim to conclude this paper and present some
perspectives and future works.
2 BACKGROUND
In this section we are going to give an outlook on
some background knowledge, we start by Multi-
Entity Bayesian Networks (Section 2.1), here after
we present the fuzzy logic (Section 2.2)
2.1 Multi-Entity Bayesian Networks
Multi-Entity Bayesian Networks extends Bayesian
networks to achieve the high level of expressivity of
First Order Logic (FOL). Where the capability of
BN to model uncertainty is combined with the
expressivity of FOL, in MEBN knowledge’s are
represented as a collection of MEBN Fragments
(MFrags) and a set of MFrags are organized into
MEBN Theories (MTheories).
An MFrag contains a collection of random
variables (RVs) and the dependencies among these
RVs are represented into fragment graph. In
addition, an MFrag can be considered as a template
or pattern to represents repeatable piece of
knowledge fragments of a Bayesian network; an
MFrag is defined as F = (C; I; R; G; D) (Laskey,
2008)
. It includes three types of nodes (RVs):
resident, input and context nodes. The local
conditional distribution also called local probability
distribution (LPD) for Resident nodes is defined in
the home MFrag, while an input node has its LPD
defined in another MFrag (it is a resident node
defined in another MFrag). The context nodes
defined in order to represent a set of logical
constraints that must be satisfied for the distributions
represented in the MFrag be valid. Furthermore, G
represents an MFrag graph, and D is a set of local
distributions.
MEBN theory represents a coherent probability
distribution; while Bayes theorem provides a
mathematical foundation for learning and inference,
the inference in MEBN consists to instantiated it, i.e.
generate a Situation Specific Bayesian Network
(SSBN) in order to models the situation that has
been observed as evidence. Hence, this instantiation
overcomes the non-flexibility nature of Bayesian
networks where the structure kept fixed in the
classical Bayesian networks. Thus, the generated
SSBNs can use regular BN inference engines to
answer the query.
In (Laskey, 2008) the author presents a Bottom-
Up algorithm to generate SSBNs. More recent work
presented in (Santos et al., 2016), a new algorithm to
generate SSBNs based on the Bayes-Ball method,
this solution overcome the limitation presented in
the Bottom-Up algorithm, by focusing on the
scalability problem.
2.2 Fuzzy Logic
In the classical logic the variables are binary where
each variable can belong or not to a set, however, in
the fuzzy logic and fuzzy set theory an element can
belong in more than one set at the same time with
some degrees. This property allows to an element to
more or less strongly belong to a set, fuzzy logic and
fuzzy set theory were proposed by Zadeh (Zadeh,
1975) to manage imprecise and vague knowledge. It
is proposed as an extension of the binary logic, this
logic does not consist to be precise in the
affirmations, for example let ask this question” is the
speed of the car fast? “in the classical logic to
answer to this question we have to say “yes” if the
speed of the car is fast or “no” if the speed of the
car slow, however, in the fuzzy logic we can
represent the cases when the speed of the car is too
slow, slow, medium, fast, and too fast.
In fuzzy logic the variable speed can take many
values, and if we interpreted this variable as
“linguistic variable” the corresponding values
“linguistic values “are {too slow, slow, medium,
fast, and too fast}.
Each linguistic variable called fuzzy variable and
the linguistic value can be seen as a label to a fuzzy
sets.
The fuzzy sets can be represented with a
membership function μA.
Ax: x 0,1
Where μA(x) = 1 if x is belongs totally in A, μA(x)
= 0 if x does not belongs to A, and 0< μA(x) < 1 to
represent the partial belonging of x in the fuzzy set A.
Examples of membership functions presented in
Figure 1.
FzMEBN: Toward a General Formalism of Fuzzy Multi-Entity Bayesian Networks for Representing and Reasoning with Uncertain
Knowledge
521

Figure 1: membership functions (a) trapezoidal function
(b) triangular function (c) linear function.
3 RELATED WORK
The fuzzy Bayesian networks have been applied
successfully in many field such as fuzzy Bayesian
classification (Moura et al., 2015) and the Risk
analysis (Zhang et al., 2016)… etc. However,
combining of fuzzy logic with Bayesian networks is
a very difficult task due to the difference between
the two formalisms. In addition, the proposed
approaches are completely different because each
author used different notations from the others thus
there is no unified model to define the fuzzy
Bayesian networks as the classical Bayesian
networks, which makes this model very difficult to
understand and to work with.
To incorporate the fuzzy logic in Bayesian
networks several approaches have been proposed, an
approach based on weighted method, another
approach based on Fuzzy Probability Distribution,
and finally the virtual evidence method.
In the Weighted method (Tang et al., 2007; Mrad
et al., 2012), the main idea is to extend the different
rules used in the Bayesian networks by associating a
membership degree value to each rule as weight;
then the fuzzy Bayesian rules can be defined to
support the fuzzy Bayesian inference in FBN
model. As a limitation of this approach, the
algorithms of inference in Bayesian networks must
be also changed and updated. Because these
algorithms based on the standard Bayesian Equation.
In Fuzzy Probability Distribution method
(Fogelberg et al., 2008; Ryhajlo et al., 2013 ) the
fuzzy membership integrated directly in the
probability distribution, where in the first step the
fuzzy membership degree must be represented like a
probability distribution, then this later will be
integrated in the probability distribution in order to
generate the Fuzzy Probability Distribution, where
the Fuzzy Probability Distribution is a hybrid
representation of the fuzzy membership degree and
the probability distribution.
The virtual evidence it’s a method proposed in
(Pearl, 1988), in order to incorporate external
knowledge such as the uncertainty of evidence into
Bayesian networks as it mentioned in (Li, 2009).
Hence, this technique is used in (Pan et al., 1999) in
order to incorporate fuzzy membership values into a
Bayesian network. It consists to add a new node in
the DAG called virtual evidence node. And then we
can incorporate the fuzzy evidence in this later, the
fuzzy evidence will be represented as a probability
distribution in the conditional probability table
(CPT) of the virtual node. After adding the virtual
nodes and constructing the CPT of the virtual nodes
a standard Bayesian inference can be applied in
order to calculate the fuzzy inference, we can apply
a classical inference. We use this method in the
step of inference in the proposed FzMEBN due to its
effectiveness and its simplicity. An illustrative
example is considered in (section 3.2).
Furthermore, the matter of how to extend the
Multi-Entity Bayesian Networks is already devoted
in (Golestan et al., 2013; Golestan et al., 2015),
where the authors tried to enhance the classical
MEBN to support fuzzy logic and apply this later in
the context of the data-fusion, in their extension they
replaced the First Order Logic by the First Order
Fuzzy Logic (FOFL) when defining the contextual
and semantic constraints. Moreover, they extend the
definition of MFrag by adding fuzzy rules “if-then
rules” in this extension where the crisp MFrags were
slightly modified by annotating each MFrag F by a
set of fuzzy if-then rules that are used by a Fuzzy
Inference System (FIS).
The inference process in the Fuzzy MEBN is
also been discussed, after the generation of the
SSFBN (Situation Specific Fuzzy Bayesian
networks), we can apply the new version of the
modified Clique Tree (CT) algorithm to tackle
inference in FBNs. In addition the modified
algorithm based on the belief propagation where the
authors treated three cases and all these three cases
based on weighted formulas using both the
membership degrees and the probability
distributions. As drawback of this modification, the
inference must be done only by the modified Clique
Tree. However, in our extension we use the virtual
evidence method in order to allow the possibility to
the use of both an exact and approximate inference,
without any changes in these algorithms. And as we
know that the inference is an NP-complete problem
(Cooper, 1999). So, if we are limited in one exact
algorithm as their extension we may risk of a
computational explosion when the complexity of the
problem arise. Moreover, in the contrast to FMEBNs
cited above, in our extension we focus on extending
the components of the classical MEBN, especially
the most important one the MEBN fragments
(MFrags). Where in our extension a Fuzzy-Mfrag
ICEIS 2017 - 19th International Conference on Enterprise Information Systems
522

can be seen as template for repeatable Fuzzy small
knowledge, Based on hybrid Mfrags (a combination
of fuzzy and crisp nodes) and in the step of the
inference and after the instantiating we will have a
hybrid directed acyclic graph (DAG) and this later
contains two type of node (fuzzy, and crisp). The
next section will be devoted to the presentation of
our solution.
4 THE PROPOSED FUZZY
MULTI-ENTITY BAYESIAN
NETWORKS (FzMEBN)
The contribution in this paper is to propose a new
extension of the classical Multi-Entity Bayesian
networks (MEBN) as an answer to the need of
representing randomness, vague and imprecise
knowledge at the same time, we have chosen to
extend this model due to their expressiveness and
power of reasoning. The idea behind our extension is
to add new types of nodes in Multi-Entity Bayesian
Networks to represent the vague and imprecise
knowledge’s as it illustrated in the figure 2.
4.1 Modeling with FzMEBN
FuZzy Multi-Entity Bayesian Network is
enhancement of the classical Multi-Entity Bayesian
Network to benefit the power of the fuzzy logic, thus
improve the expressiveness of classical MEBNs in
order to well represent knowledge’s of the real
world’s problems and situations. As the classical
MEBN the FuZzy Mutli-Entity Bayesian Network
contains a set of FuZzy MFrags (FzMfrags)
organized into MTheories.
4.1.1 FuZzy MFrags 
Fuzzy MFrag (FzMFrag) is an extension which
enables the crisp MFrags to deal with vague and
imprecise knowledge’s, a Fuzzy MFrags F it’s a
hybrid template in which contains both the vague
and crisp nodes.
FzMFrag is a 7-tuple<C, R, I, F
R
, F
I,
G, D>:
 C is a set of crisp context nodes,
 R is a set of crisp resident nodes,
 Iis a set of crisp Input nodes.
 F
R
is a set of fuzzy resident nodes.
 F
I
is a set of fuzzy Input nodes.
 G represents a hybrid MFrag Graph (Fuzzy
MFrag Graph), and
 D represents the local distributions.
Context Nodes: these types of nodes are
Boolean random variables representing conditions
and constraints that must be satisfied to make a
distribution in an FzMFrag valid.
Input Nodes: these nodes can be seen as
«foreign nodes" or "pointers" referring to a resident
node defined in another FzMFrag. Its own
distributions defined in its home FzMFrag.
Fuzzy input Nodes:fuzzy input nodes are fuzzy
resident nodes defined in another FzMFrag, the
fuzzy input nodes can also influence the probability
distribution of the resident nodes, but its probability
Distribution and own membership functions are
defined in its own home FzMFrag.
Resident Nodes: Resident Node can be defined
as Function, Predicate, or Formula of First Order Logic
(FOL), and this node is attached by a probability
distribution.
Fuzzy resident Nodes: are extensions of the
classical resident nodes enabling the FzMFrag to
cope the vagueness and imprecise knowledge. As
the classical resident nodes the fuzzy resident nodes
are attached with a probability distribution. In
addition, they can represent the vagueness by using
the membership functions.
LEGEND
Figure 2: structure of the proposed Fuzzy MFrag.
FzMEBN: Toward a General Formalism of Fuzzy Multi-Entity Bayesian Networks for Representing and Reasoning with Uncertain
Knowledge
523

Formally a fuzzy resident node is 4-tuple <T, P,
Sfs, M>, where:
 T can be predicate or function or a first order
logic expression,
 P represents the probability distribution of the
fuzzy resident node,
 Sfs represent a set of fuzzy states of the resident
node, and
 M is a mapping rule which map every fuzzy state
of each fuzzy resident node to a fuzzy set. Per
each state ∈Sfs is attached with its own
membership function.
An example of Danger MFrag belongs to
Vehicle Identification MTheory (Park et al., 2013)
is presented in Figure 03.The Danger MFrags
contains:
a) Context nodes, where isA(obj, vehicle) and
isA(rgn, Region) are used in order to represent the
types of the ordinary variables (obj and rgn),
rgn=location (obj) represent a condition about the
variable rgn must be satisfied, and
b) An Input node called VehiculeType(obj) its
defined in another Mfrag, and
c) A resident node named Danger-level (rgn) to
represent the danger level of a region and this later
depends on the type of the vehicle located in this
region
Figure 3: Danger MFrag.
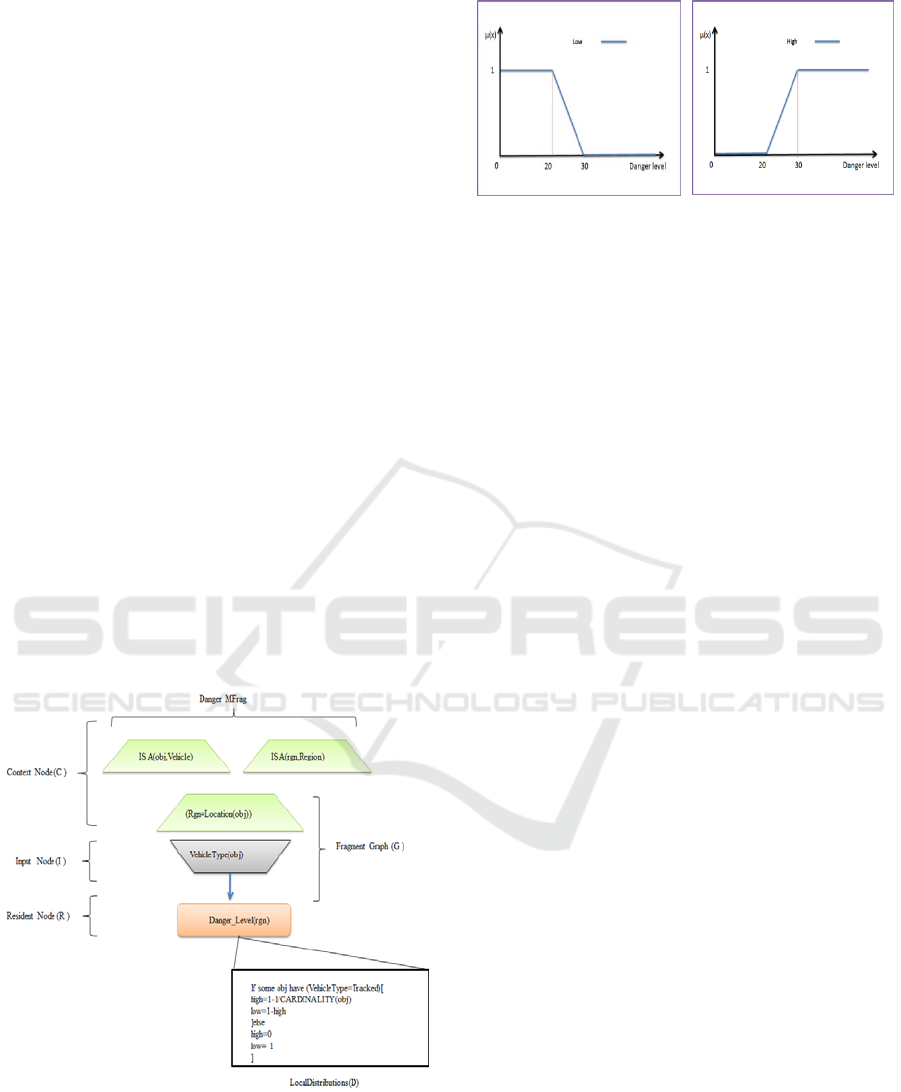
The Danger-level (rgn) node is fuzzy by nature and
it can take this set of Fuzzy states {high, low}.
The member ship functions to represent the fuzzy
states {low, high} presented in Figures 4, and 5.
Figure 4: Low danger
member ship function.
Figure 5: High danger
member ship function.
4.2 Fuzzy Probabilistic Inference in
FzMEBN
We believe strongly that the success of our
extension depends on it capability to provide a
strong mechanism for Fuzzy probabilistic reasoning.
Thus in this section we will explain how the fuzzy
probabilistic inference can be done in the FuZzy
Multi-Entity Bayesian networks (FzMEBN).
The inference in our extension consists to
generate a Fuzzy Situation Specific Bayesian
Networks (FSSBN) where the FSSBN is a fuzzy
Bayesian network contains the crisp and fuzzy
nodes, and then a fuzzy probabilistic inference based
on the virtual evidence method can applied in this
later in order to answer the queries. The process of
the inference in the FuZzy Multi-Entity Bayesian
Networks illustrated in the Figure 6.
Step 1 - Generating Fuzzy SSBN
The purpose of this step is to generate a Fuzzy
SSBN by executing a query, thus the generation of
the FSSBN achieved with the same manner as the
classical SSBN using Laskey algorithm (Laskey,
2008). Furthermore, each instance of a fuzzy
Resident node must be attached with a set of
membership functions and these last are similar to
the membership functions attached to the resident
node in which it belong.
The generation of the Fuzzy SSBN is held
according to algorithm 1.
ICEIS 2017 - 19th International Conference on Enterprise Information Systems
524

Figure 6: The inference process in the FuZzy MEBN.
Algorithm 1: Generating Fuzzy SSBN.
Inputs : <query List: L, knowledge base: k, FuZzyMEBN:
m, Fuzzy resident nodes list: FL >
Output: Probabilistic Network Net;
Begin:
01: Net=LaskeySSBNGenerator.generateSSBN (L, k, m);
02: For all N ∈ Net do
03: RgetResidentNodeName (N)
//Get the resident name in which this node was instantiated.
04: If (R ∈ FL) Then
//If the resident node is fuzzy.
05: Attach N with the same membership functions than R.
06: Endif
07: Done
End
Example of a Fuzzy Situation Specific Bayesian
Network FSSBN is presented in figures 7.
Figure 7: Fuzzy Situation Specific Bayesian Network
(FSSBN) (given v1, v2, and v3 as vehicle, and region1_1
as region).
Step 2- Computing Fuzzy Evidence
For each fuzzy node appear in the query the agent
must give the observed value, hereafter, the degrees
of membership of every state of every fuzzy node
can be calculated using the membership functions
attached to each fuzzy node.
Let LFMD be a list of fuzzy membership degrees
for all fuzzy node in the query i.e. The fuzzy
evidence, so FLMD can be defined as:
LFMD={ FMD
node1
, FMD
node2
………….FMD
noden
} where node
i
1< i<n are a fuzzy nodes and
FMD
nodei
=<
state1
,
state2
,………….
statem
>
represent the membership degrees for a fuzzy node
i
.
Occasionally, the sums of the membership degrees
of a linguistic variable are not well-defined as it’s
discussed in (Waltman et al., 2005). To deal with
this problem we normalize each membership degree
μ



as flows:

̅
satatejx 
μ
∑
μstateix
||


(1)
For example the agent executes this query on the
generated Fuzzy SSBN:
P (VhiculeType_v2=tracked| Danger_level_region1_1=high).
In this case the danger level node is fuzzy and it
appear in the query, so let assume that the observed
level of danger is 27 %, so 
high
(27)=0.7and

low
(27) = 0.3 calculated using “Low”, and “High”
membership functions attached to the
Danger_leve_region1_1 node.
LFMD= {FMD
Danger_leve_region1_1
}={ <
low
,
high
>}={<0.3,0.7>}.
The computation of the fuzzy evidence is held
according to the algorithm 2.
FzMEBN: Toward a General Formalism of Fuzzy Multi-Entity Bayesian Networks for Representing and Reasoning with Uncertain
Knowledge
525

Algorithm 2: Computing the Fuzzy evidence
Input : < list of observed values: L, Fuzzy resident nodes list:
FL >
Output: LFMD Lmd.
Begin:
01: Lmd= Φ.
02: i  1.
03: While i < = |FL| do //Get the observed value for the
node i 04: ObservedVi getVlaueL(i);
//Calculate the membership degrees for each state i ∈ node i
05: FMD
nodei
=<μ
state
1
(ObservedVi)…… μ
state
m
(ObservedVi )>;
06: If (FMD
nodei
is not normalized) Then
07: Normalize each state using equation (1);
08: Update FMDnodei;
09: Endif
10: ADD (FMD
nodei,
Lmd) ;
11: Done
End
Step 3- Adding the virtual nodes
For each fuzzy node appear in the query of the
agent, a child node will be added automatically, then
the normalized membership degrees calculated using
step 2 will be incorporated in the CPT of the virtual
node as probability distributions.
The “Danger_level_region1_1” node appears in
the query of the agent and it is fuzzy. So a virtual
node will be added as it illustrated in the figure 8.
The step of adding the virtual nodes is held
according to the algorithm 3.
Algorithm 3: Adding the virtual nodes.
Input :< FLMD: Flm,Fuzzy resident nodes list: FL , FSSBN :
BN>
Begin:
01: For all nodei ∈ Fl do
//Get the membership degrees for the node i
02: FMD
nodei
=getFMD(Flm,i);
//Create a virtual node of the node i as a child
03: child create_Child (nodei, BN);
04: Incorporate FMD
nodei
in the CPT of child node;
05: ADD (child, FMD
nodei
);
06: Done
End
Figure 8: Fuzzy Situation Specific Bayesian Network
(FSSBN) with a virtual node.
Step 4- Fuzzy Probabilistic Inference
The fuzzy probabilistic inference can be done by
substituting each fuzzy node appears in the query by
its virtual node. Then a classical probabilistic
inference approximate or exact will be tackled.
The fuzzy probabilitic inference can be done
using the algorithm 4.
Algorithm 4: Fuzzy probabilistic inference.
Input :< query nodes X, Fuzzy Evidence Y, Fuzzy resident
nodes list: FL, FSSBN BN >
Output: Probability value;
Begin:
01: If( X ∈ FL) Then // if the query node is fuzzy
02: VgetVirtualNodeName(X, BN);
03: Substitute X by V;
04 Endif
05: For all N ∈ Y do
06: If (n ∈ FL) Then {if the node is fuzzy}
//Get the virtual node name of the node N from FSSBN
07: VgetVirtualNodeName(N, BN);
08: Substitute N by V in Y;
09: Endif
10: Done
11: Run a classical Bayesian inference using X and the new
evidence Y;
End.
In our example the Danger_level_region1_1 is fuzzy
so it will be substituted in the evidence by its chilled
virtual node “VirtualDanger_level_region1_1”.To
make the notation easy we note VhiculeType_v2 as
V2, Danger_level_region1_1 as D1,
Virtual_Danger_level_region1_1 as V_D1, High as H
and Low as L.
Then the new query taken V_D1 as evidence:
PV2  Tracked|D1  H  PVT2  Tracked|V_D1  H.
ICEIS 2017 - 19th International Conference on Enterprise Information Systems
526


_|∗
_
.

_|∗
_|∗



_|∗
.
Noting that
PV_D1  H|D1  H and P

V

H
|
D1  L

represents the membership degrees incorporated in
step 3 in the CPT of the virtual node respectively 
high
and 
low
.
5 CONCLUSIONS
The overall goal of this paper is to develop a
solution to deal with vague and imprecise
knowledge in MEBNs, thus dealing with tow kind of
uncertainty at the same time, for this, we have
introduced a new extension of the Multi-Entity
Bayesian Networks based on fuzzy logic in order to
improve the classical MEBN by extending the
classical MFrags to a FuZzy MFrags, our approach
based on a strong probabilistic graphical model
enabling the reasoning with uncertainty under a
complex problems. Moreover, we have proposed a
complete process to do the fuzzy inference in the
extended MEBNs, where the inference task in
FzMEBN is divided in four steps, the first one
consist to generate a minimal fuzzy Bayesian
networks (Fuzzy SSBN) capable to answer the query
as the classical MEBN using Laskey algorithm . The
second one consists to computing the fuzzy
evidence, the third consist to incorporate the fuzzy
evidence in the Fuzzy SSBN and finally, fuzzy
Bayesian inference can be done using classical
Bayesian inference on the generated Fuzzy SSBN.
Currently, we are focusing on evaluating the
ability of the proposed FuZzy Multi-Entity Bayesian
Networks by apply it on a complex real world
problems, thus in our next work we are interesting to
evaluate the performance of our solution taking the
diabetes disease as a case of study.
REFERENCES
Cooper, G. F. (1990). The computational complexity of
probabilistic inference using Bayesian belief
networks. Artificial intelligence, 42(2), 393-405.
Delcroix, V., Sedki, K., &Lepoutre, F. X. (2013). A
Bayesian network for recurrent multi-criteria and
multi-attribute decision problems: Choosing a manual
wheelchair. Expert systems with applications, 40(7),
2541-2551.
Fogelberg, C., Palade, V., &Assheton, P. (2008).Belief
propagation in fuzzy bayesian networks. In 1st
International Workshop on Combinations of
Intelligent Methods and Applications (CIMA) at
ECAI’08 (pp. 19-24).
Golestan, K., Karray, F., &Kamel, M. S. (2013, July).
High level information fusion through a fuzzy
extension to multi-entity Bayesian networks in
vehicular ad-hoc networks. In Information Fusion
(FUSION), 2013 16th International Conference
on (pp. 1180-1187).IEEE.
Golestan, K., Karray, F., &Kamel, M. S. (2015, August).
An integrated approach for fuzzy multi-entity bayesian
networks and semantic analysis for soft and hard data
fusion.In Fuzzy Systems (FUZZ-IEEE), 2015 IEEE
International Conference on (pp. 1-8).IEEE.
Koller, D. and Pfeffer, A. (1997).Object-oriented Bayesian
networks. In Uncertainty in Artificial Intelligence:
Proceedings of the Thirteenth Conference, San
Francisco, CA: Morgan Kaufmann.
Laskey, K. B. (2008). MEBN: A language for first-order
Bayesian knowledge bases. Artificial
intelligence, 172(2), 140-178.
Li, X. (2009, August). On the use of virtual evidence in
conditional random fields. In Proceedings of the 2009
Conference on Empirical Methods in Natural
Language Processing: Volume 3-Volume 3 (pp. 1289-
1297).Association for Computational Linguistics.
Liu, Q., Tchangani, A., &Pérès, F. (2016).Modelling
complex large scale systems using object oriented
Bayesian networks (OOBN). IFAC-
PapersOnLine, 49(12), 127-132.
Moura, G., &Roisenberg, M. (2015, August). Probabilistic
Fuzzy Bayesian Network. In Fuzzy Systems and
Knowledge Discovery (FSKD), 2015 12th
International Conference on (pp. 476-482). IEEE.
Mrad, A. B., Delcroix, V., Maalej, M. A., Piechowiak, S.,
&Abid, M. (2012, July). Uncertain evidence in
Bayesian networks: Presentation and comparison on a
simple example. In International Conference on
Information Processing and Management of
Uncertainty in Knowledge-Based Systems (pp. 39-48).
Springer Berlin Heidelberg.
Pan, H., & Liu, L. (1999). Fuzzy bayesian networks-a
general formalism for representation, inference and
learning with hybrid bayesian networks. In Neural
Information Processing, 1999. Proceedings.
ICONIP'99. 6th International Conference on (Vol. 1,
pp. 401-406). IEEE.
Park, C. Y., Laskey, K. B., Costa, P., & Matsumoto, S.
(2013). Multi-entity bayesian networks learning in
predictive situation awareness. George mason univ
Fairfax va volgenau school of Information technology
and engineering.
Pearl J (1988) Probabilistic reasoning in intelligent
systems: networksof plausible inference. Morgan
Kaufmann Publishers, SanMateo.
Ryhajlo, N., Sturlaugson, L., & Sheppard, J. W. (2013,
September). Diagnostic Bayesian networks with fuzzy
evidence. In 2013 IEEE AUTOTESTCON (pp. 1-
8).IEEE.
Santos, L. L., Carvalho, R. N., Ladeira, M.,
&Weigang,(2016) L. A New Algorithm for Generating
FzMEBN: Toward a General Formalism of Fuzzy Multi-Entity Bayesian Networks for Representing and Reasoning with Uncertain
Knowledge
527

Situation-Specific Bayesian Networks Using Bayes-
Ball Method.
Tang, H., & Liu, S. (2007, August). Basic theory of fuzzy
Bayesian networks and its application in machinery
fault diagnosis. In Fuzzy Systems and Knowledge
Discovery, 2007.FSKD 2007. Fourth International
Conference on(Vol. 4, pp. 132-137). IEEE.
Waltman, L., Kaymak, U., & Van Den Berg, J. (2005). A
theoretical analysis of probabilistic fuzzy
systems (Doctoral dissertation, Master thesis
Informatics &Economics.Erasmus University
Rotterdam).
Zadeh L. (1975). The Concept of a Linguistic Variable
and its Application to Approximate Reasoning,
International Journal of Information Science, vol. 4, n°
4, p. 301-357.
Zhang, L., Wu, X., Qin, Y., Skibniewski, M. J., & Liu, W.
(2016). Towards a Fuzzy Bayesian Network Based
Approach for Safety Risk Analysis of Tunnel-Induced
Pipeline Damage. Risk Analysis, 36(2), 278-301.
ICEIS 2017 - 19th International Conference on Enterprise Information Systems
528