Investigating the Prioritization of Unit Testing Effort

using Software Metrics

Fadel Toure

, Mourad Badri

and Luc Lamontagne

Department of Mathematics and Computer Science, University of Quebec, Trois-Rivières, Canada

Department of Software Engineering and Computer Science, University of Laval, Quebec, Canada

Keywords: Tests Prioritization, Unit Tests, Source Code Metrics, Logistic Regression, Machine Learning.

Abstract: In object-oriented software, unit testing is a level of software testing where each individual class is tested by

a dedicated unit test class. Unfortunately, due to time and resources constraints, this phase does not cover all

classes. The testing efforts are often focused on particular classes. In this paper, we investigate an approach

based on software information history to support the prioritization of classes to be tested. To achieve this

goal, we first analyzed different attributes of ten open-source Java software systems for which JUnit test

cases have been developed for several classes. We used the mean and the logistic regression analysis to

characterize the classes for which JUnit test classes have been developed by testers. Second, we used two

classifiers trained on metrics values and unit tests information collected from the selected systems. The

classifiers provide, for each software, a set of classes on which unit testing efforts have to be focused. The

obtained sets have been compared to the sets of classes for which JUnit test classes have been developed by

testers. Results show that: (1) the metrics average values of tested classes are significantly different from the

metrics average values of other classes, (2) there is a significant relationship between the fact that a JUnit

test class has been developed for a class and its attributes, and (3) the sets of classes suggested by classifiers

reflect the testers’ selection properly.

1 INTRODUCTION

Testing plays a crucial role in software quality

assurance. It is, however, a time and resource-

consuming process. Unit testing is one of the main

phases of the testing process where each software

unit is early and individually tested using dedicated

unit test cases. In object-oriented (OO) software

systems, units are software classes and testers

usually write a dedicated unit test class for each

software class they decided to test. The main goal of

unit testing is to early reveal the faults of software

classes. In the case of large-scale OO software

systems, because of resources limitation and time

constraints, the unit testing efforts are often focused.

Testers usually select a limited set of software

classes for which they write dedicated unit tests.

Knowing that it is often difficult and not realistic to

test equally all software classes, it is important for

testers to target the most critical and fault-prone

ones. Unfortunately, the task is not obvious and

requires a deep analysis of software. In this paper,

we focus on unit testing of classes and particularly

on how to automatically target suitable classes for

unit testing using classifiers algorithms trained from

unit tests information and source code metrics.

A large number of OO metrics were proposed in

literature (Chidamber and Kemerer, 1994;

Henderson-Sellers, 1996). Some of these metrics,

related to different OO internal class attributes, were

already used in recent years to predict unit testability

of classes in OO software systems (Gupta et al.,

2005; Bruntink and Van Deursen, 2006; Badri et al.,

2010; Badri and Toure, 2011; Badri and Toure,

2012; Toure et al., 2014a; Toure et al., 2014b).

These studies have analyzed various open source

Java software systems and corresponding JUnit test

classes. One of the observations that have been made

in these studies is that unit test cases have been

developed only for a subset of classes. To the best

of our knowledge, no study focused on how the

selection of classes for which JUnit test cases have

been developed is made by testers, which criteria

have been considered for the selection of these

classes and how to automate or improve the

selection of classes on which unit testing efforts

have to be focused using source code metrics. One

Toure, F., Badri, M. and Lamontagne, L.

Investigating the Prioritization of Unit Testing Effort using Software Metrics.

DOI: 10.5220/0006319300690080

In Proceedings of the 12th International Conference on Evaluation of Novel Approaches to Software Engineering (ENASE 2017), pages 69-80

ISBN: 978-989-758-250-9

of the research questions we consider in this paper

is: can the selection of these classes (made by

testers) for unit tests be predicted or explained by

software classes’ attributes? As far as we know, this

issue has not been empirically investigated.

Understanding the testers’ selection criteria using

software metrics could help to: (1) know whether

these criteria are similar (reproducible) or not (from

one system to another), (2) characterize typical

software classes that require unit test cases to be

written, and (3) automate the selection of suitable

classes for the unit testing phase. In this case, we

could automatically determine the classes requiring

a more unit testing effort on which testers have to

focus to ensure software quality. We used, in this

study, some OO metrics to characterize software

classes. We considered three class attributes: size,

complexity and coupling, which we believe to be

determinative factors in the choice of testers. The

objective is first to identify the metrics that best

distinguish the classes for which unit test cases have

been developed by testers from other classes.

Software metrics will be used in a second step, in

combination with test information history, to explore

an automatic approach to prioritize the classes on

which the unit testing efforts have to be focused.

The rest of the paper is organized as follows.

Section 2 presents some related works. Section 3

presents the OO software metrics we used in our

study. Section 4 describes the data collection

procedure. Section 5 presents the empirical study

that we conducted. Section 6 focuses on the main

threats to validity related to the empirical

experimentations. Finally, Section 7 concludes the

paper, summarizes the contributions of this work

and outlines several directions for future

investigations.

2 RELATED WORK

Many researchers have proposed different tests

prioritization techniques in the literature. Test cases

prioritization has been widely discussed in the

context of regression testing, and from different

perspectives. The various proposed techniques are

based on different criteria such as fault detection,

coverage rates, software history information, and

risk analysis.

In fault detection based techniques, the main goal

is to run test cases that target the most fault prone

components.

Since these components are not known

in practice, the proposed techniques use different

factors of fault exposure as proxies, which can be

estimated in different ways from the software

artifacts. In a controlled environment, Rothermel et

al. (1999) showed that rescheduling test cases

improve the fault detection rate during regression

testing. The authors analyzed different test cases

scheduling techniques and used the APFD (Average

Percentage of Faults Detected) metric to compare

models’ performance. Yu and Lau (2012) proposed

a fault-based test cases prioritization that directly

utilizes the theoretical knowledge of their fault-

detecting ability. The technique is based on the

relationships between test cases and faults.

In coverage based techniques, the main goal is to

run test suites that cover most modified software

artefacts during regression testing. This goal leads to

fault detection rate improvement. Wong et al. (1997)

suggest a first prioritization strategy for regression

test case suites which optimizes the factor "cost

coverage" (branches that have undergone the

change). The authors focus on the prioritization of a

subset of test cases of a test suite by using a "safe

regression selection" technique. More complex

algorithms will be proposed by Mirarab et al.

(2007). The authors used Bayesian Networks to

build a unified model based on information provided

by CK metrics (Chidamber and Kemerer, 1994),

changes, and coverage rates. The defined approach

optimizes the coverage and, as a corollary, improves

the fault detection rate when compared to the

random test cases scheduling. The authors integrated

later an information feedback mechanism in the

Bayesian model in order to improve its

performances. However, the feedback mechanism

led to a relative slight improvement from the basic

Bayesian approach. Walcott and Kapfhammer

(2006) integrated time constraints in their

prioritization technique and used genetic algorithms

with artifact coverage rate as fitness function. The

authors considered different levels of software

artifacts granularity. Results showed a better APFD

value when considering the source code block level

of granularity. Rothermel et al. (1999) compared the

performances of different techniques. They describe

nine test cases prioritization techniques based on

random prioritization, coverage prioritization and

fault detection (using proxy) prioritization. They

reported the empirical results by measuring the

effectiveness of these techniques to improving fault

detection rate (AFPD). Results provide insights into

the tradeoffs among various techniques for test cases

prioritization.

The history based prioritization uses information

from the previous regression testing of the same

software system and current modification

information in order to prioritize the new test suites.

This makes the technique unsuitable for the first

ENASE 2017 - 12th International Conference on Evaluation of Novel Approaches to Software Engineering

regression testing of software. Porter and Kim

(2002) used the historical execution data to prioritize

test cases in a suite of regression tests. The authors

investigated the long run performance of

prioritization techniques based on data history

within environment under time and resources

constraints. The regression tests selection is driven

by the probabilities that integrate model features and

results of the previous test case execution. Lin et al.

(2013) investigate the weight of used information

between two versions of history based prioritization

techniques. The authors propose an approach that

mitigates the weight of information by integrating

the source code history of faults. Results indicated

that the approach provides a better fault detection

rate.

Some studies proposed mixing techniques based

on the history of faults detection and coverage

information. Carlson et al. (2011) conjectured that if

test cases have common properties, then test cases

within the same group may have similar fault

detection ability. The authors proposed a clustering

based prioritization technique that incorporates code

complexity, code coverage and system data history

of real faults. Applied to industrial software

products, results show that the approach could

improve the effectiveness of test cases prioritization

techniques.

Elbaum et al. (2004) analyzed the conditions into

which techniques are relevant. The authors observed

that the effectiveness of orientation techniques

varies a lot depending on various attributes of the

software and test suites. This makes difficult for a

practitioner to choose an appropriate prioritization

technique for a testing scenario. The problem has

been addressed by analyzing the fault detection rates

that result from applying several different

prioritization techniques to different programs and

their modified versions. Results provide insights and

conditions into which types of prioritization

techniques are or are not appropriate under specific

testing scenarios.

All previous techniques prioritize test suites in

the context of regression testing.

Some other

techniques allow, upstream, the prioritizing of

components to be tested. The main objective is to

optimize the testing effort to target the most fault

prone components. Boehm and Basili (2001)

proposed a Pareto distribution in which 80% of all

defects within software are found in 20% of the

modules. Ray and Mohapatra (2012) rely on the

Pareto distribution proposed by Boehm and Basili

(2001) to address the question of components

prioritization. The objective was to locate critical

parts of software code that present high risks of

faults (because of their complexity) and high impact

(because of their severity). The authors conducted an

empirical study on three small software systems.

Results indicated that the proposed approach

improves the test efficiency by targeting critical

bugs on systems. Shihab et al. (2010) explored the

prioritization for unit testing phase in the context of

legacy systems. They presented an approach that

assists testers with limited resources, to test legacy

systems efficiently. The technique leverages the

development history of a project to generate a

prioritized list of functions that managers should

focus their unit tests writing resources on. The

approach has been evaluated on two software

systems. The findings suggest that heuristics based

on the function size, modification frequency and bug

fixing frequency should be used to prioritize the unit

tests writing efforts for legacy systems.

The approach of Ray and Mohapatra (2012)

ignores the history of the software, whereas the

approach of Shihab et al. (2010) is not suitable for

new software because it requires own software

history information. Moreover, neither approach

takes advantage of the large amounts of information

available in software public repositories, coming

from the tests of various open-source software

systems. In this paper, we study the prioritization of

software classes to be tested for OO software

systems in the context of unit tests. We conjecture

that testers generally rely on class characteristics

which are captured by source code metrics, in order

to select the component for which they will write

dedicated unit tests. Thus, we propose an approach

that takes advantage of the experience of different

software testers as well as objective attributes of

software classes (metrics), in order to prioritize

classes for which unit test cases should be written.

3 SOFTWARE METRICS

We present, in this section, the OO source code

metrics we selected for the empirical study. These

metrics have received considerable attention from

researchers and are also being increasingly adopted

by practitioners. In fact, several studies have shown

that considered metrics are related to testability

(Bruntink and Van Deursen, 2004; Gupta et al.,

2005; Bruntink and Van Deursen, 2006; Badri et al.,

2010; Badri and Toure, 2011; Badri and Toure,

2012; Toure et al., 2014a; Toure et al., 2014b),

maintainability (Li and Henry, 1993; Dagpinar and

Jahnke, 2003; Zhou and Leung, 2007), and fault

proneness (Basili et al., 1996; Zhou and Leung,

2006; Aggarwal et al., 2009; Shatnawi, 2010).

Investigating the Prioritization of Unit Testing Effort using Software Metrics

Furthermore, these metrics have been incorporated

into several development tools. Two of the selected

metrics were proposed by Chidamber and Kemerer

(1994). We also include in our study the well-known

LOC metric. We give in what follows a brief

definition of each metric. The selected source code

metrics are related to three class attributes: coupling,

complexity and size.

Coupling between Objects: The CBO metric counts

for a given class, the number of other classes to

which it is coupled (and vice versa).

Weighted Methods per Class: The WMC metric

gives the sum of complexities of the methods of a

given class, where each method is weighted by its

cyclomatic complexity (McCabe, 1976). Only

methods specified in the class are considered.

Lines of Code per class: The LOC metric counts for

a given class its number of source lines of code.

The selected metrics have been computed using the

Borland Together Tool (http://www.borland.com).

4 DATA COLLECTION

4.1 Data Collection Procedure

The systems we selected for our study are of

different sizes and from different domains. In

addition, these systems have been developed by

different teams in Java. The selected systems have

been tested using JUnit framework. JUnit

(

http://www.junit.org/) is a simple Framework for

writing and running automated unit tests for Java

classes. The unit test cases in JUnit are written by

testers in Java. JUnit gives testers some support so

that they can write the test cases more conveniently.

A typical usage of JUnit is to test each class C

the software by means of a dedicated test class C

To actually test a class C

, we need to execute its test

class C

. This is done by calling JUnit’s test runner

tool. JUnit will report how many of the test methods

in C

succeeded, and how many failed.

By analyzing the code of the JUnit test cases of

the selected systems, we noticed that developers

usually name the JUnit dedicated test case classes by

adding the prefix (suffix) “Test” (“TestCase”) into

the name of the classes for which JUnit test cases

were developed. This observation has been the basis

for the identification of the link between classes and

corresponding JUnit test classes in other previous

studies (Bruntink and Van Deursen, 2006; Mockus

et al., 2009; Rompaey and Demeyer, 2009). In our

study, we adopted the same approach. The matching

procedure has been performed on the subject

systems by three research assistants separately in a

first step. Results have been checked, discussed and

validated in a second step. The software classes for

which JUnit test classes have such naming

mechanism are referred as tested classes. So, these

classes are the classes on which (in each system)

testers have deliberately focused while developing

unit test cases. We assign the modality 1 to the set of

tested classes and the modality 0 to the other classes.

In what follows, we will characterize and analyze

both categories of classes using statistics based on

source code metrics.

4.2 Selected Systems

We extracted information from the repositories of 10

open source OO software systems that were

developed in Java. For each system, only a part of

the classes has been tested using JUnit framework.

The selected systems are:

 ANT (http://www.apache.org/). ANT is a Java

library and command-line tool that drives processes

described in build files as target and extension points

dependent upon each other. This system consists of

713 classes with a total of roughly 64,000 lines of

code.

 DBU (http://dbunit.sourceforge.net/). DbUnit is a

JUnit extension (also usable with Ant) used in

database-driven projects that, among other things,

put a database into a known state between test runs.

This system consists of 238 classes with a total of

roughly 12,300 lines of code.

 IO

(https://commons.apache.org/proper/commons-io/).

Commons IO is a library of utilities for developing

Input/Output functionalities. It is developed under

Apache Software Foundation (ASF). This system

consists of 104 classes with a total of roughly 7,600

lines of code.

 IVY (http://ant.apache.org/ivy/). The agile

dependency manager known as IVY, is a popular

dependency manager. It is characterized by

flexibility, simplicity and tight integration with

Apache Ant. This system consists of 610 classes

with a total of roughly 50,080 lines of code.

 LOG4J (http://wiki.apache.org/logging-log4j/).

Log4j is a fast and flexible framework for logging

applications debugging messages. This system

consists of 252 classes with a total of roughly 20,300

lines of code.

 JFC (http://www.jfree.org/jfreechart/). JFreechart

is a free chart library for Java platform. This system

consists of 496 classes with a total of roughly 68,000

lines of code.

ENASE 2017 - 12th International Conference on Evaluation of Novel Approaches to Software Engineering

 JODA (http://joda-time.sourceforge.net/). JODA-

Time is the de facto standard library for advanced

date and time in Java. Joda-Time provides a quality

replacement for the Java date and time classes. The

design supports multiple calendar systems, while

still providing a simple API. This system consists of

225 classes with a total of roughly 31,000 lines of

code.

 POI (http://poi.apache.org/). POI is a Java APIs

for manipulating various file formats based upon the

Office Open XML standards (OOXML) and

Microsoft's OLE 2 Compound Document format

(OLE2). It can read and write MS Excel files using

Java. This system consists of 1,539 classes with a

total of roughly 136,000 lines of code.

 MATH (http://commons.apache.org/proper/

commons-math/). Commons MATH is a library of

lightweight, self-contained mathematics and

statistics components addressing the most common

problems not available in the Java programming

language or Commons Lang. This system consists of

125 classes with a total of roughly 8,106 lines of

code.

 LUCENE (http://lucene.apache.org/). LUCENE

is a high-performance, full-featured text search

engine library. It is a technology suitable for nearly

any application that requires full-text search,

especially cross-platform. This system consists of

659 classes with a total of roughly 56,900 lines of

code.

4.3 Descriptive Statistics

Table 1 summarizes the statistics of selected metrics

for the 10 systems. Note that for our investigations,

trivial artifacts like interfaces and pure abstract

classes have been removed from the data.

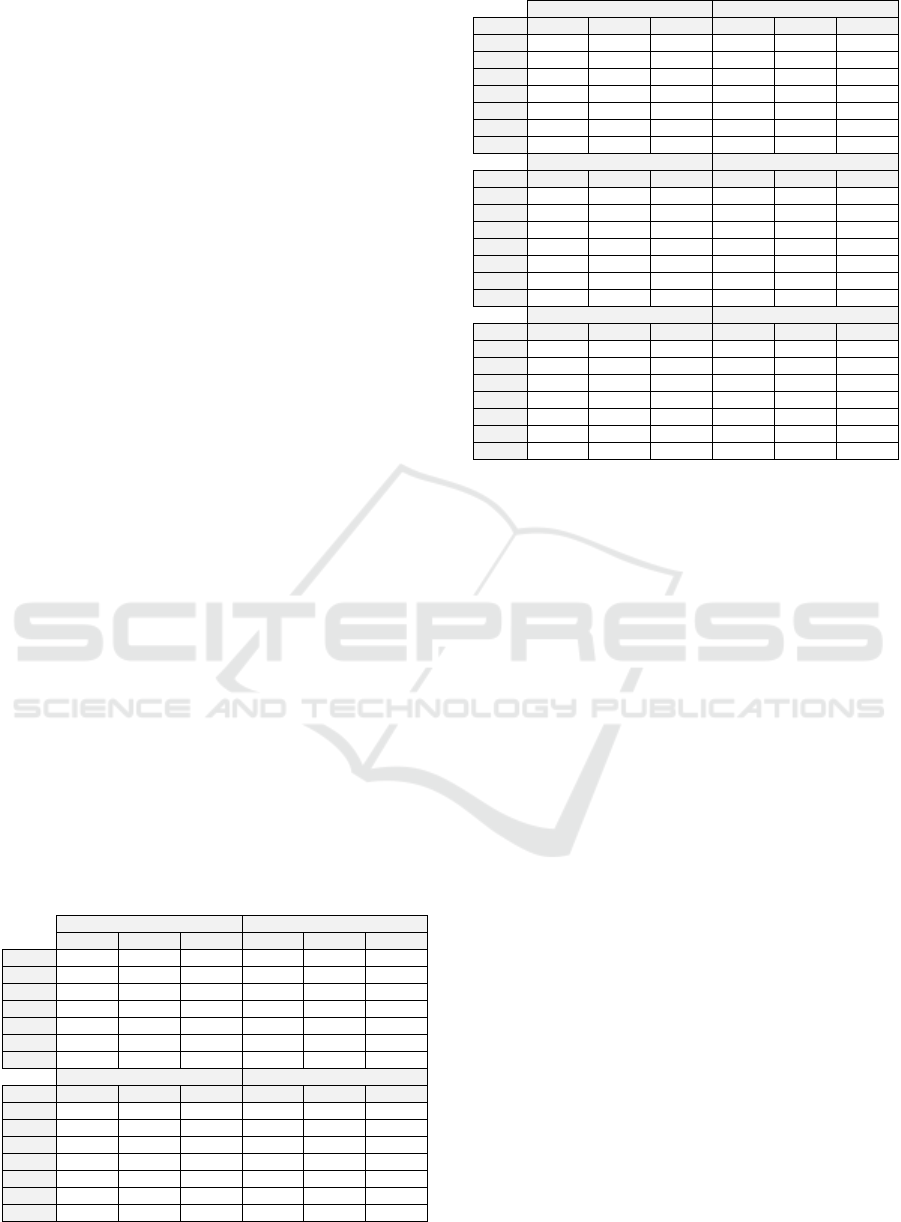
Table 1: Descriptive statistics of the source code metrics.

ANT JFC

CBO LOC WMC CBO LOC WMC

Obs. 663 663 663 411 411 411

Min. 0 1 0 0 4 0

Max. 41 1252 245 101 2041 470

Sum 4613 63548 12034 4861 67481 13428

µ 6.958 95.849 18.151 11.827 164.187 32.672

σ 7.25 132.915 24.168 14.066 228.056 46.73

Cv 1.042 1.387 1.332 1.189 1.389 1.43

DBU JODA

DBU CBO LOC WMC CBO LOC WMC

Obs. 213 213 213 201 201 201

Min. 0 4 1 0 5 1

Max. 24 488 61 36 1760 176

Sum 1316 12187 1989 1596 31339 6269

µ 6.178 57.216 9.338 7.94 155.915 31.189

σ 5.319 60.546 9.451 6.443 210.974 30.553

Cv 0.861 1.058 1.012 0.811 1.353 0.98

IO POI

IO CBO LOC WMC CBO LOC WMC

Obs. 100 100 100 1382 1382 1382

Min. 0 7 1 0 2 0

Max. 39 968 250 168 1686 374

Sum 405 7604 1817 9660 130185 23810

µ 4.05 76.04 18.17 6.99 94.2 17.229

σ 5.702 121.565 31.751 10.782 154.282 28.319

Cv 1.408 1.599 1.747 1.543 1.638 1.644

IVY MATH

IVY CBO LOC WMC CBO LOC WMC

Obs. 610 610 610 94 94 94

Min. 0 2 0 0 2 0

Max. 92 1039 231 18 660 174

Sum 5205 50080 9664 306 7779 1824

µ 8.533 82.098 15.843 3.255 82.755 19.404

σ 11.743 141.801 27.38 3.716 97.601 25.121

Cv 1.376 1.727 1.728 1.141 1.179 1.295

LOG4J LUCENE

LOG4J CBO LOC WMC CBO LOC WMC

Obs. 231 231 231 615 615 615

Min. 0 5 1 0 1 0

Max. 107 1103 207 55 2644 557

Sum 1698 20150 3694 3793 56108 10803

µ 7.351 87.229 15.991 6.167 91.233 17.566

σ 10.119 130.419 25.7 7.243 192.874 35.704

Cv 1.377 1.495 1.607 1.174 2.114 2.033

Table 1 shows that the selected software systems

are of different sizes. The lines of code vary from

7,600 lines spread over 100 software classes for IO

system, to more than 130,185 lines of code over

1,382 software classes for POI system. The number

of classes and their cyclomatic complexity follow

the same trend. Descriptive statistics also show 4

groups of systems according to the systems’ size: (1)

the small-size systems, about 100 software classes

such as IO and MATH, (2) the medium-size systems

around 200 classes as LOG4J, DBU and JODA, (3)

the large-size systems, between 400 and 600 classes

as LUCENE, IVY, ANT and JFC, and (4) the very

large-size systems over than 1,000 software classes

as POIs.

Note that the average cyclomatic complexity

varies widely between systems with similar sizes.

For example, JODA and DBU have a similar

number of classes (around 200) but quite a different

average of cyclomatic complexity (9.34 vs 31.18).

The systems LUCENE and JFC also have this

characteristic. In our data set, each observation

(software class) has, in addition to the metrics CBO,

LOC, and WMC, a binary attribute TESTED taking

modalities 1 or 0 to indicate whether it has been

tested (JUnit test class has been developed) or not.



5 EMPIRICAL ANALYSIS

5.1 Research Questions

We investigated the following research questions:

Investigating the Prioritization of Unit Testing Effort using Software Metrics

Q1: Can the sets of tested classes (in comparison to

the other classes) be characterized by source code

attributes?

Q2: Are there common criteria (in terms of class

attributes) used by testers to select the classes for

which they explicitly write unit test classes?

Q3: Can we automatically learn from the history of

the selection made by other testers on different

software systems using a suitable set of class

attributes to generate a set of classes similar to the

set of tested classes given by the testers of a new

system?

5.2 Goals

We investigate, in this section, the relationship

between class attributes and the fact that the class is

tested or not. We considered the source code metrics

CBO, LOC and WMC described previously as

observable (measurable) characteristics of software

classes. In a first step, we performed a Z-Test to

compare the mean values of the set of tested classes

to the mean values of the set of not-tested classes

(classes for which JUnit test classes have not been

developed). In a second step, we performed a

univariate binary logistic regression analysis. The

objective was to study the significance level of these

relationships with each metric. Finally, we used

machine learning classifiers in a third step, to

suggest a set of classes to be tested for a system

from its source code metrics and history test

information of other systems. The goal, in this case,

is to investigate to what extent the selection criteria

of classes to be tested in a given system are reusable

to support the test prioritization of classes for

another software system.

5.3 Mean Analysis

We relied on Z-Test of related samples to compare

the set of tested classes to the other classes for each

system. The Z-Test is typically used to compare the

means values of two large samples (>32

observations) of known variances. In our case, the

test will determine whether the set of tested classes

has a mean value of CBO, LOC and WMC

significantly different from the set of other classes.

We wanted to know whether the selected metrics

could significantly characterize both sets of classes.

We thus made the following null and alternative

hypotheses for each given system s and metric ms:

 H0: The ms mean value of tested classes

(modality 1) is not significantly different from the

ms mean value of other classes (modality 0).

 H1: The ms mean value of tested-classes is

significantly different from the ms mean value of

other classes.

The Z-Test determines a p-value that is

compared with the typical significance level α = 5%.

The p-value is the probability that the difference δ

between the mean values (μ) of two sets is not equal

to 0 by chance. The computed Z coefficient is

compared to a reference threshold (Z/Cree = 1.96 in

our case) for a normal distribution. We also

determined the standard deviation σ of each set.

Table 2 shows the results of the 10 analyzed

systems. The modalities 1 and 0 indicate

respectively the set of tested and not-tested classes.

We note that for almost all systems (except MATH),

the WMC and LOC mean values of tested classes

are significantly higher than those of not-tested

classes. For only MATH system, the difference of

WMC and LOC mean values of the two sets was not

significant: p-value of 0.092 and 0.143 (≥ 0.05). We

can generally, in the case of WMC and LOC, reject

the null hypothesis. The CBO metric seems to be

less discriminating between the two sets of classes.

Indeed, the mean differences between the sets are

not significant for LOG4J, MATH and IO systems.

This is not surprising and can be explained, among

other, by the level of observability of the software

source code attributes. Indeed, the lines of code

(LOC) and the high cyclomatic complexity (WMC)

are directly and more visible in the source code than

the level of coupling between classes. The incoming

coupling, captured by CBO, is not easily visible in a

single class source code. Indeed, identifying

coupling between classes requires global and deep

analysis of the system architecture. These

preliminary results suggest that the mean values of

software metrics of both sets of classes are

significantly different. The considered software

metrics (especially LOC and WMC) can distinguish

the set of tested classes from the set of not-tested

classes. This suggests the existence of relationship

between the software attributes captured by metrics

and the selection criteria considered by testers when

selecting software classes for which unit tests will be

written. We explore these relationships individually

in the following section.

5.4 Univariate Logistic Regression

Analysis

After characterizing the metrics mean values of

tested classes and not-tested classes sets, we present

in this section the empirical study we conducted to

evaluate individual relationship between each of

ENASE 2017 - 12th International Conference on Evaluation of Novel Approaches to Software Engineering

source code metrics (LOC, WMC and CBO) and the

status (tested or not) of software classes. We used

univariated logistic regression to analyze the

relationship between the considered OO metrics and

TESTED binary variable. Logistic Regression (LR)

is a standard statistical modelling method in which

the dependent variable can take on only one of two

different values. It is suitable for building software

quality classification models. It is used to predict the

dependent variable from a set of independent

variables to determine the percent of variance in the

dependent variable explained by the independent

variables. This technique has been widely applied to

the prediction of fault-prone classes (Basili et al.,

1996; Zhou and Leung, 2006; Aggarwal et al., 2009;

Shatnawi, 2010). LR is of two types: Univariate LR

and Multivariate LR. A multivariate LR model is

based on the following equation:









,



,…











∑



















∑















 

The Xis are the independent variables and the

(normalized) bis are the estimated regression

coefficients (approximated contributions)

corresponding to the independent variables Xis. The

larger the absolute value of the coefficient, the

stronger the impact of the independent variable on

the probability P. In our case, P is the probability of

a class to be tested. The univariate regression

analysis we used is, in fact, a special case of the

multivariate regression analysis, where there is only

one independent variable (one OO metric). The p-

value related to the statistical hypothesis is the

probability of the coefficient being different from

zero by chance and is also an indicator of the

accuracy of the estimated coefficient. To decide

whether a metric is a statistically significant

predictor of tested classes, we compared the

obtained p-value to α = 0.05. Nagelkerke R

defined as the proportion of the total variance in the

dependent variable that is explained by the model.

The higher R

is, the higher the effect of the

independent variables, and the more accurate the

model. We also calculated the area under ROC

(Hosmer and Lemeshow, 2000) curve (AUC) to

evaluate the model adjustment level with data. A

model is considered to be well-adjusted if the AUC

value is greater than 0.70 (Hosmer and Lemeshow,

2000). The results are summarized in Table 3. The

results indicate that ANT and JODA have a

significant R

values for all metrics (p-values <5%),

with an AUC value < 70%. The significant value of

suggests that the information provided by metrics

has significantly improved the baseline model.

Baseline model is the prediction model in which

probabilities are based on the distribution of

dependent variable modalities. The b coefficients are

all significant according to their p-values. However,

the models are not good predictors (AUC < 0.70) of

TESTED variable. For ANT system, this result may

be explained by the low unit test class coverage

(about 16.9%). For JODA, the explanation may lie

in the low rate of tested classes among the complex

classes. Indeed, the average WMC complexity of

JODA’s not-tested classes is of 22.94 vs 15.52 for

ANT. Finally, for both systems, a key factor of

classes that have been tested is related to their

cyclomatic complexity (WMC).

Logistic models derived from that metric have

the highest R

value (7.7% for ANT and 16% for

JODA). For the most of models, the IO and MATH

systems present a no-significant R

and b values and

a low predictive ability (AUC < 70%). For IO

system, the size factor (LOC), is an exception and

has a good performance (significant R

of 15.4%,

significant b of 1.053 and significant AUC of 0.710

> 0.7). The size seems to be one of the main factors

that explain the choice of the software classes to be

tested by testers.

The positive sign of the b coefficients indicates

that large classes were tested while the small classes

were not. The AUC greater than 0.70 suggests that

the model derived from LOC fits the data, which

means that obtained model could be a good predictor

of TESTED variable. The average size ratio of tested

over not-tested classes is of 2.55 with the absolute

highest Z value (3.08) according to Table 2. This

confirms the performance of the size (LOC) factor.

For JFC, DBU, POI, IVY, LOG4J and LUCENE

systems, we observe a significant b, and R

coefficients with higher AUC scores (> 0.70). In

these systems, the selection criteria of classes to be

tested are significantly explained by the considered

software metrics. We also note, when considering

previous results in Table 2, that the Z scores of these

systems are particularly high. This result can be

explained by the multiplicity of selection criteria for

unit testing or the existence of a strong correlation

between software metrics of the systems. JFC and

IVY have significant performance for all metrics. In

both systems, all the metrics appear to have been

considered during the selection of classes to be

tested (at least the attributes they capture). Note that

the coupling is the worst performing metric.

Coupling seems to be the least considered factor

when selecting classes to be tested.

Investigating the Prioritization of Unit Testing Effort using Software Metrics

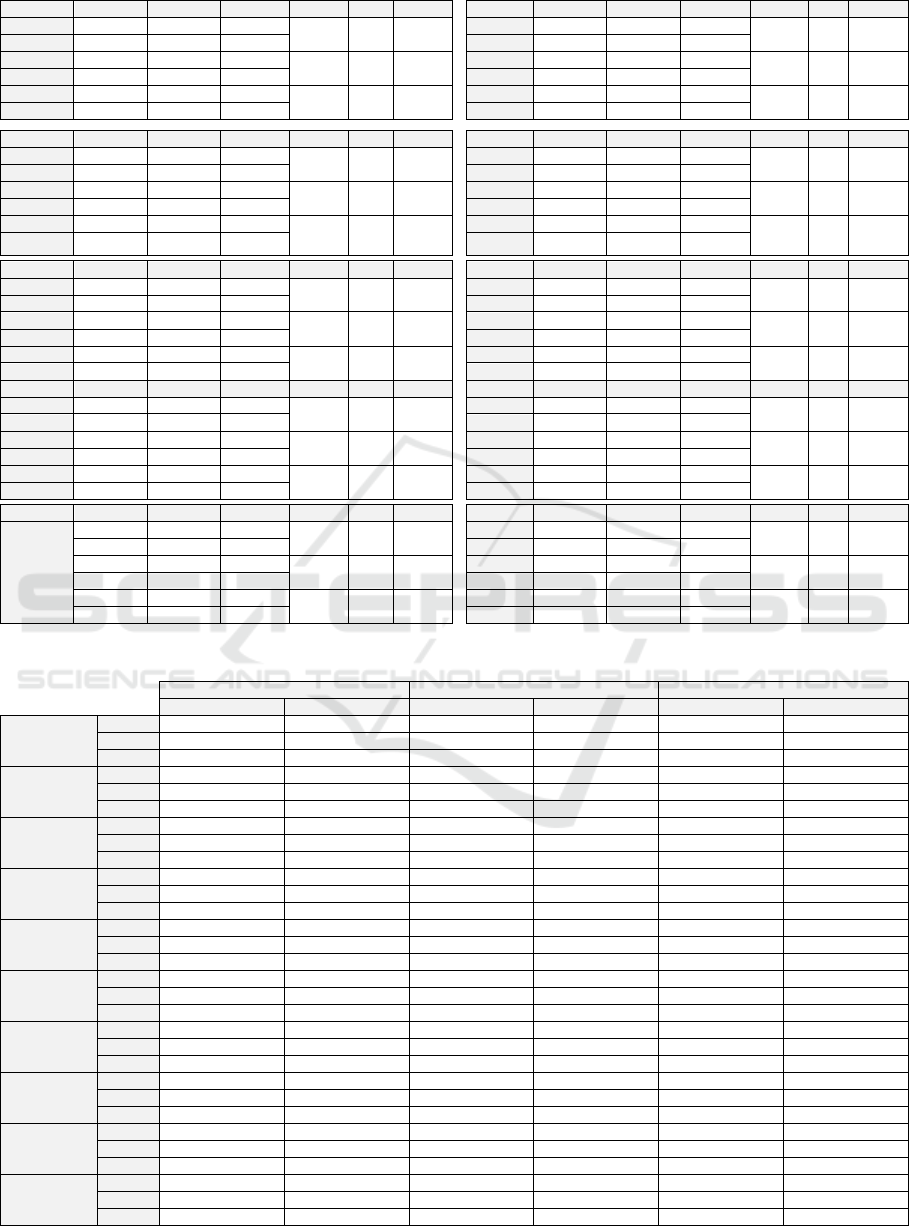
Table 2: Results of Z-Test.

ANT Obs. µ σ δ Z p-value JFC Obs. µ σ δ Z p-value

CBO | 1 112 10.41 8.6

-4.15 4.82 < 0.0001

CBO | 1 229 15.98 15.29

-0.4 -2.88 0.004

CBO | 0 551 6.26 6.75 CBO | 0 182 6.6 10.27

LOC | 1 112 157.45 154.72

-74.12 4.77 < 0.0001

LOC | 1 229 232 273.2

-74.12 -4.77 < 0.0001

LOC | 0 551 83.33 124.64 LOC | 0 182 78.86 104.61

WMC | 1 112 31.11 31.18

-15.59 5.05 < 0.0001

WMC | 1 229 46.28 57.17

-15.59 -5.05 < 0.0001

WMC | 0 551 15.52 21.61 WMC | 0 182 15.55 17.7

DBU Obs. µ σ δ Z p-value JODA Obs. µ σ δ Z p-value

CBO | 1 86 8.78 5.48

-4.36 -6.14 < 0.0001

CBO | 1 76 10.62 7.34

-4.31 -4.47 < 0.0001

CBO | 0 127 4.42 4.46 CBO | 0 125 6.31 5.26

LOC | 1 86 72.93 49.08

-26.36 -3.35 0.001

LOC | 1 76 231.89 279.65

-122.17 -3.55 0

LOC | 0 127 46.57 65.49 LOC | 0 125 109.72 138.41

WMC | 1 86 11.41 7.17

-3.47 -2.86 0.004

WMC | 1 76 44.75 39.98

-21.81 -4.46 < 0.0001

WMC | 0 127 7.94 10.56 WMC | 0 125 22.94 19.11

IO Obs. µ σ δ Z p-value POI Obs. µ σ δ Z p-value

CBO | 1 66 4.68 6.27

-1.86 -1.73 0.083

CBO | 1 387 10.76 13.72

-5.24 -6.96 < 0.0001

CBO | 0 34 2.82 4.34 CBO | 0 995 5.52 8.99

LOC | 1 66 95.85 144.34

-58.26 -3.08 0.002

LOC | 1 387 150.89 200.23

-78.74 -7.2 < 0.0001

LOC | 0 34 37.59 37.88 LOC | 0 995 72.15 125.65

WMC | 1 66 22.45 37.82

-12.6 -2.5 0.013

WMC | 1 387 29.08 37.94

-16.46 -8.03 < 0.0001

WMC | 0 34 9.85 11.37 WMC | 0 995 12.62 21.91

IVY Obs. µ σ δ Z p-value MATHS Obs. µ σ δ Z p-value

CBO | 1 95 18.23 16.1

-11.49 -6.73 < 0.0001

CBO | 1 58 3.24 3.82

-0.04 -0.05 0.963

CBO | 0 515 6.74 9.78 CBO | 0 36 3.28 3.65

LOC | 1 95 189.97 209.36

-127.77 -5.79 < 0.0001

LOC | 1 58 92.95 114.66

-26.61 -1.46 0.143

LOC | 0 515 62.2 115.33 LOC | 0 36 66.33 61.02

WMC | 1 95 34.47 38.66

-22.07 -5.39 < 0.0001

WMC | 1 58 22.31 30.35

-7.59 -1.69 0.092

WMC | 0 515 12.41 23.24 WMC | 0 36 14.72 12.56

LOG4J Obs. µ σ δ Z p-value LUCENE Obs. µ σ δ Z p-value

CBO | 1 44 8.41 8.1

-1.31 -0.9 0.366

CBO | 1 114 9.9 10.72

-4.59 -4.42 < 0.0001

CBO | 0 187 7.1 10.57 CBO | 0 501 5.32 5.89

LOC | 1 44 175.27 176.85

-108.76 -3.91 < 0.0001

LOC | 1 114 193.84 340.65

-125.96 -3.89 0

LOC | 0 187 66.51 107.84 LOC | 0 501 67.88 128.78

WMC | 1 44 34.16 43.04

-22.44 -3.4 0.001

WMC | 1 114 35.89 61.18

-22.49 -3.85 0

WMC | 0 187 11.72 17.19 WMC | 0 501 13.4 25.06

Table 3: Univariate logistic regression results.

CBO LOC WMC

values p-value values p-value values p-value

ANT

R² 0.066 < 0.0001 0.057 < 0.0001 0.077 < 0.0001

b 0.264 < 0.0001 0.238 < 0.0001 0.284 < 0.0001

AUC 0.667 0.684 0.694

JFC

R² 0.168 < 0.0001 0.235 < 0.0001 0.253 < 0.0001

b 0.532 < 0.0001 0.999 < 0.0001 1.124 < 0.0001

AUC 0.723 0.768 0.771

DBU

R² 0.214 < 0.0001 0.062 0.002 0.043 0.009

b 0.533 < 0.0001 0.266 0.004 0.207 0.012

AUC 0.762 0.756 0.755

JODA

R² 0.138 < 0.0001 0.116 < 0.0001 0.160 < 0.0001

b 0.392 < 0.0001 0.430 0.001 0.456 < 0.0001

AUC 0.670 0.690 0.679

R² 0.041 0.083 0.154 0.001 0.095 0.008

b 0.269 0.145 1.053 0.010 0.762 0.049

AUC 0.620 0.710 0.684

POI

R² 0.065 < 0.0001 0.071 < 0.0001 0.097 < 0.0001

b 0.284 < 0.0001 0.307 < 0.0001 0.389 < 0.0001

AUC 0.686 0.739 0.756

IVY

R² 0.160 < 0.0001 0.131 < 0.0001 0.105 < 0.0001

b 0.417 < 0.0001 0.369 < 0.0001 0.332 < 0.0001

AUC 0.792 0.805 0.779

MATH

R² 0.000 0.963 0.027 0.167 0.035 0.115

b -0.005 0.963 0.193 0.221 0.241 0.187

AUC 0.533 0.557 0.546

LOG4J

R² 0.004 0.465 0.136 < 0.0001 0.149 < 0.0001

b 0.061 0.450 0.419 0.000 0.471 0.000

AUC 0.599 0.786 0.799

LUCENE

R² 0.079 < 0.0001 0.086 < 0.0001 0.085 < 0.0001

b 0.284 < 0.0001 0.366 < 0.0001 0.391 < 0.0001

AUC 0.657 0.749 0.750

ENASE 2017 - 12th International Conference on Evaluation of Novel Approaches to Software Engineering

Overall, the logistic regression analysis

suggests that the criteria that guide the testers when

selecting software classes to be tested can be, in

most cases, well explained by cyclomatic

complexity, size and coupling.

5.5 Classifiers and Cross-System

Validation

We used machine learning classifiers trained on a

system’s test information data to provide a set of

classes to be tested for other software systems. The

objective of this experiment is to see to what extent

the criteria used by the testers to decide which

software classes they will test can be reused on

different systems. The hypothesis is the following:

Considering the values of CBO, LOC and WMC

metrics for all classes of a system S

for which

testers have already provided a set of tested classes,

is it possible to build a learner automatically which

is able to suggest, for another system S

, a set of

classes (to be tested) "similar" to the set of tested

classes that would have been proposed by S

testers?

Validating this hypothesis would indicate the

existence of class attributes that determine the

testers’ selection. From these attributes, it will then

be possible to build an automated tool that could

help to prioritize software classes during unit testing.

Such tool could rely on tests information and

associated class metrics automatically gathered from

different open source software repositories to

support automatic unit tests orientation.

We chose multivariate logistic (LR) regression

and Naive Bayesian (NB) classifier. Multivariate LR

is particularly suitable for the binary variables

prediction. It allows analyzing multiple output

parameters that may explain the classifier model

performance. Even if the NB classifier assumes a

strong hypothesis on sample data, the classifier is

particularly efficient and fast for large observations

size such as in our case. Furthermore, it requires a

relatively small training set, which is an advantage

when trainings are done on small systems. For both

classifiers, data collected from each of the 10

systems will be used in turn as training set and the

derived model will be cross-validated on the 9

remaining systems. In Table 4, LR and NB represent

the Multivariate Logistic Regression and Naïve

Bayes classifiers. The table presents, in each box,

the accuracy (1-error) of classifications obtained for

both classifiers, trained on the system dataset of

rows i, validated on the dataset’s system on column

j. The boxes in the diagonal (k, k) present the

adjustment (1 – optimistic error) of classifiers on the

dataset of system k. We interpret the performance of

classifiers by analyzing the results obtained

according to the training data (rows) and validating

data (columns). We consider the models with

accuracy values greater than 0.70 (error < 0.30) as

good classifiers. From Table 4, the analysis of

training and test data shows 4 groups of systems.

IO and MATH compose the first group. Both

systems have unpredictable testing information.

Furthermore, the unit test information from these

systems forms bad training sets. Indeed, the

classifiers trained from these datasets have no

predictive ability on the sets of tested classes of

other systems. Overfitting problems may explain the

low performances. Indeed, both classifiers provide a

good adjustment (LR: 0.74, NB: 0.71 for IO, LR:

0.745, NB: 0.723 for MATH), but cannot predict

any dataset from other systems (rows 4 and 9).

Furthermore, the small size of both systems reduces

the training data set (100 observations for IO and

125 for MATH) and may also explain the poor

performances observed on the 4

and 9

rows. In

software testing perspective, the overfitting results

of IO and MATH as training sets indicate that the

testers took into account specific criteria of the

systems when selecting the classes to be tested.

Those specific criteria are captured by our metrics

(Good adjustment values of classifiers) but are not

considered by testers of other systems. The fact that

no classifier trained on other systems were able to

accurately predict the test information of both

systems (columns 4 and 9) confirms the specificity

of the criteria used by IO and MATH testers.

In the second group, we find DBU system. The

trained classifiers have a little predictive ability on

other systems. LR and NB classifiers do not have the

same performances depending on the validating

systems. The LR classifier predicts IVY and

LUCENE test information accurately when NB

classifier provides good adjustment on DBU test set

(0.756). NB seems to overfitting DBU dataset as in

first group systems, but LR classifier does not over

fit the training data, according to the adjustment

values (0.664). The selection made by testers seems

to consider some of common and DBU specific

criteria captured by considered metrics.

The third group is composed of JFC and JODA

systems. The classifiers trained on the group have a

good predictive ability on other systems but their

testing information is not well predicted by other

groups (<0.7). The result may be obtained when the

selection made by testers mix common criteria

captured by metrics for some selected classes with a

random or different criteria that are not captured by

LOC, WMC and CBO for other classes.

Investigating the Prioritization of Unit Testing Effort using Software Metrics

The last group is formed of ANT, IVY, LOG4J,

LUCENE and POI. The classifiers trained on the

data from the fourth group of systems can accurately

predict test information of the other systems of the

group. This result indicates that the testers of

different systems used similar criteria that are

captured by the considered metrics. LR and NB

classifiers trained on JFC and JODA (from the third

group of systems) accurately predicted the unit test

information of this group, even if they are not well-

adjusted on their dataset.

The learning algorithms and cross-validation

results, especially for systems of the 4

group, show

that it is possible, based on only several metrics, to

construct classifier models from existing software

datasets that automatically suggest, for another

software system, a set of classes to be tested. For the

last group, the suggested set is more than 70%

similar to the set of tested classes that would have

proposed a tester knowing the system. Results also

indicate that the criteria for selecting tested classes

are relatively the same (consistent) and significantly

captured by CBO, LOC and WMC metrics.

6 THREATS TO VALIDITY

The study we conducted in this paper was performed

on 10 open-source systems containing almost a half

million of lines of code (453K). The sample is large

to allow obtaining significant results, but the

measuring methods and approaches have limitations

that can restrict the generalization of certain

conclusions. We have identified external validity

threats that can prevent the generalization of results

and construct validity threats which can skew the

measurements.

For external validity, the threats are mainly

related to the type and the domain of considered

systems. The application domains (Calculus, Code

Parsers, Graphic Charts, etc.) and types (Standalone

application, libraries, plugins etc.) of analyzed

systems may impact the selected metrics and reduce

the classifier performances during the cross system

validation. Indeed, some analyzed systems are

mathematical algorithms libraries (IO), while others

have more complex architectures and involve many

OO-technology specific artifacts such as inheritance

and polymorphism (JFC). Thus, the learning

algorithms that trained on some types of systems can

greatly adjust to validation datasets from systems of

similar domain and not able to suggest a good set of

classes (to be tested) for other types and domain

systems. It would be interesting, in this context, to

include the domain and the type of systems as

classifier parameters to take into account this bias.

On the other hand, the data we analyzed from the

different repositories does not provide any

information on selection criteria of tested classes. It

may be that, for some systems, tested classes were

randomly selected. In these cases, obtained models

and results cannot be generalized, even for software

systems in the same domain and type.

For construct validity, the main threat lies in the

technique used for matching JUnit test suites to

software classes to identifying the tested classes.

Indeed, unpaired software classes that are tested by

transitive method calls, are ignored by our approach.

Table 4: Cross-System Validations.

ANT JFC DBU JODA IO POI IVY MATH LOG4J LUCENE

ANT

0.833

0.513 0.596 0.692 0.360

0.728 0.820

0.404

0.823 0.816

0.778

0.628 0.629 0.692 0.390

0.735 0.814

0.394

0.779 0.813

JFC

LR 0.697 0.698 0.601 0.602 0.500

0.724 0.766

0.511

0.736 0.771

NB 0.632 0.689 0.685 0.597 0.530

0.707 0.730

0.511

0.701 0.736

DBU

LR 0.677 0.664 0.671 0.622 0.490 0.681

0.743

0.457 0.645

0.725

NB 0.511 0.684

0.756

0.448 0.600 0.627 0.617 0.489 0.589 0.571

JODA

0.796

0.620 0.620

0.711

0.390

0.721 0.814

0.415

0.779 0.807

0.742

0.681 0.620 0.692 0.420

0.721 0.799

0.457

0.771 0.800

LR 0.359 0.623 0.624 0.458

0.740

0.395 0.418 0.617 0.329 0.403

NB 0.403 0.652 0.667 0.413

0.710

0.505 0.454 0.628 0.494 0.433

POI

0.837

0.582 0.596 0.682 0.370

0.728 0.822

0.415

0.823 0.816

NB 0.605 0.681

0.709

0.527 0.540

0.718 0.725

0.511

0.714 0.712

IVY

0.828

0.511 0.596 0.622 0.340

0.726 0.822

0.383

0.801 0.820

0.707

0.696 0.634 0.667 0.480

0.728 0.786

0.479

0.749 0.772

MATH

LR 0.193 0.414 0.404 0.338 0.590 0.295 0.188

0.745

0.160 0.184

NB 0.363 0.606 0.521 0.478 0.620 0.418 0.400

0.723

0.411 0.405

LOG4J

0.804

0.577 0.554 0.647 0.440

0.728 0.818

0.436

0.840 0.816

NB 0.692 0.672 0.629 0.637 0.490

0.744 0.783

0.468

0.758 0.774

LUCENE

0.706

0.533 0.596 0.657 0.360

0.730 0.823

0.394

0.814 0.820

0.706

0.689 0.615 0.662 0.500

0.736 0.784

0.468

0.753 0.777

ENASE 2017 - 12th International Conference on Evaluation of Novel Approaches to Software Engineering

It would be possible to reduce this bias if we

consider a larger set formed by the union of classes

for which JUnit test classes have been written and

the classes that have been implicitly tested by

methods transitive calls.

7 CONCLUSIONS

We analyzed 10 open source software systems

containing more than 4400 classes for which testers

developed dedicated unit test classes using JUnit for

several classes of each system. The selection criteria

of classes that have been tested are not known. We

explored the possibility of explaining and reusing

these criteria for different systems through three

experiments using three source code metrics. We

first analyzed, for each system, the set of tested

classes and not-tested classes using the Z-Test.

Results show that for all metrics except CBO, the

mean values are significantly different and

consistent (the tested sets have higher average values

for LOC and WMC). Secondly, we performed a

binary univariate logistic regression analysis to

determine the individual effect of each metric on the

tested classes’ selection made by testers. Results

show a significant relationship with the considered

software metrics. We finally used multivariate LR

and NB classifiers to build models that support unit

tests prioritization. The goal was to compare classes

suggested by classifiers and the set of tested classes

provided by systems’ testers. The classifiers were

trained on each system dataset taken individually

and validated on the 9 remaining systems. Results

suggest that more than 70% of classes provided by

testers (tested classes) can be automatically

suggested by the classifiers. The results of this

experiment suggest the viability of a unit tests

prioritization automation technique using classifiers

trained on different software source code metrics

and history of the unit tests information. It would be

interesting to group systems according to their

domains, types and include other software source

code metrics such as RFC (Response For Class) to

observe the changes on results. It would also be

interesting to apply an adapted Leave-One-Out-

Validation technique (LOOV) by validating one

system with a classifier trained on the test

information of the remaining systems. We could

improve classifier performances, prevent overfitting

problems and be able to use more classifiers that

require a larger training datasets. Moreover, since

the proposed prioritization technique suggests a

slightly different (30%) set of classes from the

testers set of tested classes, it would be pertinent to

analyze and compare their actual performance on

covering faulty classes. This topic will be the next

direction of our investigations.

REFERENCES

Aggarwal K.K., Singh Y., Kaur A., and Malhotra R.,

2009. Empirical Analysis for Investigating the Effect

of Object-Oriented Metrics on Fault Proneness: A

Replicated Case Study, Software Process

Improvement and Practice, vol. 14, no. 1, pp. 39-62.

Badri L., Badri M. and Toure F., 2010. Exploring

Empirically the Relationship between Lack of

Cohesion and Testability in Object-Oriented Systems,

JSEA Eds., Advances in Software Engineering,

Communications in Computer and Information

Science, Vol. 117, Springer, Berlin.

Badri M. and Toure F., 2011. Empirical analysis for

investigating the effect of control flow dependencies

on testability of classes, in Proceedings of the 23rd

International Conference on Software Engineering and

Knowledge Engineering (SEKE '11).

Badri M. and Toure F., 2012. Empirical analysis of object

oriented design metrics for predicting unit testing

effort of classes, Journal of Software Engineering and

Applications (JSEA), Vol. 5 No. 7, pp.513-526.

Basili V.R., Briand L.C. and Melo W.L., 1996. A

Validation of Object-Oriented Design Metrics as

Quality Indicators, IEEE Transactions on Software

Engineering. vol. 22, no. 10, pp. 751-761.

Boehm B. and Basili V. R., 2001. Software defect

reduction top-10 list, Computer, vol. 34, no. 1, pp.

135–137.

Bruntink M., and Deursen A.V., 2004. Predicting Class

Testability using Object-Oriented Metrics, 4th Int.

Workshop on Source Code Analysis and Manipulation

(SCAM), IEEE.

Bruntink M. and Van Deursen A., 2006. An Empirical

Study into Class Testability, Journal of Systems and

Software, Vol. 79, No. 9, pp. 1219-1232.

Carlson R., Do H., and Denton A., 2011. A clustering

approach to improving test case prioritization: An

industrial case study, Software Maintenance, 27th

IEEE International Conference, ICSM, pp. 382-391.

Chidamber S.R. and Kemerer C.F., 1994. A Metrics Suite

for Object Oriented Design, IEEE Transactions on

Software Engineering, vol. 20, no. 6, pp. 476–493.

Dagpinar M., and Jahnke J., 2003. Predicting

maintainability with object-oriented metrics – an

empirical comparison, Proceedings of the 10th

Working Conference on Reverse Engineering

(WCRE), IEEE Computer Society, pp. 155–164.

Elbaum S., Rothermel G., Kanduri S. and Malishevsky

A.G., 2004. Selecting a cost-effective test case

prioritization technique, Software Quality Control,

12(3):185–210.

Gupta V., Aggarwal K.K. and Singh Y., 2005. A Fuzzy

Approach for Integrated Measure of Object-Oriented

Investigating the Prioritization of Unit Testing Effort using Software Metrics

Software Testability, Journal of Computer Science,

Vol. 1, No. 2, pp. 276-282.

Henderson-Sellers B., 1996. Object-Oriented Metrics

Measures of Complexity, Prentice-Hall, Upper Saddle

River.

Hosmer D. and Lemeshow S., 2000. Applied Logistic

Regression, Wiley-Interscience, 2nd edition.

Kim J. and Porter A., 2002. A history-based test

prioritization technique for regression testing in

resource constrained environments, In Proceedings of

International Conference on Software Engineering.

Li W., and Henry S., 1993. Object-Oriented Metrics that

Predict Maintainability Journal of Systems and

Software, vol. 23 no. 2 pp. 111-122.

Lin C.T., Chen C.D., Tsai C.S. and Kapfhammer G. M.,

2013. History-based Test Case Prioritization with

Software Version Awareness, 18th International

Conference on Engineering of Complex Computer

Systems.

McCabe T. J., 1976. A Complexity Measure, IEEE

Transactions on Software Engineering: 308–320.

Mirarab S. and Tahvildari L., 2007. A prioritization

approach for software test cases on Bayesian

networks, In FASE, LNCS 4422-0276, pages 276–

290.

Mockus A., Nagappan N. and Dinh-Trong T. T., 2009.

Test coverage and post-verification defects: a multiple

case study, in Proceedings of the 3rd International

Symposium on Empirical Software Engineering and

Measurement (ESEM), pp. 291– 301.

Ray M. and Mohapatra D.P., 2012. Prioritizing Program

elements: A pretesting effort to improve software

quality, International Scholarly Research Network,

ISRN Software Engineering.

Rompaey B. V. and Demeyer S., 2009. Establishing

traceability links between unit test cases and units

under test, in Proceedings of the 13th European

Conference on Software Maintenance and

Reengineering (CSMR ’09), pp. 209–218.

Rothermel G., Untch R.H., Chu C. and Harrold M.J.,

1999. Test case prioritization: an empirical study,

International Conference on Software Maintenance,

Oxford, UK, pp. 179–188.

Shatnawi R., 2010. A Quantitative Investigation of the

Acceptable Risk Levels of Object-Oriented Metrics in

Open-Source Systems, IEEE Transactions On

Software Engineering, Vol. 36, No. 2.

Shihaby E., Jiangy Z. M., Adamsy B., Ahmed E. Hassany

A. and Bowermanx R., 2010. Prioritizing the Creation

of Unit Tests in Legacy Software Systems, Softw.

Pract. Exper., 00:1–22.

Toure F., Badri M. and Lamontagne L., 2014a. Towards a

metrics suite for JUnit Test Cases. In Proceedings of

the 26th International Conference on Software

Engineering and Knowledge Engineering (SEKE

Vancouver, Canada. Knowledge Systems Institute

Graduate School, USA pp 115–120.

Toure F., Badri M. and Lamontagne L., 2014b. A metrics

suite for JUnit test code: a multiple case study on open

source software, Journal of Software Engineering

Research and Development, Springer, 2:14.

Walcott K.R., Soffa M.L., Kapfhammer G.M. and Roos

R.S., 2006. Time aware test suite prioritization,

Proceedings of the International Symposium on

Software Testing and Analysis (ISSTA 2006). ACM

Press, New York, 1–12.

Wong W., Horgan J., London S., and Agrawal, H., 1997.

A study of effective regression in practice,

Proceedings of the 8th International Symposium on

Software Reliability Engineering, November, p. 230–

238.

Yu Y. T. and Lau M. F., 2012. Fault-based test suite

prioritization for specification-based testing,

Information and Software Technology Volume 54,

Issue 2, Pages 179–202.

Zhou Y. and Leung H., 2006. Empirical Analysis of

Object-Oriented Design Metrics for Predicting High

and Low Severity Faults, IEEE Transaction Software

Engineering, vol. 32, no. 10, pp. 771-789.

Zhou Y., and Leung H., 2007. Predicting object-oriented

software maintainability using multivariate adaptive

regression splines, Journal of Systems and Software,

Volume 80, Issue 8, August 2007, Pages 1349-1361,

ISSN 0164-1212.

ENASE 2017 - 12th International Conference on Evaluation of Novel Approaches to Software Engineering