
Skyline Modeling and Computing over Trust RDF Data
Amna Abidi
1
, Mohamed Anis Bach Tobji
1,2
, Allel Hadjali
3
and Boutheina Ben Yaghlane
4
1
Universit
´
e de Tunis, Institut Sup
´
erieur de Gestion de Tunis, LARODEC, Tunis, Tunisia
2
Univ. Manouba, ESEN, Manouba, Tunisia
3
ENSMA, LIAS, Chasseneuil-du-Poitou, France
4
University of Carthage, IHEC, LARODEC, Carthage, Tunisia
Keywords:
Preference Queries, Semantic Web, RDF Data, Trustworthiness, Skyline.
Abstract:
Resource Description Framework (RDF) data come from various sources whose reliability is sometimes ques-
tionable. Therefore, several researchers enriched the basic RDF data model with trust information. New meth-
ods to represent and reason with trust RDF data are introduced. In this paper, we are interested in querying
trust RDF data. We particularly tackle the skyline problem, which consists in extracting the most interesting
trusted resources according to user-defined criteria. To this end, we first redefined the dominance relationship
in the context of trust RDF data. Then, we proposed an appropriate semantics of the trust-skyline; the set
of most interesting resources in a trust RDF dataset. Efficient methods to compute the trust-skyline are pro-
vided and compared to some existing approaches as well. Experiments led on the algorithms’ implementations
showed promising results.
1 INTRODUCTION
The large adoption of Semantic Web in research and
industry has led to the development of a large amount
of Resource Description Framework (RDF) data on
the Web (Berners-Lee et al., 1998; Frauenfelder,
2009; Antoniou and vanHarmelen, 2004). However,
due to te openness of the web and variety of sources
in internet, the reliability of collected data is ques-
tioned. To control information trustworthiness, new
metrics were introduced in RDF representation to ex-
press intention of information provider about infor-
mation trust (Hartig, 2009a; Tomaszuk et al., 2012;
Fionda and Greco, 2015).
To reason in presence of trust information, we
need new methods to query RDF data. In this pa-
per, we are interested in preference-based queries
(Chomicki, 2002; Kiessling, 2002; Chomicki, 2011;
Chomicki et al., 2013) that show motivating results to
personalize and filter the massive amount of informa-
tion contained in data. Skyline operator, introduced in
(B
¨
orzs
¨
onyi et al., 2001) is an important kind of prefer-
ence queries that returns the most interesting objects
according to user-defined criteria based on the Pareto
dominance operator.
The aim of this paper is to adapt the skyline opera-
tor to trust weighted RDF data. First of all, we define
the dominance between such data. While this oper-
ator produces a binary result in case of certain data,
in the context of trust RDF data, it produces a de-
gree of dominance rather than a boolean (true/false)
result. Then, we provide a semantics for the trust-
skyline, i.e., the set of resources that are dominated
by no other resource with a degree exceeding a user-
defined threshold denoted α. Up to our knowledge the
only work proposed in the literature to extend skyline
queries over RDF data to filter the massive amount
of resources among the web is the proposal of (Chen
et al., 2011). However, this method does not consider
trust measures and is based on the basic definition of
the RDF data.
To compute the trust-skyline, we proposed a new
algorithm TRDF-Skyline. This algorithm is based on
properties we checked and proved over the new re-
defined dominance relationship. We compared the
proposed method to the naive solution for computing
the trust-skyline, and also with an SQL query where
data were assumed to be stored in a relational table
of quadruples. The experiments showed interesting
results.
The rest of the paper is organized as follows: In
the second section, we present our background mate-
rial. In the third section we review the related work
in the literature. In section 4, we introduce our new
634
Abidi, A., Tobji, M., Hadjali, A. and Yaghlane, B.
Skyline Modeling and Computing over Trust RDF Data.
DOI: 10.5220/0006320706340643
In Proceedings of the 19th International Conference on Enterprise Information Systems (ICEIS 2017) - Volume 2, pages 634-643
ISBN: 978-989-758-248-6
Copyright © 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
model, the Trust-Skyline and we show how it operates
over uncertain RDF data. Then, in section 5, we il-
lustrate our experimental study. Finally, we conclude
and present some perspectives in section 6.
2 BACKGROUND MATERIAL
2.1 Trust RDF Data
RDF is a W3C framework to represent informa-
tion in the Web in a meaningful (semantic) way.
An RDF statement is a triple < s, p, o > where s,
p, and o stand for sub ject, property and ob ject
respectively. RDF describes Web resources (sub-
ject) related/characterized (property) to other re-
sources/literals (object).
A set of RDF statements is a graph for repre-
senting Meta-Data and describing the semantics of
information in a machine-accessible way. Therefore,
RDF data can be thought in terms of a decentral-
ized directed labelled graph. The edges’ labels
are the as ”properties”, also called ”predicates” or
”attributes”. The RDF data are stored as a set of
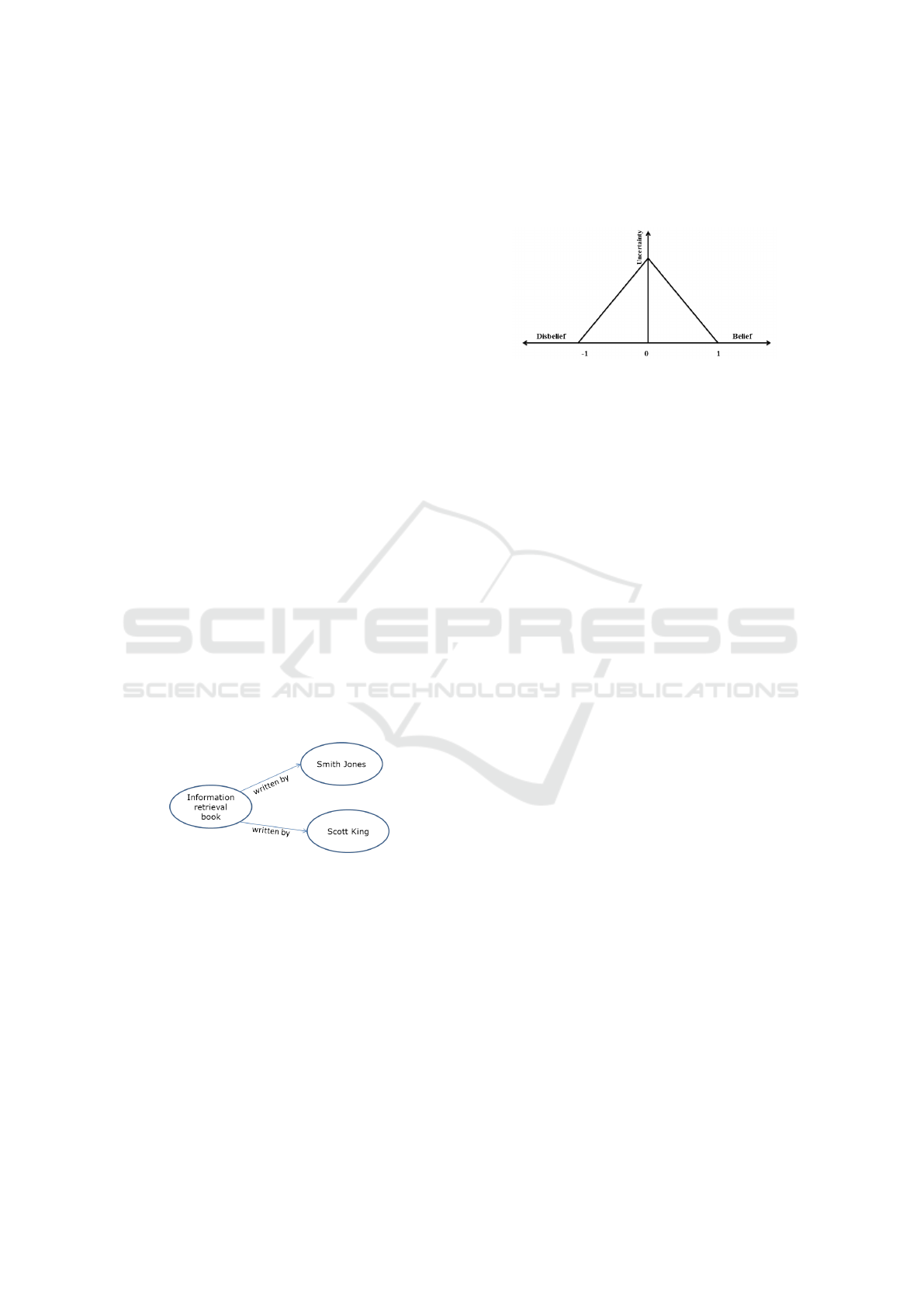
Subject(Node)-Property(Edge)-Object(Node)
triples, often called SPO triples < s, p, o > and
represented graphically as illustrated in figure 1. This
later is an example of a simplified RDF graph that
describes relation (co-writing) between the resource
”Information retrieval book” on the one hand, and
”Smith Jones” and ”Scott King” on the other hand.
To rate the trustworthiness of an RDF information,
Figure 1: RDF Graph example.
Olaf Hartig introduced the trust model of RDF data
in (Hartig, 2009a). He introduces the trust measure
that quantifies the subjective belief/disbelief of an
RDF information. Belief (disbelief) of an RDF triple
is the degree of confidence in the truth (untruth) of
the information. The trust RDF model was developed
in several works such as (Hartig, 2009b; Tomaszuk
et al., 2012; Fionda and Greco, 2015).
As mentioned above, trustworthiness of an RDF
triple is represented by a trust degree. This measure,
denoted t, is either unknown or a value in the interval
[−1,1] as shown in figure 2. If t = 1, the user is ab-
solutely sure about the truth of the triple. A positive
value less than 1 still represents belief in the infor-
mation truth. A negative value expresses a disbelief,
while t = −1 represents a certitude in the information
untruth.
Figure 2: Meaning of trust values.
In the trust RDF model the triple < s, p, o > is ex-
tended to a quadruple < s, p, o,t > where the value t
represents the trust degree of the triple < s, p,o >. We
call the quadruple a ”SPOT”.
Definition 1. RDF SPOT. An RDF SPOT X is a
quadruple < s, p, o,t >, where o is a value of a pred-
icate p related to a subject s, with a trust t. The triple
< s, p,o > is denoted by X
∗
.
A SPOT describes a unique property of a subject.
However, to compare two resources, we should con-
sider all common properties. That is why we intro-
duce the notion of point which is the set of SPOTs
related to a unique resource (subject). In a multi-
dimensional space, a point is characterized by several
dimensions, as well as RDF resources, characterized
by several properties.
Definition 2. Trust RDF Point. A trust RDF tuple
P
s
is the set of SPOTs related to a unique subject s
that has n properties p
i
, having the values o
i
and the
trusts t
i
with 1 ≤ i ≤ n. P
∗
s
denotes the set of SPOs
related to the subject s, i.e., without considering the
trust measures.
Example 1. Consider the RDF data set in table 1.
Four hotels are considered, each one has two prop-
erties that are ”HasPrice” and ”HasDistance”. The
quadruple
< h
1
,HasPrice,20,0.8 > is a SPOT.
We denote it X. Consequently, X
∗
is the
SPO < h
1
,HasPrice,20 >. Let the pat-
tern matching P be the set of SPOTs related
to h
1
. P = {< h
1
,HasPrice,20,0.8 >, <
h
1
,HasDistance,100,0.9 >}. P
∗
is the set of
SPOs related to h
1
:
P
∗
= {< h
1
,HasPrice,20 >,<
h
1
,HasDistance,100 >}.
2.2 The Skyline Operator
The skyline operator is based on the Pareto domi-
nance. In a set of database objects denoted by S, the
Skyline Modeling and Computing over Trust RDF Data
635
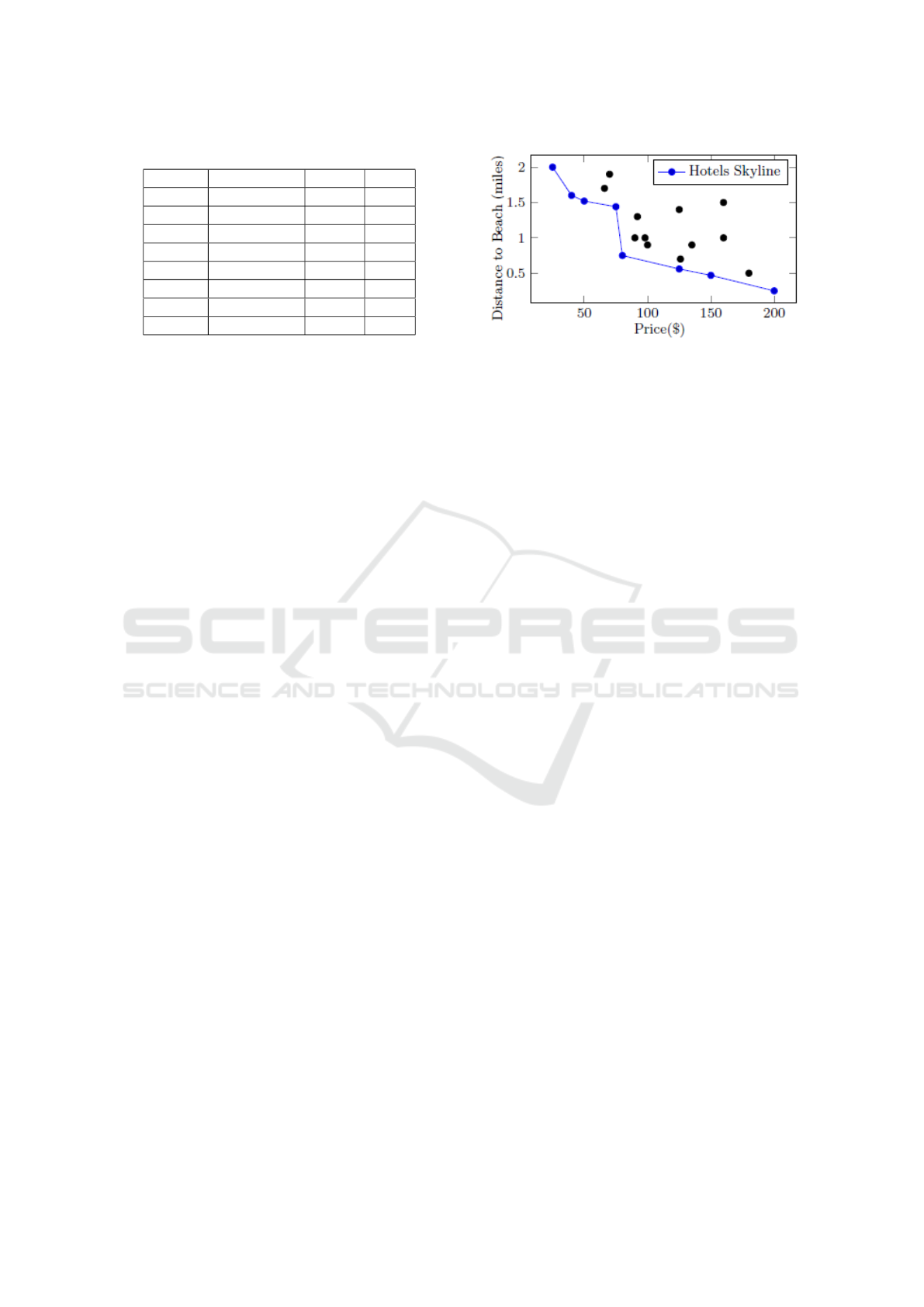
Table 1: Example of trust RDF data.
Subject Predicate Object Trust
h
1
HasPrice 20 0.8
h
1
HasDistance 100 0.9
h
2
HasPrice 30 0.5
h
2
HasDistance 110 0.2
h
3
HasPrice 20 0.2
h
3
HasDistance 120 0.7
h
4
HasPrice 30 0.8
h
4
HasDistance 60 0.3
skyline consists of the objects dominated by no other
object. The skyline copes with applications that in-
volve multi-criteria decision making. It consists in
finding the most interesting objects according to user-
defined criteria.
Definition 3. Pareto Dominance.
Let P and Q be two points in a set of points denoted
O with n attributes. A point Q dominates a point P
denoted by Q P, if ∀i ∈ [1, n] q
i
≥ p
i
∧∃ j, q
j
> p
j
.
The logical dominance concept between two points is
modeled as follows:
Q P =
^
(
^
1≤i≤n
q
i
≥ p
i
,
_
1≤i≤n
q
i
> p
i
)
The skyline is the set of points that are dominated
by no other points. It is defined as follows:
Definition 4. Skyline.
Let O be a set of points having n attributes. The sky-
line of O denoted by S is defined as:
S = {P ∈ O/@Q ∈ O,Q P}
Example 2. We illustrate the well known example
presented in (B
¨
orzs
¨
onyi et al., 2001). Given a list
of hotels with the attributes price and distance (to
the beach), we aim to find the cheapest and nearest
hotels to the sea. Figure 3 illustrates the set of all
hotels where each point is characterized by a price
and a distance. Points in the curve represent the sky-
line, i.e., the set of hotels dominated by no other one
according to the above-mentioned criteria (minimum
distance and price).
3 RELATED WORK
Up to our knowledge, there is no earlier work about
computing skyline queries over trust RDF data. We
present in this section 2 kind of works that cope at
most with our concern: (1) modeling and managing
uncertain RDF data, and (2) modeling and computing
skyline queries over RDF data.
Figure 3: Hotels’ prices and distances to beach (B
¨
orzs
¨
onyi
et al., 2001).
Uncertainty can result from either impreci-
sion/inaccuracy of sources or from inconsistency be-
tween them. The last two decades have witnessed a
profusion of research works on this topic. There is
an urgent need of a uniform way to manage uncer-
tainty of the Web data and standardized mechanisms
to evaluate data trustworthiness. (Richardson et al.,
2003; Golbeck, 2006) introduced the web of trust. In
(Richardson et al., 2003), authors estimate user be-
lieves in statements supplied by any other user and de-
fine properties for combination functions for merging
trusts. The work of (Golbeck, 2006) copes with so-
cial networks for which authors present an approach
to integrate trust, provenance and annotations in se-
mantic web systems. Other works are based on on-
tologies such as (Golbeck et al., 2003) where authors
investigate the applicability of social network anal-
ysis to the semantic web. They discuss the multi-
dimensional networks evolving from ontological trust
specifications. Olaf Hartig in (Hartig, 2009a) advo-
cated the need of a uniform way to rate the trustwor-
thiness of RDF Data. The author introduced a trust
model that associates RDF statements with trust val-
ues. He also extended the semantics of SPARQL (the
RDF query language) to manage trustworthiness of
RDF data. The trust RDF model was then developed
in several works such as (Hartig, 2009b; Tomaszuk
et al., 2012; Fionda and Greco, 2015). In (Fionda
and Greco, 2015), authors tackled the properties of
the trust model related to semantic and complexity
issues. Finally, in (Huang and Liu, 2009; Lian and
Chen, 2011; Yuan et al., 2014) authors proposed to
model uncertainty over RDF data using the probabil-
ity theory.
On the other hand, the only existing work about
extending skyline queries over RDF data is the pro-
posal of (Chen et al., 2011). The authors introduced
a skyline model over RDF data stored in a multiple
relations way. They proposed an earlier filtering of
the skyline candidate subjects using a new mecha-
nism called the Header Point. The objective of the
ICEIS 2017 - 19th International Conference on Enterprise Information Systems
636

Header Point is to maintain a concise summary of the
already visited regions of the data space, and to prune
a great number of subject without checking them with
the whole of subjects in the RDF data set.
Although absence of works on skyline queries over
uncertain RDF data, the literature is abundant on
works about skyline queries over uncertain relational
data, such as (Jiang et al., 2012), (Bosc et al., 2011),
(Zhang et al., 2013). The extension of skyline queries
over uncertain RDF has not been advocated in litera-
ture, in this paper we fill the gap.
4 TRUST-SKYLINE MODEL
In this section, we propose to extend the classic model
of skyline queries to cope with the trust RDF model.
We introduce the Trust-Skyline in which we extract
the set of resources that are dominated by no other
resource according to user-defined properties. As the
skyline query is based on the Pareto dominance oper-
ator, we start by defining the dominance operator in
the context of trust RDF data.
4.1 Trust Dominance
The dominance operator is based on comparison be-
tween the properties’ values (see definition 3). In the
context of certain data, the comparison between two
values produces a binary result; 0 if false, and 1 if
true. However, when data are uncertain, compari-
son is not binary. The comparison is rather quanti-
fied with a degree. For example, assume we have
two SPOTs, p
1
= (h
1
,
0
distance
0
,20,0.4) and p
2
=
(h
2
,
0
distance
0
,15,0.3). That means distance that sep-
arates hotels h
1
and h
2
from the beach are 20 with
the trust 0.4, and 15 with the trust 0.3, respectively.
We cannot conclude that h
1
.distance is greater than
h
2
.distance. We just quantify the trustworthiness of
that comparison as shown in definition 5.
Definition 5. Comparison Trust. Let a and b be
two properties’ values, having the trusts Trust(a)
and Trust(b). Let λ be an arbitrary value such that
λ ≤ −1. Trust degree of the comparison between a
and b, denoted by Trust(a φ b) , where the operator
φ ∈ {≤,<,≥,>,=,6=}, is defined as follows:
Trust(a φ b) =
min(Trust(a), Trust(b)) i f aφb = true
λ else
In the rest of the paper, λ is arbitrary fixed to λ=-1.
We need now to define the dominance between
two RDF triples. To consider the uncertain nature
of the data, we adapt the Pareto dominance shown in
definition 3. The logical connectors
V
and
W
, that
represents the conjunction and disjunction of two bi-
nary comparisons, are changed to the minimum and
maximum functions, respectively, to deal with the un-
certain context.
Definition 6. Trust Dominance Degree. Let P and
Q be two subjects having n properties p
i
and q
i
, re-
spectively with 1 ≤ i ≤ n. The degree of dominance
between P and Q, denoted by d(Q P) is defined as
follows
1
:
d(Q P) = min( min
1≤i≤n
Trust(q
i
≤ p
i
), max
1≤i≤n
Trust(q
i
< p
i
))
Example 3. We illustrate an example of two hotels h
1
and h
2
, having the properties price and distance. We
take four cases in order to test all scenarios between
h
1
and h
2
as shown in the table2.
Table 2: Example of hotels properties.
Hotels case 1 case 2 case 3 case 4
price distance price distance price distance price distance
h
1
20(0.2) 100(0.4) 20(0.6) 80(0.7) 20(0.3) 100(0.5) 20(0.3) 70(0.5)
h
2
30(0.3) 110(0.5) 25(0.3) 70(0.1) 20(0.4) 100(0.6) 25(0.4) 70(0.5)
We proceed on computing the Trust-Skyline over
those cases:
• case 1:
d(h
1
h
2
)= min(min(0.2,0.4), max(0.2,0.4))=0.2
• case 2:
d(h
1
h
2
)= min(min(0.3,-1), max(0.3,-1))=-1
• case 3:
d(h
1
h
2
)= min(min(0.3,0.5), max(-1,-1))=-1
• case 4:
d(h
1
h
2
)= min(min(0.3,0.5), max(0.3,-1))=0.3
To simplify the computation of dominance degree
between two triples, we introduce the concept of trust
of point.
Definition 7. Trust of a Point. Given an RDF point P
with n properties p
i
such that 1 ≤ i ≤ n. Each property
is associated with a trust value t
i
. The trust of a point,
denoted by P.t
−
is the minimum trust degree among
all its properties.
P.t
−
= min
1≤i≤n
(p
i
.t)
The notion of point trust simplifies the computa-
tion of the trust dominance as presented in the follow-
ing proposition.
Proposition 1. Given two points P and Q having the
trusts Q.t
−
and P.t
−
.
d(Q P) =
min(Q.t
−
,P.t
−
) i f Q∗ P∗
−1 else
1
We assume in this paper, that the smaller value, the
more preferable
Skyline Modeling and Computing over Trust RDF Data
637

Proof 1. For two RDF points P and Q,
d(Q P) is the minimum between two
measures; min
1≤i≤n
Trust(q
i
≤ p
i
), and
max
1≤i≤n
Trust(q
i
< p
i
).
For the first measure(min
1≤i≤n
Trust(q
i
≤ p
i
)),
we have two scenarios:
• if there exists any property i where q
i
≤ p
i
is false,
then the measure is equal to -1.
• if for each property i, q
i
≤ p
i
is true, then the mea-
sure is equal to the smallest trust among all prop-
erties of P and Q. It is equal to min(Q.t
−
,P.t
−
)
For the second measure(max
1≤i≤n
Trust(q
i
< p
i
)),
we have two scenarios:
• if there exists at least one property i such that q
i
<
p
i
, then the measure is equal to the greatest value
between the trusts of all comparisons q
i
< p
i
that
return true.
• if there is no property i such that q
i
≤ p
i
is true,
then the measure is equal to -1.
The scenarios above are combined in the table 3.
The only case that returns a value different from λ
occurs when ∀i,q
i
≤ p
i
and ∃i,q
i
< p
i
. In this case,
we return:
min(min
1≤i≤n
Trust(q
i
≤ p
i
),max
1≤i≤n
Trust(q
i
< p
i
)).
We are sure that min
1≤i≤n
Trust(q
i
≤ p
i
) is less or
equal than max
1≤i≤n
Trust(q
i
< p
i
).
Hence, the measure min
1≤i≤n
Trust(q
i
≤ p
i
) returns
the minimal trust among all properties’ values
of P and Q (see definition 5), that is simply
min(P.t
−
,Q.t
−
). The case where ∀i,q
i
≤ p
i
and
Table 3: Dominance degree function.
∃i,q
i
< p
i
@i,q
i
< p
i
∀i,q
i
≤ p
i
min(min
1≤i≤n
Trust(q
i
≤ p
i
),max
1≤i≤n
Trust(q
i
< p
i
)) -1
∃i,q
i
> p
i
-1 -1
∃i,q
i
< p
i
, corresponds in fact to Q
∗
P
∗
. In this
case, d(Q P) is equal to the smallest trust among all
properties’ trusts of P and Q (see definitions 6 and 7),
which is the minimum value between Q.t
−
and P.t
−
.
Example 4. If we take the same cases shown in example
3 using proposition 1, we obtain:
• case 1: h
∗
1
h
∗
2
then d(h
1
h
2
) = min(Q.t
−
,P.t
−
) =
min(0.2,0.3) = 0.2
• case 2: h
∗
1
h
∗
2
then d(h
1
h
2
)=-1
• case 3: h
∗
1
h
∗
2
then d(h
1
h
2
)=-1
• case 4: h
∗
1
h
∗
2
then d(h
1
h
2
) = min(Q.t
−
,P.t
−
) =
min(0.3,0.4) = 0.3
Note that we obtain same results of example 3.
Proposition 2. The trust dominance is transitive.
Given two RDF triples P and Q, and a threshold
α ∈ [−1,1]
if d(R Q) > α and
d(Q P) > α;− −→ d(R P) > α
Proof 2. d(R Q) > α and d(Q P) > α (1)
d(R Q) = min(R.t
−
,Q.t
−
) and d(Q P) =
min(Q.t
−
,P.t
−
) (2)
(1) and (2) imply min(R.t
−
,Q.t
−
) > α and
min(Q.t
−
,P.t
−
) > α (3)
(3) implies min(R.t
−
,Q.t
−
,P.t
−
) > α (4)
(4) implies d(R P) > α
Proposition 3. The trust dominance is asymmetric.
Given two RDF triples P and Q, and a threshold α ∈
[−1,1]
d(Q P) > α Then d(P Q) = −1
Proof 3. d(Q P) > α −→ Q
∗
P
∗
Q
∗
P
∗
−→ P
∗
Q
∗
P
∗
Q
∗
−→ d(P Q) = −1
4.2 Trust-Skyline Model
In (B
¨
orzs
¨
onyi et al., 2001), skyline is defined as the
set of database objects dominated by no other object.
In such perfect context, dominance is binary. How-
ever, in context of trust RDF data (Hartig, 2009a),
dominance has a degree in [-1, 1]. Thus, skyline is de-
fined as the set of points dominated by no other point
according to a trust threshold α.
Definition 8. Trust-Skyline. The T-Skyline of a data
set D, denoted by T − Sky
α
, contains each point P
in D such there is no point Q that dominates P with
a trust degree greater than a user defined threshold
α ∈ [−1,1].
T − sky
α
= {P ∈ D/@Q ∈ D,d(Q P) ≥ α}
Example 5. We illustrate the example of five hotels,
with two properties each one (Price and Distance).
For each property we specify a trust degree to de-
scribe the data trustworthiness.
Table 4: Example of hotels candidate list of T-Sky.
Hotel Price Distance
h
1
23 (0.5) 5 (0.3)
h
2
50 (0.2) 4 (0.6)
h
3
50 (0.7) 3 (0.5)
h
4
40 (0.1) 1 (0.3)
h
5
50 (0.6) 2 (0.4)
We want to compute the T-Skyline of the above
RDF data set when α is fixed to 0.1.
• h
1
dominates h
2
with a degree equal to 0.2 (≥ α).
As the trust-dominance is asymetric h
2
does not
dominate h
1
. We conclude that h
2
could not inte-
grate the skyline. We prune it.
• d(h
1
h
3
) = 0.3, thus h
3
is also pruned.
ICEIS 2017 - 19th International Conference on Enterprise Information Systems
638

• d(h
1
h
4
) = −1 and d(h
4
h
1
) = −1. We make
no pruning.
• d(h
1
h
5
) = 0.3. h
5
is pruned.
We conclude that the Trust-Skyline list includes h
1
and
h
4
which are dominated by no other point.
Remark in example 5 that some points could en-
ter the trust-Skyline directly without comparing them
with other ones. Indeed, if the trust of a point P (see
definition 7) is less than the trust threshold α, then we
conclude directly that P is in the skyline because we
are sure there is no other point Q able to dominate it
with a degree greater than α, even if Q
∗
P
∗
.
Proposition 4. . Given a data set D and its T-Skyline
T − Sky
α
and a point P ∈ D. If P.t
−
< α then P ∈
T − Sky
α
.
Proof 4. . If P.t
−
< α, then we are sure there exists
no point Q ∈ D such that d(Q P) ≥ α since d(Q
P)isequaltomin(Q.t
−
,P.t
−
)or − 1. In this case, (there
is no Q ∈ D such that d(Q P) ≥ α), we are sure that
P ∈ T − Sky
α
.
4.3 Trust-Skyline Computation
In order to compute the Trust-Skyline, we introduced
two algorithms; the Naive T-Skyline algorithm and
the TRDF-Skyline algorithm. In addition, for an eval-
uation matter, we present a non-native solution that
consists in representing trust-RDF data in relational
table and then extract the trust-Skyline using SQL.
In the next subsection, we show how the Trust-
Skyline can be implemented on a relational database
using an SQL query. We illustrate in table 5 the stored
functions used in the query.
4.3.1 Extracting Trust-Skyline through SQL
Trust RDF data could be stored in a relational table
as quadruplets (table 1 is an example). To implement
our SQL method, we created a table named T
RDF
with
four attributes; s for Subject, p for Predicate, o for
Object and t for Trust (SPOT). As the comparison be-
tween objects is not binary, we implemented two spe-
cific comparison operators to deal with the uncertain
context; the less and lessorequal functions which re-
turn a degree between −1 and 1. The two functions
are described in table5.
Below is the SQL query that returns the trust-
skyline of the table T
RDF
according to the threshold
α. This latter selects each subject A such there
is no subject B dominating A. B dominates A if
two conditions are satisfied. First, there exists no
predicate whose value for A is better or equal than
its value for B. And second, it exists at least one
Table 5: Used functions Meaning.
returns the least trust degree
less(v
1
,v
2
) between two points v1 and v2
if v1 < v2
returns the least trust degree
lessorequal(v
1
,v
2
) between two points v1 and v2
if v1 ≤ v2
predicate whose value for A is strictly better than its
value for B. We recall here that the smaller values,
the more preferable are, hence the use of functions
less and lessorequal.
SELECT DISTINCT s FROM T
RDF
A WHERE NOT EXISTS(
SELECT * FROM T
RDF
B WHERE B.s = A.s AND NOT EXISTS(
SELECT * FROM T
RDF
C WHERE C.s= A.s AND NOT EXISTS(
SELECT * FROM T
RDF
D WHERE D.s= B.s AND C.p= D.p
AND lessorequal(D.o, D.t, C.o, C.t)>=&α))
AND EXISTS
(SELECT * FROM T
RDF
E WHERE E.s=A.s AND EXISTS(
SELECT * FROM T
RDF
F WHERE F .s=B.s AND F.p= E.p
AND less( F.o, F .t, E .o, E.t)>=&α)));
We present below the SQL code of the functions
less and lessorequal.
CREATE OR REPLACE FUNCTION less(v1 IN NUMBER, t1
NUMBER, v2 IN NUMBER, t2 NUMBER) RETURN NUMBER IS
inferior NUMBER := -1;
BEGIN
IF (v1<v2) THEN
inferior := least(t1,t2);
END IF;
RETURN inferior;
END;
CREATE OR REPLACE FUNCTION lessorequal(v1 IN NUMBER, t1
NUMBER, v2 IN NUMBER, t2 NUMBER) RETURN NUMBER IS
inferior NUMBER := -1;
BEGIN
IF (v1<=v2) THEN
inferior := least(t1,t2);
END IF;
RETURN inferior;
END;
4.3.2 Naive T-Skyline Algorithm
A naive approach to solve the problem of extracting
the trust skyline, is to compare each pair of points.
When a point is dominated, it is rejected. Only points
that are dominated by no other points in the data set
are kept in the trust skyline.
Based on proposition 4, we optimized the naive
method by adding directly all points which trusts are
less or equal to the threshold α. These points could
not be dominated with a degree greater than α. Note
that Complexity of this method is O(n
2
).
Based on the same example presented on the table
4 we proceed on modifying α to check its influence
on the Skyline resulting list. If we choose α = 0.1,
Skyline Modeling and Computing over Trust RDF Data
639

each point that could be a part of the T-Skyline should
be dominated by no other point with a degree greater
than 0.1. The T-Skyline result list is {h
1
,h
4
}. If we
increase α, points with trust measure inferior than α
are in the Skyline because no other point could dom-
inate them over this degree. The trust degree α has
a big influence on computing the T-Skyline resulting
list. Therefore, we used this measure in our Naive T-
Skyline algorithm to make an earlier filtering of the
candidate list.
Algorithm 1: The Naive T-Skyline Algorithm.
1: INPUT: n RDF triples.
2: OUTPUT: TSky Trust-Skyline points.
3: for each point P ∈ DB P do
4: SKY= true;
5: if P.t
−
< α then
6: Add P to TSky
7: else
8: for each point Q ∈ DB such that Q 6= P do
9: if (dominates(Q,P)=> α) then /*Using function
dominates*/
10: SKY=false;
11: Break;
12: end if
13: end for
14: if(SKY=true) then
15: Add P to TSky
16: end if
17: end for
4.3.3 TRDF-Skyline Algorithm
TRDF-Skyline is a new algorithm that uses, in addi-
tion to the optimization (based on property 4) in the
naive T-Skyline method, a second optimization based
on the transitivity property (proposition 2). Indeed,
we are not obliged to compare all the pairs of points.
If a point U dominates a point W , then W is eliminated
and U is added to the trust skyline. Then, when we
find that a point Z dominates U, then U is eliminated
and Z is added to the skyline. Here the comparison
between Z and W in useless because W cannot domi-
nate U. We even know that Z dominates W thanks to
the transitivity property (U W and Z U implies
Z W ).
Even if the complexity of this method is O(n
2
),
we are sure we pruned useless points thanks to the
transitivity property. Algorithm of the TRDF-Skyline
method is presented below.
5 EXPERIMENTAL EVALUATION
In this section, we evaluate the methods introduced in
subsection 4.3, which are exact methods. That’s why
Algorithm 2: The TRDF-Skyline Algorithm.
1: NPUT: n RDF triples.
2: OUTPUT: TSky Trust-Skyline points.
3: for each point P ∈ DB do
4: if P.t
−
< α then
5: Add P to TSky
6: else
7: inSKY=true;
8: for each point Q ∈ TSky, Q 6= P do
9: if (dominates(P,Q)=> α) then
10: Remove (Q) from TSky
11: else if (dominates(Q,P)=> α) then
12: inSKY=false;
13: Break;
14: end if
15: end for
16: if (inSKY=true) then
17: Add P to TSky
18: end if
19: end for
evaluation doesn’t cope with the output quality. In-
deed, the produced skyline is exactly the same re-
gardless of the used method. Consequently, the ex-
periments we led were about (1) the performance of
the methods (time execution), and (2) the size of the
skyline (readability of the result). For each measure,
we varied (1) the trust threshold, (2) the size of the
database and (3) the number of properties in the sky-
line query. The idea is to understand the effects of
these parameters on the execution time and the re-
sulted skyline.
5.1 Experimental Setup
Due to the lack of trust RDF databases, we generated
synthetic data sets according to the parameters in ta-
ble 6. For each experiment, we vary one parameter
and set the others to the default values ()referred in the
above-mentioned table). Note that data are generated
following the uniform law. We used the triple stor-
age approach (Sakr and Al-Naymat, 2009), extended
to a quadruple format to deal with the trust measure.
The data generator and the algorithms 2 and 1 were
implemented in Java. The SQL query were imple-
mented under Oracle 11g. Stored functions were im-
plemented using PL/SQL. All experiments were con-
ducted under Windows 7 on a 2.10 GHz Intel Core
Duo processor computer with 4GB of RAM.
Table 6: Parameters under investigation.
Symbol Parameter Default
P Number of properties 6
D Number of quadruples 300 K
T Size of T-Skyline data -
α Trust measure 0.2
X Time execution (ms) -
ICEIS 2017 - 19th International Conference on Enterprise Information Systems
640
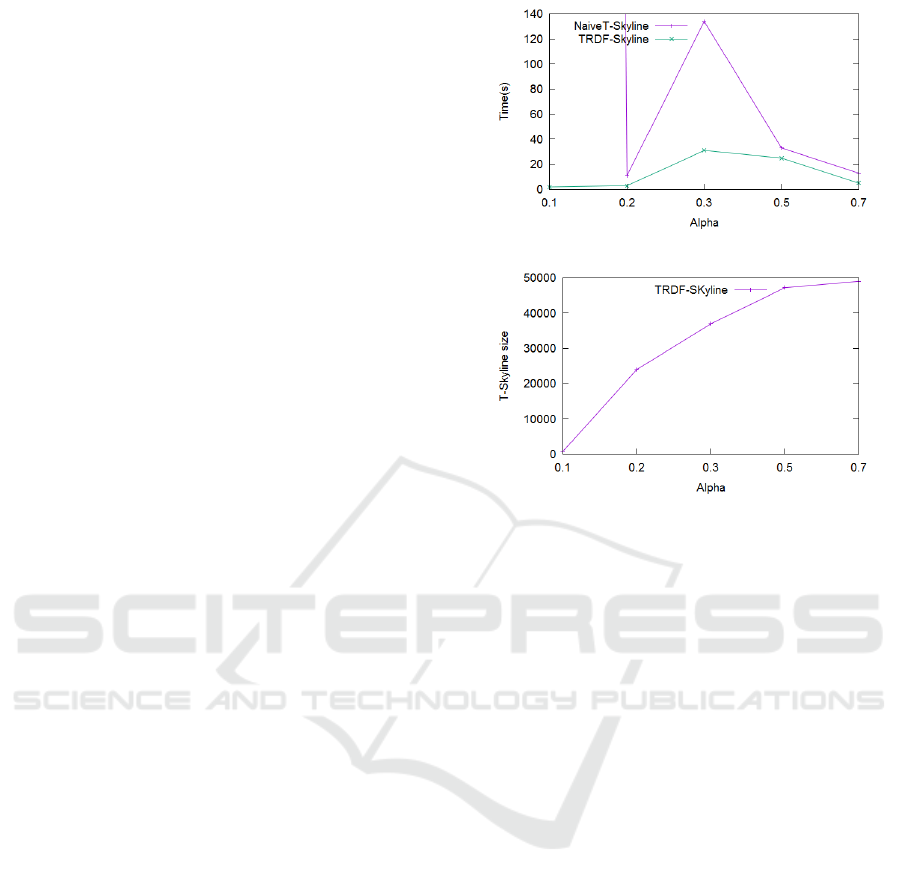
5.2 Impact of the Trust Threshold
Variation
As we presented previously in this paper, we defined
the Trust-Skyline as the set of points dominated by
no other point according to a trust threshold α. In
this experiment, we varied α in order to measure its
impact on the execution time and on the trust skyline,
as shown in figure 4.
When α has a great value, the two methods per-
form quickly (figure 4(a)). This is due to the fact that
points’ trusts are more probably less than α, and thus
enter directly to the skyline without processing. In
this case, thanks to proposition 4, the search space is
considerably pruned. Size of the trust skyline (figure
4(b)) is important, because it is rare to check a dom-
inance between two points, according to a threshold
whose value is important. If there is rare dominance
between points, then we obtain a great number of sky-
line points.
On the other hand, when α has a small value, sev-
eral points are dominated and so do not enter to the
skyline. That is why skyline size is small in this case.
The Naive T-Skyline do not benefit from the proposi-
tion 4 pruning method, and execution time is very im-
portant. However, for TRDF-skyline, execution time
is very acceptable, since pruning based on the transi-
tivity property is always efficient and doesn’t depend
from α.
For the SQL query, with a database of 6k tuples
the execution time exceeds 12.10
3
ms. SQL query
is logically costly since we do not use a native en-
vironment, and we don’t optimize computation as in
the other methods. The SQL query compare all the
points’ pairs in the database.
5.3 Size of the Data Set
In this experiment, we study the impact of the data
size on the performance and size of the trust skyline.
We varied the input data size from 100k, to 500k tu-
ples as shown in figure 5. Figure 5 depicts a com-
parison between our two algorithms. As in the pre-
vious experiment, TRDF-Skyline algorithm performs
better than the Naive Trust-Skyline algorithm. When
the data size reaches 300k, the execution time of the
Naive T-Skyline becomes exponential. At 500k it ex-
ceeded 223s, for the TRDF-Skyline it does not ex-
ceed 50s. The execution time of the SQL query is the
worst, it is very high over a size greater than 12K.
When data set are very huge, we think that dis-
tributed methods are recommended. Since Pareto
dominance is transitive, data set could be divided, ex-
traction of trust-Skyline is computed in parallel, and
(a) Effect on time execution
(b) Effect on skyline size
Figure 4: Effect of α on skyline computation.
then a smart fusion of the results is operated. An in-
teresting perspective of this work is to model and im-
plement distributed methods to extract trust-Skyline.
5.4 Number of Properties in the Skyline
Query
In this experiment, we study the effect of properties
(criteria) number in the skyline query over the result
computation. For this purpose, we increased the num-
ber of skyline query’s properties as shown in figure 6.
The trust skyline size increased with the increase of P
(see figure 6(b)), because a subject has more chance to
be not dominated when comparison copes with a high
number of criteria. Figure 6(a) shows again the per-
formance of the TRDF-Skyline that takes advantage
from the transitivity property. The naive algorithm,
even worst, outperforms the SQL query which com-
pares all pairs of points, without pruning using the
property 4.
6 CONCLUSION
In this paper, we proposed an extension of the skyline
to the context of trust RDF data. A new variant of the
skyline, called the trust-Skyline is introduced. To this
end, semantics of Pareto dominance relationship and
(traditional) skyline were redefined.
Skyline Modeling and Computing over Trust RDF Data
641
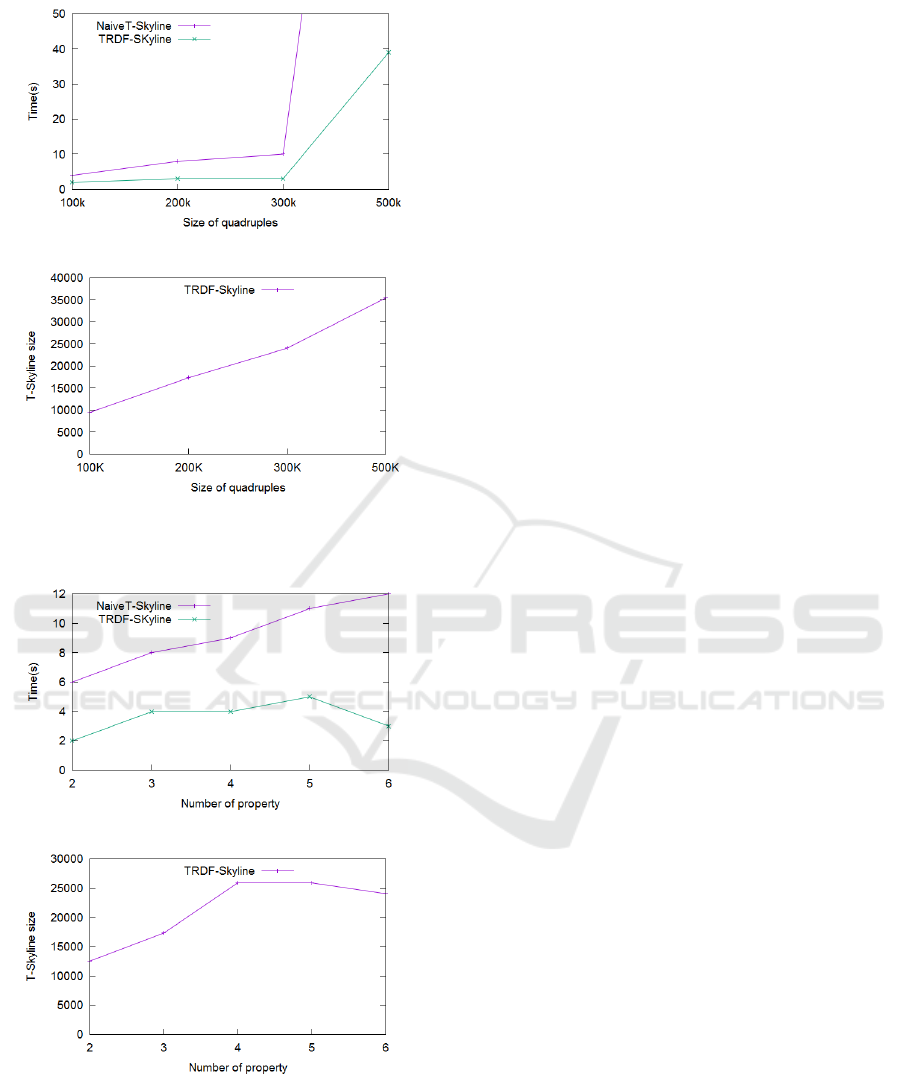
(a) Effect on time execution
(b) Effect on skyline size
Figure 5: Effect of data size on skyline computation.
(a) Effect on time execution
(b) Effect on skyline size
Figure 6: Effect of criteria number on skyline computation.
To compute the trust-Skyline, we implemented
two algorithms that take into account the trust mea-
sures to compute the trust-Skyline set. The Naive
T-Skyline algorithm that uses points’ trust degrees
to make an early filtering of data. And the TRDF-
Skyline algorithm that is optimized based on the tran-
sitivity property of the trust dominance operator. We
also presented an SQL query to show how Trust-
Skyline can be implemented on a relational database
system.
Our experiments showed the efficiency of the
TRDF-Skyline algorithm. The naive T-Skyline
method is acceptable if the input data size is not huge
and if the trust threshold is medium or high. However,
the SQL query showed very limited performance.
As future work, two points attracted our attention.
First, performance of all methods decreases when
data set are voluminous. We think that distributed
methods could perform better in this case. The transi-
tivity property of the dominance operator encourage
such solution. Second, when the trust threshold has
an important value, the trust-Skyline size increases
considerably. If the skyline is huge, our objective of
filtering the initial data set to present only the most
interesting points is not reached. In this case, we need
a second analysis to refine the initial result (skyline).
A top-k trust skyline query could be a promising so-
lution.
REFERENCES
Antoniou, G. and vanHarmelen, F. (2004). A Semantic Web
Primer. MIT Press, Cambridge, MA, USA.
Berners-Lee, T., Fielding, R., and Masinter, L. (1998). Uni-
form resource identifiers (uri): Generic syntax.
B
¨
orzs
¨
onyi, S., Kossmann, D., and Stocker, K. (2001). The
skyline operator. In Proceedings of the 17th Interna-
tional Conference on Data Engineering, pages 421–
430, Washington, DC, USA. IEEE Computer Society.
Bosc, P., Hadjali, A., and Pivert, O. (2011). On possibilistic
skyline queries. In Proceedings of the 9th Interna-
tional Conference on Flexible Query Answering Sys-
tems, FQAS’11, pages 412–423, Berlin, Heidelberg.
Springer-Verlag.
Chen, L., Gao, S., and Anyanwu, K. (2011). Efficiently
evaluation skyline queries on rdf databases. In 8th Ex-
tended Semantic Web Conference, ESWC 2011, pages
123–138, Heraklion, Crete, Greece.
Chomicki, J. (2002). Querying with intrinsic preferences.
In Proceedings of the 8th International Conference
on Extending Database Technology: Advances in
Database Technology, EDBT ’02, pages 34–51, Lon-
don, UK, UK. Springer-Verlag.
Chomicki, J. (2011). Logical foundations of preference
queries. volume 34, pages 3–10.
Chomicki, J., Ciaccia, P., and Meneghetti, N. (2013). Sky-
line queries, front and back. SIGMOD Rec., 42(3):6–
18.
Fionda, V. and Greco, G. (2015). Trust models for RDF
data: Semantics and complexity. In Proceedings of
ICEIS 2017 - 19th International Conference on Enterprise Information Systems
642

the Twenty-Ninth AAAI Conference on Artificial In-
telligence, January 25-30, 2015, Austin, Texas, USA.,
pages 95–101.
Frauenfelder, M. (2009). A Smarter Web.
Golbeck, J. (2006). Combining provenance with trust in
social networks for semantic web content filtering. In
Proceedings of the 2006 International Conference on
Provenance and Annotation of Data, pages 101–108,
Berlin, Heidelberg. Springer-Verlag.
Golbeck, J., Parsia, B., and Hendler, J. A. (2003). Trust
networks on the semantic web. In Cooperative Infor-
mation Agents VII, 7th International Workshop, CIA
2003, Helsinki, Finland, August 27-29, 2003, Pro-
ceedings, pages 238–249.
Hartig, O. (2009a). Querying trust in rdf data with tsparql.
In The Semantic Web: Research and Applications,
6th European Semantic Web Conference, ESWC 2009,
Heraklion, Crete, Greece, May 31-June 4, 2009, Pro-
ceedings, pages 5–20.
Hartig, O. (2009b). Towards a data-centric notion of trust
in the semantic web (a position statement). In The
Semantic Web: Research and Applications,the 7th Ex-
tended Semantic Web Conference , ESWC 2010, Her-
aklion, Greece, May 2010, pages 5–20.
Huang, H. and Liu, C. (2009). Query evaluation on prob-
abilistic rdf databases. In Proceedings of the 10th In-
ternational Conference on Web Information Systems
Engineering, WISE ’09, pages 307–320.
Jiang, B., Pei, J., Lin, X., and Yuan, Y. (2012). Probabilis-
tic skylines on uncertain data: Model and bounding-
pruning-refining methods. volume 38, pages 1–39.
Kluwer Academic Publishers.
Kiessling, W. (2002). Foundations of preferences in
database systems. In Proceedings of the 28th Interna-
tional Conference on Very Large Data Bases, VLDB
’02, pages 311–322. VLDB Endowment.
Lian, X. and Chen, L. (2011). Efficient query answering in
probabilistic rdf graphs. In Proceedings of the 2011
ACM SIGMOD International Conference on Manage-
ment of Data, SIGMOD ’11, pages 157–168, New
York, NY, USA. ACM.
Richardson, M., Agrawal, R., and Domingos, P. (2003).
Trust management for the semantic web. In Proceed-
ings of the Second International Conference on Se-
mantic Web Conference, pages 351–368, Berlin, Hei-
delberg. Springer-Verlag.
Sakr, S. and Al-Naymat, G. (2009). Relational processing
of rdf queries: a survey. volume 38, pages 23–28.
Tomaszuk, D., Pak, K., and Rybinski, H. (2012). Trust in
RDF graphs. In Advances in Databases and Informa-
tion Systems - 16th East European Conference, AD-
BIS 2012, Pozna
´
n, Poland, September 18-21, 2012.
Proceedings II, pages 273–283.
Yuan, Y., Wang, G., Chen, L., and Wang, H. (2014). Graph
similarity search on large uncertain graph databases.
The VLDB Journal, 24(2):271–296.
Zhang, Q., Ye, P., Lin, X., and Zhang, Y. (2013). Skyline
probability over uncertain preferences. In Proceed-
ings of the 16th International Conference on Extend-
ing Database Technology, pages 395–405, New York,
NY, USA. ACM.
Skyline Modeling and Computing over Trust RDF Data
643
