University Student Progressions and First Year Behaviour

R. Campagni, D. Merlini and M. C. Verri

Dipartimento di Statistica, Informatica, Applicazioni, Universit

a di Firenze, Viale Morgagni 65, 50134, Firenze, Italia

Keywords:

Educational Data Mining, Clustering, Student Progressions, Self Assessment Test.

Abstract:

Advanced mining techniques are used on educational data concerning university students. In particular, cluster

analysis is used to predict the university careers of students starting from their ﬁrst year performance and

the results of the self assessment test. The analysis of the entire careers highlights three groups of students

strongly affected by the results of the ﬁrst year: high achieving students who start medium-high and increase

their performance over the time, medium achieving students who maintain their performance throughout the

entire course of study, low achieving students unable to improve their performance who often abandon their

studies. This kind of knowledge can have practical implications on the involved laurea degree.

1 INTRODUCTION

Many ﬁelds and sectors, from economic and busi-

ness activities to public administration, are involved

with the growth of data in computer systems, result-

ing in the need to develop new technologies to man-

age and analyse all the information from this large

amount of data. For what concerns the ﬁeld of edu-

cation, EDM (Educational Data Mining) is a recent

area of research that, starting from data stored in the

schools and universities databases for administrative

purposes, is designed to extract knowledge with the

aim to understand and improve the performance of

the student learning process (see (Baker, 2014; Pe

na-

Ayala, 2014; Romero et al., 2014; Romero and Ven-

tura, 2013) for recent surveys on the state of the art of

educational data mining and on preprocessing educa-

tional data).

The recent literature reveals that predicting per-

formance at a university degree level has attracted

considerable attention and interest. For example,

(Kabakchieva et al., 2011; Zimmermann et al., 2011;

Zimmermann et al., 2015) use regression and clas-

siﬁcation models to analyse how well indicators of

undergraduate achievements and university perfor-

mance characteristics can predict graduate-level per-

formance; in (Bower, 2010), hierarchical cluster anal-

ysis is used to provide school leaders and researchers

a method to make better informed decisions in schools

earlier, using data already collected on students.

The present study uses data mining methods, in

particular partitional clustering, to analyse the per-

formance of students in the Computer Science laurea

degree of the University of Florence (Italy), by us-

ing an explorative approach to mine information from

students data. Two aspects of students performance

are considered. First, we analyse the performance of

students during their ﬁrst year for 5 cohorts, starting

from the academic year 2010-2011 up to 2014-2015.

In particular, we combine results achieved by students

in the courses of the ﬁrst year with the results of a self-

assessment test they are required to take before enter-

ing the university. This is done by clustering analysis

using the K-means implementation of software WEKA

(see (Witten et al., 2011)); the obtained results allows

us to identify a few courses which can serve as indi-

cators of good and low performance and to point out

the inﬂuence of the self-assessment test in being suc-

cessful in the ﬁrst year exams.

Second, we concentrate on the ﬁrst three cohorts

of students and study their progressions during the

ﬁrst, second and third year of university. Three im-

portant groups of students have been identiﬁed: stu-

dents who achieve quite high results during all the pe-

riod under examination, medium achieving students

who maintain a medium proﬁle throughout the entire

course of study, low achieving students which often

abandon their studies (see (Campagni et al., 2015)

for a similar study treated with a different approach).

This analysis is done by clustering students of the

ﬁrst year according to the number of credits and the

grades achieved during the ﬁrst year, together with

the result of the self-assessment test. Then we use

this model to classify students during the other two

Campagni, R., Merlini, D. and Verri, M.

University Student Progressions and First Year Behaviour.

DOI: 10.5220/0006323400460056

In Proceedings of the 9th International Conference on Computer Supported Education (CSEDU 2017) - Volume 2, pages 46-56

ISBN: 978-989-758-240-0

years and thus identify the three typical behaviors.

This second analysis is performed by using the Clus-

ter Assigner node function of the software KNIME (see

https://www.knime.org).

In Section 2 we introduce data used for the anal-

ysis and in particular we illustrate the operations per-

formed on the original data to obtain the ﬁnal data

sets for the application of the appropriate algorithms.

In Sections 3 and 4 we explain the methodology and

present the results obtained on a real case study. Fi-

nally, in Section 5 we present our conclusions.

2 DATA SETS FOR ANALYSIS

In this section, we describe how university students’

data are organized, referring to a laurea degree of the

University of Florence, Italy; in particular we deal

with data of the Computer Science degree of the Sci-

ence School, under the Italian Ministerial Decree n.

270/2004. This academic degree is structured over

three years and every academic year is organized with

several courses, each course has assigned some cred-

its (CFU) for an amount of 60 credits in each year.

Each student, before enrolling in the degree

course, has to take an entrance test to self-evaluate

his background in mathematics

. This test consists

of 25 multiple choice questions (one correct answer

out of four possible options) on mathematics argu-

ments usually studied in high school: arithmetic, el-

ementary algebra, equations, inequalities, elementary

logic, combinatorics, functions, geometry, probabil-

ity. Each correct answer counts as 1 point while a

wrong or no given answer counts as 0 points: the test

is passed with 12 points.

Data under analysis concern university students

enrolled from academic year 2010-2011 (afterwards

cohort 2010) up to 2014-2015 (afterwards cohort

2014), updated to 31th December 2015. We start with

two different data sets: the ﬁrst contains information

about students and their school career before entering

university, together with information on the entrance

test; the second, with information about exams taken

by students.

Table 1 illustrates an example of students data set

after a preprocessing phase which allows us to inte-

grate all the attributes related to students in a single

table. Table 2 contains, for each student, the exams

data with the grade and the credits obtained. As of-

ten happens, we deal with data which need a prepro-

cessing step to ﬁx errors and to reorganize the data

See http://www.scienze.unifi.it/upload/sub/

testdiaccesso/syllabus-conoscenze-matematiche.

pdf for more details, in Italian.

for the purposes of analysis, before applying the var-

ious analysis techniques, such that clustering, classi-

ﬁcation and several others (see (Romero et al., 2014)

for a survey on preprocessing educational data). Dur-

ing this preprocessing phase we join Tables 1 and 2

and aggregate the data to obtain the productivity of

the student in a year, in terms of credits and the av-

erage grade obtained in the corresponding exams.At

the end of this phase the resulting data set is orga-

nized as shown in Table 3, where, for example, the

student 100 obtained 24 credits in the ﬁrst year (at-

tribute credits) with a average grade of 25.5 (at-

tribute avggrade); in the second year the same stu-

dent obtained 60 credits with an average grade of 28.

The attribute test grade corresponds to the grade in

the entrance test.

In this paper we present two different analyses

based on two different data sets. The ﬁrst analysis,

by concerning the student productivity during the ﬁrst

year, considers all cohorts from 2010 to 2014 and is

based on the data set related to students who took at

least an exam in their ﬁrst year. The data set, analysed

by the K-means implementation of the software WEKA,

contains the detail about the grades obtained in each

exam taken by students and is illustrated in Table 4.

The second analysis concerns the student pro-

ductivity during the ﬁrst three years; for each year

we consider the credits and the average grade of

exams and we analyse the way students behave in

the different years in terms of the corresponding at-

tributes. This analysis is based on students enrolled

from 2010 up to 2012 and takes into account the en-

trance test and the examinations over the three years,

as shown in Table 5. The indices I, II and III refer

to the different years; the column names CreditsI,

CreditsII, CreditsIII are for CreditsIgrade,

CreditsIIgrade, CreditsIIIgrade, that is, they

represent credits obtained in exams with grade. In

particular we analyse how the career of the ﬁrst year

affects the entire career by using the Cluster Assigner

node function of the software KNIME.

3 ANALYSIS OF THE FIRST

YEAR PRODUCTIVITY

In this section, we examine the ﬁrst year active stu-

dents of the 5 cohorts from 2010 up to 2014, for a to-

tal of 289 students. The term active refers to the fact

that students under examination have given at least an

exam within the month of December of the second

year (for example, December 2011 for students of co-

horts 2010). For some of these students, this fact cor-

responds to passing the English exam, which is a 3

University Student Progressions and First Year Behaviour

Table 1: A sample of students data. The attributes in the table refer to the student identiﬁer, Student, the grade obtained in

the entrance test, varying in the range 0..25, Test grade, the ﬁnal grade obtained at the high school, varying in the range

60..100, Hgrade, and the typology of high school, Hschool.

Student Test grade Hgrade Hschool

100 18 80 LS

200 22 100 IT

300 15 78 IT

400 24 100 LS

500 19 90 LC

Table 2: A sample of exams data. The attributes in the table refer to the student identiﬁer, Student, the exam code, Exam,

the exam date, Date, the grade obtained in the exam, varying in the range 18..30, Grade, and the corresponding number of

credits, Credits.

Student Exam Date Grade Credits

100 10 2011-01-14 24 12

100 20 2011-02-20 27 12

200 20 2011-02-20 21 12

300 10 2012-01-29 26 12

100 40 2012-02-15 26 6

Table 3: A sample of student productivity in the years. The attributes in the table refer to the student identiﬁer, Student, the

academic year under examination, Year, the number of credits achieved during the year, Credits, the average grade, varying

in the range 18..30, Avggrade, and the grade obtained in the entrance test, varying in the range 0..25, Test grade.

Student Year Credits Avggrade Test grade

100 2011 24 25.5 18

200 2011 12 21 22

300 2012 26 12 15

100 2012 60 28 18

Table 4: A sample of data set for the analysis on ﬁrst year. The attributes in the table refer to the student identiﬁer, Student, the

student cohort, Cohort, the number of credits corresponding to exams with a grade achieved during the year, Credits

grade,

the average grade, varying in the range 18..30, Avggrade, the grade obtained in the entrance test, varying in the range 0..25,

Test grade, and the grade obtained in the ith exam, exam i.

Student Cohort Credits grade Avggrade Test grade exam 1 . . . exam n

100 2010 60 26 18 27 . . . 24

200 2010 12 21 15 21 . . . 0

300 2011 12 26 12 26 . . . 0

CFU course without grade assignment. From our anal-

ysis are therefore excluded all the students that enroll

at the Computer Science degree of the University of

Florence and remain inactive within December of the

next year: most of these students abandon their stud-

ies or make a different choice. However, among the

active students just deﬁned, there are some which are

yet at risk of dropping out, due to the very low results

CSEDU 2017 - 9th International Conference on Computer Supported Education

Table 5: A sample of data set for the analysis on ﬁrst three years. The attributes in the table refer to the student identiﬁer,

Student, the student cohort, Cohort, the number of credits corresponding to exams with a grade achieved during the I, II

or III year, CreditsI, CreditsII, CreditsIII, the average grade, varying in the range 18..30, achieved during the I, II or

III year, AvggradeI, AvggradeII and AvggradeIII, and the grade obtained in the entrance test, varying in the range 0..25,

Test.

Student Cohort CreditsI CreditsII CreditsIII AvggradeI AvggradeII AvggradeIII Test

100 2010 60 60 60 26 28 28 18

200 2010 12 36 48 21 23 25 15

300 2011 12 24 36 21 23 24 12

during their ﬁrst year. Understanding the productivity

of ﬁrst year students can point out these difﬁculties

and gives an opportunity to improve the teaching and

learning processes of the Laurea Degree. The data set

we analyse is not big, however, as focused in (Natek

and Zwilling, 2014), a data mining analysis is useful

also in such small contexts. Moreover, the case study

allows us to describe the methodology on a real situ-

ation.

In particular, we perform a cluster analysis by us-

ing the K-means implementation of the software WEKA.

In our analysis we measure cluster validity with cor-

relation, by using the concept of proximity and inci-

dence matrices: in the proximity matrix P = (P

i, j

each element P

i, j

represents the Euclidean distance

between elements i and j in the data set; in the in-

cidence matrix I = (I

i, j

), each element I

i, j

is 1 or 0

if the elements i and j belong to the same cluster or

not. We then compute the Pearson’s correlation, as

deﬁned in (Tan et al., 2006, page 77), between the

linear representation by rows of matrices P and I and

we expect to ﬁnd a negative value, where -1 means a

perfect negative linear relationship.

We tried the K-means algorithm with several val-

ues of k and with k = 3 we obtained the cluster for

the ﬁrst year students of the 5 cohorts from 2010 up

to 2014, illustrated in Figure 1. As cluster attributes

we used the number of credits corresponding to ex-

ams with a grade, attribute credits grade, the av-

erage grade, attribute avggrade, and the grade of the

self-assessment test, attribute test grade.

The centroids of the cluster are illustrated in Ta-

ble 6 and, in particular, cluster 0 identiﬁes medium

achieving students, cluster 1 corresponds to students

that during the ﬁrst year had success only with the

exam of English and therefore have no credits and

no grade in this clustering, ﬁnally, cluster 2 identiﬁes

high achieving students. The clusters are character-

ized by colours blue, red and green in Figure 1, re-

spectively. The Pearsons correlation between the lin-

ear representation of the proximity and incidence ma-

trices is -0.66, a good value of correlation.

The following Figures 2,3,4,5 and 6 illustrate the

relation between the students in the cluster of Fig-

ure 1 and the exams of the ﬁrst year: Algorithms

and Data Structures (ADS), Programming (PRG), Cal-

culus (CAL), Architectures (ARC), Discrete mathemat-

ics and Logic (DML). In these ﬁgures, the blue colour

means that the exam has not been given (the grade is

0) and the orange colour means that the exam has been

passed with a grade between 18 and 30 (31 means 30

cum laude). As can be seen, there are some courses,

such as ADS, organized in a such a way that most stu-

dents in clusters 0 and 2 are able to give the corre-

sponding exams, while there are two exams, ARC and

DML, which are given mainly by students in cluster 2

and that therefore present some critical aspects.

Figure 7 puts in evidence the results of the self as-

sessment test, however such ﬁgure should be accom-

panied with the results of the Pearson correlation be-

tween the test grade and the number of credits and the

average grade, respectively: for the ﬁve years 2010-14

the value corresponding to attributes credits grade

and test grade shows a positive correlation of 0.49

while the value corresponding to attributes avggrade

and test grade shows a positive correlation of 0.39.

A more detailed analysis, shows a particular positive

correlation with the average grade of CAL and DML,

that is, the mathematics courses of the ﬁrst year. The

self assessment test is mainly concerned with prob-

lems of logic, calculus, probability and the previ-

ous correlations between mathematics courses and the

test are quite natural. These facts are summarized

in Table 7 which shows the values of the correla-

tion between each of the attributes credits grade,

avggrade, ADS, ARC, PRG, CAL, DML and the attribute

test

grade, during the academic years from 2010 up

to 2014, the three years 2010-12, which will be ex-

amined in the next section and, ﬁnally, the ﬁve years

2010-14.

University Student Progressions and First Year Behaviour

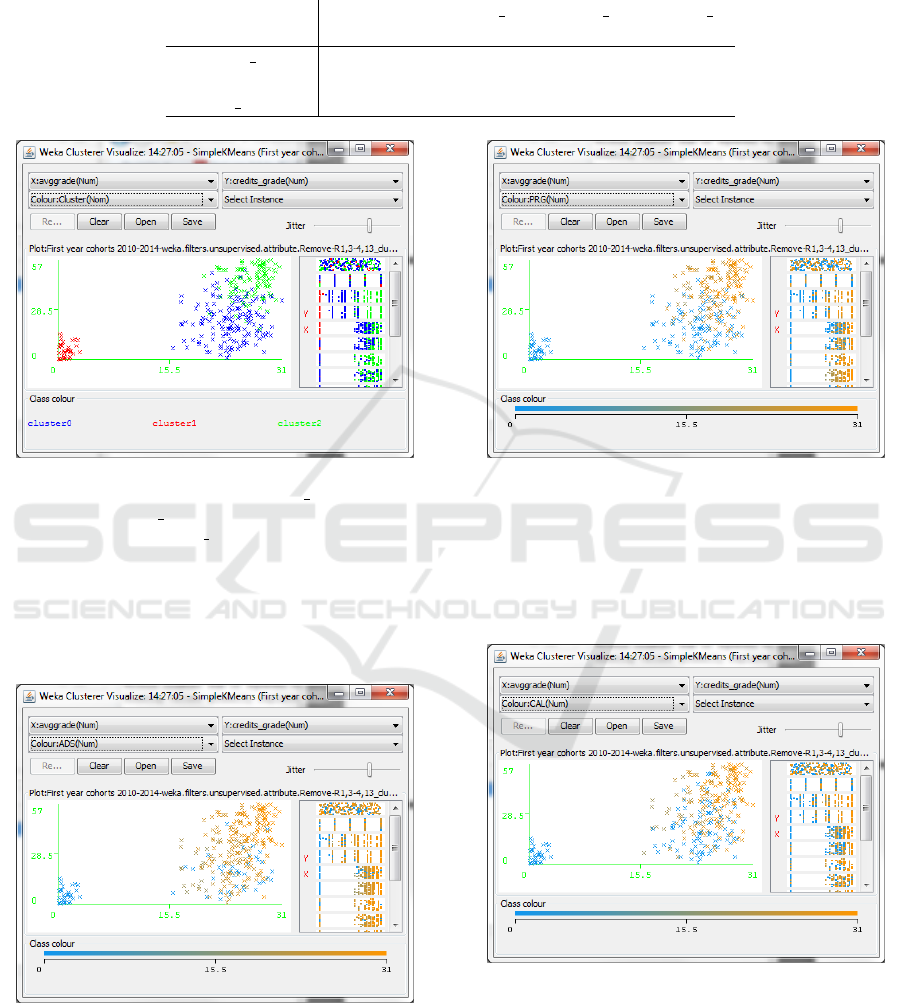
Table 6: Centroids corresponding to Figure 1 and corresponding to ﬁrst year results of cohorts 2010-2014. The cluster 0

identiﬁes medium achieving students, cluster 1 corresponds to students that during the ﬁrst year had success only with the

exam of English and therefore have no credits and no grade in this clustering, ﬁnally, cluster 2 identiﬁes high achieving

students.

Attribute Full Data Cluster 0 Cluster 1 Cluster 2

(289) (154) (32) (103)

credits grade 28.55 21.99 0 47.21

avggrade 22.52 24.23 0 26.97

test grade 14.39 13.08 11.28 17.32

Figure 1: Clusters for the ﬁrst year students of cohorts 2010-

2014 with respect to attributes credits grade, attribute

avggrade, and test grade and their projection with re-

spect to attributes credits grade and avggrade. In red

the students that during the ﬁrst year had success only with

the exam of English and therefore have no credits and no

grade in this clustering; in blue medium achieving students

and in green high achieving students. (For interpretation of

the references to colours in this ﬁgure legend, the reader is

referred to the electronic version of this article).

Figure 2: Clusters of cohorts 2010-2014 illustrated in Fig-

ure 1 with the Algorithms and Data Structures course, ADS,

in evidence. The blue colour means that the exam has not

been given (the grade is 0) and the orange colour means that

the exam has been passed with a grade between 18 and 30

(31 means 30 cum laude). (For interpretation of the refer-

ences to colours in this ﬁgure legend, the reader is referred

to the electronic version of this article).

Figure 3: Clusters of cohorts 2010-2014 illustrated in Fig-

ure 1 with the Programming course, PRG, in evidence. The

blue colour means that the exam has not been given (the

grade is 0) and the orange colour means that the exam has

been passed with a grade between 18 and 30 (31 means 30

cum laude). (For interpretation of the references to colours

in this ﬁgure legend, the reader is referred to the electronic

version of this article).

Figure 4: Clusters of cohorts 2010-2014 illustrated in Fig-

ure 1 with the Calculus course, CAL, in evidence. The blue

colour means that the exam has not been given (the grade

is 0) and the orange colour means that the exam has been

passed with a grade between 18 and 30 (31 means 30 cum

laude). (For interpretation of the references to colours in

this ﬁgure legend, the reader is referred to the electronic

version of this article).

CSEDU 2017 - 9th International Conference on Computer Supported Education

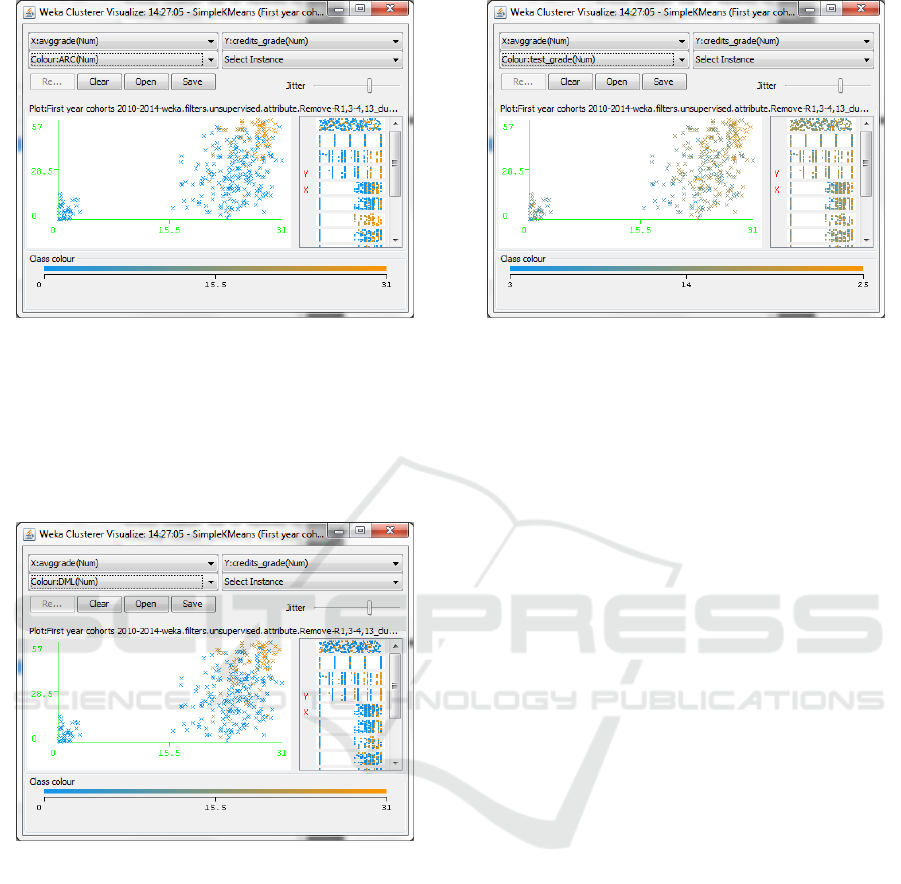
Figure 5: Clusters of cohorts 2010-2014 illustrated in Fig-

ure 1 with the Architectures course, ARC, in evidence. The

blue colour means that the exam has not been given (the

grade is 0) and the orange colour means that the exam has

been passed with a grade between 18 and 30 (31 means 30

cum laude). (For interpretation of the references to colours

in this ﬁgure legend, the reader is referred to the electronic

version of this article).

Figure 6: Clusters of cohorts 2010-2014 illustrated in Fig-

ure 1 with the Discrete mathematics and Logic course, DML,

in evidence. The blue colour means that the exam has not

been given (the grade is 0) and the orange colour means that

the exam has been passed with a grade between 18 and 30

(31 means 30 cum laude). (For interpretation of the refer-

ences to colours in this ﬁgure legend, the reader is referred

to the electronic version of this article).

For completeness, we computed also the Spear-

man and Kendall correlations between the same at-

tributes as before and the test grade. The results are

illustrated in Table 8 and reveal that the Kendall val-

ues are worse than Pearson values while the Spearman

values are quite similar to Pearson values illustrated in

Table 7.

A behavior similar to that illustrated in the previ-

ous ﬁgures, relative to cohorts 2010-2014 examined

Figure 7: Clusters of cohorts 2010-2014 illustrated in Fig-

ure 1 with self assessment test in evidence. The blue colour

means that the test has not been passed (the grade is 0) and

the orange colour means that the test has been passed with

the maximum grade 25. (For interpretation of the references

to colours in this ﬁgure legend, the reader is referred to the

electronic version of this article).

all together, can also be ﬁnd on the single cohorts.

4 ANALYSIS OF THE FIRST

THREE YEARS

PRODUCTIVITY

In this section we analyse the ﬁrst three cohorts of

students from 2010 up to 2012, for a total of 125 stu-

dents, by studying their progressions during the ﬁrst,

second and third year of university. As in Section 3,

we consider only active students during the ﬁrst year,

that is, students that have taken at least an exam in

the same year. We point out that a student active in

the ﬁrst year can stop to be active during the second

and/or third year, thus becoming inactive in that year.

In particular, for the third year we consider exams and

credits matured up to the end of April of the fourth

year after enrollment; this date represents the end of

the third academic year.

As already observed for the analysis of Section 3,

the data set we study is not very big but we wish to

underline the methodological approach that, as far as

we know, is new. The analysis starts by clustering the

results of students during their ﬁrst year, obtaining a

model that is the input for the next steps that classify

students according to their results during the second

and third years. This process allows us to analyse the

way in which the student careers evolve over the three

years and to understand how the performance during

the ﬁrst year affects the following ones. We devel-

oped a KNIME ﬂow, illustrated in Figure 8, that starts

University Student Progressions and First Year Behaviour

Table 7: Pearson’s correlation between various attributes and the test grade, test, relative to the ﬁrst year of the cohorts 2010

up to 2014, of the three cohorts 2010-12 and of the ﬁve cohorts 2010-14. In particular, Credits grade is the number of

credits corresponding to exams with a grade achieved during the year, Avggrade is the average grade and ADS, ARC, PRG, CAL

and DML are the grades in the corresponding exams (the grade is 0 if the exam is not been passed).

Cohort Credits grade/test Avggrade/test ADS/test ARC/test PRG/test CAL/test DML/test

2010 0.49 0.40 0.08 0.23 0.56 0.51 0.46

2011 0.15 0.22 0.06 -0.12 0.07 0.20 0.17

2012 0.41 0.45 0.28 0.26 0.30 0.33 0.43

2013 0.55 0.39 0.22 0.43 0.42 0.51 0.47

2014 0.61 0.40 0.39 0.37 0.57 0.55 0.53

2010-12 0.33 0.38 0.18 0.15 0.27 0.29 0.36

2010-14 0.49 0.39 0.26 0.31 0.41 0.43 0.44

Table 8: Spearman (S) and Kendall (K) correlations between various attributes and the test grade, test, relative to the ﬁrst

year of the three cohorts 2010-12 and of the ﬁve cohorts 2010-14. In particular, Credits grade is the number of credits

corresponding to exams with a grade achieved during the year, Avggrade is the average grade and ADS, ARC, PRG, CAL and

DML are the grades in the corresponding exams (the grade is 0 if the exam is not been passed).

Cohort Credits grade/test Avggrade/test ADS/test ARC/test PRG/test CAL/test DML/test

S 2010-12 0.26 0.34 0.18 0.11 0.25 0.32 0.35

S 2010-14 0.47 0.48 0.36 0.30 0.41 0.48 0.43

K 2010-12 0.20 0.25 0.14 0.09 0.19 0.25 0.28

K 2010-14 0.35 0.36 0.27 0.25 0.32 0.37 0.35

with the K-means node to analyse data of the ﬁrst year

and produces an output model; this model represents

the input for a ﬁrst Cluster Assigner node, that clas-

siﬁes students of the second year, and for a second

node which classiﬁes students of the third one. In the

ﬁgure, these tree nodes are evidenced in green. As in

the previous analysis, we applied the K-means algo-

rithm with k = 3 and we considered the same cluster

attributes, that is, test

grade, credits grade and

avggrade.

More precisely, the input to the KNIME ﬂow con-

sists of three data sets, evidenced in orange in Fig-

ure 8; the input for the K-means node contains in-

formation about active students in the ﬁrst year and

concerns exams taken by students up to 31th Decem-

ber of the year following their enrollment. A sample

of these data is illustrated in Table 9, where the at-

tributes creditsI grade and avggradeI contain re-

spectively the credits and the average grade obtained

from students in exams taken during their ﬁrst year.

The inputs for the ﬁrst and second Cluster Assigner

nodes are analogous; in this case we consider the at-

tributes creditsII grade and avggradeII, indicat-

ing the credits and the average grade obtained from

students in exams taken in the second year, and the

similar attributes corresponding to the exams taken in

the third year, that is, up to the 30th April of the fourth

year after the year of enrollment. We wish to point out

that we still consider active students, therefore the car-

dinalities of these input ﬁles can decrease from year

to year.

The result of the K-means step of the KNIME ﬂow,

expressed in terms of coordinates of the centroids, is

showed in Table 10. We can observe that the attribute

credits grade separates very well the three cen-

troids; the cluster 2 identiﬁes high achieving stu-

dents, cluster 1 medium achieving students and ﬁ-

nally cluster 0 corresponds to students that during

their ﬁrst year had success only with the exam of En-

glish and therefore have no credits and no grade in

this clustering.

Table 11 represents the output data set obtained

from the clustering step, where the new attribute

cluster indicates the cluster to which each student

has been assigned: this data set corresponds to the

ﬁrst red node in Figure 8, starting from above. The

output data sets of the two Cluster Assigner nodes are

similar and correspond to the other two red nodes, one

for the second and one for the third year. This process

is concluded by a last postprocessing phase which

joins the previous data sets and produces a ﬁnal output

illustrated in Table 12: a triplet of cluster values is as-

sociated to each student, indicating the path followed

over the three years under analysis. This path takes

into account also the inactivity of students during a

year. This data set is visualized in Figure 9, where the

green colour corresponds to hight proﬁle students, the

yellow colour to medium proﬁle students and the or-

ange colour to low proﬁle students; the blue colour

represents inactive students. According to our deﬁni-

tion of active students, a student can be inactive dur-

ing the second year but become active again during

CSEDU 2017 - 9th International Conference on Computer Supported Education

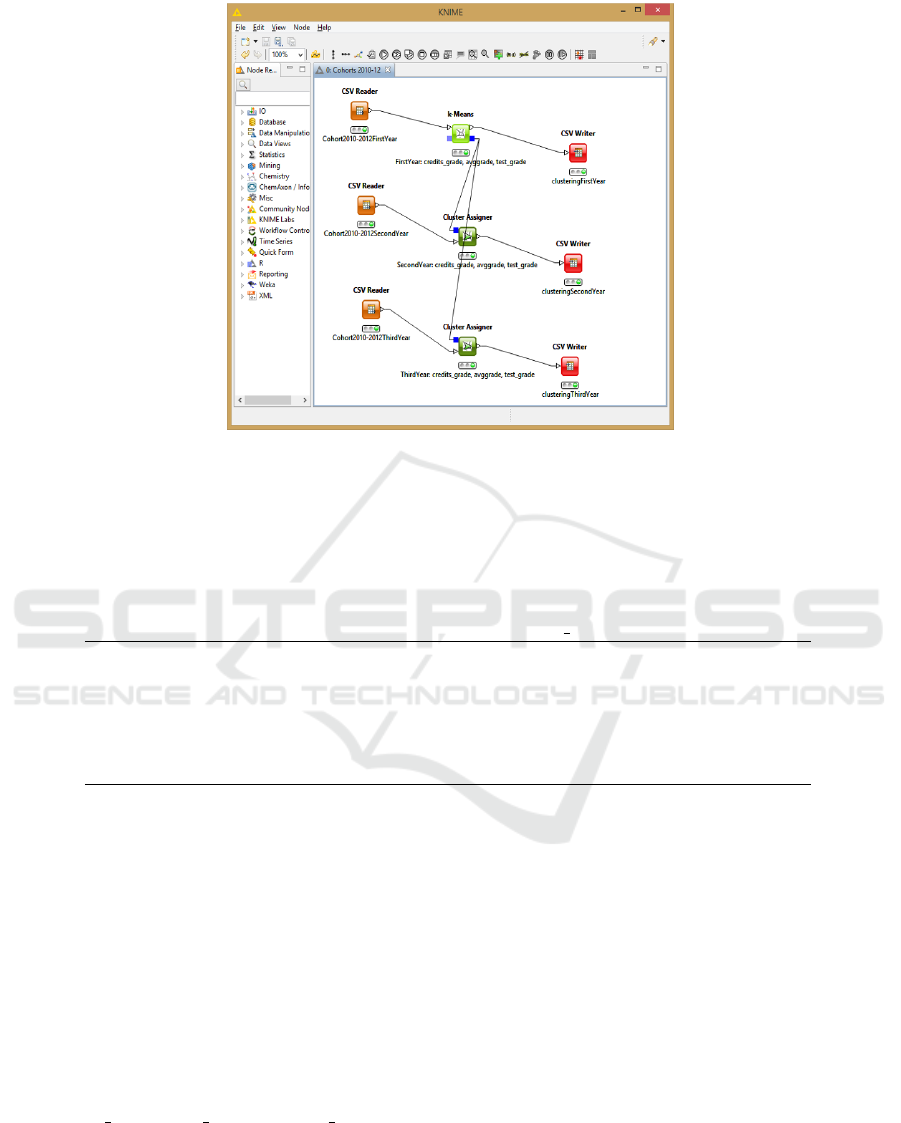
Figure 8: The KNIME ﬂow: the orange nodes are the input to the ﬂow and contain information about active students in ﬁrst,

second and third year, respectively (see also Table 9); the ﬁrst green node on the top is the K-means node where the clustering

step is performed; the other green nodes are the Cluster Assigner nodes which classify students according to the previous

clustering by using the results of second and third year; ﬁnally, the red nodes partition the students of each year according to

the clustering (see also Table 11). (For interpretation of the references to colours in this ﬁgure legend, the reader is referred to

the electronic version of this article).

Table 9: A sample of input data set for the K-means node of Figure 8.

Student Cohort CreditsIgrade AvggradeI Test grade Hgrade Hschool

100 2010 48 27 19 69 LS

200 2010 60 27 17 75 IT

300 2012 60 26 16 75 PS

the third. Figure 9 suggests that students inactive dur-

ing the second year remain inactive also in the next

year; moreover, students in the green cluster conﬁrm

their good trend in the subsequent years, students in

the orange cluster tends to become inactive and, ﬁ-

nally, some of the students in the yellow cluster move

to the adjacent clusters, improving or getting worse.

This hypothesis suggested by Figure 9 is conﬁrmed

both by an analytic inspection of the data set and by

a new clustering step performed on data organized

as in Table 12. In fact, by using again the K-means

implementation of WEKA with k = 4 and attributes

clusterI, clusterII and clusterIII, where val-

ues cluster 0, cluster 1 and cluster 2 have been

transformed into the numeric values 0, 1 and 2 respec-

tively, and the value -1 has been assigned to inactivity,

we obtain the centroids illustrated in Table 13. With

this choice of k, the Pearsons correlation between the

linear representation of the proximity and incidence

matrices gives the value -0.63, a quite good value.

The cluster 0 represents students starting as yel-

low and becoming green, cluster 1 represent the ever

green students, cluster 2 corresponds to students at

risk of dropping out and, ﬁnally, cluster 3 represents

the ever yellow students. In other words, clusters 0

and 1 represent students who had overall very posi-

tive results during the three years, students of cluster

3 represent the medium achieving students throughout

the entire course of study and, ﬁnally, cluster 2 corre-

sponds to students who started with low or medium

results and were not be able to improve their perfor-

mance, often dropping out.

5 CONCLUSIONS

The analysis presented in Section 3 can be summa-

rized in the following steps: 1) we performed a pre-

University Student Progressions and First Year Behaviour

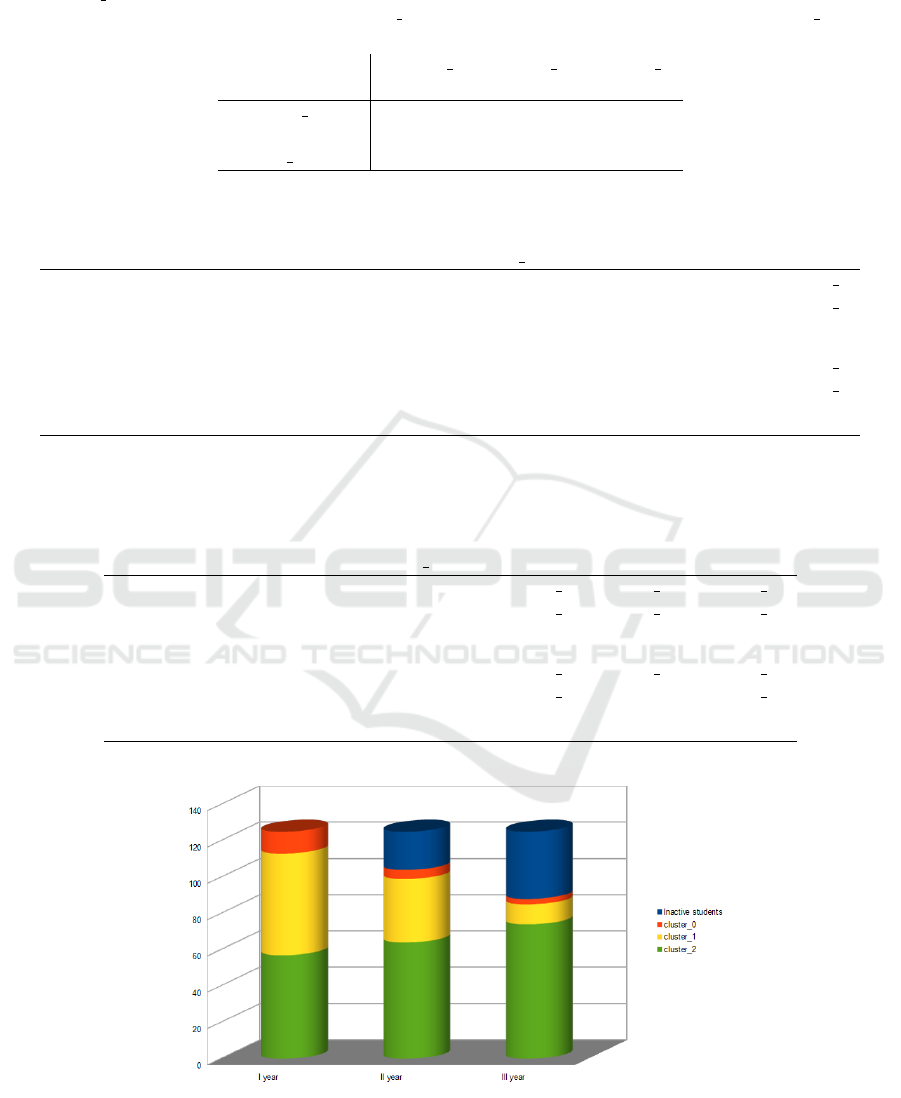
Table 10: Centroids resulting from the ﬁrst step of the KNIME ﬂow and corresponding to ﬁrst year results of cohorts 2010-2012.

The cluster 0 corresponds to students that during their ﬁrst year had success only with the exam of English and therefore

have no credits and no grade in this clustering, cluster 1 corresponds to medium achieving students and cluster 2 identiﬁes

high achieving students. See Table 6 for the centroids of the analogous clusters on cohorts 2010-2014.

Attribute Cluster 0 Cluster 1 Cluster 2

(12) (57) (57)

credits grade 0 18.69 43.89

avggrade 0 24.42 26.42

test grade 11.67 14.45 15.33

Table 11: A sample of data set resulting from the K-means node of Figure 8.

Student Cohort CreditsIgrade AvggradeI Test grade Hgrade Hschool Cluster

100 2010 48 27 19 69 LS cluster 1

200 2010 60 27 17 75 IT cluster 2

300 2011 0 0 12 65 IT cluster 0

400 2012 60 26 16 75 PS cluster 2

Table 12: A sample of the ﬁnal data set resulting from the KNIME ﬂow and the postprocessing phase. A triplet of cluster values

is associated to each student, indicating the path followed over the three years under analysis. This path takes into account

also the inactivity of students during a year, as in the case of student 400.

Student Cohort . . . . . . Test grade ClusterI ClusterII ClusterIII

100 2010 . . . . . . 19 cluster 1 cluster 1 cluster 2

200 2010 . . . . . . 17 cluster 2 cluster 2 cluster 2

300 2011 . . . . . . 12 cluster 0 cluster 1 cluster 1

400 2012 . . . . . . 16 cluster 2 inactive cluster 2

Figure 9: A visualization of data corresponding to Table 12. The green colour corresponds to hight proﬁle students, the

yellow colour to medium proﬁle students and the orange colour to low proﬁle students; the blue colour represents inactive

students. (For interpretation of the references to colours in this ﬁgure legend, the reader is referred to the electronic version

of this article).

CSEDU 2017 - 9th International Conference on Computer Supported Education

Table 13: Centroids corresponding to data organized as in Table 12. By referring to Figure 9, the cluster 0 represents students

starting as yellow and becoming green, cluster 1 represent the ever green students, cluster 2 corresponds to students at risk of

dropping out and, ﬁnally, cluster 3 represents the ever yellow students. (For interpretation of the references to colours in this

ﬁgure legend, the reader is referred to the electronic version of this article).

Attribute Full Data Cluster 0 Cluster 1 Cluster 2 Cluster 3

(125) (16) (52) (37) (20)

clusterI 1.36 0.94 2 0.81 1.05

clusterII 1.14 2 1.85 -0.03 0.75

clusterIII 0.98 1.94 1.96 -1 1.3

processing phase on students information to obtain

data organized as in Table 4, relative to students re-

sults on ﬁrst year; 2) we performed a clustering step

to classify students according to the results of the self-

assessment test and the university performance dur-

ing the ﬁrst year, by using K-means algorithm; 3) we

deepened the analysis on the partition obtained at the

previous step by exploring each exam dimension and

by computing correlations between attributes.

For the cohorts of students considered in this pa-

per, this analysis puts in evidence that the self assess-

ment test is an important indicator to predict both the

performance of the ﬁrst year, in particular for what

concerns mathematical courses, and the progress of

the students career. On the other hand, courses of

the ﬁrst year in which students have more difﬁcul-

ties seem to give an important indication on the stu-

dent success. The laurea degree course could use this

information to support students having this kind of

problems.

The analysis proposed in Section 4 can be sum-

marized in the following steps: 1) we performed a

preprocessing phase on students information to obtain

data organized as in Table 5, relative to the results of

students during their ﬁrst, second and third year; 2)

we performed a clustering step to classify students ac-

cording to the results of the self-assessment test and

the university performance during their ﬁrst year, by

using K-means algorithm; 3) we applied the model ob-

tained at the previous step to the results of students

during their second and third year and associated to

each student the sequence of traversed clusters; 4) we

performed a second clustering step according to the

traversed clusters. Step 2 and 3 were realized by a

Knime ﬂow.

The observations made as conclusion of the anal-

ysis presented in Section 3 are conﬁrmed by the anal-

ysis of Section 4 that highlights three different trends

strongly affected from the performance of the ﬁrst

year. As before, supporting ﬁrst year students seems

to be a way to face the problem of inactive students

and dropping out. We think that the proposed method-

ology could be possibly applied to similar university

contexts to give suggestions for the deﬁnition of man-

agement strategies aiming to improve the students

productivity.

A practical implication of the results obtained

from this research could be the introduction of tutors

to support ﬁrst year students, with special attention to

the most critical courses. Another aspect not to be un-

derestimated concerns the orientation and information

for incoming students: if it is true that the entrance

test gives important information on the students pro-

gressions, then the laurea degree should try to make

it clear to young people willing to join, what are the

difﬁculties that they will encounter, in order to help

them to make an informed choice.

ACKNOWLEDGMENTS

We wish to thank the anonymous referees whose com-

ments and suggestions helped us to improve the con-

tents and readability of the paper.

REFERENCES

Baker, R. S. J. D. (2014). Educational data mining: an ad-

vance for intelligent systems in education. IEEE In-

telligent Systems, 29(3):78–82.

Bower, A. (2010). Analyzing the Longitudinal K-12 Grad-

ing Histories of Entire Cohorts of Students: Grades,

Data Driven Decision Making, Dropping Out and Hi-

erarchical Cluster Analysis. Practical Assessment, Re-

search & Evaluation, 15(7):1–18.

Campagni, R., Merlini, D., Sprugnoli, R., and Verri, M. C.

(2015). Data mining models for student careers. Ex-

pert Systems with Applications, 42(13):5508–5521.

Kabakchieva, D., Stefanova, K., and Kisimov, V. (2011).

Determining Student Proﬁles and Predicting Perfor-

mance. In Proceedings of EDM 2011, 4th Interna-

tional Conference on Educational Data Mining, Eind-

hoven, the Netherlands.

Natek, S. and Zwilling, M. (2014). Student data min-

ing solution-knowledge management system related

to higher education institutions. Expert Systems with

Applications, 41:6400–6407.

University Student Progressions and First Year Behaviour

na-Ayala, A. (2014). Educational data mining: a survey

and a data mining-based analysis. Expert Systems with

Applications, 41:1432–1462.

Romero, C., Romero, J. R., and Ventura, S. (2014). A

survey on pre-processing educational data. In Edu-

cational Data Mining. Studies in Computational In-

telligence, volume 524, pages 29–64, A. Pe

na-Ayala

(Ed.), Springer.

Romero, C. and Ventura, S. (2013). Data mining in educa-

tion. Wiley Interdisc. Rew.: Data Mining and Knowl-

edge Discovery, 3(1):12–27.

Tan, P. N., Steinbach, M., and Kumar, V. (2006). Introduc-

tion to Data Mining. Addison-Wesley.

Witten, I. H., Frank, E., and Hall, M. A. (2011). Data

Mining: Practical Machine Learning Tools and Tech-

niques, Third Edition. Morgan Kaufmann.

Zimmermann, J., Brodersen, K. H., Heinimann, H. R., and

Buhmann, J. M. (2015). A model-based approach to

predicting graduate-level performance using indica-

tors of undergraduate-level performance. Journal of

Educational Data Mining, 7(3):151–176.

Zimmermann, J., Brodersen, K. H., Pellet, J. P., August,

E., and Buhmann, J. M. (2011). Predicting graduate

level performance from undergraduate achievements.

In Proceedings of EDM 2011, 4th International Con-

ference on Educational Data Mining, Eindhoven, the

Netherlands.

CSEDU 2017 - 9th International Conference on Computer Supported Education