Extraction of Conservative Rules for Translation Initiation Site

Prediction using Formal Concept Analysis

Leandro M. Ferreira

, Cristiano L. N. Pinto

1,3

, S´ergio M. Dias

2,4

, Cristiane N. Nobre

and Luis E. Z´arate

1,2

UNA University Center, Belo Horizonte, Brazil

Pontiﬁcal Catholic University of Minas Gerais (PUC Minas), Belo Horizonte, Brazil

School of Engeneering of Minas Gerais (EMGE), Belo Horizonte, Brazil

Federal Service of Data Processing (SERPRO), Belo Horizonte, Brazil

Keywords:

Data Mining, Bioinformatics, Formal Concept Analysis, Machine Learning, Translation Initiation Site.

Abstract:

The search for conservative features that deﬁne the translation and transcription processes used by cells to

interpret and express their genetic information is one of the great challenges in the molecular biology. Each

transcribed mRNA sequence has only one part translated into proteins, called Coding Sequence. The detec-

tion of this region is what motivates the search for conservative characteristics in an mRNA sequence. In

eukaryotes, this region usually begins with the ﬁrst occurrence of the sequence of three nucleotides, being

Adenine, Uracil and Guanine, the nucleotide set that it is called Translation Initiation Site. One way to look

for conservative rules that deﬁne this region is to use the formal concept analysis that can have implications

that indicate a coexistence between the positions of the sequence with the presence of the translation start site.

This paper analyze the use of this technique to extract conservative rules to predict the translation initiation

site in eukaryotes.

1 INTRODUCTION

The use of computational techniques for the molecu-

lar biology analysis information has contributed sig-

niﬁcantly to the area of bioinformatics. Among the

main processes that have received attention are those

of translation and transcription, which are mecha-

nisms used by cells to interpret and express their ge-

netic information (Tzanis et al., 2007). The entire

mRNA sequence transcribed only a part called Cod-

ing Sequence (CDS) is translated into proteins. One

of the main problems of molecular biology corre-

sponds to the search for conservative characteristics

in an mRNA sequence that allows the detection of a

CDS region. In eukaryotes, this region usually starts

at a AUG (sequence of 3 nucleotides Adenine (A),

Uracil (U) and Guanine (G)), with a nucleotide set

that we call Translation Initiation Site (TIS).

The extraction of conservative characteristics can

be done by exploiting dependencies in sequences con-

taining TIS. In this paper, it will be considered the

Formal Concept Analysis (FCA), which is a mathe-

matical technique introduced in the early 1980s by

Rudolf Wille (Wille, 1982). The FCA has been ap-

plied in different areas of knowledge (Poelmans et al.,

2010; Poelmans et al., 2013; Kuznetsov and Poel-

mans, 2013). The application of the FCA depends

on the construction of the formal context to represent

a speciﬁc problem. From this context, it is possible to

apply a speciﬁc algorithm for the extraction of knowl-

edge from formal concepts it is possible to obtain

rules of implication (commonly called implications

), which are rules indicative of a relation between

subsets of attributes related to objects. In this work,

the formal context is constructed from the mRNA se-

quences, where the objects are the sequences them-

selves and each position is transformed into a multi-

valued attribute of 4 positions: Adenine (A), Uracil

(U), Cytosine (C) or Guanine (G). The extracted im-

plication rules are given in the form Y → Z, where Y

and Z attribute subsets, when its found the subset Y it

has Z with conﬁdence of 100%. In this way, could

achieve new conservative characteristics that deter-

mine the TIS, besides those found by (Kozak, 1984).

The purpose of this article is to verify if the con-

servative characteristics obtained from implications

extracted using FCA can improve the prediction of

TIS using the Support Vector Machine (SVM) classi-

Ferreira, L., Pinto, C., Dias, S., Nobre, C. and Zárate, L.

Extraction of Conservative Rules for Translation Initiation Site Prediction using Formal Concept Analysis.

DOI: 10.5220/0006326202650271

In Proceedings of the 19th International Conference on Enterprise Information Systems (ICEIS 2017) - Volume 1, pages 265-271

ISBN: 978-989-758-247-9

265

ﬁer.

This paper is organized as follows: Section 2 gives

a brief introduction to the formal concept analysis. In

section 3 a review about related work is presented.

Section 4 presents the description of the methodology

and the experiments carried out. Finally, discussion

of results obtained is showed.

2 FORMAL CONCEPT ANALYSIS

This section presents the main concepts of formal

concept analysis (FCA). The notation and terminol-

ogy are based on the formulations of Ganter and Wille

(Ganter and Wille, 1999).

2.1 Formal Context

Deﬁnition 1. A formal context consists of two sets

and a binary relation between them. Generally speak-

ing, a formal context is a triple (G,M,I) where I ⊆

G × M, the elements of the set G are called objects,

the elements of the set M calls for attributes and I

called incidence relation. In other words (g,m) ∈ I

or simply gIm should be read as ”object g contains

attribute m”.

Table 1 shows an example of formal context. Each

row of the table represents a sequence (TIS or non-

TIS), the columns represent the positions of the se-

quence, and each position can assume one of the four

nucleotides (A, C, G or U), each marking (X) in-

dicates if there is a nucleotide in that position. To

demonstrate the nucleotide present in a multivalued

position is used the notation P. N, where P is se-

quence’s position and N is the nucleotide’s identiﬁer.

Deﬁnition 2. Given a set B ⊆ G, of objects of a for-

mal context (G,M, I), we can identify which attributes

of M are common to all objects of B. Similarly, that

can be identiﬁed for a set D ⊆ M, which are the ob-

jects of G that have the attributes of D. These ques-

tions are answered by the derivation operators, de-

ﬁned by Equations 1 and 2.

′

= {m ∈ M|gIm ∀g ∈ B} (1)

′

= {g ∈ G|gIm ∀m ∈ D} (2)

2.2 Formal Concepts

The formal concepts obtainable from a formal context

(G,M,I) are ordered pairs (B,D), where B ⊆ G and

D ⊂ M, Each object in B has all the attributes in D

and each attribute in D is the attribute of all objects

in B. In other words, (B, D) is a formal concept if

and only if B

′

= D and D

′

= B. The sets B and D are

denominated extension and intention of the concept,

respectively.

Exemple 1. Following the formal context of Table 1,

it can be made the formal concept (2, 3, 4, -9.G, -

8.C) where the elements of the subset D are {-9.G,

-8.C }. Hence, by derivation (Equation 2), B = 2,3,4

represents the subset of the sequences having as char-

acteristics the nucleotide G in the position 9 and the

nucleotide C in the position -8. It should be noted that

the formal concept corresponds to any aspect within

the domain of the problem, represented by attributes

and objects, where there may be an understanding or

a comprehension.

2.3 Concept Lattice

When the set of all formal concepts of a formal con-

text is hierarchically ordered, it receives the denom-

ination of concept lattice. Its formal concepts are

related as (A1,B1) ≤ (B2,D2), when B1 ⊆ B2 and

D2 ⊆ D1, where (B1, D1) is called subconcept and

(B2, D2) is called superconcept.

Figure 1 shows the diagram of the concept lattice

obtained from the TIS prediction problem (presented

in a simpliﬁed way in the table 1). We can observe

that all object that has the attributes -7.G and -6.G

also has -8.C and -9.G.

Figure 1: Example of concept lattice in the TIS prediction

context.

While a formal context is represented by a table,

such as the Table 1, a concept lattice is represented

by a diagram shown as a graph, where each vertex

is a formal concept and the edge shows its relations

(B1,D1) ≤ (B2, D2). When two concepts relate as

subconcept and superconcept without any other for-

mal concept between them, their vertices must be con-

nected by an edge in the diagram. The highest vertex

of the diagram represents the formal concept whose

extension contains all objects, while the lowest vertex

contains all the attributes in its intention.

ICEIS 2017 - 19th International Conference on Enterprise Information Systems

266

Table 1: Example of an formal context.

Position of nucleotides in sequence

Sequences -9 -8 ... TIS ... 1083

A U C G A U C G ... ... A U C G

1 X . . . X . . . ... X ... X . . .

. . . X . . X . ... X ... . X . .

. . . X . . X . ... X ... . . X .

. . . X . . X . ... ... . . . X

2.4 Implication Rules

Deﬁnition 3. In a formal context whose set of at-

tributes is M, one implication is an expression P → Q,

where P,Q ⊆ M.

An implication P → Q, extracted from a formal

context, must be such that P

′

⊆ Q

′

. In other words,

every object that has the attributes of P has the at-

tributes of Q.

Exemple 2. An example of an implication rule

is given by {−4.C, −3.A,4.G} → {1.A,2.U,3.G},

whose premise is formed by the set of attributes

{−4.C, −3.A,4.G} indicating that in positions −4,

−3 and 4 we have the nucleotides C, A and G, re-

spectively. The conclusion is represented by the set

of attributes {1.A,2.U,3.G} indicating the TIS. From

the example we can infer that when this premise is

found in the mRNA sequence we have the TIS, with a

conﬁdence rate of 100%.

3 RELATED WORKS

In (Cur´e et al., 2015), the authors used an approach

based on FCA and on semantic query expansion to

determine diseases from their symptoms. The ap-

proach proved to be efﬁcient for the detection of dis-

eases with greater sensitivity and support especially

for cases of presence or absence of obesity.

The use of FCA was also addressed by (Hris-

toskova et al., 2014) as a cluster analysis technique,

derived from several sets of genetic microarrays.

These data sets were initially divided into groups that

have characteristics related to a predeﬁned criterion.

As result, the FCA proved to be a robust data inte-

gration technique capable of producing a good and

representative grouping solution for the entire set of

genetic expression matrices. In addition, the use of

FCA enabled a subsequent analysis of the data, pro-

viding useful information about the biological role of

genes contained in the same concepts of the FCA.

The biggest problem of mining of numeric data

using FCA is caused by binarization of data. This can

cause a loss of information or produce a large volume

of data, difﬁcult to process. In (Kaytoue et al., 2011),

the authors studied two methods based on FCA for

the mining of numerical data in contexts of genetic

data expressions. The ﬁrst uses interordial scaling,

encoding all possible attribute ranges in a formal con-

text without losing information, but ends up produc-

ing a large and dense volume of data. The second

constructs a concept lattice directly from the origi-

nal data.The author shown that the two methods are

equivalent, but the second method was shown to be

computationally more efﬁcient.

After an exhaustive search, it was not possible to

ﬁnd papers using FCA in the biological domain con-

sidered in this work. Thus, we intend to show that

this theory can be used to improve the performance of

methods and techniques in the context of TIS predic-

tion.

4 MATERIALS AND METHODS

4.1 Materials

The used databases in our experiments were ex-

tracted from the NCBI RefSeq (Pruitt and Ma-

glott, 2001) repository on April 22, 2014. The ex-

tracted data refer to four organisms Rattus Novergicus

(1383 molecules), Mus musculus (1097 molecules),

Homo sapiens (21528 molecules) and Drosophila

melanogaster (27764 molecules).

In this work, each molecule is identiﬁed according

to the level of inspection, and classiﬁed as: Model,

Inferred, Predicted, Provisional, Reviewed, Validated

and WGSk. In this work only mRNA molecules

with inspection level reviewed were used. Table 2

shows the sequence amount for each species. Posi-

tive sequences are those that synthesize proteins (TIS)

and the negative sequences do not synthesize proteins

(Non-TIS).

Table 2: Number of sequences for each database.

Positives Negatives Total

Rattus Novergicus 66 101 167

Mus musculos 398 632 1030

Homo sapiens 9716 16085 25801

Drosophila melanogaster 10122 25725 35847

Extraction of Conservative Rules for Translation Initiation Site Prediction using Formal Concept Analysis

267

4.2 Window Size Deﬁnition

The size of the nucleotide sequence used in training

has a direct inﬂuence on the quality of the prediction

model (Silva et al., 2011; LIU and WONG, 2003).

Extraction windows can be symmetric, with the same

number of nucleotides in the upstream regions ( re-

gion of the sequence before TIS ) and downstream

(region after of TIS), or asymmetric, with a number

other than nucleotides for each region. Preliminary

studies indicate that asymmetric-sized windows pro-

vide greater accuracy (Silva et al., 2011). We will

adopt asymmetric windows in this work being the re-

gion upstream with the lowest number of nucleotides.

For the deﬁnition of the nucleotide number of

the upstream region, we use the ribosome scan-

ning model and the Kozak’s consensus (Kozak,

1984), that identiﬁes a conservative pattern at the

−6,−5, −4,−3,−2,−1, 1, 2, 3, 4 positions with the

sequence (GCC[A or G]CCAUGG), where predom-

inance of the nucleotides [A/G] and [G] in the posi-

tions of −3 and 4, respectively. A greater number of

nucleotides in the upstream region was used by (Tza-

nis et al., 2007), where the conservation of the −7

position was also identiﬁed. For the experiments of

this work, we adopted a window with 9 nucleotides in

the upstream region, since the mRNA scanning model

is done by codon and, besides that, we guarantee the

conservative positions identiﬁed in other works.

For the downstream region, it was found in (Pinto

et al., 2017) that the larger is the region the greater

is the accuracy achieved by the SVM classiﬁer, thus

adopting the size of 1081 nucleotides in the down-

stream region, so that we can have a better ﬁt in the

classiﬁer. For the extraction of the conservative rules,

we used the 20 nucleotide downstream size to ease

the computational time of extraction, due to the high

computational cost of the algorithm used in rule ex-

traction.

4.3 Extraction of Conservative

Characteristics

In this work, we used the ’Find Implications’ algo-

rithm, proposed by (Carpineto et al., 1999). This al-

gorithm allows to extract implications using formal

concept analysis for the extraction of all rules. Given

a formal concept (X,Y), and a concept lattice, the al-

gorithm looks for implications of (X,Y) where there

are implications P → Q, with P

Q =

0, R ⊂ Y,=

Y − P, so that this implication can not be obtained

from the concept (W,Z). This algorithm requires a

large computational effort due to its complexity that

is proportional to O(|C|k

|M|q), where C is the con-

cept number, k is the largest number of attributes in

the premise, M is the number of attributes and q is

the largest number of relation per concept. Since the

database was very large, causing a great computa-

tional effort, we divided the base into groups of 500

sequences and, in the end, we made an intersection

between the implications generated for each analyzed

organism.

Since the TIS attribute is common to all positive

sequences, it was possible to observe rules where TIS

is the conclusion of a certain premise as exempli-

ﬁed in the 2.4 section. After obtaining the impli-

cations of each organism, the common rules among

all organisms were collected. This extraction was

made through the intersection between the sets of

rules acquired from each organism. We also con-

sider that rules with support greater than or equal to

30%, within all bases, should be used as conserva-

tive characteristics to increase classiﬁer performance

(25% would be considered random since they are four

nucleotides).

It were added characteristics as supporting vector

G in our base as binary values demonstrating the ex-

istence of that rule in the sequence. The vector G is

formed by Equation 3.

G(n) =

(

1 if V (n) == N (n)

0 Otherwise

(3)

where V is a vector with the values of the sequence in

the positions of the conservative characteristics found

and N is the vector with the values that each position

must have according to the implications found.

4.4 Support Vector Machines Classiﬁer

SVM is a machine learning technique capable of solv-

ing linear and non-linear classiﬁcation problems. It

separates examples using a linear decision surface and

increasing the distance between training points (Silva

et al., 2011).

The efﬁciency of SVM classiﬁer depends on the

proper selection of the parameters of the kernel func-

tion used and the smoothing parameter of the optimal

hyperplane separation margin, represented by sym-

bol C. In this work, the Gaussian RBF (Radial Basis

Function) kernel function was used, which acts as a

structural regulator. The RBF function is deﬁned by

the Equation 4 and its parameter is represented by the

symbol gamma (γ)

K(x

) = exp(−γkx− x

′

) (4)

To deﬁne the parameters C and γ, was used the

’Grid Search’ method, implemented for the class lib-

ICEIS 2017 - 19th International Conference on Enterprise Information Systems

268

SVM

. This method deﬁnes the best set of parame-

ters through an exhaustive search within a predeﬁned

range of values for each of the parameters. The execu-

tion time of this tool can be prohibitive. To decrease

this time, the grid search method was executed in a

cluster, consisting of 12 machines

4.5 Evaluation Methods

The evaluation of the results was performed from the

precision, sensitivity, and F-measure metrics. Preci-

sion evaluates among all the sequences classiﬁed as

TIS those that are truly TIS (Equation 5).

Precision = 100·

TP+ FP

(5)

The sensibility is relative to the hit rate in the pos-

itive class (TIS). It is also called rate of true positives

(Equation 6).

Sensitivity = 100·

TP+ FN

(6)

where TP, TN, FP and FN denote the number of True

Positives, True Negatives, False Positives and False

Negatives, respectively.

F-measure considers the precision and sensitivity

metrics to evaluate the model, performing a harmonic

average between the two metrics (Equation 7).

F − measure = 2 ·

Precision· Sensitivity

Precision+ Sensitivity

(7)

For the validation of the proposed model, it was

used the cross-validation (10-fold cross-validation)

technique, which guarantees a statistical validation of

the model. The procedure consists in subdividing the

available dataset into ten folds of the same size, 9 of

which folds are used for training and one fold for val-

idation.

5 RESULTS

After determining the subset of implications of the in-

tersection between the set of rules of each organism,

the main rules for TIS prediction, in the range stipu-

lated, were obtained (Table 3), while still retaining the

characteristics demonstrated by Kozak. For example,

the ﬁrst line of Table 3 represents −8.C → TIS. This

indicates that whenever there is a nucleotide C at the

Available in https://www.csie.ntu.edu.tw/cjlin/Libsvm/

Intel Core2 duo 2.2 GHz x2, 4 GB of RAM memory

Ubuntu 14.04 64 bits

-8 position, the AUG begins the traduction. This oc-

curs with a support of 34.3% of the base Rattus nover-

gicus and 31.1% support when considering all species

bases. The values of the brackets for each rule found

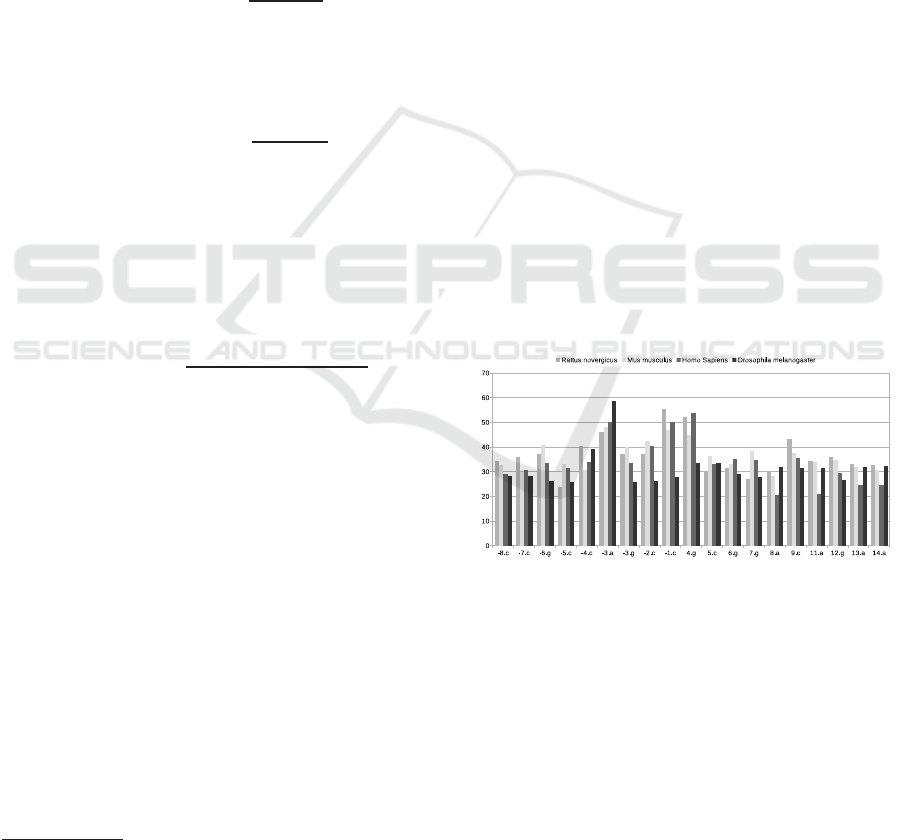
in the positives sequences can be visualized in Figure

It can be noted the predominance of the conser-

vative Kozak characteristics in the −3 positions, con-

taining A or G and 4 containing G, and T with the val-

ues of greater support among the bases analyzed. It

is also observed 11 new conservative characteristics,

besides those indicated by Kozak, among which the 9

position is a C nucleotide (with a support of 37%).

As for the negative sequences (Non-TIS), two

conservative positions were identiﬁed: positions -2

and 4 with the presence of nucleotide A, with a sup-

port of 30.6% and 31.3%, respectively. This shows

how negative sequences can be random and not fol-

low a pattern, unlike positive sequences (TIS).

In preliminary tests, it was decided to add features

with greater support within all the bases, positives

and negatives, to value its main characteristics. Thus,

the -3.A, -3.G, 4.G and 9.C, 1.C characteristics were

added in the positives sequences and the -2.C and 4.C

characteristics were added in the negatives sequences.

However, in doing so, it was noted that there was an

increase in noise in the data and an increase in clas-

siﬁcation error. Thus it was decided to add only the

features that value the positive characteristics, shown

in the Table 3.

Figure 2: Values of the brackets for each rule found in the

positives sequences.

Table 4 presents the parameters used for the SVM,

obtained by ’Grid search’ method.

The use of the implication rules found allowed

a small increase in the metrics evaluated in this

work (see Table 5). The biggest difference between

the results with and without the characteristics hap-

pens in the organisms Mus muscules and Drosophila

melanogaster, where we see an increase around 1 %.

This is due to the fact that in none of the rules found,

the appearance of them in the negative sequence is

greater than in the positive ones while this happens

twice in the other bases. Even so, the organism Homo

Extraction of Conservative Rules for Translation Initiation Site Prediction using Formal Concept Analysis

269

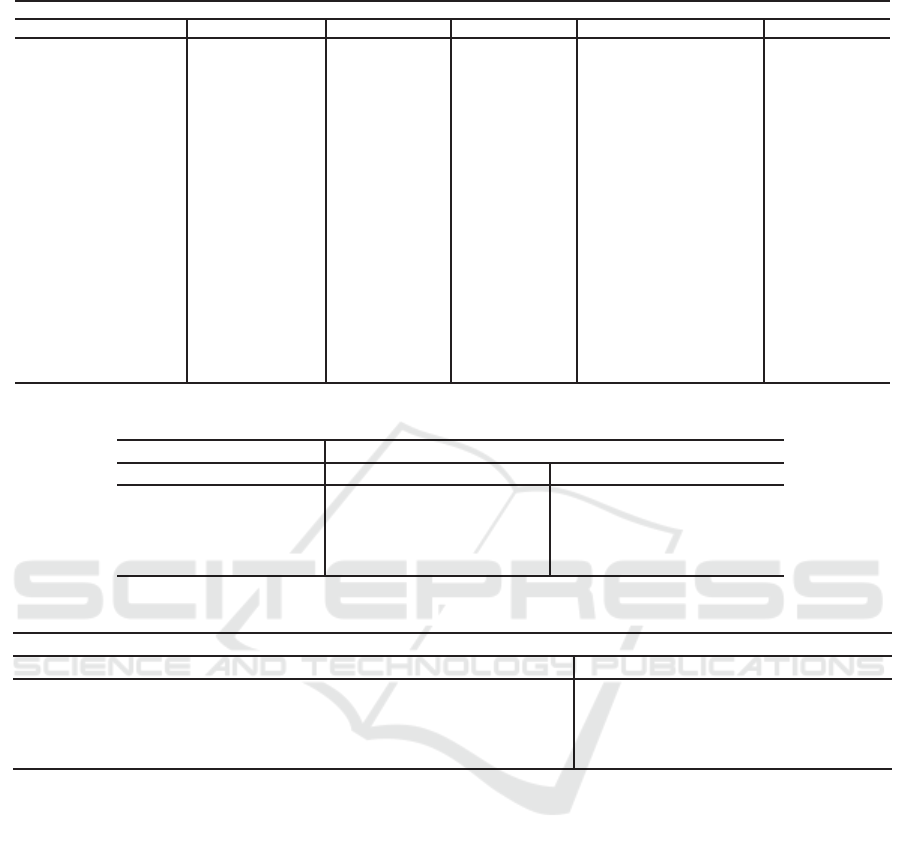
Table 3: Implications rules extracted and their support.

Premisse Rattus novergicus Mus musculus Homo Sapiens Drosophila melanogaster General

Position Nucleotides Pos Neg Pos Neg Pos Neg Pos Neg Pos Neg

-8 C 34.3% 21.6% 32.8% 22.3% 29.1% 26.7% 28.1% 21.7% 31.1% 23.0%

-7 C

35.8% 27.5% 29.7% 21.1% 30.6% 25.7% 28.3% 21.6% 31.1% 24.0%

-6 G

37.3% 17.6% 40.8% 31.3% 33.6% 28.7% 26.1% 21.2% 34.5% 24.7%

-5 C

23.9% 28.4% 33.0% 28.5% 31.3% 25.4% 25.9% 19.9% 28.5% 25.6%

-4 C

40.3% 18.6% 30.5% 25.4% 34.0% 24.8% 39.1% 18.5% 35.9% 21.8%

-3 A

46.3% 23.5% 48.2% 26.9% 50.2% 25.4% 58.6% 26.5% 50.8% 25.5%

-3 G

37.3% 27.5% 40.1% 25.7% 33.3% 28.3% 26.0% 18.5% 34.1% 25.0%

-2 C

37.3% 16.6% 42.5% 22.3% 40.5% 21.9% 26.3% 20.0% 36.7% 20.2%

-1 C

55.2% 25.5% 46.9% 23.5% 50.2% 27.7% 27.7% 17.3% 45.0% 23.3%

4 G

52.2% 33.3% 45.0% 24.6% 53.7% 28.5% 33.6% 17.4% 46.1% 25.9%

5 C

29.8% 20.6% 36.5% 25.4% 33.0% 24.6% 33.7% 19.2% 33.2% 22.5%

6 G

31.3% 26.5% 33.2% 21.9% 35.3% 30.7% 28.9% 19.9% 32.2% 24.7%

7 G

26.9% 26.5% 38.2% 27.7% 34.5% 28.2% 27.6% 20.7% 31.8% 25.8%

8 A

29.8% 39.2% 28.2% 27.3% 20.6% 24.1% 31.7% 30.2% 27.6% 30.2%

9 C

43.2% 19.6% 37.5% 21.8% 35.6% 23.8% 31.6% 20.0% 37.0% 21.3%

11 A

34.3% 18.6% 33.9% 23.8% 20.9% 23.9% 31.7% 31.6% 30.2% 24.5%

12 G

35.8% 22.5% 34.7% 31.2% 29.3% 28.7% 26.6% 22.2% 31.6% 26.2%

13 A

32.9% 24.5% 31.7% 21.1% 24.6% 24.1% 31.8% 30.6% 30.2% 25.0%

14 A

32.8% 28.4% 30.6% 22.3% 24.6% 23.1% 32.2% 30.1% 30.1% 26.0%

Table 4: Parameters obtained using the ’Grid Search’ method.

Without characteristics With characteristics

C Gamma C Gamma

Rattus norvegicus 128 3.051757812× 10

−5

32 3.0517578125× 10

−5

Mus musculus

8 1.220703125× 10

−4

8 4.8828125× 10

−4

Homo sapiens

2 4.8828125× 10

−4

128 4.8828125×10

−4

Drosophila melanogaster

32 4.8828125× 10

−4

8 4.8828125× 10

−4

Table 5: Results of SVM classiﬁer.

Without characteristics With characteristics

Precision Sensitivity F-measure Precision Sensitivity F-measure

Rattus norvegicus 89.4% 89.2% 89.1% 89.4% 89.2% 89.1%

Mus musculus 97.9% 97.9% 97.8%

98.8% 98.7% 98.8%

Homo sapiens 98.0% 97.7% 97.9%

98.2% 98.2% 98.2%

Drosophila melanogaster 96.9% 96.8% 96.8%

98.2% 98.2% 98.2%

sapiens had a small increase, while the Rattus nover-

gicus organism they continued with the same values,

because of its low amount of data.

6 CONCLUSIONS

In this work it was proposed the extraction of conser-

vative mRNA characteristics from eukaryotes organ-

isms to improve the prediction of TIS, using formal

concept analysis. Using a downstream region of 20

nucleotides and 9 nucleotides upstream, it was possi-

ble to ﬁnd a total of 19 rules of implication, including

the rules of Kozak. The results show shows that the

addition of conservative characteristics, even using a

small window, improves SVM results, although the

increase is little in this work.

In future works, it would be important to test

larger windows, both in the upstream and downstream

regions for rule extraction. In this work, by compu-

tational limitation, we use only 20 nucleotides in the

downstream region. But for this, it is necessary to im-

plement more optimized versions of the algorithm in

order to consider more characteristics.

ACKNOWLEDGEMENTS

The authors acknowledge the ﬁnancial support re-

ceived from the Foundation for Research Support of

Minas Gerais state, FAPEMIG; the National Council

for Scientiﬁc and TechnologicalDevelopment, CNPq;

Coordination for the Improvement of Higher Educa-

tion Personnel, CAPES. We would also express grati-

tude to the Federal Service of Data Processing, SER-

PRO.

ICEIS 2017 - 19th International Conference on Enterprise Information Systems

270

REFERENCES

Carpineto, C., Romano, G., and d’Adamo, P. (1999). In-

ferring dependencies from relations: a conceptual

clustering approach. Computational Intelligence,

15(4):415–441.

Cur´e, O. C., Maurer, H., and Shah, Nigam H.and LeP-

endu, P. (2015). A formal concept analysis and se-

mantic query expansion cooperation to reﬁne health

outcomes of interest. BMC Medical Informatics and

Decision Making, 15(1):1–6.

Ganter, B. and Wille, R. (1999). Formal Concept Analy-

sis: Mathematical Foundations. Springer-Verlag, Ger-

many.

Hristoskova, A., Boeva, V., and Tsiporkova, E. (2014). A

formal concept analysis approach to consensus clus-

tering of multi-experiment expression data. BMC

Bioinformatics, 15(1):1–16.

Kaytoue, M., Kuznetsov, S. O., Napoli, A., and Duplessis,

S. (2011). Mining gene expression data with pattern

structures in formal concept analysis. Information Sci-

ences, 181(10):1989 – 2001. Special Issue on Infor-

mation Engineering Applications Based on Lattices.

Kozak, M. (1984). Compilation and analysis of sequences

upstream from the translational start site in eukaryotic

mrnas. Nucleic Acids Research, 12(2):857–872.

Kuznetsov, S. O. and Poelmans, J. (2013). Knowledge rep-

resentation and processing with formal concept anal-

ysis. Wiley Interdisciplinary Reviews: Data Mining

and Knowledge Discovery, 3(3):200–215.

LIU, H. and WONG, L. (2003). Data mining tools for bi-

ological sequences. Journal of Bioinformatics and

Computational Biology, 01(01):139–167.

Pinto, C. L. N., Nobre, C. N., and Z´arate, L. E. (2017).

Transductive learning as an alternative to translation

initiation site identiﬁcation. BMC Bioinformatics,

18(1):81.

Poelmans, J., Elzinga, P., Viaene, S., and Dedene, G.

(2010). Formal Concept Analysis in Knowledge Dis-

covery: A Survey. Springer Berlin Heidelberg, Berlin,

Heidelberg.

Poelmans, J., Ignatov, D. I., Kuznetsov, S. O., and Dedene,

G. (2013). Formal concept analysis in knowledge pro-

cessing: A survey on applications. Expert Systems

with Applications, 40(16):6538 – 6560.

Pruitt, K. D. and Maglott, D. R. (2001). Refseq and lo-

cuslink: Ncbi gene-centered resources. Nucleic Acids

Research, 29(1):137–140.

Silva, L. M., de Souza Teixeira, F. C., Ortega, J. M., Z´arate,

L. E., and Nobre, C. N. (2011). Improvement in the

prediction of the translation initiation site through bal-

ancing methods, inclusion of acquired knowledge and

addition of features to sequences of mrna. BMC Ge-

nomics, 12(4):1–20.

Tzanis, G., Berberidis, C., and Vlahavas, I. (2007). Mantis:

a data mining methodology for effective translation

initiation site prediction. In Engineering in Medicine

and Biology Society, 2007. EMBS 2007. 29th Annual

International Conference of the IEEE, pages 6343–

6347. IEEE.

Wille, R. (1982). Restructuring lattice theory: an approach

based on hierarchies of concepts. I. Rival (Ed.): Or-

dered Sets, pages 445–470.

Extraction of Conservative Rules for Translation Initiation Site Prediction using Formal Concept Analysis

271